A Dynamic Approach to Sustainable Knitted Footwear Production in Industry 4.0: Integrating Short-Term Profitability and Long-Term Carbon Efficiency
Abstract
:1. Introduction
Research Background and Motivation
- (1)
- Section 1, Introduction: This section explains the research background and motivation of this research.
- (2)
- Section 2, Literature: This section mainly discusses the impact and transformation of the footwear industry on the environment, carbon tax and carbon rights, and the combination of the constraint theory of the activity-based cost system.
- (3)
- Section 3, Research Design and Methods: This section defines the single-period model, multi-period model, and model parameter data hypothesis.
- (4)
- Section 4, Research Results and Analysis: This section describes the model results and model analysis.
- (5)
- Section 5, Discussion and Conclusions: This section describes the research conclusions and research limitations.
2. Literature
2.1. Carbon Emissions, Carbon Taxes, Carbon Rights
2.2. The Relationship among Activity-Based Costing, Constraint Theory, and Industry 4.0
3. Research Design and Methods
3.1. Single-Period Model Assumptions
3.1.1. Objective Function
- (1)
- A carbon tax cost scheme with a smoothly escalating tax rate, excluding the mechanism for carbon emissions trading—referred to as Model 1.
- (2)
- A carbon tax cost model characterized by a gradually increasing tax rate, including provisions for trading carbon emission rights—referred to as Model 2.
- (3)
- A carbon tax cost framework featuring a stepped, progressive tax rate without the option for carbon emissions trading—referred to as Model 3.
- (4)
- A carbon tax cost model with a tiered, step-increasing tax rate, incorporating carbon emission trading—referred to as Model 4.
3.1.2. Carbon Emission Cost Function
3.1.3. Carbon Tax Cost Function
- (1)
- A carbon tax cost function with a smoothly increasing tax rate.
| CEim | For each i-th product, CEim represents the carbon emissions produced by the m-th process (where m equals 1, 2, or 5). |
| CT | The expenses incurred by a corporation due to the carbon tax. |
| CEQ3 | Without a maximum cap in the third carbon tax structure, significant emissions cannot be modeled without defining CEQ3. |
| CT3 | Substantial carbon emissions cannot be accounted for in the mathematical model without defining CEQ3. |
| TRi | At the CEQ3 point, the carbon tax cost is determined by the applicable tax rate for the segment i that the emissions fall into. |
| Each is a dummy variable (0, 1), and only one of the three can be 1. | |
| Each is a variable that cannot be negative, where no more than two consecutive variables can have a non-zero value. |
- (2)
- A carbon tax cost function featuring a stepwise increasing tax rate.
| This variable indicates carbon emissions in the i-th segment (i = 1, 2, 3), allowing detailed analysis by emission levels. | |
| CEim | CEim denotes the quantity of carbon emissions generated by a single unit of the i-th product undergoing the m-th process, where m can be 1, 2, or 5. This parameter captures the specific carbon footprint associated with each product and process combination. |
| TRi | This term denotes the tax rate for carbon emissions in the i-th segment, enabling a flexible, tiered tax policy. |
| These are dummy variables (0, 1), and only one of the three can be 1. |
3.1.4. Carbon Right Trading Consideration
- Models 1 and 3 assess carbon tax impacts without trading.
- Models 2 and 4 incorporate carbon trading, evaluating costs and benefits.
- Models 1 and 2 feature continuous tax rates.
- Models 3 and 4 apply stepwise rates at specific emission levels.
| The amount of product i (where i equals 1, 2, or 3). | |
| CEim | CEim represents the carbon emissions per unit of process m for product i (with m being 1, 2, or 5). |
| Corresponds to the maximum level of carbon emissions permitted by regulatory authorities. |
| The company’s total carbon emissions, when . | |
| The company’s total carbon emissions, when . | |
| These are dummy variables (0, 1), and only one of the two can be 1. |
3.1.5. Unit Level Operation—Direct Labor Cost Function
| The amount of the i-th product, where i equals 1, 2, or 3. | |
| Each is a variable that cannot be less than zero, with no more than two consecutive variables having values greater than 0. | |
| Each is a dummy variable (0, 1), where only one of them can be 1. | |
| In tasks related to pruning, which involve the variable m equaling 4, the quantity of labor hours needed to finish one unit of the i-th product is specified. | |
| For tasks that involve combining components, where m is equal to 5, the text outlines the labor hours required to complete one unit of the i-th product. | |
| This refers to the aggregate labor hours available for tasks without considering any rush or delayed orders. | |
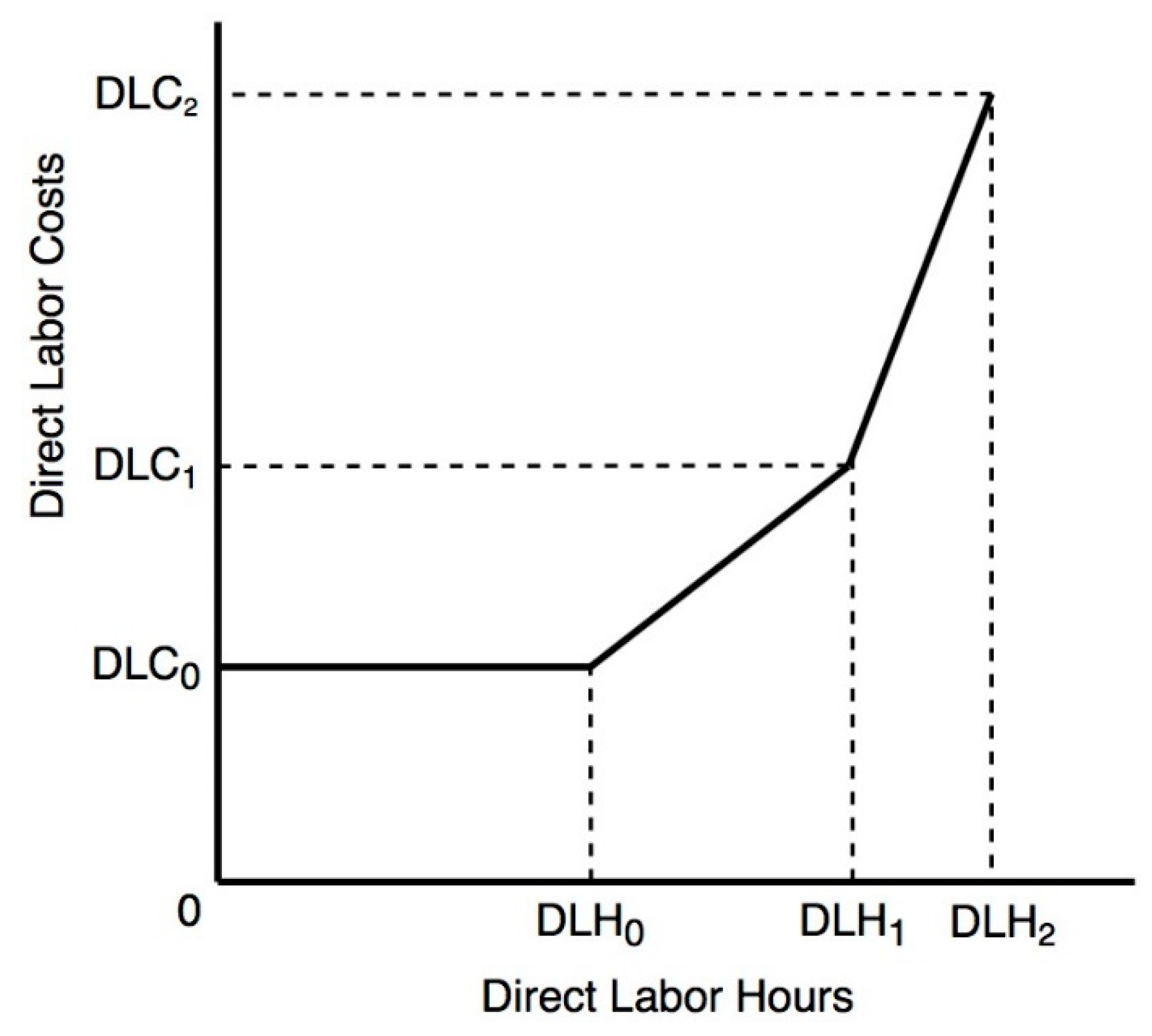
| This denotes the maximum labor hours allocated during the initial overtime phase, as depicted in Figure 4. | |
| This signifies the greatest amount of labor hours allocated during the second overtime phase, as illustrated in Figure 4. | |
| The total direct labor cost at this point in = WR0 * . | |
| The total direct labor cost at this point in = + WR1 * ( − ). | |
| The total direct labor cost at this point in = + WR2 * ( − ). |
3.1.6. Capacity per Machine Hour
| The duration, in machine hours, that the knitting machine takes to produce a single unit of product i. | |
| The amount of time, in machine hours, needed by the press to manufacture a single unit of product i. | |
| The machine hours necessary for the automatic gluing machine to finish producing a single unit of product i. | |
| The maximum capacity of machine hours that the knitting machine can operate. | |
| The ceiling on the operational machine hours for the press. | |
| The maximum available machine hours for the automatic gluing machine to function. |
3.1.7. Batch Level Operation—Formulating a Cost Function for Setup and Material Management
| For each type of product, the number of batches processed at each specific batch-level activity is denoted (for product types 1, 2, and 3; during batch processes 3, 6, and 7). | |
| The production output for each batch corresponding to each type of product during the specific batch-level stage is detailed (for product types 1, 2, and 3; at batch stages 3, 6, and 7). | |
| Resource use for each batch of product types 1, 2, and 3 is detailed at stages 3, 6, and 7. | |
| The maximum capacity of resources that can be allocated for each batch-level operation is specified (for batch processes 3, 6, and 7). |
3.1.8. Product Level Activity—Product Design Cost Function
| The existing demand in the market for each type of product. | |
| A binary variable, represented as either 0 or 1, used to decide the production status of each product. A Γi value of 1 implies the product is in production, whereas a value of 0 indicates that the product is not being produced. | |
| The amount of resources expended on the operations at the level of each specific product (for products 1, 2, and 3). The maximum quantity of resources that can be utilized for operations at the product level. | |
| The amount of resources expended on the operations at the level of each specific product (for products 1, 2, and 3). The maximum quantity of resources that can be utilized for operations at the product level. |
3.1.9. Direct Raw Material Cost Function
| The cost associated with one unit of each type of raw material (categorized as types 1, 2, and 3). | |
| The quantity of each type of raw material required to manufacture a single unit of product i (for products 1, 2, and 3, corresponding to raw material types 1, 2, and 3). | |
| The maximum available quantity for each category of raw material (for raw material types 1, 2, and 3). |
3.2. Multi-Period Model
- (1)
- Model 1 is an objective function.
- (2)
- Model 2 evaluates a carbon tax system with increasing rates and carbon credit trading.
- (3)
- Model 3 is a carbon tax pricing model with a tiered, incrementally increasing tax rate without the option for trading carbon emission allowances.
- (4)
- Model 4 is a carbon tax framework using a segmented, progressively increasing rate, integrating the ability to trade carbon emission permits.
4. Research Results and Analysis
4.1. Assumptions of Single-Period and Multi-Period Model Parameter Data
- Model 1: Continuous and progressive carbon tax cost function without carbon emission trading. The carbon tax cost increases continuously with emissions.
- Model 2: Single-period model with a continuous carbon tax rate based on emission levels and the option for carbon trading.
- Model 3: Single-period model with a stepwise carbon tax rate structure. The tax rate remains constant within each emission range but increases abruptly when emissions exceed predetermined threshold.
- Model 4: Combines a stepped progressive tax rate with carbon rights trading.
4.2. Model Analysis
4.2.1. Model Description
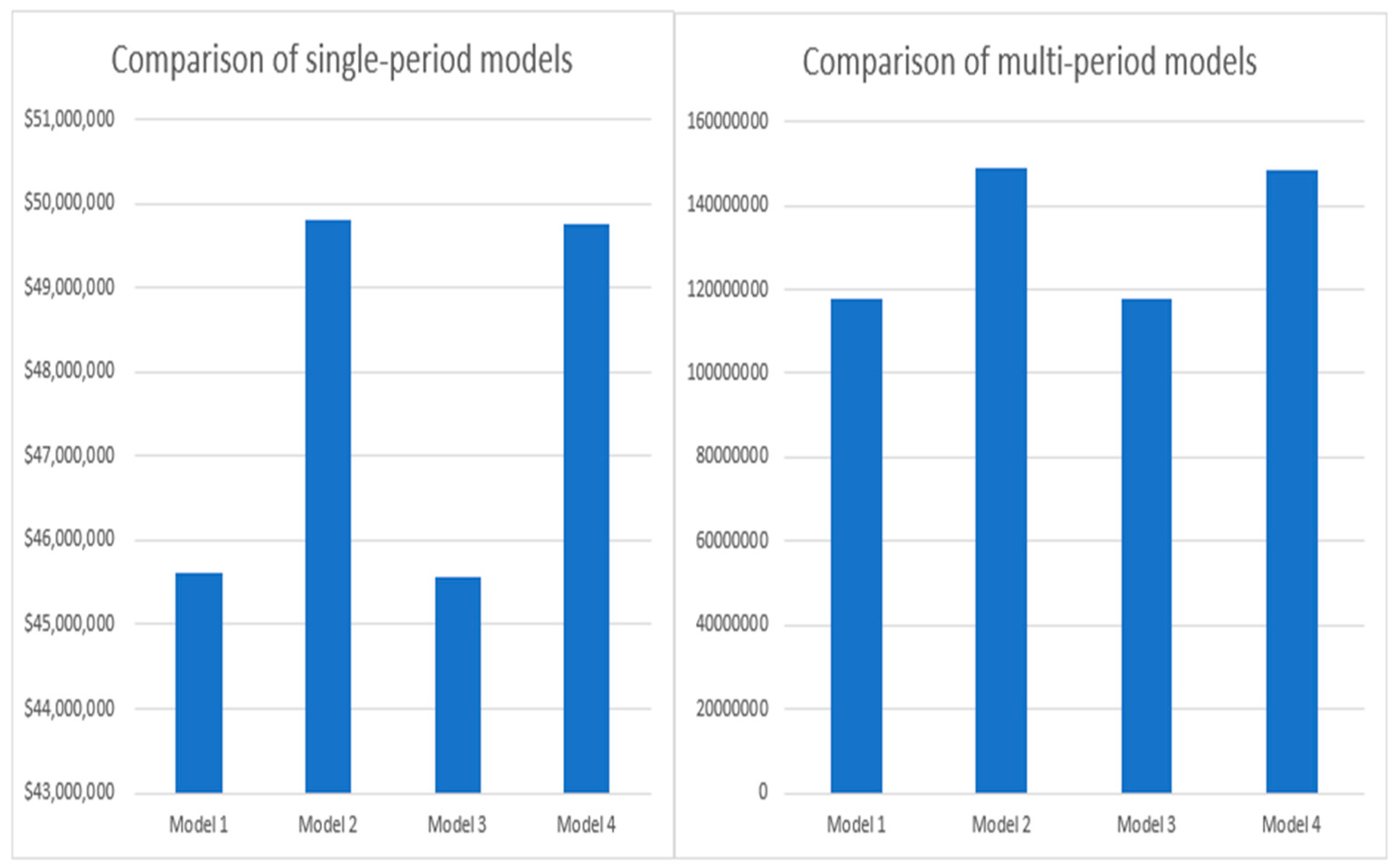
4.2.2. Comparison of Single-Period and Multi-Period Models
5. Discussion and Conclusions
5.1. Discussion
5.2. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Bockorny, M.; Raber, M.; Vos, Y. The use of Dimethylformamide (DMF) in the shoe production and its effects on health and environment. RIVM Lett. Rep. 2017, 2017, 136. [Google Scholar] [CrossRef]
- Ellen MacArthur Foundation. A New Textiles Economy: Redesigning Fashion’s Future. Available online: https://www.ellenmacarthurfoundation.org/assets/downloads/publications/A-New-Textiles-Economy_Full-Report_Updated_1-12-17.pdf (accessed on 1 July 2024).
- Moretto, A.; Macchion, L.; Lion, A.; Caniato, F.; Danese, P.; Vinelli, A. Designing a roadmap towards a sustainable supply chain: A focus on the fashion industry. J. Clean. Prod. 2018, 193, 169–184. [Google Scholar] [CrossRef]
- Bianchi, I.; Forcellese, A.; Simoncini, M.; Vita, A.; Castorani, V.; Cafagna, D.; Buccoliero, G. Comparative life cycle assessment of safety shoes toe caps manufacturing processes. Int. J. Adv. Manuf. Technol. 2022, 120, 7363–7374. [Google Scholar] [CrossRef]
- Ghimouz, C.; Kenné, J.P.; Hof, L.A. On sustainable design and manufacturing for the footwear industry–Towards circular manufacturing. Mater. Des. 2023, 233, 112224. [Google Scholar] [CrossRef]
- Caniato, F.; Caridi, M.; Crippa, L.; Moretto, A. Environmental sustainability in fashion supply chains: An exploratory case based research. Int. J. Prod. Econ. 2012, 135, 659–670. [Google Scholar] [CrossRef]
- Dissanayake, G.; Sinha, P. An examination of the product development process for fashion remanufacturing. Resour. Conserv. Recycl. 2015, 104, 94–102. [Google Scholar] [CrossRef]
- Lee, M.J.; Rahimifard, S. An air-based automated material recycling system for postconsumer footwear products. Resour. Conserv. Recycl. 2012, 69, 90–99. [Google Scholar] [CrossRef]
- Bhavan, S.; Rao, J.R.; Nair, B.U. A potential new commercial method for processing leather to reduce environmental impact. Environ. Sci. Pollut. Res. 2008, 15, 293–295. [Google Scholar] [CrossRef]
- Chen, K.W.; Lin, L.C.; Lee, W.S. Analyzing the carbon footprint of the finished bovine leather: A case study of aniline leather. Energy Proc. 2014, 61, 1063–1066. [Google Scholar] [CrossRef]
- Kılıç, E.; Puigb, R.; Zengin, G.; Zengin, C.A.; Fullana-I-Palmer, P. Corporate carbon footprint for country climate change mitigation: A case study of a tannery in Turkey. Sci. Total Environ. 2018, 635, 60–69. [Google Scholar] [CrossRef] [PubMed]
- Milà I Canals, L.; Domènèch, X.; Rieradevall, J.; Puig, R.; Fullana, P. Use of life cycle assessment in the procedure for the establishment of environmental criteria in the catalan eco-label of leather. Int. J. Life Cycle Assess. 2002, 7, 39–46. [Google Scholar] [CrossRef]
- Bodoga, A.; Nistorac, A.; Loghin, M.C.; Isopescu, D.N. Environmental Impact of Footwear Using Life Cycle Assessment—Case Study of Professional Footwear. Sustainability 2024, 16, 6094. [Google Scholar] [CrossRef]
- Perdijk, E.W.; Luijten, J.; Selderijk, A.J. An Eco-Label for Footwear. Background Report (Report Number: 9041); CEA, Communication and Consultancy on Environment and Energy, Centrum TNO Leather and Shoes: Rotterdam, The Netherlands, 1994. [Google Scholar]
- Van Rensburg, M.L.; Nkomo SP, L.; Mkhize, N.M. Life cycle and End-of-Life management options in the footwear industry: A review. Waste Manag. Res. 2020, 38, 599–613. [Google Scholar] [CrossRef] [PubMed]
- Gottfridsson, M.; Zhang, Y. Environmental Impacts of Shoe Consumption—Combining Product Flow Analysis with an LCA Model for Sweden; Department of Energy and Environment, Division of Environmental Systems Analysis, Chalmers University of Technology: Gothenburg, Sweden, 2015. [Google Scholar]
- Bhat, R.A.; Dervash, M.A.; Mehmood, M.A.; Hakeem, K.R. Municipal solid waste generation and its management a growing threat to fragile ecosystem in Kashmir Himalaya. Am. J. Environ. Sci. 2017, 13, 388–397. [Google Scholar] [CrossRef]
- Kazuva, E.; Zhang, J. Analyzing municipal solid waste treatment scenarios in rapidly urbanizing cities in developing countries: The case of Dar es Salaam, Tanzania. Int. J. Environ. Res. Public Health 2019, 16, 2035. [Google Scholar] [CrossRef] [PubMed]
- Oelofse, S.H.H.; Nahman, A. Waste production and disposal in South Africa. Environ. Sci. Policy 2019, 94, 46–56. [Google Scholar]
- O’Neill, K. The global environmental injustice of fast fashion. Environ. Health 2018, 17, 92. [Google Scholar] [CrossRef]
- Ozc1an, K.; Suthar, S.; Singh, S. Household waste categorization and its environmental impact: A comprehensive analysis. Waste Manag. 2016, 56, 234–245. [Google Scholar]
- Behrendt, G.; Naber, B.W. The chemical recycling of polyurethanes. J. Chem. Technol. Metall. 2009, 44, 3–23. [Google Scholar]
- Chrobot, P.; Faist, M.; Gustavus, L.; Martin, A.; Stamm, A.; Zah, R.; Zollinger, M. Measuring Fashion: Environmental Impact of the Global Apparel and Footwear Industries Study; Quantis. Available online: https://quantis.com/report/measuring-fashion-report/ (accessed on 1 July 2024).
- World Footwear Yearbook 2023. Global Footwear Production Reaches 23.9 Billion Pairs and Is Back to Pre-Pandemic Levels. Retrieved from World Footwear. Available online: https://www.worldfootwear.com/news/2022-global-footwear-production-reaches-239-billion-pairs-back-to-pre-pandemic-levels/9025.html (accessed on 1 July 2024).
- Mwinyihija, M. An analysis of the synthetic leather footwear industry in Kenya. J. Clean. Prod. 2018, 196, 953–960. [Google Scholar]
- Cheah, L.; Ciceri, N.D.; Olivetti, E.; Matsumura, S.; Forterre, D.; Roth, R.; Kirchain, R. Manufacturing-focused emissions reductions in footwear production. J. Clean. Prod. 2013, 44, 18–29. [Google Scholar] [CrossRef]
- Wang, Z.; Wang, L.H. Low-carbon economic development under carbon emission trading system—Analysis based on non-expected DEA and DID model. J. Southwest Univ. 2019, 41, 85–95. [Google Scholar] [CrossRef]
- Verde, S.F. The impact of the EU emissions trading system on competitiveness and carbon leakage: The econometric evidence. J. Econ. Surv. 2020, 34, 320–343. [Google Scholar] [CrossRef]
- Lin, T.J.; Wang, J.S.; Hsieh, P.H.; Hsu, T.S. Advantage analysis and integration planning of Taiwan carbon trading platform. Qtly. J. Bus. Manag. 2015, 16, 269–289. [Google Scholar]
- Albino, V.; Ardito, L.; Dangelico, R.M.; Petruzzelli, A.M. Understanding the development trends of low-carbon energy technologies: A patent analysis. Appl. Energy 2014, 135, 836–854. [Google Scholar] [CrossRef]
- De Marchi, V. Environmental innovation and R&D cooperation: Empirical evidence from Spanish manufacturing firms. Res. Policy 2012, 41, 614–623. [Google Scholar] [CrossRef]
- Yan, Z.; Yi, L.; Du, K.; Yang, Z. Impacts of low-carbon innovation and its heterogeneous components on CO2 emissions. Sustainability 2017, 9, 548. [Google Scholar] [CrossRef]
- Yin, H.; Zhao, J.; Xi, X.; Zhang, Y. Evolution of regional low-carbon innovation systems with sustainable development: An empirical study with big-data. J. Clean. Prod. 2019, 209, 1545–1563. [Google Scholar] [CrossRef]
- Borghesi, S.; Cainelli, G.; Mazzanti, M. Linking emission trading to environmental innovation: Evidence from the Italian manufacturing industry. Res. Policy 2015, 44, 669–683. [Google Scholar] [CrossRef]
- Calel, R.; Dechezlepretre, A. Environmental policy and directed technological change: Evidence from the European carbon market. Rev. Econ. Stat. 2016, 98, 173–191. [Google Scholar] [CrossRef]
- Kim, W.; Yu, J. The effect of the penalty system on market prices in the Korea ETS. Carbon Manag. 2018, 9, 145–154. [Google Scholar] [CrossRef]
- Luthra, S.; Mangla, S.K. Evaluating the impact of industry 4.0 on supply chain sustainability. Proc. Manuf. 2018, 21, 563–570. [Google Scholar]
- Kiel, D.; Müller, J.M.; Arnold, C.; Voigt, K.I. Sustainable industrial value creation: Benefits and challenges of industry 4.0. Int. J. Innov. Manag. 2017, 21, 1740015. [Google Scholar] [CrossRef]
- Dalenogare, L.S.; Benitez, G.B.; Ayala, N.F.; Frank, A.G. The expected contribution of industry 4.0 technologies for industrial performance. Int. J. Prod. Econ. 2018, 204, 383–394. [Google Scholar] [CrossRef]
- Gabriel, M.; Pessl, E. Industry 4.0 and sustainability impacts: Critical discussion of sustainability aspects with a special focus on future of work and ecological consequences. Ann. Fac. Eng. Hunedoara 2016, 14, 131–136. [Google Scholar]
- Müller, J.M.; Kiel, D.; Voigt, K.I. What drives the implementation of industry 4.0? The role of opportunities and challenges in the context of sustainability. Sustainability 2018, 10, 247. [Google Scholar] [CrossRef]
- de Sousa Jabbour, A.B.L.; Jabbour, C.J.C.; Foropon, C.; Godinho Filho, M. When titans meet—Can industry 4.0 revolutionise the environmentally-sustainable manufacturing wave? The role of critical success factors. Technol. Forecast. Soc. Change 2018, 132, 18–25. [Google Scholar] [CrossRef]
- Beltrami, M.; Orzes, G. A systematic review of industry 4.0 and sustainability. In Proceedings of the 2019 IEEE International Conference on Engineering, Technology and Innovation (ICE/ITMC), Valbonne, France, 17–19 June 2019; pp. 1–9. [Google Scholar]
- Park, J.; Sarkis, J.; Wu, Z. Creating integrated business and environmental value within the context of China’s circular economy and ecological modernization. J. Clean. Prod. 2010, 18, 1494–1501. [Google Scholar] [CrossRef]
- Cooper, R.; Kaplan, R.S. Activity-based costing: Introducing a new cost management system. J. Cost Manag. 1988, 2, 4–15. [Google Scholar]
- Kim, G.; Ballard, G. Applying ABC to construction projects. J. Constr. Eng. Manag. 2001, 127, 176–185. [Google Scholar]
- Fichman, M.; Kemerer, C.F. Software development: Using ABC for cost management. Inform. Syst. Res. 2002, 13, 267–283. [Google Scholar]
- AlMaryani, M.A.K.; Sadik, Z. Environmental protection costs: Insights from the ABC method. Environ. Resour. Econom. 2012, 52, 549–564. [Google Scholar]
- Goldratt, E.M.; Cox, J. The Theory of Constraints and Its Implications for Management Accounting; The North River Press: Great Barrington, MA, USA, 1984. [Google Scholar]
- Tsai, W.H.; Jhong, S.Y. Production decision model with carbon tax for the knitted footwear industry under activity-based costing. J. Clean. Prod. 2019, 207, 1150–1162. [Google Scholar] [CrossRef]
- Hsieh, C.L.; Tsai, W.H. Sustainable Decision Model for Circular Economy towards Net Zero Emissions under Industry 4.0. Processes 2023, 11, 3412. [Google Scholar] [CrossRef]
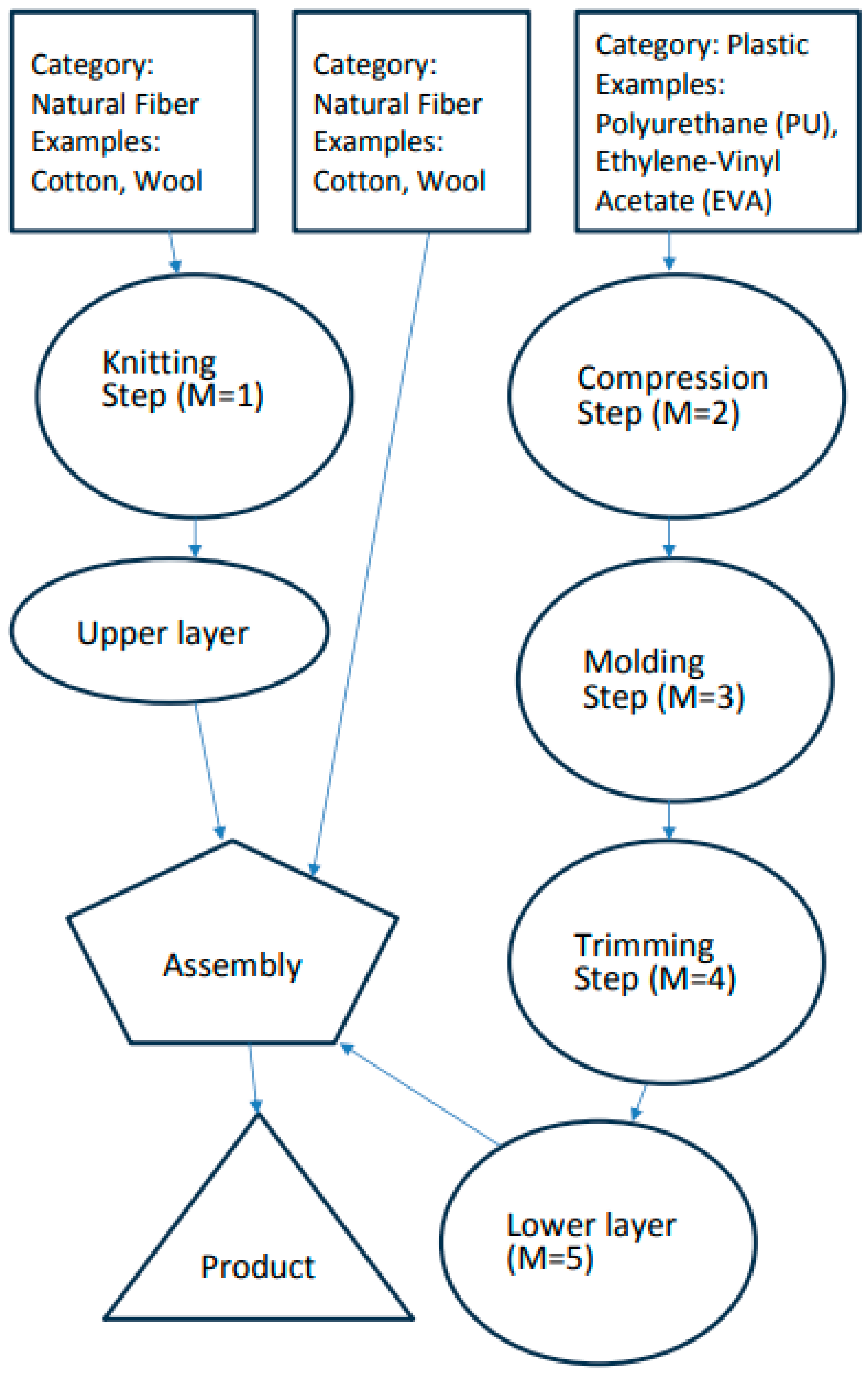


| Maximum Available Resources | Product 1 (i = 3) | Product 2 (i = 2) | Product 3 (i = 1) | |||||
|---|---|---|---|---|---|---|---|---|
| Market price of product | m | Pi | TWD 2178 | TWD 1974 | TWD 1705 | |||
| Fundamental resources (unit level) | j equal to 1 (string) | M1 = TWD 58/unit | RMi1 | LMQ1 = | ||||
| j equal to 2 (PU) | M2 = TWD 116/unit | RMi2 | LMQ2 = 364,000 | |||||
| j equal to 3 (glue) | M3 = TWD 39/unit | RMi3 | LMQ3 = 156,000 | |||||
| Unit level job | ||||||||
| labor hours | m equal to 4 (trimming) | 4 | RLHi4 | |||||
| m equal to 5 (combination) | 5 | RLHi5 | ||||||
| machine hour | m equal to 1 (knitting) | 1 | RMHi1 | LMH1 = 401,500 | 8 | 4 | 1 | |
| m equal to 2 (pressing) | 2 | RMHi2 | LMH2 = 24,024 | 0.2 | 0.14 | 0.1 | ||
| m equal to 5 (combination) | 5 | RMHi5 | LMH5 = 64,064 | 0.5 | 0.4 | 0.2 | ||
| Batch level | job element | |||||||
| forming | forming hours | C3 = TWD 100/h | 3 | i3 | R3 = 120,900 | 2 | 2 | 2 |
| i3 | 2 | 3 | 4 | |||||
| setting | setting hours | C6 = TWD 40/h | 6 | i6 | R6 = 713,284 | 2 | 3 | 6 |
| i6 | 2 | 3 | 6 | |||||
| material handling | handling hours | C7 = TWD 15/h | 7 | i7 | R7 = 436,800 | 2 | 4 | 6 |
| i7 | 3 | 4 | 6 | |||||
| Product level | product design | d8 = TWD 150/h | 8 | i8 | C8 = 10,000 | 5000 | 1500 | 3000 |
| Labor cost cap on costs for direct labor | DLC0 = TWD 15,960,000 | DLC1 = TWD 22,910,790 | DLC2 = TWD 31,589,640 | |||||
| allocated hours for direct labor | DLH0 = 120,000 | DLH1 = 39,270 | DLH2 = 78,540 | |||||
| hourly wage rate | WR0 = TWD 133/h | WR1 = TWD 177/h | WR2 = TWD 221/h | |||||
| Carbon emissions | ||||||||
| carbon emissions during production | m = 1 (knitting) | CEi1 | MCEQ = 250,000 kg | 1.43 | 0.98 | 0.53 | ||
| m = 2 (pressing) | CEi2 | SMCEQ = 677,500 kg | 0.95 | 0.65 | 0.35 | |||
| m = (combination) | CEi5 | 2.39 | 1.64 | 0.89 | ||||
| Carbon tax cost | CT1 = TWD 135,000 | CT2 = TWD 425,000 | T3 = TWD 313,667,020 | |||||
| Carbon emission caps for each level | CEQ1 = 150,000 kg | CEQ2 = 400,000 kg | CEQ3 = 221,460,000 kg | |||||
| Carbon tax rates for each level | TR1 = TWD 0.9/kg | TR2 = TWD 1.16/kg | TR3 = TWD 1.417/kg | |||||
| Carbon rights cost | LPCRC = TWD 36,500 | LPCEQ = 50,000 kg | = TWD 0.73/kg | MPCEQ = 300,000 kg | ||||
| SLPCRC = TWD 98,910 | LPCEQ = 135,500 kg | SMPCEQ = 813,000 kg | ||||||
| π | = (1705 * X1 + 1974 * X2 + 2178 * X3) − [(58 + 232 + 20)X1 + (87 + 232 + 39)X2 + (116 + 232 + 47)X3] − (15,960,000 + 6,950,7901 + 15,629,6402) − [(4 * 100) + (3 * 100) + (2 * 100)] − [(6 * 40) + (3 * 40) + (2 * 40)] + [(6 * 15) + (4 * 15) + (3 * 15))] − (450,000 + 225,000 + 750,000) − (135,000 + 425,000 + 313,667,020) − 44,996,392; |
| carbon tax constraints: (1.77 * X1 + 3.27 * X2 + 4.77 * X3) = 150,000 + 400,000 + 221,460,000; (1.77 * X1 + 3.27 * X2 + 4.77 * X3) ≤ 250,000; − ≤ 0; − − ≤ 0; − − ≤ 0; − ≤ 0; + + + = 1; + + = 1 | |
| π | = (1705X1 + 1974X2 + 2178X3) − [(58 + 232 + 20)X1 + (87 + 232 + 39)X2 + (116 + 232 + 47)X3] − (15,960,000 + 6,950,7901 + 15,629,6402) − [(4 * 100) + (3 * 100) + (2 * 100)] − [(6 * 40) + (3 * 40) + (2 * 40)] + [(6 * 15) + (4 * 15) + (3 * 15))] − (450,000 + 225,000 + 750,000) − ((135,000 + 425,000 + 313,667,020) − (250,000 − ()) * 0.73) − ((135,000 + 425,000 + 313,667,020) + (() − 250,000) * 0.73) − 44,996,392; |
| carbon tax constraints: (1.77 * X1 + 3.27 * X2 + 4.77 * X3) = 150,000 + 400,000 + 221,460,000; − ≤ 0; − − ≤ 0; − − ≤ 0; − ≤ 0; + + + = 1; + + = 1 | |
| carbon right constraint: (1.77 * X1 + 3.27 * X2 + 4.77 * X3) = ; ≤ 250,000; ; ≤ 300,000; + 1 | |
| π | = (1705 * X1 + 1974 * X2 + 2178 * X3) − [(58 + 232 + 20)X1 + (87 + 232 + 39)X2 + (116 + 232 + 47)X3] − (15,960,000 + 6,950,7901 + 15,629,6402) − [(4 * 100) + (3 * 100) + (2 * 100)] − [(6 * 40) + (3 * 40) + (2 * 40)] + [(6 * 15) + (4 * 15) + (3 * 15))] − (450,000 + 225,000 + 750,000) − () − 44,996,392; |
| carbon tax constraints: (1.77 * X1 + 3.27 * X2 + 4.77 * X3) = Q1 + Q2 + Q3; (1.77 * X1 + 3.27 * X2 + 4.77 * X3) ≤ 250,000; ; ; ; ≤ 400,000; ; ; | |
| π | = (1705 * X1 + 1974 * X2 + 2178 * X3) − [(58 + 232 + 20)X1 + (87 + 232 + 39)X2 + (116 + 232 + 47)X3] − (15,960,000 + 6,950,7901 + 15,629,6402) − [(4 * 100) + (3 * 100) + (2 * 100)] − [(6 * 40) + (3 * 40) + (2 * 40)] + [(6 * 15) + (4 * 15) + (3 * 15))] − (450,000 + 225,000 + 750,000) − (() − (250,000 − ()) * 0.73) − (() + (() − 250,000) * 0.73) − 44,996,392; |
| carbon tax constraints: (1.77 * X1 + 3.27 * X2 + 4.77 * X3) = Q1 + Q2 + Q3; ; ; ; ≤ 400,000; ; ; | |
| carbon right constraint: (1.77 * X1 + 3.27 * X2 + 4.77 * X3) = ; ≤ 250,000; ; ≤ * 300,000; + 1; | |
| The target equation is constrained by the following: Direct raw material restrictions 1 * X1 + 1.5 * X2 + 2 * X3 ≤ 265,938; 2 * X1 + 2 * X2 + 2 * X3 ≤ 364,000; 0.5 * X1 + 1 * X2 + 1.2 * X3 ≤ 156,000; |
| Direct manual restriction (1 * X1 + 1.8 * X2 + 2 * X3) ≤ (120,000 +39,270 + * 78,540); ; ; ; ; |
| Machine hour limit 1 * X1 + 4 * X2 + 8 * X3 ≤ 401,500; 0.1 * X1 + 0.14 * X2 + 0.2 * X3 ≤ 24,024; 0.2 * X1 + 0.4 * X2 + 0.5 * X3 ≤ 64,064; |
| Batch-level job limits (forming) X1 − 2 * ≤ 0; X2 − 2 * ≤ 0; X3 − 2 ≤ 0; 4 + 3 + 2 ≤ 120,900; |
| Batch-level job limits (settings) X1 − 6 ≤ 0; X2 − 3 ≤ 0; X3 − 2 ≤ 0; 6 + 3 + 2 ≤ 713,284; |
| Batch-level job limits (material handling) X1 − 6 ≤ 0; X2 − 4 ≤ 0; X3 − 3 ≤ 0; 6 + 4 + 3 ≤ 436,800; |
| Product-level assignments (product design) X1 − 100,000 ≤ 0; X2 − 25,000 ≤ 0; X3 − 30,000 ≤ 0; 3000 + 1500 + 5000 ≤ 10,000; |
| Profit | The Output of Each Product | Carbon Emission | Carbon Tax Cost | The Cost of Carbon Rights | Labor Hours | Forming (Forming Hours) | Setting (Setting Hours) | Material Handling (Handling Hours) | |
|---|---|---|---|---|---|---|---|---|---|
| Model 1 Continuous carbon tax | TWD 45,614,175 | X1: 34,818 X2: 14,454 X3: 29,582 | 249,999 | TWD 250,998 | 0 | 119,999 | 120,899 | 78,854 | 78,857 |
| Model 2 Continuous carbon tax with carbon trading | 49,807,842 | X1: 26,700 X2: 25,000 X3: 30,000 | 272,109 | 276,646 | 16,140 | 131,700 | 120,900 | 81,702 | 81,700 |
| Model 3 Discontinuous carbon tax | 45,575,175 | X1: 34,818 X2: 14,454 X3: 29,582 | 249,999 | 289,998 | 0 | 119,999 | 120,899 | 78,854 | 78,857 |
| Model 4 Discontinuous carbon tax with carbon trading | 49,768,842 | X1: 26,700 X2: 25,000 X3: 30,000 | 272,109 | 315,646 | 16,140 | 131,700 | 120,900 | 81,702 | 81,700 |
| Profit | The Output of Each Product | Carbon Emission | Carbon Tax Cost | Pre-Borrow or Store Carbon Emissions | Expense Related to Carbon Credits | Labor Hours | Forming (Forming Hours) | (Adjustment Duration) Management of Materials | (Management Duration) | |
|---|---|---|---|---|---|---|---|---|---|---|
| Model 1 Continuous carbon tax | TWD 118,037,916 | X11: 30,600 X21: 25,000 X31: 22,198 | 241,797 | TWD 241,483 | (8204) | 0 | 119,996 | 120,898 | 77,800 | 77,800 |
| X12: 36,768 X22: 24,996 X32: 9870 | 193,896 | 185,920 | (31,104) | 114,950 | 120,900 | 71,634 | 71,634 | |||
| X13: 30,600 X23: 25,000 X33: 22,200 | 241,806 | 241,495 | 39,306 | 120,000 | 120,900 | 77,802 | 77,800 | |||
| Model 2 Continuous carbon tax with carbon trading | 148,742,200 | X11: 26,712 X21: 24,984 X31: 30,000 | 272,078 | 276,610 | X | 16,117 | 131,683 | 120,900 | 81,696 | 81,696 |
| X12: 26,730 X22: 24,960 X32: 30,000 | 272,031 | 276,556 | 34,333 | 131,658 | 120,900 | 81,690 | 81,690 | |||
| X13: 27,942 X23: 23,343 X33: 30,000 | 268,889 | 272,911 | 48,464 | 129,959 | 120,900 | 81,285 | 81,286 | |||
| Model 3 Discontinuous carbon tax | 117,920,900 | X11: 30,624 X21: 24,996 X31: 22,158 | 241,635 | 280,297 | (8365) | 0 | 119,933 | 120,900 | 77,778 | 77,778 |
| X11: 30,606 X21: 25,000 X31: 22,188 | 241,759 | 280,441 | 16,759 | 119,982 | 120,900 | 77,796 | 77,794 | |||
| X11: 36,738 X21: 25,000 X31: 9922 | 194,104 | 225,161 | (8396) | 101,582 | 120,898 | 71,662 | 71,662 | |||
| Model 4 Discontinuous carbon tax with carbon trading | 148,625,179 | X11: 26,730 X21: 24,960 X31: 30,000 | 272,031 | 315,556 | X | 16,083 | 131,658 | 120,900 | 81,690 | 81,690 |
| X11: 26,712 X21: 24,984 X31: 30,000 | 272,078 | 315,610 | 34,367 | 131,683 | 120,900 | 81,696 | 81,696 | |||
| X11: 27,942 X21: 23,343 X31: 30,000 | 268,889 | 311,911 | 48,464 | 129,959 | 120,900 | 81,285 | 81,286 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tsai, W.-H.; Su, P. A Dynamic Approach to Sustainable Knitted Footwear Production in Industry 4.0: Integrating Short-Term Profitability and Long-Term Carbon Efficiency. Sustainability 2024, 16, 7120. https://doi.org/10.3390/su16167120
Tsai W-H, Su P. A Dynamic Approach to Sustainable Knitted Footwear Production in Industry 4.0: Integrating Short-Term Profitability and Long-Term Carbon Efficiency. Sustainability. 2024; 16(16):7120. https://doi.org/10.3390/su16167120
Chicago/Turabian StyleTsai, Wen-Hsien, and Poching Su. 2024. "A Dynamic Approach to Sustainable Knitted Footwear Production in Industry 4.0: Integrating Short-Term Profitability and Long-Term Carbon Efficiency" Sustainability 16, no. 16: 7120. https://doi.org/10.3390/su16167120
APA StyleTsai, W.-H., & Su, P. (2024). A Dynamic Approach to Sustainable Knitted Footwear Production in Industry 4.0: Integrating Short-Term Profitability and Long-Term Carbon Efficiency. Sustainability, 16(16), 7120. https://doi.org/10.3390/su16167120






