Nature-Based Secondary Resource Recovery under Climate Change Uncertainty: A Robust Multi-Objective Optimisation Methodology
Abstract
1. Introduction
2. Previous Works
2.1. Remediation Domain
2.2. Resource Recovery Domain
2.3. NbS Domain
2.4. Interdisciplinary Studies
2.5. Research Gaps and Objectives
3. Methodology
3.1. Problem Statement
3.2. Deterministic Mathematical Formulation
3.2.1. Economic Objective
3.2.2. Social Well-Being Objective
3.2.3. Climate Risk Resilience Objective
3.2.4. Constraints
- ▪
- All the bulk materials from blast furnaces at legacy sites are collected and recovered.
- ▪
- Processing facilities have the technological specifications to process all the recoverable resources.
3.3. Robust Mathematical Formulation
- No global mean temperature increases by 2080 (1961–1990 baseline as assumed in UKCP09).
- Approximately 2 °C global mean temperature increases by 2080.
- Approximately 4 °C global mean temperature increases by 2080.
3.4. Solution Approach
3.5. Illustrative Case Study
- ▪
- The bulk materials’ (blast furnace) density is assumed to be 1.5 t/m3, and around 85% is assumed to be inert materials (i.e., not containing critical materials).
- ▪
- All the recovery brownfields will be remediated within the 30-year project duration [65].
- ▪
- Bulk materials will be layered vertically to a depth of 2 m over an area of 1 m2 on brownfields.
- ▪
- ▪
- The land value of the remediated recovery brownfields is not considered due to the high variability of real estate value at the national scale [70].
- ▪
- Exactly N1 = 50 recovery brownfields should be selected, and up to N2 ≤ 59 processing facilities can be selected.
| Parameter | Description | Category | Source |
|---|---|---|---|
| Brownfield sites | Locations of brownfields | Spatial data | [71] |
| Capital expenses of nature-based solutions | Capital expense factor of NbS per unit area | Cost | [46] |
| Climate change risk indicators spatial dataset | Climate change risk factors per climate change projections | Hydroclimatic data | [60] |
| Earthmoving cost factors | Loading cost per unit volume | Cost | [72] |
| Transport GHG emission factor | Carbon emission factors of transport | Cost | [73] |
| Legacy industrial sites | Locations of legacy industrial sites | Spatial data | [74] |
| Nature-based solution employment multiplier | Implementation and maintenance phases | Area multiplier | [75] |
| Passive carbon sequestration by brownfield factor | Carbon sequestered by unit area of brownfields | Area multiplier | [76] |
| Processing facilities | Locations of processing facilities | Spatial data | [77] |
| Recoverable resources prices | Low, central, and high estimates | Profit | [78,79,80,81] |
| UK borough boundary lines | Vector dataset of UK roads | Spatial data | [82] |
| UK road network vector spatial dataset | Vector dataset of UK roads | Spatial data | [83] |
| Valuation of greenhouse gas emissions | Low, central, and high estimates | Cost | [84] |
3.6. Sensitivity Analysis
3.6.1. Number of Grid Points for AUGMECON2
3.6.2. Variability in Recovery Revenue, Resource Concentration, and Carbon Pricing
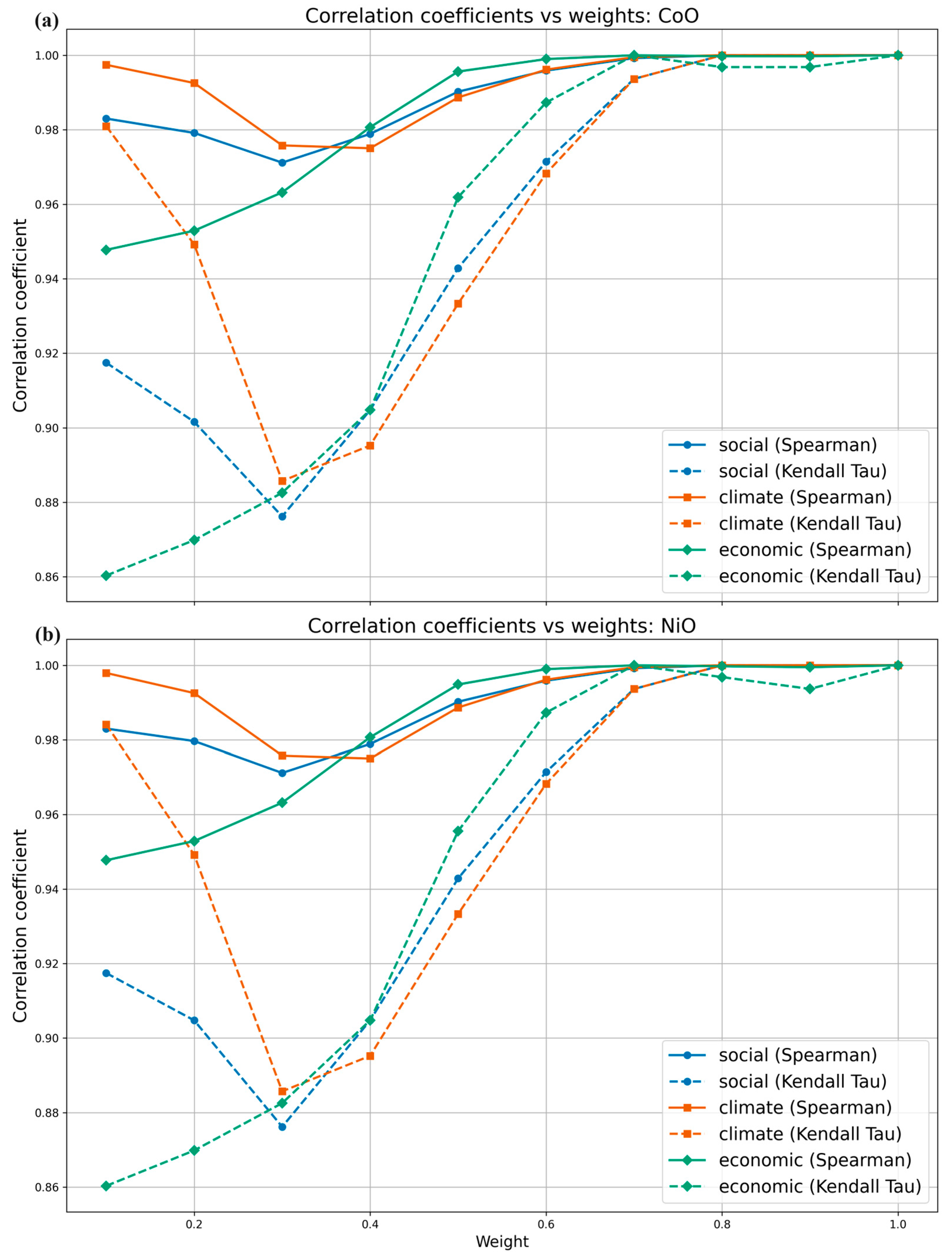
3.6.3. Weights of Ranking Methods
3.7. Computational Implementation
4. Results
4.1. Pareto Sets of AUGMECON2
4.2. Sensitivity Analysis
4.2.1. AUGMECON2 Performance Sensitivity to Grid Size
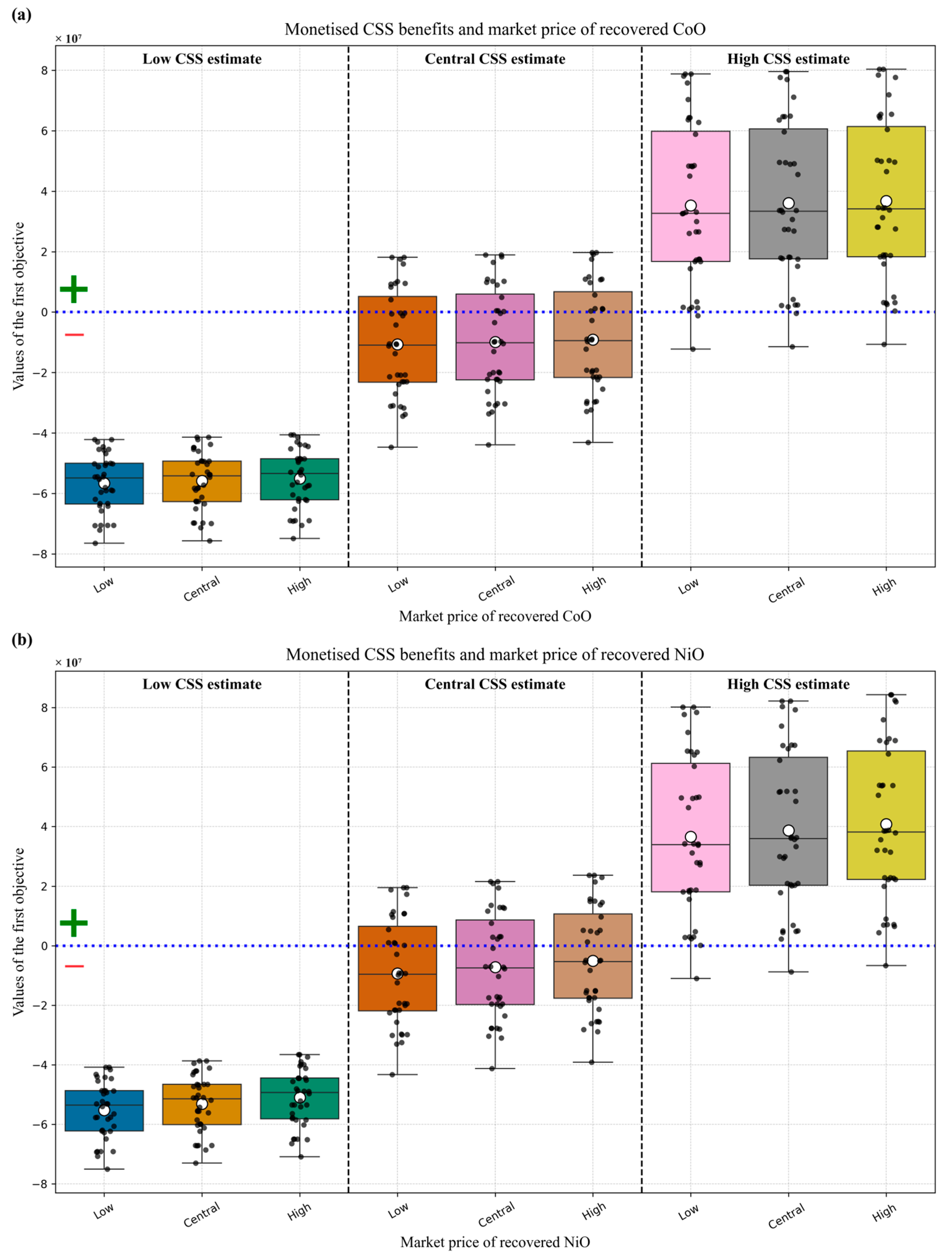
4.2.2. Variability in Recovery Revenue, Resource Concentration, and Carbon Pricing
4.2.3. Multi-Criteria Analysis of Pareto Sets: Compromise Programming
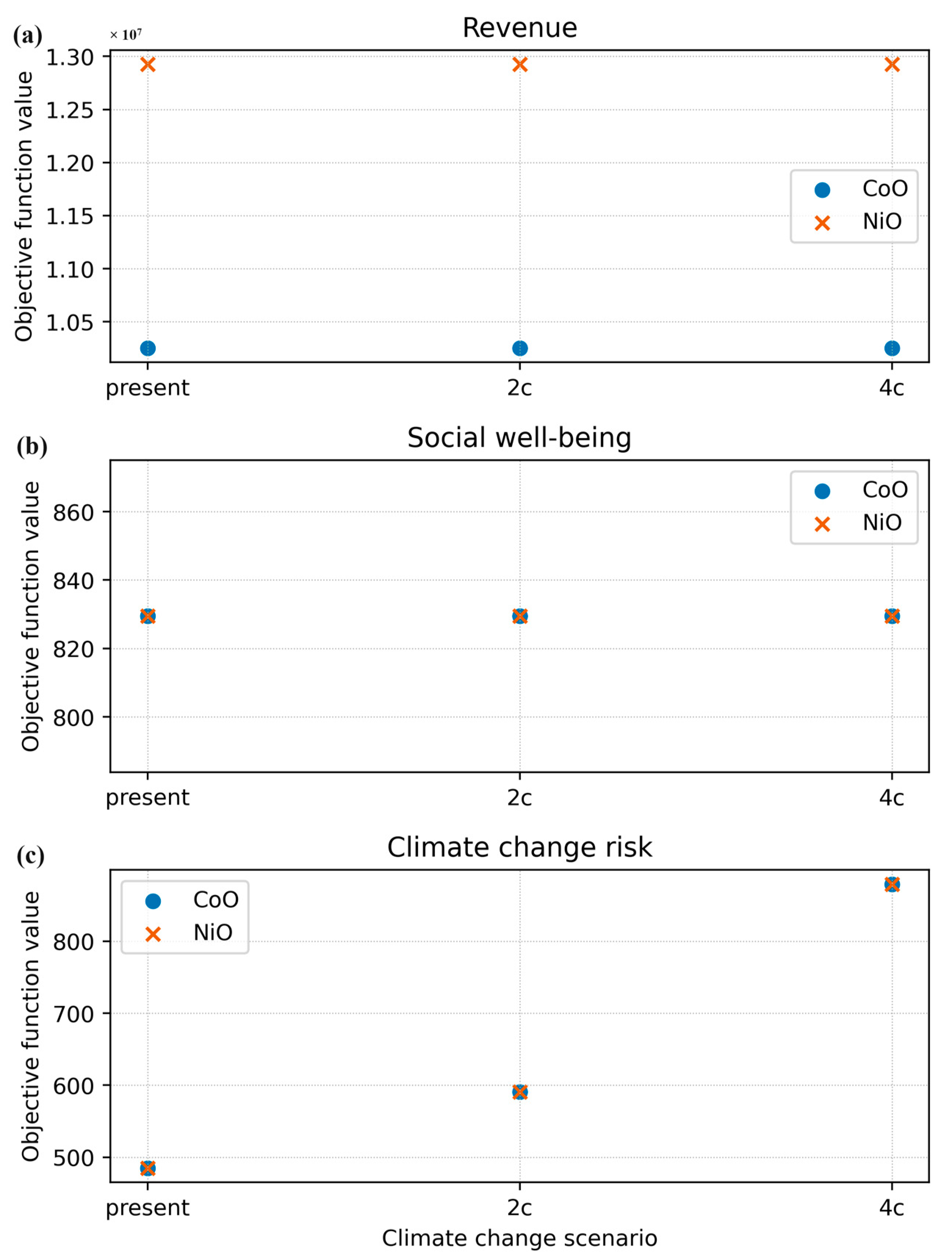
4.3. Robust Optimisation of Climate Change Uncertainty
5. Discussion
5.1. Performance of AUGMECON2
5.2. Impacts of Resource Value and Carbon Pricing
5.3. Impact of Decision-Maker Preferences on Selected Solutions
5.4. Robust Optimisation under Climate Change Uncertainty
6. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
| Set | Description |
|---|---|
| I | Set of legacy sites where materials are available. |
| J | Set of recovery brownfield sites available for nature-based solutions. |
| J | Set of processing facilities available for final processing of materials. |
| K | Set of climate change scenarios. |
| Parameter | Description |
|---|---|
| Revenue from recovered materials based on market prices. | |
| Monetised value of carbon sequestration and storage from NbS. | |
| Capital expense for NbS implementation per hectare. | |
| Transportation cost from legacy site i to brownfield site j. | |
| Transportation cost from brownfield site j to processing facility k. | |
| Loading cost for materials at brownfields for transportation. | |
| Employment multiplier per hectare of NbS implementation at brownfield j. | |
| Climate risk factor for brownfield site j. | |
| Climate risk factor for processing facility k. | |
| Volume of materials available at legacy site i. | |
| Temporary storage capacity at brownfield site j. | |
| Processing capacity at processing facility k. | |
| period | Duration of the project. |
| Number of brownfield sites to be selected. | |
| Maximum number of processing facilities that can be selected. |
| Variable | Description |
|---|---|
| Continuous variable representing the fraction of materials from legacy site iii allocated to brownfield site j. | |
| Continuous variable representing the amount of materials transported from brownfield site j to processing facility k. | |
| Binary variable indicating whether brownfield site j is selected. | |
| Binary variable indicating whether processing facility k is selected. |
| Objective | Description |
|---|---|
| Economic objective | |
| Social well-being objective | |
| Climate risk resilience objective |
| Objective | Description |
|---|---|
| Robust climate risk resilience objective |
| Constraint | Description |
|---|---|
| Selection constraint (1) | |
| Selection constraint (2) | |
| Capacity constraint (1) | The total volume of materials transported to each brownfield site must not exceed its capacity: |
| Capacity constraint (2) | The total volume of materials processed by each facility must not exceed its capacity: |
| Flow balance constraint | Ensure material flow balance from legacy sites through brownfields to processing facilities |
| Service constraint | Ensure all material from legacy sites is allocated to brownfield sites: |
| Decision variable constraint (1) | |
| Decision variable constraint (2) | |
| Decision variable constraint (3) | |
| Decision variable constraint (4) |
| Parameter | Low | Central | High | Unit | Source |
|---|---|---|---|---|---|
| Capital expenses of nature-based solutions | n.a. * | 123 | n.a. | GBP/hectare | [46] |
| Earth-moving cost factor (a 1 m3 crawler assuming 10 loadings per hour) | n.a. | 26.84 | n.a. | GBP/hour | [72] |
| Transport GHG emission factor (assuming average laden rigid lorry) | n.a. | 0.9635 | n.a. | kgCO2e/km | [73] |
| Nature-based solution employment multiplier (implementation phase) | n.a. | 0.04 | n.a. | Full-time equivalent/hectare/year | [75] |
| Nature-based solution employment multiplier (maintenance phase) | n.a. | 0.01 | n.a. | Full-time equivalent/hectare/year | [75] |
| Passive carbon sequestration by brownfield factor | n.a. | 4 | n.a. | tCO2e/hectare | [76] |
| Recoverable resources prices (CoO) | 2000 | 4500 | 6000 | GBP/ton | [78,79] |
| Recoverable resources prices (NiO) | 2500 | 5000 | 7500 | GBP/ton | [80,81] |
| Valuation of greenhouse gas emissions | 189 | 378 | 568 | GBP/tCO2e | [80] |
References
- Sapsford, D.J.; Stewart, D.I.; Sinnett, D.E.; Burke, I.T.; Cleall, P.J.; Harbottle, M.J.; Mayes, W.; Owen, N.E.; Sardo, A.M.; Weightman, A. Circular economy landfills for temporary storage and treatment of mineral-rich wastes. Proc. Inst. Civ. Eng. Waste Resour. Manag. 2023, 176, 77–93. [Google Scholar] [CrossRef]
- Wastling, T.; Charnley, F.; Moreno, M. Design for Circular Behaviour: Considering Users in a Circular Economy. Sustainability 2018, 10, 1743. [Google Scholar] [CrossRef]
- Bjørnbet, M.M.; Skaar, C.; Fet, A.M.; Schulte, K.Ø. Circular economy in manufacturing companies: A review of case study literature. J. Clean. Prod. 2021, 294, 126268. [Google Scholar] [CrossRef]
- Kirchherr, J.; Reike, D.; Hekkert, M. Conceptualizing the circular economy: An analysis of 114 definitions. Resour. Conserv. Recycl. 2017, 127, 221–232. [Google Scholar] [CrossRef]
- Lambiase, N.; Barbera, F. The Anatomy of the Circular Economy: Goals, Strategies, Values and Scales. In Innovations for Circularity and Knowledge Creation: Participation and Cooperative Approaches for Sustainability; Bernardi, A., Mazzanti, M., Monni, S., Eds.; Springer Nature: Cham, Switzerland, 2024; pp. 21–41. [Google Scholar] [CrossRef]
- Kisser, J.; Wirth, M.; De Gusseme, B.; Van Eekert, M.; Zeeman, G.; Schoenborn, A.; Vinnerås, B.; Finger, D.C.; Repinc, S.K.; Bulc, T.G.; et al. A review of nature-based solutions for resource recovery in cities. Blue-Green Syst. 2020, 2, 138–172. [Google Scholar] [CrossRef]
- Mohammad, A.; Sapsford, D.; Harbottle, M.; Cleall, P.; Stewart, D.I.; Sepúlveda, F. Effect of Different Physical and Geochemical Parameters on Mobilisation of Metals: A Crucial Step Towards Resource Recovery from Waste. In Proceedings of the 9th International Congress on Environmental Geotechnics, Chania, Greece, 25–28 June 2022. [Google Scholar] [CrossRef]
- Shaw, R.A.; Petavratzi, E.; Bloodworth, A.J. Resource Recovery from Mine Waste. In Waste as a Resource; Hester, R.E., Harrison, R.M., Harrison, R., Hester, R., Eds.; The Royal Society of Chemistry: London, UK, 2013; pp. 44–65. [Google Scholar] [CrossRef]
- Sapsford, D.; Cleall, P.; Harbottle, M. In Situ Resource Recovery from Waste Repositories: Exploring the Potential for Mobilization and Capture of Metals from Anthropogenic Ores. J. Sustain. Met. 2017, 3, 375–392. [Google Scholar] [CrossRef]
- Krook, J.; Svensson, N.; Eklund, M. Landfill mining: A critical review of two decades of research. Waste Manag. 2012, 32, 513–520. [Google Scholar] [CrossRef]
- Dermatas, D. Waste management and research and the sustainable development goals: Focus on soil and groundwater pollution. Waste Manag. Res. 2017, 35, 453–455. [Google Scholar] [CrossRef]
- Sinnett, D. Going to waste? The potential impacts on nature conservation and cultural heritage from resource recovery on former mineral extraction sites in England and Wales. J. Environ. Plan. Manag. 2019, 62, 1227–1248. [Google Scholar] [CrossRef]
- Wuana, R.A.; Okieimen, F.E. Heavy Metals in Contaminated Soils: A Review of Sources, Chemistry, Risks and Best Available Strategies for Remediation. ISRN Ecol. 2011, 2011, 402647. [Google Scholar] [CrossRef]
- Osra, F.A.; Elbisy, M.S.; Mosaıbah, H.A.; Osra, K.; Ciner, M.N.; Ozcan, H.K. Environmental Impact Assessment of a Dumping Site: A Case Study of Kakia Dumping Site. Sustainability 2024, 16, 3882. [Google Scholar] [CrossRef]
- Yin, C.; Zhao, W.; Pereira, P. Soil conservation service underpins sustainable development goals. Glob. Ecol. Conserv. 2022, 33, e01974. [Google Scholar] [CrossRef]
- Mead, I.; Apted, J.; Sharif, S. Delivering London 2012: Contaminated soil treatment at the Olympic Park. Proc. Inst. Civ. Eng. Geotech. Eng. 2013, 166, 8–17. [Google Scholar] [CrossRef]
- Apted, M.J.; Ahn, J. (Eds.) Geological Repository Systems for Safe Disposal of Spent Nuclear Fuels and Radioactive Waste, 2nd ed.; Woodhead Publishing: Sawston, UK, 2017. [Google Scholar]
- Alshehri, K.; Harbottle, M.; Sapsford, D.; Beames, A.; Cleall, P. Integration of ecosystem services and life cycle assessment allows improved accounting of sustainability benefits of nature-based solutions for brownfield redevelopment. J. Clean. Prod. 2023, 413, 137352. [Google Scholar] [CrossRef]
- Alshehri, K.; Gao, Z.; Harbottle, M.; Sapsford, D.; Cleall, P. Life cycle assessment and cost-benefit analysis of nature-based solutions for contaminated land remediation: A mini-review. Heliyon 2023, 9, e20632. [Google Scholar] [CrossRef]
- Ahmed, R.O.; Al-Mohannadi, D.M.; Linke, P. Multi-objective resource integration for sustainable industrial clusters. J. Clean. Prod. 2021, 316, 128237. [Google Scholar] [CrossRef]
- Huntington, V.E.; Coulon, F.; Wagland, S.T. Innovative Resource Recovery from Industrial Sites: A Critical Review. Sustainability 2022, 15, 489. [Google Scholar] [CrossRef]
- Fortunati, S.; Morea, D.; Mosconi, E.M. Circular economy and corporate social responsibility in the agricultural system: Cases study of the Italian agri-food industry. Agric. Econ. 2020, 66, 489–498. [Google Scholar] [CrossRef]
- Alamerew, Y.A.; Kambanou, M.L.; Sakao, T.; Brissaud, D. A Multi-Criteria Evaluation Method of Product-Level Circularity Strategies. Sustainability 2020, 12, 5129. [Google Scholar] [CrossRef]
- Basirati, M.; Jokar, M.R.A.; Hassannayebi, E. Bi-objective optimization approaches to many-to-many hub location routing with distance balancing and hard time window. Neural Comput. Appl. 2020, 32, 13267–13288. [Google Scholar] [CrossRef]
- Baratsas, S.G.; Pistikopoulos, E.N.; Avraamidou, S. A systems engineering framework for the optimization of food supply chains under circular economy considerations. Sci. Total. Environ. 2021, 794, 148726. [Google Scholar] [CrossRef] [PubMed]
- Holzkämper, A.; Klein, T.; Seppelt, R.; Fuhrer, J. Assessing the propagation of uncertainties in multi-objective optimization for agro-ecosystem adaptation to climate change. Environ. Model. Softw. 2015, 66, 27–35. [Google Scholar] [CrossRef]
- Zolghadr-Asli, B.; Bozorg-Haddad, O.; Enayati, M.; Goharian, E. Developing a Robust Multi-Attribute Decision-Making Framework to Evaluate Performance of Water System Design and Planning under Climate Change. Water Resour. Manag. 2021, 35, 279–298. [Google Scholar] [CrossRef]
- Beh, E.H.; Zheng, F.; Dandy, G.C.; Maier, H.R.; Kapelan, Z. Robust optimization of water infrastructure planning under deep uncertainty using metamodels. Environ. Model. Softw. 2017, 93, 92–105. [Google Scholar] [CrossRef]
- Alshehri, K.; Harbottle, M.; Sapsford, D.; Cleall, P. Nature-based secondary resource recovery decision-making from regional and national lens: A mini-review. Front. Sustain. 2024. under review. [Google Scholar]
- Bayer, P.; Duran, E.; Baumann, R.; Finkel, M. Optimized groundwater drawdown in a subsiding urban mining area. J. Hydrol. 2009, 365, 95–104. [Google Scholar] [CrossRef]
- Morano, P.; Tajani, F. The Transfer of Development Rights for the Regeneration of Brownfield Sites. Appl. Mech. Mater. 2013, 409–410, 971–978. [Google Scholar] [CrossRef]
- De Mare, G.; Nesticò, A.; Tajani, F. The Rational Quantification of Social Housing. In Computational Science and Its Applications—ICCSA 2012; Murgante, B., Gervasi, O., Misra, S., Nedjah, A., Rocha, M.A.C., Taniar, D., Apduhan, B.O., Eds.; Lecture Notes in Computer Science; Springer: Berlin/Heidelberg, Germany, 2012; Volume 7334, pp. 27–43. [Google Scholar] [CrossRef]
- Jeyasingh, J.; Somasundaram, V.; Philip, L.; Bhallamudi, S.M. Bioremediation of Cr(VI) contaminated soil/sludge: Experimental studies and development of a management model. Chem. Eng. J. 2010, 160, 556–564. [Google Scholar] [CrossRef]
- Guo, M. Multi-scale system modelling under circular bioeconomy. Comput. Aided Chem. Eng. 2018, 43, 833–838. [Google Scholar] [CrossRef]
- Robles, I.; Guo, M. Development of Systems Modelling Framework for Waste-to-Resource Transformation. Comput. Aided Chem. Eng. 2020, 48, 1597–1602. [Google Scholar] [CrossRef]
- Robles, I.; Durkin, A.; Guo, M. Stochastic optimisation of organic waste-to-resource value chain. Environ. Pollut. 2021, 273, 116435. [Google Scholar] [CrossRef]
- Huang, Y.; Xu, J. Bi-level multi-objective programming approach for bioenergy production optimization towards co-digestion of kitchen waste and rice straw. Fuel 2022, 316, 123117. [Google Scholar] [CrossRef]
- Capraz, O.; Polat, O.; Gungor, A. Planning of waste electrical and electronic equipment (WEEE) recycling facilities: MILP modelling and case study investigation. Flex. Serv. Manuf. J. 2015, 27, 479–508. [Google Scholar] [CrossRef]
- Wu, H.; Wan, Z. A multiobjective optimization model and an orthogonal design–based hybrid heuristic algorithm for regional urban mining management problems. J. Air Waste Manag. Assoc. 2018, 68, 146–169. [Google Scholar] [CrossRef]
- Hernández, I.F.; Ordóñez, J.I.; Robles, P.A.; Gálvez, E.D.; Cisternas, L.A. A Methodology for Design and Operation Of Heap Leaching Systems. Miner. Process. Extr. Met. Rev. 2017, 38, 180–192. [Google Scholar] [CrossRef]
- O’Dwyer, E.; Chen, K.; Wang, H.; Wang, A.; Shah, N.; Guo, M. Optimisation of wastewater treatment strategies in eco-industrial parks: Technology, location and transport. Chem. Eng. J. 2020, 381, 122643. [Google Scholar] [CrossRef]
- Misrol, M.A.; Alwi, S.R.W.; Lim, J.S.; Manan, Z.A. Optimization of energy-water-waste nexus at district level: A techno-economic approach. Renew. Sustain. Energy Rev. 2021, 152, 111637. [Google Scholar] [CrossRef]
- Singh, A.; Sarma, A.K.; Hack, J. Cost-Effective Optimization of Nature-Based Solutions for Reducing Urban Floods Considering Limited Space Availability. Environ. Process. 2020, 7, 297–319. [Google Scholar] [CrossRef]
- Alves, A.; Vojinovic, Z.; Kapelan, Z.; Sanchez, A.; Gersonius, B. Exploring trade-offs among the multiple benefits of green-blue-grey infrastructure for urban flood mitigation. Sci. Total. Environ. 2020, 703, 134980. [Google Scholar] [CrossRef]
- McClymont, K.; Cunha, D.G.F.; Maidment, C.; Ashagre, B.; Vasconcelos, A.F.; de Macedo, M.B.; dos Santos, M.F.N.; Júnior, M.N.G.; Mendiondo, E.M.; Barbassa, A.P.; et al. Towards urban resilience through Sustainable Drainage Systems: A multi-objective optimisation problem. J. Environ. Manag. 2020, 275, 111173. [Google Scholar] [CrossRef] [PubMed]
- Liu, L.; Dobson, B.; Mijic, A. Optimisation of urban-rural nature-based solutions for integrated catchment water management. J. Environ. Manag. 2023, 329, 117045. [Google Scholar] [CrossRef] [PubMed]
- Liu, Y.; Xia, C.; Ou, X.; Lv, Y.; Ai, X.; Pan, R.; Zhang, Y.; Shi, M.; Zheng, X. Quantitative structure and spatial pattern optimization of urban green space from the perspective of carbon balance: A case study in Beijing, China. Ecol. Indic. 2023, 148, 110034. [Google Scholar] [CrossRef]
- Castro, C. Optimizing nature-based solutions by combining social equity, hydro-environmental performance, and economic costs through a novel Gini coefficient. J. Hydrol. X 2022, 16, 100127. [Google Scholar] [CrossRef]
- Yang, S.; Ruangpan, L.; Torres, A.S.; Vojinovic, Z. Multi-objective Optimisation Framework for Assessment of Trade-Offs between Benefits and Co-benefits of Nature-based Solutions. Water Resour. Manag. 2023, 37, 2325–2345. [Google Scholar] [CrossRef]
- Yang, G.; Best, E.P. Spatial optimization of watershed management practices for nitrogen load reduction using a modeling-optimization framework. J. Environ. Manag. 2015, 161, 252–260. [Google Scholar] [CrossRef] [PubMed]
- Feng, S.; Shen, J.; Sheng, S.; Hu, Z.; Wang, Y. Spatial Prioritizing Brownfields Catering for Green Infrastructure by Integrating Urban Demands and Site Attributes in a Metropolitan Area. Land 2023, 12, 802. [Google Scholar] [CrossRef]
- Bhakuni, P.; Das, A. An Innovative Algorithm-Driven Optimization Framework for Landfill Mining: Aiming Sustainable Profitability Expeditiously. IEEE Access 2023, 11, 122792–122820. [Google Scholar] [CrossRef]
- Hutahaean, J.; Demyanov, V.; Christie, M. Reservoir development optimization under uncertainty for infill well placement in brownfield redevelopment. J. Pet. Sci. Eng. 2019, 175, 444–464. [Google Scholar] [CrossRef]
- Seddon, N.; Smith, A.; Smith, P.; Key, I.; Chausson, A.; Girardin, C.; House, J.; Srivastava, S.; Turner, B. Getting the message right on nature-based solutions to climate change. Glob. Chang. Biol. 2021, 27, 1518–1546. [Google Scholar] [CrossRef]
- García, J.; Peña, A. Robust Optimization: Concepts and Applications. In Nature-Inspired Methods for Stochastic, Robust and Dynamic Optimization; Del Ser, J., Osaba, E., Eds.; IntechOpen: London, UK, 2018. [Google Scholar] [CrossRef]
- Meysami, R.; Niksokhan, M.H. Evaluating robustness of waste load allocation under climate change using multi-objective decision making. J. Hydrol. 2020, 588, 125091. [Google Scholar] [CrossRef]
- Wang, M.; Yu, H.; Jing, R.; Liu, H.; Chen, P.; Li, C. Combined multi-objective optimization and robustness analysis framework for building integrated energy system under uncertainty. Energy Convers. Manag. 2020, 208, 112589. [Google Scholar] [CrossRef]
- Alshehri, K.; Chen, I.-C.; Rugani, B.; Sapsford, D.; Harbottle, M.; Cleall, P. A novel uncertainty assessment protocol for integrated ecosystem services-life cycle assessments: A comparative case of nature-based solutions. Sustain. Prod. Consum. 2024, 47, 499–515. [Google Scholar] [CrossRef]
- Mišković, S.; Stanimirović, Z.; Grujičić, I. Solving the robust two-stage capacitated facility location problem with uncertain transportation costs. Optim. Lett. 2017, 11, 1169–1184. [Google Scholar] [CrossRef]
- Sayers, P.; Penning-Rowsell, E.C.; Horritt, M. Flood vulnerability, risk, and social disadvantage: Current and future patterns in the UK. Reg. Environ. Chang. 2018, 18, 339–352. [Google Scholar] [CrossRef]
- Mavrotas, G. Effective implementation of the ε-constraint method in Multi-Objective Mathematical Programming problems. Appl. Math. Comput. 2009, 213, 455–465. [Google Scholar] [CrossRef]
- Basirati, M.; Billot, R.; Meyer, P.; Bocher, E. Exact Zoning Optimization Model for Marine Spatial Planning (MSP). Front. Mar. Sci. 2021, 8, 726187. [Google Scholar] [CrossRef]
- Mavrotas, G.; Florios, K. An improved version of the augmented ε-constraint method (AUGMECON2) for finding the exact pareto set in multi-objective integer programming problems. Appl. Math. Comput. 2013, 219, 9652–9669. [Google Scholar] [CrossRef]
- Riley, A. Slag Composition Data for: Legacy Iron and Steel Wastes in the UK: Extent, Resource Potential, and Management Futures. Available online: https://data.mendeley.com/datasets/dzxx4wh75n/1 (accessed on 10 October 2023).
- Carey, M.A. Guidance on the Assessment and Monitoring of Natural Attentuation of Contaminants in Groundwater; Environment Agency: Bristol, UK, 2000. [Google Scholar]
- Johnson, D.B. Biomining—Biotechnologies for extracting and recovering metals from ores and waste materials. Curr. Opin. Biotechnol. 2014, 30, 24–31. [Google Scholar] [CrossRef]
- Johnson, D.B. The Evolution, Current Status, and Future Prospects of Using Biotechnologies in the Mineral Extraction and Metal Recovery Sectors. Minerals 2018, 8, 343. [Google Scholar] [CrossRef]
- Lusty, P.; Shaw, R.; Gunn, A.; Idoine, N. UK Criticality Assessment of Technology Critical Minerals and Metals; British Geological Survey: Nottingham, UK, 2021. [Google Scholar]
- European Commission. Directorate General for Internal Market, Industry, Entrepreneurship and SMEs. Study on the Critical Raw Materials for the EU 2023: Final Report. LU: Publications Office. 2023. Available online: https://data.europa.eu/doi/10.2873/725585 (accessed on 27 May 2024).
- Sigman, H. Environmental Liability and Redevelopment of Old Industrial Land. J. Law Econ. 2010, 53, 289–306. [Google Scholar] [CrossRef]
- UK Government. Brownfield Land Dataset|Planning Data. Available online: https://www.planning.data.gov.uk/dataset/brownfield-land (accessed on 21 May 2024).
- Schedules of Contractors Equipment, Rates for Use on Construction Contracts, Civil Engineering Contractors Association, London, 978-1-9161584-2-9. 2019. Available online: http://www.ceca.co.uk/ (accessed on 15 September 2023).
- Greenhouse Gas Reporting: Conversion Factors 2023. Available online: https://www.gov.uk/government/publications/greenhouse-gas-reporting-conversion-factors-2023 (accessed on 15 August 2023).
- Riley, A.L.; MacDonald, J.M.; Burke, I.T.; Renforth, P.; Jarvis, A.P.; Hudson-Edwards, K.A.; McKie, J.; Mayes, W.M. Legacy iron and steel wastes in the UK: Extent, resource potential, and management futures. J. Geochem. Explor. 2020, 219, 106630. [Google Scholar] [CrossRef]
- Raes, L.; Mittempergher, D.; Piaggio, M.; Siikamäki, J. Nature-Based Recovery Can Create Jobs, Deliver Growth and Provide Value for Nature; IUCN: Gland, Switzerland, 2021. [Google Scholar]
- Jorat, M.E.; Goddard, M.A.; Manning, P.; Lau, H.K.; Ngeow, S.; Sohi, S.P.; Manning, D.A. Passive CO2 removal in urban soils: Evidence from brownfield sites. Sci. Total. Environ. 2020, 703, 135573. [Google Scholar] [CrossRef]
- UK Critical Minerals Intelligence Centre. CMIC Web GIS Live. CMIC INTERACTIVE MAP. Available online: https://experience.arcgis.com/experience/6306721821554bbd8447802676695588 (accessed on 21 May 2024).
- The London Metal Exchange. LME Cobalt. Available online: https://www.lme.com/Metals/EV/LME-Cobalt (accessed on 12 January 2024).
- SMM Metal Market. Refined Cobalt Price Today|Historical Refined Cobalt Price Charts. Available online: https://www.metal.com/Cobalt/201102250375 (accessed on 12 January 2024).
- The London Metal Exchange. LME Nickel. Available online: https://www.lme.com/Metals/Non-ferrous/LME-Nickel (accessed on 12 January 2024).
- SMM Metal Market. Nickel Price Today|Historical Base Metals Price Charts. Available online: https://www.metal.com/price/Base%20Metals/Nickel (accessed on 12 January 2024).
- Boundary-LineTM [SHAPE Geospatial Data], Scale 1:10000’, Tiles: GB. Ordnance Survey (GB), Mar. 28, 2023. Available online: https://digimap.edina.ac.uk (accessed on 23 August 2023).
- OS Open Roads [SHAPE Geospatial Data], Scale 1:25000’, Tiles: Hp, ht, hu, hy, hz, na, nb, nc, nd, nf, ng, nh, nj, nk, nl, nm, nn, no, nr, ns, nt, nu, nw, nx, ny, nz, sd, se, sh, sj, sk, sm, sn, so, sp, sr, ss, st, su, sv, sw, sx, sy, sz, ta, tf, tg, tl, tm, tq, tr, tv. Ordnance Survey (GB), Apr. 21, 2023. Available online: https://digimap.edina.ac.uk (accessed on 21 August 2023).
- Valuation of Greenhouse Gas Emissions: For Policy Appraisal and Evaluation. Available online: https://www.gov.uk/government/publications/valuing-greenhouse-gas-emissions-in-policy-appraisal/valuation-of-greenhouse-gas-emissions-for-policy-appraisal-and-evaluation (accessed on 1 November 2023).
- Nikas, A.; Fountoulakis, A.; Forouli, A.; Doukas, H. A robust augmented ε-constraint method (AUGMECON-R) for finding exact solutions of multi-objective linear programming problems. Oper. Res. 2022, 22, 1291–1332. [Google Scholar] [CrossRef]
- Zitzler, E.; Thiele, L.; Laumanns, M.; Fonseca, C.; da Fonseca, V. Performance assessment of multiobjective optimizers: An analysis and review. IEEE Trans. Evol. Comput. 2003, 7, 117–132. [Google Scholar] [CrossRef]
- Basirati, M.; Billot, R.; Meyer, P. An Extension of NSGA-II for Scaling up Multi-objective Spatial Zoning Optimization. In Learning and Intelligent Optimization; Simos, D.E., Rasskazova, V.A., Archetti, F., Kotsireas, I.S., Pardalos, P.M., Eds.; Lecture Notes in Computer Science; Springer: Cham, Switzerland, 2022; Volume 13621, pp. 205–219. [Google Scholar] [CrossRef]
- Pătrăușanu, A.; Florea, A.; Neghină, M.; Dicoiu, A.; Chiș, R. A Systematic Review of Multi-Objective Evolutionary Algorithms Optimization Frameworks. Processes 2024, 12, 869. [Google Scholar] [CrossRef]
- Basirati, M.; Billot, R.; Meyer, P. Two parameter-tuned multi-objective evolutionary-based algorithms for zoning management in marine spatial planning. Ann. Math. Artif. Intell. 2023, 1–32. [Google Scholar] [CrossRef]
- Ishibuchi, H.; Imada, R.; Setoguchi, Y.; Nojima, Y. How to Specify a Reference Point in Hypervolume Calculation for Fair Performance Comparison. Evol. Comput. 2018, 26, 411–440. [Google Scholar] [CrossRef]
- Udías, A.; Efremov, R.; Cano, J. Methodological Review of Multicriteria Optimization Techniques: Aplications in Water Resources; Technical Report 2012.1; Centro de Servicios en Gestión de Información (CESGI): Buenos Aires, Argentina, 2012. [Google Scholar]
- Opricovic, S.; Tzeng, G.-H. Compromise solution by MCDM methods: A comparative analysis of VIKOR and TOPSIS. Eur. J. Oper. Res. 2004, 156, 445–455. [Google Scholar] [CrossRef]
- Štilić, A.; Puška, A. Integrating Multi-Criteria Decision-Making Methods with Sustainable Engineering: A Comprehensive Review of Current Practices. Eng 2023, 4, 1536–1549. [Google Scholar] [CrossRef]
- Hwang, C.-L.; Yoon, K. Multiple Attribute Decision Making: Methods and Applications a State-of-the-Art Survey; Springer Science & Business Media: Berlin, Germany, 2012; Volume 186. [Google Scholar]
- Brans, J.-P.; Vincke, P. A Preference Ranking Organisation Method: (The PROMETHEE Method for Multiple Criteria Decision-Making). Manag. Sci. 1985, 31, 647–656. [Google Scholar] [CrossRef]
- Monardes, V.; Sepúlveda, J.M. Multi-Criteria Analysis for Circular Economy Promotion in the Management of Tailings Dams: A Case Study. Minerals 2023, 13, 486. [Google Scholar] [CrossRef]
- Wismans, L.J.; Brands, T.; Van Berkum, E.C.; Bliemer, M.C. Pruning and ranking the Pareto optimal set, application for the dynamic multi-objective network design problem. J. Adv. Transp. 2014, 48, 588–607. [Google Scholar] [CrossRef]
- Spearman, C. The Proof and Measurement of Association between Two Things. Am. J. Psychol. 1904, 15, 72–101. [Google Scholar] [CrossRef]
- Kendall, M.G. A New Measure of Rank Correlation. Biometrika 1938, 30, 81. [Google Scholar] [CrossRef]
- Mitchell, S.; OSullivan, M.; Dunning, I. Pulp: A linear Programming Toolkit for Python; The University of Auckland: Auckland, New Zealand, 2011; Volume 65. [Google Scholar]
- Raffler, C. QNEAT3—QGIS Network Analysis Toolbox 3. GitHub. 2023. Available online: https://github.com/root676/QNEAT3 (accessed on 21 May 2024).
- IBM. ILOG CPLEX Optimization Studio V22.1: User’s Manual. 2019. Available online: https://www.ibm.com/docs/en/icos/12.9.0 (accessed on 21 May 2024).
- Virtanen, P.; Gommers, R.; Oliphant, T.E.; Haberland, M.; Reddy, T.; Cournapeau, D.; Burovski, E.; Peterson, P.; Weckesser, W.; Bright, J.; et al. SciPy 1.0 Contributors. SciPy 1.0 Fundamental Algorithms for Scientific Computing in Python. Nat. Methods 2020, 17, 261–272. [Google Scholar] [CrossRef]
- Kizielewicz, B.; Shekhovtsov, A.; Sałabun, W. pymcdm—The universal library for solving multi-criteria decision-making problems. SoftwareX 2023, 22, 101368. [Google Scholar] [CrossRef]
- Demir, I.; Ergin, F.C.; Kiraz, B. A New Model for the Multi-Objective Multiple Allocation Hub Network Design and Routing Problem. IEEE Access 2019, 7, 90678–90689. [Google Scholar] [CrossRef]
- Maadanpour Safari, F.; Etebari, F.; Pourghader Chobar, A. Modelling and optimization of a tri-objective Transportation-Location-Routing Problem considering route reliability: Using MOGWO, MOPSO, MOWCA and NSGA-II. J. Optim. Ind. Eng. 2021, 14, 83–98. [Google Scholar] [CrossRef]
- Li, P.; Qian, H.; Wu, J.; Chen, J. Sensitivity analysis of TOPSIS method in water quality assessment: I. Sensitivity to the parameter weights. Environ. Monit. Assess. 2013, 185, 2453–2461. [Google Scholar] [CrossRef]
- Genc, T. Sensitivity analysis on PROMETHEE and TOPSIS weights. Int. J. Manag. Decis. Mak. 2014, 13, 403. [Google Scholar] [CrossRef]
- Venkat, V.; Jacobson, S.H.; Stori, J.A. A Post-Optimality Analysis Algorithm for Multi-Objective Optimization. Comput. Optim. Appl. 2004, 28, 357–372. [Google Scholar] [CrossRef]
- Deb, K.; Jain, H. An Evolutionary Many-Objective Optimization Algorithm Using Reference-Point-Based Nondominated Sorting Approach, Part I: Solving Problems with Box Constraints. IEEE Trans. Evol. Comput. 2014, 18, 577–601. [Google Scholar] [CrossRef]
- Basirati, M. Zoning Management in Marine Spatial Planning: Multi-Objective Optimization and Agent-Based Conflict Resolution. Ph.D. Thesis, IMT Atlantique, Nantes, France, 2022. [Google Scholar]
- Raidl, G.R.; Puchinger, J.; Blum, C. Handbook of Metaheuristics. In International Series in Operations Research & Management Science; Springer: Cham, Switzerland, 2019; Volume 272. [Google Scholar]
- Kwatra, S.; Kumar, A.; Sharma, S.; Sharma, P. Stakeholder participation in prioritizing sustainability issues at regional level using analytic hierarchy process (AHP) technique: A case study of Goa, India. Environ. Sustain. Indic. 2021, 11, 100116. [Google Scholar] [CrossRef]
- Kibria, A.S.; Seekamp, E.; Xiao, X.; Dalyander, S.; Eaton, M. Multi-criteria decision approach for climate adaptation of cultural resources along the Atlantic coast of the southeastern United States: Application of AHP method. Clim. Risk Manag. 2024, 43, 100587. [Google Scholar] [CrossRef]
- Iacovidou, E.; Velis, C.A.; Purnell, P.; Zwirner, O.; Brown, A.; Hahladakis, J.; Millward-Hopkins, J.; Williams, P.T. Metrics for optimising the multi-dimensional value of resources recovered from waste in a circular economy: A critical review. J. Clean. Prod. 2017, 166, 910–938. [Google Scholar] [CrossRef]
- Greco, S.; Ishizaka, A.; Tasiou, M.; Torrisi, G. On the Methodological Framework of Composite Indices: A Review of the Issues of Weighting, Aggregation, and Robustness. Soc. Indic. Res. 2019, 141, 61–94. [Google Scholar] [CrossRef]
- Kahraman, C.; Ruan, D.; Dogan, I. Fuzzy group decision-making for facility location selection. Inf. Sci. 2003, 157, 135–153. [Google Scholar] [CrossRef]
- Anjum, M.; Min, H.; Ahmed, Z. Healthcare Waste Management through Multi-Stage Decision-Making for Sustainability Enhancement. Sustainability 2024, 16, 4872. [Google Scholar] [CrossRef]
- Yousefpour, R.; Temperli, C.; Jacobsen, J.B.; Thorsen, B.J.; Meilby, H.; Lexer, M.J.; Lindner, M.; Bugmann, H.; Borges, J.G.; Palma, J.H.N.; et al. A framework for modeling adaptive forest management and decision making under climate change. Ecol. Soc. 2017, 22, art40. [Google Scholar] [CrossRef]
- Bertsimas, D.; Goyal, V. On the Power of Robust Solutions in Two-Stage Stochastic and Adaptive Optimization Problems. Math. Oper. Res. 2010, 35, 284–305. [Google Scholar] [CrossRef]



| Resource | Grid Size | Objective | Mean | Std. Dev. | Min. | Max. | Range |
|---|---|---|---|---|---|---|---|
| CoO | 5 × 5 | Objective 1 | −7.97 × 106 | 1.57 × 107 | −3.31 × 107 | 1.57 × 107 | 4.88 × 107 |
| 5 × 5 | Objective 2 | 7.03 × 102 | 1.36 × 102 | 5.26 × 102 | 8.80 × 102 | 3.54 × 102 | |
| 5 × 5 | Objective 3 | −3.01 × 102 | 5.08 × 102 | −9.62 × 102 | 3.59 × 102 | 1.32 × 103 | |
| 7 × 7 | Objective 1 | −9.89 × 106 | 1.78 × 107 | −4.39 × 107 | 1.89 × 107 | 6.28 × 107 | |
| 7 × 7 | Objective 2 | 7.03 × 102 | 1.46 × 102 | 4.92× 102 | 9.14 × 102 | 4.21 × 102 | |
| 7 × 7 | Objective 3 | −3.01 × 102 | 5.45 × 102 | −1.09 × 103 | 4.85 × 102 | 1.57 × 103 | |
| 10 × 10 | Objective 1 | −1.25 × 107 | 2.21 × 107 | −6.48 × 107 | 2.08 × 107 | 8.56 × 107 | |
| 10 × 10 | Objective 2 | 7.03 × 102 | 1.53 × 102 | 4.67 × 102 | 9.39 × 102 | 4.72 × 102 | |
| 10 × 10 | Objective 3 | −3.01 × 102 | 5.72 × 102 | −1.18 × 103 | 5.79 × 102 | 1.76 × 103 | |
| 15 × 15 | Objective 1 | −1.97 × 107 | 4.00 × 107 | −1.47 × 108 | 2.23 × 107 | 1.69 × 107 | |
| 15 × 15 | Objective 2 | 7.03 × 102 | 1.59 × 102 | 4.47 × 102 | 9.59 × 102 | 5.11 × 102 | |
| 15 × 15 | Objective 3 | −3.75 × 102 | 5.51 × 102 | −1.26 × 103 | 5.06 × 102 | 1.76 × 103 | |
| 20 × 20 | Objective 1 | −1.15 × 107 | 2.10 × 107 | −6.51 × 107 | 2.26 × 107 | 8.77 × 107 | |
| 20 × 20 | Objective 2 | 7.03 × 102 | 1.62 × 102 | 4.38 × 102 | 9.69 × 102 | 5.31 × 102 | |
| 20 × 20 | Objective 3 | −3.56 × 102 | 5.08 × 102 | −1.18 × 103 | 4.69 × 102 | 1.65 × 103 | |
| 30 × 30 | Objective 1 | −1.67 × 107 | 3.33 × 107 | −1.47 × 108 | 2.28 × 107 | 1.70 × 108 | |
| 30 × 30 | Objective 2 | 7.03 × 102 | 1.65 × 102 | 4.28 × 102 | 9.78 × 102 | 5.51 × 102 | |
| 30 × 30 | Objective 3 | −4.11 × 102 | 5.08 × 102 | −1.26 × 103 | 4.33 × 102 | 1.69 × 103 |
| Resource | Grid Size | Objective | Mean | Std. Dev. | Min. | Max. | Range |
|---|---|---|---|---|---|---|---|
| NiO | 5 × 5 | Objective 1 | −5.30 × 106 | 1.57 × 107 | −3.03 × 107 | 1.83 × 107 | 4.85 × 107 |
| 5 × 5 | Objective 2 | 7.03 × 102 | 1.36 × 102 | 5.26 × 102 | 8.80 × 102 | 3.54 × 102 | |
| 5 × 5 | Objective 3 | −3.01 × 102 | 5.08 × 102 | −9.62 × 102 | 3.59 × 102 | 1.32 × 103 | |
| 7 × 7 | Objective 1 | −7.21 × 106 | 1.78 × 107 | −4.12 × 107 | 2.16 × 107 | 6.28 × 107 | |
| 7 × 7 | Objective 2 | 7.03 × 102 | 1.46 × 102 | 4.92 × 102 | 9.14 × 102 | 4.21 × 102 | |
| 7 × 7 | Objective 3 | −3.01 × 102 | 5.45 × 102 | −1.09 × 103 | 4.85 × 102 | 1.57 × 103 | |
| 10 × 10 | Objective 1 | −9.81 × 106 | 2.21 × 107 | −6.21 × 107 | 2.34 × 107 | 8.56 × 107 | |
| 10 × 10 | Objective 2 | 7.03 × 102 | 1.53 × 102 | 4.67 × 102 | 9.39 × 102 | 4.72 × 102 | |
| 10 × 10 | Objective 3 | −3.01 × 102 | 5.72 × 102 | −1.18 × 103 | 5.79 × 102 | 1.76 × 103 | |
| 15 × 15 | Objective 1 | −1.71 × 107 | 4.00 × 107 | −1.45 × 108 | 2.49 × 107 | 1.70 × 108 | |
| 15 × 15 | Objective 2 | 7.03 × 102 | 1.59 × 102 | 4.47 × 102 | 9.59 × 102 | 5.11 × 102 | |
| 15 × 15 | Objective 3 | −3.75 × 102 | 5.51 × 102 | −1.26 × 103 | 5.06 × 102 | 1.76 × 103 | |
| 20 × 20 | Objective 1 | −8.80 × 106 | 2.10 × 107 | −6.24 × 107 | 2.53 × 107 | 8.77 × 107 | |
| 20 × 20 | Objective 2 | 7.03 × 102 | 1.62 × 102 | 4.38 × 102 | 9.69 × 102 | 5.31 × 102 | |
| 20 × 20 | Objective 3 | −3.56 × 102 | 5.08 × 102 | −1.18 × 103 | 4.69 × 102 | 1.65 × 103 | |
| 30 × 30 | Objective 1 | −1.40 × 107 | 3.32 × 107 | −1.45 × 108 | 2.55 × 107 | 1.70 × 108 | |
| 30 × 30 | Objective 2 | 7.03 × 102 | 1.65 × 102 | 4.28 × 102 | 9.78 × 102 | 5.51 × 102 | |
| 30 × 30 | Objective 3 | −4.11 × 102 | 5.08 × 102 | −1.26 × 103 | 4.33 × 102 | 1.69 × 103 |
| Grid Size | ||||||
|---|---|---|---|---|---|---|
| CoO | 5 × 5 | 7 × 7 | 10 × 10 | 15 × 15 | 20 × 20 | 30 × 30 |
| Optimal solutions | 16 | 36 | 81 | 182 | 304 | 696 |
| Infeasibilities | 4 | 6 | 9 | 14 | 38 | 58 |
| Skipped solutions | 5 | 7 | 10 | 29 | 58 | 146 |
| Hypervolume | 9.279 × 1015 | 1.083 × 1016 | 1.248 × 1016 | 1.423 × 1016 | 1.482 × 1016 | 2.088 × 1016 |
| Solution time (s) | 1324 | 2468 | 5220 | 11,754 | 14,368 | 47,881 |
| NiO | 5 × 5 | 7 × 7 | 10 × 10 | 15 × 15 | 20 × 20 | 30 × 30 |
| Feasible solutions | 16 | 36 | 81 | 182 | 304 | 696 |
| Infeasibilities | 4 | 6 | 9 | 14 | 38 | 58 |
| Skipped solutions | 5 | 7 | 10 | 29 | 58 | 146 |
| Hypervolume | 9.366 × 1015 | 1.093 × 1016 | 1.259 × 1016 | 1.435 × 1016 | 1.482 × 1016 | 2.100 × 1016 |
| Solution time (s) | 1006 | 3019 | 5574 | 12,927 | 14,086 | 32,403 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Alshehri, K.; Basirati, M.; Sapsford, D.; Harbottle, M.; Cleall, P. Nature-Based Secondary Resource Recovery under Climate Change Uncertainty: A Robust Multi-Objective Optimisation Methodology. Sustainability 2024, 16, 7220. https://doi.org/10.3390/su16167220
Alshehri K, Basirati M, Sapsford D, Harbottle M, Cleall P. Nature-Based Secondary Resource Recovery under Climate Change Uncertainty: A Robust Multi-Objective Optimisation Methodology. Sustainability. 2024; 16(16):7220. https://doi.org/10.3390/su16167220
Chicago/Turabian StyleAlshehri, Khaled, Mohadese Basirati, Devin Sapsford, Michael Harbottle, and Peter Cleall. 2024. "Nature-Based Secondary Resource Recovery under Climate Change Uncertainty: A Robust Multi-Objective Optimisation Methodology" Sustainability 16, no. 16: 7220. https://doi.org/10.3390/su16167220
APA StyleAlshehri, K., Basirati, M., Sapsford, D., Harbottle, M., & Cleall, P. (2024). Nature-Based Secondary Resource Recovery under Climate Change Uncertainty: A Robust Multi-Objective Optimisation Methodology. Sustainability, 16(16), 7220. https://doi.org/10.3390/su16167220






