A Cooperative Game Approach for Optimal Design of Shared Energy Storage System

Abstract

The energy sector’s long-term sustainability increasingly relies on widespread renewable energy generation. Shared energy storage embodies sharing economy principles within the storage industry. This approach allows storage facilities to monetize unused capacity by offering it to users, generating additional revenue for providers, and supporting renewable energy prosumers’ growth. However, high investment costs and long payback periods often hinder the development of battery storage. To address this challenge, we propose a shared storage investment framework. In this framework, a storage investor virtualizes physical storage equipment, enabling prosumers to access storage services as though they owned the batteries themselves. We adopt a cooperative game approach to incorporate storage sharing into the design phase of energy systems. To ensure a fair distribution of cooperative benefits, we introduce a benefit allocation mechanism based on contributions to energy storage sharing. Utilizing realistic data from three buildings, our simulations demonstrate that the shared storage mechanism creates a win–win situation for all participants. It also enhances the self-sufficiency and self-consumption of renewable energy. This paper provides valuable insights for shared storage investors regarding optimal design and benefit allocation among multiple stakeholders.

1. Introduction

The implementation of China’s ambitious “dual carbon” goals has catalyzed a substantial increase in the deployment of distributed renewable energy systems within the framework of the emerging power infrastructure [1]. There has been a significant increase in renewable energy systems operating as prosumers within local communities, such as microgrids, in the pursuit of a low-carbon society [2]. These systems, which both consume and produce energy, are emerging as pivotal elements in the energy transition towards low-carbon and sustainable paradigms [3]. Despite the numerous advantages of renewable energy sources, their inherent variability and intermittency pose significant challenges to the stability and reliability of community power systems [4,5]. In response to these challenges, the concept of shared energy storage has emerged as a promising approach, leveraging the principles of the sharing economy to provide crucial support for renewable energy development. It effectively mitigates the temporal and spatial imbalances between stochastic power generation and consumption in communities, and it capitalizes on the fact that the net loads of multiple prosumers can differ at the same time [6,7]. In light of the Chinese government’s strong policy support for both energy storage and renewable energy development, coupled with the demonstrated advantages of the sharing economy model, there is a pressing need for comprehensive research into the planning and operation of shared storage systems in community settings [8,9].

The operational intricacies of shared energy storage systems have garnered substantial scholarly interest within the domain of energy storage sharing [10]. Researchers typically approach the management of these systems by formulating it as an optimization problem, which is generally categorized as either single-level or bi-level in nature [11,12]. In the case of bi-level structures, researchers often employ the alternating direction multiplier method to address the intricate interactions between different levels [13]. Game theory has emerged as a powerful alternative framework for analyzing storage-sharing dynamics among multiple stakeholders [14]. For instance, Modified auction-based methods have been proposed to examine storage ownership sharing between multiple shared facility controllers and residents [15]. A periodically organized auction mechanism has been developed to allocate shared storage resources among various market players and their associated applications [16]. Drawing inspiration from the sharing economy model, researchers have introduced the concept of an energy bank system. This system serves as a trading platform for multiple microgrids and energy storage devices, utilizing a call-auction method for energy sharing [17]. In auction-based mechanisms, participants can place single bids or combinations of bids called packages [18]. Furthermore, coalitional game theory has been applied to investigate the potential benefits of power systems where end-users share storage resources. These studies have demonstrated the effectiveness of cooperative storage sharing in enhancing overall system performance [19]. To optimize the utilization of shared storage, researchers have proposed an energy capacity trading and operation game. This approach aims to minimize energy operation costs by allowing each participant to determine capacity trading and day-ahead charging–discharging profiles based on their assigned capacity [20]. While the existing literature has made significant strides in addressing the optimal operation of shared storage systems, there is a notable gap in research concerning the investment planning of energy storage facilities. This oversight is particularly significant given that effective planning for shared energy storage is crucial for achieving optimal economic performance during the operational stage.

The rapid proliferation of renewable energy systems has underscored the critical importance of designing robust energy storage systems capable of managing high penetrations of variable renewable energy generation [21]. Conventional planning models typically encompass installation, operation, and maintenance costs [22] while also incorporating scenarios such as ancillary services participation [23], demand response mechanisms [24], and network reconfiguration strategies [25]. However, there remains a notable paucity of research addressing the investment planning of shared storage. In the context of shared storage design, two primary cooperation frameworks have emerged: one where end-users individually invest in battery storage and share their unused capacities within the community [26], and another where a third-party investor installs the storage and interacts with prosumers [27]. The latter framework involves a third-party investor coordinating storage information to implement energy storage sharing within the community. An investment decision model under this framework analyzes sizing strategies for shared storage systems and energy trading behaviors among participants, with the Nash bargaining solution method allocating collective benefits [28]. Furthermore, a Stackelberg game-theoretic approach embedded in the shared storage planning model has been proposed, considering storage sharing among energy prosumers at the design phase, with the storage investor as the leader and energy prosumers as followers [29]. Focusing on the role of community storage systems, a cooperative game model is developed to study the investment cost sharing among consumers who invest in the storage [30]. The cost sharing is based on three factors: investment cost, the correlation coefficient between consumer i and others, and the variance of energy deviation. Despite the exploration of shared storage planning in existing literature, little literature focus on cooperative game theory, which integrates local supply and demand resources to maximize social welfare, the primary concern of sharing participants.

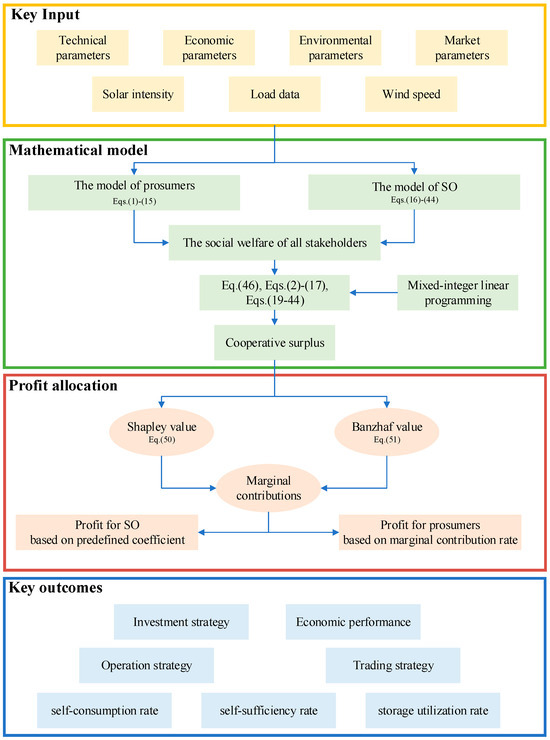
In light of these research gaps, two key challenges emerge: (1) Optimizing the investment strategy of shared storage systems by effectively coordinating prosumer resources; (2) developing a fair and efficient method for allocating the cooperative surplus of the shared storage mechanism among participants. To address these challenges, this paper optimizes the design strategy of shared storage systems among prosumers with renewable generators in community settings while ensuring equitable profit allocation. The proposed storage capacity sharing mechanism coordinates economic interactions among stakeholders and balances participant interests, providing valuable guidelines for managers to allocate cooperative surplus among sharing participants.

The main contributions of this paper are two-fold:

(1) Development of a comprehensive demand-side storage sharing framework that encompasses both the investment model and profit allocation method for shared energy storage systems, designed to maximize resource utilization efficiency;

(2) Application of cooperative game theory to the planning of shared energy storage, with the introduction of the Shapley value and Banzhaf value to evaluate each participant’s contribution to storage sharing. The proposed approach ensures a realistic and cost-effective maximization of resource utilization.

The structure of this paper is organized as follows. Section 2 introduces the storage-sharing framework. Section 3 establishes the mathematical models for prosumers and the storage investor. Section 4 develops the benefit allocation scheme for storage sharing among the investors and prosumers. Section 5 presents a case study as an illustrative example of the proposed framework. Section 6 summarizes the main findings and draws conclusions.

2. Storage Sharing Framework

In community-based energy systems, prosumers typically employ grid-connected renewable energy systems without integrated storage capabilities. These prosumers can purchase electricity from the utility grid and export excess power back to it. However, to maximize renewable energy utilization and further reduce costs, prosumers are increasingly incentivized to invest in storage technologies.

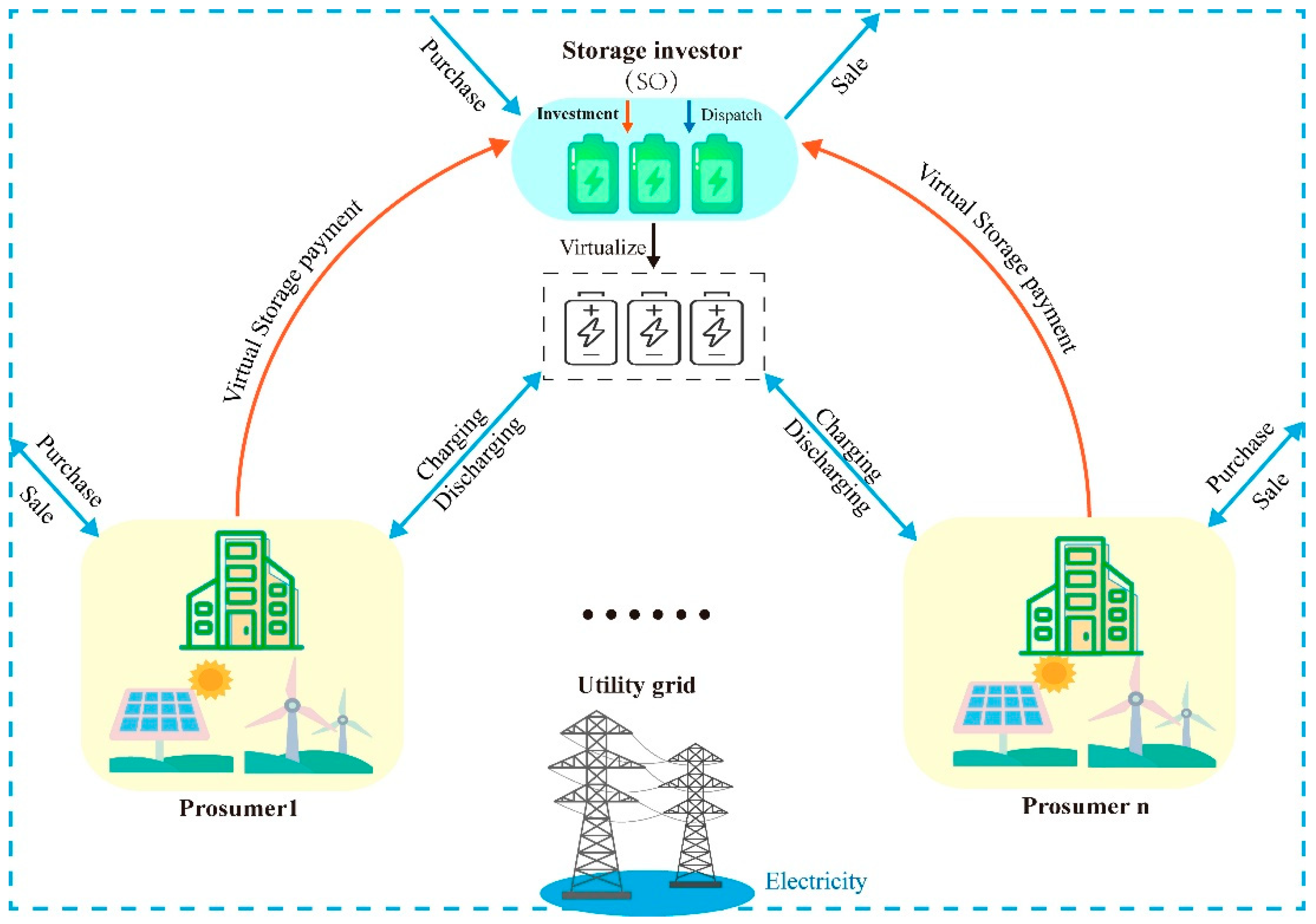
This paper examines two distinct models for energy storage investment within a community setting. (1) Individual Storage Mode: in this model, individual prosumers invest in their own battery ESS for exclusive personal use. This approach allows for a degree of decoupling between supply and demand, thereby enhancing energy system flexibility. The individual mode serves as the baseline for comparison in this study. (2) Shared Storage Mode: this mode introduces the concept of storage capacity sharing as a service provided by a third-party investor, referred to as the Storage Operator (SO), as illustrated in Figure 1. The SO invests in and operates the shared storage. The shared energy storage mode is characterized by the following key features. (a) Contractual agreement: The SO and prosumers enter into a contractual arrangement wherein prosumers purchase capacities from the SO. (b) Virtual storage service: The SO manages a shared ESS, offering charging and discharging services to all energy prosumers who signed the contract. This service is essentially virtual, not solely dependent on a physical storage system. (c) Complementary behavior exploitation: The SO capitalizes on the complementary charging and discharging behaviors among all prosumers, arising from their varying renewable generation and load curves, to offset a portion of the storage demands. (d) Grid interaction: The SO engages in real-time electricity trading with the grid to provide storage services when the prosumers’ total charging or discharging requirements exceed the physical storage capacity. (e) Virtual capacity: The SO does not need to own all the storage capacity it sells to prosumers; it just needs to satisfy the charging and discharging schedules of prosumers, effectively making the storage virtually shared.

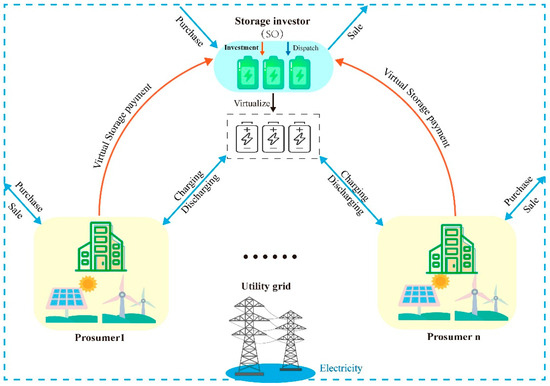
Figure 1. System structure of shared energy storage mode.

Despite the virtual nature of the storage service, prosumers can perform real-time charging and discharging operations as if using actual batteries without compromising their comfort. The shared storage mode offers several advantages over the personal energy storage mode. (a) Economic efficiency: The SO creates profit margins by leveraging both the discrepancy between real and virtual storage capacities and market price variations. (b) Win–Win scenario: The shared model creates a mutually beneficial situation for both the SO and prosumers.

The establishment of the storage-sharing mode necessitates the development of an appropriate profit allocation mechanism. To address this critical aspect and balance individual and collective interests, we employ cooperative game theory to design a fair and efficient profit allocation mechanism. This approach not only optimizes the economic benefits for all participants but also ensures the long-term sustainability of the shared energy storage model. By leveraging cooperative game theory, we can account for the diverse contributions and needs of each participant, fostering a more equitable and robust energy-sharing ecosystem.

The subsequent sections of this paper will delve into the mathematical formulation of this model, the specific allocation mechanisms derived from cooperative game theory, and a case study demonstrating the practical implications of this innovative approach to community energy storage.

3. Mathematical Model for Shared Storage Framework

3.1. The Prosumers Model

This study aims to elucidate the investment strategy and economic performance associated with shared energy storage systems. Our analysis is based on the assumption that prosumers have installed renewable generation devices, thereby excluding the investment costs of these systems from our considerations. Within this framework of shared storage, the primary objective for individual prosumers is to minimize their overall costs. These costs can be categorized into three main components: virtual storage purchase cost, grid trading cost, and carbon tax. The mathematical formulation is expressed as follows:

$$\min C_i^{ses,pro}={\pi }_i^{ses,buy}+C_i^{ses,Grid}+C_i^{ses,carbon} \forall i\in I$$

(1)

where $C_i^{ses,pro}$ is the overall cost of prosumer $i$. ${\pi }_i^{ses,buy}$ represents the shared storage buying cost paid to the SO. The cost, ${\pi }_i^{ses,buy}\ge 0$, will be described in the benefit allocation scheme in Section 4.

Prosumers have the flexibility to engage in electricity trading with the municipal power grid. This trading activity incurs costs or generates revenue, depending on whether electricity is purchased from or sold to the grid. We can represent the net trade cost with the utility grid, denoted as $C_i^{ses,Grid}$, using the following Equation:

$$C_i^{ses,Grid}={\displaystyle \sum _{t\in T}\left({\lambda }_t^{gb}{P}_{i,t}^{ses,gb}-{\lambda }_t^{gs}{P}_{i,t}^{ses,gs}\right)} \forall i\in I$$

(2)

where $P_{i,t}^{ses,gb}$ is the electricity quantity purchased from the grid, $P_{i,t}^{ses,gs}$ is the electricity sold to the grid. ${\lambda }_t^{gb}$ denotes the retail price set by the grid for electricity purchases, ${\lambda }_t^{gs}$ is the feed-in tariff offered by the grid for electricity sales.

Additionally, the environmental impact should be considered, specifically in terms of carbon emissions. The cost associated with these emissions is calculated based on three factors: the amount of electricity purchased from the grid, the CO₂ emission factor of grid electricity, and the applicable carbon tax. The carbon emission cost, $C_i^{ses,carbon}$, for a prosumer i as follows:

$$C_i^{ses,carbon}=c^{carbon}\beta {\displaystyle \sum _{t\in T}{P}_{i,t}^{ses,gb}} \forall i\in I$$

(3)

where $\beta$ represents the carbon emission factor of the municipal power grid and $c^{carbon}$ is the carbon tax rate.

Renewable energy systems include solar photovoltaic (PV) systems and wind power generation systems.

$$P_{i,t}^{pv}={\eta }_i^{pv}{N}_i^{pv}{E}_i^{pv}{\displaystyle \frac{I_t}{I^{stc}}}\left(1+0.005\times \left(T{c}_t-25\right)\right) \forall i\in I,t\in T$$

(4)

$$P_{i,t}^{wind}=\left\{\begin{array}{ll}0& 0\le v_t\le v_{in}\\ P_i^{wind}\cdot {\displaystyle \frac{v_t-v_{in}}{v_r-v_{in}}}& v_{in} \le v_t\le v_r\\ P_i^{wind}& v_r \le v_t\le v_{out}\\ 0& v_t \ge v_{out}\end{array}\right. \forall i\in I,t\in T$$

(5)

where $I_t$ denotes the intensity of solar radiation at time $t$, $P_{i,t}^{pv}$ is the PV’s output power, ${\eta }_i^{pv}$ is the conversion efficiency of PV inverter, $N_i^{pv}$ is the number of PV panels, $E_i^{pv}$ is the rated power of one PV panel, $I^{stc}$ represents the intensity of solar irradiation at standard test conditions, $T{c}_t$ is the ambient temperature. $v_t$ is the wind speed at time $t$, $P_{i,t}^{wind}$ is the electricity output of wind power systems, $P_i^{wind}$ is the rated capacity, $v_{in}$ and $v_{out}$ are the cut-in speed and cut-out speed, $v_r$ is the rated wind speed.

As outlined in the previous section, the storage acquired by prosumers is virtual in nature. This virtualization of storage resources introduces a novel paradigm in energy management, wherein prosumers are liberated from the technical complexities associated with physical storage systems. Specifically, when formulating their operational strategies, prosumers need not account for charging and discharging efficiencies or the specific technological constraints of physical storage systems. To ensure effective management of prosumers’ charging and discharging behaviors within this virtual framework, the SO must establish clear operational parameters: the bounds and initial values of the state of charge (SOC). The operational constraints are delineated as follows:

$$E_{i,t}^{ses}=E_{i,t-1}^{ses}+\Delta t\left(P_{i,t}^{ses,ch}-P_{i,t}^{ses,dch}\right) \forall i\in I,t\in T$$

(6)

$$E_i^{\min }\le E_{i,t}^{ses}\le E_i^{\max } \forall i\in I,t\in T$$

(7)

$$E_i^{\min }=SO{C}^{\min }{E}_{i,so}^{ses,cap} \forall i\in I$$

(8)

$$E_i^{\max }=SO{C}^{\max }{E}_{i,so}^{ses,cap} \forall i\in I$$

(9)

$$E_{i,0}^{ses}=SO{C}^0{E}_{i,so}^{ses,cap} \forall i\in I$$

(10)

$$E_{i,T}^{ses}=E_{i,0}^{ses} \forall i\in I$$

(11)

$$P_{i,t}^{ses,ch}\le {\alpha }_{i,t}^{ses,ch}{P}_{i,so}^{ses,cap} \forall i\in I,t\in T$$

(12)

$$P_{i,t}^{ses,dch}\le {\alpha }_{i,t}^{ses,dch}{P}_{i,so}^{ses,cap} \forall i\in I,t\in T$$

(13)

$${\alpha }_{i,t}^{ses,dch}+{\alpha }_{i,t}^{ses,ch}\le 1 \forall i\in I,t\in T$$

(14)

where $E_{i,t}^{ses}$ is the virtual storage level. $E_{i,0}^{ses}$ is the initial level of virtual battery storage. $E_i^{\min }$ and $E_i^{\max }$ are the lower and upper bounds of the storage level. $SO{C}^{\min }$ and $SO{C}^{\max }$ are the bounds and $SO{C}^0$ represents the initial value of the state of charge. $E_{i,so}^{ses,cap}$ and $P_{i,so}^{ses,cap}$ denote the virtual energy and power capacity bought from the SO. ${\alpha }_{i,t}^{ses,ch}$ and ${\alpha }_{i,t}^{ses,dch}$ are binary variables.

Equation (15) is built to balance the energy supply and demand:

$$P_{i,t}^{pv}+P_{i,t}^{wind}+P_{i,t}^{ses,gb}-P_{i,t}^{ses,gs}+P_{i,t}^{ses,dch}-P_{i,t}^{ses,ch}=P_{i,t}^{load} \forall i\in I,t\in T$$

(15)

where $P_{i,t}^{load}$ is the electrical load. $P_{i,t}^{ses,gb}$ and $P_{i,t}^{ses,gs}$ are the purchased electricity and sold electricity of the prosumer $i$ while trading with the utility grid.

3.2. The Shared Storage Model

The SO plays a crucial role in the energy ecosystem, responsible for both the investment in and operation of the physical storage infrastructure that supports virtual storage services. The SO’s primary goal is to optimize its financial position by minimizing total costs, which effectively maximizes profit. This optimization process involves balancing several key economic factors. (1) Capital Expenditure: The upfront investment required for the physical storage system. (2) Operational Expenses: Ongoing costs associated with running and maintaining the storage infrastructure. (3) Grid Interaction Costs: Financial implications of electricity trading with the municipal grid. (4) Environmental Impact: Expenses related to carbon emissions, often in the form of taxes or penalties. It is crucial to understand that the SO’s revenue model is primarily built around the sale of virtual storage capacity to prosumers. This creates a symbiotic economic relationship between the SO and its prosumer clients. Thus, the objective function of SO can be built as follows:

$$\min C_{so}^{ses}=C_{so}^{ses,inv}+C_{so}^{ses,OM}+C_{so}^{ses,Grid}+C_{so}^{ses,carbon} +{\displaystyle \sum _{i\in I}{\pi }_i^{ses,sell}}$$

(16)

where $C_{so}^{ses}$ is the overall cost of SO, ${\pi }_i^{ses,sell}$ represents the selling cost, ${\pi }_i^{ses,sell}\le 0$ and ${\pi }_i^{ses,sell}+{\pi }_i^{ses,buy}=0$.

The investment cost of the shared storage comprises the energy and power capacity costs. It is important to note that the unit costs for batteries and inverters are typically provided over their respective lifetimes. Since this paper employs an annual planning model, it is vital to convert these costs to annual values. Therefore, the cost of investing in shared storage, $C_{so}^{ses,inv}$, can be expressed as follows:

$$C_{so}^{ces,inv}={\displaystyle \frac{r}{1-{\left(1+r\right)}^{-l_y}}}{c}^{einv}{E}_{so}^{ses,cap}+{\displaystyle \frac{r}{1-{\left(1+r\right)}^{-l_x}}}{c}^{pinv}{P}_{so}^{ses,cap}$$

(17)

where $c^{einv}$ and $c^{pinv}$ denote the unit battery investment cost and unit inverter investment cost, $r$ denotes the discount rate, $E_{so}^{ses,cap}$ and $P_{so}^{ses,cap}$ are the battery capacity and inverter capacity, $l_y$ and $l_x$ represent the lifetime.

The optimal configuration of the energy storage is optimized according to the existing capacity ($E$ and $P$). Thus, $E_{so}^{ses,cap}$ and $P_{so}^{ses,cap}$ are constrained by Equation (18) and Equation (19), respectively.

$$E_{so}^{ses,cap}=M_{so}E$$

(18)

$$P_{so}^{ses,cap}=N_{so}P$$

(19)

where $M_{so}$ and $N_{so}$ are the number of the battery and inverter.

The mathematical expression of the physical storage O&M cost ($C_{so}^{ses,OM}$) is as follows:

$$C_{so}^{ses,OM}={\displaystyle \sum _{t\in T}{c}^{OM}\left(P_{so,t}^{ses,ch}+P_{so,t}^{ses,dch}\right)}$$

(20)

where $c^{OM}$ is the unit cost for O&M, $P_{so,t}^{ses,ch}$ and $P_{so,t}^{ses,dch}$ are the SO’s charging and discharging schedules.

The SO has the flexibility to interact with the utility power grid when the physical storage capacity is insufficient to meet the aggregate charge or discharge demands of the prosumers. This interaction involves buying from or selling electricity to the grid, resulting in a trading cost ($C_{so}^{ses,Grid}$) that can be quantified using the following Equation:

$$C_{so}^{ses,Grid}={\displaystyle \sum _{t\in T}\left({\lambda }_t^{gb}{P}_{so,t}^{ses,gb}-{\lambda }_t^{gs}{P}_{so,t}^{ses,gs}\right)}$$

(21)

where $P_{so,t}^{ses,gb}$ and $P_{so,t}^{ses,gs}$ are electricity purchased from grid and sold back to the power grid.

Additionally, the SO must account for the environmental impact of these grid interactions. The carbon emission cost ($C_{so}^{ses,carbon}$) associated with the SO’s operations can be expressed as follows:

$$C_{so}^{ses,carbon}=c^{carbon}\beta {\displaystyle \sum _{t\in T}{P}_{so,t}^{ses,gb}}$$

(22)

A key responsibility of the SO is to manage the overall charging and discharging schedules for all prosumers. This decision-making process is informed by the individual charging and discharging profiles submitted by each prosumer. The SO meets the prosumers’ charging and discharging demands by optimizing the investment and grid trade strategies. The SO can reduce the cost by rationally utilizing shared storage and taking advantage of time-of-use electricity pricing schemes. The detailed constraints are as follows:

$$P{s}_t^{ch}={\left[{\displaystyle \sum _{i\in I}{P}_{i,t}^{ses,ch}-{\displaystyle \sum _{i\in I}{P}_{i,t}^{ses,dch}}}\right]}^{+} \forall t\in T$$

(23)

$$P{s}_t^{dch}={\left[{\displaystyle \sum _{i\in I}{P}_{i,t}^{ses,dch}-{\displaystyle \sum _{i\in I}{P}_{i,t}^{ses,ch}}}\right]}^{+} \forall t\in T$$

(24)

$$P{s}_t^{ch}=P_{so,t}^{ses,ch}+P_{so,t}^{ses,gs}-P_{so,t}^{ses,dch}-P_{so,t}^{ses,gb} \forall t\in T$$

(25)

$$P{s}_t^{dch}=P_{so,t}^{ses,dch}+P_{so,t}^{ses,gb}-P_{so,t}^{ses,ch}-P_{so,t}^{ses,gs} \forall t\in T$$

(26)

$$0\le P_{so,t}^{ses,ch}\le {\alpha }_{so,t}^{ses,ch}M \forall t\in T$$

(27)

$$0\le P_{so,t}^{ses,dch}\le {\alpha }_{so,t}^{ses,dch}M \forall t\in T$$

(28)

$${\alpha }_{so,t}^{ses,ch}+{\alpha }_{so,t}^{ses,dch}\le 1$$

(29)

$$0\le P_{so,t}^{ses,gb}\le {\alpha }_{so,t}^{ses,gb}M \forall t\in T$$

(30)

$$0\le P_{so,t}^{ses,gs}\le {\alpha }_{so,t}^{ses,gs}M \forall t\in T$$

(31)

$${\alpha }_{so,t}^{ses,gb}+{\alpha }_{so,t}^{ses,gs}\le 1$$

(32)

where ${\left[f\right]}^{+}=\max \left(f,0\right)$, $P{s}_t^{ch}$ is the net charging power, $P{s}_t^{dch}$ is the net discharging electricity, $P_{so,t}^{ses,dch}$ and $P_{so,t}^{ses,ch}$ denote the discharging and charging behavior of shared storage. ${\alpha }_{so,t}^{ses,ch}$ and ${\alpha }_{so,t}^{ses,gb}$ are binary variables used to prevent simultaneous charging/discharging and purchasing/selling of electricity.

The physical storage is mainly limited by the following:

$$E_{so,t}^{ses}=E_{so,t-1}^{ses}+\Delta t\left({\eta }^c{P}_{so,t}^{ses,ch}-P_{so,t}^{ses,dch}/{\eta }^d\right) \forall t\in T$$

(33)

$$E_{so}^{\min }\le E_{so,t}^{ses}\le E_{so}^{\max } \forall t\in T$$

(34)

$$E_{so}^{\min }=SO{C}^{\min }{E}_{so}^{ses,cap}$$

(35)

$$E_{so}^{\max }=SO{C}^{\max }{E}_{so}^{ses,cap}$$

(36)

$$E_{so,0}^{ses}=SO{C}^0{E}_{so}^{ses,cap}$$

(37)

$$E_{so,t}^{ses}={\displaystyle \sum E_{so,t}^{ses}} \forall t\in T$$

(38)

$$E_{so,T}^{ses}=E_{so,0}^{ses}$$

(39)

$$0\le P_{so,t}^{ses,ch}\le P_{so}^{ses,cap} \forall t\in T$$

(40)

$$0\le P_{so,t}^{ses,dch}\le P_{so}^{ses,cap} \forall t\in T$$

(41)

$$P_{so,t}^{ses,ch}\le {\alpha }_{so,t}^{ses,ch}M \forall t\in T$$

(42)

$$P_{so,t}^{ses,dch}\le {\alpha }_{so,t}^{ses,dch}M \forall t\in T$$

(43)

$${\alpha }_{so,t}^{ses,ch}+{\alpha }_{so,t}^{ses,dch}\le 1 \forall t\in T$$

(44)

where $E_{so,t}^{ses}$ is the storage level, ${\eta }^c,{\eta }^d$ are the charging/discharging efficiency. $E_{so}^{\max }$ and $E_{so}^{\min }$ are the maximum and minimum storage levels. $SO{C}^0$, ${SOC}^{\min }$, and ${SOC}^{\max }$ are the initial SOC, the lower bound of SOC, and the upper bound of SOC, respectively. $E_{so,t}^{ses}$ and $E_{so,0}^{ses}$ represent the storage level and initial storage level of batteries. ${\alpha }_{so,t}^{ses,ch}$ and ${\alpha }_{so,t}^{ses,dch}$ denote binary variables.

4. Benefit Allocation Scheme for Shared Storage

This scheme is proposed for the optimal coordination of supply, demand, and storage resources at the district level. Central to this approach is the presence of an independent system operator, envisioned as a nonprofit entity, which assumes a supervisory role in system operations and benefit allocation. This model acknowledges the diverse array of stakeholders, each representing distinct interest groups, and ingeniously consolidates their varied objectives and constraints into a unified, centralized optimization problem. The primary aim of this scheme is to maximize the integration of all available resources, thereby optimizing overall system profit under the aegis of fair contracts mutually agreed upon by all stakeholders. In the context of increasingly distributed energy landscapes, particularly those dominated by renewable energy sources, this approach is pivotal in ensuring the effective utilization of all distributed energy resources.

At the core of this framework lies the concept of full cooperation, which harnesses the synergistic potential of collaboration among key actors in the energy system. Under this coordination scheme, the objective function is articulated in terms of social welfare—a metric defined as the aggregate willingness-to-pay of all stakeholders involved. This holistic approach transcends individual profit motives, aligning the system’s operation with broader societal benefits.

$$\begin{array}{l}S{C}^{ses}=\min \left({\displaystyle \sum _{i\in I}{C}_i^{ses,pro}}+C_{so}^{ses}\right) \\ ={\displaystyle \sum _{i\in I}\left({\pi }_i^{ses,buy}+C_i^{ses,Grid}+C_i^{ses,carbon}\right)}+\\ C_{so}^{ses,inv}+C_{so}^{ses,OM}+C_{so}^{ses,Grid}+C_{so}^{ses,carbon} +{\displaystyle \sum _{i\in I}{\pi }_i^{ses,sell}}\end{array}$$

(45)

where $S{C}^{ses}$ is the social cost. Due to ${\pi }_i^{ses,sell}+{\pi }_i^{ses,buy}=0$, the social cost can also be expressed as follows:

$$S{C}^{ses}=\min \left(\begin{array}{l}{\displaystyle \sum _{i\in I}\left(C_i^{ses,Grid}+C_i^{ses,carbon}\right)}+\\ C_{so}^{ses,inv}+C_{so}^{ses,OM}+C_{so}^{ses,Grid}+C_{so}^{ses,carbon}\end{array}\right)$$

(46)

Subject to Equations (2)–(17), Equations (19)–(44).

After optimization, the social welfare of the cooperative community is determined. Stable and sustainable cooperation hinges on a fair profit allocation plan. To develop the trading structure within the district, we introduce the concept of a cooperative game. Without shared storage, there would be no energy interactions among the prosumers, meaning prosumers could only buy or sell electricity to the municipal power grid without trading with each other.

In a cooperative framework, the core represents a set of stable payoff distributions where no stakeholder has the incentive to leave the coalition, and no coalition can improve its situation by changing the actions of its members. Let $N=\left\{1,2,\dots ,n\right\}$ denote the set of players, and let a coalition $S\subset N$ represent a subset of N. $C=\left\{c_1,c_2,\dots ,c_n\right\}$ is a payoff vector related to profit allocation under a cooperative coalition. For a coalition to be stable, it must satisfy individual, group, and subgroup rationalities. Therefore, the following constraints are strictly enforced:

$$c_j\ge v\left(\left\{j\right\}\right) \forall j\in N$$

(47)

$${\displaystyle \sum _{j=1}^n{c}_j}=v\left(N\right) \forall j\in N$$

(48)

$${\displaystyle \sum _{j=1}^s{c}_j}\ge v\left(S\right) \forall S\subset N$$

(49)

In the context of cooperative game theory applied to energy systems, the function v represents the aggregate cost or profit of the system. Equation (47) encapsulates a fundamental principle of cooperative game theory: the synergistic effect of collaboration. It stipulates that a player will derive greater economic benefit by participating in a coalition than by operating independently. Furthermore, the model adheres to the principle of efficiency in Equation (48), which mandates that the sum of profits allocated to each player should equate to the maximum attainable profit of the entire system. This condition ensures that all benefits derived from cooperation are fully distributed among the participants, leaving no surplus unallocated. A critical constraint in this framework is the subgroup coalition rationality, expressed in Equation (49). This condition necessitates that the total profit earned by any formed coalition should not exceed the cumulative allocated profits of its constituent players. This requirement serves as a safeguard against the formation of splinter groups that might destabilize the grand coalition.

The simultaneous satisfaction of Equations (47)–(49) is paramount in determining the existence of a core solution. The core, a central concept in cooperative game theory, delineates the set of feasible and stable allocations that no coalition can improve upon. If these equations cannot be concurrently satisfied, it indicates the absence of a core under the current imputation scheme.

To allocate the cooperative surplus, we introduce the Shapley value and Banzhaf value, which are two classical and well-known tools. Both methods are used for the fair distribution of payoffs in cooperative games and are applied in fields such as economics and political science. The Shapley value considers all possible orderings of participants and weighs their marginal contributions accordingly. The Banzhaf value, like the Shapley value, is a concept from cooperative game theory used to measure the power or influence of each participant in a system. While the Shapley value considers all possible permutations of players, the Banzhaf value simplifies the calculation by focusing on the power of a player to change outcomes in different coalitions.

The Shapley value for stakeholder i (${\phi }_i\left(v\right)$) in an n-person cooperative game is expressed as follows:

$${\phi }_i^s\left(v\right)={\displaystyle \sum _{s\subseteq N\backslash i}\frac{s!\left(n-s-1\right)!}{n!}\left[v\left(S\cup i\right)-v\left(S\right)\right]} \forall i=1,2,\dots ,n$$

(50)

The Banzhaf value for stakeholder i (${\psi }_i\left(v\right)$) is defined by

$${\phi }_i^b\left(v\right)={\displaystyle \sum _{S\subseteq N\backslash i}\frac{1}{2^{n-1}}\left[v\left(S\cup i\right)-v\left(S\right)\right]} \forall i=1,2,\dots ,n$$

(51)

where $v\left(S\right)$ is the profit or cost of coalition S.

Here are the steps to calculate the Shapley and Banzhaf values.

(1) Define the Value Function. Based on solving the model, including Equations (46), (2)–(17), (19)–(44), the value to each subset of participants is assigned;

(2) Calculate Marginal Contributions. For each sharing participant, compute their marginal contribution to every possible subset of participants that do not already include them;

(3) Calculate each stakeholder’s contribution. The Shapley and Banzhaf values for each participant are then computed using Equations (50) and (51), respectively.

After calculating the Shapley value or Banzhaf value, we can determine the contribution of each stakeholder. Considering that the SO plays a special role by bearing the investment cost, a rule-based benefit allocation scheme is proposed. It is assumed that the marginal contribution of prosumer i is ${\phi }^i$, and the cooperative surplus is $v\left(N\right)$. The payoff of the SO under a cooperative coalition is first defined by multiplying $v\left(N\right)$ by a predefined coefficient ${\epsilon }_{so}$, which will be decided before investment and described in the contract. The rule-based allocation scheme ensures that investors receive an appropriate income. The remaining surplus $\left(1-{\epsilon }_{so}\right)v\left(N\right)$ is then allocated according to the marginal contribution of each prosumer. The payoff expression of prosumer i is calculated as follows:

$$c_i={\displaystyle \frac{{\phi }^i}{{\displaystyle \sum _{i\in N\backslash so}{\phi }^i}}}\left(1-{\epsilon }_{so}\right)v\left(N\right) \forall i=1,2,\dots ,n$$

(52)

It can be observed that prosumers participating in the group benefit compared to the non-cooperation scenario if the cooperative surplus is greater than zero. In summary, the decision-making process for shared storage planning and profit allocation among sharing participants is illustrated in Figure 2.

Figure 2. The decision-making framework.

In this paper, we propose a shared storage planning approach based on cooperative game theory. This method offers a different perspective compared to two well-established approaches: Nash bargaining [28] and Stackelberg game-based [29] planning.

The proposed approach in this paper centers on full cooperation among all participants, with the primary objective of maximizing collective benefit. This cooperative framework ensures that participants’ interests are aligned, leading to fair and stable solutions. By focusing on total utility rather than individual gains, the method achieves efficient resource allocation. Furthermore, it facilitates collective decision-making, resulting in more sustainable long-term solutions.

In contrast, the Nash bargaining approach relies on the bargaining power of each participant. While it can lead to an equitable distribution based on initial endowments or bargaining strength, it may not always maximize collective benefit. The efficiency of this method depends on the bargaining process, which can be time-consuming and may not consistently yield optimal resource allocation. The Stackelberg game-based approach establishes a leader-follower dynamic, where the investor (leader) sets terms that participants (followers) must accept. Although effective in hierarchical settings, this approach may not fully consider the collective welfare of all participants. Efficiency is driven by the leader’s decisions, which can be swift but may overlook optimal resource allocation from a collective standpoint. Moreover, while both Nash bargaining and Stackelberg game-based approaches can theoretically protect privacy through distributed algorithms, their complex iterative processes may lead to convergence issues.

In summary, our proposed method offers several advantages. (1) It promotes a holistic view of the storage planning problem by focusing on full cooperation, ensuring that all participants’ needs are considered and addressed. (2) The use of cooperative game theory guarantees that all participants receive a fair share of the benefits, enhancing satisfaction and long-term sustainability. (3) By maximizing collective benefit, the method leads to outcomes that are more advantageous for the entire community.

5. Case Study

5.1. Data Description

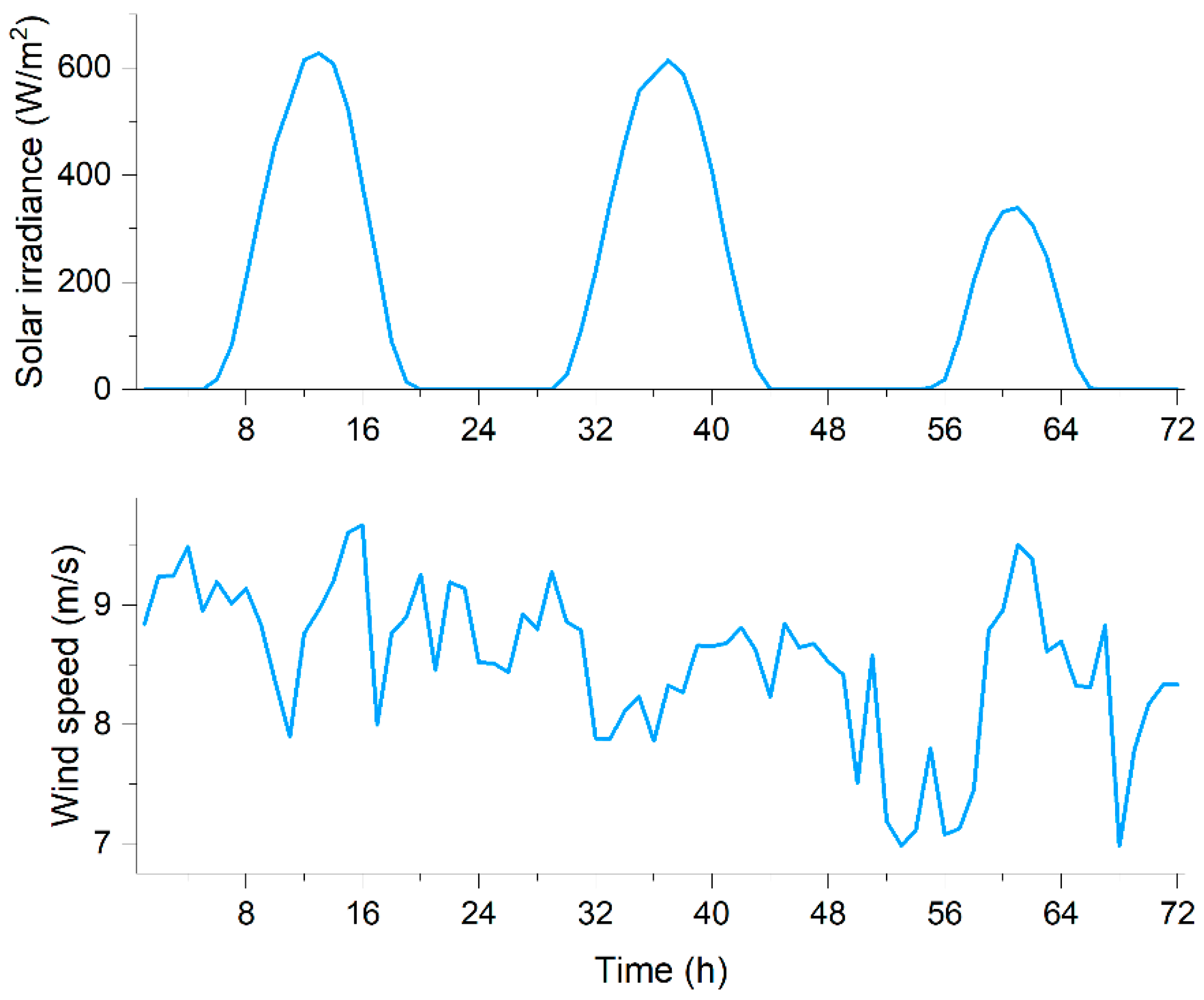
To assess the efficacy of the proposed shared framework, three prosumers were selected. Prosumer 1 has a PV system with an installed capacity of 250 kW and no wind turbine. Prosumer 2 possesses a PV system with a 200 kW installed capacity and a wind turbine with a 150 kW capacity. Prosumer 3 has a PV system with a 250 kW installed capacity and a wind turbine with a 1000 kW capacity. The battery has a rated capacity of 13.2 kWh, with charging and discharging efficiencies of 94%. The maximum, minimum, and initial state of charge (SOC) are 0.95, 0.05, and 0.2, respectively. The battery has a 10-year lifetime and costs $216.27 per kWh. Load data for three buildings within the community were sourced from the literature [31]. Our simulation focused on the investment and operational strategies of the energy storage system across three distinct seasonal scenarios. We chose a typical day from spring, summer, and winter to capture the varying energy demands and usage patterns throughout the year. Solar irradiance and wind speed data are presented in Figure 3. The time-of-use power prices ($/kWh) for different periods are as follows: from 1–4 h and 22–24 h: $0.06; from 5–7 h and 11–16 h: $0.12; from 8–10 h and 17–21 h: $0.18. The feed-in tariff is set at $0.04/kWh [32]. Additional parameters can be referenced in [28].

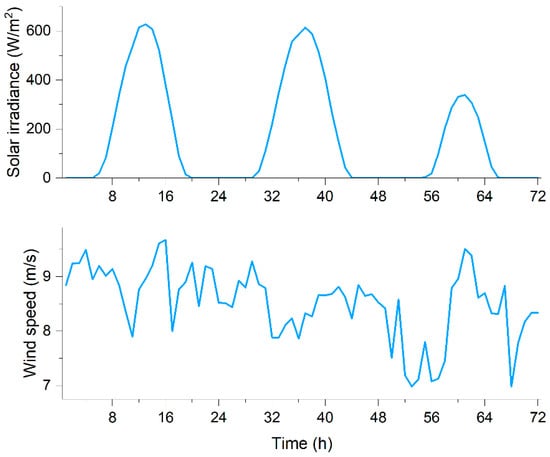
Figure 3. Hourly solar irradiance and wind speed.

Two scenarios, individual and shared, were defined to assess the performance of shared storage. In the individual scenario, each prosumer installs its own energy storage system. In contrast, in the shared scenario, prosumers share a storage system, with the physical storage device being invested in and controlled by a storage operator. This operator provides energy storage services to the prosumers in the form of virtual storage capacity, fully capitalizing on the inherent complementarity and diversity of charging and discharging behaviors among different prosumers. This approach optimizes the utilization of idle resources.

5.2. Optimal Configuration of Energy Storage

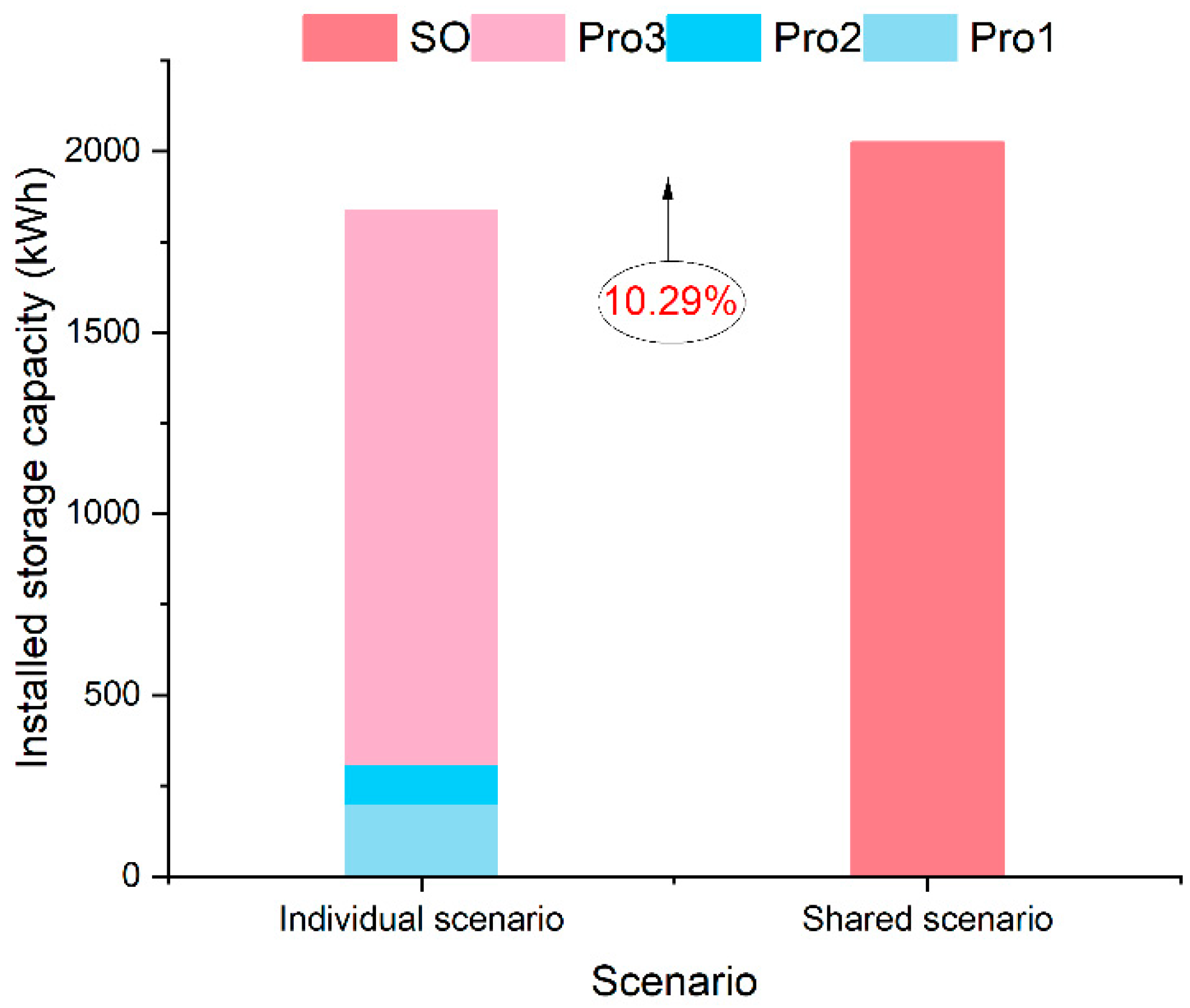
The investment strategies under individual and shared scenarios are illustrated in Figure 4. Based on the generation and consumption characteristics of each prosumer, the storage capacities for prosumers 1, 2, and 3 are 202.5 kWh, 108 kWh, and 1525.5 kWh, respectively. The cumulative storage capacity in this individual approach totaled 1836 kWh. Contrastingly, the shared scenario yielded an optimal storage capacity of 2025 kWh. This represents a notable 10.29% increase over the individual scenario. The primary reason for this increase is that all participants share the physical storage cost of investment. It can be inferred that the costs of storage for prosumers are lower than the cost of investing in individual energy storage systems. Additionally, under the shared scenario, prosumers do not bear the O&M costs as well as the power losses incurred by charging and discharging. Consequently, prosumers have more flexible charging and discharging decisions and can achieve greater storage capacities compared to the individual scenario. In conclusion, the shared model incentivizes greater investment in battery storage.

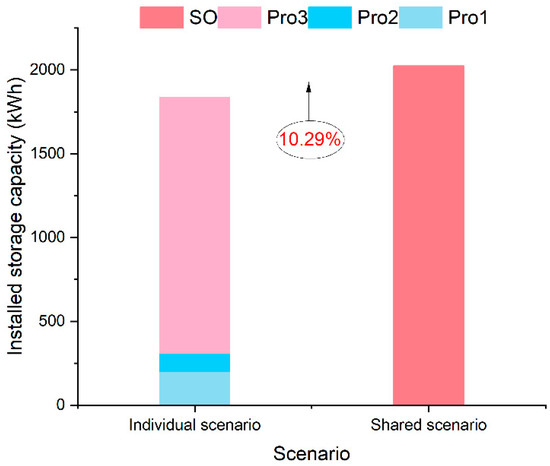
Figure 4. The optimal storage capacity under the individual scenario and shared scenario.

5.3. Optimal Scheduling of Energy Storage

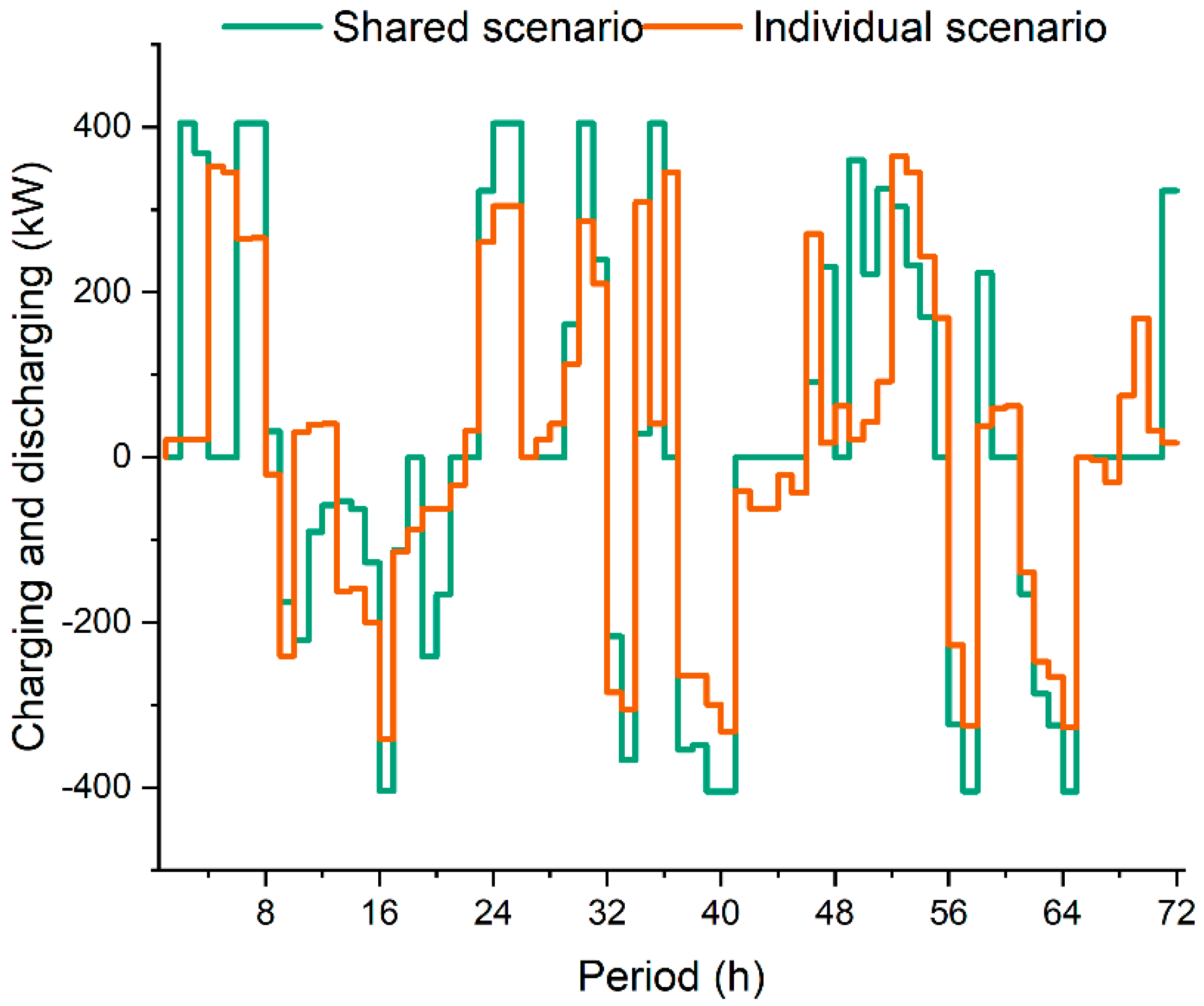
Figure 5 shows the optimal storage schedule of each prosumer in three typical days under individual and shared scenarios. The positive and negative kilowatts represent the charging and discharging quantity. The charging and discharging decisions of three prosumers in the individual scenario are summarized, with the orange line representing the total charging and discharging electricity of all participants. It can be seen that the charging and discharging schedules of prosumers in the individual scenario are similar to those in the shared scenario. Moreover, in the shared scenario, the charging and discharging quantity is higher, indicating better utilization of storage in the shared scenario.

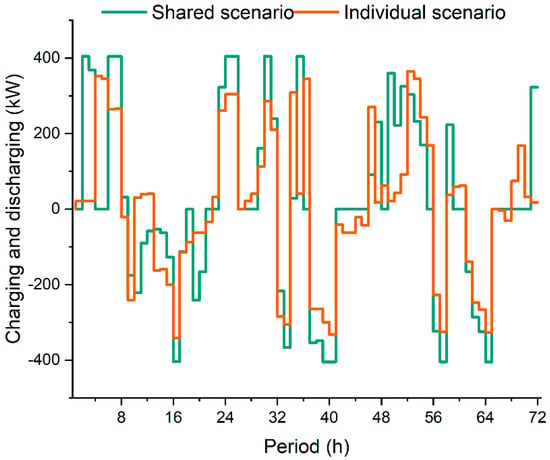
Figure 5. Charging and discharging schedules of stakeholders in two scenarios.

In addition, three criteria are introduced to assess the performance of shared storage.

The self-consumption rate (sc) measures the proportion of locally generated renewable energy that is consumed on-site to meet the community’s energy needs. This indicator shows how much of the locally produced renewable energy is directly used by the community rather than being exported to the grid.

$$sc={\displaystyle \frac{{\displaystyle \sum _{i,t}\left(P_{i,t}^{d,ren}+P_{i,t}^{dch,ren}\right)}}{{\displaystyle \sum _{i,t}\left(P_{i,t}^{pv}+P_{i,t}^{wind}\right)}}}$$

(53)

where $P_{i,t}^{d,ren}$ is the renewable electricity used directly to satisfy the load, $P_{i,t}^{dch,ren}$ is the renewable electricity discharged from storage to meet the load, $P_{i,t}^{pv}$ is the photovoltaic power generated, and $P_{i,t}^{wind}$ is the wind power generated.

The self-sufficiency rate (ss) indicates the extent to which the community’s energy demand can be satisfied by its own renewable energy production. This metric reflects how much of the total energy demand is met by local renewable sources, either directly or through stored energy.

$$ss={\displaystyle \frac{{\displaystyle \sum _{i,t}\left(P_{i,t}^{d,ren}+P_{i,t}^{dch,ren}\right)}}{{\displaystyle \sum _{i,t}{P}_{i,t}^{load}}}}$$

(54)

where $P_{i,t}^{load}$ is the total electricity demand at time t for participant i.

The energy storage utilization rate (eu) measures the percentage of energy demand that is fulfilled through discharging stored energy. It reflects the community’s reliance on energy storage systems to meet its energy needs.

$$eu={\displaystyle \frac{{\displaystyle \sum _{i,t}{P}_{i,t}^{dis,load}}}{{\displaystyle \sum _{i,t}{P}_{i,t}^{load}}}}$$

(55)

where $P_{i,t}^{dis,load}$ represents the quantity of electricity discharged from energy storage to meet the load at time t for participant i.

These indicators are important for evaluating the performance of renewable energy systems and the efficiency of energy storage solutions in a community setting. They provide insight into how well a community is utilizing its renewable resources and how dependent it is on energy storage.

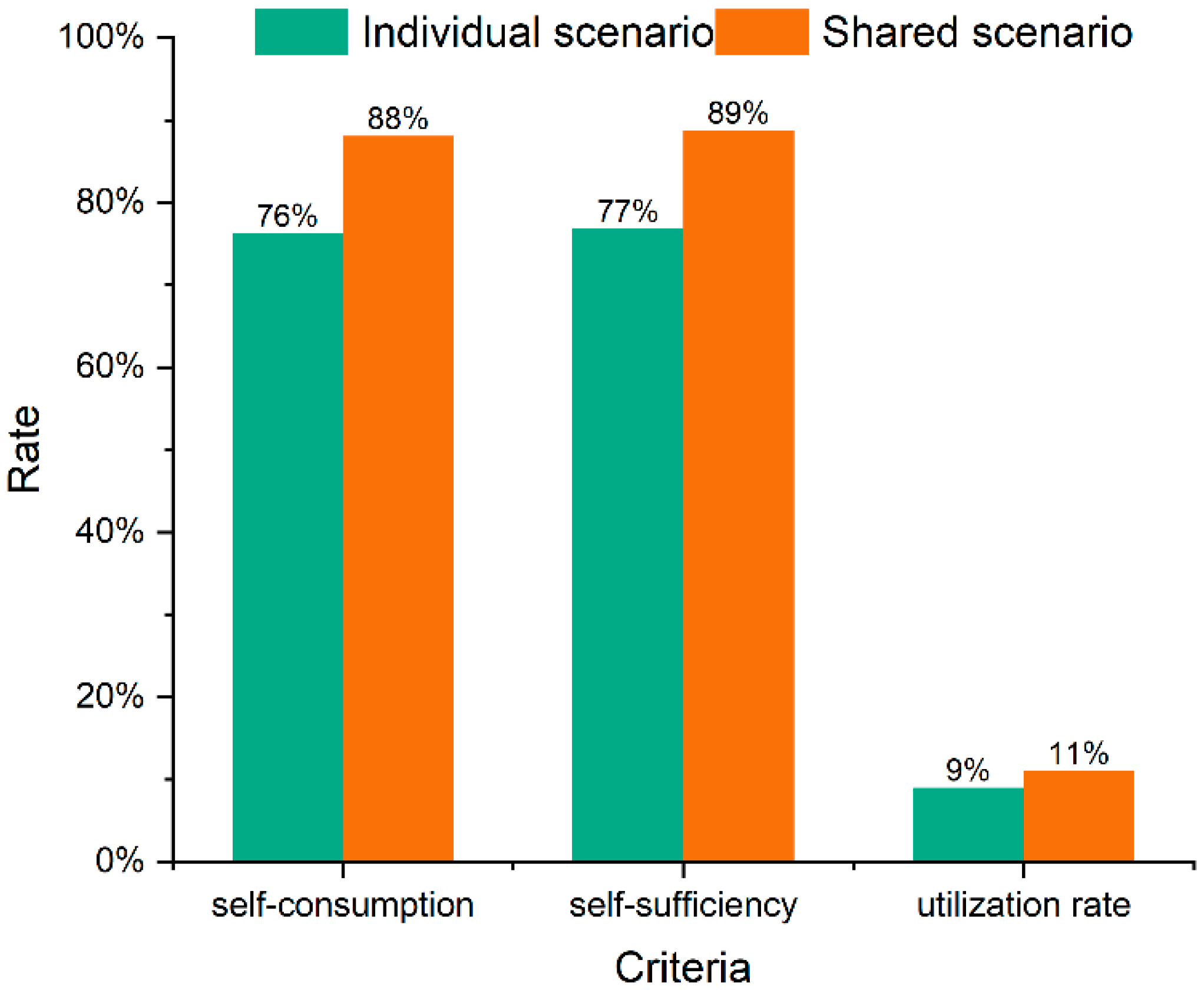
The implementation of storage sharing significantly enhances prosumers’ willingness to utilize storage systems, as illustrated in Figure 6. Compared to the individual scenario, the shared approach increases the community’s self-consumption rate by 11.82% and the self-sufficiency rate by 12.01%. In the shared scenario, prosumers more effectively utilize storage capacities. Most excess renewable energy is stored in batteries to meet future demand, thereby improving renewable energy utilization. Moreover, by primarily sharing charging/discharging needs, prosumers avoid storing all surplus electricity in storage systems, eliminating power losses and consequently boosting the community’s self-consumption and self-sufficiency rates. The utilization rate of energy storage in the shared scenario reaches 11.04%, surpassing the individual scenario by 2.06%. This metric indicates the community’s reliance on stored energy to meet power demands. For prosumers, most energy needs are met through renewable power and grid electricity, resulting in utilization rates below 12% in both scenarios. Despite this seemingly low percentage, it can be inferred that prosumers in the shared scenario make more efficient use of energy storage compared to those in the individual scenario.

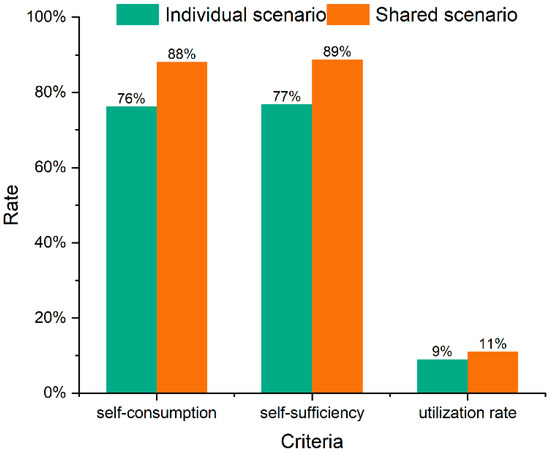
Figure 6. The assessment criteria for the community under two scenarios.

5.4. Economic Performance of Shared Storage

A comprehensive cooperation scheme is devised using cooperative game theory. The game comprises four players: one storage operator (SO) and three prosumers, denoted as N = {SO, Pro1, Pro2, Pro3}. These players can form 15 distinct non-empty coalitions, as detailed in Table 1. The SO is tasked with storage installation. It is assumed that without shared storage, each prosumer can only engage in transactions with the utility grid, precluding inter-prosumer interactions. Table 1 outlines the costs associated with different alliances. To align with the aforementioned objective function, all values are expressed as costs rather than profits.

Table 1. Costs of coalitions.

Coalitions	Costs (Million $)	Coalitions	Costs (Million $)
{SO}	0.00	{Pro 1}	0.08
{Pro 2}	0.02	{Pro 3}	0.11
{SO, Pro 1}	0.07	{SO, Pro 2}	0.02
{SO, Pro 3}	0.09	{Pro 1, Pro 2}	0.09
{Pro 1, Pro 3}	0.15	{Pro 2, Pro 3}	0.09
{SO, Pro 1, Pro 2}	0.09	{SO, Pro 1, Pro 3}	0.14
{SO, Pro 2, Pro 3}	0.08	{Pro 1, Pro 2, Pro 3}	0.14
{SO, Pro 1, Pro 2, Pro 3}	0.13

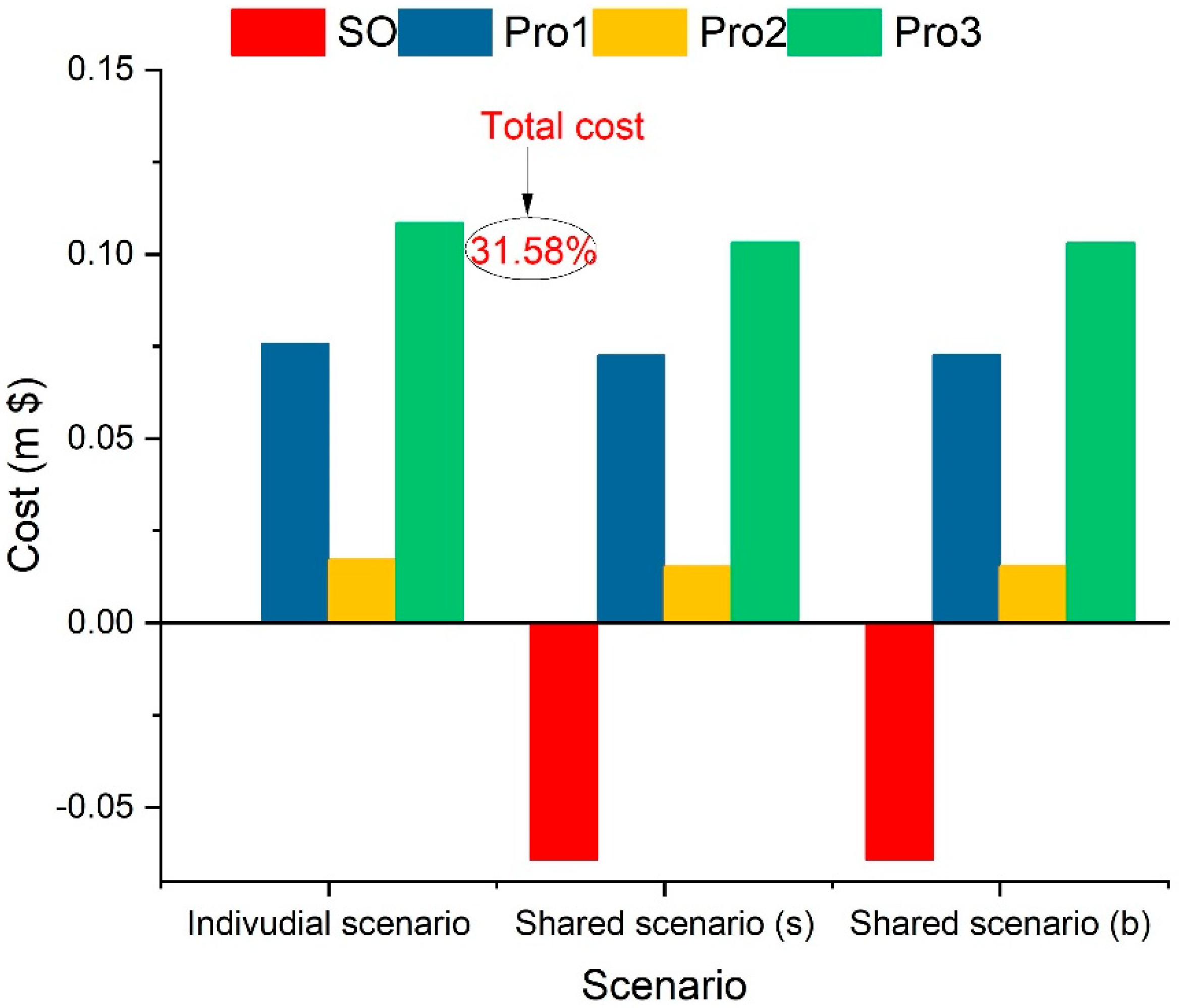
The Shapley value and Banzhaf value methods are employed to derive cost allocation strategies for storage-sharing participants. For any rational allocation scheme, each player’s cost must fall within the Core. Equations (47)–(49) confirm that the cost post-allocation strategy satisfies the Core requirements. Figure 7 illustrates a cost comparison between the two scenarios. In the shared scenario, the allocation strategies based on Shapley value (s) and Banzhaf value (b) are also depicted.

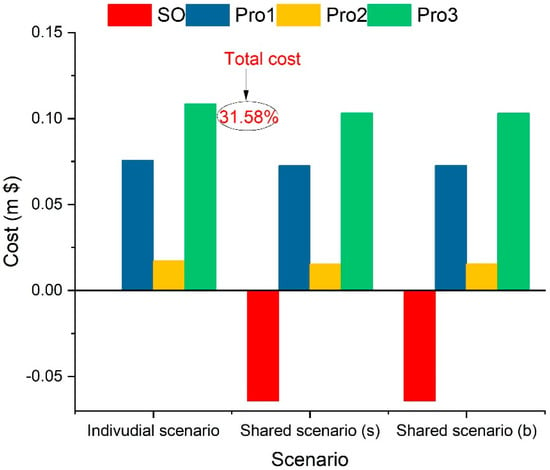
Figure 7. The cost of stakeholders in individual and shared scenarios.

The grand coalition’s total annual cost amounts to $0.89 million, representing a 31.58% reduction compared to the individual scenario. Notably, the SO derives the greatest benefit among all participants. The SO, investing in and providing the physical infrastructure for inter-prosumer sharing, is a crucial stakeholder and justifiably receives a higher profit than the prosumers. Based on the current allocation strategies, we calculate the payback period and the net present value for the SO. The payback period for investing in physical storage is 6.73 years, and the net present value is $0.037 million. This indicates that the project is feasible and that the SO’s profit is reasonable.

Based on the Shapley value, the cost savings for Pro1, Pro2, and Pro3 are 4.71%, 13.15%, and 4.98%, respectively, compared to their costs in the individual scenario. When considering the Banzhaf value method, the cost savings for the three prosumers are 4.45%, 12.90%, and 5.20%, respectively. It can be observed that the marginal contributions of prosumers are similar under both the Shapley and Banzhaf values. Among the prosumers, Pro2 achieves the most cost-saving ratio. This is primarily due to Pro2’s lower costs compared to the others. In terms of actual cost-saving contribution, from largest to smallest, the order is Pro3, Pro1, and Pro2. This is attributed to Pro3 having the highest generation capacity among the three and making a substantial marginal contribution due to complementary supply and demand dynamics from the perspective of the whole system. However, due to the high cost of Pro3, although it has obtained the most profit distribution, its cost-saving rate is still low. In conclusion, full cooperation optimally coordinates resource dispatch at the district level, generating considerable cooperative surplus. This shared scheme demonstrates the potential for significant cost savings and improved resource utilization through collaborative energy management strategies.

5.5. Practical Implications and Potential Applications

The findings from this study present several practical implications and potential applications for the shared energy storage model. The implementation of shared energy storage, as outlined in our proposed framework, has the potential to significantly enhance the efficiency and financial viability of renewable energy systems. By allowing storage facilities to monetize unused capacity, the shared storage model not only generates additional revenue streams for storage providers but also provides renewable energy prosumers with affordable and accessible storage solutions.

Practical Implications: (1) The virtualization of physical storage equipment allows investors to distribute the high costs and long payback periods associated with battery storage over multiple users. This cost-sharing mechanism makes the investment in battery storage more attractive and financially feasible. Investors can achieve quicker returns on investment through the additional revenue generated by offering storage services to prosumers. (2) The shared storage model promotes the efficient use of renewable energy by increasing the self-sufficiency and self-consumption rates among prosumers. By having access to shared storage, prosumers can store excess energy generated from renewable sources and use it during periods of low generation or high demand. This capability reduces reliance on the grid and enhances the overall stability and reliability of the energy system. (3) The cooperative game approach used in our framework ensures the optimal allocation and utilization of storage resources. By incorporating storage sharing into the design phase of energy systems, we can achieve a more balanced and efficient distribution of storage capacity. This leads to a reduction in energy waste and improves the overall performance of the energy system.

Potential Applications: (1) The shared storage model can be applied to residential, office, and commercial buildings to optimize energy usage and reduce costs. For example, multiple buildings within a community or business park can share a centralized storage facility, enabling them to collectively manage their energy needs more effectively. This application not only lowers individual energy costs but also enhances the community’s energy resilience. (2) Shared storage can be a crucial component in the development of microgrid and VPP projects. By integrating shared storage into these projects, system operators can better manage their energy resources, improve grid stability, and support the transition to renewable energy sources. This model fosters participants cooperation and investment, leading to more sustainable and resilient energy systems.

6. Conclusions

The primary objective of this paper is to strategically plan the optimal investment size for shared energy storage under various investment models and to effectively distribute the cooperative surplus among storage-sharing participants, aiming for a mutually beneficial outcome. To this end, we propose a comprehensive storage-sharing framework involving key stakeholders, including a storage investor and multiple prosumers, all bound by a contractual agreement. The storage investor determines the optimal storage capacity by integrating the charging and discharging profiles of all participants and subsequently provides storage services to them. Moreover, we introduce a benefit allocation method with Shapley value and Banzhaf value to quantify the contributions of different stakeholders within the storage-sharing arrangement.

Numerical simulations indicate that our proposed model achieves a total cost reduction of 31.58%, with all participants benefiting from the shared storage arrangement compared to individual investment scenarios. Additionally, there are marked improvements in self-sufficiency rates, self-consumption rates, and storage utilization rates. Prosumers gain more flexibility in their charging and discharging decisions and can access greater storage capacities tailored to their needs, leading to more efficient storage utilization compared to the individual investment scenario.

While our methodology demonstrates significant potential, it is important to acknowledge its limitations. The model assumes perfect information and rational decision-making, which may not always hold in real-world scenarios. Furthermore, the study does not account for potential regulatory barriers or changes in energy policies that could impact the implementation of shared storage systems. Future research directions could include exploring the impact of bounded rationality on storage sharing in a cooperative manner and investigating the effects of different regulatory frameworks and policy scenarios on the viability of shared storage systems.