Optimizing Cross-Regional Lockdown Policies for Epidemics: Balancing Economic and Public Health Costs
Abstract
1. Introduction
2. Literature Review
3. Method
3.1. Model Overview
3.2. Data and Hypothesis Testing
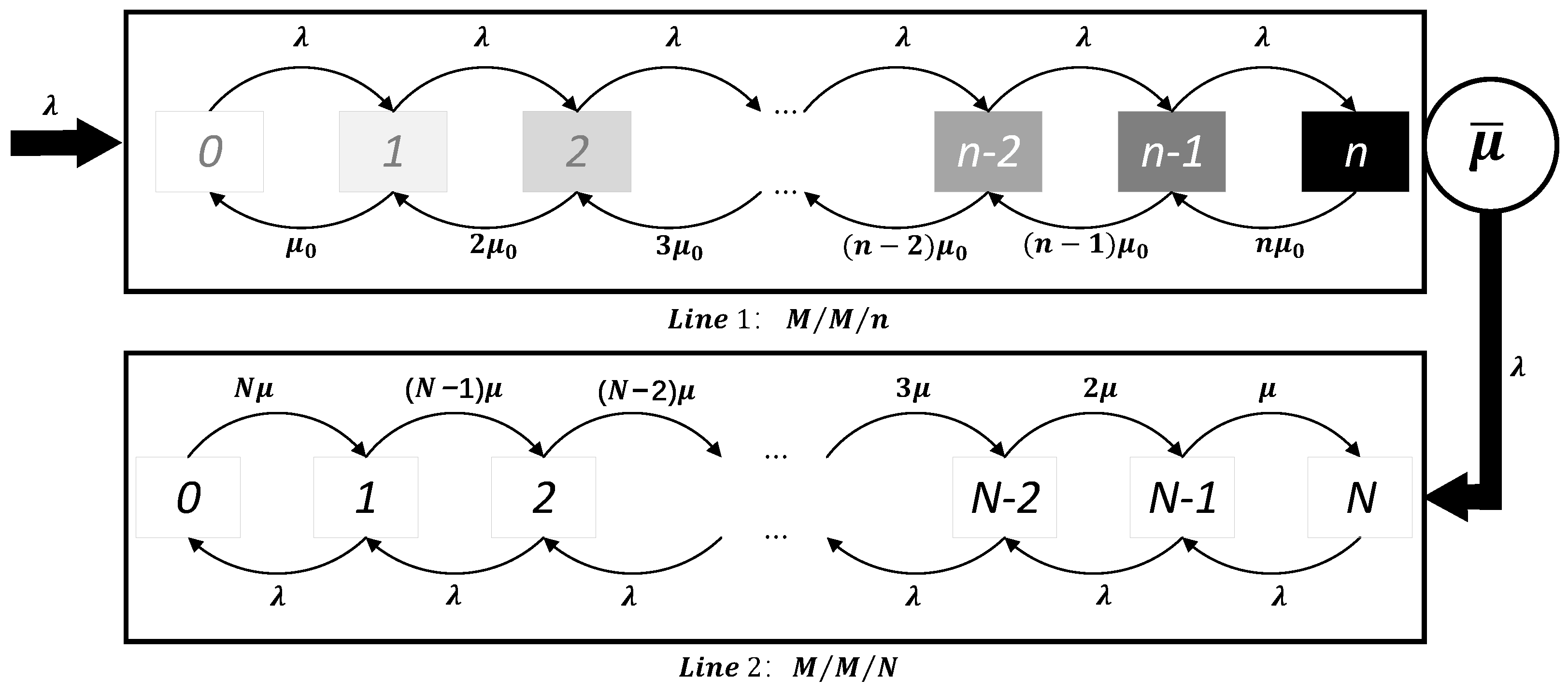
3.3. Queuing Network
3.4. SIR Network
4. Numerical Results
4.1. Parameter Settings
4.2. Results
5. Discussion
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A. Main Proof
References
- Sandford, A. Half of Humanity Now on Lockdown as 90 Countries Call for Confinement. 2020. Available online: https://www.euronews.com/2020/04/02/coronavirus-in-europe-spain-s-death-toll-hits-10-000-after-record-950-new-deaths-in-24-hou (accessed on 2 April 2020).
- Al-Jubari, I.; Mosbah, A.; Salem, S.F. Employee well-being during COVID-19 pandemic: The role of adaptability, work-family conflict, and organizational response. Sage Open 2022, 12, 3. [Google Scholar] [CrossRef]
- Joseph, E.; Levenson, E. New York Gov. Cuomo Extends Stay-at-Home Order Until at Least May 15. 2020. Available online: https://www.cnn.com/2020/04/16/us/new-york-coronavirus/index.html (accessed on 16 April 2020).
- Di Domenico, L.; Pullano, G.; Sabbatini, C.E.; Boëlle, P.Y.; Colizza, V. Impact of lockdown on COVID-19 epidemic in Île-de-France and possible exit strategies. BMC Med. 2020, 18, 240. [Google Scholar] [CrossRef] [PubMed]
- Meo, S.A.; Abukhalaf, A.A.; Alomar, A.A.; AlMutairi, F.J.; Usmani, A.M.; Klonoff, D.C. Impact of lockdown on COVID-19 prevalence and mortality during 2020 pandemic: Observational analysis of 27 countries. Eur. J. Med. Res. 2020, 25, 56. [Google Scholar] [CrossRef] [PubMed]
- Atalan, A. Is the lockdown important to prevent the COVID-19 pandemic? Effects on psychology, environment and economy-perspective. Ann. Med. Surg. 2020, 56, 38–42. [Google Scholar] [CrossRef] [PubMed]
- Eichenbaum, M.S.; Rebelo, S.; Trabandt, M. The macroeconomics of testing and quarantining. J. Econ. Dyn. Control 2022, 138, 104337. [Google Scholar] [CrossRef]
- Kharroubi, S.; Saleh, F. Are lockdown measures effective against COVID-19? Front. Public Health 2020, 8, 549692. [Google Scholar] [CrossRef] [PubMed]
- Moser, C.; Yared, P. Pandemic lockdown: The role of government commitment. Rev. Econ. Dyn. 2022, 46, 27–50. [Google Scholar] [CrossRef]
- Zhang, Y.; Jiang, B.; Yuan, J.; Tao, Y. The impact of social distancing and epicenter lockdown on the COVID-19 epidemic in mainland China: A data-driven SEIQR model study. MedRxiv 2020. [Google Scholar] [CrossRef]
- Eichenbaum, M.S.; Rebelo, S.; Trabandt, M. The macroeconomics of epidemics. Rev. Financ. Stud. 2021, 34, 5149–5187. [Google Scholar] [CrossRef]
- Kaplan, G.; Moll, B.; Violante, G.L. The Great Lockdown and the Big Stimulus: Tracing the Pandemic Possibility Frontier for the US; NBER: Cambridge, MA, USA, 2020. [Google Scholar]
- Hall, R.E.; Jones, C.I.; Klenow, P.J. Trading off Consumption and COVID-19 Deaths; NBER: Cambridge, MA, USA, 2020. [Google Scholar]
- Barrero, J.M.; Bloom, N.; Davis, S.J. COVID-19 Is Also a Reallocation Shock; NBER: Cambridge, MA, USA, 2020. [Google Scholar]
- Kozlowski, J.; Veldkamp, L.; Venkateswaran, V. Scarring Body and Mind: The Long-Term Belief-Scarring Effects of Covid-19; NBER: Cambridge, MA, USA, 2020. [Google Scholar]
- Alvarez, F.; Argente, D.; Lippi, F. A simple planning problem for COVID-19 lock-down, testing, and tracing. Am. Econ. Rev. Insights 2021, 3, 367–382. [Google Scholar] [CrossRef]
- Berger, D.W.; Herkenhoff, K.F.; Mongey, S. An SEIR Infectious Disease Model with Testing and Conditional Quarantine; NBER: Cambridge, MA, USA, 2020. [Google Scholar]
- Chari, V.V.; Kirpalani, R.; Phelan, C. The hammer and the scalpel: On the economics of indiscriminate versus targeted isolation policies during pandemics. Rev. Econ. Dyn. 2021, 42, 1–14. [Google Scholar] [CrossRef]
- Ren, X. Pandemic and lockdown: A territorial approach to COVID-19 in China, Italy and the United States. Eur. Geo. Econ. 2020, 61, 423–434. [Google Scholar] [CrossRef]
- La Torre, D.; Liuzzi, D.; Marsiglio, S. Epidemic outbreaks and the optimal lockdown area: A spatial normative approach. Econ. Theory 2024, 77, 349–411. [Google Scholar] [CrossRef]
- Conant, G.C.; Wolfe, K.H. Self-tests for COVID-19: What is the evidence? A living systematic review and meta-analysis (2020–2023). PLoS Glob. Public Health 2024, 4, e0002336. [Google Scholar]
- Gail, H.R.; Hantler, S.L.; Taylor, B.A. Spectral analysis of M/G/1 and G/M/1 type markov chains. Adv. Appl. Probab. 1996, 28, 114–165. [Google Scholar] [CrossRef]
- Ross, S.M. Introduction to Probability Models, 11th ed.; Academic Press: San Diego, CA, USA, 2014; pp. 1–784. [Google Scholar]
- Ellison, G. Implications of heterogeneous SIR models for analyses of COVID-19. Rev. Econ. Des. 2024, 1–37. [Google Scholar] [CrossRef]
- Kermack, W.O.; McKendrick, A.G. Contributions to the mathematical theory of epidemics IV: Analysis of experimental epidemics of the virus disease mouse ectromelia. Epidemiol. Infect. 1937, 37, 172–187. [Google Scholar] [CrossRef] [PubMed]
- Piunovskiy, A.B.; Clancy, D. An explicit optimal intervention policy for a deterministic epidemic model. Optim. Contr. Appl. Met. 2008, 29, 413–428. [Google Scholar] [CrossRef]
- Rees, E.M.; Nightingale, E.S.; Jafari, Y.; Waterlow, N.R.; Clifford, S.; Pearson, C.A.B.; CMMID Working Group; Jombart, T.; Procter, S.R.; Knight, G.M. COVID-19 length of hospital stay: A systematic review and data synthesis. BMC Med. 2020, 18, 270. [Google Scholar] [CrossRef] [PubMed]
- Liu, Y.; Rocklöv, J. The effective reproduction number for the omicron SARS-CoV-2 variant of concern is several times higher than Delta. J. Travel Med. 2022, 29, taac037. [Google Scholar] [CrossRef] [PubMed]




| Null Hypothesis | The number of spillover cases follows a Poisson distribution |
| Sample Size | 23 |
| Mean | 5.260 |
| Chi-Square Statistic | 2.820 |
| Degrees of Freedom | 2 |
| p-value | 0.244 |
| Conclusion | Accept the null hypothesis |
| Date | Confirmed Cases | Cumulative Cases |
|---|---|---|
| 4 March 2022 | 8 | 8 |
| 5 March 2022 | 32 | 40 |
| 6 March 2022 | 37 | 77 |
| Time Period (T) | Jilin | Changchun | Shanghai | Average |
|---|---|---|---|---|
| T = 3 days | 7.45 | 7.05 | 7.80 | 7.43 |
| T = 7 days | 3.90 | 3.55 | 3.44 | 3.63 |
| T = 14 days | 2.20 | 2.13 | 2.06 | 2.13 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Qin, T.; Gan, X.; Li, Y.; Qin, C. Optimizing Cross-Regional Lockdown Policies for Epidemics: Balancing Economic and Public Health Costs. Sustainability 2024, 16, 7682. https://doi.org/10.3390/su16177682
Qin T, Gan X, Li Y, Qin C. Optimizing Cross-Regional Lockdown Policies for Epidemics: Balancing Economic and Public Health Costs. Sustainability. 2024; 16(17):7682. https://doi.org/10.3390/su16177682
Chicago/Turabian StyleQin, Taojie, Xianghua Gan, Yuchen Li, and Changsheng Qin. 2024. "Optimizing Cross-Regional Lockdown Policies for Epidemics: Balancing Economic and Public Health Costs" Sustainability 16, no. 17: 7682. https://doi.org/10.3390/su16177682
APA StyleQin, T., Gan, X., Li, Y., & Qin, C. (2024). Optimizing Cross-Regional Lockdown Policies for Epidemics: Balancing Economic and Public Health Costs. Sustainability, 16(17), 7682. https://doi.org/10.3390/su16177682








