Optimizing EV Powertrain Performance and Sustainability through Constraint Prioritization in Nonlinear Model Predictive Control of Semi-Active Bidirectional DC-DC Converter with HESS
Abstract
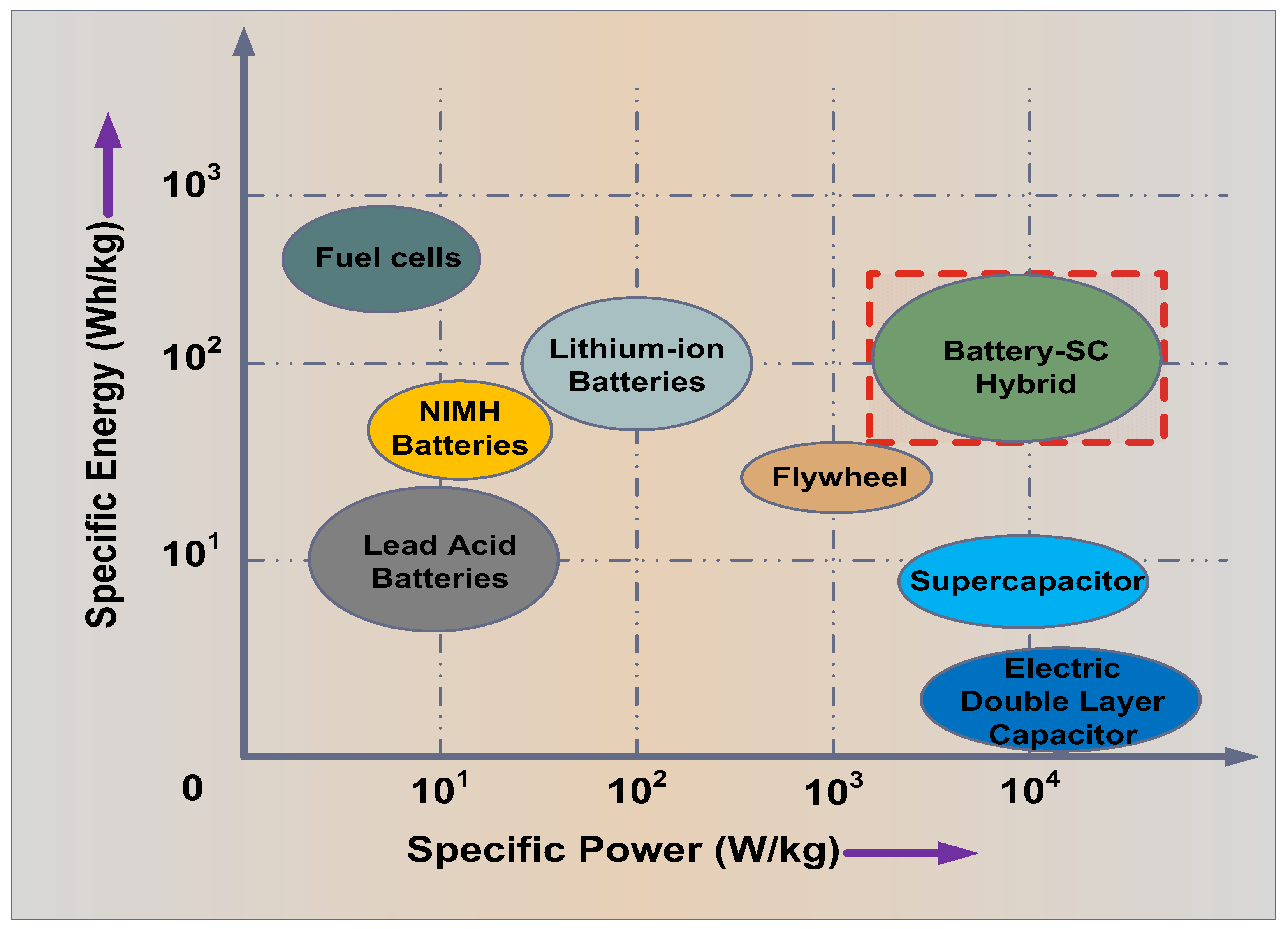
1. Introduction
- Modelling and design of semi-active topology of the bidirectional DC–DC converter (SAT-BDC) to transfer energy from a HESS incorporating the mathematically modelled lithium–ion battery and supercapacitor (SC) to a variable load model in the open loop to validate the concept.
- Investigation of the performance of the applied nonlinear model predictive control (NMPC) to enhance the operation and life span of the lithium–ion battery pack by simultaneously maintaining constant battery current and regulating DC link voltage at the output by tracking its reference value with different prioritizations.
- Simulation of individual case studies to validate the impact of different prioritizations of the selected variables and the difference in the performance of the system.
2. Modelling of the System Components
2.1. Battery
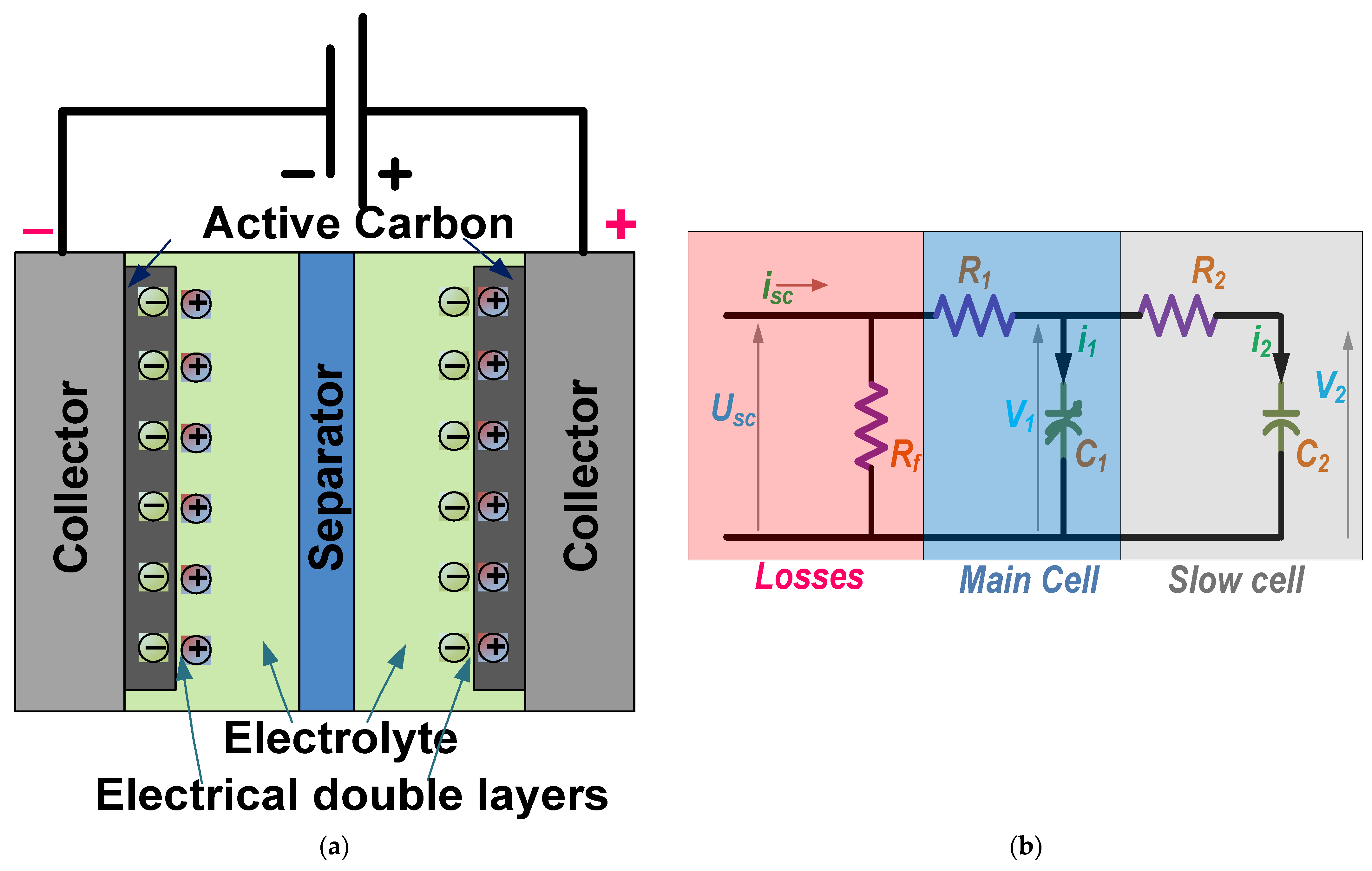
2.2. Supercapacitor
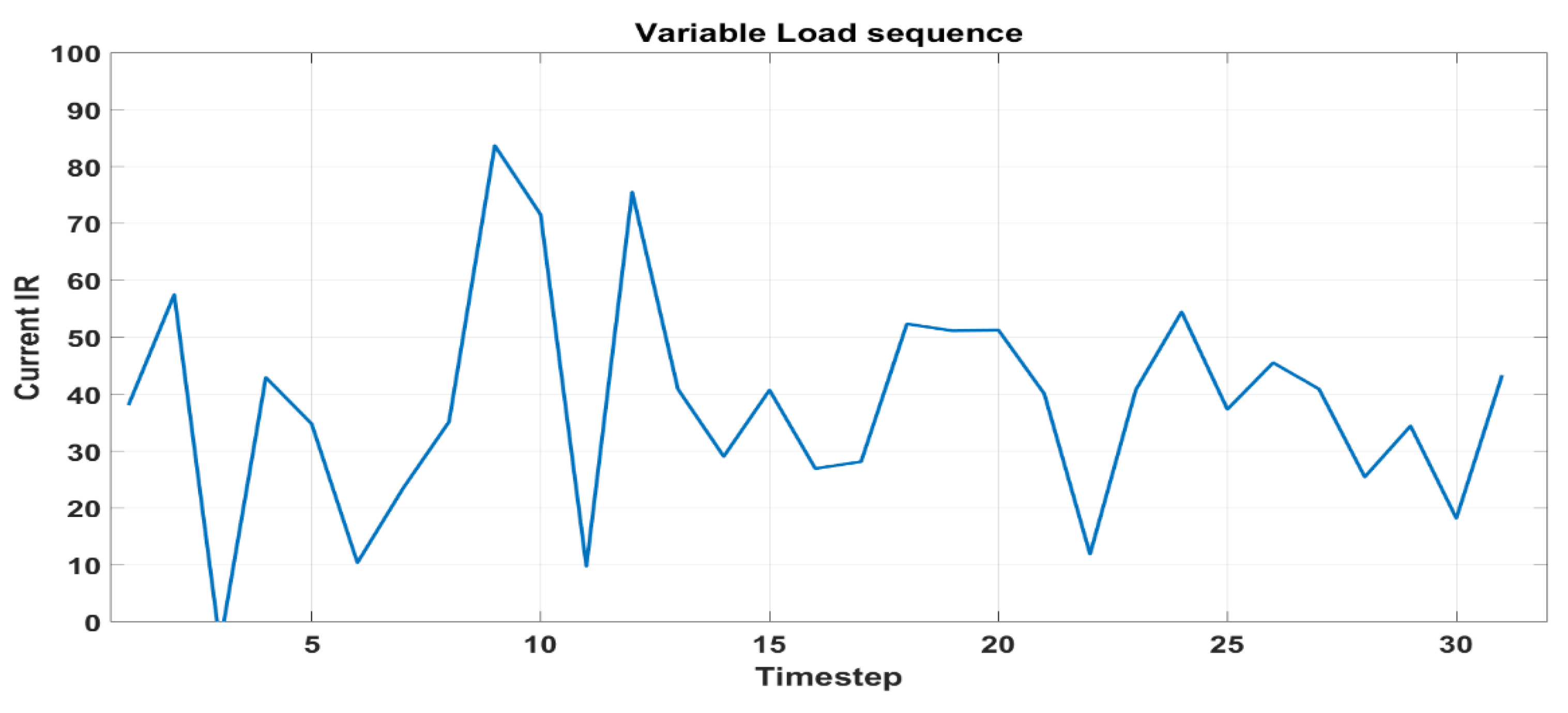
2.3. DC-Link Load Current Generation
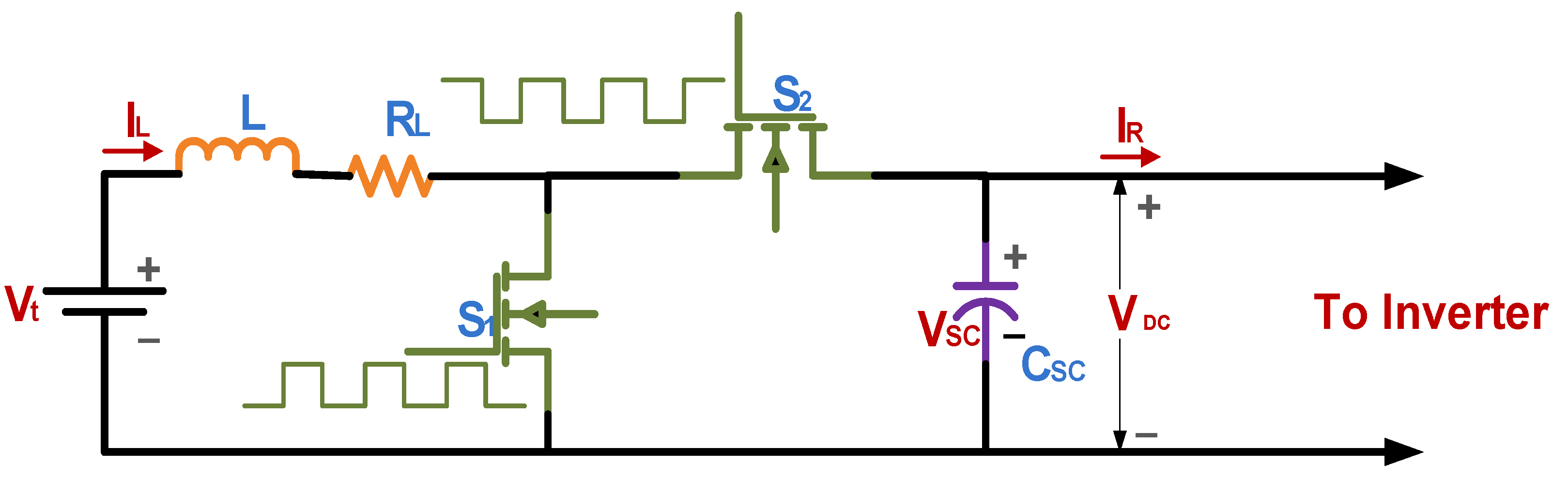
2.4. Semi-Active Topology of Bidirectional DC-DC Converter (SAT-BDC)
3. Configuration of the Proposed System with Nonlinear Model Predictive Control
Proposed Nonlinear Model Predictive Control Strategy
4. Results and Analysis
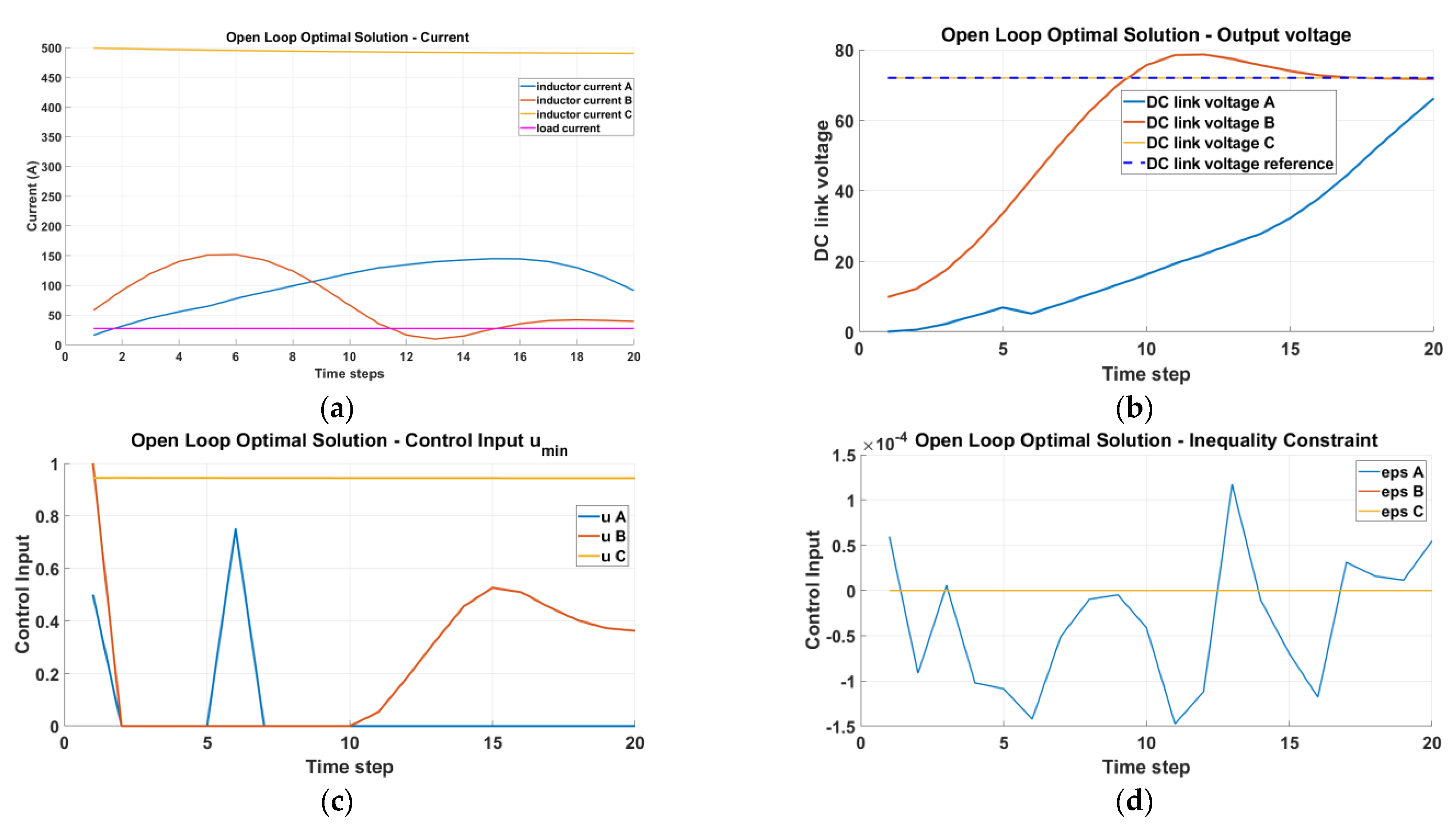
4.1. Open-Loop Optimal Solution without Supercapacitor
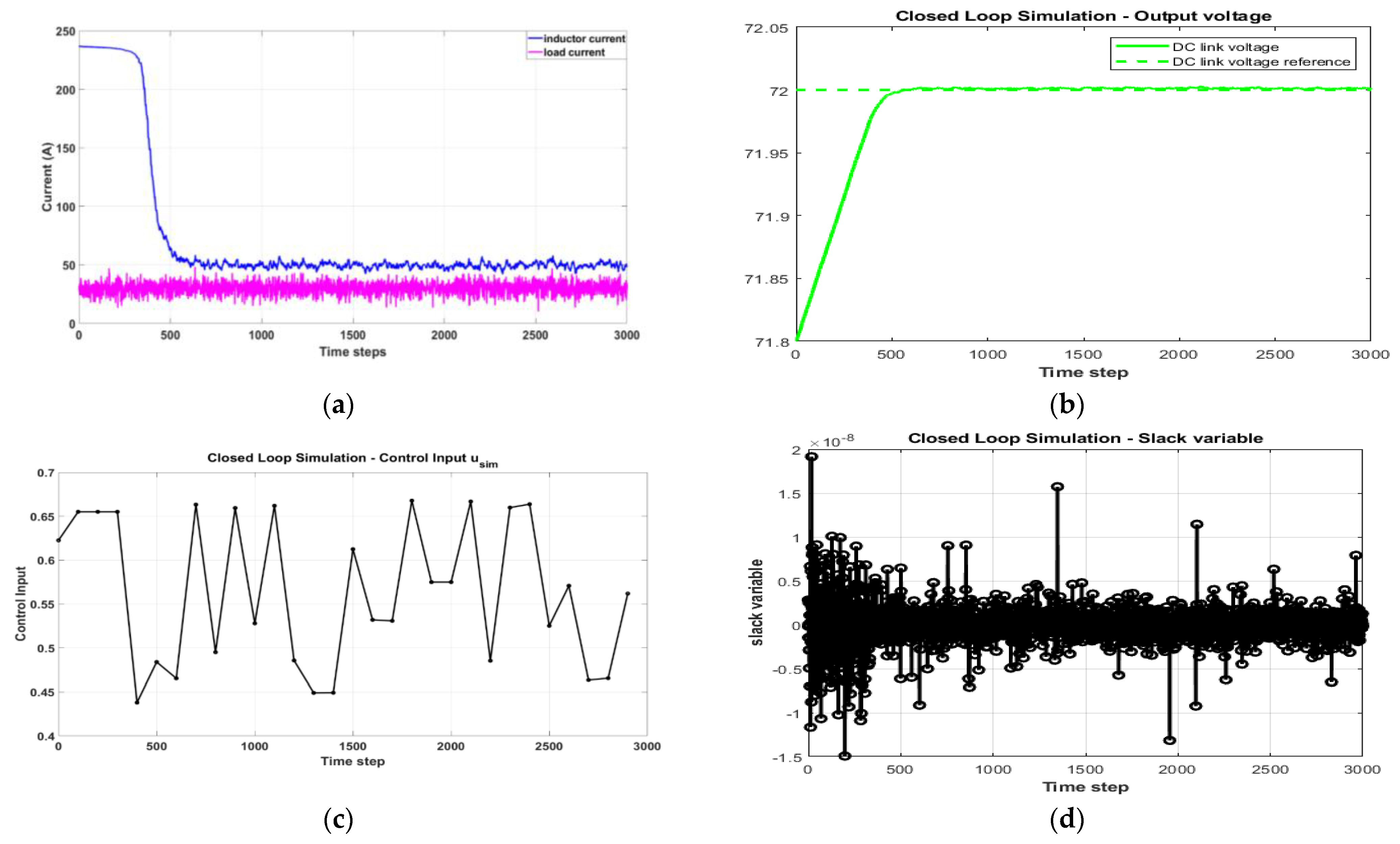
4.2. Closed Loop Simulation, without Supercapacitor
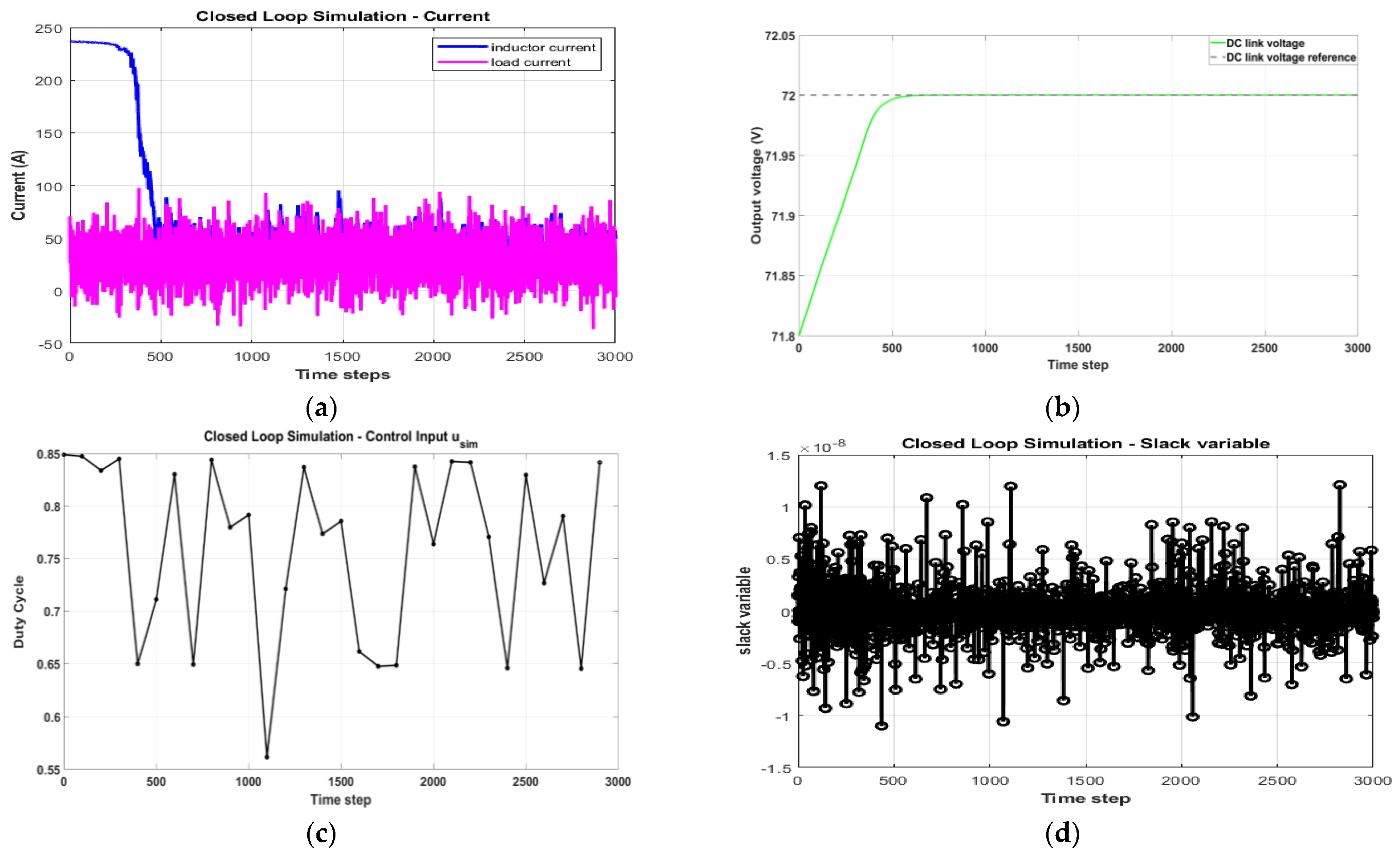
4.3. Closed-Loop Simulation with the Integration of Supercapacitor
4.4. Closed-Loop Simulation of HESS with Voltage Prioritization
4.5. Closed-Loop Simulation of HESS with Current Prioritization
5. Discussion
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Alanazi, F. Electric Vehicles: Benefits, Challenges, and Potential Solutions for Widespread Adaptation. Appl. Sci. 2023, 13, 6016. [Google Scholar] [CrossRef]
- Agajie, T.F.; Ali, A.; Fopah-Lele, A.; Amoussou, I.; Khan, B.; Velasco, C.L.R.; Tanyi, E. A Comprehensive Review on Techno-Economic Analysis and Optimal Sizing of Hybrid Renewable Energy Sources with Energy Storage Systems. Energies 2023, 16, 642. [Google Scholar] [CrossRef]
- Abdelqawee, I.M.; Emam, A.W.; ElBages, M.S.; Ebrahim, M.A. Implementation of a novel hybrid optimizer for energy management of fuel cell/battery/supercapacitor system. Energy Syst. 2022. [Google Scholar] [CrossRef]
- Pedrayes, J.F.; Melero, M.G.; José, M.C.; Norniella, J.G.; Orcajo, G.A.; Cabanas, M.F.; Rojas, C.H. Optimization of supercapacitor sizing for high-fluctuating power applications by means of an internal-voltage-based method. Energy 2019, 183, 504–513. [Google Scholar] [CrossRef]
- Hossain Lipu, M.S.; Hannan, M.A.; Karim, T.F.; Hussain, A.; Md Saad, M.H.; Ayob, A.; Miah, M.S.; Mahlia, T.M.I. Intelligent algorithms and control strategies for battery management system in electric vehicles: Progress, challenges and future outlook. J. Clean. Prod. 2021, 292, 126044. [Google Scholar] [CrossRef]
- Tran, M.-K.; Mathew, M.; Janhunen, S.; Panchal, S.; Raahemifar, K.; Fraser, R.; Fowler, M. A comprehensive equivalent circuit model for batteries, incorporating the effects of state of health, state of charge, and temperature on model parameters. J. Energy Storage 2021, 43, 103252. [Google Scholar] [CrossRef]
- Hannan, M.A.; Hoque, M.M.; Mohamed, A.; Ayob, A. Review of energy storage systems for electric vehicle applications: Issues and challenges. Renew. Sustain. Energy Rev. 2017, 69, 771–789. [Google Scholar] [CrossRef]
- Zhao, X.L.; Wang, L.; Zhou, Y.L.; Pan, B.X.; Wang, R.C.; Wang, L.M.; Yan, X.Q. Energy management strategies for fuel cell hybrid electric vehicles: Classification, comparison, and outlook. Energy Convers. Manag. 2022, 270, 116179. [Google Scholar] [CrossRef]
- Badji, A.; Abdeslam, D.O.; Becherif, M.; Eltoumi, F.; Benamrouche, N. Analyze and Evaluate of Energy Management System for Fuel Cell Electric Vehicle based on Frequency Splitting. Math. Comput. Simul. 2020, 169, 65–77. [Google Scholar] [CrossRef]
- Hossain Lipu, M.S.; Mamun, A.A.; Ansari, S.; Miah, M.S.; Hasan, K.; Meraj, S.T.; Abdolrasol, M.G.M.; Rahman, T.; Maruf, M.H.; Sarker, M.R.; et al. Battery Management, Key Technologies, Methods, Issues, and Future Trends of Electric Vehicles: A Pathway toward Achieving Sustainable Development Goals. Batteries 2022, 8, 119. [Google Scholar] [CrossRef]
- Collath, N.; Tepe, B.; Englberger, S.; Jossen, A.; Hesse, H. Aging aware operation of battery energy storage systems: A review. J. Energy Storage 2022, 55, 105634. [Google Scholar] [CrossRef]
- Robayo, M.; Mueller, M.; Sharkh, S.; Abusara, M. Assessment of supercapacitor performance in a hybrid energy storage system with an EMS based on the discrete wavelet transform. J. Energy Storage 2023, 57, 106200. [Google Scholar] [CrossRef]
- Alobeidli, K.; Khadkikar, V. A new ultracapacitor state of charge control concept to enhance battery lifespan of dual storage electric vehicles. IEEE Trans. Veh. Technol. 2018, 67, 10470–10481. [Google Scholar] [CrossRef]
- Sundén, B. Battery Technologies. In Hydrogen, Batteries and Fuel Cells, 1st ed.; Academic Press: Cambridge, MA, USA, 2019; pp. 57–79. [Google Scholar] [CrossRef]
- Nguyen, B.H.; German, R.; Trovao, J.P.F.; Bouscayrol, A. Real-time energy management of battery/supercapacitor electric vehicles based on an adaptation of pontryagin’s minimum principle. IEEE Trans. Veh. Technol 2019, 68, 203–212. [Google Scholar] [CrossRef]
- Dong, Z.; Zhang, Z.B.; Li, Z.; Li, X.M.; Qin, Z.W.; Liang, C.X.; Han, M.H.; Yin, Y.F.; Bai, J.Z.; Wang, C.Y.; et al. A Survey of Battery–Supercapacitor Hybrid Energy Storage Systems: Concept, Topology, Control and Application. Symmetry 2022, 14, 1085. [Google Scholar] [CrossRef]
- Gorji, S.A.; Sahebi, H.G.; Ektesabi, M.; Rad, A.B. Topologies and control schemes of bidirectional DC–DC power converters: An overview. IEEE Access 2019, 7, 117997–118019. [Google Scholar] [CrossRef]
- Nguyen, N.D.; Yoon, C.; Lee, Y.-I. A standalone energy management system of battery/supercapacitor hybrid energy storage system for electric vehicles using model predictive control. IEEE Trans. Ind. Electron. 2022, 70, 5104–5114. [Google Scholar] [CrossRef]
- Momayyezan, M.; Abeywardana, D.B.W.; Hredzak, B.; Agelidis, V.G. Integrated reconfigurable configuration for battery/ultracapacitor hybrid energy storage systems. IEEE Trans. Energy Convers. 2016, 31, 1583–1590. [Google Scholar] [CrossRef]
- Song, Z.Y.; Hofmann, H.; Li, J.Q.; Han, X.B.; Zhang, X.W.; Ouyang, M.G. A comparison study of different semi-active hybrid energy storage system topologies for electric vehicles. J. Power Sources 2015, 274, 400–411. [Google Scholar] [CrossRef]
- Sankarkumar, R.S.; Natarajan, R. Energy management techniques and topologies suitable for hybrid energy storage system powered electric vehicles: An overview. Int. Trans. Electr. Energy Syst. 2021, 31, e12819. [Google Scholar] [CrossRef]
- Punna, S.; Mailugundla, R.; Salkuti, S.R. Design, Analysis and Implementation of Bidirectional DC–DC Converters for HESS in DC Microgrid Applications. Smart Cities 2022, 5, 433–454. [Google Scholar] [CrossRef]
- Ranjan, A.; Bodkhe, S.B.; Goyal, G.N.; Aware, M.V. Heuristics EMS for HESS of Electric Vehicle to Extended Battery Operation Using Rate Limiter. Adv. Electr. Comput. Eng. 2022, 22, 11–22. [Google Scholar] [CrossRef]
- Hossain Lipu, M.S.; Faisal, M.; Ansari, S.; Hannan, M.A.; Karim, F.A.; Ayob, A.; Hussain, A.; Miah, M.S.; Md Saad, M.H. Review of electric vehicle converter configurations, control schemes and optimizations: Challenges and suggestions. Electronics 2021, 10, 477. [Google Scholar] [CrossRef]
- Cordoba-Arenas, A.; Onori, S.; Rizzoni, G. A control-oriented battery pack model for plug-in hybrid electric vehicle cycle-life studies and system design with consideration of health management. J. Power Sources 2015, 279, 791–808. [Google Scholar] [CrossRef]
- Sankar, R.S.R.; Deepika, K.; Alsharef, M.; Alamri, B. A Smart ANN-Based Converter for Efficient Bidirectional Power Flow in Hybrid Electric Vehicles. Electronics 2022, 11, 3564. [Google Scholar] [CrossRef]
- Karami-Mollaee, A.; Barambones, O. Dynamic Sliding Mode Control of DC-DC Converter to Extract the Maximum Power of Photovoltaic System Using Dual Sliding Observer. Electronics 2022, 11, 2506. [Google Scholar] [CrossRef]
- Trinh, H.-A.; Nguyen, D.G.; Phan, V.-D.; Duong, T.-Q.; Truong, H.-V.-A.; Choi, S.-J.; Ahn, K.K. Robust Adaptive Control Strategy for a Bidirectional DC-DC Converter Based on Extremum Seeking and Sliding Mode Control. Sensors 2023, 23, 457. [Google Scholar] [CrossRef]
- Song, Z.Y.; Hofmann, H.; Li, J.Q.; Han, X.B.; Ouyang, M.G. Optimization for a hybrid energy storage system in electric vehicles using dynamic programing approach. Appl. Energy 2015, 139, 151–162. [Google Scholar] [CrossRef]
- Taheri, B.; Sedaghat, M.; Bagherpour, M.A.; Farhadi, P. A New Controller for DC-DC Converters Based on Sliding Mode Control Techniques. J. Control Autom. Electr. Syst. 2019, 30, 63–74. [Google Scholar] [CrossRef]
- Praveena, K.P.S.; Jayalakshmi, N.S.; Adarsh, S. Fuzzy Logic Based Hysteresis Current Control and Regenerative Braking of BLDC Motor with Battery Equivalent Cell Modelling for Electric Vehicles. Int. J. Renew. Energy Res. 2023, 13, 1406–1417. [Google Scholar] [CrossRef]
- Lakshmi Narayana, R.; Sreeramulu Mahesh, G.; KCheepati, K.R.; Yuvaraj, T. A fuzzy logic based controller for the bidirectional converter in an electric vehicle. Int. J. Eng. Adv. Technol. 2019, 9, 58–62. [Google Scholar] [CrossRef]
- Škugor, B.; Deur, J. Dynamic programming-based optimisation of charging an electric vehicle fleet system represented by an aggregate battery model. Energy 2015, 92, 456–465. [Google Scholar] [CrossRef]
- Stachowicz, K.; Theodorou, E.A. Optimal-Horizon Model Predictive Control with Differential Dynamic Programming. Energies 2021, 15, 498. [Google Scholar] [CrossRef]
- Heydari, A. Optimal Switching of DC-DC Power Converters Using Approximate Dynamic Programming. IEEE Trans. Neural Netw. Learn. Syst. 2018, 29, 586–596. [Google Scholar] [CrossRef]
- Akter, P.; Uddin, M.; Mekhilef, S.; Tan, N.M.L.; Akagi, H. Model predictive control of bidirectional isolated DC-DC converter for energy conversion system. Int. J. Electron. 2015, 102, 1407–1427. [Google Scholar] [CrossRef]
- Shan, Y.H.; Hu, J.F.; Chan, K.W.; Fu, Q.; Guerrero, J.M. Model Predictive Control of Bidirectional DC-DC Converters and AC/DC Interlinking Converters-A New Control Method for PV-Wind-Battery Microgrids. IEEE Trans. Sustain. Energy 2019, 10, 1823–1833. [Google Scholar] [CrossRef]
- Mande, D.; Trovão, J.P.F.; Ta, M.C.; Van Do, T. Dual-Source Bidirectional Quasi-Z-Source Inverter Development for Off-Road Electric Vehicles. World Electr. Veh. J. 2022, 13, 174. [Google Scholar] [CrossRef]
- Zhao, F.; Li, D.; Chen, X.Q.; Wang, Y. Energy Storage Bidirectional DC-DC Converter Model Predictive Control. J. Appl. Sci. Eng. 2024, 27, 1975–1983. [Google Scholar]
- Li, Y.; Sahoo, S.; Ou, S.Y.; Leng, M.R.; Vazquez, S.; Dragičević, T.; Blaabjerg, F. Flexible Transient Design-Oriented Model Predictive Control for Power Converters. IEEE Trans. Ind. Electron. 2023, 71, 11377–11387. [Google Scholar] [CrossRef]
- Karami, Z.; Shafiee, Q.; Sahoo, S.; Yaribeygi, M.; Bevrani, H.; Dragicevic, T. Hybrid Model Predictive Control of DC-DC Boost Converters with Constant Power Load. IEEE Trans. Energy Convers. 2021, 36, 1347–1356. [Google Scholar] [CrossRef]
- Chen, M.; Rincón-Mora, G.A. Accurate electrical battery model capable of predicting runtime and I-V performance. IEEE Trans. Energy Convers. 2006, 21, 504–511. [Google Scholar] [CrossRef]
- Zhang, R.F.; Xia, B.Z.; Li, B.H.; Lai, Y.Z.; Zheng, W.W.; Wang, H.W.; Wang, W.; Wang, M.W. Study on the Characteristics of a High-Capacity Nickel Manganese Cobalt Oxide (NMC) Battery—An Experimental Investigation. Energies 2018, 11, 2275. [Google Scholar] [CrossRef]
- Sun, F.C.; Xiong, R.; He, H.W. A systematic state-of-charge estimation framework for multi-cell battery packs in electric vehicles using bias correction techniques. Appl. Energy 2016, 162, 1399–1409. [Google Scholar] [CrossRef]
- Meng, J.W.; Boukhnifer, M.; Diallo, D. Comparative study of lithium-ion battery open-circuit-voltage online estimations methods. IET Electr. Syst. Transp. Res. 2019, 10, 162–169. [Google Scholar] [CrossRef]
- Argyrou, M.C.; Christodoulides, P.; Marouchos, C.C.; Kalogirou, S.A. Hybrid battery-supercapacitor mathematical modeling for PV application using Matlab/Simulink. In Proceedings of the Power Engineering Conference. International Universities, Glasgow, UK, 4–7 September 2018. [Google Scholar] [CrossRef]
- Plett, G.L. Battery Management Systems Volume I Battery Modeling; Artech House: Norwood, MA, USA, 2015; pp. 1–325. [Google Scholar]
- Tian, Y.; Li, D.; Tian, J.D.; Xia, B.Z. State of charge estimation of batteries using an optimal adaptive gain nonlinear observer. Electrochim. Acta 2017, 225, 225–234. [Google Scholar] [CrossRef]
- Cabrane, Z.; Lee, S.H. Electrical and Mathematical Modeling of Supercapacitors: Comparison. Energies 2022, 15, 693. [Google Scholar] [CrossRef]
- Datasheet 125V Heavy Transportation Module. Available online: https://www.mouser.com/datasheet/2/257/datasheet_bmod0063_1014696-1179787.pdf (accessed on 21 January 2024).
- Deepak, P.; Viswadev, R.; Venkatesaperumal, B.; Arjun, M. A Novel Bi-Directional Converter for Electric Vehicle to Grid Applications. In Proceedings of the 2020 IEEE International Conference on Power Electronics, Smart Grid and Renewable Energy (PESGRE2020), Cochin, India, 2–4 January 2020. [Google Scholar] [CrossRef]





| Control Approach Their Features | Model of BDC | Ease of Implementation | Flexibility | Realtime Applicability | Computational Complexity | Tuning Complexity |
|---|---|---|---|---|---|---|
| Sliding mode control [27,28,30] | Necessary | Medium | Not Flexible | Well suited | Low | Medium |
| Extremum-Seeking Control [28] | Not Necessary | Medium | Less flexible | No | Medium | Medium |
| Artificial Neural Network [26] | Not Necessary | Depends on the training of the input data | Flexible | Depends on the accuracy of data | High | High |
| Fuzzy logic control [31,32] | Not Necessary | Depends on sophistication of the rule base | Flexible | Depends on training procedure | High | High |
| Dynamic programming [33,34,35] | Not Necessary | Easy | Flexible | No | Low but expensive | Low |
| Model Predictive Control [36,37,38] | An accurate model is necessary | Easy | Less Flexible | Well suited | It depends on the complexity of the model, but efficient | Low |
| Parameter | Value | Remarks |
|---|---|---|
| Battery voltage Vt | 48 V | [18] |
| Battery output current IL | 80 A | Average value consideration |
| DC-link voltage reference VDC | 72 V | Based on motor consideration |
| a0 | 3.2416 | [48] Values of Panasonic NCR18650PF lithium–ion battery |
| a1 | 1.3905 | |
| a2 | 1.3781 | |
| a3 | 0.9206 | |
| R0 | 0.0314 Ω | |
| R1 | 0.0181 Ω | |
| R2 | 0.0281 Ω | |
| C0 | 0.1712 F | |
| CV | 0.55257 F |
| Parameter | Value | Remarks |
|---|---|---|
| DC link Voltage VDC | 72 V | [49] |
| Maximum output current IR | 100 A | [50] |
| Rated capacitance CSC | 63 F | Values are taken from the datasheet of the BMOD0063 P125 B08 model. |
| Maximum initial capacitance | 100 F | |
| Rf | 18 mΩ | |
| R1 | 0.8 Ω | |
| R2 | 1 Ω | |
| C1 | 0.1712 F | |
| C2 | 0.55257 F |
| Parameter | Value | Remarks |
|---|---|---|
| Number of switches | 2 | |
| Switching frequency, f | 20,000 | |
| Inductor L | 490 µH | [18] |
| Series Resistance of inductor RL | 90 mΩ | |
| Capacitor CSC | 0.0063 F/ 63 F | |
| Average load current IL | 50 A | |
| Output Voltage (DC link) VDC | 72 V | |
| Input or source voltage Vt | 48 V |
| Parameter | Value |
|---|---|
| Time horizon, N | 20 timestep |
| One timestep for MPC | 0.0005 s |
| Weightage of voltage, current, and slack variables | 1, 1, 1000 respectively |
| Parameter | Value |
|---|---|
| Time horizon, N | 30 timestep |
| One timestep for MPC | 0.0005 s |
| Weightage of voltage, current, and slack variables | 100, 1, 1000 respectively |
| Parameter | Value |
|---|---|
| Time horizon, N | 3000 timestep |
| One timestep for MPC | 0.0005 s |
| Weightage of voltage, current, and slack variables | 1, 1, 1000 respectively |
| The capacitance C | 63 F |
| Parameter | Value |
|---|---|
| Time horizon, N | 3000 timestep |
| One timestep for MPC | 0.0005 s |
| Weightage of voltage, current, and slack variables | 100, 1, 1000 respectively |
| The capacitance C | 63 F |
| Parameter | Value |
|---|---|
| Time horizon, N | 1000 timesteps |
| One timestep for MPC | 0.005 s |
| Weightage of voltage, current, and slack variables | 1, 100, 1000 respectively |
| The capacitance C | 63 F |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Praveena Krishna, P.S.; Sabhahit, J.N.; Rao, V.S.; Saraswat, A.; Laugaland, H.C.; Nempu, P.B. Optimizing EV Powertrain Performance and Sustainability through Constraint Prioritization in Nonlinear Model Predictive Control of Semi-Active Bidirectional DC-DC Converter with HESS. Sustainability 2024, 16, 8123. https://doi.org/10.3390/su16188123
Praveena Krishna PS, Sabhahit JN, Rao VS, Saraswat A, Laugaland HC, Nempu PB. Optimizing EV Powertrain Performance and Sustainability through Constraint Prioritization in Nonlinear Model Predictive Control of Semi-Active Bidirectional DC-DC Converter with HESS. Sustainability. 2024; 16(18):8123. https://doi.org/10.3390/su16188123
Chicago/Turabian StylePraveena Krishna, P. S., Jayalakshmi N. Sabhahit, Vidya S. Rao, Amit Saraswat, Hannah Chaplin Laugaland, and Pramod Bhat Nempu. 2024. "Optimizing EV Powertrain Performance and Sustainability through Constraint Prioritization in Nonlinear Model Predictive Control of Semi-Active Bidirectional DC-DC Converter with HESS" Sustainability 16, no. 18: 8123. https://doi.org/10.3390/su16188123
APA StylePraveena Krishna, P. S., Sabhahit, J. N., Rao, V. S., Saraswat, A., Laugaland, H. C., & Nempu, P. B. (2024). Optimizing EV Powertrain Performance and Sustainability through Constraint Prioritization in Nonlinear Model Predictive Control of Semi-Active Bidirectional DC-DC Converter with HESS. Sustainability, 16(18), 8123. https://doi.org/10.3390/su16188123






