The Impact of Environmental Social Responsibility on Total Factor Productivity: Evidence from Listed Companies in China
Abstract
1. Introduction
2. Literature Review and Hypotheses
2.1. Theoretical Framework
2.1.1. Company Environmental Protection Behaviors Promote TFP
2.1.2. Company Environmental Protection Behaviors May Inhibit TFP
2.1.3. An Exploration of U-Shape
2.1.4. Impact of Greenwashing
3. Materials and Methods
3.1. Indicators of Environmental Social Responsibility
3.2. Measurements of Total Factor Productivity
3.3. Basic Regression Model
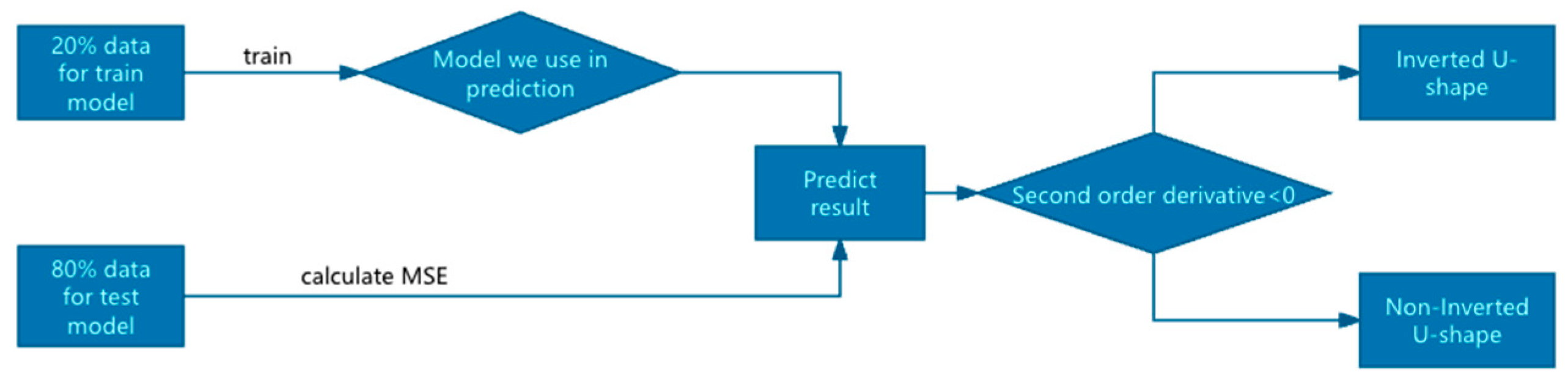
3.4. Inverted U-Shape Analysis Model
3.5. Data Description
4. Results
4.1. Descriptive Statistics and Correlation Analysis
4.2. Basic Fixed Effects Model Regression
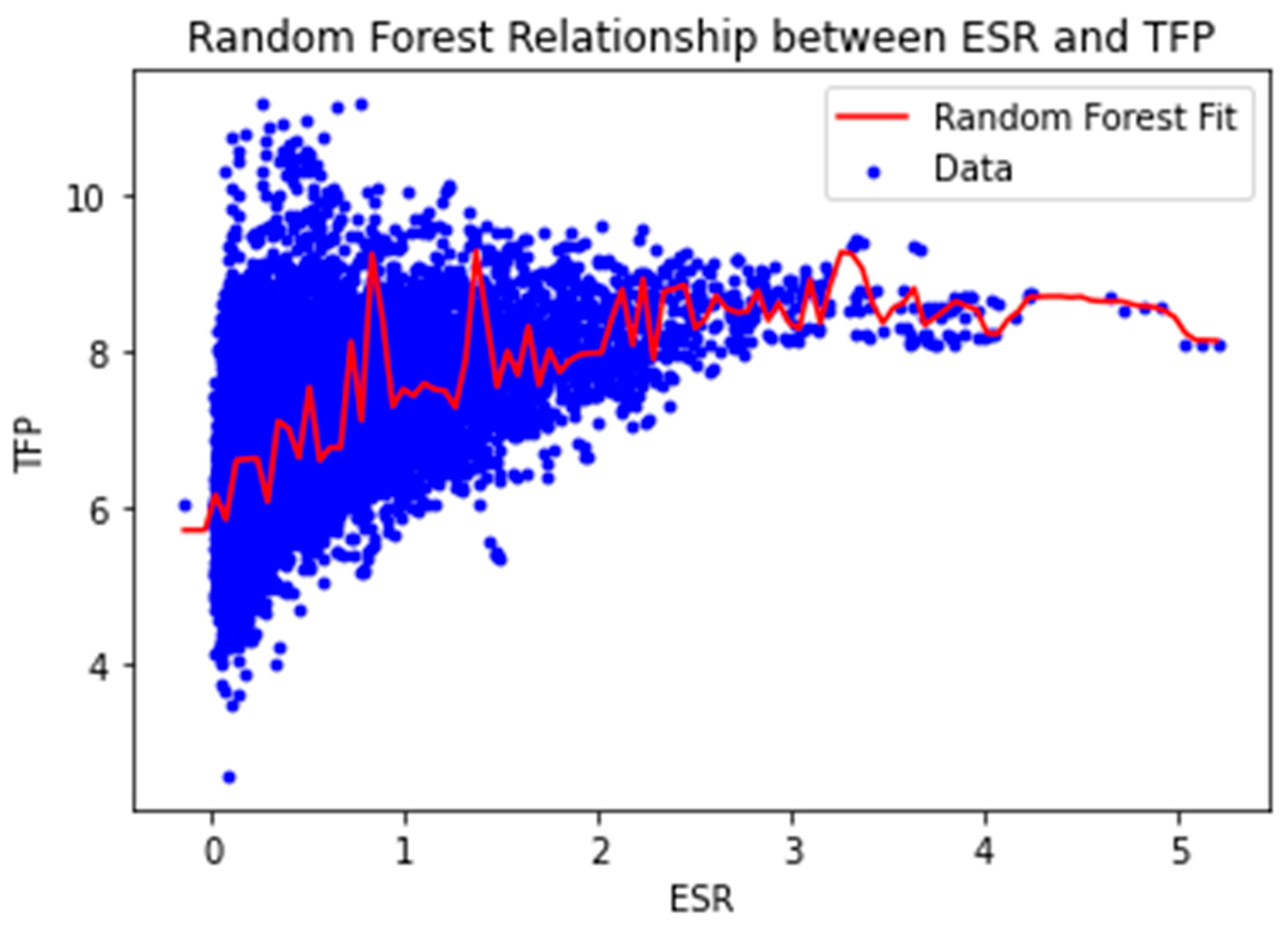
4.3. Inverted U-Shaped Curve Analysis
4.4. Robustness Analysis
4.5. Analysis of Company Size and Industry Type
4.6. The Impact of Greenwashing
5. Discussion
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A
Appendix B


References
- DiSegni, D.M.; Huly, M.; Akron, S. Corporate social responsibility, environmental leadership and financial performance. Soc. Responsib. J. 2015, 11, 131–148. [Google Scholar] [CrossRef]
- Kong, D.; Liu, S.; Dai, Y. Environmental policy, company environment protection, and stock market performance: Evidence from China. Corp. Soc. Responsib. Environ. Manag. 2014, 21, 100–112. [Google Scholar] [CrossRef]
- Ball, C.; Burt, G.; De Vries, F.; MacEachern, E. How environmental protection agencies can promote eco-innovation: The prospect of voluntary reciprocal legitimacy. Technol. Forecast. Soc. Change 2018, 129, 242–253. [Google Scholar] [CrossRef]
- Baier, S.L.; Dwyer Jr, G.P.; Tamura, R. How important are capital and total factor productivity for economic growth? Econ. Inq. 2006, 44, 23–49. [Google Scholar] [CrossRef]
- He, Y.; Zhu, X.; Zheng, H. The influence of environmental protection tax law on total factor productivity: Evidence from listed firms in China. Energy Econ. 2022, 113, 106248. [Google Scholar] [CrossRef]
- Li, Z.; Zou, F.; Mo, B. Does mandatory CSR disclosure affect enterprise total factor productivity? Econ. Res. Ekon. Istraživanja 2022, 35, 4902–4921. [Google Scholar] [CrossRef]
- Tunio, R.A.; Jamali, R.H.; Mirani, A.A.; Das, G.; Laghari, M.A.; Xiao, J. The relationship between corporate social responsibility disclosures and financial performance: A mediating role of employee productivity. Environ. Sci. Pollut. Res. 2021, 28, 10661–10677. [Google Scholar] [CrossRef]
- Padilla-Lozano, C.P.; Collazzo, P. Corporate social responsibility, green innovation and competitiveness–causality in manufacturing. Compet. Rev. Int. Bus. J. 2022, 32, 21–39. [Google Scholar] [CrossRef]
- Ge, Z. Research on corporate environmental responsibility, media coverage, and corporate performance. Manag. Adm. 2024, 4, 54–60. [Google Scholar] [CrossRef]
- Wu, X. China’s OFDI, R&D spillovers and TFP growth. In Proceedings of the 2018 10th International Conference on Information Management and Engineering, Salford, UK, 22–24 September 2018; pp. 146–150. [Google Scholar]
- Liu, H.; Liu, W.; Chen, G. Environmental information disclosure, digital transformation, and total factor productivity: Evidence from Chinese heavy polluting listed companies. Int. J. Environ. Res. Public Health 2022, 19, 9657. [Google Scholar] [CrossRef]
- Zhao, L.; Wang, D.; Wang, X.; Zhang, Z. Impact of green finance on total factor productivity of heavily polluting enterprises: Evidence from green finance reform and innovation pilot zone. Econ. Anal. Policy 2023, 79, 765–785. [Google Scholar] [CrossRef]
- Li, Y.; Zhang, X.; Jin, C.; Huang, Q. The influence of reverse technology spillover of outward foreign direct investment on green total factor productivity in China’s manufacturing industry. Sustainability 2022, 14, 16496. [Google Scholar] [CrossRef]
- Velte, P. Does ESG performance have an impact on financial performance? Evidence from Germany. J. Glob. Responsib. 2017, 8, 169–178. [Google Scholar] [CrossRef]
- Tarmuji, I.; Maelah, R.; Tarmuji, N.H. The impact of environmental, social and governance practices (ESG) on economic performance: Evidence from ESG score. Int. J. Trade Econ. Financ. 2016, 7, 67. [Google Scholar] [CrossRef]
- Giese, G.; Lee, L.E.; Melas, D.; Nagy, Z.; Nishikawa, L. Foundations of ESG investing: How ESG affects equity valuation, risk, and performance. J. Portf. Manag. 2019, 45, 69–83. [Google Scholar] [CrossRef]
- Jiang, S. Research on the Impact of Corporate Environmental Responsibility on the Risk-Taking of Heavily Polluting Listed Companies. Master’s Thesis, Henan University, Kaifeng, China, 2022. [Google Scholar]
- Chen, X. Environmental Responsibility, Media Attention, and Corporate Value. Master’s Thesis, Yangtze University, Jingzhou, China, 2022. [Google Scholar]
- Cao, X.; Deng, M.; Li, H. How does e-commerce city pilot improve green total factor productivity? Evidence from 230 cities in China. J. Environ. Manag. 2021, 289, 112520. [Google Scholar] [CrossRef]
- Hao, X.; Fu, W. Innovation with ecological sustainability: Does corporate environmental responsibility matter in green innovation? J. Econ. Anal. 2023, 2, 21–42. [Google Scholar] [CrossRef]
- Li, J. Research on the relationship between corporate environmental responsibility and financial performance under supply-side reform. Econ. Res. Guide 2019, 6, 102–105. [Google Scholar]
- Siregar, I. CSR-based corporate environmental policy implementation. Br. J. Environ. Stud. 2021, 1, 51–57. [Google Scholar]
- Deng, X.; Li, W.; Ren, X. More sustainable, more productive: Evidence from ESG ratings and total factor productivity among listed Chinese firms. Financ. Res. Lett. 2023, 51, 103439. [Google Scholar] [CrossRef]
- Yu, X.; Chen, Y. Does ESG advantage promote total factor productivity (TFP)? Empirical evidence from China’s listed enterprises. Appl. Econ. 2024, 1–17. [Google Scholar] [CrossRef]
- Halkos, G.; Papageorgiou, G. Extraction of Non-Renewable Resources: A Differential Game Approach. 2008. Available online: https://mpra.ub.uni-muenchen.de/37596/ (accessed on 23 March 2012).
- Linh, D.T. The effects of political connections on entrepreneurial venture operations, employee productivity and investment decisions. J. Small Bus. Enterp. Dev. 2023, 30, 786–803. [Google Scholar] [CrossRef]
- Ding, S.; Guariglia, A.; Harris, R. The determinants of productivity in Chinese large and medium-sized industrial firms, 1998–2007. J. Product. Anal. 2016, 45, 131–155. [Google Scholar] [CrossRef]
- Huang, J.; Cai, X.; Huang, S.; Tian, S.; Lei, H. Technological factors and total factor productivity in China: Evidence based on a panel threshold model. China Econ. Rev. 2019, 54, 271–285. [Google Scholar] [CrossRef]
- Fan, M.; Yang, P.; Li, Q. Impact of environmental regulation on green total factor productivity: A new perspective of green technological innovation. Environ. Sci. Pollut. Res. 2022, 29, 53785–53800. [Google Scholar] [CrossRef] [PubMed]
- Yang, W.; Yang, S. An empirical study on the relationship between corporate social responsibility and financial performance in China: A comparative analysis of large, medium, and small listed companies. Chin. Manag. Sci. 2016, 24, 143–150. [Google Scholar]
- Shan, L.; Li, F.; Ding, Y. Can corporate environmental responsibility achieve a win-win situation for environmental and economic benefits? From the perspective of equity capital cost. Investig. Res. 2021, 40, 71–91. [Google Scholar]
- Liu, Y.; Failler, P.; Chen, L. Can mandatory disclosure policies promote corporate environmental responsibility?—Quasi-natural experimental research on China. Int. J. Environ. Res. Public Health 2021, 18, 6033. [Google Scholar] [CrossRef]
- Al-Shammari, M.; Rasheed, A.A.; Banerjee, S.N. Are all narcissistic CEOs socially responsible? An empirical investigation of an inverted U-shaped relationship between CEO narcissism and corporate social responsibility. Group Organ. Manag. 2022, 47, 612–646. [Google Scholar] [CrossRef]
- Pareek, R.; Sahu, T.N. How far the ownership structure is relevant for CSR performance? An empirical investigation. Corporate Governance. Int. J. Bus. Soc. 2022, 22, 128–147. [Google Scholar]
- Li, Z.; Wang, F.; Yang, L. Looking in and looking out: Effects of (in) congruent corporate social responsibility on organizational cynicism. Soc. Behav. Personal. Int. J. 2021, 49, 1–15. [Google Scholar] [CrossRef]
- Ersoy, E.; Swiecka, B.; Grima, S.; Özen, E.; Romanova, I. The impact of ESG scores on bank market value? Evidence from the US banking industry. Sustainability 2022, 14, 9527. [Google Scholar] [CrossRef]
- Bhatnagar, C.S.; Bhatnagar, D.; Bhullar, P.S. Social expenditure, business responsibility reporting score and firm performance: Empirical evidence from India. Corp. Gov. Int. J. Bus. Soc. 2023, 23, 1404–1436. [Google Scholar] [CrossRef]
- De la Fuente, G.; Ortiz, M.; Velasco, P. The value of a firm’s engagement in ESG practices: Are we looking at the right side? Long Range Plan. 2020, 55, 102143. [Google Scholar] [CrossRef]
- Lee, M.T.; Raschke, R.L. Stakeholder legitimacy in firm greening and financial performance: What about greenwashing temptations? J. Bus. Res. 2023, 155, 113393. [Google Scholar] [CrossRef]
- Lin, Y.; Fu, C.; Zheng, J. New structural environmental economics: An initial exploration of a theoretical framework. J. Nanchang Univ. (Humanit. Soc. Sci. Ed.) 2021, 52, 25–43. [Google Scholar]
- Lin, Y.; Mao, Y.; Tan, H. Environmental investment decision-making in politically connected firms: Leading by example or retreating behind? Account. Res. 2021, 6, 159–175. [Google Scholar]
- Corso, A. Logarithmic Scales. Science 1996, 271, 15. [Google Scholar]
- Zhao, L.; Wang, X. Can corporate green investment and green expenses improve operating performance? An empirical analysis based on EBM and panel Tobit model. J. Beijing Inst. Technol. (Soc. Sci. Ed.) 2022, 24, 28–42. [Google Scholar]
- Zhang, Q.; Zheng, Y.; Kong, D. Regional environmental governance pressure, executive experience, and corporate environmental investment: A quasi-natural experiment based on the “Ambient Air Quality Standards (2012)”. Econ. Res. J. 2019, 54, 183–198. [Google Scholar]
- Mundlak, Y. Empirical production function free of management bias. J. Farm Econ. 1961, 43, 44–56. [Google Scholar] [CrossRef]
- Hoch, I. Estimation of production function parameters combining time-series and cross-section data. Econom. J. Econom. Soc. 1962, 30, 34–53. [Google Scholar] [CrossRef]
- Griliches, Z. R&D and productivity: The unfinished business. In R&D and Productivity: The Econometric Evidence; University of Chicago Press: Chicago, IL, USA, 1998; pp. 269–283. [Google Scholar]
- Blundell, R.; Bond, S. GMM estimation with persistent panel data: An application to production functions. Econom. Rev. 2000, 19, 321–340. [Google Scholar] [CrossRef]
- Olley, G.S.; Pakes, A. The Dynamics of Productivity in the Telecommunications Equipment Industry. Econometrica 1996, 64, 1263. [Google Scholar] [CrossRef]
- Levinsohn, J.; Petrin, A. Estimating production functions using inputs to control for unobservables. Rev. Econ. Stud. 2003, 70, 317–341. [Google Scholar] [CrossRef]
- Lu, X.; Lian, Y. Estimation of total factor productivity of Chinese industrial enterprises: 1999–2007. China Econ. Q. 2012, 11, 541–558. [Google Scholar]
- De Loecker, J. Do exports generate higher productivity? Evidence from Slovenia. J. Int. Econ. 2007, 73, 69–98. [Google Scholar] [CrossRef]
- Swaab, R.I.; Schaerer, M.; Anicich, E.M.; Ronay, R.; Galinsky, A.D. The too-much-talent effect: Team interdependence determines when more talent is too much or not enough. Psychol. Sci. 2014, 25, 1581–1591. [Google Scholar] [CrossRef]
- Lind, J.T.; Mehlum, H. With or without U? The appropriate test for a U-shaped relationship. Oxf. Bull. Econ. Stat. 2010, 72, 109–118. [Google Scholar] [CrossRef]
- Simonsohn, U.; Nelson, L.D.; Simmons, J.P. P-curve: A key to the file-drawer. J. Exp. Psychol. Gen. 2014, 143, 534. [Google Scholar] [CrossRef]
- Kostyshak, S. Non-Parametric Testing of U-Shaped Relationships. 2017. Available online: https://papers.ssrn.com/sol3/papers.cfm?abstract_id=2905833 (accessed on 20 July 2017).
- Rigby, R.A.; Stasinopoulos, D.M. A semi-parametric additive model for variance heterogeneity. Stat. Comput. 1996, 6, 57–65. [Google Scholar] [CrossRef]
- Zhao, M.; Liu, F.; Sun, W.; Tao, X. The relationship between environmental regulation and green total factor productivity in China: An empirical study based on the panel data of 177 cities. Int. J. Environ. Res. Public Health 2020, 17, 5287. [Google Scholar] [CrossRef] [PubMed]
- Heffernan, S.A.; Fu, X. Determinants of financial performance in Chinese banking. Appl. Financ. Econ. 2010, 20, 1585–1600. [Google Scholar] [CrossRef]
- Hu, X.; Hua, R.; Liu, Q.; Wang, C. The green fog: Environmental rating disagreement and corporate greenwashing. Pac. Basin Financ. J. 2023, 78, 101952. [Google Scholar] [CrossRef]
- Douglas, P.H. The Cobb-Douglas production function once again: Its history, its testing, and some new empirical values. J. Political Econ. 1976, 84, 903–915. [Google Scholar] [CrossRef]
- Bellman, R. Dynamic programming. Science 1966, 153, 34–37. [Google Scholar] [CrossRef]
| TFP Measurement Method | Description |
|---|---|
| OLS | Endogeneity is not considered. |
| FE | Endogeneity and selectivity bias cannot be solved. |
| OP | Endogeneity and sample selection can be solved without loss of data. |
| LP | Expanding the absolute value of TFP |
| GMM | Data will be lost, and suitable instrumental variables need to be found. |
| DEA | Suitable for balanced panels, mostly used in industry and geographical studies |
| Variables | Observation | Meaning of Indicators | Mean | Std | Min | Max |
|---|---|---|---|---|---|---|
| TFP | 25,962 | Total factor productivity | 6.706 | 0.868 | 2.560 | 11.160 |
| ESR | 25,962 | Environmental social responsibility | 0.408 | 0.462 | 0.000 | 5.204 |
| Assets | 25,962 | Natural logarithm of total corporate assets which can reflect company size | 22.290 | 1.261 | 19.570 | 26.452 |
| ROA | 25,962 | Return on assets | 0.042 | 0.063 | −0.382 | 0.255 |
| Fixed | 25,962 | Percentage of fixed assets | 0.221 | 0.152 | 0.002 | 0.725 |
| BM | 25,962 | Book-to-market ratio | 1.050 | 1.174 | 0.052 | 10.089 |
| Mfee | 25,962 | Management cost ratio | 0.084 | 0.065 | 0.007 | 0.641 |
| ROE | 25,962 | Return on equity | 0.066 | 0.125 | −0.962 | 0.415 |
| ATO | 25,962 | Total asset turnover | 0.657 | 0.426 | 0.055 | 2.891 |
| TFP | ESR | Size | ROA | Fixed | BM | Mfee | ROE | ATO | |
|---|---|---|---|---|---|---|---|---|---|
| TFP | 1.000 | ||||||||
| ESR | 0.567 *** | 1.000 | |||||||
| Assets | 0.729 *** | 0.790 *** | 1.000 | ||||||
| ROA | 0.113 *** | 0.017 *** | −0.001 | 1.000 | |||||
| Fixed | −0.143 *** | 0.045 *** | 0.071 *** | −0.094 *** | 1.000 | ||||
| BM | 0.479 *** | 0.480 *** | 0.624 *** | −0.228 *** | 0.068 *** | 1.000 | |||
| Mfee | −0.597 *** | −0.111 *** | −0.344 *** | −0.179 *** | −0.067 *** | −0.255 *** | 1.000 | ||
| ROE | 0.207 *** | 0.099 *** | 0.107 *** | 0.903 *** | −0.082 *** | −0.119 *** | −0.221 *** | 1.000 | |
| ATO | 0.557 *** | 0.166 *** | 0.083 *** | 0.173 *** | −0.010 | 0.019 *** | −0.434 *** | 0.206 *** | 1.000 |
| Variables | (1) TFP | (2) TFP | (3) TFP | (4) TFP | (5) TFP |
|---|---|---|---|---|---|
| ESR | 0.789 *** | 0.162 *** | 0.677 *** | 0.919 *** | 0.233 *** |
| (0.041) | (0.038) | (0.035) | (0.036) | (0.030) | |
| Size control variables | YES | YES | |||
| Remaining performance controls | YES | YES | |||
| Remaining control variables | YES | YES | |||
| Time fixed effects | YES | YES | YES | YES | YES |
| Individual fixed effects | YES | YES | YES | YES | YES |
| Observations | 25,962 | 25,962 | 25,962 | 25,962 | 25,962 |
| 0.355 | 0.452 | 0.609 | 0.622 | 0.793 |
| Variables | (1) | (2) |
|---|---|---|
| TFP | TFP | |
| ESR | 1.438 *** | 0.549 *** |
| (0.075) | (0.053) | |
| −0.316 *** | −0.127 *** | |
| (0.031) | (0.017) | |
| Control variables | NO | YES |
| Time fixed effects | YES | YES |
| Individual fixed effects | YES | YES |
| Observations | 25,962 | 25,962 |
| 0.570 | 0.940 | |
| U-test | t = 5.85 ***, p = 0 ***, ESR = 2.17 when curve get max | |
| Goodness of Fit of the Model | Inverted U-Shape Test | |
|---|---|---|
| GAM | 0.459 | Pass |
| Random forest | 0.659 | Pass |
| Variables | (1) | (2) | (3) | (4) | (5) |
|---|---|---|---|---|---|
| TFP-OLS | TFP-LP | TFP-GMM | TFP-FE | TFP-RF | |
| ESR | 0.468 *** | 0.437 *** | 0.224 *** | 0.493 *** | 0.502 *** |
| (0.028) | (0.029) | (0.034) | (0.028) | (0.028) | |
| Control variables | YES | YES | YES | YES | YES |
| Time fixed effects | YES | YES | YES | YES | YES |
| Individual fixed effects | YES | YES | YES | YES | YES |
| Observations | 25,962 | 25,962 | 25,962 | 25,962 | 25,962 |
| 0.929 | 0.884 | 0.688 | 0.690 | 0.933 |
| Variables | (1) | (2) | (3) | (4) |
|---|---|---|---|---|
| Step 1 ESR | Step 2 TFP | Step 1 ESR | Step 2 TFP | |
| L.ESR | 0.564 *** | |||
| (0.013) | ||||
| L2.ESR | 0.312 *** | |||
| (0.018) | ||||
| ESR | 0.271 *** | 0.227 *** | ||
| (0.042) | (0.061) | |||
| Control variables | YES | YES | YES | YES |
| Time fixed effects | YES | YES | YES | YES |
| Individual fixed effects | YES | YES | YES | YES |
| Kleibergen–Paap rk LM | 147.422 *** | 69.924 *** | ||
| Kleibergen–Paap rk Wald F | 1876.489 [16.38] | 315.344 [16.38] | ||
| Observations | 19,126 | 19,126 | 16,078 | 16,078 |
| Variables | (1) | (2) | (3) | (4) | (5) |
|---|---|---|---|---|---|
| TFP-OLS | TFP-GMM | TFP-LP | TFP-FE | TFP-RF | |
| ESR | 1.014 *** | 0.984 *** | 0.595 *** | 1.058 *** | 1.065 *** |
| (0.048) | (0.048) | (0.057) | (0.049) | (0.049) | |
| −0.218 *** | −0.218 *** | −0.147 *** | −0.227 *** | −0.228 *** | |
| (0.019) | (0.018) | (0.018) | (0.020) | (0.020) | |
| Control variables | YES | YES | YES | YES | YES |
| Time fixed effects | YES | YES | YES | YES | YES |
| Individual fixed effects | YES | YES | YES | YES | YES |
| Observations | 25,962 | 25,962 | 25,962 | 25,962 | 25,962 |
| 0.934 | 0.891 | 0.694 | 0.940 | 0.938 |
| Variables | (1) | (2) | (3) | (4) | (5) | (6) |
|---|---|---|---|---|---|---|
| Step 1 | Step 1 | Step 2 | Step 1 | Step 1 | Step 2 | |
| ESR | TFP | ESR | TFP | |||
| L.ESR | 0.455 *** | −0.266 * | ||||
| (0.029) | (0.126) | |||||
| L.ESR2 | 0.0484 *** | 0.778 *** | ||||
| (0.013) | (0.072) | |||||
| L2.ESR | 0.265 *** | −0.111 | ||||
| (0.033) | (0.170) | |||||
| L2.ESR2 | 0.0222 | 0.457 *** | ||||
| (0.018) | (0.109) | |||||
| ESR | 1.194 *** | 1.139 *** | ||||
| (0.073) | (0.111) | |||||
| −0.234 *** | −0.198 *** | |||||
| (0.026) | (0.035) | |||||
| Control variables | YES | YES | YES | YES | YES | YES |
| Time fixed effects | YES | YES | YES | YES | YES | YES |
| Individual fixed effects | YES | YES | YES | YES | YES | YES |
| Kleibergen–Paap rk LM | 423.413 *** | 228.476 *** | ||||
| Kleibergen–Paap rk Wald F | 767.543 [7.03] | 199.574 [7.03] | ||||
| Observations | 19,126 | 19,126 | 19,126 | 16,078 | 16,078 | 16,078 |
| Variables | (1) | (2) | (3) | (4) | (5) | (6) |
|---|---|---|---|---|---|---|
| TFP | ||||||
| Adding Interaction Effects | Replacement Regression Model | Time Intervals | ||||
| OLS | Poisson | 2012–2019 | 2020–2022 | |||
| ESR | 1.433 *** | 0.550 *** | 0.147 *** | 0.0964 *** | 0.580 *** | 1.002 *** |
| (0.075) | (0.053) | (0.023) | (0.008) | (0.067) | (0.094) | |
| −0.314 *** | −0.128 *** | −0.0138 * | −0.0244 *** | −0.137 *** | −0.211 *** | |
| (0.030) | (0.017) | (0.006) | (0.003) | (0.022) | (0.027) | |
| Control variables | NO | YES | YES | YES | YES | YES |
| Time fixed effects | YES | YES | NO | YES | YES | YES |
| Individual fixed effects | YES | YES | NO | YES | YES | YES |
| interaction fixed effects | YES | YES | NO | NO | NO | NO |
| Observations | 25,962 | 25,962 | 25,962 | 25,962 | 15,194 | 10,768 |
| 0.374 | 0.796 | 0.853 | 0.030 | 0.739 | 0.777 | |
| Variables | (1) | (2) | (3) |
|---|---|---|---|
| TFP | TFP | TFP | |
| Small Company | Large Company | Chow Test | |
| ESR | 2.618 ** | 0.270 *** | 1.352 *** |
| (0.273) | (0.028) | (0.159) | |
| Large×ESR | −1.119 *** | ||
| (0.151) | |||
| Large | 0.089 *** | ||
| (0.021) | |||
| Control variables | YES | YES | YES |
| Time fixed effects | YES | YES | YES |
| Individual fixed effects | YES | YES | YES |
| Observations | 3638 | 22,324 | 25,962 |
| 0.756 | 0.779 | 0.795 | |
| Between-group coefficient difference test | Chi = 3.38 * | ||
| Variables | (1) | (2) | (3) |
|---|---|---|---|
| TFP | TFP | TFP | |
| High-Tech | Non-High-Tech | Chow Test | |
| ESR | 0.322 *** | 0.205 *** | 0.227 *** |
| (0.041) | (0.039) | (0.033) | |
| High-tech×ESR | 0.0244 | ||
| (0.034) | |||
| High-tech | 0.0309 | ||
| (0.027) | |||
| Control variables | YES | YES | YES |
| Time fixed effects | YES | YES | YES |
| Individual fixed effects | YES | YES | YES |
| Observations | 11,202 | 14,760 | 25,962 |
| 0.792 | 0.788 | 0.793 | |
| Between-group coefficient difference test | Chi = 12.09 *** | ||
| Variables | (1) | (2) | (3) | (4) | (5) | (6) |
|---|---|---|---|---|---|---|
| TFP | TFP | TFP | TFP | TFP | TFP | |
| Small Company | Large Company | Chow Test | High-Tech | Non-High-Tech | Chow Test | |
| ESR | 3.481 *** | 0.595 *** | 0.536 *** | 0.586 *** | 0.532 *** | 0.552 *** |
| (0.474) | (0.055) | (0.053) | (0.090) | (0.068) | (0.054) | |
| −1.596 *** | −0.129 *** | 2.121 ** | −0.127 *** | −0.120 *** | −0.125 *** | |
| (0.569) | (0.018) | (0.395) | (0.035) | (0.020) | (0.017) | |
| −2.246 *** | ||||||
| (0.395) | ||||||
| Large | 0.003 | |||||
| (0.012) | ||||||
|
High-tech× | −0.01 | |||||
| (0.014) | ||||||
| High-tech | 0.038 | |||||
| (0.023) | ||||||
| Control variables | YES | YES | YES | YES | YES | YES |
| Time fixed effects | YES | YES | YES | YES | YES | YES |
| Individual fixed effects | YES | YES | YES | YES | YES | YES |
| Observations | 3638 | 22,324 | 25,962 | 11,202 | 14,760 | 25,962 |
| 0.759 | 0.783 | 0.797 | 0.794 | 0.790 | 0.796 | |
| Between-group coefficient difference test | Chi = 6.69 ** | Chi = 0.10 | ||||
| Variables | (1) | (2) | (3) | (4) |
|---|---|---|---|---|
| TFP | TFP | TFP | TFP | |
| Full Sample | Heavy “Greenwashing” | Weak “Greenwashing” | No ”Greenwashing” | |
| ESR | 0.246 *** | 0.065 | 0.265 ** | 0.315 *** |
| (0.033) | (0.065) | (0.100) | (0.093) | |
| Control variables | YES | YES | YES | YES |
| Time fixed effects | YES | YES | YES | YES |
| Individual fixed effects | YES | YES | YES | YES |
| Observations | 7211 | 836 | 5027 | 1348 |
| 0.801 | 0.710 | 0.811 | 0.776 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cao, Y.; Xu, T. The Impact of Environmental Social Responsibility on Total Factor Productivity: Evidence from Listed Companies in China. Sustainability 2024, 16, 8137. https://doi.org/10.3390/su16188137
Cao Y, Xu T. The Impact of Environmental Social Responsibility on Total Factor Productivity: Evidence from Listed Companies in China. Sustainability. 2024; 16(18):8137. https://doi.org/10.3390/su16188137
Chicago/Turabian StyleCao, Yuanyu, and Tao Xu. 2024. "The Impact of Environmental Social Responsibility on Total Factor Productivity: Evidence from Listed Companies in China" Sustainability 16, no. 18: 8137. https://doi.org/10.3390/su16188137
APA StyleCao, Y., & Xu, T. (2024). The Impact of Environmental Social Responsibility on Total Factor Productivity: Evidence from Listed Companies in China. Sustainability, 16(18), 8137. https://doi.org/10.3390/su16188137





