Ground Surface Effect of Earth Pressure Balance Tunnelling in Deltaic Deposits: A Case Study of Line 9 of the Barcelona Metro
Abstract
1. Introduction and Engineering Background
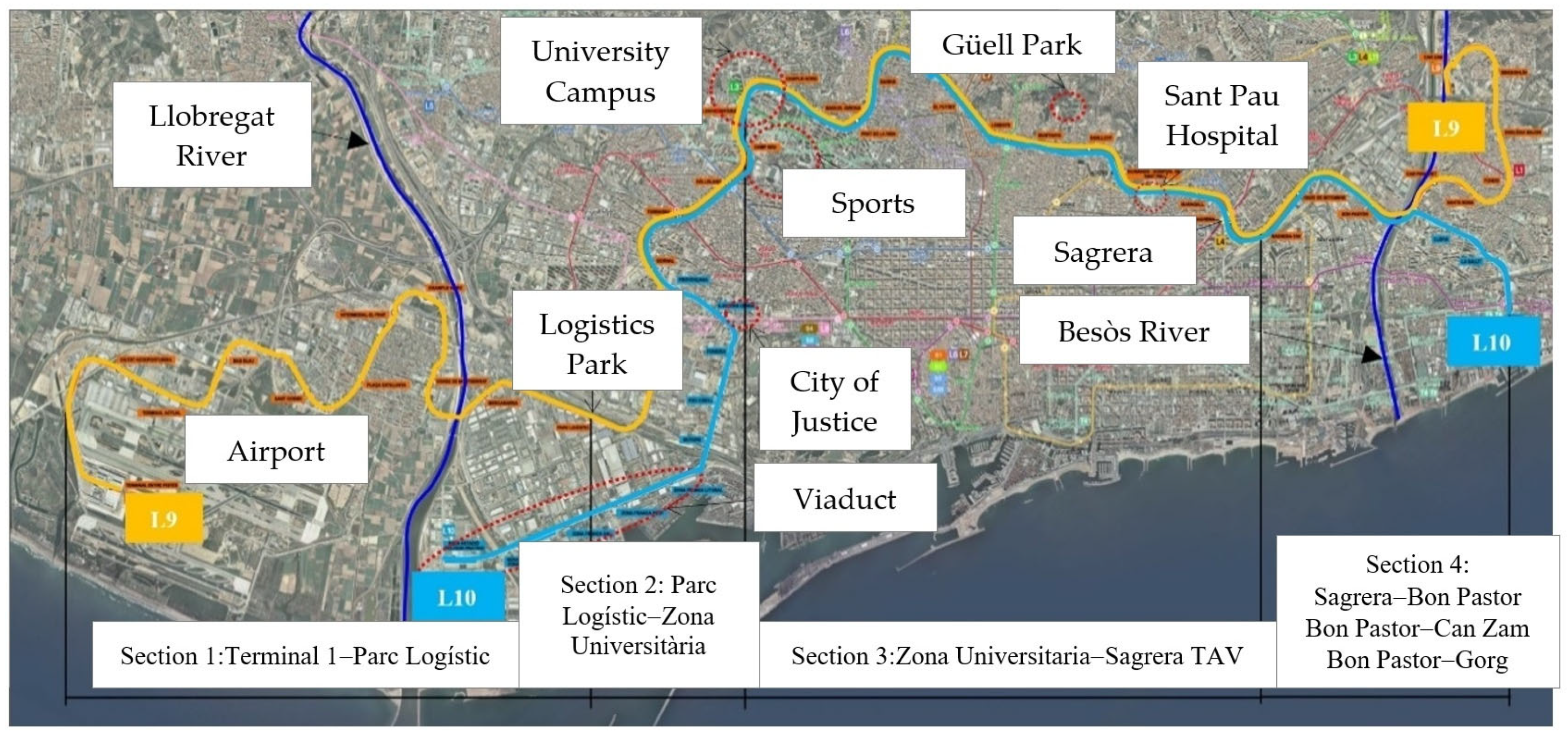
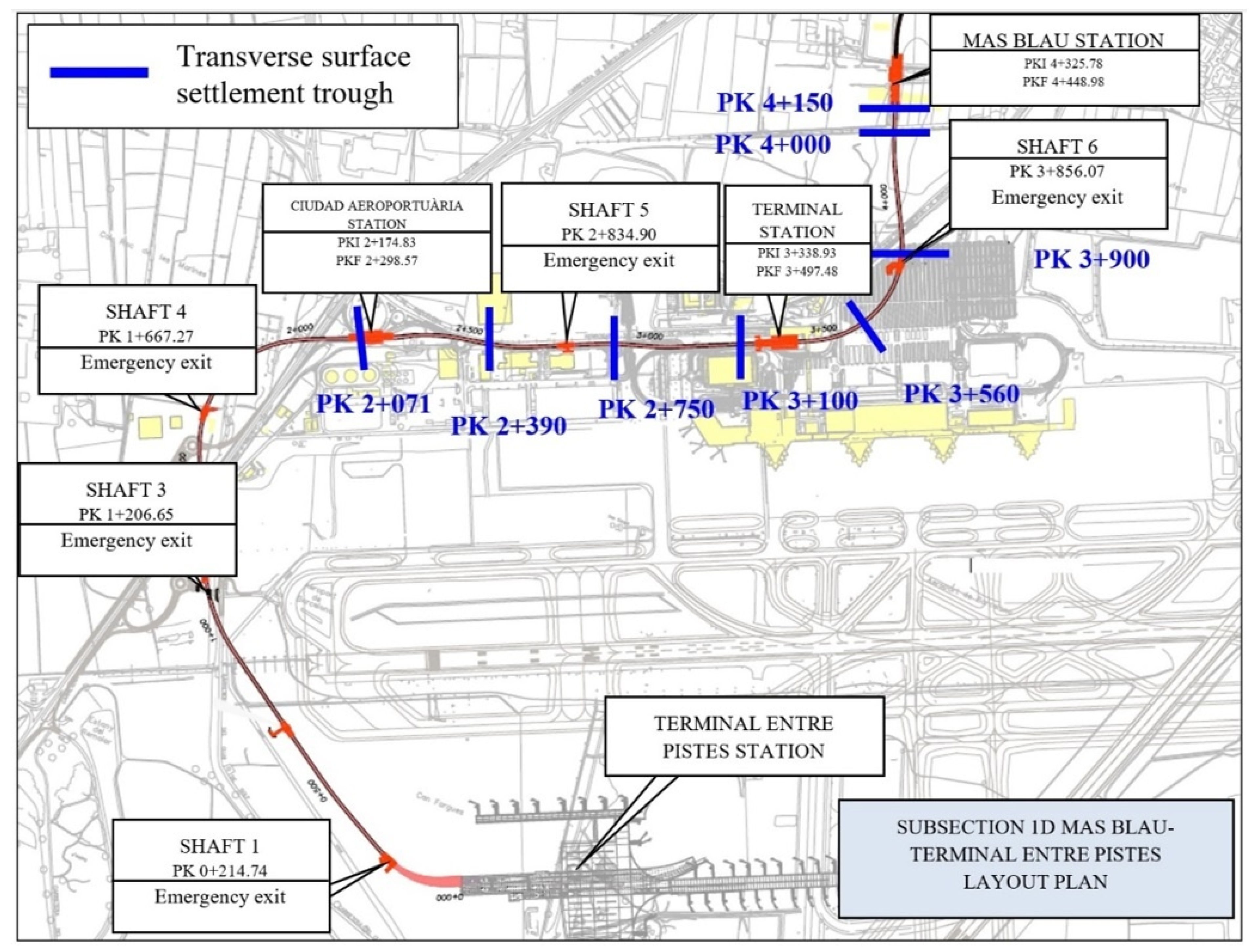
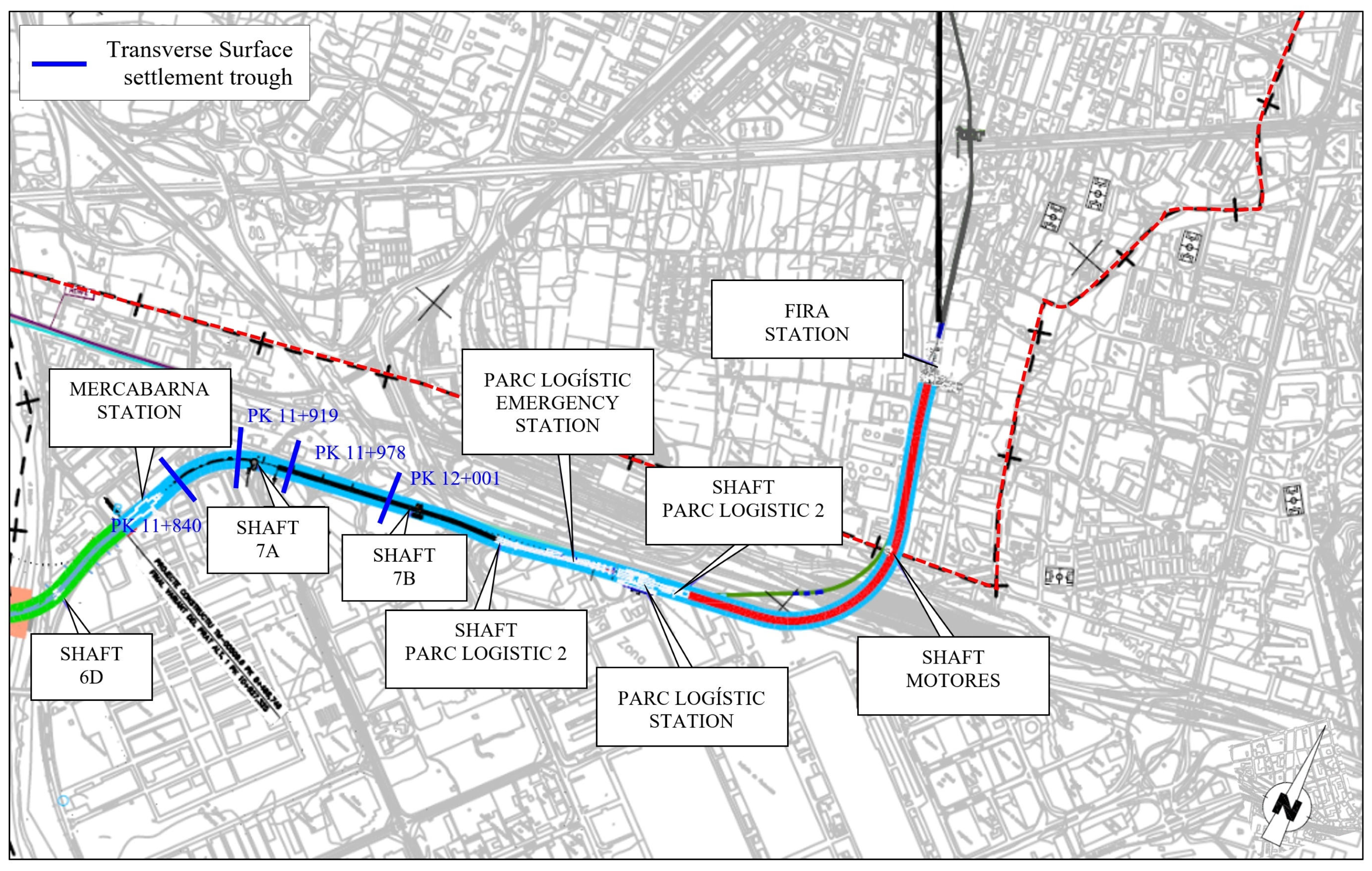
2. Study Area and Tunnelling Details
2.1. Project Overview
2.2. Operational Control Parameters Used in EPBs
2.2.1. Face Pressure (P1)
2.2.2. Bentonite Slurry Pressure around the Shield (P2) and (V2)
2.2.3. Pressure and Volume of Grout Injected into the Shield Tail (P3) and (V3)
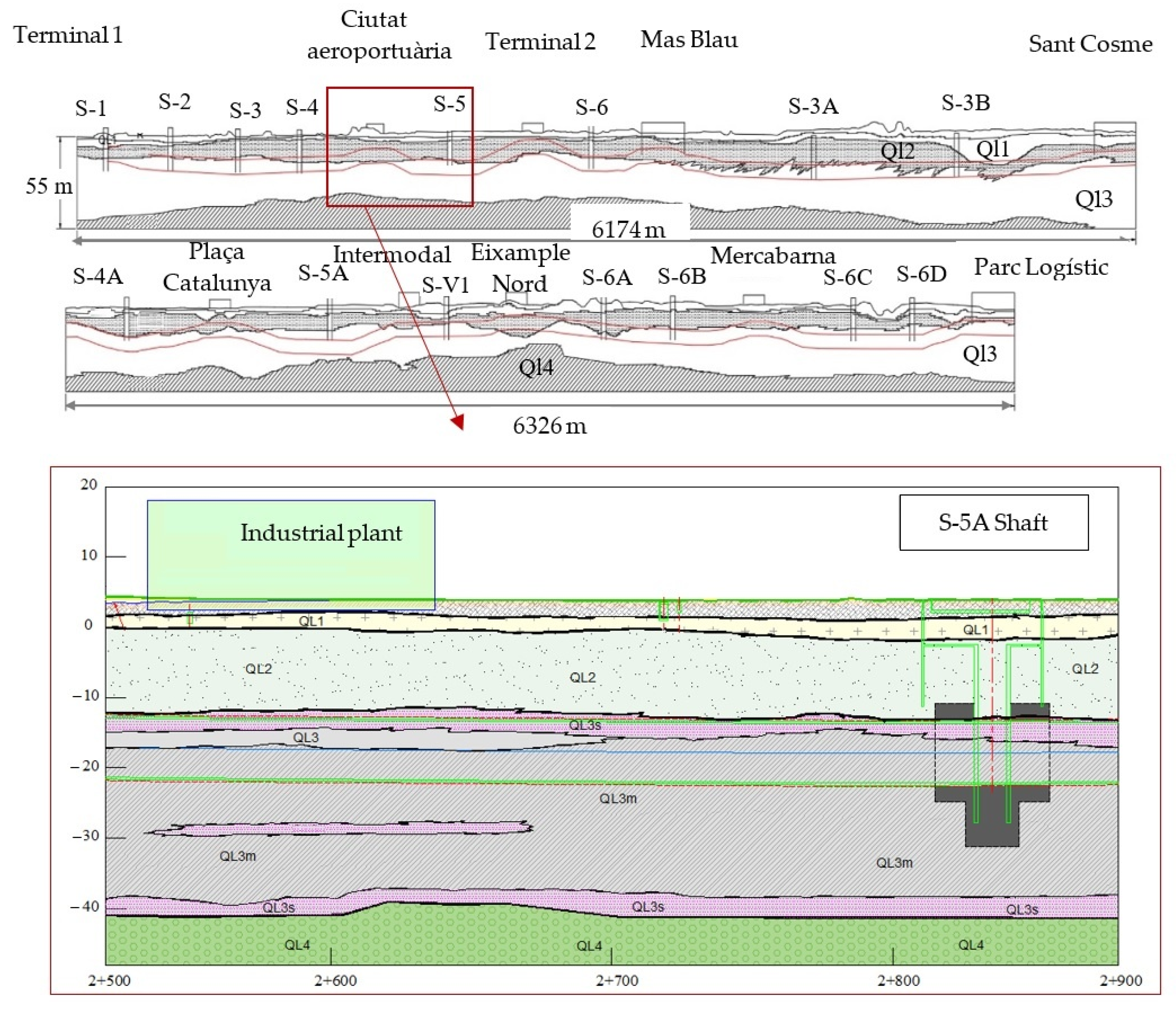
3. Geological Conditions
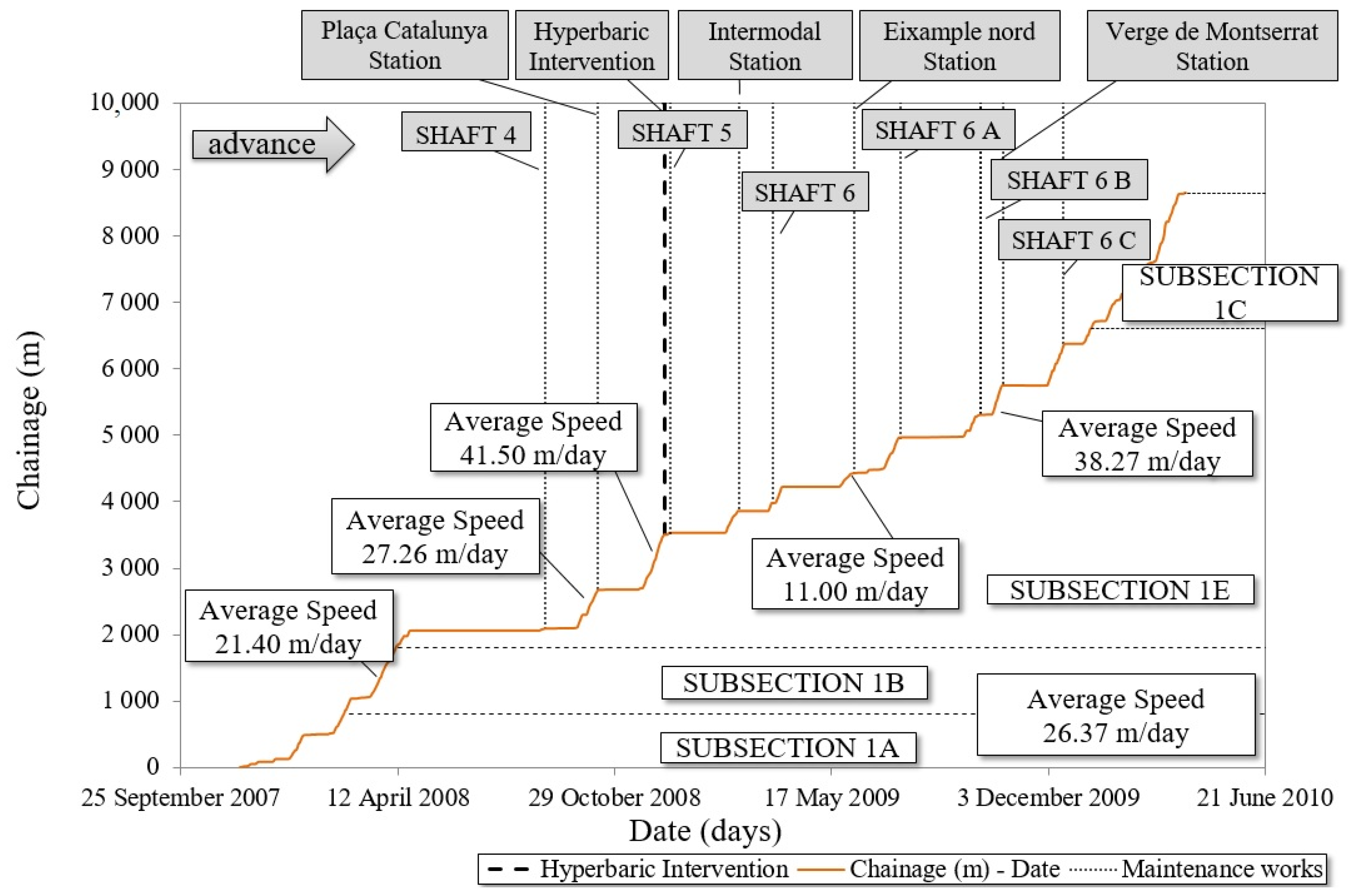
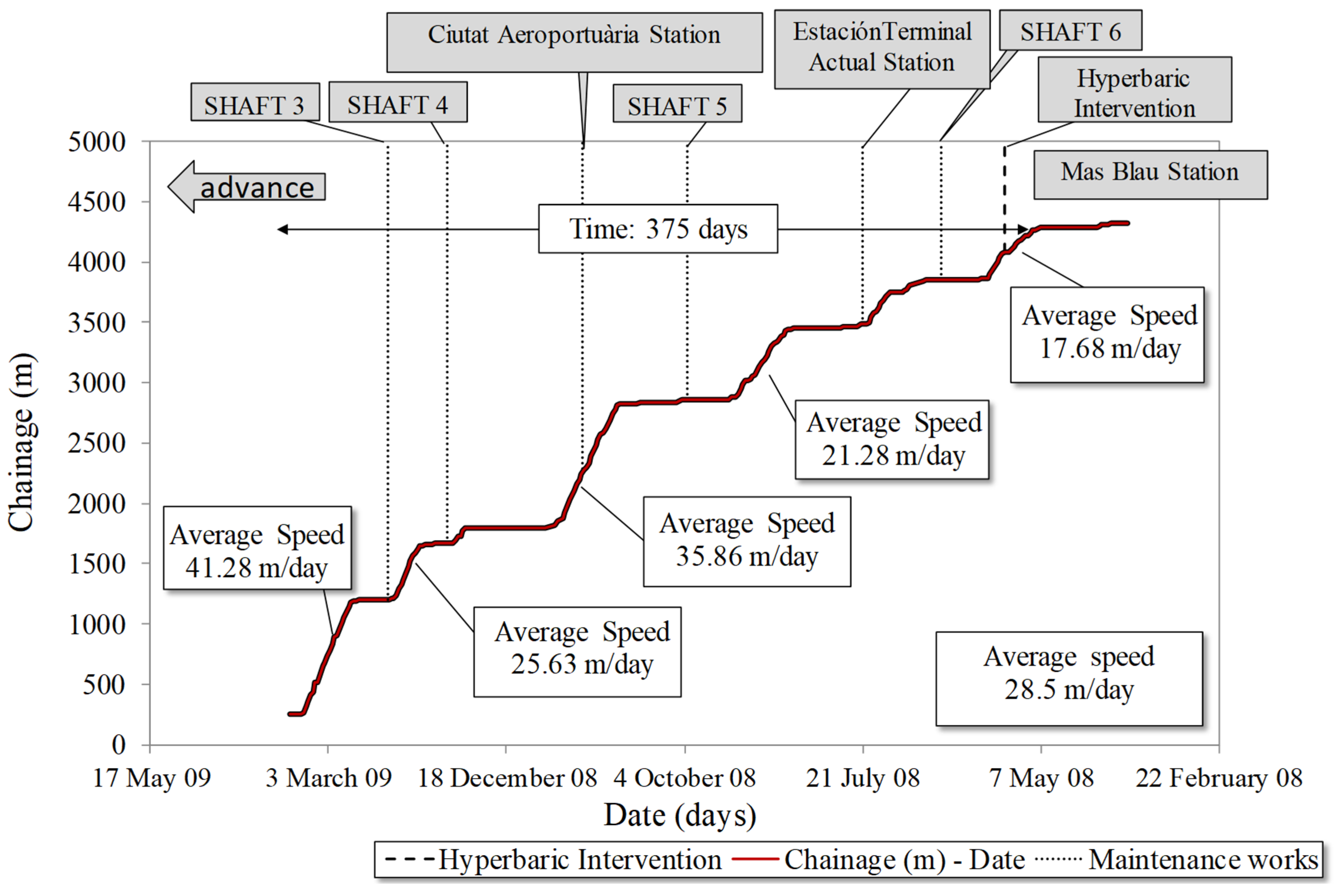
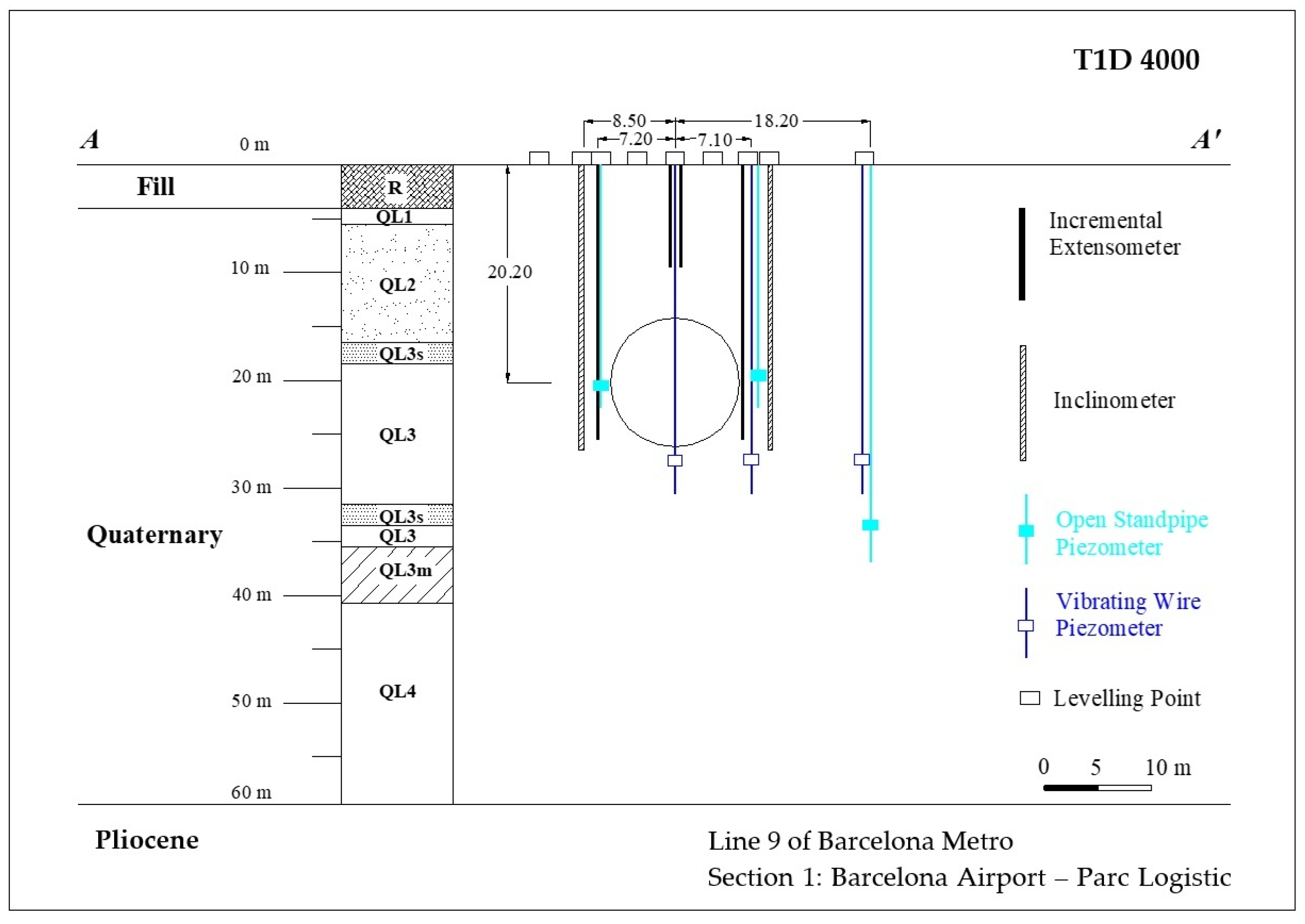
4. In Situ Measurement Equipment
5. Results of Surface Control and Discussions
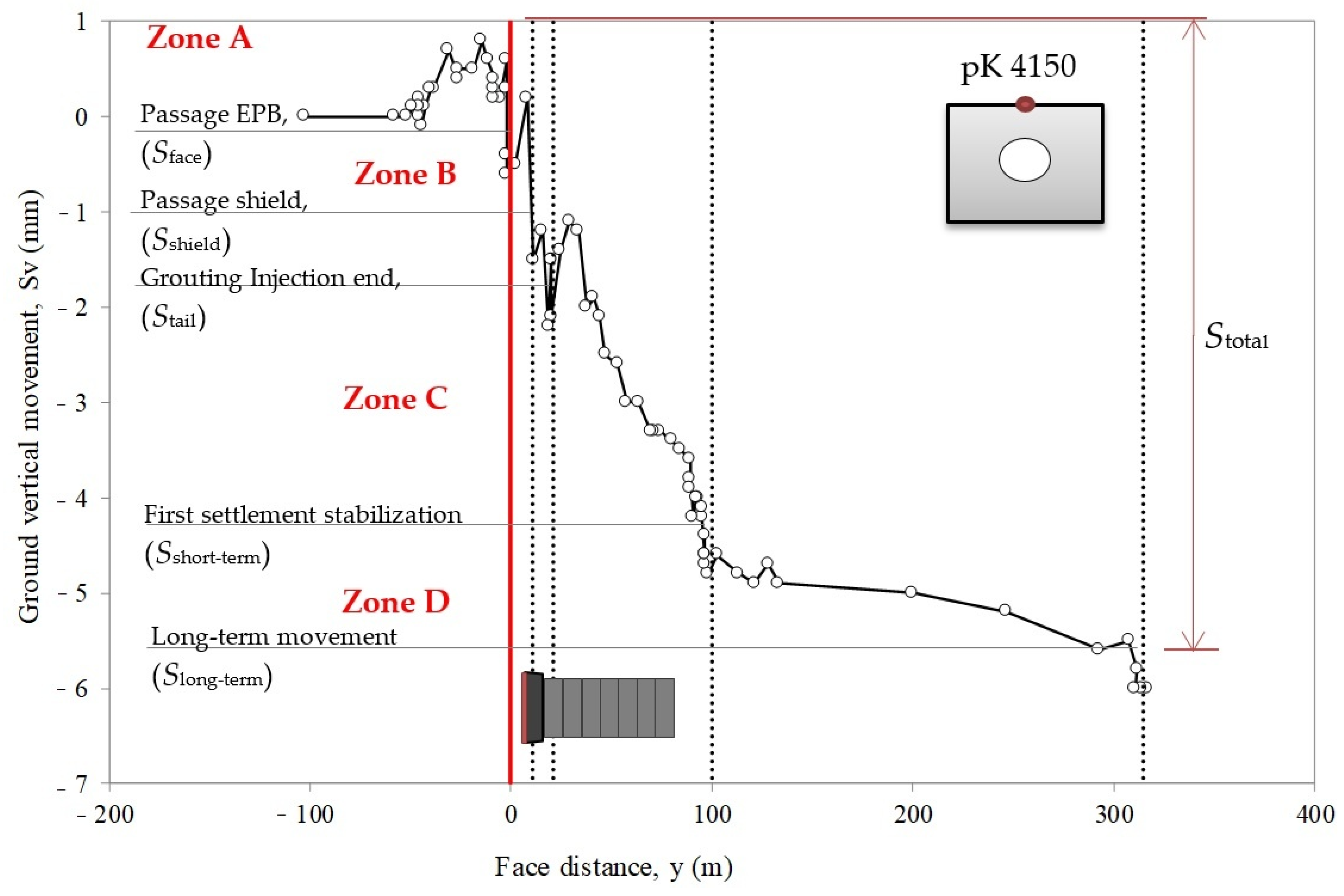
5.1. Vertical Displacements Parallel to the Tunnel Axis
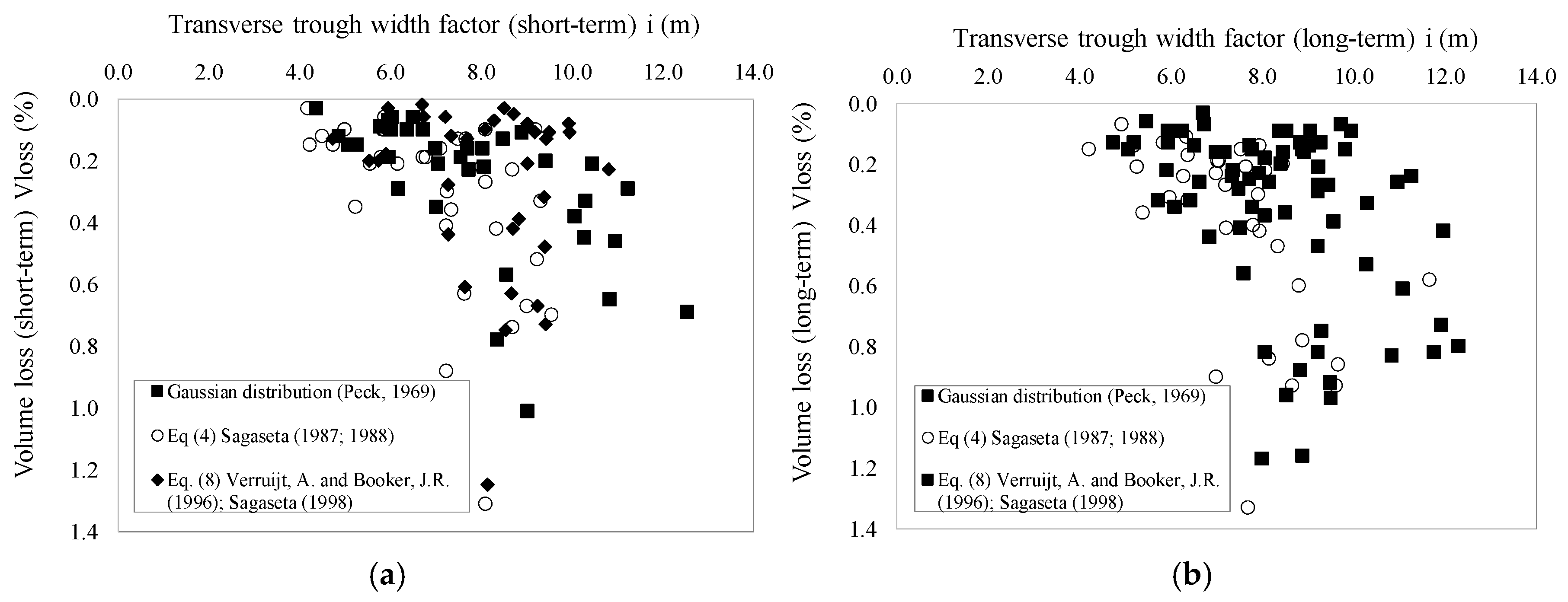
5.2. Volume Loss
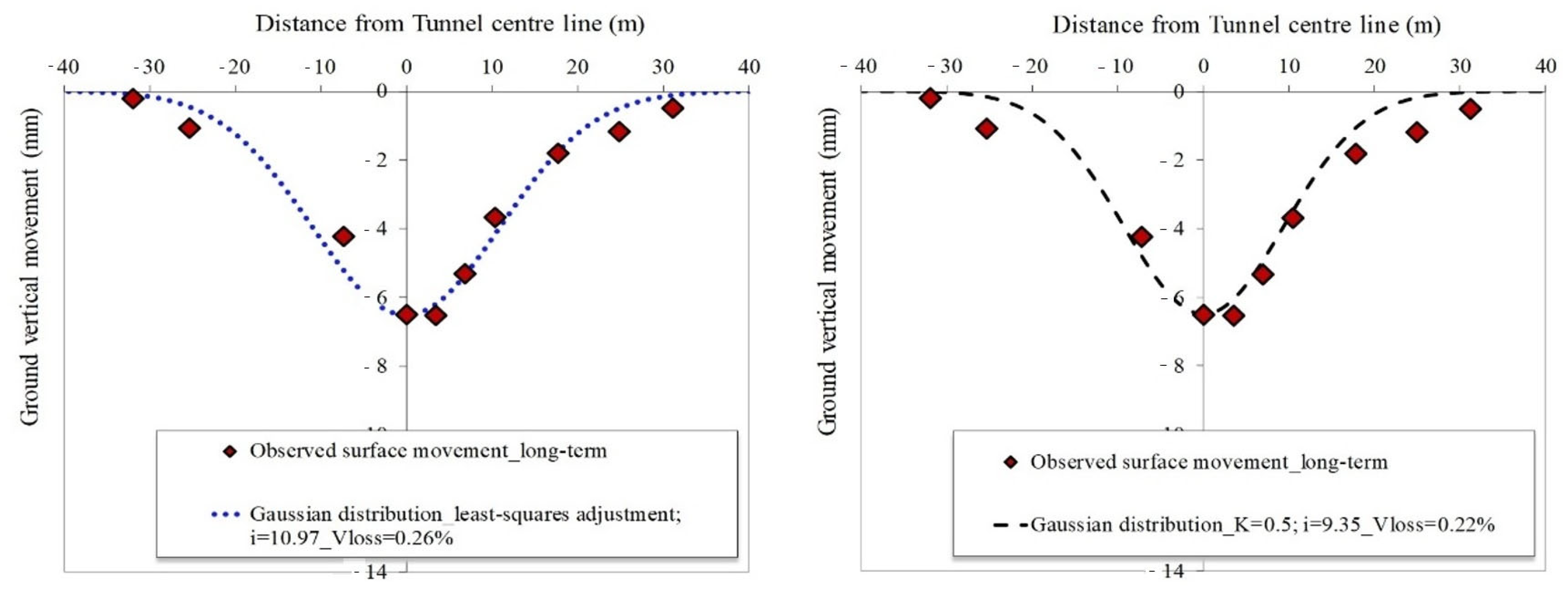
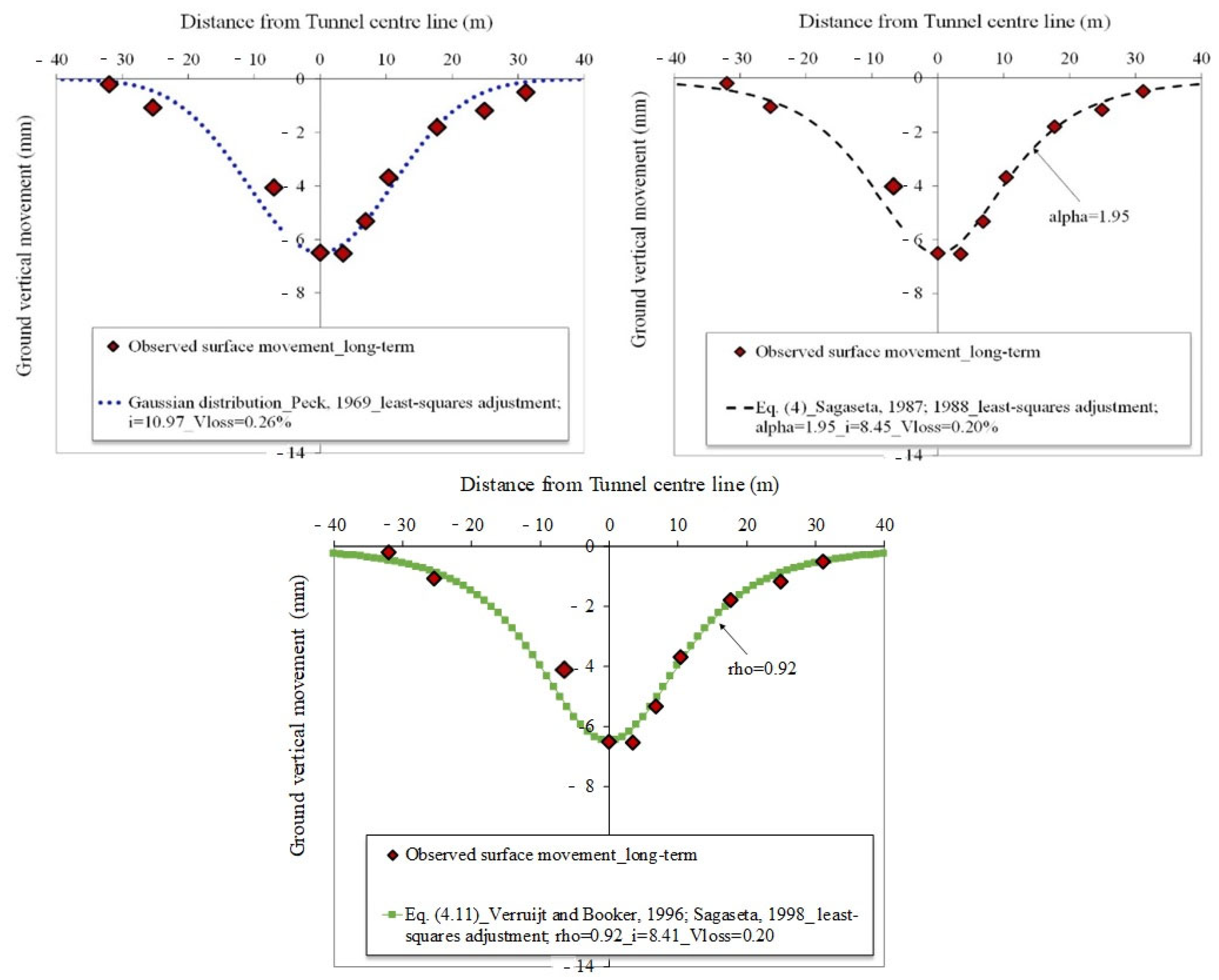
5.3. Vertical Displacements Perpendicular to the Tunnel Axis
6. Theoretical Approach with Analytics Solutions
6.1. Tunnel Non-Symmetric Deformation: Ovalisation
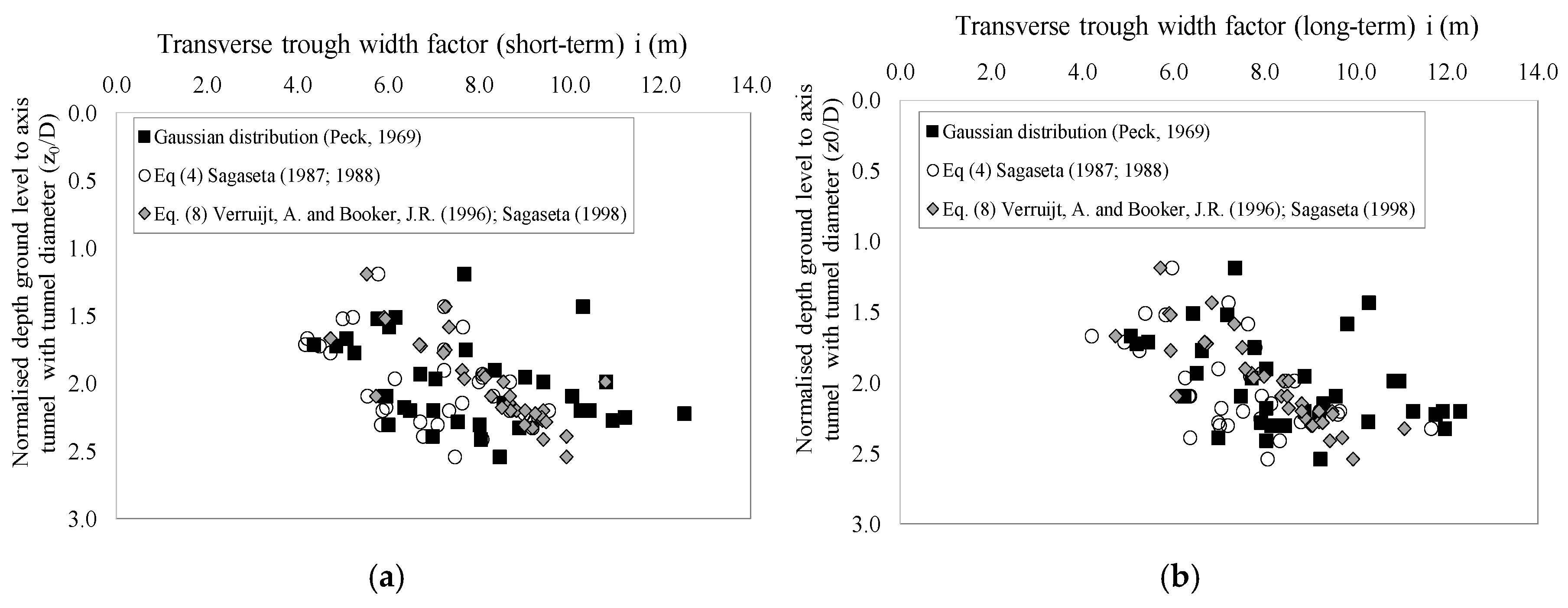
6.2. Results from Analytics Solutions
7. Comparison with Other Surface Settlement Cases


| Case Nº | Location | Geology | Method Used | Prof z0 (m) | Diameter D (m) | Width iz (m) | Máx. Settlement Svmax (mm) | K | Vloss (%) | References |
|---|---|---|---|---|---|---|---|---|---|---|
| 0 | Line 9, Barcelona (Spain) | Fine sand, silty clays, sandy silts, and silty sands | EPB | 20.7 | 9.40 | 11.10 | 18.10 | 0.54 | 0.73 | |
| 1 | Contract CR3, (Up-track), Kaohsiung, Taiwan | Alluvial: silt, sand, and clay | EPB | 13.0–20.0 | 6.3 | 7.52 | 27.0 | 0.35–0.55 | 0.20–1.05 | [59] |
| Contract CR3, (Down-track), Kaohsiung, Taiwan | Alluvial: silt, sand, and clay | EPB | 13.0–20.0 | 6.3 | 7.60 | 27.0 | 0.35–0.54 | 0.18–1.27 | [59] | |
| 2 | Taipei Rapid Transit System (TRTS) CA450A, Taipei, Taiwan | Silty clay and silty sand | EPB | 5.0–25.0 | 6.42 | 6.0 | 50.9 | N/A | 0.71–1.82 | [6] |
| 3 | MRT, CH218, Taipei, Taiwan | Silty clay and silty sand | EPB | 18.5 | 6.0 | 8.9 | 25.0 | 0.40 | 1.3 | [55] |
| 4 | MRTA, Bangkok Sewer Tunnel, Thailand | Soft clay, very stiff clay, hard clay, and dense sand | EPB | 8.0–25.0 | 6.3 | 9.5 | 0.3–0.6 | 0.5–2.5 | [3] | |
| 5 | Hangzhou Metro, Right Line, Hangzhou, China | Alluvial deposits (sandy silt, silty clay, fine sand, and rounded gravel) | Mud shield | 21.0–26.5 | 11.30 | N/A | 6.0–20.0 | 0.26–0.30 | 0.093–0.32 | [60] |
| 6 | Line 5, Milan (Italy) | Glacial and alluvial deposits (sands, gravels, and silt) | EPB | 15.0 | 6.69 | 5.60 | 12.4 | 0.35–0.40 | 0.50 | [5] |
| 7 | Line 1, Milan (Italy) | Glacial and alluvial deposits (sands, gravels, and silt) | EPB | 10–20 | 6.56 | 4.0–10.0 | N/A | N/A | N/A | [4] |
| 8 | Passante Ferroviario, Milan (Italy) | Glacial and alluvial deposits (sands, gravels, and silt) | EPB | 4–16 | 8.03 | 4.0–6.0 | N/A | 0.43–0.46 | N/A | [4] |
| 9 | Line 2, El Cairo (Egypt) | Alluvial deposits followed by layers of clay, silt, and silty sands | Escudo de lodos | 16–18 | 9.48 | 4.0–10.0 | 20.0 | 0.52–1.22 | 0.5–0.8 | [63] |
8. Conclusions
- The observed settlement troughs can be reasonably modelled using the empirical Gaussian formulation, adjusted using least squares with K (an empirical proportionality constant, depending on the soil type, with value of 0.5).
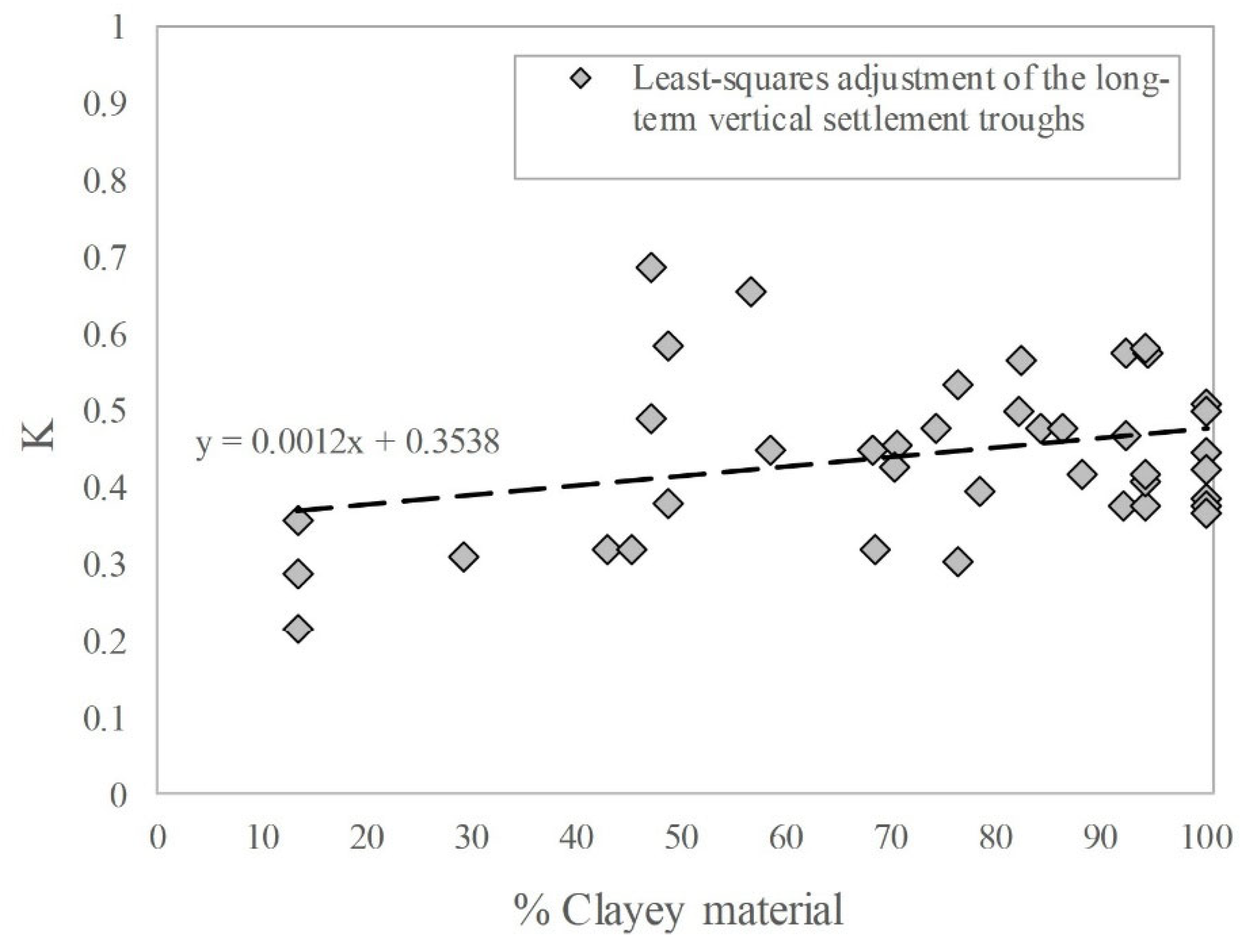
- The parameter K for the original ground, determined through least-squares fitting, ranges from 0.30 to 0.58.
- In sections where the tunnel alignment consists of more than 50% clayey materials, a value of K = 0.5 is representative for calculating ground loss volume.
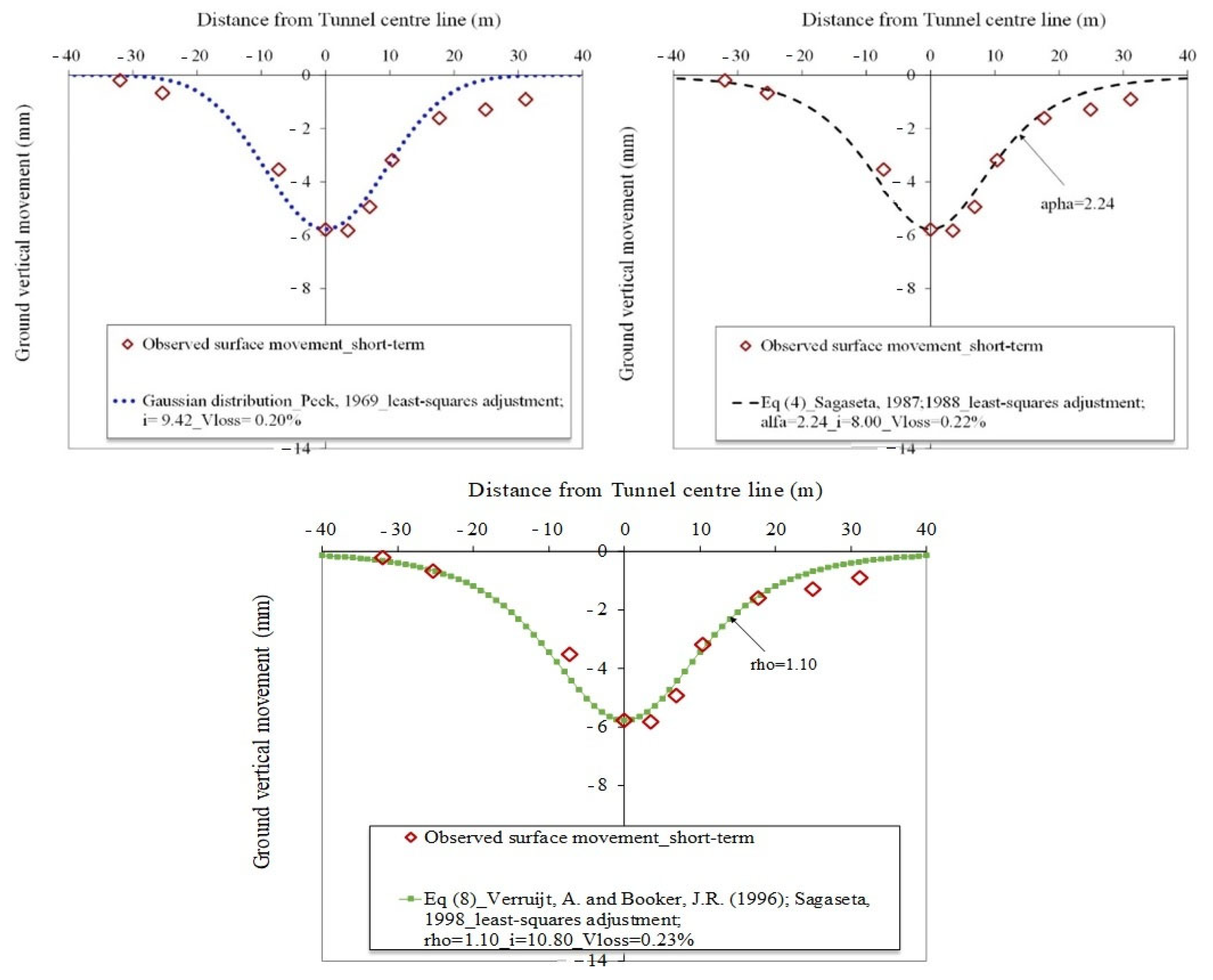
- The values of the parameter α from the Sagaseta [48] method is positive and range between 0.98 and 2.56, aligning with the guidelines for sandy soils.
- The degree of the ovalisation parameter ρ ranges from 0.18 to 2.07, indicating some degree of ovalisation (ρ > 0).
- The analysis of the 43 settlement troughs and the corresponding calculation of ground loss volume show that all methods yield very similar results, with only a few exceptions where the ground loss volume exceeds 1%.
- A slight tendency for the settlement trough width to increase with the tunnel depth is observed, although the variation in excavation depth is minimal, making it difficult to corroborate this trend.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Dimmock, P.S. Tunnelling-Induced Ground and Building Movement on the Jubilee Line Extension; University of Cambridge: Cambridge, UK, 2003. [Google Scholar]
- Wongsaroj, J. Three-Dimensional Finite Element Analysis of Short and Long-Term Ground Response to Open-Face Tunnelling in Stiff Clay. PhD Thesis, University of Cambridge, Cambridge, UK, 2005. [Google Scholar]
- Phienwej, N.; Sirivachiraporn, A.; Timpong, S.; Tavaranum, S. Characteristics of Ground Movements from Shield Tunnelling of the First Bangkok Subway Line. In Proceedings of the International Symposium on Underground Excavation and Tunnelling, Bangkok, Thailand, 2–4 February 2006; pp. 319–330. [Google Scholar]
- Antiga, A.; Chiorboli, M. Tunnel face stability and settlement control using earth pressure balance shield in cohesionless soil. In Geotechnical Aspects Underground Construction Soft Ground, Balkema, Shanghai (China); Ng, C.W.W., Huang, H.W., Liu, G.B., Eds.; Taylor & Francis Group: Shanghai, China, 2009; pp. 365–371. [Google Scholar]
- Fargnoli, V.; Boldini, D.; Amorosi, A. TBM tunnelling-induced settlements in coarse-grained soils: The case of the new Milan underground line 5. Tunn. Undergr. Space Technol. 2013, 38, 336–347. [Google Scholar] [CrossRef]
- Gui, M.-W.; Chen, S.-L. Estimation of transverse ground surface settlement induced by DOT shield tunneling. Tunn. Undergr. Space Technol. 2013, 33, 119–130. [Google Scholar] [CrossRef]
- Standing, J.R.; Selemetas, D.; Shirlaw, J.N. Greenfield ground response to EPBM tunnelling in London Clay. Géotechnique 2014, 64, 581–583. [Google Scholar] [CrossRef]
- Wan, M.S.P.; Standing, J.R.; Potts, D.M.; Burland, J.B. Mesured short-term ground surface response to EPBM tunnelling in London Clay. Géotechnique 2017, 67, 420–445. [Google Scholar] [CrossRef]
- Díez, F. Nuevo Modelo Madrid para la Estimación de Asientos en Túneles con Tuneladoras EPB de Gran Diámetro. Ph.D. Thesis, Universidad Politécnica de Madrid, E.T.S.I. Caminos, Canales y Puertos (UPM), Madrid, Spain, 2010. [Google Scholar]
- Gens, A.; Persio, R.; Di Mariano, A.; Castellanza, R.; Arroyo Alvarez de Toledo, M. Relación enre parámetros de una tuneladora EPB y los movimientos del terreno. In 3as Jornadas Hispano-Portuguesas de Geotecnia; Cedex: Madrid, Spain, 2009; pp. 433–441. [Google Scholar]
- Gens, A. Soil–environment interactions in geotechnical engineering. Géotechnique 2010, 60, 3–74. [Google Scholar] [CrossRef]
- Clough, G.W.; Sweeney, B.P.; Finno, R.J. Measured soil response to EPB shield tunnelling. ASCE J. Geotech. Eng. 1983, 109, 131–149. [Google Scholar] [CrossRef]
- Lee, K.M.; Ji, H.W.; Shen, C.K.; Liu, J.H.; Bai, T.H. Ground response to the construction of Shanghai Metro Tunnel-Line 2. Soil Found. 1999, 39, 113–134. [Google Scholar] [CrossRef]
- Cording, E.J. Control of ground movements around tunnels in soil. In Proceedings of the 9th Pan American Conference, Vina del Mar, Chile, 26–30 August 1991; pp. 2195–2244. [Google Scholar]
- Matsushita, Y.; Iwasaki, Y.; Ashimoto, T.; Imanishi, H. Behaviour of subway tunnel driven by large slurry shield. Underground Construction in Soft Ground. From CiNNII Researh, Balkema: Rotterdam, The Netherlands, 1995; 253–256. [Google Scholar]
- Mair, R.J.; Taylor, R.N. “Theme Lecture: Bored tunnelling inthe urban environment” Plenar Session 4. In Proceedings of the 14th International Conference on Soil Mechanics and Foundation Engineering (Hamburg), Hamburg, Germany, 6–12 September 1997; Volume 4, pp. 2353–2385. [Google Scholar]
- Wongsaroj, A.; Borghi, F.X.; Soga, K.; Mair, R.J.; Sugiyama, T.; Hagiwara, T.; Bowers, K.H. Effect of TBM driving parameters on ground surface movements: Channel Tunnel Rail Link Contract 220. In Geothecnicak Aspects of Underground Construction in Soft Ground; Bakken, K.J., Bezuijen, A., Broere, W., Kwast, E.A., Eds.; Taylor & Francis Group: London, UK, 2006; ISBN 0-415-39124-5. [Google Scholar]
- Gens, A.; Di Mariano, A.; Yubero, M.T. EPB tunneling in deltaic deposits: Observations of ground movements. In Geotechnical Aspects of Underground Construction in Soft Ground; Viggiani, G., Ed.; Taylor & Francis Group: Abingdon, UK, 2011. [Google Scholar]
- Nyren, R.J. Field Measurements above Twin Tunnels in London Clay. Ph.D. Thesis, Imperial College, Universtiy of London, London, UK, 1998. [Google Scholar]
- Selemetas, D. The Response of Ful-Scale Piles and Piled Structures to Tunnelling. Ph.D. Thesis, University of Cambridge, Cambridge, UK, 2005. [Google Scholar]
- Attewell, P.; Farmer, I. Ground Deformations Resulting from Shield Tunnelling in London Clay. Can. Geotech. J. 1974, 11, 380–395. [Google Scholar] [CrossRef]
- Peck, R.B. Deep Excavations and Tunneling insoft Ground. In Proceedings of the 7th International Conference on Soil Mechanics and Foundation Engineering, Mexico City, Mexico, 28 August–3 September 1969; pp. 225–290. [Google Scholar]
- Marshall, A.M.; Farrell, R.; Klar, A.; Mair, R. Tunnels in sands: The effect of size, depth and volume loss on greenfield displacements. Géotechnique 2012, 62, 385–399. [Google Scholar] [CrossRef]
- Di Mariano, A.; Gesto, J.M.; Gens, A.; Schwarz, H. Ground deformation and mitigating measures associated with the excavation of a new Metro line. In Proceedings of the 14th European Conference on Soil Mechanics and Geotechnical Engineering, Madrid, Spain, 24–27 September 2007; pp. 1901–1906. [Google Scholar]
- Deulofeu, C.; Schwarz, H.; Comulada, M. Data management for highly mechanized shield tunnelling in the construction of the Line 9 Metro Barcelona. In Underground Space, Proceedings of the 33rd ITA-AITES World Tunnel Congress, Prague, Czech Republic, 5–10 May 2007; Barták, J., Hrdina, I., Romancov, G., Ziámal, J., Eds.; Taylor and Francis Group: London, UK, 2007; pp. 1603–1608, ISBN 978-0-415-40807-3. [Google Scholar]
- Gens, A.; Di Mariano, A.; Gesto, J.M.; Schwarz, H. Ground movement control in the construction of a new metro line in Barcelona. In International Symposium Geothecnical Aspects of Underground Construction in Soft Ground; Bakker, K.J., Bezuijen, W., Kwast, E.A., Eds.; Balkema: Rotterdam, The Netherlands, 2006; pp. 389–395. [Google Scholar]
- Borràs, X.; Boté, R.; Maidl, B.; Della Valle, N. Metro Barcelona Línea 9-Europe’s greatest metro project with shield tunnel boring machines of large diameters. In (Re) Claiming the Underground Space; Saveur, J., Ed.; Routledge: Amsterdam, The Netherlands, 2003; pp. 637–643. [Google Scholar]
- Schwarz, H.; Bote, R.; Gens, A. Construction of a new Metro line in Barcelona: Design criteria, excavation and monitoring system. In Geotechnical Aspects of Underground Construction in Soft Ground—Proceedings of the 5th International Conference of TC28 of the ISSMGE, Netherlands, 15–17 June 2005; Bakker, K.J., Bezuijen, A., Kwast, E.A., Eds.; Taylor & Francis Group: London, UK, 2006; pp. 757–762. [Google Scholar] [CrossRef]
- Mendaña, F. La construcción de túneles en terrenos mixtos con tuneladoras de gran diámetro. Experiencias recientes de algunas obras Boring of tunnels in mixed face conditions with large diameter TBMs. Rev. Obras Públicas 2009, 65–78, ISSN 0034-8619. [Google Scholar]
- Naitoh, K. The development of earth pressure balanced shields in Japan. Tunn. Tunn. 1985, 17, 15–18. [Google Scholar]
- Krause, T. Schildvortrieb mit Flüssigkeits-Underdgestütxter Ortsbrust. Ph.D. Thesis, Technische Universitaet Braunschweig, Institut fuer Grundbau und Bodenmechanik, Bergisch Gladbach, Germany, 1987. (In German). [Google Scholar]
- Bono, R.; Ortu, M.; Valdemarin, F. Surface settlement minimization in soft soil when excavating with an earth pressure balance shield. Jornada Técnica: Túneles con EPB Simulacion y Control de la Tuneladora; Universitat Politècnica de Catalunya: Barcelona, Spain, 2008; pp. 129–148. Available online: https://deca.upc.edu/ca/el-departament/seccions/etcg/docencia/aula-paymacotas/pdf/publicacions/EPB.pdf (accessed on 20 August 2024).
- Maidl, B.; Herrenknecht, M.; Anheuser, L. Mechanised Shield Tunnelling; Wiley VCH: Weinheim, Germany, 1996; ISBN 343301292X. [Google Scholar]
- Shah, R.; Lavasan, A.A.; Peila, D.; Todaro, C.; Luciani, A.; Schanz, T. Numerical Study on Backfilling the Tail Void Using a Two-Component Grout. J. Mater. Civ. Eng. 2018, 30, 04018003. [Google Scholar] [CrossRef]
- Kravitz, B.; Mooney, M.; Karlovsek, J.; Danielson, I.; Hedayat, A. Void detection in two-component annulus grout behind a pre-cast segmental tunnel liner using Ground Penetrating Radar. Tunn. Undergr. Space Technol. 2019, 83, 381–392. [Google Scholar] [CrossRef]
- Wang, S.; He, C.; Nie, L.; Zhang, G. Study on the long-term performance of cement-sodium silicate grout and its impact on segment lining structure in synchronous backfill grouting of shield tunnels. Tunn. Undergr. Space Technol. 2019, 92, 1–13. [Google Scholar] [CrossRef]
- Shao, X.; Yang, Z.; Jiang, Y.; Yang, X.; Qi, W. Field test and numerical study of the effect of shield tail-grouting parameters on surface settlement. Geomech. Eng. 2022, 29, 509–522. [Google Scholar]
- Loganathan, N.; Poulos, H.G. Analytical prediction for tunneling-induced ground movements in clays. J. Geotech. Geoenviron. Eng. ASC 1998, 124, 846–856. [Google Scholar]
- Komiya, K.; Soga, K.; Akagi, H. Soil consolidation associated with grouting during shield tunnelling in soft clayey ground. Geotechnique 2001, 53, 447–448. [Google Scholar] [CrossRef]
- Liu, X.X.; Shen, S.L.; Xu, Y.S.; Zhou, A.N. Non-linear spring model for backfill grout-consolidation behind shield tunnel lining. Comput. Geotech. 2021, 136, 104235. [Google Scholar] [CrossRef]
- Zheng, G.; Zhang, T.; Diao, Y. Mechanism and countermeasures of preceding tunnel distortion induced by succeeding EPBS tunnelling in close proximity. Comput. Geotech. 2015, 66, 53–65. [Google Scholar] [CrossRef]
- He, S.; Lai, J.; Wang, L.; Wang, K. A literature review on properties and applications of grouts for shield tunnel. Constr. Build. Mater. 2020, 239, 117782. [Google Scholar] [CrossRef]
- Mao, J.; Yuan, D.; Jin, D.; Zeng, J. Optimization and application of backfill grouting material for submarine tunnel. Constr. Build. Mater. 2020, 265, 120281. [Google Scholar] [CrossRef]
- Cui, Y.; Tan, Z.; Han, D.; Song, J. Investigation and application of a high-performance grouting material in water-rich silty fine sand stratum. Constr. Build. Mater. 2022, 329, 127100. [Google Scholar] [CrossRef]
- Wongsaroj, J.; Soga, K.; Mair, R.J. Tunnelling-induced consolidation settlements in London Clay. Geotechnique 2013, 63, 1103–1115. [Google Scholar] [CrossRef]
- O’Reilly, M.P.; New, B.M. Settlements above tunnels in the United Kingdom-their magnitude and prediction. In Tunnelling’82; The Institution of Mining and Metallurgy: London, UK, 1982; pp. 173–181. [Google Scholar]
- Sagaseta, C. Analysis of undrained soil deformation due to ground loss. Géotechnique 1987, 37, 301–320. [Google Scholar] [CrossRef]
- Sagaseta, C. Author’s reply to Schmidt (1988). Géotechnique 1988, 38, 647–649. [Google Scholar] [CrossRef]
- Verruijt, A.; Booker, J.R. Surface settlements due deformation of a tunnel in an elastic half plane. Géotechnique 1996, 46, 753–756. [Google Scholar] [CrossRef]
- Uriel, A.O.; Sagaseta, C. Selection of Parameters for Underground Construction. AA Balkema: Rotterdam, The Netherlands, 1989; Volume 4, pp. 2521–2551. [Google Scholar]
- Sagaseta, C. Discusion to Verruijt and Booker (1996). Géotechnique 1998, 48, 709–713. [Google Scholar]
- Xie, T.-C.; Zhu, H.-H.; Tan, D.-Y.; Shukla, S.K. Modeling pipe-soil interaction under surface loading using material point method. Tunn. Undergr. Space Technol. 2024, 147, 105709. [Google Scholar] [CrossRef]
- Sugiyama, T.; Hagiwara, T.; Nomoto, T.; Nomoto, M.; Ano, Y.; Mair, R.J.; Bolton, M.D.; Soga, K. Observations of Ground Movements During Tunnel Construction by Slurry Method at the Docklands Light Railway Lewisham Extension-East London. Soils Found. 1999, 39, 99–112. [Google Scholar] [CrossRef]
- Clough, G.W.; Schmidt, B. Design and performance of excavation and tunnels in soft clay. In Soft Clay Engineering; Cording, E.J., Ed.; Developments in Geotechnical Engineering; Elsevier: Amsterdam, The Netherlands, 1981; Volume 20, pp. 569–634. [Google Scholar]
- Moh, Z.C.; Ju, D.H.; Hwang, R.N. Ground movements around tunnels in soft ground. In Proceedings of the International Symposium on Geotechnical Aspects of Underground Construction in Soft Ground, London, UK, 15–17 April 1996; pp. 15–17. [Google Scholar]
- Hergarden, H.J.A.M.; Van der Poel, J.T.; Vand der Schrier, J.S. Ground movements due to tunneling: Influence on pile foundations. In Proceedings of the 2nd International Symposium on Geotechnical Aspects of Underground Construction in Soft Ground, London, UK, 15–17 April 1996; AA Balkema: Rotterdam, The Netherlands; pp. 519–524. [Google Scholar]
- Jacobsz, S.W.; Standing, J.R.; Mair, R.J.; Hagiwara, T.; Sugiyama, T. Centrifuge modelling of tunnelling near driven piles. Soils Found. 2004, 44, 49–56. [Google Scholar] [CrossRef]
- Vorster, T.E.B.; Klar, A.; Soga, K.; Mair, R.J. Estimating the Effects of Tunneling on Existing Pipelines. J. Geotech. Geoenvironmental Eng. 2005, 131, 1399–1410. [Google Scholar] [CrossRef]
- Hsiung, B.C.B. Analysis of Ground Movements Induced by Tunnels in Sand Based on Contract CR3 in Kaohsiung Metro. Geotechnical Aspects of Underground Construction in Soft Ground. 2011, pp. 869–875. Available online: http://www.scopus.com/inward/record.url?eid=2-s2.0-84867157741&partnerID=tZOtx3y1 (accessed on 20 August 2024).
- Lin, C.G.; Zhang, Z.M.; Wu, S.M.; Yu, F. Key techniques and important issues for slurry shield under-passing embankments: A case study of Hangzhou Qiantang River Tunnel. Tunn. Undergr. Space Technol. 2013, 38, 306–325. [Google Scholar] [CrossRef]
- Wu, P.C.; Hsieh, M.B.; Yang, W.; Liu, P.E. Study on Double-O-Tube tunnel construction. Tunn. Constr. China 2011, 31, 265–273. [Google Scholar]
- Sirivachiraporn, A.; Phienwej, N. Ground movements in EPB shield tunneling of Bangkok subway project and impacts on adjacent buildings. Tunn. Undergr. Space Technol. 2012, 30, 10–24. [Google Scholar] [CrossRef]
- Hamza, M.; Ata, A.; Roussin, A. Ground Movements Due to the Constuction of Cut-and-Cover Structures and Slurry Shield Tunnel of the Cairo Metro. Tunn. Undergr. Space Technol. 1999, 14, 281–289. [Google Scholar] [CrossRef]
- Wang, L.; Chen, W.; Tan, X.; Tan, X.; Yang, J.; Yang, D.; Zhang, X. Numerical investigation on the stability of deforming fractured rocks using discrete fracture networks: A case study of underground excavation. Bull. Eng. Geol. Environ. 2020, 79, 133–151. [Google Scholar] [CrossRef]





| Client | Civil Work | Construction Company | Shield Type | Diameter (m) |
|---|---|---|---|---|
| Generalitat de Catalunya | L9 Metro | UTE Triangle | EPB | 11.90 |
| Generalitat de Catalunya | L9 Metro | UTE Gorg 1 | EPB | 12.00 |
| Generalitat de Catalunya | L9 Metro | UTE Gorg 2 | EPB | 12.00 |
| Generalitat de Catalunya | L9 Metro | UTE Airport 1 | EPB | 9.40 |
| Generalitat de Catalunya | L9 Metro | UTE Airport 2 | EPB | 9.40 |
| FCG | Terrassa Railway | UTE Terrassa | 2 EPB | 6.40 |
| FCG | Sabadell Railway | Acciona | 2 EPB | 6.40 |
| Adif | High-Speed Rail | UTE Montcada | EPB | 11.90 |
| Adif | High-Speed Rail | UTE Sagrada Familia | EPB | 11.90 |
| Adif | High-Speed Rail | UTE Girona | EPB | 10.00 |
| Excavation Parameter | Average Value |
|---|---|
| Pressure at the excavation face (bar) | 2.6 |
| Bentonite injection pressure (bar) | 2.0 |
| Bentonite injection volume (m3) | 1.0–2.5 |
| Tail pressure (bar) | 3.1 |
| Grouting injection volume (m3) | 8.23 |
| Foam expansion rate (FER) | min 25 |
| Foam Injection rate (FIR) | min 20 |
| Work density chamber (ton/m3) | 1.60–1.80 |
| Machine stops/ring (min) | 178 |
| Installation ring time (min) | 19 |
| Drilling time/ring (min) | 28 |
| Cycle time/ring (min) | 225 |
| Wheel thrust force (kN) | 6217.57 |
| Propulsion force (kN) | 25,600 |
| PAR (kNm) | 4475 |
| Ratio advance (mm/min) | 63 |
| Penetration (mm/rpm) | 53 |
| Geological Unit | R | QL1 | QL2 | QL3 | QL3s | QL3m | |
|---|---|---|---|---|---|---|---|
| Granulometry | % fines | 91.35 | 28.55 | 28.61 | 90.81 | 81.5 | 91.62 |
| % sands | 8.61 | 67.67 | 63.54 | 9.14 | 18.39 | 8.36 | |
| % gravel | 0.04 | 3.78 | 7.85 | 0.05 | 0.11 | 0.03 | |
| Limits | LL | 30.1 | 39 | 25.9 | 25.8 | 33–21.6 | 23.7 |
| LP | 19–23 | 21.4 | 18.72 | 16.2–25 | 12.4–21.9 | 17.9 | |
| Humidity | % | 18 | 18 | 21 | 26 | 25 | 27 |
| Density (γn) | g/cm3 | 2.06 | 1.95 | 2.53 | 1.9 | 1.6 | 1.83 |
| Dry Density (γd) | g/cm3 | 1.75 | 1.47 | 1.75 | 1.54 | 1.47 | 1.44 |
| NSPT | Average | 14.44 | 8.16 | 13.5 | 12.76 | 9.8 | 11.55 |
| Simple Compression | qu (Kg/cm2) | 0.84 | 1.05 | 0.24 | 0.65 | 0.35 | 0.25 |
| Direct Cutting | c (Kg/cm2) | 0.13–0.37 | 0.15–0.20 | 0.15–0.40 | 0.3 | 0–0.07 | 0.2 |
| φ (0) | 26 | 38.1 | 34.7 | 28.5 | 28 | 26.7 | |
| Oedometer | e0 | 0.5 | 0.65 | 0.7 | 0.67 | 0.73 | 0.62 |
| Cc | 0.09 | 0.08 | 0.15 | 0.12 | 0.09 | 0.09 | |
| mv | 0.01 | 0.01 | 0.002 | 0.001 | 0.002 | 0.01 | |
| Triaxial | c | 0–1.50 | 0.47 | 0.38 | 0.32 | ||
| φ (0) | 31–39.00 | 17.19 | 24.8 | 21.01 | |||
| Sulphates | % | 0.12 | <0.1 | 0.1–0.48 | 0.1–0.26 | 0.19–0.59 | 0.1–0.26 |
| Organic Material | % | 0.12 | 0.1–0.33 | 0.22–0.40 | 0.29–1.2 | 0.07–0.91 | 0.74 |
| Pressure Meter | MPa | 10.3 | 14.2 | 15.2 | 11.9 | 15.1 | |
| Permeability | cm/s | 5.71 × 10−5 | 2.29 × 10−4 | 1.29 × 10−8 | 4.27 × 10−6 | 2.79 × 10−7 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yubero, M.T.; Bonet, E. Ground Surface Effect of Earth Pressure Balance Tunnelling in Deltaic Deposits: A Case Study of Line 9 of the Barcelona Metro. Sustainability 2024, 16, 8275. https://doi.org/10.3390/su16188275
Yubero MT, Bonet E. Ground Surface Effect of Earth Pressure Balance Tunnelling in Deltaic Deposits: A Case Study of Line 9 of the Barcelona Metro. Sustainability. 2024; 16(18):8275. https://doi.org/10.3390/su16188275
Chicago/Turabian StyleYubero, Maria Teresa, and E. Bonet. 2024. "Ground Surface Effect of Earth Pressure Balance Tunnelling in Deltaic Deposits: A Case Study of Line 9 of the Barcelona Metro" Sustainability 16, no. 18: 8275. https://doi.org/10.3390/su16188275
APA StyleYubero, M. T., & Bonet, E. (2024). Ground Surface Effect of Earth Pressure Balance Tunnelling in Deltaic Deposits: A Case Study of Line 9 of the Barcelona Metro. Sustainability, 16(18), 8275. https://doi.org/10.3390/su16188275





