Design of a Misalignment-Tolerant Inductor–Capacitor–Capacitor-Compensated Wireless Charger for Roadway-Powered Electric Vehicles
Abstract
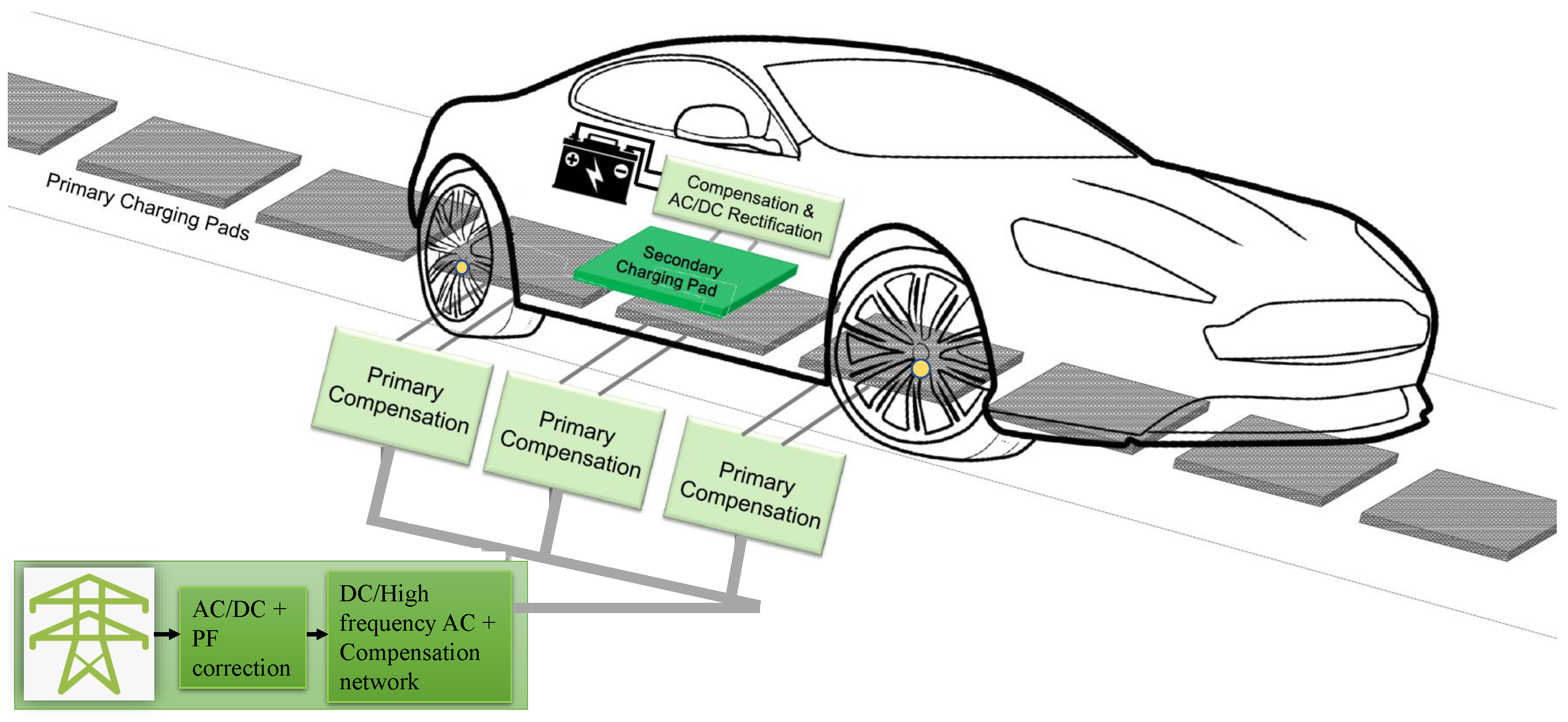
:1. Introduction
1.1. Related Works
1.1.1. Coil Geometry
1.1.2. Compensation Networks
1.1.3. Integrated DWC Designs
1.2. This Work
- Expand on the earlier work by the authors in [19] by providing a comprehensive description of the proposed design of a high-efficiency RIPT system for EV DWC using a multi-coil DDQ receiver structure. In the proposed design, the DD and Q components are connected to separate LCC compensation and regulation circuits to offer additional design degrees of freedom for optimal tuning.
- Propose a minimum-coupling-based tuning of the LCC compensation networks on the primary and secondary sides while designing the corresponding power and current control loops. This helps improve the system’s misalignment tolerance by maintaining zero-phase angle (ZPA) operation, constant output current and maximum received power at different misalignment conditions.
- Study the variations in the output AC power and AC-AC power transfer efficiency at different misalignment levels for a downscaled experimental prototype to validate the proposed design against simulation results.
2. Materials and Methods
2.1. LCC-LCC Compensation Design
2.2. Dual-Side Control
2.2.1. Primary-Side Control
2.2.2. Secondary-Side Control
3. Model Simulations
4. Experimental Verification
4.1. Prototype Construction
4.2. Results and Discussions
4.3. Cost Analysis
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Nomenclature
| DWC | Dynamic Wireless Charging |
| ESR | Equivalent Series Resistance |
| EV | Electric Vehicle |
| PWM | Pulse Width Modulation |
| RIPT | Resonant Inductive Power Transfer |
| SoC | State-of-Charge |
| ZPA | Zero Phase Angle |
| ZVS | Zero Voltage Switching |
References
- Saber, A.Y.; Venayagamoorthy, G.K. One million plug-in electric vehicles on the road by 2015. In Proceedings of the 2009 12th International IEEE Conference on Intelligent Transportation Systems, St. Louis, MO, USA, 4–7 October 2009; pp. 1–7. [Google Scholar]
- Chan, C.C. The state of the art of electric, hybrid, and fuel cell vehicles. Proc. IEEE 2007, 95, 704–718. [Google Scholar] [CrossRef]
- Wang, X.; Shahidehpour, M.; Jiang, C.; Li, Z. Coordinated Planning Strategy for Electric Vehicle Charging Stations and Coupled Traffic-Electric Networks. IEEE Trans. Power Syst. 2019, 34, 268–279. [Google Scholar] [CrossRef]
- Zhang, T.Y.; Yang, Y.; Zhu, Y.T.; Yao, E.J.; Wu, K.Q. Deploying Public Charging Stations for Battery Electric Vehicles on the Expressway Network Based on Dynamic Charging Demand. IEEE Trans. Transp. Electrif. 2022, 8, 2531–2548. [Google Scholar] [CrossRef]
- Elghanam, E.; Ndiaye, M.; Hassan, M.S.; Osman, A.H. Location Selection for Wireless Electric Vehicle Charging Lanes Using an Integrated TOPSIS and Binary Goal Programming Method: A UAE Case Study. IEEE Access 2023, 11, 94521–94535. [Google Scholar] [CrossRef]
- Dharmakeerthi, C.; Mithulananthan, N.; Saha, T. A comprehensive planning framework for electric vehicle charging infrastructure deployment in the power grid with enhanced voltage stability. Int. Trans. Electr. Energy Syst. 2015, 25, 1022–1040. [Google Scholar] [CrossRef]
- Tavakoli, A.; Saha, S.; Arif, M.T.; Haque, M.E.; Mendis, N.; Oo, A.M. Impacts of grid integration of solar PV and electric vehicle on grid stability, power quality and energy economics: A review. IET Energy Syst. Integr. 2020, 2, 243–260. [Google Scholar] [CrossRef]
- Chen, X.; Wang, H.; Wu, F.; Wu, Y.; González, M.C.; Zhang, J. Multi-Microgrids Load Balancing through EV Charging Networks. IEEE Internet Things J. 2021, 9, 5019–5026. [Google Scholar] [CrossRef]
- Duarte, G.; Silva, A.; Baptista, P. Assessment of wireless charging impacts based on real-world driving patterns: Case study in Lisbon, Portugal. Sustain. Cities Soc. 2021, 71, 102952. [Google Scholar] [CrossRef]
- Yi, Z.; Bauer, P.H. Optimal Stochastic Eco-Routing Solutions for Electric Vehicles. IEEE Trans. Intell. Transp. Syst. 2018, 19, 3807–3817. [Google Scholar] [CrossRef]
- Sun, C.; Wen, X.; Lu, Z.; Zhang, J.; Chen, X. A Graphical Game Approach to Electrical Vehicle Charging Scheduling: Correlated Equilibrium and Latency Minimization. IEEE Trans. Intell. Transp. Syst. 2021, 22, 505–517. [Google Scholar] [CrossRef]
- ElGhanam, E.; Sharf, H.; Odeh, Y.; Hassan, M.S.; Osman, A.H. On the Coordination of Charging Demand of Electric Vehicles in a Network of Dynamic Wireless Charging Systems. IEEE Access 2022, 10, 62879–62892. [Google Scholar] [CrossRef]
- Yu, R.; Zhong, W.; Xie, S.; Yuen, C.; Gjessing, S.; Zhang, Y. Balancing Power Demand Through EV Mobility in Vehicle-to-Grid Mobile Energy Networks. IEEE Trans. Ind. Inform. 2016, 12, 79–90. [Google Scholar] [CrossRef]
- Mude, K.N. Battery charging method for electric vehicles: From wired to on-road wireless charging. Chin. J. Electr. Eng. 2018, 4, 1–15. [Google Scholar] [CrossRef]
- Mi, C.C.; Buja, G.; Choi, S.Y.; Rim, C.T. Modern advances in wireless power transfer systems for roadway powered electric vehicles. IEEE Trans. Ind. Electron. 2016, 63, 6533–6545. [Google Scholar] [CrossRef]
- ElGhanam, E.; Hassan, M.; Osman, A. Design of a high power, LCC-compensated, dynamic, wireless electric vehicle charging system with improved misalignment tolerance. Energies 2021, 14, 885. [Google Scholar] [CrossRef]
- Chandra Majhi, R.; Ranjitkar, P.; Sheng, M. Optimal Allocation of Dynamic Wireless Charging Facility for Electric Vehicles. Transp. Res. Part D Transp. Environ. 2022, 111, 103461. [Google Scholar] [CrossRef]
- Newbolt, T.M.; Mandal, P.; Wang, H.; Zane, R. Diverse Effects of Dynamic Wireless Power Transfer Roadway In-Motion Electric Vehicle Charging. In Proceedings of the 2023 IEEE Power & Energy Society Innovative Smart Grid Technologies Conference (ISGT), Washington, DC, USA, 16–19 January 2023; pp. 1–5. [Google Scholar] [CrossRef]
- Abdulhameed, M.; ElGhanam, E.; Osman, A.H.; Hassan, M.S. Design and Testing of Wireless EV Charging System with Improved Lateral Misalignment Tolerance. In Proceedings of the 2022 IEEE Vehicle Power and Propulsion Conference (VPPC), Merced, CA, USA, 1–4 November 2022; pp. 1–6. [Google Scholar] [CrossRef]
- Moon, S.; Kim, B.C.; Cho, S.Y.; Ahn, C.H.; Moon, G.W. Analysis and design of a wireless power transfer system with an intermediate coil for high efficiency. IEEE Trans. Ind. Electron. 2014, 61, 5861–5870. [Google Scholar] [CrossRef]
- Triviño-Cabrera, A.; Aguado, J.; González, J. Analytical characterisation of magnetic field generated by ICPT wireless charger. Electron. Lett. 2017, 53, 871–873. [Google Scholar] [CrossRef]
- Patil, D.; McDonough, M.K.; Miller, J.M.; Fahimi, B.; Balsara, P.T. Wireless Power Transfer for Vehicular Applications: Overview and Challenges. IEEE Trans. Transp. Electrif. 2018, 4, 3–37. [Google Scholar] [CrossRef]
- Ahmad, A.; Alam, M.S.; Chabaan, R. A Comprehensive Review of Wireless Charging Technologies for Electric Vehicles. IEEE Trans. Transp. Electrif. 2018, 4, 38–63. [Google Scholar] [CrossRef]
- Marco, D.; Dolara, A.; Longo, M.; Yaici, W. Design and Performance Analysis of Pads for Dynamic Wireless Charging of EVs using the Finite Element Method. Energies 2019, 12, 4139. [Google Scholar] [CrossRef]
- Bandyopadhyay, S.; Venugopal, P.; Dong, J.; Bauer, P. Comparison of Magnetic Couplers for IPT-Based EV Charging Using Multi-Objective Optimization. IEEE Trans. Veh. Technol. 2019, 68, 5416–5429. [Google Scholar] [CrossRef]
- Lu, J.; Zhu, G.; Wang, H.; Lu, F.; Jiang, J.; Mi, C.C. Sensitivity Analysis of Inductive Power Transfer Systems With Voltage-Fed Compensation Topologies. IEEE Trans. Veh. Technol. 2019, 68, 4502–4513. [Google Scholar] [CrossRef]
- ElGhanam, E.; Hassan, M.; Osman, A.; Kabalan, H. Design and performance analysis of misalignment tolerant charging coils for wireless electric vehicle charging systems. World Electr. Veh. J. 2021, 12, 89. [Google Scholar] [CrossRef]
- Nguyen, T.; Li, S.; Li, W.; Mi, C.C. Feasibility study on bipolar pads for efficient wireless power chargers. In Proceedings of the 2014 IEEE Applied Power Electronics Conference and Exposition—APEC 2014, Fort Worth, TX, USA, 16–20 March 2014; pp. 1676–1682. [Google Scholar] [CrossRef]
- Bouanou, T.; El Fadil, H.; Lassioui, A.; Assaddiki, O.; Njili, S. Analysis of Coil Parameters and Comparison of Circular, Rectangular, and Hexagonal Coils Used in WPT System for Electric Vehicle Charging. World Electr. Veh. J. 2021, 12, 45. [Google Scholar] [CrossRef]
- Zhang, X.; Yuan, Z.; Yang, Q.; Li, Y.; Zhu, J.; Li, Y. Coil design and efficiency analysis for dynamic wireless charging system for electric vehicles. IEEE Trans. Magn. 2016, 52, 1–4. [Google Scholar] [CrossRef]
- Ongayo, D.; Hanif, M. Comparison of circular and rectangular coil transformer parameters for wireless Power Transfer based on Finite Element Analysis. In Proceedings of the 2015 IEEE 13th Brazilian Power Electronics Conference and 1st Southern Power Electronics Conference (COBEP/SPEC), Fortaleza, Brazil, 29 November–2 December 2015; pp. 1–6. [Google Scholar]
- Ahmad, A.; Alam, M.S.; Mohamed, A.A. Design and interoperability analysis of quadruple pad structure for electric vehicle wireless charging application. IEEE Trans. Transp. Electrif. 2019, 5, 934–945. [Google Scholar] [CrossRef]
- Zaheer, A.; Neath, M.; Beh, H.Z.Z.; Covic, G.A. A dynamic EV charging system for slow moving traffic applications. IEEE Trans. Transp. Electrif. 2016, 3, 354–369. [Google Scholar] [CrossRef]
- Abou Houran, M.; Yang, X.; Chen, W. Magnetically coupled resonance WPT: Review of compensation topologies, resonator structures with misalignment, and EMI diagnostics. Electronics 2018, 7, 296. [Google Scholar] [CrossRef]
- Trivino, A.; Sanchez, J.; Delgado, A. Efficient Methodology of the Coil Design for a Dynamic Wireless Charger. IEEE Access 2022, 10, 83368–83378. [Google Scholar] [CrossRef]
- Hassanin, W.S.; Enany, M.A.; Shaier, A.A.; Ahmed, M.M. Performance analysis of rectangular and double-D transmitters with various receivers for electric vehicle static charging. Alex. Eng. J. 2023, 78, 438–452. [Google Scholar] [CrossRef]
- Shin, J.; Shin, S.; Kim, Y.; Ahn, S.; Lee, S.; Jung, G.; Jeon, S.J.; Cho, D.H. Design and implementation of shaped magnetic-resonance-based wireless power transfer system for roadway-powered moving electric vehicles. IEEE Trans. Ind. Electron. 2013, 61, 1179–1192. [Google Scholar] [CrossRef]
- Chen, W.; Lin, F.; Covic, G.A. A Modified DDQ Track for Interoperable EV Dynamic Charging. IEEE Trans. Power Electron. 2023, 38, 11738–11750. [Google Scholar] [CrossRef]
- Luo, Z.; Nie, S.; Pathmanathan, M.; Han, W.; Lehn, P.W. 3-D Analytical Model of Bipolar Coils With Multiple Finite Magnetic Shields for Wireless Electric Vehicle Charging Systems. IEEE Trans. Ind. Electron. 2022, 69, 8231–8242. [Google Scholar] [CrossRef]
- Lee, S.H.; Lorenz, R.D. Development and validation of model for 95%-efficiency 220-W wireless power transfer over a 30-cm air gap. IEEE Trans. Ind. Appl. 2011, 47, 2495–2504. [Google Scholar] [CrossRef]
- Tsai, J.S.; Hu, J.S.; Chen, S.L.; Huang, X. Directional antenna design for wireless power transfer system in electric scooters. Adv. Mech. Eng. 2016, 8, 1687814016632693. [Google Scholar] [CrossRef]
- Zhang, W.; Mi, C.C. Compensation topologies of high-power wireless power transfer systems. IEEE Trans. Veh. Technol. 2015, 65, 4768–4778. [Google Scholar] [CrossRef]
- Movagharnejad, H.; Mertens, A. Design metrics of compensation methods for contactless charging of electric vehicles. In Proceedings of the 2017 19th European Conference on Power Electronics and Applications (EPE’17 ECCE Europe), Warsaw, Poland, 11–14 September 2017. [Google Scholar]
- Shevchenko, V.; Husev, O.; Strzelecki, R.; Pakhaliuk, B.; Poliakov, N.; Strzelecka, N. Compensation topologies in IPT systems: Standards, requirements, classification, analysis, comparison and application. IEEE Access 2019, 7, 120559–120580. [Google Scholar] [CrossRef]
- Li, W.; Zhao, H.; Deng, J.; Li, S.; Mi, C.C. Comparison Study on SS and Double-Sided LCC Compensation Topologies for EV/PHEV Wireless Chargers. IEEE Trans. Veh. Technol. 2016, 65, 4429–4439. [Google Scholar] [CrossRef]
- Esteban, B.; Sid-Ahmed, M.; Kar, N.C. A comparative study of power supply architectures in wireless EV charging systems. IEEE Trans. Power Electron. 2015, 30, 6408–6422. [Google Scholar] [CrossRef]
- Li, S.; Li, W.; Deng, J.; Nguyen, T.D.; Mi, C.C. A double-sided LCC compensation network and its tuning method for wireless power transfer. IEEE Trans. Veh. Technol. 2014, 64, 2261–2273. [Google Scholar] [CrossRef]
- Li, W.; Zhao, H.; Li, S.; Deng, J.; Kan, T.; Mi, C.C. Integrated LCC compensation topology for wireless charger in electric and plug-in electric vehicles. IEEE Trans. Ind. Electron. 2014, 62, 4215–4225. [Google Scholar] [CrossRef]
- Zhu, Q.; Wang, L.; Guo, Y.; Liao, C.; Li, F. Applying LCC compensation network to dynamic wireless EV charging system. IEEE Trans. Ind. Electron. 2016, 63, 6557–6567. [Google Scholar] [CrossRef]
- Li, Y.; Hu, J.; Lin, T.; Li, X.; Chen, F.; He, Z.; Mai, R. A new coil structure and its optimization design with constant output voltage and constant output current for electric vehicle dynamic wireless charging. IEEE Trans. Ind. Inform. 2019, 15, 5244–5256. [Google Scholar] [CrossRef]
- Deng, J.; Mao, Q.; Wang, W.; Li, L.; Wang, Z.; Wang, S.; Guidi, G. Frequency and Parameter Combined Tuning Method of LCC–LCC Compensated Resonant Converter With Wide Coupling Variation for EV Wireless Charger. IEEE J. Emerg. Sel. Top. Power Electron. 2021, 10, 956–968. [Google Scholar] [CrossRef]
- Yenil, V.; Cetin, S. Load Independent Constant Current and Constant Voltage Control of LCC-Series Compensated Wireless EV Charger. IEEE Trans. Power Electron. 2022, 37, 8701–8712. [Google Scholar] [CrossRef]
- Yang, J.; Zhang, X.; Zhang, K.; Cui, X.; Jiao, C.; Yang, X. Design of LCC-S Compensation Topology and Optimization of Misalignment Tolerance for Inductive Power Transfer. IEEE Access 2020, 8, 191309–191318. [Google Scholar] [CrossRef]
- Yang, L.; Li, X.; Liu, S.; Xu, Z.; Cai, C. Analysis and Design of an LCCC/S-Compensated WPT System With Constant Output Characteristics for Battery Charging Applications. IEEE J. Emerg. Sel. Top. Power Electron. 2021, 9, 1169–1180. [Google Scholar] [CrossRef]
- Wang, W.; Deng, J.; Chen, D.; Wang, Z.; Wang, S. A Novel Design Method of LCC-S Compensated Inductive Power Transfer System Combining Constant Current and Constant Voltage Mode via Frequency Switching. IEEE Access 2021, 9, 117244–117256. [Google Scholar] [CrossRef]
- Nguyen, H.T.; Alsawalhi, J.Y.; Hosani, K.A.; Al-Sumaiti, A.S.; Jaafari, K.A.A.; Byon, Y.J.; Moursi, M.S.E. Review Map of Comparative Designs for Wireless High-Power Transfer Systems in EV Applications: Maximum Efficiency, ZPA, and CC/CV Modes at Fixed Resonance Frequency Independent From Coupling Coefficient. IEEE Trans. Power Electron. 2022, 37, 4857–4876. [Google Scholar] [CrossRef]
- Song, K.; Wei, R.; Yang, G.; Zhang, H.; Li, Z.; Huang, X.; Jiang, J.; Zhu, C.; Du, Z. Constant Current Charging and Maximum System Efficiency Tracking for Wireless Charging Systems Employing Dual-Side Control. IEEE Trans. Ind. Appl. 2020, 56, 622–634. [Google Scholar] [CrossRef]
- Vu, V.B.; Tran, D.H.; Choi, W. Implementation of the Constant Current and Constant Voltage Charge of Inductive Power Transfer Systems With the Double-Sided LCC Compensation Topology for Electric Vehicle Battery Charge Applications. IEEE Trans. Power Electron. 2018, 33, 7398–7410. [Google Scholar] [CrossRef]
- Tavakoli, R.; Pantic, Z. Analysis, design, and demonstration of a 25-kW dynamic wireless charging system for roadway electric vehicles. IEEE J. Emerg. Sel. Top. Power Electron. 2017, 6, 1378–1393. [Google Scholar] [CrossRef]
- Corti, F.; Reatti, A.; Nepote, A.; Pugi, L.; Pierini, M.; Paolucci, L.; Grasso, F.; Grasso, E.; Nienhause, M. A secondary-side controlled electric vehicle wireless charger. Energies 2020, 13, 6527. [Google Scholar] [CrossRef]
- Diekhans, T.; De Doncker, R.W. A dual-side controlled inductive power transfer system optimized for large coupling factor variations and partial load. IEEE Trans. Power Electron. 2015, 30, 6320–6328. [Google Scholar] [CrossRef]
- Hu, X.; Wang, Y.; Jiang, Y.; Lei, W.; Dong, X. Maximum efficiency tracking for dynamic wireless power transfer system using LCC compensation topology. In Proceedings of the 2018 IEEE Energy Conversion Congress and Exposition (ECCE), Portland, OR, USA, 23–27 September 2018; pp. 1992–1996. [Google Scholar]
- Jiang, J.; Li, Z.; Song, K.; Song, B.; Dong, S.; Zhu, C. A cascaded topology and control method for two-phase receivers of dynamic wireless power transfer systems. IEEE Access 2020, 8, 47445–47455. [Google Scholar] [CrossRef]
- Bagchi, A.C.; Kamineni, A.; Zane, R.A.; Carlson, R. Review and Comparative Analysis of Topologies and Control Methods in Dynamic Wireless Charging of Electric Vehicles. IEEE J. Emerg. Sel. Top. Power Electron. 2021, 9, 4947–4962. [Google Scholar] [CrossRef]
- Shanmugam, Y.; Narayanamoorthi, R.; Vishnuram, P.; Bajaj, M.; AboRas, K.M.; Thakur, P. A Systematic Review of Dynamic Wireless Charging System for Electric Transportation. IEEE Access 2022, 10, 133617–133642. [Google Scholar] [CrossRef]
- Keil, P.; Jossen, A. Charging protocols for lithium-ion batteries and their impact on cycle life—An experimental study with different 18650 high-power cells. J. Energy Storage 2016, 6, 125–141. [Google Scholar] [CrossRef]
- Dai, H.; Zhang, X.; Gu, W.; Wei, X.; Sun, Z. A semi-empirical capacity degradation model of EV Li-ion batteries based on eyring equation. In Proceedings of the 2013 IEEE Vehicle Power and Propulsion Conference (VPPC), Beijing, China, 15–18 October 2013; pp. 1–5. [Google Scholar]
- Wan, L. Modelling and analysis of power battery. AIP Conf. Proc. 2019, 2066, 020027. [Google Scholar]
- J2954 Taskforce; Wireless Power Transfer for Light-Duty Plug-In/Electric Vehicles and Alignment Methodology. SAE International: Warrendale, PA, USA, 2016.
- Aditya, K.; Williamson, S.S. Design Guidelines to Avoid Bifurcation in a Series–Series Compensated Inductive Power Transfer System. IEEE Trans. Ind. Electron. 2018, 66, 3973–3982. [Google Scholar] [CrossRef]
- Chen, Y.; Zhang, H.; Shin, C.S.; Seo, K.H.; Park, S.J.; Kim, D.H. A comparative study of S-S and LCC-S compensation topology of inductive power transfer systems for EV chargers. In Proceedings of the 2019 IEEE 10th International Symposium on Power Electronics for Distributed Generation Systems (PEDG), Xi’an, China, 3–6 June 2019; pp. 99–104. [Google Scholar]
- Li, Y.; Xu, Q.; Lin, T.; Hu, J.; He, Z.; Mai, R. Analysis and design of load-independent output current or output voltage of a three-coil wireless power transfer system. IEEE Trans. Transp. Electrif. 2018, 4, 364–375. [Google Scholar] [CrossRef]
- Jiang, Y.; Wang, L.; Fang, J.; Li, R.; Han, R.; Wang, Y. A High-Efficiency ZVS Wireless Power Transfer System for Electric Vehicle Charging WithVariable Angle Phase Shift Control. IEEE J. Emerg. Sel. Top. Power Electron. 2021, 9, 2356–2372. [Google Scholar] [CrossRef]
- Cai, J.; Wu, X.; Sun, P.; Deng, Q.; Sun, J.; Zhou, H.; Wang, X. Zero-Voltage Switching Regulation Strategy of Full-Bridge Inverter of Inductive Power Transfer System Decoupled From Output Characteristics. IEEE Trans. Power Electron. 2022, 37, 13861–13873. [Google Scholar] [CrossRef]
- Abdulhameed, M.; ElGhanam, E.; Osman, A.; Hassan, M.S. Design and Tuning of LCC Compensation Networks for DD-DDQ Coils in Dynamic Wireless EV Charging Systems. In Proceedings of the 2022 IEEE Transportation Electrification Conference & Expo (ITEC), Anaheim, CA, USA, 15–17 June 2022; pp. 579–583. [Google Scholar] [CrossRef]
- Jovanovic, M.M.; Jang, Y. State-of-the-art, single-phase, active power-factor-correction techniques for high-power applications—An overview. IEEE Trans. Ind. Electron. 2005, 52, 701–708. [Google Scholar] [CrossRef]
- Zhou, S.; Mi, C.C. Multi-paralleled LCC reactive power compensation networks and their tuning method for electric vehicle dynamic wireless charging. IEEE Trans. Ind. Electron. 2015, 63, 6546–6556. [Google Scholar] [CrossRef]
- IDTechEx. Wireless Charging Market for Electric Vehicles 2023–2033: Technology, Players and Forecasts; IDTechEx: Cambridge, UK, 2022. [Google Scholar]
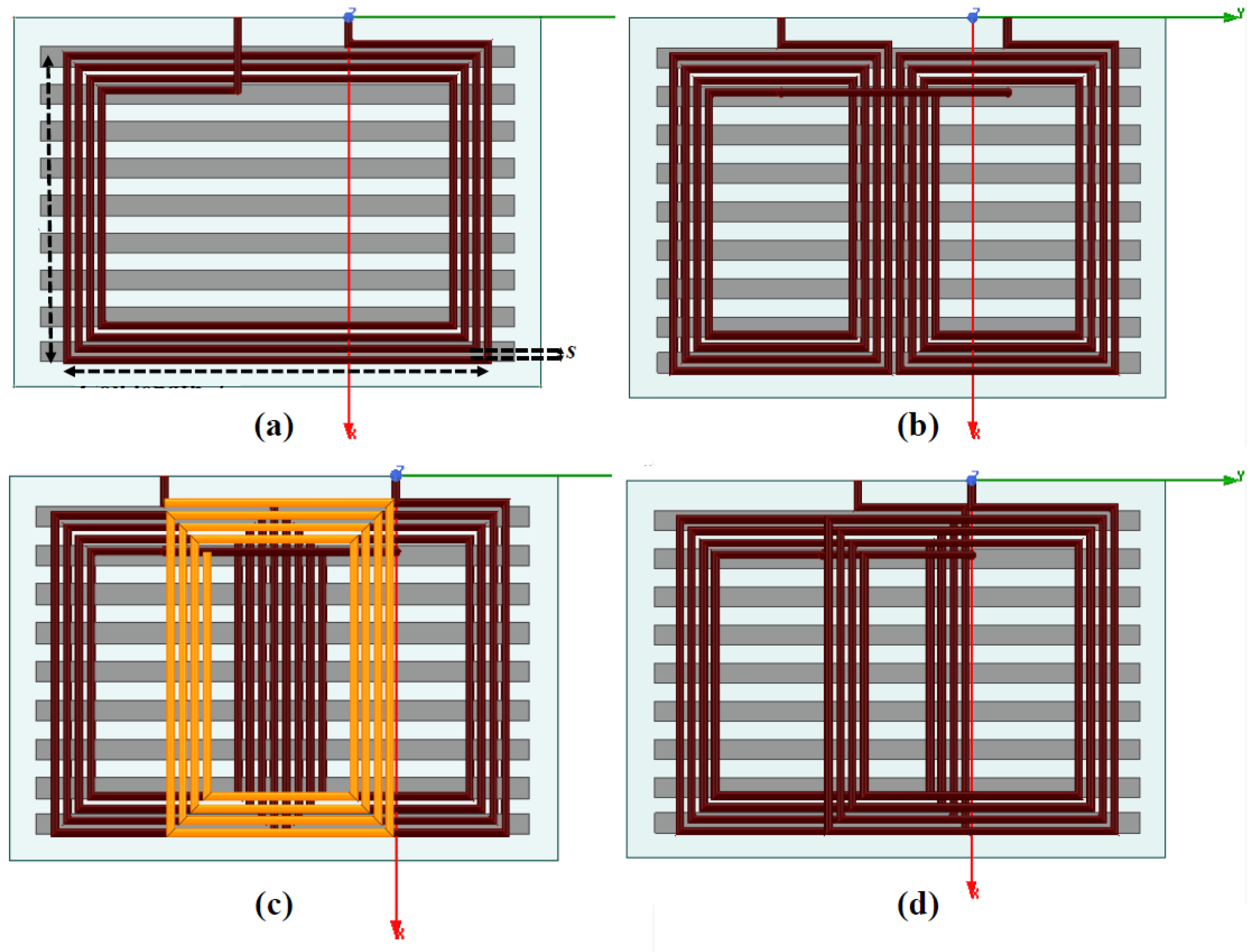



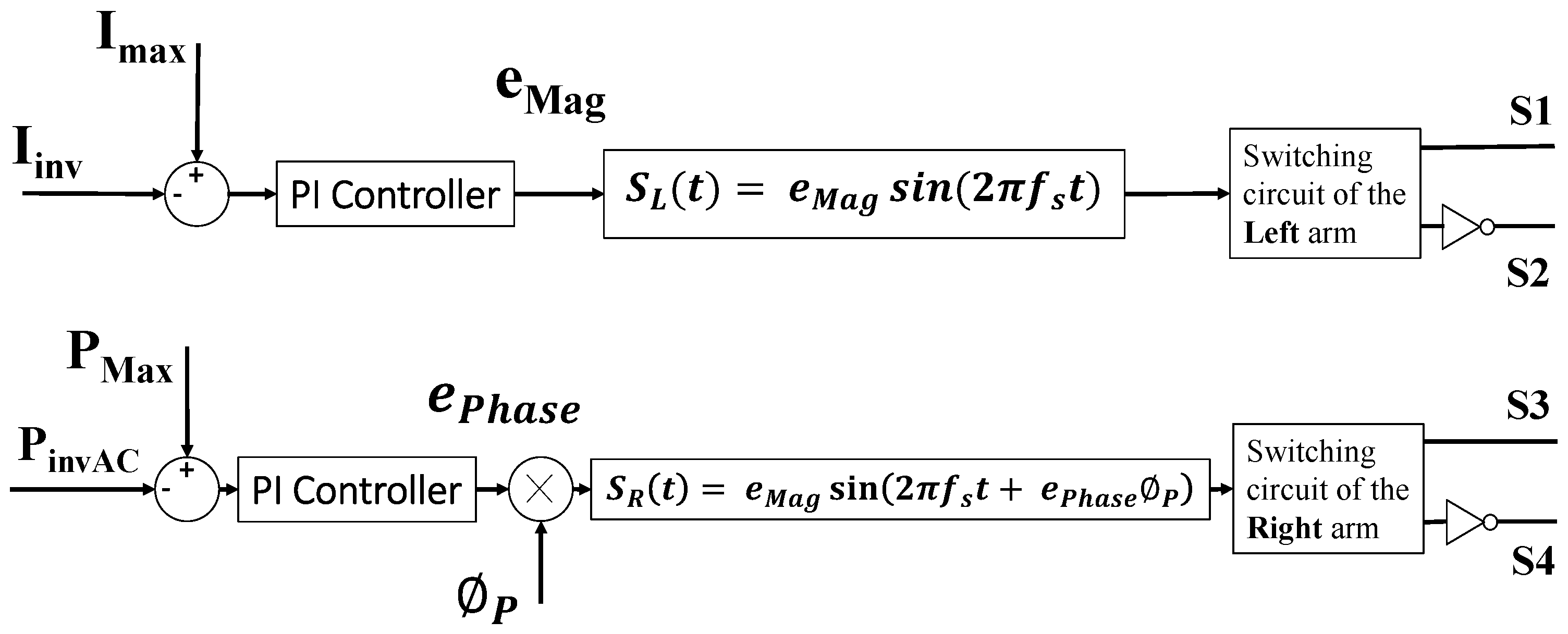
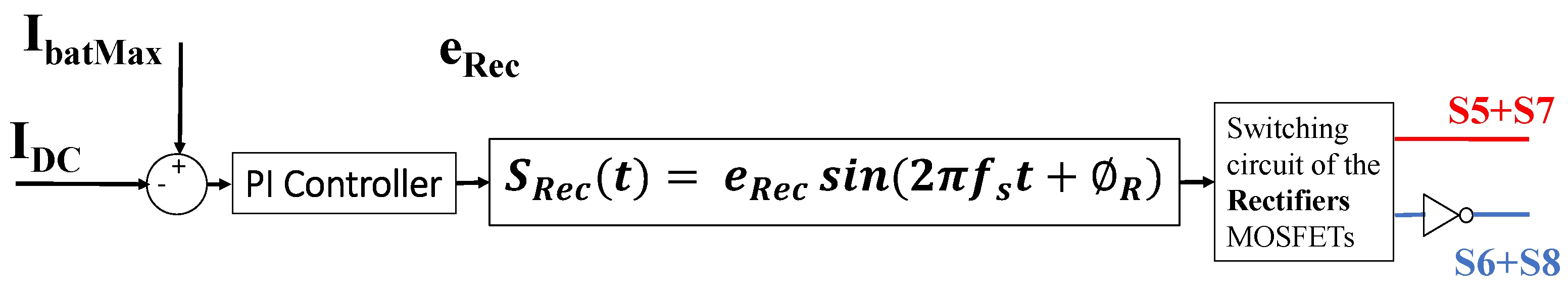
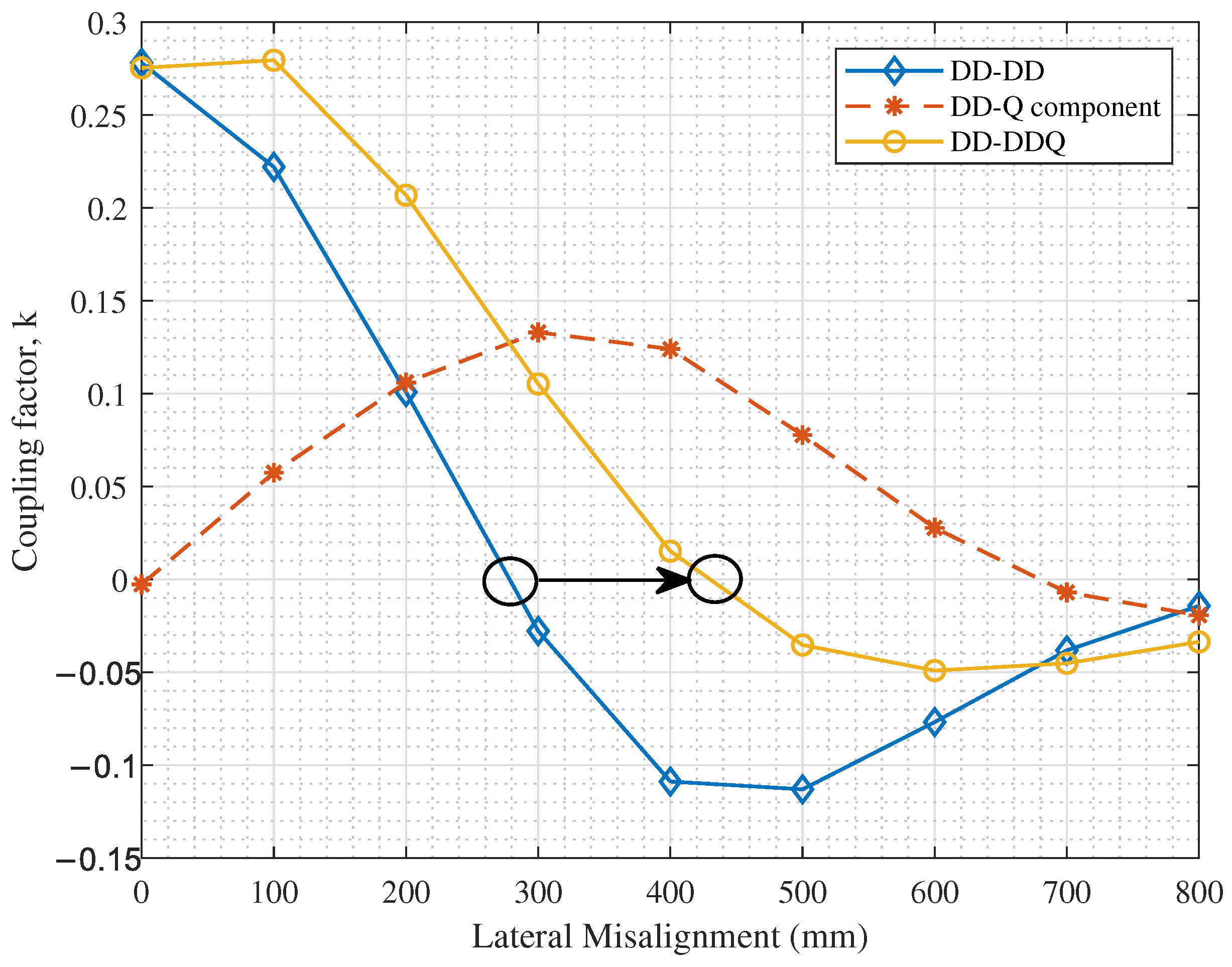








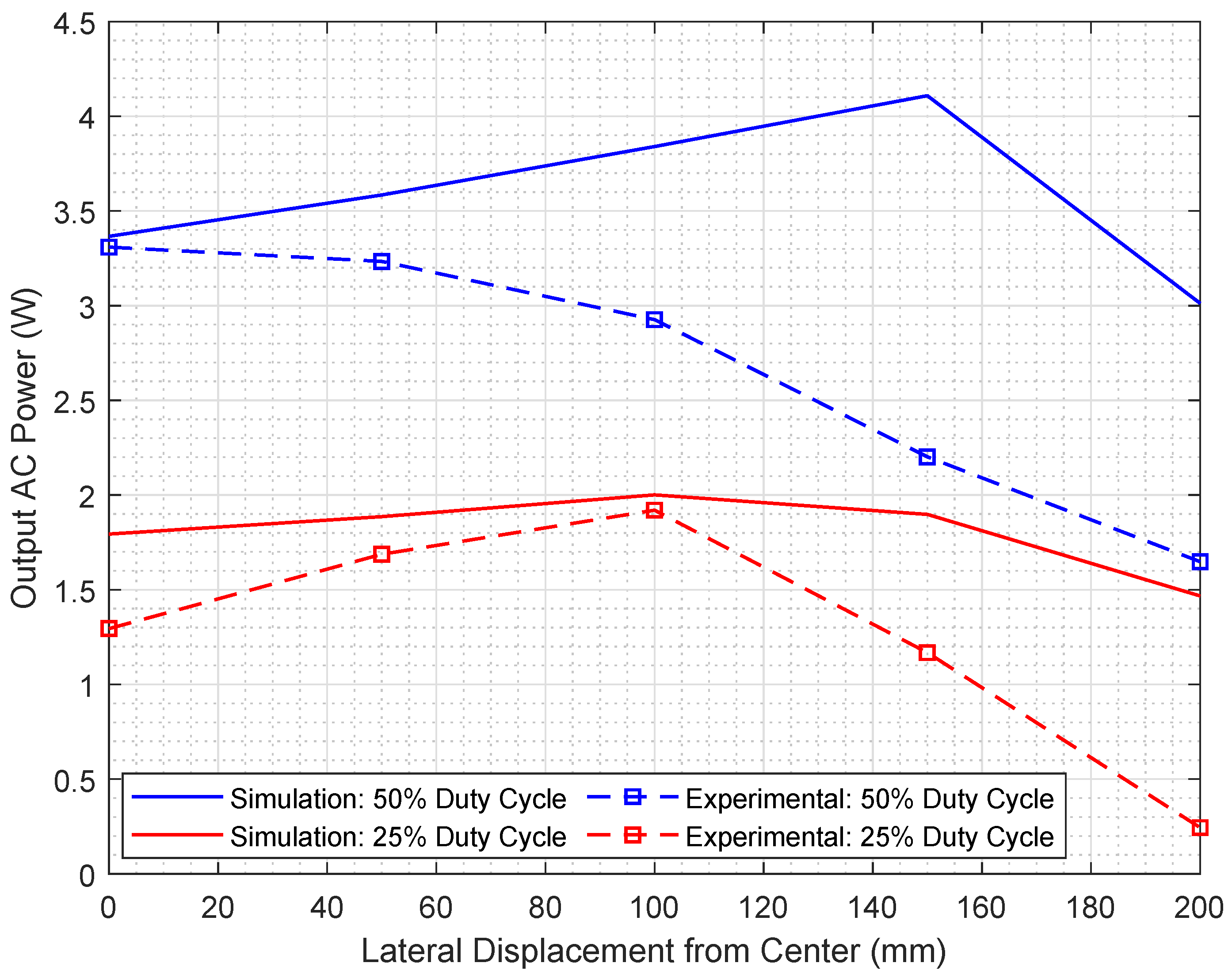

| Parameter | Value |
|---|---|
| Surface area per D coil | mm |
| Number of turns, N | 13 |
| Wire diameter, d | 4 mm |
| Edge-to-edge spacing, s | 6 mm |
| Component | Symbol | Value |
|---|---|---|
| Rated power | 25 kW | |
| Input DC voltage | 500 V | |
| Input DC current | 50 A | |
| Nominal DC battery voltage | V | |
| Battery charging current | A | |
| Primary-side compensation inductor | H | |
| Secondary-side DD compensation inductor | H | |
| Secondary-side Q compensation inductor | H | |
| Primary-side parallel comp. capacitor | nF | |
| Secondary-side parallel DD comp. capacitor | nF | |
| Secondary-side parallel Q comp. capacitor | nF | |
| Primary-side series comp. capacitor | nF | |
| Secondary-side series DD comp. capacitor | nF | |
| Secondary-side series Q comp. capacitor | nF |
| Criteria | [30] | [77] | [50] | [16] | This Work |
|---|---|---|---|---|---|
| Frequency | 85 kHz | 85 kHz | 85 kHz | 85 kHz | 85 kHz |
| Compensation | LCC-LCC | LCC-LCC | LCC-Hybrid | LCC-LCC | LCC-LCC |
| IL design | D-D | DD-DDQ | DDQ-DDQ | DD-DDQ | DD-DDQ |
| Number of secondary coils | 1 | 1 | 2 | 1 | 2 |
| Power rating | kW | <150 W | 384 W | 40 kW | 25 kW |
| Max LTMA tolerance (mm) | - | 0–150 | - | 0–200 | 0–200 |
| AC power fluctuation | - | - | |||
| AC efficiency at 0 LTMA | - | - | - | ||
| AC efficiency at Max LTMA | - | - | - | ||
| DC power variation | - | - | <2% | ||
| DC efficiency | - |
| Parameter | Symbol | Value |
|---|---|---|
| Rated power | W | |
| DC input voltage | 10 V | |
| Operating frequency | 85 kHz | |
| Primary-side compensation inductor | H | |
| Secondary-side DD compensation inductor | 16 H | |
| Secondary-side Q compensation inductor | 11 H | |
| Primary-side parallel comp. capacitor | 300 nF | |
| Secondary-side parallel DD comp. capacitor | 243 nF | |
| Secondary-side parallel Q comp. capacitor | 380 nF | |
| Primary-side series comp. capacitor | 20 nF | |
| Secondary-side series DD comp. capacitor | 27 nF | |
| Secondary-side series Q comp. capacitor | 51 nF |
| 0 mm | Experimental | Simulation | ||
|---|---|---|---|---|
| Duty Cycle | V | V | V | V |
| 12 | ||||
| 15 | ||||
| (±100 mm) | Experimental | Simulation | ||
|---|---|---|---|---|
| Duty Cycle | V | V | V | V |
| (±200 mm) | Experimental | Simulation | ||
|---|---|---|---|---|
| Duty Cycle | V | V | V | V |
| 1 | ||||
| 10 | ||||
| 1 | ||||
| Component | Quantity | Unit Price (USD) | Total Price (USD) |
|---|---|---|---|
| Transmitter pad | 1 | 100 | 100 |
| Receiver pad | 1 | 150 | 150 |
| MOSFET devices | 12 | 5 | 60 |
| Diodes | 8 | 2.5 | 20 |
| TLP250H Gate drivers | 4 | 40 | 160 |
| Compensation components | 9 | 2 | 18 |
| Other accessories | 1 | 30 | 30 |
| Total | 538 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Abdulhameed, M.; ElGhanam, E.; Osman, A.H.; Hassan, M.S. Design of a Misalignment-Tolerant Inductor–Capacitor–Capacitor-Compensated Wireless Charger for Roadway-Powered Electric Vehicles. Sustainability 2024, 16, 567. https://doi.org/10.3390/su16020567
Abdulhameed M, ElGhanam E, Osman AH, Hassan MS. Design of a Misalignment-Tolerant Inductor–Capacitor–Capacitor-Compensated Wireless Charger for Roadway-Powered Electric Vehicles. Sustainability. 2024; 16(2):567. https://doi.org/10.3390/su16020567
Chicago/Turabian StyleAbdulhameed, Mustafa, Eiman ElGhanam, Ahmed H. Osman, and Mohamed S. Hassan. 2024. "Design of a Misalignment-Tolerant Inductor–Capacitor–Capacitor-Compensated Wireless Charger for Roadway-Powered Electric Vehicles" Sustainability 16, no. 2: 567. https://doi.org/10.3390/su16020567
APA StyleAbdulhameed, M., ElGhanam, E., Osman, A. H., & Hassan, M. S. (2024). Design of a Misalignment-Tolerant Inductor–Capacitor–Capacitor-Compensated Wireless Charger for Roadway-Powered Electric Vehicles. Sustainability, 16(2), 567. https://doi.org/10.3390/su16020567








