Abstract
In response to the escalating global energy crisis, the motivation for this research has been derived from the need for sustainable and efficient energy solutions. A gap in existing renewable energy systems, particularly in terms of stability and efficiency under variable environmental conditions, has been recognized, leading to the introduction of a novel hybrid system that combines photovoltaic (PV) and wind energy. The innovation of this study lies in the methodological approach that has been adopted, integrating dynamic modeling with a sophisticated control mechanism. This mechanism, a blend of model predictive control (MPC) and particle swarm optimization (PSO), has been specifically designed to address the fluctuations inherent in PV and wind power sources. The methodology involves a detailed stability analysis using Lyapunov’s theorem, a critical step distinguishing this system from conventional renewable energy solutions. The integration of MPC and PSO, pivotal in enhancing the system’s adaptability and optimizing the maximum power point tracking (MPPT) process, improves control efficiency across key components like the doubly fed induction generator (DFIG), rectifier-sourced converter (RSC), and grid-side converter (GSC). Through rigorous MATLAB simulations, the system’s robust response to changing solar irradiance and wind velocities has been demonstrated. The key findings confirm the system’s ability to maintain stable power generation, underscoring its practicality and efficiency in renewable energy integration. Not only has this study filled a crucial gap in renewable energy control systems, but it has also set a precedent for future research in sustainable energy technologies.
1. Introduction
The relentless growth of the global population and continuous industrial advancements have led to a steep increase in energy demand, emphasizing the essential role of energy in our modern lives [1,2,3]. This burgeoning demand, paired with diminishing fossil fuel reserves and escalating environmental concerns, has hastened the transition towards cleaner and more sustainable energy sources such as solar, hydro, and wind energy [4]. Among these, solar and wind energies stand out in the renewable energy sector, with photovoltaic (PV) systems and wind power systems, particularly wind farms, experiencing significant global growth [5,6]. PV systems have revolutionized the conversion of solar energy into electricity, with substantial advancements and cost reductions in solar modules [5,7,8]. Similarly, wind energy, particularly through innovations in wind farms using Doubly Fed Induction Generators (DFIGs), is shaping the future of energy due to its efficiency, adaptability, and cost-effectiveness [6,9]. However, the inherent variability and unpredictability of both solar and wind energy sources pose significant challenges to system stability and efficiency. To optimize these renewable energy sources’ efficiency, accurate modeling and effective control mechanisms are indispensable. In PV systems, maximum power point tracking (MPPT) is crucial for maximizing electricity extraction under various environmental conditions [10,11,12,13]. In wind power systems, effectively managing power on both the generator and grid sides is critical, with power converters enabling DFIGs to operate at variable speeds [14,15,16]. Addressing these challenges, our study introduces a novel hybrid system that synergistically integrates photovoltaic and wind energy systems. Our approach leverages model predictive control (MPC) enhanced by particle swarm optimization (PSO) to efficiently manage the complex dynamics of this integrated system. Unlike traditional methods, MPC’s ability to predict system behavior and adapt control actions is coupled with PSO for optimizing the cost function of the controller, ensuring enhanced performance and stability [17,18,19,20,21]. This hybrid system promises improved energy harvesting from both solar and wind sources while addressing their variability challenges. The paper is structured to detail the hybrid energy system’s components and operations, with Section 2 introducing the PSO-enhanced MPC strategy. Subsequent sections include a comprehensive overview of the PV system and control methodology (Section 2), an evaluation of a grid-tied wind system under varying conditions (Section 3), an in-depth look at the DFIG wind system and PSO control technique (Section 4), and simulation methodology and results (Section 5). The final section (Section 6) synthesizes our key findings and discusses potential future research directions.
Key Contributions:
- Development of an innovative hybrid solar and wind energy system, distinct in its use of MPC combined with PSO. This approach is novel in its ability to address the unpredictable nature of renewable energy sources, a gap in existing methodologies.
- Application of Lyapunov’s theorem for rigorous stability analysis, providing a mathematical validation of our system’s stability, a feature often overlooked in similar hybrid systems.
- Comprehensive MATLAB simulations demonstrate the system’s resilience and adaptability to changing environmental conditions, confirming its practicality and efficiency in renewable energy integration.
2. Configuration of Hybrid System
This study unveils a hybrid solar PV/wind system, an elegantly integrated framework that marries the advantages of solar and wind energy to facilitate consistent and efficient power production. The solar facet is composed of photovoltaic panels that efficiently convert sunlight into electrical power. A boost converter then optimizes this power, enhancing the voltage from the solar array, as detailed in reference [22]. The subsequent DC output is converted to AC through a precise DC–AC inverter, maintaining a power factor of one. This AC is then conditioned through a transformer to meet grid voltage standards, as outlined in reference [23].
Parallel to this, the wind component is built around a doubly fed induction generator (DFIG), a system favored for its efficiency and versatility in harnessing wind energy, as cited in reference [24]. The DFIG integrates a pair of back-to-back converters—the rotor-side converter (RSC) and the grid-side converter (GSC)—which are pivotal in achieving optimal energy conversion and facilitating grid integration. The GSC is particularly crucial for maintaining a stable DC-link voltage and for its ability to supply reactive power to the grid, therefore improving the system’s overall power factor.
As depicted in Figure 1, each element of the system plays an integral role: the solar array employs MPPT technology to maximize power output under variable solar conditions, while the DFIG-based wind subsystem is adept at adapting to changing wind speeds. The RSC is tasked with maximizing energy extraction, and the GSC is responsible for ensuring smooth grid integration and voltage stability. This cohesive strategy not only bolsters efficiency but also secures a reliable and uniform power supply, making it suitable for diverse applications.

Figure 1.
Diagram of a hybrid PV/wind energy system integrated with the grid.
The subsequent sections will delve into the modeling, operational performance, and control strategies of this hybrid system. The intricate cooperation between the PV modules, wind generator, power converters, and their respective control methodologies underpins this pioneering energy solution, marking an important step toward sustainable and reliable power generation.
3. Description of Photovoltaic System Configuration
This study explores a multifaceted photovoltaic (PV) system intricately designed to harness solar energy effectively. The system initiates the energy conversion process through PV panels, which capture sunlight and convert it into electrical power. These panels play a pivotal role, as they are the primary interface with the renewable energy source. Following the initial conversion, the electrical output, primarily in DC form, undergoes voltage regulation via a boost converter. This critical component elevates the voltage to an optimal level, ensuring that the power delivery is both efficient and consistent with the system requirements. A crucial transition from DC to AC power is managed by a DC–AC inverter. This stage is vital for integrating solar energy into standard power grids or for use in AC-dependent applications. The inverter is meticulously engineered to maintain a unity power factor, signifying efficient and reliable conversion without unnecessary power loss. An additional aspect of the system is the employment of a transformer. This device adapts the output voltage from the inverter, aligning it with the requirements of the power grid or the end-use application. This step is essential for the safe and effective distribution of the generated power. At the core of the system’s efficiency is the array of control techniques employed. These techniques are designed to maximize power extraction, retain an optimal power factor, and modulate the system’s response to changing operational conditions. Of particular importance is maximum power point tracking (MPPT) technology, which dynamically adjusts the operation of the PV modules to ensure maximum power output under varying environmental conditions, including changes in sunlight and temperature. This comprehensive PV system not only focuses on the conversion and enhancement of solar energy but also places significant emphasis on the control and regulation aspects. Each component, from the solar panels to the boost converter and the DC–AC inverter, is analyzed for optimal performance, ensuring the system operates at peak efficiency regardless of external factors [22,23]. The configuration’s detailed design and strategic component integration highlight the meticulous approach toward optimizing solar energy conversion, marking a significant stride in renewable energy technology and its application. Figure 2 displays the comprehensive setup of the photovoltaic system.

Figure 2.
Diagram of a PV energy system integrated with the grid.
3.1. Photocell Panel
Typically, the conceptual model of a photovoltaic (PV) system is represented through an idealized circuit diagram, often illustrated by a PNPN or Shockley diode, as shown in Figure 3. This model encompasses several key components: a current source that reflects the generation of current induced by sunlight and temperature variations, a diode in reverse bias illustrating the P-N junction’s characteristic impedance, and intrinsic series and parallel resistances that account for energy dissipation within the system [25]. The electrical behavior of a PV module is effectively modeled to mirror the impact of varying meteorological factors such as ambient temperature and solar irradiance [26]. By employing Kirchhoff’s law of currents, one can derive the mathematical expressions that accurately characterize the current–voltage (I–V) relationship under different operational conditions [27,28].
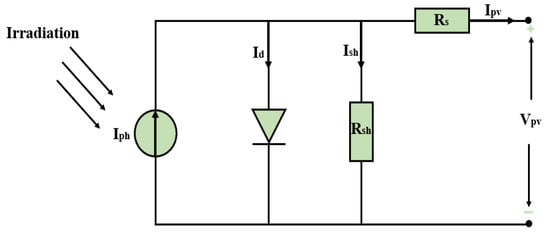
Figure 3.
Basic equivalent circuit diagram of a single-diode photovoltaic module.
The photovoltaic cell’s functionality is encapsulated in a simplified single-diode model, as illustrated in Figure 3 [29]. Central to this model is the photogenerated current, which is contingent upon both solar irradiance and ambient temperature variations. A diode characterizes the inherent non-linearity of the P-N junction, while resistances in series and parallel capture the cell’s resistive loss characteristics. The ensuing equations succinctly represent the photovoltaic cell’s electrical output, showcasing its sensitivity to the surrounding environmental conditions [30,31,32].
The output current , as delineated in these equations, is a composite function that includes the photogenerated current , and considers the influences of series resistance , the number of cells in series , and the ideality factor , alongside the thermal voltage .
Here, is formulated by adding the temperature coefficient to the nominal short-circuit current , then adjusting for the actual temperature and irradiance .
Temperature profoundly affects the saturation current , altering it based on the cubic temperature ratio and an exponential factor influenced by the semiconductor’s bandgap energy . The cell’s thermal voltage derives from a fundamental equation incorporating the Boltzmann constant , temperature , and the electron charge . Furthermore, the shunt current is determined by the photovoltaic voltage and the series resistance , divided by the shunt resistance .
The significance of each parameter is as follows:
- : The current output from the PV generator.
- : The temperature-dependent saturation current of the diode.
- : The current induced by photon absorption.
- : The current flowing through the shunt resistance.
- : The benchmark short-circuit current at standard test conditions.
- : The current’s response coefficient to temperature variations.
- : The Boltzmann constant.
- : The charge of an electron.
- : The quality factor of the diode, also known as the ideality factor.
- : The thermal voltage.
- and : The number of modules connected in parallel and cells connected in series, respectively.
- : The rated saturation current at a reference temperature.
- : The bandgap energy of the semiconductor material used.
- and : The inherent series and shunt resistances within the PV module.
The characteristics and specifications of the photovoltaic system are delineated in Table 1. Illustrated in Figure 4 are the current–voltage (I–V) and power–voltage (P–V) curves of the photovoltaic array, which were determined through simulation under various conditions of solar irradiance.

Table 1.
Attributes and performance metrics of the photovoltaic module.
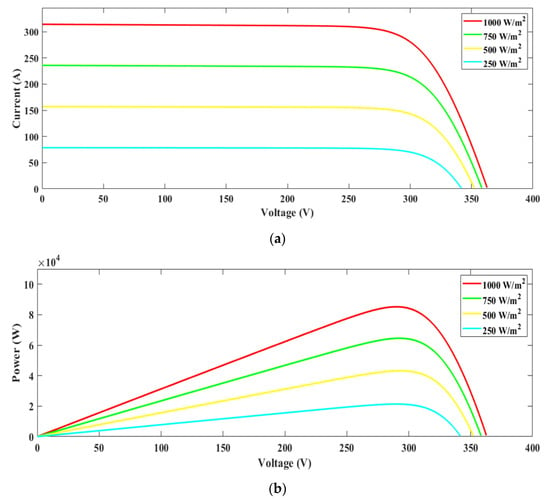
Figure 4.
Photovoltaic cell performance: (a) current–voltage and (b) power–voltage relationships across different solar irradiance levels.
3.2. MPPT
In the study detailed herein, a DC–DC conversion mechanism is utilized for maximum power point tracking (MPPT). Owing to the relatively low voltage output of the photovoltaic (PV) system, which requires amplification for effective conversion to AC via a DC–AC inverter, the chosen converter design elevates the PV array’s voltage to a more suitable level. This conversion process is characterized by minimal ripple current at the PV interface, ensuring a smoother operation [33]. The integration of the DC–DC boost converter with the PV assembly is illustrated in Figure 5. The modulation of the duty cycle within this system is governed by an MPPT controller that operates on the principles of the MPC algorithm.
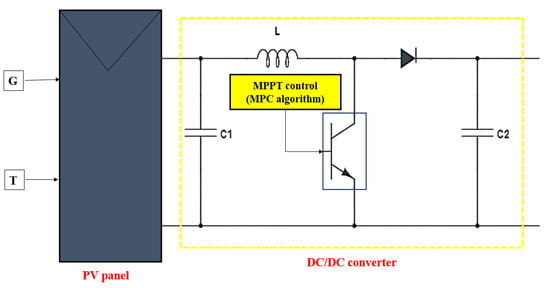
Figure 5.
Photovoltaic panel coupled with a boost converter configuration.
The boost converter’s primary role within the photovoltaic system is to escalate the output voltage from the solar panels, which in turn has a proportional impact on the power yield. Illustrated in Figure 6 is the schematic of the boost converter, which is composed of key components such as an inductor, diode, switch (transistor), and capacitor. By applying the principles of Kirchhoff’s circuit laws, the operational dynamics of the converter can be captured through a set of equations [33]:
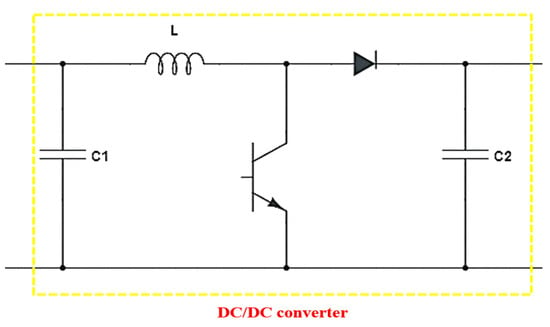
Figure 6.
Boost converter configuration.
Although the switch is engaged (S = 1), the rate of change in voltage across the capacitor is described by the equation:
Conversely, when the switch is disengaged (S = 0), the change is given by:
The duty cycle (D) of the converter is then defined as:
Hence, the voltage across the capacitor can be calculated using the relation:
where
- : Voltage generated by the photovoltaic system;
- : Current produced by the photovoltaic system;
- : Voltage across the capacitance in the boost converter, representing the output voltage target for the boost converter;
- : Capacitance within the boost converter circuit.
In examining the electrical properties of the DC—DC boost converter, Table 2 succinctly outlines the critical parameters.

Table 2.
DC–DC boost converter parameters.
3.3. MPPT MPC
The analytical exploration of the BOOST converter has yielded a set of equations that delineate the relationship between certain inputs and their corresponding outputs. This relationship is encapsulated in the equation below [33]:
Applying Euler’s method for the discretization of derivatives present in Equations (2), (3), and (6), they can be approximated by the finite difference formula [34]:
where
- : represents the parameter subject to discretization.
- : denotes the sampling period.
- : signifies the discrete time steps.
The actual current expression is contingent on the switch state (ON or OFF), leading to the derivation of the following equations:
When the switch is ON (S = 1):
And when the switch is OFF (S = 0):
During the OFF state of the switch:
Conversely, during the ON state of the switch:
Upon establishing these equations, it is possible to configure the model predictive control (MPC) algorithm for maximum power point tracking (MPPT). The intricacies of the MPC algorithm are detailed in Figure 7. Furthermore, the optimization within the MPC framework is guided by a cost function, as shown in Equation (14), which aims to minimize the discrepancy between the projected voltage and a predefined reference voltage:
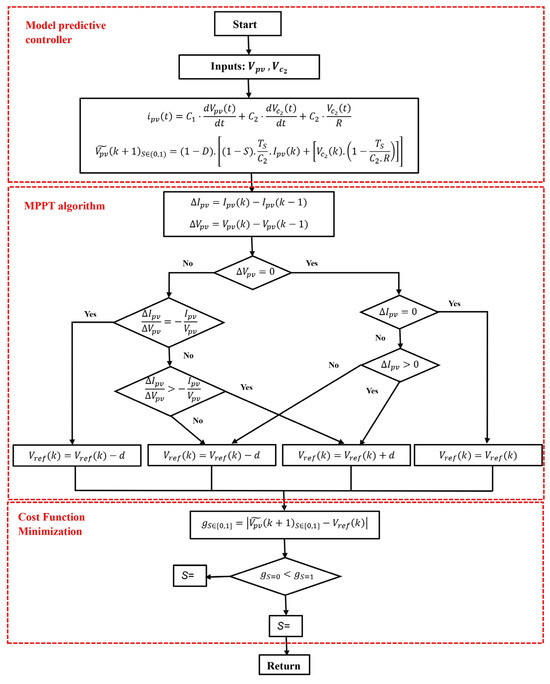
Figure 7.
Design of the MPPT controller algorithm utilizing the MPC approach.
3.4. Stability of MPPT MPC “Lyapunov”
3.4.1. Selection of the Lyapunov Function
Lyapunov’s direct approach is applied to secure the stability of the boost converter system. A Lyapunov function, denoted as , is conceived to reflect the system’s energy status at the k-th interval, predominantly predicated on the capacitive energy. The function is expressed as , which capitalizes on the intrinsic energy storage characteristic of capacitor .
3.4.2. Affirmation of Lyapunov Function’s Positivity
Inherently, due to its quadratic formulation in terms of capacitor voltage, the Lyapunov function maintains a positive value across all except when , signifying the system’s state of balance.
3.4.3. Determination of the Lyapunov Function’s Discrete Differential
The discrete variation of the Lyapunov function denoted as , is evaluated under the converter’s ON and OFF states. In the ON state, this differential is ascertained from the system dynamics as outlined in Equation (15). During the OFF state, the system’s dynamics per Equation (13) are incorporated, recognizing the photovoltaic current as a contributing factor.
3.4.4. Criterion for the Non-Positive Differential
To meet stability criteria, it is imperative that does not exceed zero for any . The analysis involves simplifying and inspecting both and , affirming their non-positivity, which guarantees the system’s trajectory will not result in an increased , therefore upholding stability under both operational states.
3.4.5. Global Stability Overview
Upon ensuring stability within each discrete mode, a comprehensive assessment of the system’s global stability is conducted. This assessment takes into account the interplay between modal transitions, which is dictated by the control methodology and the modulation of the duty cycle . The cost function, , is instrumental in steering the system towards decisions that favor stability.
3.4.6. Cost Function’s Role in Promoting Stability
Lastly, the focus shifts to the optimization of the cost function, which is instrumental in aligning the system operations with the pre-set reference voltage . The minimization of this cost function is pivotal, as it aids in the global stabilization of the system by ensuring that the operational point converges towards the targeted reference, solidifying the system’s overall stability.
3.5. DC/AC Inverter Control Strategy
This research integrates the photovoltaic assembly with the public power network through a tri-phase DC–AC voltage source inverter (VSI). The chosen VSI for exploration, a bi-level, tri-phase model, is depicted in the provided diagram (refer to Figure 8). The conversion of energy from DC to AC is accomplished through gate signals labeled a, a’, b, b’, c, and c’, which correspond to the actuation of six power semiconductor switches (S1–S6) within the VSI configuration.
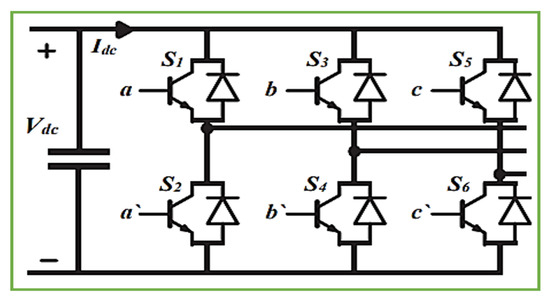
Figure 8.
DC–AC inverter.
The DC–AC voltage source inverter is crucial in the infrastructure of grid-tied PV systems, overseeing the transformation and dispatch of energy into the utility grid. The essence of this research lies in the VSI’s control strategy, aiming to fulfill several targets: enhancing the power factor to approximate unity, managing the flow of active power into the grid efficiently, and maintaining the DC-bus voltage within the desired range. A sophisticated control mechanism, as shown in Figure 9, has been engineered to meet these control endpoints.
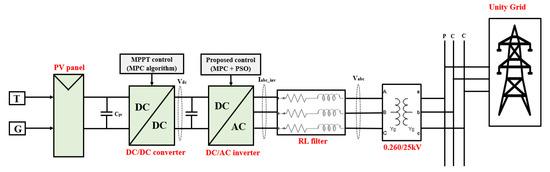
Figure 9.
MPC+PSO-controlled DC–AC inverter system configuration.
Within this controller architecture lies an outer loop focused on voltage regulation and an inner loop dedicated to current modulation. This dual-loop control framework ensures that the photovoltaic system performs at its peak efficacy and stability when interfaced with the grid infrastructure.
As illustrated in Figure 9, the schematic outlines the proposed control methodology for the inverter. Its chief aims are the stabilization of DC-link voltage, the meticulous administration of real power delivery, and the establishment of a unity power factor at the Point of Common Coupling (PCC). Noteworthy is this method’s provision for isolated control and its swift response to dynamic changes, as highlighted in the literature [35].
3.6. MPC Controller for DC–AC Inverter
3.6.1. Model Predictive Control Implementation
In this work, we unveil a model predictive control (MPC) strategy tailored for the DC–AC inverter module. The framework of the MPC is articulated through the mathematical models delineated in Equations (15) and (16):
These foundational equations evolve into:
Applying the MPC method transforms these equations as follows:
The cost function proposed to steer the optimization is expressed as:
3.6.2. MPC Optimization with PSO
The particle swarm optimization (PSO) algorithm, introduced by Kennedy and Eberhart, is based on the principles of swarm intelligence [36]. It has demonstrated effectiveness in rapidly pinpointing extreme values and global minima within a search space, even with a limited number of iterations. PSO’s robustness to initial conditions and its ability to discern both local and global optima makes it particularly valuable for complex optimization tasks, including those within the realm of MPC.
MPC’s primary aim is to minimize a predefined objective function across a set horizon, considering both the system’s dynamics and constraints. The objective function can encapsulate various control aspirations, such as error minimization, energy conservation, or cost efficiency.
In the context of MPC, PSO operates by emulating a group of particles. Each particle in this group signifies a potential solution for voltage references. The particles advance towards the most optimal solution by considering both their personal best performance (local best) and the best found by the entire group (global best). The process of adjustment and movement for each particle is governed by a fitness function, influencing both their velocity and position within the solution space with each iteration of Figure 10.

Figure 10.
Process diagram of PSO.
3.6.3. Stability Analysis of DC–AC Inverter Control System
To ascertain the stability of the DC–AC inverter control system that employs a model predictive control (MPC) approach, we undertake a methodical procedure underpinned by Lyapunov’s theorem. The theorem’s applicability hinges on identifying an appropriate Lyapunov function which must be inherently positive and whose derivative along the system’s trajectories is non-positive.
The system under consideration is defined by discretized Equations (19) and (20) for the direct and quadrature currents and , respectively. We also have a cost function J articulated in Equation (21), which is instrumental in generating a control action that minimizes the cost.
- Proposition of a Lyapunov Function: For the given system, we propose a Lyapunov function rooted in the stored energy within the inductances, corresponding to the sum of the squares of the currents and :
- Affirmation of Function Positivity: It is evident that is positive across all and values, as it constitutes a sum of squares of these current components.
- Calculation of the Lyapunov Function Difference: The change in the Lyapunov function, , is expressed as:
Implementing Equations (19) and (20), we articulate and within the difference expression to derive .
- D.
- Verification of Non-Positive Difference: The subsequent step involves demonstrating that remains non-positive for all k.
A negative suggests that the Lyapunov function is diminishing over time, signaling the system’s stability.
- E.
- Correlation of Cost Function to Stability: The cost function J aims to minimize the discrepancy between the predicted currents and and their reference counterparts and . Theoretically, perfect minimization at each step should steer the system towards the reference values, suggesting stability in terms of error convergence towards zero.
Precision in this analysis mandates an explicit computation of using the provided equations, followed by a mathematical verification that this quantity is consistently non-positive, irrespective of the control action rendered by the MPC methodology. Satisfying this condition through rigorous validation establishes Lyapunov stability for the system.
4. Description of Wind System Configuration
The doubly fed induction generator (DFIG) system anchors the architecture of modern wind turbines and is heralded for its advanced design that effectively captures wind energy for electrical conversion. Its market prominence is attributed to the system’s ability to allow variable speed operation and its efficient energy modulation, facilitated by a dual-winding rotor design within the induction generator. One winding connects directly to the grid, promoting an uninterrupted flow of electricity, while the other interfaces through a sophisticated set of power electronics converters, namely the rotor-side converter (RSC) and the grid-side converter (GSC), as elaborated in reference [24]. The GSC is particularly critical in the DFIG configuration. It meticulously manages the direct current (DC) voltage across the DC link, a vital aspect that ensures the RSC is supplied with a stable voltage. This regulation is essential for harmonizing the power exported to the grid by the generator. Additionally, the GSC’s control mechanism is adept at enhancing grid stability by providing necessary reactive power compensation, therefore enriching the power quality and improving the system’s power factor. The DFIG’s innovative capacity lies in its variable speed operation enabled by the RSC, which adeptly modulates the rotor’s extracted power. This modulation is responsive to the fluctuating nature of wind speeds, optimizing the generator’s output for a range of wind conditions. A transformer is judiciously incorporated within the system to align the generated power’s voltage with that of the Point of Common Coupling (PCC), thus ensuring a seamless integration of wind-generated electricity into the grid’s existing infrastructure. The integration of this wind system with a photovoltaic (PV) setup and the grid poses a sophisticated challenge due to the intermittent nature of both wind and solar resources. The study, shown in Figure 11, presents a system that is robust and adaptable enough to accommodate the variability of wind speeds while ensuring smooth grid integration. Advanced control strategies like the model predictive control (MPC) and particle swarm optimization (PSO) algorithms are employed to finely tune the performance of both the DFIG and the PV systems. MPC utilizes a predictive model of the system’s behavior to optimize the control inputs proactively, while PSO optimizes the system’s operational parameters by simulating the social dynamics observed in natural swarms. The interaction between the wind and PV systems, particularly when coupled with the grid, necessitates a delicate balance. The integrated system must address the variability of the energy sources and the demand response of the grid. Solutions include deploying energy storage to mitigate intermittence and employing smart grid technologies to ensure that the power output is consistent, reliable, and meets consumption demands. Thus, the study portrays a wind power system that is not only robust and capable of adjusting to wind variability but also harmoniously integrated with the grid and complementary PV systems. The DFIG, with its advanced converters and control strategies epitomized by the MPC and PSO algorithms, stands as a testament to efficiency in wind energy generation, pointing to a sustainable trajectory for renewable power technologies.

Figure 11.
Diagram of a wind energy system integrated with the grid.
4.1. Overview of Wind Power
4.1.1. Wind Energy Model
The formula presented next defines the power available from wind under ideal flow conditions as found in the literature [37]:
Wind power is intrinsically connected to the aerodynamic torque that acts upon the turbine blades.
The power coefficient, , reflects the interplay between the turbine’s aerodynamic design and its operational conditions. Holding the pitch angle steady, the value is a function of the tip speed ratio . When the pitch angle is adjustable, becomes a function of both and as discussed in [38]:
Within these expressions, is the wind turbine’s harvested power, stands for air density, is the wind velocity, signifies the rotor’s angular velocity, and R is the blade length.
Albert Betz provided a theoretical limit for , which is cited as [34]:
The formulation for aerodynamic torque is given by:
The gearbox is essential in matching the turbine’s rotational speed to the generator’s requirements. Assuming there is minimal energy dissipation, rigidity, and resistance within the gearbox, it is represented as follows [39]:
The core dynamical equation is as stated [40]:
An illustration of the wind turbine’s aerodynamic and mechanical design is provided in the block diagram shown in Figure 12.
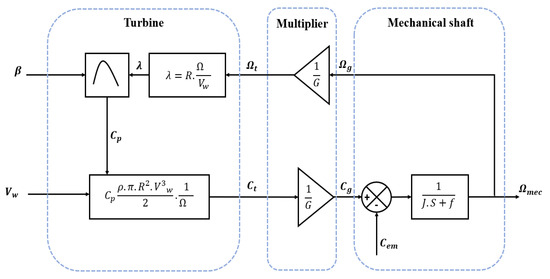
Figure 12.
Schematic of the wind turbine model.
Our investigation into enhancing energy capture efficiency has led us to examine the variable speed control within wind turbines. We introduce a control mechanism designed to optimize rotational velocity via the maximum power point tracking (MPPT) technique. The primary aim is to achieve the most favorable wind power to capture power ratio by fine-tuning the power coefficient (). Utilizing a cruise control algorithm [41,42], the system calculates the optimal rotational speed at peak torque by formulating a reference electromagnetic torque through a proportional-integral (PI) controller. This strategy enables us to accurately identify the best operational points for speed and power coefficient , thus setting the turbine’s reference rotational speed ().
Figure 13 exhibits the MPPT control system block diagram incorporating mechanical rotational speed regulation.
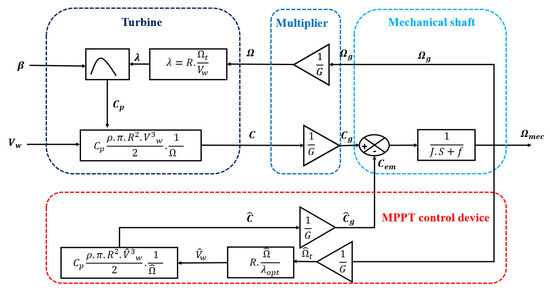
Figure 13.
Schematic of the wind turbine model with MPPT.
4.1.2. Doubly Fed Induction Generator (DFIG) Modeling
The DFIG is conceptually akin to an induction generator, with its modeling paralleling the latter’s principles. The dynamic behavior of the DFIG in a three-phase system is captured using a rotating direct-quadrature (d-q) reference frame, which can be mathematically described by the following set of equations, as referenced in the literature [43,44,45]:
These equations align with the magnetic flux linkages for both the stator and rotor circuits:
The approach involves synchronizing the stator flux with the d-axis of the rotating frame, as per the following relations [46]:
Subsequently, the current equations can be simplified as:
Considering ideal conditions where the stator resistance and stator voltage along the d-axis are negligible, we have:
The equations governing the rotor’s magnetic flux linkages, considering the influence of the stator, are:
By integrating these flux equations into the original set, we derive the comprehensive equations for the rotor voltages:
Equations (22) through (29) encapsulate the dynamic characteristics of the DFIG, illustrating the complex interactions between the stator and rotor circuits mediated by the mutual inductance. They form the basis for the simulation and control of the DFIG in various applications, particularly in wind power generation systems.
4.1.3. Rotor-Side Converter (RSC) Control in DFIG System
The rotor-side converter (RSC) plays a pivotal role in wind turbine systems employing Doubly Fed Induction Generators (DFIGs). The primary objective of the RSC is to optimize power output by adjusting the rotor’s speed so that it remains aligned with a predefined reference value. This adjustment is essential to cope with the fluctuating nature of wind speeds. The mathematical representation that governs the behavior of the RSC is provided by the following equations [47]:
In these equations, and are the d-axis and q-axis components of the stator voltage in the rotating reference frame, and is the angular frequency of the rotor.
Here, and refer to the d-axis and q-axis components of the rotor voltage. is the rotor resistance, the rotor inductance, is a scalar representing the level of magnetic coupling, is the rotor’s electrical angular velocity, the mutual inductance, and the q-axis stator flux linkage.
By manipulating these dynamic equations, the RSC can effectively control the power flow between the stator and the grid, ensuring efficient operation of the wind turbine across various operating conditions.
4.1.4. Modeling of the Grid-Side Converter (GSC)
The grid-side converter (GSC) is a crucial component of a wind turbine system, responsible primarily for transferring active power into the electrical grid and maintaining the DC-link voltage at its designated setpoint. The GSC is governed by the following equations, which form the foundation of its mathematical model [47]:
In these expressions, denotes the grid-side voltage, is the resistance associated with the grid-side converter, its inductance, and the angular frequency of the grid voltage. The variables and represent the d-axis and q-axis components of the grid-side current, respectively, and and correspond to the d-axis and q-axis rotor voltage components.
This model encapsulates the GSC’s functionality, highlighting its role in stabilizing the voltage within the wind turbine’s power circuit and ensuring the effective delivery of power to the grid.
4.2. MPC Controller Optimizing by PSO
The particle swarm optimization (PSO) algorithm is an evolutionary computation technique that draws inspiration from swarm intelligence. Devised by Kennedy and Eberhart, the algorithm demonstrates remarkable efficiency in seeking out the global minimum within a problem space, even with a limited number of iterations [38]. It showcases robust performance in identifying both local and global optimal solutions and exhibits resilience to the initial positions of the particles within the search space. Its versatility allows it to tackle various optimization challenges, one of which includes model predictive control (MPC).
MPC is an advanced method that anticipates system behavior and enforces constraints while minimizing a predefined objective function across a projected time horizon. This objective function could represent different control targets, such as minimizing tracking errors, reducing energy consumption, or lowering operational costs. Within the context of MPC, the PSO algorithm simulates a swarm of particles that search for the optimal control inputs over the prediction horizon [39]. These particles navigate towards the best solution found by the collective (global best), as well as their personal experience (local best), based on the fitness function’s evaluation. Their velocity and position are continuously updated to guide their exploration of the search space. Figure 10 depicts a flowchart illustrating the PSO process.
In the context of MPC-PSO control strategies, the objective function incorporates components related to the currents and , and is computed over a specified period, integrating the predictive results of the DC–AC currents. The optimization of this objective function is where the PSO algorithm is applied.
The movement of each particle is influenced by its own best-known position and that of the best-known position in the swarm, according to the following equations [39]:
Here, represents the directional movement of voltage at iteration , is the inertia weight, and are the cognitive and social acceleration coefficients, and and are random numbers between 0 and 1. The terms and denote the best personal voltage values for the and components for particle i, while refers to the best global voltage values found by the swarm for both components. indicates the voltage value for each particle i at iteration for both and components.
RSC Controller
In this investigation, the robustness of a rotor-side converter (RSC) controlled via a model predictive control (MPC) mechanism augmented by particle swarm optimization (PSO) is rigorously scrutinized. A structured approach unfolds as follows, entailing a combination of theoretical exposition and empirical verification.
- Defining Control Aspirations and Modeling: At the heart of RSC functionality within wind turbine applications lies the imperative to modulate rotor currents, and , to oversee the electromagnetic torque and manage reactive power. Such regulation is vital to synchronize rotor velocity with a pre-set reference, compensating for wind speed fluctuations.
- Strategizing MPC Coupled with PSO: The MPC establishes an optimization challenge with the goal of curtailing a cost metric emblematic of the control goals within a forecast horizon constrained by the dynamics inherent to the RSC. Concurrently, PSO is woven into the MPC structure, tasked with the identification of prime control stratagems, an endeavor facilitated by its heuristic nature to canvass the extensive parameter space.
- Lyapunov Function Proposition: Asserting stability involves positing a Lyapunov function, , indicative of the system’s energy reserves. For RSC systems, might encapsulate the electrical energy within the rotor’s inductive components and the rotor’s kinetic vigor:
Here, represents the rotor’s inductance, and J stands for the rotor’s moment of inertia.
- D.
- Lyapunov Function Derivative Derivation: The crux of stability validation necessitates the derivative of , , to be non-positive along system trajectories. The exercise entails computing the temporal rate of change in and integrating the RSC’s dynamical behavior:
- E.
- Implementation of MPC+PSO for Lyapunov Derivative Minimization:
The combined might of MPC and PSO coalesces to engineer control voltages, and , that pursue the minimization of , therefore guaranteeing the attenuation of any deviations in rotor currents or velocity.
- F.
- Simulation for Empirical Corroboration:
The practical facet of this theoretical construct is tested through simulation. The applied MPC+PSO schema, when superimposed onto a simulated RSC model and subjected to disturbances like variable wind velocities, is expected to reaffirm the return of rotor speeds and currents to their designated benchmarks, signifying system stability.
In essence, the proposed framework offers a hypothetical blueprint for affirming RSC stability when controlled by an MPC+PSO amalgamation, with empirical substantiation through simulations acting as a critical component of the overall validation process.
- G.
- Enhanced Stability Assurance of Grid-Side Converters via an Integrated MPC-PSO Control Paradigm
The operational stability of Grid-Side Converters (GSCs), critical components in the electrical power conversion landscape, has been advanced through the innovative incorporation of a model predictive control (MPC) and particle swarm optimization (PSO) hybrid algorithm. This methodology has undergone rigorous validation based on the principles of Lyapunov’s second method, where the amalgamation of PSO with MPC significantly elevates the optimization process. This hybridized control strategy is designed to meticulously refine GSC control actions by meticulously navigating through a multi-dimensional search space to identify the most optimal control solutions.
Analytical modeling of GSC behavior is framed within the context of state-space formulations, encapsulating the essential dynamics of both the direct and quadrature components of grid current. These electrical currents, which are crucial to the efficacy of power conversion processes, are modulated by specific control voltage vectors , . The targeted optimization process leverages these vectors to achieve a finely tuned control mechanism.
At the core of the stability argument lies the proposition of a Lyapunov candidate function , formulated to represent the inductor-stored electromagnetic energy within the GSC system:
This selection inherently fulfills the requisite condition of positivity, as prescribed by Lyapunov’s criteria. Crucially, the stability confirmation is dependent on demonstrating the derivative of this function, , maintains a non-positive trajectory in the system’s operational pathway:
Through the strategic implementation of the MPC-PSO framework, the optimization of the control law is fine-tuned to ensure the minimization of the Lyapunov function’s derivative. PSO embarks on an exhaustive control input space exploration, pinpointing parameters that guarantee a consistent decline in , thus facilitating a dynamic adaptation that upholds system stability.
The intrinsic heuristic quality of PSO, when seamlessly integrated with the predictive nature of MPC, enables a robust global search mechanism. This search avoids potential local minima that could threaten system stability and ensures an adjustment in control voltage vectors that perpetuates the non-positive gradient of the Lyapunov function.
In conclusion, the fusion of MPC and PSO culminates in a sophisticated control schema that adeptly manages the intrinsic complexities and uncertainties present in GSC operations, securing their stable performance. The PSO component, especially, excels in traversing the intricate optimization topography and, in synergy with MPC’s forecasting precision, adheres to the strict stability guidelines as mandated by Lyapunov’s theorem. This presents a methodologically sound and reliable framework for ensuring the stability of GSCs.
5. Simulation and Results
5.1. For PV System
In this section, the operational efficiency of the system was assessed under different solar irradiance conditions, while the temperature of the photovoltaic array was maintained at a steady 25 °C. The output of the solar panels was gauged using standard test conditions (STC), which assume a baseline temperature of 25 °C. Figure 14 illustrates the fluctuating solar irradiance and its daily variation pattern.
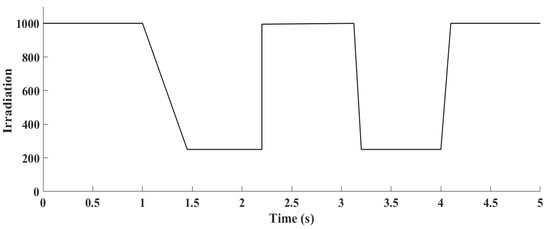
Figure 14.
Irradiance fluctuations at a constant temperature of 25 °C.
5.2. Simulation
The Simulink representation of the photovoltaic (PV) system, detailing the interconnected components and their functionality, is captured in Figure 15. This model is composed of distinct blocks that simulate the key elements of the system, including the PV module, boost converter, MPPT algorithm, and the DC–AC inverter, among others. The PV module block not only symbolizes the solar panel but also integrates the equations that define its electrical behavior, producing the respective current–voltage (I–V) and power–voltage (P–V) characteristics based on solar irradiance and temperature inputs. The boost converter block is tasked with stepping down the voltage output from the PV array and includes the control logic that dictates the operation of the converter via the MPPT strategy. This MPPT algorithm actively tracks and adjusts the operating point of the PV system to optimize power extraction. The DC–AC inverter block’s role is to convert the DC output of the PV array into AC power that is suitable for the grid, ensuring the quality and grid compatibility of the AC output with a target power factor of unity. Other elements in the model, such as transformers and grid interfacing components, are instrumental in depicting the full scope of the PV system and its integration with the electrical grid infrastructure. Figure 11 illustrates the proposed photovoltaic (PV) system, which is segmented into three primary sections labeled A, B, and C. Each of these sections plays a distinct role in ensuring the efficient production, transformation, and integration of solar energy into the power grid. They correspond to different components or phases of the system.
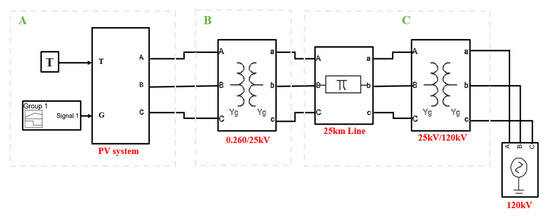
Figure 15.
Comprehensive schematic of the proposed photovoltaic system.
5.3. Results
5.3.1. Part A
In the first section, identified as Part A, we explore the core components of the photovoltaic (PV) system. It begins with the PV panels, tasked with the critical function of transforming sunlight into electric power. The system integrates a boost converter, working in unison with an MPPT controller guided by an MPC algorithm. The boost converter’s primary objective is to elevate the voltage output from the PV array, therefore enhancing the overall efficacy of the energy conversion process. The MPPT controller’s role is pivotal, as it relentlessly pursues the maximum power point of the PV system, dynamically adjusting the operational variables of the boost converter to capitalize on the maximum available power amid fluctuating environmental conditions. Furthermore, the setup encompasses a DC–AC inverter, responsible for transmuting the DC electricity produced by the PV array into AC power compatible with grid distribution. This inverter is also calibrated to maintain a unity power factor, ensuring efficient power delivery and compliance with grid interconnection standards, thus facilitating a seamless merger of sustainable energy into the conventional power grid.
Continuing to Figure 16, the sinusoidal current waveforms for the three-phase injection into the grid are depicted. These waveforms are critical for verifying that the injected currents are in harmony with grid requirements.
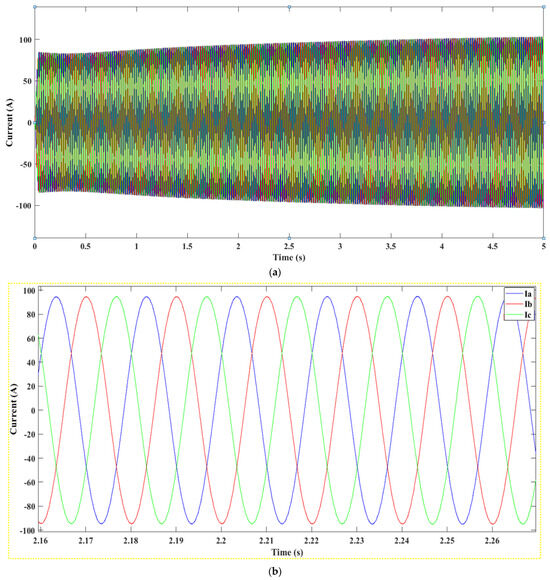
Figure 16.
(a) Current Output from Section A of the system, (b): Zoomed-In Current Oscillation from Selected Interval in Section A.
Figure 17 details the actual power output produced by Component A of the system, offering a quantitative look at the energy generation efficiency.
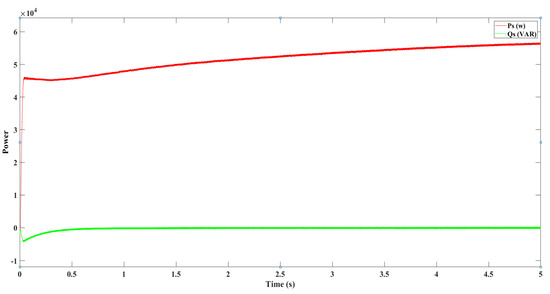
Figure 17.
Active and reactive powers produced by Part A.
Lastly, Figure 18 portrays the electrical characteristics of the voltage and current produced, encapsulating a comprehensive overview of the operational dynamics and the system’s electrical performance.
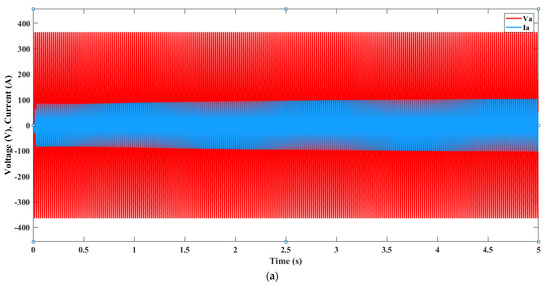
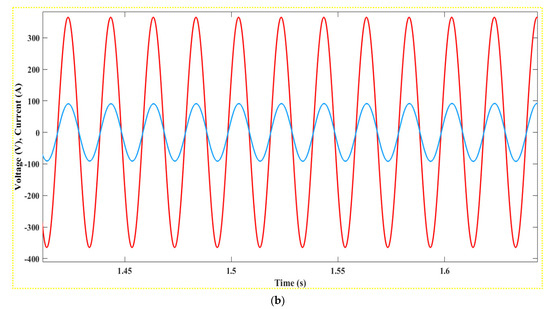
Figure 18.
(a): Current and voltage produced by Part A, (b): Detailed Oscillation Analysis of Current and Voltage from Part A.
5.3.2. Part B
Within Component B of the PV system, the transformer plays a crucial role by stepping up the voltage to meet the specifications of the power grid, therefore facilitating efficient power transfer. Elevating the voltage level reduces the current, which in turn minimizes power losses incurred during transmission. Furthermore, a higher voltage enables electricity to be conveyed over longer distances with reduced energy dissipation. The performance outcomes of incorporating a transformer rated at 0.26/25 kV into the PV system are documented in Figure 19, Figure 20 and Figure 21, demonstrating its impact on the system’s efficiency.
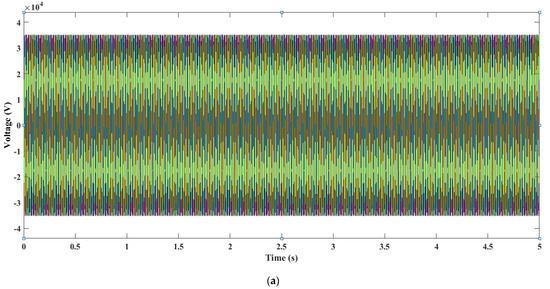
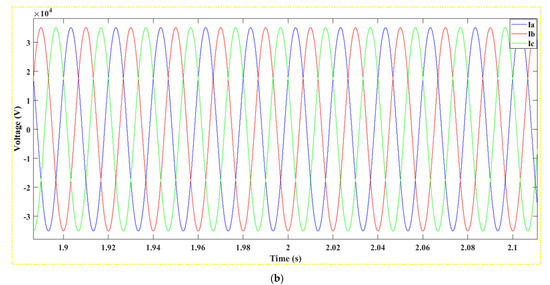
Figure 19.
(a): Voltage produced after the transformer 0.26/25 kV, (b): Close-Up on Voltage Oscillation after the 0.26/25 kV Transformer.

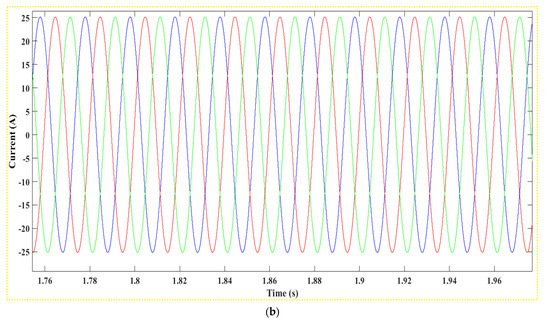
Figure 20.
(a): Current produced after the transformer 0.26/25 kV, (b): Close-Up on Current Oscillation after the 0.26/25 kV Transformer.
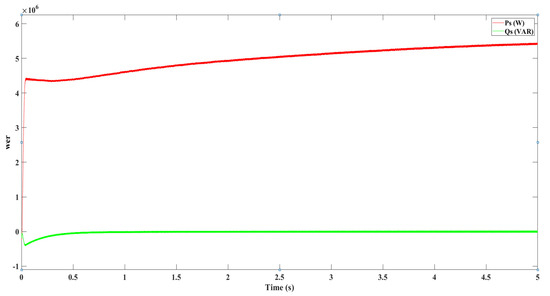
Figure 21.
Active and reactive powers produced after the transformer 0.26/25 kV.
5.3.3. Part C
Part C of the PV system is composed of two primary elements. The initial component entails a transmission line stretching 25 km, serving as the conduit to connect the system’s generated electrical power to the broader grid. The second element is a step-up transformer tasked with boosting the voltage before the power is introduced into the grid. The transmission line is pivotal for bridging the considerable distance to the grid, minimizing losses and voltage drops to preserve the integrity and efficiency of the power being transmitted. Concurrently, the transformer’s role is to elevate the voltage to the required standards for grid compatibility, a critical step for ensuring the efficient distribution and transmission of electricity within the system.
The integration of the 25 km transmission line and the step-up transformer into Part C is quantitatively depicted in Figure 22, Figure 23 and Figure 24, showcasing the enhancements in system performance subsequent to their implementation.
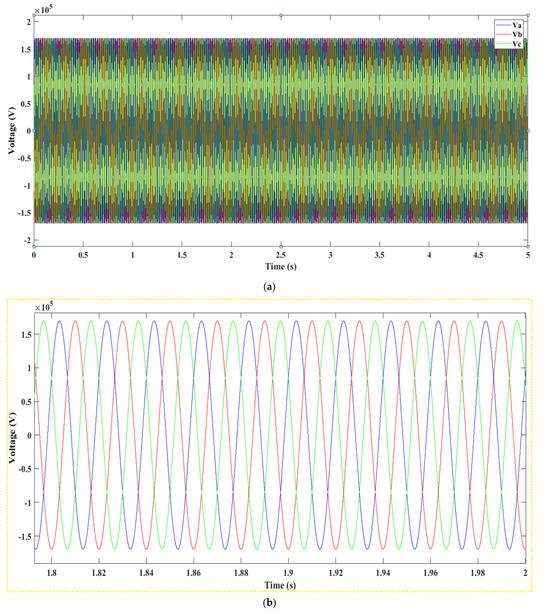
Figure 22.
(a): Voltage produced after the transformer 25/120 kV, (b): Close-Up on Voltage Oscillation after the 25/120 kV Transformer.
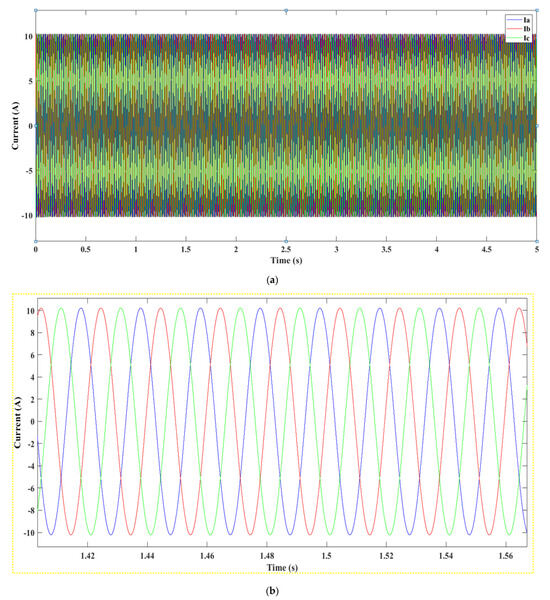
Figure 23.
(a): Current produced after the transformer 25/120 kV, (b): Close-Up on Current Oscillation after the 25/120 kV Transformer.
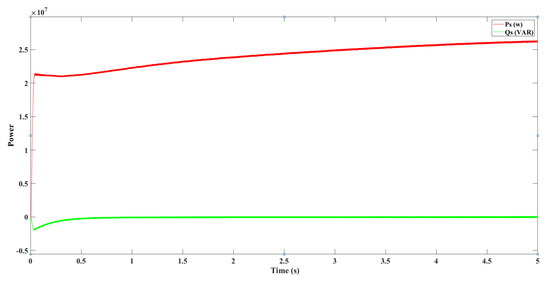
Figure 24.
Active and reactive powers produced after the transformer 25/120 kV.
5.4. Simulation
The energy generation and subsequent financial viability of a wind turbine system are critically dependent on the wind as its primary energy source. Grasping the dynamic behavior of the wind is vital for a comprehensive appreciation of the entire energy conversion process, given that the power potential of wind is theoretically proportional to the cube of the wind speed. This cubic relationship, as highlighted in the associated research, underscores the exponential impact of wind velocity on the turbine’s power output.
where .
Figure 25 presents the wind speed variability over a five-second interval, as recorded by the system.
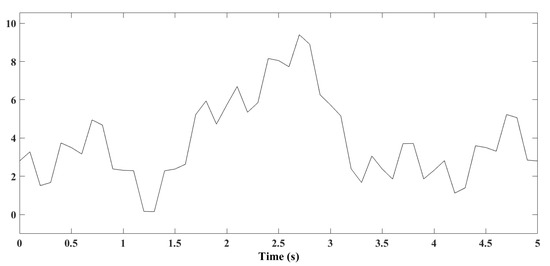
Figure 25.
Wind speed profile (m/s).
The model is meticulously constructed with separate blocks representing critical elements like the doubly fed induction generator (DFIG), the rotor-side converter (RSC), the grid-side converter (GSC), and their associated control strategies.
The DFIG block models the generator’s electrical characteristics using sophisticated mathematical representations, delivering insights into its performance across a spectrum of wind conditions. This encompasses the simulation of current and voltage outputs that adapt to the changing wind dynamics.
The RSC and GSC blocks are integral to the system, orchestrating the two-way flow of energy between the DFIG and the electrical grid. The model encapsulates the advanced control techniques that regulate these converters, optimizing power conversion and ensuring compliance with grid connection standards.
Additional components, such as transformers and grid interfacing equipment, are also incorporated into the model, completing the picture of the wind energy system’s infrastructure. The Simulink model, as illustrated, thus serves as a valuable tool for simulating and analyzing the system’s behavior under a variety of operating conditions and for evaluating different control approaches.
5.5. Results
Figure 26 illustrates the segmented design of the proposed wind energy system, which is divided into three primary sections labeled A, B, and C. Each segment performs distinct functions vital to the overall process of generating, converting, and delivering wind energy to the power grid. These segments encompass the various stages and components of the system, ensuring a streamlined operation from wind capture to electricity distribution.
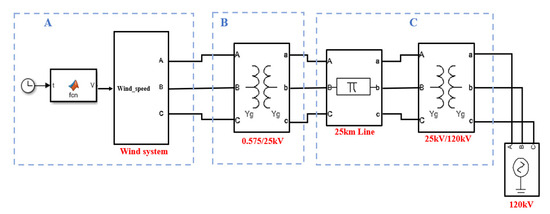
Figure 26.
Comprehensive schematic of the proposed wind system.
5.5.1. Part A
Figure 27 presents the wind turbine system, which is composed of several key components. Central to the control mechanism of the turbine is the maximum power point tracking (MPPT) system, depicted as the “Turbine + MPPT” block in the diagram. Concurrently, the system implements vector control for the doubly fed induction generator (DFIG), a method that involves a regulator ensuring the decoupling of rotor current to enable precise adjustments in power output. The control architecture utilizes a cascade control strategy that adeptly manages power and rotor current along each axis, facilitating the regulation of individual currents (, ) and power outputs (, ) in a closed-loop system. Before this process, the currents and from the rotor’s d and q axes are converted to and in the and axes. This conversion is accomplished by the “d/q to /” block, contributing to the generation of outputs with minimal ripple and enhanced smoothness. The “MPC-PSO” block integrates the model predictive control-particle swarm optimization algorithm for control purposes. Lastly, the “DFIG + inverter” block represents the end-point of the system, which is responsible for the final conversion of the generated electrical power, ensuring it is ready for integration into the grid.
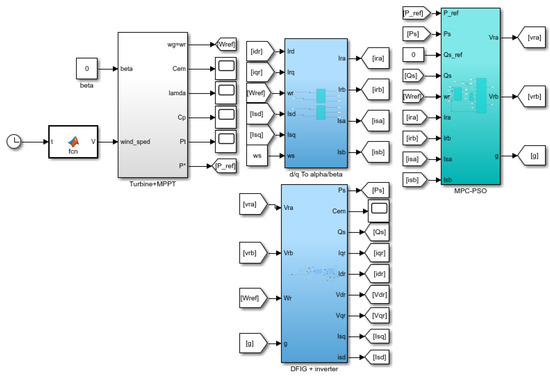
Figure 27.
Model of DFIG in MATLAB/Simulink.
Table 3 presents an organized summary of the parameters associated with the doubly fed induction generator (DFIG) being analyzed. Table 4 also presents the variables relevant to the particle swarm optimization (PSO) algorithm. And Table 5 presents the parameters of the DFIG controller.

Table 3.
DFIG and PSO configuration specifications.

Table 4.
PSO parameters.

Table 5.
Parameters of DFIG controller.
The depicted graph, as referenced in Figure 28, provides insights into the voltage trends over time, illustrating the efficacy of the boost converter in modulating and optimizing the voltage of the wind system. The data captured on the voltage behavior is instrumental in assessing the converter’s performance, its consistency, and its responsiveness to variations in environmental factors. Moving to Figure 29, the sinusoidal patterns of the three-phase current injection are presented. Then, Figure 30 quantifies the actual power output generated by Part A of the system. Finally, Figure 31 displays the profiles of the produced voltage and current. Together, these visuals offer a comprehensive view of the wind system’s electrical dynamics and operational capabilities.
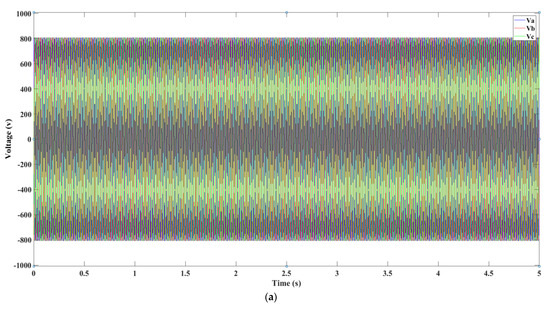
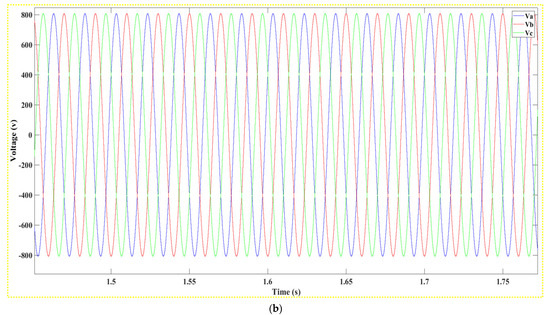
Figure 28.
(a): Voltage output from Section A of the system, (b): Zoomed-In Voltage Oscillation from Selected Interval in Section A.
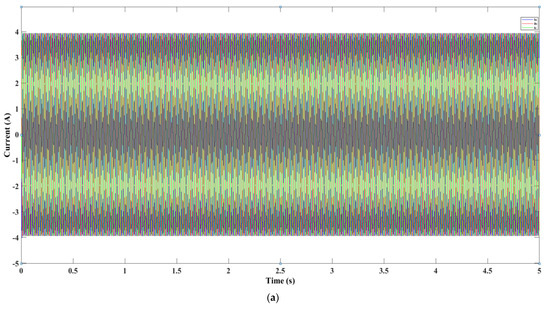
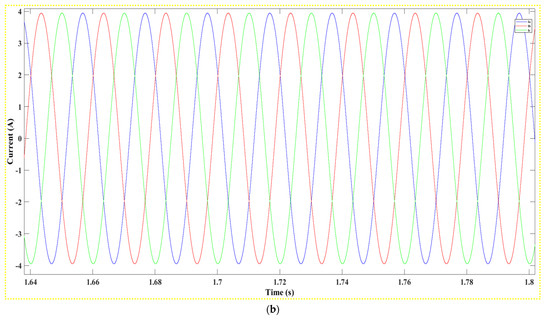
Figure 29.
(a): Current output from Section A of the system, (b): Zoomed-In Current Oscillation from Selected Interval in Section A.
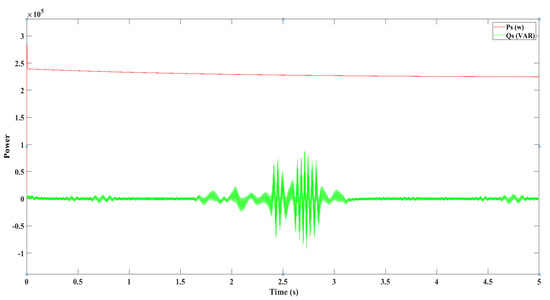
Figure 30.
Active and reactive power from Section A of the system.
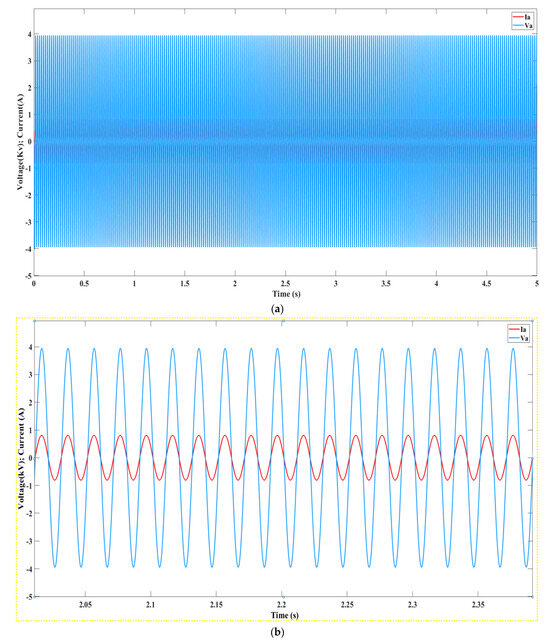
Figure 31.
(a): Voltage and current from Section A of the system, (b): Detailed Oscillation Analysis of Voltage and Current from Part A.
5.5.2. Part B
In the wind energy system, the transformer within Component B plays a crucial role in escalating the voltage to meet the grid’s voltage standards, facilitating efficient power distribution. Elevating the voltage level concurrently diminishes the current, which in turn minimizes transmission losses. Moreover, a higher voltage enables the long-distance transmission of electricity with reduced dissipation of power. The impact of integrating a transformer with a 0.575/25 kV specification on the system’s operation is demonstrated in Figure 32, Figure 33 and Figure 34, revealing the enhanced performance of the wind energy system.
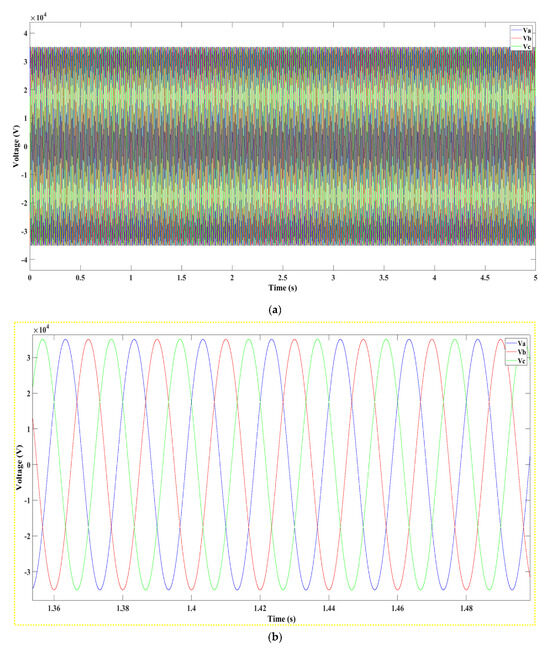
Figure 32.
(a): Voltage from Section B of the system, (b): Close-Up on Voltage Oscillation after the Section B.
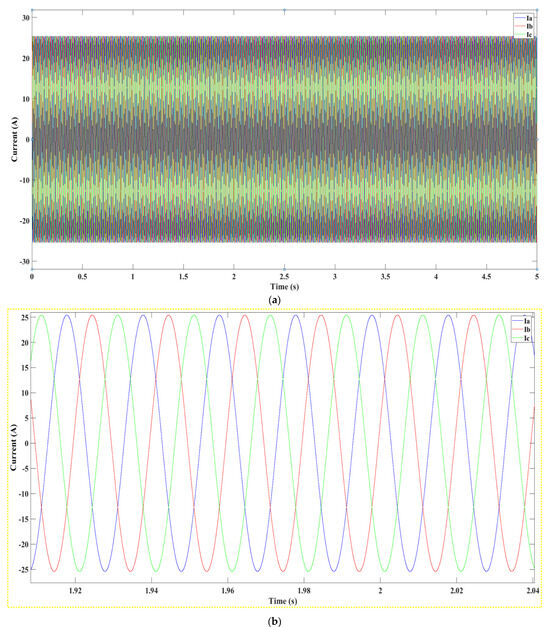
Figure 33.
(a): Current from Section B of the system, (b): Close-Up on Current Oscillation after the Section B.
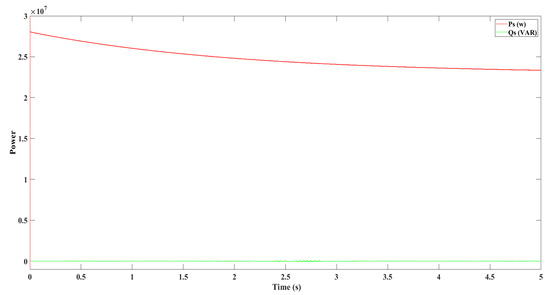
Figure 34.
Active and reactive power from Section B of the system.
5.5.3. Part C
Component C of the wind system encompasses two distinct sections. The first is a 25-km transmission line, which establishes a conduit between the wind energy grid and the broader electrical network. The second consists of a transformer tasked with voltage elevation, ensuring that power enters the grid at the necessary voltage level. This extensive transmission line is vital to efficiently deliver electricity over substantial distances to the grid, minimizing energy loss and preventing voltage sag, therefore ensuring consistent and effective power delivery. Concurrently, the transformer’s role in Component C is to augment the voltage to match grid specifications, a crucial step for maintaining the integrity of power distribution and transmission within the system. The efficacy of the wind system, inclusive of the transmission line and the step-up transformer, is illustrated in Figure 35, Figure 36 and Figure 37, detailing the operational results post-installation.
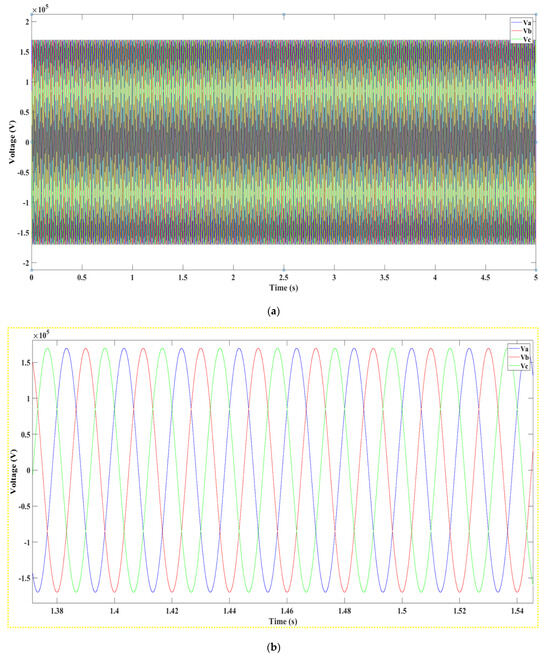
Figure 35.
(a): Voltage from Section C of the system, (b): Close-Up on Voltage Oscillation after the Section C.
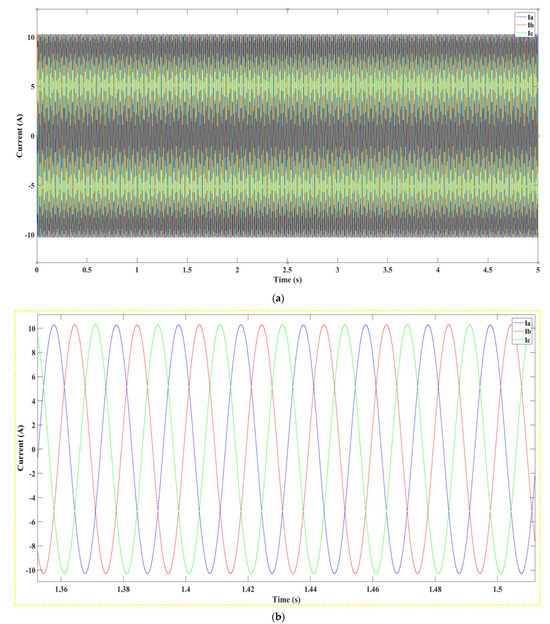
Figure 36.
(a): Current from Section C of the system, (b): Close-Up on Current Oscillation after the Section C.

Figure 37.
Active and reactive powers from Section C of the wind system.
5.6. Hybrid System
5.6.1. Simulation
The hybrid PV/wind system model depicted in Figure 1 was subjected to simulation via MATLAB to evaluate its operational efficacy. The system underwent thorough analysis under various environmental conditions, including changes in wind velocity and solar irradiance. This investigation delved into the intricate dynamic modeling, control, and simulation of a hybrid system combining solar PV and DFIG-based wind energy, integrated with the utility grid and responding to fluctuations in AC load power and power distribution to the grid. Three distinct case studies were conducted to assess the system’s behavior: examining the solar PV, wind, and integrated PV/wind systems, respectively. The results from the simulations indicated that the implemented control strategies adeptly managed the system’s responses, fulfilling the set performance criteria.
5.6.2. Results
The chart showcases (Figure 38) the active and reactive power outputs from a hybrid energy system, where the active power, depicted in red, exhibits commendable stability, signifying consistent and efficient energy conversion. Meanwhile, the reactive power, illustrated in green, remains low, indicating a well-optimized system, except for a brief spike that suggests a transient system event. This stability in active power, coupled with the brief fluctuation in reactive power, warrants further analysis to ensure the system’s robustness and reliability in long-term operation.

Figure 38.
Active and reactive powers from Section A of the hybrid system.
Figure 39 displays the power characteristics of a hybrid energy system post the initial transformer, where the active power demonstrates a decreasing trend over the observed five-second span, potentially indicating a reduction in energy production or consumption. In contrast, the reactive power remains consistently low, suggesting that the transformer effectively minimizes energy storage within the system, a sign of efficiency. The nearly flat line for reactive power close to zero implies a capacitive-inductive balance, contributing to a stable power supply with minimal wasted energy in the form of reactive power.

Figure 39.
Active and reactive powers from Section B of the hybrid system.
In Figure 40, the red line represents the active power (Ps), which remains largely constant throughout the duration, indicative of a stable and consistent energy output after the second transformer in the hybrid system. The active power’s steadiness suggests that the system’s conversion processes and load demands are well-balanced. The green line, illustrating the reactive power (Qs), maintains a position close to the baseline, signifying an insignificant level of reactive power post the second transformation stage. The negligible fluctuation in reactive power implies that the system is effectively managing the phase alignment between current and voltage, optimizing power factor and thus minimizing wasted reactive energy. This balance between active and reactive power, especially after the second transformer, suggests a well-designed system capable of maintaining high efficiency and power quality suitable for grid distribution. The system’s ability to keep reactive power minimal points to enhanced operational performance and potential cost savings in energy transmission.
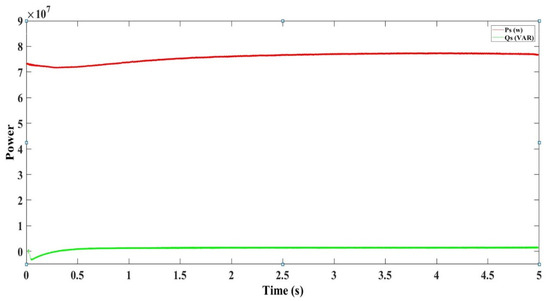
Figure 40.
Active and reactive powers from Section C of the hybrid system.
6. Conclusions
In grappling with the urgent global energy demands and the quest for environmental stewardship, this study represents a significant advancement in renewable energy system integration. Our work synthesizes solar photovoltaic (PV) and wind energy technologies into a cohesive hybrid system, setting a benchmark for sustainable development. Central to our research was the careful crafting and simulation of the system’s intricate dynamics, underpinned by the stability and efficiency secured through Lyapunov’s theorem. This principle has proven vital in affirming the dependability of our control mechanisms, equipping the system with the resilience to withstand fluctuations and maintain steady operation under diverse conditions.
The architecture of our hybrid system, which integrates a PV array, a doubly fed induction generator (DFIG), and essential power electronic converters, has undergone extensive MATLAB simulations. These simulations have rigorously evaluated the system’s adaptability, confirming a reliable and consistent energy provision. The crux of our system’s superior performance is the harmonious amalgamation of model predictive control (MPC) with particle swarm optimization (PSO). This fusion leverages the strengths of both techniques to refine control operations and elevate efficiency.
Our results validate the system’s proficiency in delivering stable energy output, adeptly adjusting to variations in solar and wind energy inputs. The combined use of PV and wind resources not only fulfills current energy requirements but also illustrates the vast capabilities of sophisticated control systems to cater to emergent energy needs. This research lays a groundwork that invites further investigation and enhancement of control strategies, with the goal of achieving more advanced and dependable energy systems. Looking ahead, we envision a landscape where comparative studies will elucidate the full capabilities of these innovative control methods, potentially redefining standards for renewable energy production and integration into the power grid.
To summarize, this investigation enriches the dialogue surrounding renewable energy, underscoring the critical role of cutting-edge control systems in forging paths to sustainability. It stands as a testament to the transformative impact that state-of-the-art approaches can have on our energy future, propelling us toward an era that promises sustainability, resilience, and heightened efficiency.
Author Contributions
Conceptualization, C.B.; Methodology, C.B. and H.K.; Software, C.B. and A.E.; Validation, B.B. and A.E.; Investigation, I.E.K., B.E.B. and K.M.A.; Resources, I.E.K., B.B., B.N. and K.M.A.; Data curation, K.M.A.; Writing—original draft, C.B.; Visualization, H.K.; Supervision, I.E.K., R.B. and B.B.; Project administration, R.B.; Funding acquisition, H.K. and A.E. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Data is contained within the article.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Ishaque, K.; Salam, Z. A review of maximum power point tracking techniques of PV system for uniform insolation and partial shading condition. Renew. Sustain. Energy Rev. 2013, 19, 475–488. [Google Scholar] [CrossRef]
- Tolba, M.; Rezk, H.; Diab, A.A.Z.; Al-Dhaifallah, M. A Novel Robust Methodology Based Salp Swarm Algorithm for Allocation and Capacity of Renewable Distributed Generators on Distribution Grids. Energies 2018, 11, 2556. [Google Scholar] [CrossRef]
- Tolba, M.A.; Rezk, H.; Tulsky, V.; Diab, A.A.Z.; Abdelaziz, A.Y.; Vanin, A. Impact of Optimum Allocation of Renewable Distributed Generations on Distribution Networks Based on Different Optimization Algorithms. Energies 2018, 11, 245. [Google Scholar] [CrossRef]
- Cheng, Z.; Zhou, H.; Yang, H. Research on MPPT control of PV system based on PSO algorithm. In Proceedings of the 2010 Chinese Control and Decision Conference, Xuzhou, China, 26–28 May 2010; pp. 887–892. [Google Scholar]
- Singh, G.K. Solar power generation by PV (photovoltaic) technology: A review. Energy 2013, 53, 1–13. [Google Scholar] [CrossRef]
- Baloch, M.H.; Chauhdary, S.T.; Ishak, D.; Kaloi, G.S.; Nadeem, M.H.; Wattoo, W.A.; Younas, T.; Hamid, H.T. Hybrid Energy Sources Status of Pakistan: An Optimal Technical Proposal to Solve the Power Crises Issues. Energy Strategy Rev. 2019, 24, 132–153. [Google Scholar] [CrossRef]
- Lun, S.; Du, C.; Sang, J.; Guo, T.; Wang, S.; Yang, G. An improved explicit I–V model of a solar cell based on symbolic function and manufacturer’s datasheet. Sol. Energy 2014, 110, 603–614. [Google Scholar] [CrossRef]
- Bai, J.; Liu, S.; Hao, Y.; Zhang, Z.; Jiang, M.; Zhang, Y. Development of a new compound method to extract the five parameters of PV modules. Energy Convers. Manag. 2014, 79, 294–303. [Google Scholar] [CrossRef]
- Baloch, M.; Abro, S.; Sarwar Kaloi, G.; Mirjat, N.; Tahir, S.; Nadeem, M.; Gul, M.; Memon, Z.; Kumar, M. A Research on Electricity Generation from Wind Corridors of Pakistan (Two Provinces): A Technical Proposal for Remote Zones. Sustainability 2017, 9, 1611. [Google Scholar] [CrossRef]
- Vidhya, K.; Arfan, G.; Erping, Z. Modelling and simulation of maximum power point tracking algorithms and review of MPPT techniques for PV applications. In Proceedings of the 5th International Conference on Electronic Devices, Systems and Applications (ICEDSA), Ras Al Khaimah, United Arab Emirates, 6–8 December 2016; pp. 1–4. [Google Scholar]
- Nandurkar, S.R.; Rajeev, M. Modeling simulation & design of photovoltaic array with MPPT control techniques. Int. J. Appl. Power Eng. (IJAPE) 2014, 3, 41–50. [Google Scholar]
- Babaa, S.E.; Armstrong, M.; Pickert, V. Overview of maximum power point tracking control methods for PV systems. J. Power Energy Eng. 2014, 2, 59–72. [Google Scholar] [CrossRef]
- Faranda, R.; Leva, S. Energy comparison of MPPT techniques for PV systems. WSEAS Trans. Power Syst. 2008, 3, 446–455. [Google Scholar]
- Singh, G.; Lentijo, S.; Sundaram, K. The impact of the converter on the reliability of a wind turbine generator. In Proceedings of the ASME 2019 Power Conference, Salt Lake City, UT, USA, 15–18 July 2019; V001T06A016. ASME: New York, NY, USA, 2019. [Google Scholar]
- Singh, G.; Matuonto, M.; Sundaram, K. Impact of imbalanced wind turbine generator cooling on reliability. In Proceedings of the 2019 10th International Renewable Energy Congress (IREC), Sousse, Tunisia, 26–28 March 2019; IEEE: New York, NY, USA, 2019; pp. 1–6. [Google Scholar] [CrossRef]
- Singh, G.; Saleh, A.; Amos, J.; Sundaram, K.; Kapat, J. IC6A1A6 vs. IC3A1 Squirrel Cage Induction Generator Cooling Configuration Challenges and Advantages for Wind Turbine Application. In Proceedings of the ASME 2018 Power Conference Collocated with the ASME 2018 12th International Conference on Energy Sustainability and the ASME 2018 Nuclear Forum, Lake Buena Vista, FL, USA, 24–28 June 2018; V001T06A002. ASME: New York, NY, USA, 2018. [Google Scholar]
- Orosz, T.; Rassõlkin, A.; Kallaste, A.; Arsénio, P.; Pánek, D.; Kaska, J.; Karban, P. Robust Design Optimization and Emerging Technologies for Electrical Machines: Challenges and Open Problems. Appl. Sci. 2020, 10, 6653. [Google Scholar] [CrossRef]
- Youcef, B. Contribution à L’étude et à la Commande Robuste d’un Aérogénérateur Asynchrone à Double Alimentation. Ph.D. Thesis, Université Mohamed Khider, Biskra, Algeria, 2014. [Google Scholar]
- Guda, S.R. Modeling and Power Management of a Hybrid Wind-Microturbine Power Generation. Master’s Thesis, Université de Bozeman, Bozeman, MT, USA, 2005. [Google Scholar]
- Hirose, T.; Matsuo, H. Standalone Hybrid Wind-Solar Power Generation System Applying Dump Power Control without Dump Load. IEEE Trans. Ind. Electron. 2012, 59, 988–997. [Google Scholar] [CrossRef]
- Hossain, M.K.; Ali, M. Transient stability augmentation of PV/DFIG/SG-based hybrid power system by parallel-resonance bridge fault current limiter. Electr. Power Syst. Res. 2016, 130, 89–102. [Google Scholar] [CrossRef]
- Parida, A.; Chatterjee, D. Cogeneration topology for wind energy conversion system using doubly-fed induction generator. IET Power Electron. 2016, 9, 1406–1415. [Google Scholar] [CrossRef]
- Bakir, H.; Kulaksiz, A.A. Modelling and voltage control of the solar-wind hybrid micro-grid with optimized STATCOM using GA and BFA. Eng. Sci. Technol. Int. J. 2020, 23, 576–584. [Google Scholar] [CrossRef]
- Pena, R.S.; Asher, G.M.; Clare, J.C. A Doubly Fed induction generator using back to back PWM converters supplying an isolated load from a variable speed wind turbine. Proc. Inst. Electr. Eng. Power Appl. 1996, 143, 380–387. [Google Scholar] [CrossRef]
- Rhouma, M.B.; Gastli, A.; Ben Brahim, L.; Touati, F.; Benammar, M. A simple method for extracting the parameters of the PV cell single-diode model. Renew. Energy 2017, 113, 885–894. [Google Scholar] [CrossRef]
- Azali, S.; Sheikhan, M. Intelligent control of photovoltaic system using BPSO-GSA-optimized neural network and fuzzy-based PID for maximum power point tracking. Appl. Intell. 2016, 44, 88–110. [Google Scholar] [CrossRef]
- Koad, R.; Zobaa, A.; Shahat, A. A Novel MPPT Algorithm Based on Particle Swarm Optimisation for Photovoltaic Systems. IEEE Trans. Sustain. Energy 2017, 8, 468–476. [Google Scholar] [CrossRef]
- Calasan, M.; Jovanovic, D.; Rubezic, V.; Mujovic, S.; Dukanovic, S. Estimation of Single-Diode and Two Diode Solar Cell Parameters by Using a Chaotic Optimization Approach. Energies J. 2019, 12, 4209. [Google Scholar] [CrossRef]
- Chowdhury, S.; Chowdhury, S.P.; Taylor, G.A.; Song, Y.H. Mathematical Modeling and Performance Evaluation of a Stand-Alone Polycrystalline PV Plant with MPPT Facility. In Proceedings of the IEEE Power and Energy Society General Meeting—Conversion and Delivery of Electrical Energy in the 21st Century, Pittsburg, PA, USA, 20–24 July 2008. [Google Scholar]
- Jung, J.-H.; Ahmed, S. Model Construction of Single Crystalline Photovoltaic Panels for Real-Time Simulation. In Proceedings of the IEEE Energy Conversion Congress and Expo, Atlanta, GA, USA, 12–16 September 2010. [Google Scholar]
- Nema, S.; Nema, R.K.; Agnihotri, G. Matlab/simulink based study of photovoltaic cells/modules/array and their experimental verification. Int. J. Energy Environ. 2010, 1, 487–500. [Google Scholar]
- Mohamed, S.A.; El Sattar, M.A. A comparative study of P and O and INC maximum power point tracking techniques for grid-connected PV systems. SN Appl. Sci. 2019, 1, 174. [Google Scholar] [CrossRef]
- Boubii, C.; Kafazi, I.E.; Bannari, R.; Bhiri, B.E. A comparison between MPC, Perturb and Observe, and Incremental Conductance Method. In Proceedings of the 2023 5th Global Power, Energy and Communication Conference (GPECOM), Nevsehir, Türkiye, 14–16 June 2023; pp. 198–202. [Google Scholar] [CrossRef]
- Rodriguez, J.; Cortes, P. Predictive Control of Power Converters and Electrical Drives; John Wiley & Sons: Hoboken, NJ, USA, 2012; Volume 37. [Google Scholar]
- Oskouei, A.B.; Banaei, M.R.; Sabahi, M. Hybrid PV/wind system with quinary asymmetric inverter without increasing DC-link number. Ain Shams Eng. J. 2016, 7, 579–592. [Google Scholar] [CrossRef]
- Kennedy, J.; Eberhart, R.C. Particle swarm optimization. In Proceedings of the IEEE International Conference on Neural Networks, Perth, WA, Australia, 27 November–1 December 1995; Volume 4, pp. 1942–1948. [Google Scholar]
- Errami, Y.; Obbadi, A.; Sahnoun, S. Control of PMSG wind electrical system in network context and during the MPP tracking process. Int. J. Syst. Control Commun. 2020, 11, 200–225. [Google Scholar] [CrossRef]
- Idrissi, I.; Chafouk, H.; El Bachtiri, R.; Khanfara, M. Modeling and Simulation of the Variable Speed Wind Turbine Based on a Doubly Fed Induction Generator [Internet]. Gas Turbines—Control, Diagnostics, Simulation, and Measurements [Working Title]. IntechOpen. 2019. Available online: https://www.intechopen.com/chapters/70671 (accessed on 28 December 2019).
- Boubii, C.; El Kafazi, I.; Bannari, R.; El Bhiri, B.; Mobayen, S.; Zhilenkov, A.; Bossoufi, B. Integrated Control and Optimization for Grid-Connected Photovoltaic Systems: A Model-Predictive and PSO Approach. Energies 2023, 16, 7390. [Google Scholar] [CrossRef]
- Boualouch, A.; Essadki, A.; Nasser, T.; Boukhriss, A.; Frigui, A. Power Control of DFIG in WECS Using Backstipping and Sliding Mode Controller. Int. J. Electr. Comput. Energetic Electron. Commun. Eng. 2015, 9, 612–618. [Google Scholar]
- Bakar, A.A.; Utomo, W.M.; Taufik, T.; Aizam Jumadril, S. Dc/dc boost converter with PI controller using real-time interface. ARPN J. Eng. Appl. Sci. 2015, 10, 9078–9082. [Google Scholar]
- Rodríguez-Amenedo, J.L.; Arnaltes, S.; Rodríguez, M.A. Operation and coordinated control of fixed and variable speed wind farms. Renew. Energy 2008, 33, 406–414. [Google Scholar] [CrossRef]
- Mishra, N.K.; Husain, Z. Novel Six Phase Doubly Fed Induction Generator through Modeling and Simulation-A Comparison with Conventional Doubly Fed Induction Generator. In Proceedings of the 2019 International Conference on Power Electronics, Control and Automation (ICPECA), New Delhi, India, 16–17 November 2019; pp. 1–5. [Google Scholar] [CrossRef]
- Mensou, S.; Essadki, A.; Minka, I.; Nasser, T.; Idrissi, B.B. Backstepping controller for a variable wind speed energy conversion system Based on a DFIG. In Proceedings of the 2017 International Renewable and Sustainable Energy Conference (IRSEC), Tangier, Morocco, 4–7 December 2017; Volume 12. [Google Scholar]
- Labdai, S.; Bounar, N.; Boulkroune, A.; Hemici, B.; Nezli, L. Artificial neural network-based adaptive control for a DFIG-based WECS. ISA Trans. 2022, 128 Pt B, 171–180. [Google Scholar] [CrossRef]
- Khojet El Khil, S. Vector Control of Doubly Fed Asynchronous Machine (MADA). Ph.D. Thesis, National Polytechnic Institute of Toulouse, Toulouse, France, 4 December 2006. [Google Scholar]
- EAbdou, H.; Youssef, A.-R.; Kamel, S.; Aly, M.M. Sensorless Wind Speed Control of 1.5 MW DFIG Wind Turbines for MPPT. In Proceedings of the 2018 Twentieth International Middle East Power Systems Conference (MEPCON), Cairo, Egypt, 18–20 December 2018; pp. 700–704. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).