Wind Resistance Performance Assessment of Long-Span Cable-Supported Bridges Based on Time-Varying Reliability Theory

Abstract

Long-span cable-supported bridges constitute the most common type of bridge with a span of more than 400 m. They are generally designed as a double-tower long-span structure with good spanning capacity and economic performance. Wind resistance safety performance is the main index used to control the long-span cable-supported bridge structure. During the life of a long-span cable-supported bridge structure, because the service life of the cables is far shorter than the design life of the structure, the wind resistance performance of the structure will inevitably deteriorate significantly, which will seriously affect the structural service performance of symmetric cable-supported bridges. Under strong wind loads, the static wind stability and flutter stability of cable-stayed bridge structures are components of the limit state of bearing capacity, which directly affects the safety performance of the structure. We take the flutter and static wind stability of a long-span cable-supported bridge structure as the main design control index, use inverse reliability theory to calculate the reliability index of a symmetric cable-supported bridge structure, use inverse reliability theory to calculate the safety factor of a symmetric cable-supported bridge structure, and evaluate the time-varying wind resistance performance of a long-span cable-supported bridge structure by comprehensively considering the reliability index and safety factor. Taking a practical project concerning a long-span cable-supported bridge as a specific case, the time-varying wind resistance reliability of the bridge throughout its operation for more than 30 years is analyzed along with the parameter sensitivity. The results show that the wind resistance performance of the cable-supported bridge structure is obviously affected by its cables, and the degradation of cable performance will have a significant impact on the time-varying wind resistance performance of the structure, especially the critical wind speed of the structure, which has obvious time-varying characteristics. The safety factor and reliability index can be used to objectively evaluate the time-varying wind resistance performance of long-span cable-supported bridge structures.

1. Introduction

Cable-supported bridges are among the most common types of modern long-span bridges. As the lifeline of a cable-supported bridge, cables are among the most critical load-bearing components, as well as the most vulnerable components to damage, in the cable-supported bridge structure. In the operation stage, they are easily damaged by various environmental factors or accidents, endangering the service safety of the bridge. Therefore, it is very important to explore the impact of cable damage on the reliability of the overall structure of this type of bridge.

As China is moving steadily from being a large-bridge country to a powerful-bridge country, an ever-increasing number of long-span cable-supported bridges are being built. As the core load-bearing components, the cables have a far shorter design life than the design life of long-span cable-supported bridges. The damage inflicted on the cables during the operation period (Figure 1 and Figure 2) will inevitably pose the practical problem of cable replacement. The anchorage system is the component most vulnerable to cable damage. The complex structure of the cable anchorage system makes the damage location difficult to detect and obscures the damage mechanism, seriously affecting the safety of long-span cable-supported bridges in the operation stage.

The cable body and anchorage system are the two main areas affected by cable damage. Cable body damage will reduce the stress sectional area of the cables, while cable anchorage system damage poses the risk of cable breakage under strong winds. Therefore, once the cables are damaged, the risks of wind instability and the collapse of the structure will increase dramatically, which will directly threaten the wind resistance safety of long-span cable-supported bridges in the operation stage. The parts (different cables, anchor heads, cable bodies, etc.) and damage degree (corrosion depth and area, etc.) of cables damaged during operation exhibit strong randomness in different environments. Due to fabrication errors of the stiffening beam and the unsteady flow characteristics of wind speed, the static three-component force coefficient of the stiffening beam exhibits strong uncertainty in physical and virtual wind tunnel test results. In addition, the wind load and structural parameters of long-span cable-supported bridges have significant probability characteristics. Therefore, the wind-induced instability of long-span cable-supported bridges in the state of cable damage is essentially a random factor.

As the main load-bearing components of cable-supported bridges, the cables transfer almost all the load of the bridge structure. Once the cables and their anchorage structure are damaged or broken, the inevitable result is the redistribution of the internal force of the structure, which will have a great impact on its safety and usability. Therefore, research on the mechanical properties of cable-supported bridges with cable damage has become a hot topic in recent years. Static and dynamic performance is the focus of attention in the construction and operation stages of cable-supported bridges. Several scholars have studied the performance degradation of cable-supported bridges caused by cable damage. Xu and Chen established a model for mechanical behaviors of corroded wires and a support in relation to the corrosion distribution at cable cross sections [1]. Xu et al. proposed a method based on image processing to visualize and model surface pits of high-strength steel wire [2]. Mozos and Aparicio investigated the stress caused by a rupture on the remaining portion of a stay which fails, and the role of the rupture time on the response of the structure is discussed from a theoretical and a numerical point of view [3]. Zhang et al. studied the structural response of a long-span cable-stayed bridge to cable loss during construction; the static performance of the Chishi Bridge subjected to multiple-cable loss caused by a fire accident was investigated in detail by field inspection and finite-element simulation [4]. Li et al. presented an empirical modelling of the long-term deterioration process of steel wires in cables, with consideration of the simultaneous occurrence of uniform corrosion, pitting corrosion, and fatigue induced by the combined action of environmental aggression and cyclic loading [5]. Sun et al. proposed a numerical model to show that the actual state of a cable-stayed bridge is the key to track its time-varying mechanical properties [6]. Liu et al. proposed a new method for time-varying cable force identification of stay cables based on an improved multi-synchro-squeezing transform and an efficient ridge extraction algorithm [7]. By summarizing previous research on cable damage, it can be found that the main consequences of cable damage are a relaxation of cable pre-tension and a reduction in cable strength.

The decrease in cable performance will have a significant impact on the static and dynamic performance of cable-supported bridges. Liu et al. investigated the influence of cable resistance degradation on the system reliability of cable-stayed bridges [8,9]. Yan and Guo investigated the influence of cable damage on the reliability of existing cable-supported bridges [10]. In addition, some scholars have studied the wind resistance performance of cable-supported bridge structures under the effect of cable damage, such as the influence of cable damage on the dynamic performance of long-span cable-supported bridges under automobile and wind loads [11] and the influence of different surface damage (Figure 3) degrees of cables on aerodynamic resistance based on wind tunnel force tests [12,13]. Shi investigated the influence of time-varying damage of cables on the critical wind speed of static wind instability. The critical wind speed for static wind instability gradually decreases as the overall damage rate of the cable section increases [14].

When the structure encounters strong winds, pedestrians and vehicles are prohibited from passing, and the wind resistance safety of the structure needs to be guaranteed. In terms of the wind safety of cable-supported bridges, flutter and static wind instability belong to divergent structural failure behaviors. Under strong wind loads, the static wind stability and flutter stability of cable-stayed bridge structures are components of the limit state of bearing capacity, which directly affects the safety performance of the structure [15,16]. The parameters of the structure and wind load have strong randomness, so it is necessary to use probability methods to study the wind resistance and time-varying performance of cable-supported bridges. Therefore, on the basis of analyzing the time-varying wind resistance performance of a long-span cable-supported bridge affected by cable damage, the risk of the wind-resistance-related safety collapse of this type of bridge under such conditions is evaluated by comprehensively considering the reliability index and the probability safety factor. There are three innovative points in this paper: firstly, the time-varying effect of the wind resistance critical wind speed of the cable-stayed structure after relaxation; xecondly, time-varying reliability indicators for flutter and static wind stability of cable-supported bridges; thirdly, the time-varying probability safety factor evaluation of flutter and static wind stability.

2. Time-Varying Wind Resistance Characteristics

At present, reliability design only considers the random factors of the structure and ignores its time variation, so its reliability is independent of time variation. With the development of research on the durability and reliability evaluation of engineering structures, considering the structural resistance decaying with time during the structures’ service life, the research on the relationship between structural reliability and time variables has become a major topic of reliability research. In addition, the resistance of the structure also exhibits randomness, so it is more appropriate to study its random time-varying reliability with regard to the actual situation.

The dynamic response of time-varying structures is very complex. This is because, in structural analysis, its control equation becomes a parameter differential equation of stochastic processes, and it is generally difficult to solve this kind of equation. Therefore, for the sake of simplification, when establishing the time-varying structural vibration equation under the action of fluctuating wind pressure, it is necessary to make the following assumptions: for a multi-degree-of-freedom structure, its mass is concentrated in several particles and changes with time; the fluctuating wind load is a concentrated load acting on a particle and is assumed to be a Gaussian process [17]; and the vibration of the structure is linear over the duration of the fluctuating wind period, and the form of damping is Rayleigh complex damping.

After determining the resistance variation law, the corresponding structural safety criteria can be obtained. The resistance safety limit $R\left(t\right)$ is generally in a state of decay over time. The safety criterion of structures is defined as the resistance $S\left(t\right)$ of the structure not exceeding the resistance safety limit $R\left(t\right)$ in the time interval $\left[\tau ,\tau +∆\tau \right]$, namely,

$$\Phi =\left\{S\right(t)<R(t),t\in [\tau ,\tau +∆\tau \left]\right\}$$

(1)

Generally, $R\left(t\right)$ and $S\left(t\right)$ are stochastic processes; $R\left(t\right)$ is the time-varying wind resistance bearing capacity of cable-supported bridges, and $S\left(t\right)$ is the response of cable-supported bridge structures under equal loads.

The first-passage failure criterion is adopted. The maximum annual average wind speed considering the standard height conforms to the Bernoulli experiment and the basic assumptions such as the random time change of the structure’s stiffness and strength. The probability that the structure will not be damaged under the action of wind pressure is expressed as

$$P_s={\int }_0^{\infty }{P}_V\left\{S\left(t\right)<R\left(t\right)\right\}F\left(V\right)\mathrm{d}V$$

(2)

where $F\left(V\right)$ is the probability density function of the annual maximum average wind speed at standard altitude, and $P_V\left\{S\left(t\right)<R\left(t\right)\right\}$ is the probability that the structural response $S\left(t\right)$ will not exceed the limit $R\left(t\right)$ when the annual average wind speed is $V$.

According to an analysis of Equation (2), the critical wind speed $V_{cr}$ for flutter (or aerostatic wind) stability can be determined. The calculation of cr is very important in the time-varying wind resistance safety analysis of long-span cable-supported bridges. Because of flutter (or) static wind stability, the critical wind speed $V_{cr}$ is the implicit expression of its influencing factors. In this paper, the finite element method based on certainty is used to calculate the critical wind speed of flutter (or aerostatic wind) stability.

2.1. Flutter Instability Mechanism

According to the self-excited aerodynamic expression [18], the aerodynamic lift $L_{ae}$ acting on the unit length of the structure, aerodynamic resistance $D_{ae}$, and aerodynamic torque $M_{ae}$ can be expressed as vertical displacement h, horizontal displacement $p$, and torsional displacement $\alpha$ functions, respectively, using the dimensionless aerodynamic derivative $H_i^{\mathrm{*}}$, $P_i^{\mathrm{*}}$, $A_i^{\mathrm{*}}$(i = 1, 2,…, 6). Equations (A1)–(A3) in Appendix A are the aerodynamic self-excited force acting on the unit width of the bridge deck, U is the average wind speed of incoming flow$, \rho$ is air density, B is the dimension of the member section along the main flow direction, $K=\frac{B\omega }{U}$ is the dimensionless frequency, $\omega$ is the vibrating circular frequency, and the aerodynamic derivative $H_i^{\mathrm{*}},P_i^{\mathrm{*}},A_i^{\mathrm{*}}$(i = 1, 2,…, 6) denotes the function of dimensionless wind speed $\tilde{U}=\frac{U}{fB}$ or dimensionless frequency, whose values are related to the geometric shape of the bridge section.

2.2. Mechanism of Static Wind Instability

The static wind load acting on the unit length of the stiffening beam of a suspension bridge can be divided into horizontal wind load $P_H$, vertical wind load $P_V$, and torsional moment $M$. Under the action of static wind, the attitude of the stiffening beam will change, and the relative wind attack angles of the static wind load and the stiffening beam section will change accordingly. The concept of an effective wind attack angle is introduced, and the static wind load is expressed as a function of wind speed, the three-component coefficient, and the effective wind attack angle.

Here, $\rho$ is air density, $D$ is the lateral projection height of the stiffening beam, $B$ is stiffener width, $V$ is average wind speed, $C_H$ is the resistance coefficient, $C_V$ is the lift coefficient, $C_M$ is the lifting torque coefficient, and $\alpha$ is the effective angle of attack.

3. Symmetric Reliability Theory

When the overall structure or part of a structure exceeds a certain specific state and cannot meet a certain functional requirement specified by the design, this specific state constitutes the limit state of the function. The limit state of the structure can be described using the limit state equation, which is expressed as

g = g(R, S) = R − S = 0

(3)

where g(R, S) is the limit state function of the structure; R is the wind resistance of flutter or aerostatic stability of cable-supported bridges; and S is the effect of the wind action of cable-supported bridges.

In general, the design variables in the inverse reliability analysis problem can be deterministic variables or random variables. Equation (5) denotes the response of flutter and aerostatic stability of cable-supported bridges at the verification point corresponding to the design variables in the limit state of bearing capacity. At the same time, the wind-resistance performance of long-span cable-supported bridges can achieve the prescribed target reliability index that is to see the Equation (4).

$$\mathsf{\beta }(\mathrm{X},\mathrm{d},\mathrm{r})={\mathsf{\beta }}^{\mathrm{T}}$$

(4)

$$\mathrm{G}(\mathrm{X},\mathrm{d},\mathrm{r})=0$$

(5)

3.1. Forward Reliability

From the above analysis, it can be gleaned that the design parameters related to structural wind stability are closely related to the target reliability index. The target reliability index of long-span cable-supported bridges is a non-explicit function of the random variables corresponding to the design parameters, and in this case, the finite element reliability method is very suitable. A very important step in the iterative calculation process of reliability is determining the influence of the structural response and its partial derivatives on the design variables. In finite element reliability, the differential method can be used to numerically simulate the partial derivatives.

The relationship between the load wind effect $S$ and the basic random vector $X$ (such as flutter derivatives, aerodynamic coefficients, wind resistance safety factor, etc.) can be expressed as

$$S=S\left(X\right)$$

(6)

when applying the finite element first-order reliability method to an implicit function such as that regarding wind resistance of flutter or aerostatic instability of cable-supported bridges, the limit state function is

$$g\left[s\right(x), x]=G\left(u\right)$$

(7)

$$d_i=\frac{{\nabla }_{u_i}{G}^T{u}_i-G\left(u_i\right)}{{‖{\nabla }_{u_i}G‖}^2}{\nabla }_{u_i}G-u_i$$

(8)

where ${\nabla }_{u_i}G$ is the gradient of the structural effect on the random variables; ${\nabla }_{s}g$ is the gradient of the limit state function $g(s, x)$ with respect to $s$; ${\nabla }_{x}g$ is the gradient of the limit state function $g(s, x)$ with respect to $x$; $J_{u,x}$ is the Jacobian matrix of probability transformation; and $J_{s,x}$ is the Jacobian matrix of mechanical transformation.

3.2. Inverse Reliability

Regarding the relationship of the structural target reliability index ${\beta }_T$, the basic random variables of the vector of standard normal distribution are denoted by $u$, and $(u,\theta )$ is a function of the structure. The inverse problem of structural reliability analysis is as follows [19,20]:

$$‖u‖-{\beta }_T=0$$

(9)

$$u+\frac{‖u‖}{‖{\nabla }_{u}G(u,\theta )‖}{\nabla }_{u}G(u,\theta )=0$$

(10)

$$G(u,\theta )=0$$

(11)

where $G(u,\theta )$ is a function of the structure;${ \nabla }_u$ is the gradient operator; and $\theta$ denotes the design parameters to be determined.

Using the Taylor expansion, ${\beta }_T$ at point ${\beta }_{}^j$ can be expressed as

$${\beta }_T={\beta }_{}^j+{\left.\frac{\partial \beta }{\partial K}\right|}_{K^j}(K_{}^{j+1}-K_{}^j)$$

(12)

where K is the design parameter, and j is the number of iterations.

The iterative formula for the design parameter of the safety factor of flutter or aerostatic instability of cable-supported bridges can be expressed as follows:

$$K_{}^{j+1}=K_{}^j+\frac{{\beta }_T-{\beta }_{}^j}{{\left.\frac{\partial \beta }{\partial K}\right|}_{K^j}}$$

(13)

In order to achieve the iteration results for the safety factor, the convergence criterion using $\epsilon$ is expressed as follows:

$$\left|K^{j+1}-K^j\right|\le \epsilon$$

(14)

4. Evaluation of Time-Varying Wind Resistance Performance of Symmetrical Cable-Supported Bridges

The flutter and static wind instability of long-span cable-supported bridges correspond to the limit state of bearing capacity, corresponding to the maximum bearing capacity or the deformation that is not suitable for continuous bearing. The flutter and wind-induced instability limit state of long-span cable-supported bridges can be expressed as a problem of exceeding the limit state. When the expected wind speed (design wind speed) at the bridge site exceeds the critical wind speed for the flutter (or wind-induced) instability of the bridge in a given return period, flutter (or wind-induced) instability occurs. Therefore, for the flutter and static wind stability of long-span cable-supported bridges, the limit state function can be expressed as [21,22]

$$g=C_w\cdot V_{cr}\left(t\right)-G_s\cdot V_b$$

(15)

$$\begin{array}{l}{g}_{rf}=C_{\mathrm{w}}\cdot V_{\mathrm{cr}}(\mathrm{t})[A_i,P_i,H_i]-G_s\cdot V_b\\ g_{ra}=C_{\mathrm{w}}\cdot V_{\mathrm{cr}}(\mathrm{t})[P_h,P_v,M]-G_s\cdot V_b\end{array}\}$$

(16)

Similarly to the limit state equation established in the process of the flutter and static wind stability reliability analysis of long-span cable-supported bridges, the safety factor evaluation expression of the flutter and static wind stability of long-span cable-supported bridges can be expressed as [23,24]

$$g=C_w\cdot V_{cr}\left(t\right)-K\cdot G_s\cdot U_b$$

(17)

$$\begin{array}{l}{g}_{sf}=C_{\mathrm{w}}\cdot V_{\mathrm{cr}}(\mathrm{t})[A_i,P_i,H_i]-K\cdot G_s\cdot V_b\\ g_{sa}=C_{\mathrm{w}}\cdot V_{\mathrm{cr}}(\mathrm{t})[P_h,P_v,M]-K\cdot G_s\cdot V_b\end{array}\}$$

(18)

where$K$ is the safety factor, $V_{cr}\left(t\right)$ is time-dependent flutter (or still wind) stability critical wind speed taking into account uncertainties in structural characteristics, $C_w$ is the conversion coefficient of critical wind speed considering uncertainty factors in wind field characteristics, $G_s$ is the gust factor considering the influence of maximum fluctuating wind, and $V_b$ is the wind speed.

5. Application

The Yangpu Bridge is a bridge over a river crossing a hub on the Inner Ring Viaduct in Shanghai. The total length of the bridge is 7658 m. The main bridge is a cable-supported bridge with a composite beam, which spans the river. The main span is 602 m. The combination of spans is 40 + 99 + 144 + 602 + 144 + 99 + 44 m, with a total width of 35.5 m. It has 6 lanes and 2 m wide sidewalks on both sides. The main bridge tower is 208 m high. It was completed and opened to traffic in 1993. The general layout is shown in Figure 3.

5.1. Time-Varying Characteristics of Cable Slack

Once the structural system of the cable-supported bridge is determined, the stress state of the completed bridge is mainly determined by cable force. However, due to the influence of its own relaxation effect, the cable force will change with time. At this time, the relaxation effect of the cable will affect the stress and strain of the whole bridge. The variation law of the relaxation rate of the cable of this bridge over time is as follows [25]:

$$\mu =0.6233+0.3357\mathrm{l}\mathrm{g}t$$

(19)

5.2. Basic Information on Random Variables

According to the statistical characteristics of the structural damping ratio of symmetric cable-supported bridges, the damping ratio follows a lognormal distribution that has a mean value of 1 and a coefficient of variation of 0.4 [26,27].

In view of the statistical characteristics of the flutter derivatives of the stiffened beam sections of symmetric cable-supported bridges, it is assumed that the flutter derivatives of the stiffened beam sections of the Yangpu Bridge are independent of each other and follow a normal distribution with an average value of 1 and a coefficient of variation of 0.2.

Regarding the statistical characteristics of the static three-component force coefficients of symmetric cable-supported bridges, for the sake of simplifying the analysis, it was assumed that the drag coefficient, lift coefficient, and lifting moment coefficient are independent and obey a normal distribution with a mean value of 1 and a variation coefficient of 0.1.

The design wind speed of the Yangpu Bridge follows the Gumbel distribution, and its probability distribution function can be expressed as:

$$F\left(V\right)=\mathrm{e}\mathrm{x}\mathrm{p}[-\mathrm{e}\mathrm{x}\mathrm{p}(-\frac{V-b}{a}\left)\right]$$

(20)

where $b$ is equal to 23.7, and $a$ is equal to 4.06.

5.3. Safety Assessment of Time-Varying Wind Resistance Characteristics

(1) Critical wind speed

The flutter stability of the Yangpu Bridge was calculated using the time domain method, and the damping ratio of the first-order vertical bending and torsional vibration of the structure at various wind speeds were determined. When the wind speed is less than 62.7 m/s, the torsional damping ratio and vertical bending damping ratio of the system are positive; when the wind speed is 62.7 m/s, the torsional damping ratio of the system is 0, and the vertical bending damping ratio of the system is positive; and when the wind speed is greater than 62.7 m/s, the torsional damping ratio of the system is negative, and the vertical bending damping ratio of the system is positive. Therefore, the flutter critical wind speed of the Yangpu Bridge is 62.7 m/s. The time variation rule of the flutter critical wind speed of the Yangpu Bridge under conditions of cable relaxation is shown in

Table 1. Time-varying law of flutter critical wind speed of the Yangpu Bridge.

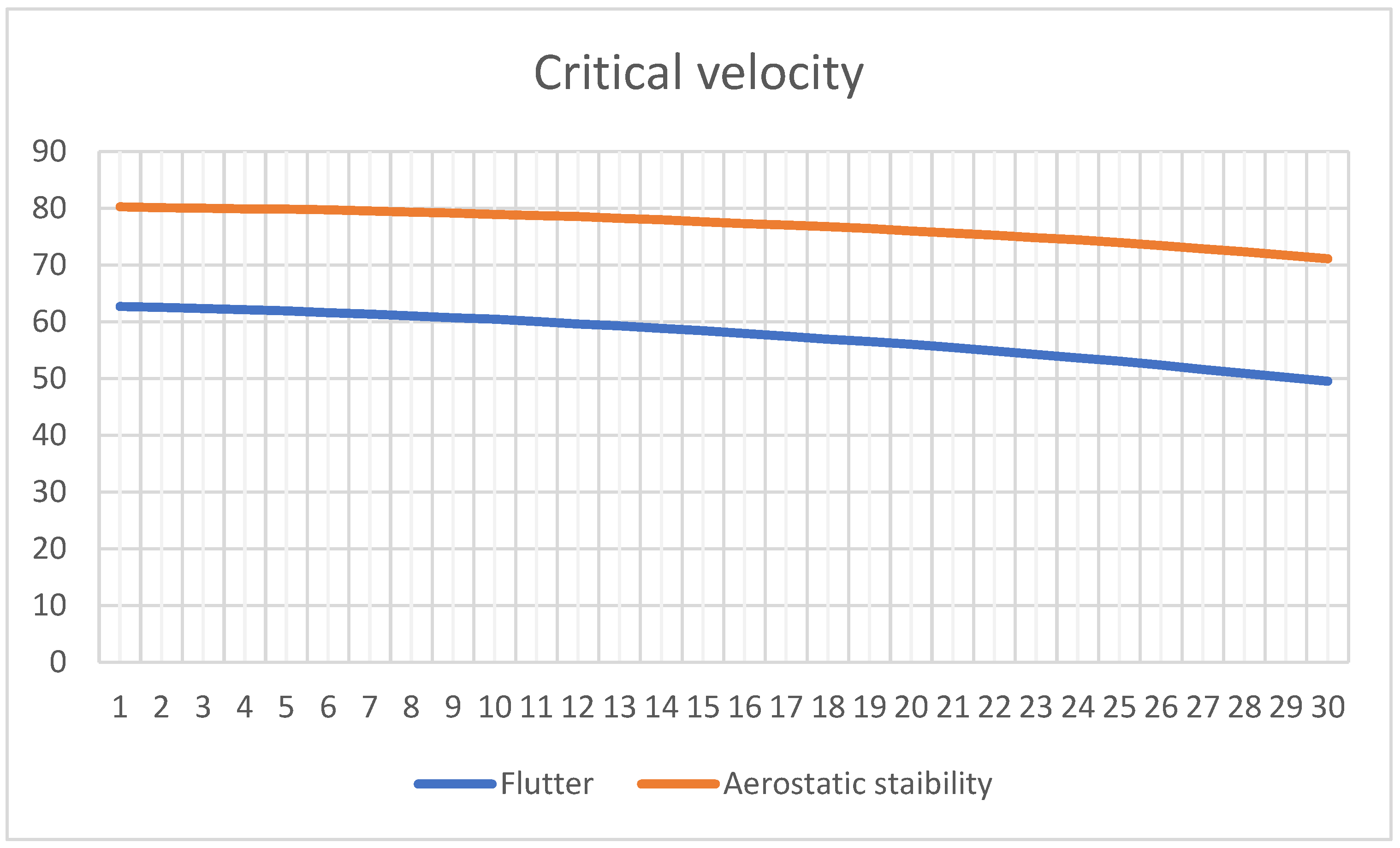
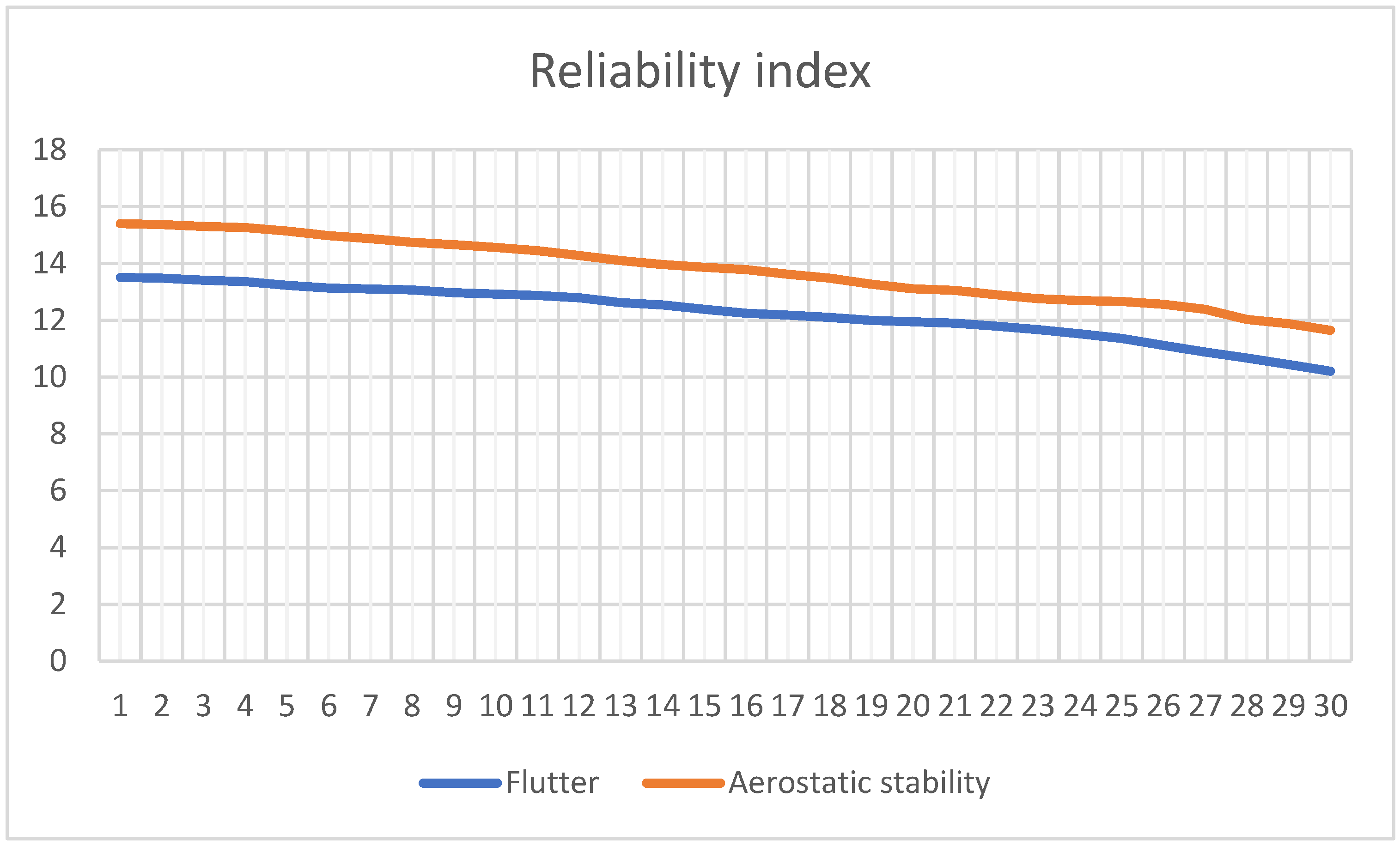
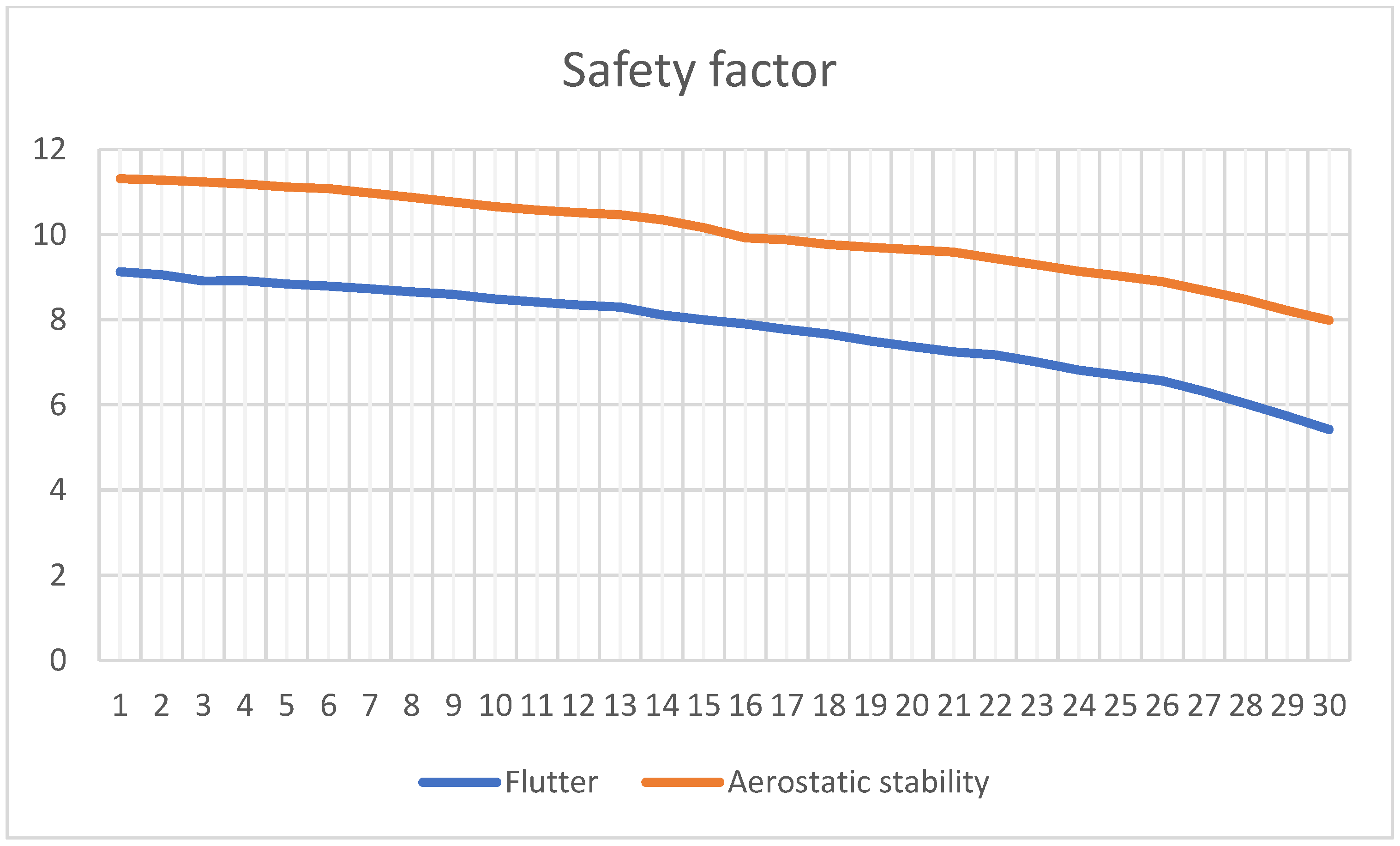
Time (Year)	Flutter Critical Wind Speed (m/s)	Time (Year)	Flutter Critical Wind Speed (m/s)	Time (Year)	Flutter Critical Wind Speed (m/s)
1	62.71	11	60.07	21	55.46
2	62.53	12	59.62	22	54.86
3	62.34	13	59.28	23	54.24
4	62.13	14	58.84	24	53.65
5	61.92	15	58.43	25	53.08
6	61.61	16	57.96	26	52.37
7	61.37	17	57.47	27	51.63
8	61.06	18	56.92	28	50.91
9	60.73	19	56.54	29	50.22
10	60.46	20	56.06	30	49.54

.

From Table 1, it can be drawn that the critical wind speed of structural flutter decreases over time, mainly because the relaxation of the cables over time weakens the constraint stiffness of the stiffened beam. Under the self-excited vibration force of flutter, the deformation of the main beam is greater, which in turn affects the wind field characteristics of the structure. The change in wind field further increases the energy absorption of the structure from the wind field, while the relaxation of the cables reduces the dissipation energy mechanism of the structure. Overall, it will lead to a decrease in the critical flutter wind speed of long-span cable-supported bridges.

In our numerical analysis of three-dimensional nonlinear static wind stability, we considered a 0° wind attack angle, took the structure-bearing dead load as the initial state, increased the wind speed incrementally, and calculated the vertical, lateral, and torsional displacement of the bridge structure under the combined action of static wind load and dead load at all wind speeds. When the wind speed is low, the displacement of the stiffening beam in all directions is low. With an increase in the wind speed, the torsional displacement and lateral displacement of the stiffening beam gradually increase, while the increase in vertical displacement is still very slow. When the wind speed increases to 60 m/s, the torsional displacement and vertical displacement begin to accelerate, until the wind degree increases to 80.28 m/s, and the torsional displacement and vertical displacement diverge, indicating that the structure has lost stability under static wind load and dead load, and the lateral displacement of the structure also tends to diverge. Therefore, the critical wind speed at a 0° wind attack angle is 80.28 m/s. See

Table 2. Time-varying law of critical wind speed of static wind instability of the Yangpu Bridge.

Time (Year)	Critical Wind Speed for Static Wind Instability (m/s)	Time (Year)	Critical Wind Speed for Static Wind Instability (m/s)	Time (Year)	Critical Wind Speed for Static Wind Instability (m/s)
1	80.28	11	78.72	21	75.63
2	80.12	12	78.56	22	75.26
3	80.03	13	78.24	23	74.82
4	79.91	14	77.98	24	74.45
5	79.85	15	77.63	25	73.97
6	79.76	16	77.32	26	73.44
7	79.53	17	77.07	27	72.88
8	79.35	18	76.79	28	72.34
9	79.18	19	76.43	29	71.73
10	78.94	20	76.01	30	71.15

for the time-varying rule of the critical wind speed for static wind instability of the Yangpu Bridge under the effect of cable relaxation.

From Table 2, it can be drawn that the critical wind speed for static wind instability of the structure decreases over time, mainly because the diagonal cables act as boundary constraints for the main beam under wind loads. Relaxation of the cables reduces the torsional stiffness of the stiffening beam to resist deformation, and the decrease in torsional stiffness exacerbates the static wind displacement of the entire structure under wind loads. Especially, the intensification of the torsional deformation of the main beam will cause rapid softening of the structural stiffness. This leads to a decrease in the critical wind speed for static wind instability.

From the comparative analysis of critical velocity of flutter and aerostatic stability of the Yangpu Bridge in Figure 4, it can be found that, due to the influence of environmental factors, cable relaxation will directly affect the structural performance of the structure under the effect of wind load during the operation of the symmetrical cable-supported bridge. With the passage of time, the critical wind speed of the symmetric cable-supported bridge structure obviously decreased. Through comprehensive comparison, it can be found that the critical wind speed of the aerostatic instability of cable-supported bridge structures is generally higher than the critical wind speed of flutter at the same time, although the critical wind speed exhibits a decreasing trend to a certain degree. For long-span cable-supported bridges, the decreasing trend in the critical wind speed for static wind instability and flutter is consistent. The common reason is that the relaxation of the cables will soften the stiffness of the structural system, and under the action of wind loads, the structural deformation will intensify, leading to a decrease in the critical wind speed for wind instability.

(2) Reliability index

The time-varying reliability index was used to evaluate the wind resistance safety performance of the symmetric cable-supported bridge structure. The results are shown in

Table 3. Time-varying characteristics of the flutter stability reliability index of the Yangpu bridge.

Time (Year)	Reliability Index	Time (Year)	Reliability Index	Time (Year)	Reliability Index
1	13.512	11	12.875	21	11.898
2	13.487	12	12.798	22	11.798
3	13.412	13	12.623	23	11.673
4	13.362	14	12.547	24	11.524
5	13.237	15	12.389	25	11.362
6	13.141	16	12.253	26	11.121
7	13.105	17	12.187	27	10.887
8	13.076	18	12.102	28	10.673
9	12.975	19	12.003	29	10.446
10	12.927	20	11.954	30	10.216

and

Table 4. Time-varying characteristics of the static wind stability reliability index of the Yangpu Bridge.

Time (Year)	Reliability Index	Time (Year)	Reliability Index	Time (Year)	Reliability Index
1	15.413	11	14.456	21	13.054
2	15.376	12	14.287	22	12.898
3	15.312	13	14.105	23	12.763
4	15.267	14	13.968	24	12.701
5	15.143	15	13.867	25	12.669
6	14.987	16	13.786	26	12.565
7	14.876	17	13.627	27	12.387
8	14.747	18	13.489	28	12.031
9	14.664	19	13.275	29	11.887
10	14.571	20	13.112	30	11.653

. Through analysis, it was found that the reliability of the symmetric cable-supported bridge structure is affected when the critical wind speed of the cable-supported bridge structure decreases due to the degradation of cable performance during the operation stage. Through the calculation of the wind resistance reliability index of the analyzed symmetric cable-supported bridge structure based on positive reliability theory, it can be found that the wind resistance reliability index of the symmetric cable-supported bridge structure obviously decreased with the passage of time. It can be gleaned from a comprehensive comparison that the aerostatic stability reliability index of the symmetric cable-supported bridge structure is generally greater than the flutter stability reliability index at the same time, indicating that the static wind stability performance of a cable-supported bridge structure is higher than its flutter stability performance.

From the comparative analysis of the reliability index of flutter and aerostatic stability of the Yangpu Bridge in Figure 5, it can be found that the critical wind speed, as the resistance part of the limit state function of bearing capacity, is the numerator of the mean critical wind speed in the calculation of structural reliability index. The decrease in numerator will lead to a decrease in the calculation result of reliability index. The decreasing trend of flutter critical wind speed and static wind instability critical wind speed is consistent, so the decreasing trend in the reliability indicators is also consistent.

(3) Probabilistic safety factor

The probabilistic safety factor was used to evaluate the wind resistance reliability of the analyzed symmetric cable-supported bridge structure, the results of which can be seen in

Table 5. Time-varying characteristics of the probability safety factor of flutter stability of the Yangpu bridge.

Time (Year)	Probabilistic Safety Factor	Time (Year)	Probabilistic Safety Factor	Time (Year)	Probabilistic Safety Factor
1	9.127	11	8.413	21	7.243
2	9.054	12	8.342	22	7.171
3	8.909	13	8.293	23	7.003
4	8.912	14	8.112	24	6.813
5	8.837	15	7.997	25	6.688
6	8.789	16	7.898	26	6.565
7	8.721	17	7.771	27	6.319
8	8.653	18	7.659	28	6.027
9	8.594	19	7.497	29	5.736
10	8.487	20	7.368	30	5.426

and

Table 6. Time-varying characteristics of the probability safety factor of static wind stability of the Yangpu Bridge.

Time (Year)	Probabilistic Safety Factor	Time (Year)	Probabilistic Safety Factor	Time (Year)	Probabilistic Safety Factor
1	11.312	11	10.569	21	9.587
2	11.276	12	10.512	22	9.431
3	11.231	13	10.462	23	9.289
4	11.185	14	10.341	24	9.135
5	11.113	15	10.161	25	9.021
6	11.076	16	9.923	26	8.889
7	10.972	17	9.872	27	8.687
8	10.868	18	9.763	28	8.472
9	10.763	19	9.701	29	8.213
10	10.654	20	9.643	30	7.988

. It was found from the analysis that the reliability of a symmetric cable-supported bridge structure will be affected when the critical wind velocity of the cable-supported bridge structure decreases due to the degradation of cable performance during the operation stage. Through the calculation of the wind resistance probability safety factor of a symmetric cable-supported bridge structure based on inverse reliability theory, it can be found that the wind resistance probability safety factor of this structure obviously decreased with the passage of time. Through comprehensive comparison, it can be drawn that the probability safety factor of the static wind stability of symmetric cable-supported bridge structures is generally greater than the probability safety factor of flutter stability at the same time, indicating that the aerostatic stability performance of cable-supported bridge structures is higher than their flutter stability performance.

From the comparative analysis of probabilistic safety factor of flutter and aerostatic stability of the Yangpu Bridge in Figure 6, it can be found that the structural flutter and wind stability and wind resistance safety of a cable-supported bridge will be directly affected after the performance degradation of its cables, which will lead to a significant reduction in the flutter critical and wind instability critical wind speed resistances of the structure. The wind resistance safety of a symmetric cable-supported bridge structure was evaluated from the perspective of probability. The flutter stability reliability index and the static wind stability reliability index decreased with time along with the flutter stability probability safety coefficient and the static wind stability probability safety coefficient. Considering the reliability index and probability safety factor, the wind resistance safety performance of a symmetric cable-supported bridge decreases with the occurrence of cable relaxation.

That is to say that, for long-span cable-stayed bridge structures, when the wind speed is very high, the operation is generally stopped. Under the action of wind load, the static wind stability and flutter stability of cable-stayed bridge structures are components of the limit state of load-bearing capacity, which directly affects the safety performance of the structure. Since the degradation of cable performance will directly affect the safety of structural wind resistance performance, it is necessary to comprehensively consider the reliability index and probability safety factor, and establish a safety performance evaluation system for the structural wind resistance stability of symmetric cable-supported bridges based on symmetric reliability theory.

(4) Sensitivity analysis of parameter variability

The probability parameter that affects the wind resistance safety of long-span cable-supported bridges is mainly the coefficient of variation, and the magnitude of variation has a significant impact on the reliability index and probability safety factor results. In order to quantitatively study the impact of the magnitude of variability on the reliability indicators and probability safety factors of structural flutter and static wind stability, parameter sensitivity analysis was only conducted on the reliability indicators and probability safety factors for 10, 20, and 30 years. The coefficient of variation is taken as 0.5, 1, and 2 times the original value, respectively. The specific results are shown in

Table 7. The effect of variability on the reliability index of flutter and aerostatic stability.

Time (Year)	Flutter Stability Reliability Index			Aerostatic Instability Reliability Index
	0.5	1	2	0.5	1	2
10	14.517	12.927	10.627	16.782	14.571	12.997
20	13.726	11.954	9.887	15.317	13.112	11.593
30	12.116	10.216	7.889	13.672	11.653	9.729

and

Table 8. The effect of variability on safety factor of flutter and aerostatic stability.

Time (Year)	Flutter Stability Reliability Index			Aerostatic Instability Reliability Index
	0.5	1	2	0.5	1	2
10	9.887	8.487	7.636	11.182	10.654	9.647
20	8.526	7.368	6.710	10.627	9.643	8.223
30	7.219	5.426	4.872	9.739	7.988	6.526

.

Through the analysis of Table 7, it can be found that the reliability index decreases with the increase in parameter variability. The reason is that the coefficient of variation reflects the discreteness of structural parameters and is located in the denominator term of the reliability index calculation expression. Therefore, the calculation result of the reliability index is inversely proportional to the magnitude of parameter variability. Similarly, through the analysis of Table 8, it can be found that the probability safety factor decreases with the increase in parameter variability. The reason is that the coefficient of variation reflects the discreteness of structural parameters, and the greater the variability, the smaller the safety reserve of the structure. Therefore, the calculation result of the probability safety factor is inversely proportional to the magnitude of parameter variability.

After conducting parameter sensitivity analysis, in order to address the issue of structural wind resistance and time-varying variability caused by cable relaxation in cable-supported bridges, if the structural reliability index or probability safety factor does not meet the design specifications, it is necessary to adjust the cable force range design value incrementally to ensure the efficiency of cable work and improve the structural stiffness, thereby ensuring that the critical wind speed of the structure can resist strong winds.

5.4. Theoretical Guidance for Practical Engineering

The bridge has been in operation for 30 years, and, based on the lifespan of the cables, the cable relaxation rate has reached 6.3%. After the relaxation of the cable, the critical wind speeds for flutter and static wind instability of the structure decreased by 21% and 11% respectively, and the corresponding probability safety factors of the structure decreased by 38% and 29%, respectively. The safety reserve for static wind instability of the structure is higher than that of flutter safety, and it is still able to resist strong winds. Considering the design service life of cable-stayed cables, although the structure can resist strong winds, the safety of the structure has significantly decreased. It is necessary to strengthen observation to ensure the wind resistance safety of the structure.

Moreover, for improving the safety degree of aerostatic and flutter instability of long-span cable-supported bridges, we could take correspondingly effective measures based on probabilistic analysis. Because the relaxation of cable tension can cause a decrease in structural stiffness, it is necessary to regularly test the cable tension and replace cables at appropriate times to ensure the efficiency of the cables. From a probabilistic perspective, the variability of structural parameters has a significant impact on wind performance, and it is important to ensure the statistical characteristics of test data, especially the probabilistic statistical analysis of structural aerodynamic parameters.

6. Conclusions

This article focuses on the wind resistance and time-varying performance of long-span cable-stayed bridges. The critical wind speeds for flutter and static wind instability of the structure are derived from the time-varying effect of cable relaxation, and the reliability and safety of flutter and static wind instability are analyzed from a probability perspective. The following conclusions are drawn.

(1) An increase in relaxation rate affects the stiffness of the structure, which in turn affects the structural response under strong wind. The critical wind speed for flutter and static wind instability will decrease with the relaxation of the cables.

(2) The reliability method is used to calculate the reliability of flutter and static wind instability of long-span cable-stayed bridges. The reliability index decreases significantly with a decrease in the critical wind speed of instability, indicating an increasing possibility of flutter and static wind instability.

(3) The probability method is used to evaluate the safety of flutter and static wind instability of long-span cable-stayed bridges, indicating that the safety reserve of static wind stability of the structure is higher than that of flutter stability. Targeted measures are taken to control the flutter safety of cable-stayed bridges and ensure structural safety.

Due to research funding and time constraints, it is necessary to consider the following issues in further research: how to accurately consider the turbulence characteristics of flutter derivatives and three component coefficients, as well as the probability correlation between different aerodynamic parameters, in the process of further probability analysis.