1. Introduction
With the rapid development of society and the economy, energy issues have become increasingly severe. The development and utilization of renewable energy have emerged as paramount concerns for nations across the world. Solar energy, characterized by its abundance, sustainability, and reliability, has assumed a significant role as a renewable energy source capable of replacing conventional energy sources. Solar energy can be applied in many fields, including architectural design, solar power generation, heat collection system design, and plant growth monitoring.
The utilization of solar energy heavily relies on the availability of precise data on incident radiation. The incident solar radiation is typically influenced by various factors, such as cloud cover, air penetration, and rugged topography [
1]. In mountainous regions with complex terrain, the shading caused by the surrounding topography is a key factor affecting the spatial and temporal distribution of solar radiation on the ground. To promote the utilization of solar energy in mountainous areas, it is essential to obtain precise data on incident solar radiation in these areas.
The conventional approach to gathering solar radiation data for a specific region involves the installation of a sufficient number of solar radiation meters in the area. However, in mountainous areas with varied topography, the geographical and economic constraints often severely limit the number of solar radiation monitoring stations. Consequently, relying on ground-based measurements to obtain incident solar radiation data for the entire mountainous region proves unfeasible. An inadequate supply of measured solar radiation data significantly impedes the utilization of solar energy in these areas [
2]. Therefore, solar radiation estimation models have become a vital approach to acquire accurate data on incident solar radiation in mountainous regions.
There are many solar radiation estimation models, broadly categorized into three classes based on their calculation principles: analytical models [
3,
4,
5], empirical models [
6,
7,
8], and statistical models [
9,
10,
11]. Analytical models are mathematical models based on physical assumptions, considering the influence of atmospheric components on solar radiation [
3]; such models include the work of Threlkeld and Jordan [
4] and that of Thevenard and Gueymard [
5]. Empirical models establish solar radiation estimation models based on the correlation between meteorological parameters and solar radiation [
6]; examples include the models by Iqbal [
7] and Bahle et al. [
8]. Statistical models iteratively adjust parameter combinations and values between the input variable and the output result to find the optimal parameters based on existing datasets, as in the models by Pang et al. [
9], Ozoegwu [
10], and Mghouchi et al. [
11]. However, these conventional solar radiation estimation models do not consider the shading effects of tall mountains on solar radiation and cannot be directly applied to estimate solar radiation in mountainous areas.
To accurately estimate data on incident solar radiation in mountainous regions, a comprehensive analysis of the shading effects of complex terrain on solar radiation is imperative. The sky-view factor (SVF) is a common parameter used to quantify terrain shading effects on solar radiation [
12,
13,
14,
15,
16]. SVF is defined as the ratio of the unobstructed surface area to the entire surface area of the hemispherical sky [
17]. For mountainous areas with complex terrain, Zhang et al. [
18] conducted an in-depth analysis of the terrain shading effects on solar radiation by using SVF, based on high-resolution digital elevation models (DEMs) and atmospheric data products from the Moderate-resolution Imaging Spectroradiometer. This algorithm demonstrated satisfactory performance in validation on the Heihe River Basin, with both the mean bias error percentage (MBE%; −6.2%) and the root mean square difference percentage (RMSD%; 7.5%) below 10% [
18]. Vartholomaios [
15] developed an efficient machine learning (ML)-based model for urban solar radiation estimation considering terrain shading effects by using the Monte Carlo method to generate 30,000 samples and calculating the SVF and solar radiation data of each sample. This model can achieve near-instant calculation, but the accuracy of its calculation is limited in geometrically complex environments. Although there is a strong correlation between SVF and terrain shading [
16,
19,
20,
21,
22,
23], their relationship is non-linear [
24]. This is primarily due to SVF reflecting the percentage of the unobstructed sky hemisphere area relative to the total area, exhibiting a stronger correlation with diffuse radiation shading than with direct radiation shading [
15]. Consequently, in heavily shaded areas, estimating solar radiation with SVF would result in a large error.
Using DEM and geographic information system (GIS) platforms to extract terrain data is a common method to quantify mountain shading effects on solar radiation [
25,
26,
27,
28,
29]. Previously, Dubayah and Rich [
30] developed a GIS-based solar radiation estimation model (SolarFlux) after considering the shading effects of mountainous terrain. Because of its simple and convenient operation, this model can be effectively applied in planning, conservation, microclimate, and basic ecology studies. However, this model simplifies the diffuse radiation to isotropic, leading to diminished calculation accuracy of solar radiation. Subsequently, Fu and Rich [
31] proposed the concept of the viewshed to quantify the visible and invisible areas of the sky affected by terrain, and they developed the Solar Analyst model. This model assumes diffuse radiation to be anisotropic radiation, leading to more precise calculation results compared to the SolarFlux model. Despite enhancements in model accuracy, the Solar Analyst model is limited to calculating solar radiation within a defined time span. When dealing with small time intervals, the issue of overlapping solar trajectories can arise, resulting in imprecise calculations [
32]. In subsequent studies, many scholars have adopted the viewshed concept to develop models for estimating solar radiation shading levels in diverse environments [
28,
29], but the limited quantity of raster data continues to pose a challenge in achieving high accuracy.
Although several relevant studies have addressed terrain shading effects on solar radiation, current methods suffer from high computational complexity and limited accuracy, particularly when applied in regions with severe terrain shading. Achieving precise and rapid quantification of terrain shading effects on solar radiation remains a challenging task. Hence, this study proposed an ML-based approach to quickly estimate terrain shading effects on solar radiation in mountainous areas. By using this method to rapidly obtain solar radiation shading rates, one can accurately correct the data calculated by conventional models, allowing the precise acquisition of solar radiation data under mountain terrain shading. It could provide essential foundational data for urban site selection and the assessment of rooftop solar potential in mountainous regions.
The study is structured in six sections.
Section 1 is the introduction.
Section 2 outlines the steps taken to develop the ML model, presenting an analytical approach for assessing terrain shading effects on solar radiation in complex mountainous terrain.
Section 3 applies this approach through a case study of western Sichuan, with complex and diverse terrain. The primary results and discussion are presented in
Section 4 and
Section 5 to demonstrate the significance of the research. Finally,
Section 6 draws conclusions from the research.
3. Case Implementation
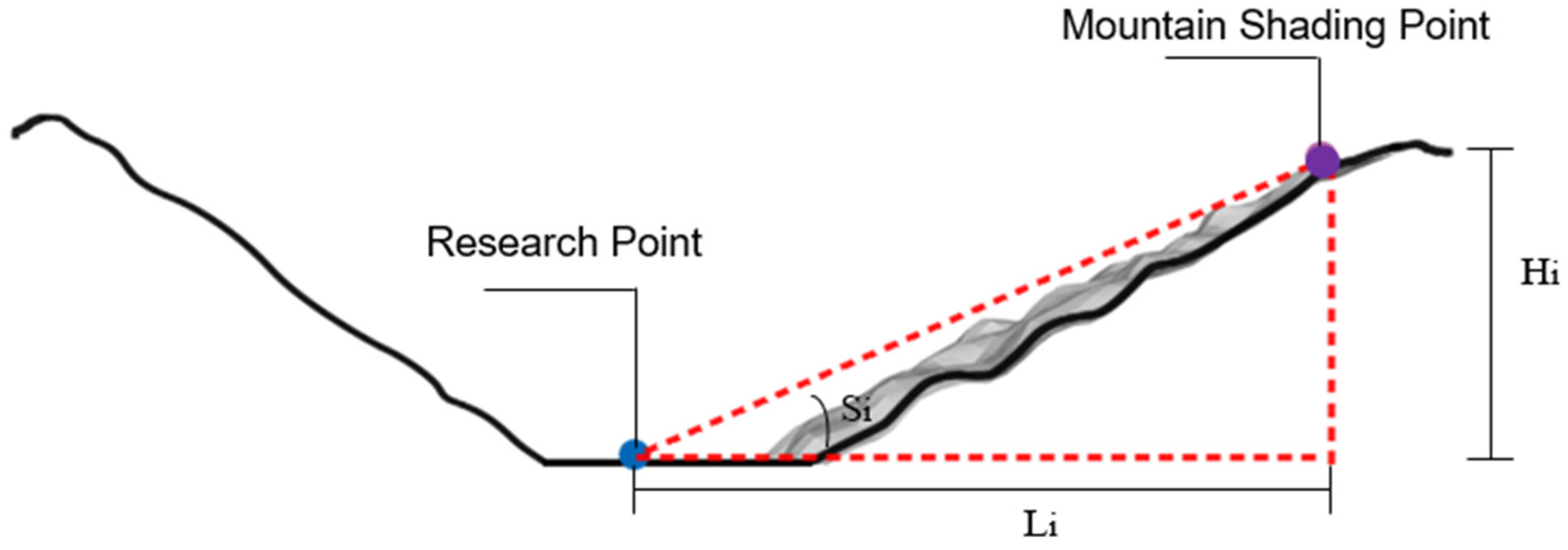
In this study, the Western Sichuan Plateau was chosen as a representative case to apply and evaluate the method proposed above. Situated in the transition area between the Qinghai-Tibet Plateau and the Sichuan Basin, the Western Sichuan Plateau is characterized by high altitude and abundant solar energy resources. However, the terrain there is complex and varied. In western Sichuan, the solar radiation received by the towns scattered among the mountains is significantly affected by the shading effects of the surrounding terrain (
Figure 2).
3.1. Terrain Factors of Western Sichuan
Based on the distribution of towns on the Western Sichuan Plateau, this study selected 139 town study sites and extracted terrain factors as inputs for training samples. First, based on DEM, ArcGIS was used to extract the terrain shading angles around the study sites at 1° interval. Taking Jianshe Town in western Sichuan as an example, the terrain shading angles around the research point are shown in
Figure 3. In the diagram, the angular coordinate represents the position of the mountains relative to the town (−180° to 180°), where 0° signifies that the mountain is to the south of the town, while ±180° indicates that the mountain is to the north of the town. The radial axis represents the slope of the mountain (0° to 40°), and the length of the line segment denotes the terrain shading angle at that direction. A longer line segment implies a greater the terrain shading angle at the azimuth angle. Subsequently, based on the terrain shading angles around the 139 town study sites, the average terrain shading angle within the range of solar azimuth angles and the terrain shading angles in the four different directions are calculated.
3.2. Solar Radiation Shading Rates
In rugged mountain areas, varying mountain shapes result in different degrees of shading effects on solar radiation. According to the topographical characteristics of western Sichuan, the direct radiation shading rates and diffuse radiation shading rates of the study sites in 139 towns were calculated by using the solar radiation model of Xu et al. [
33]. These shading rates were considered output variables of training samples, as depicted in
Figure 4. The average annual direct radiation shading rate of the 139 towns in western Sichuan was 4.6%, and the average annual diffuse radiation shading rate was 8.3%. Among these, the direct radiation shading rates of 57 urban study sites exceeded 5%, and the diffuse radiation shading rates of 95 urban study sites exceed 5%.
3.3. Selection of Input-Parameter Combinations
To determine the optimal combination of input variables for ML, the correlations between various terrain factors and solar radiation shading rates were analyzed. Five terrain factors of the 139 towns were used as input variables, with the annual direct radiation shading rates and diffuse radiation shading rates as output variables. The correlations between the five terrain factors and the annual direct radiation shading rates and diffuse radiation shading rates were analyzed.
Figure 5 illustrates the distribution of solar radiation shading rates in western Sichuan under the influence of the five terrain factors and the Pearson correlation coefficients (P) between shading rates and terrain factors. This figure demonstrates that there were linear relationships between the five terrain factors and the annual solar radiation shading rates. Obviously, the annual direct radiation shading rate and the diffuse radiation shading rate exhibited the strongest correlation with the average terrain shading angle within the solar azimuth range, with Pearson correlation coefficients of 0.901 and 0.971, respectively. The annual direct radiation shading rate and the diffuse solar radiation shading rate had the lowest correlation with the average shading angle in the northerly direction, with Pearson correlation coefficients of 0.517 and 0.786, respectively.
According to the results of the correlation analysis, selecting appropriate input variables for model training could enhance the model calculation accuracy. During the model training process, an excessive number of input variables may lead to model overfitting, compromising simulation accuracy. Therefore, to mitigate overfitting, the number of input variables was increased in turn based on the degree of correlation between the five terrain factors and solar radiation shading rates during model training. The input variables were added in the following order: the average terrain shading angle within the solar azimuth range, the terrain shading angle in the east, the terrain shading angle in the west, and the terrain shading angles in the south and north. Throughout the training process, the input variables were divided into five combinations, as shown in
Table 1.
3.4. GBDT Algorithm Hyperparameter Optimization
When using the GBDT algorithm for model training, it is crucial to adjust and optimize the hyperparameters, including the n-estimators and learning rate. Among them, the n-estimators represent the number of iterations for decision tree models. Generally, if the parameter is too small, it may lead to underfitting, and if it is too large, it might result in overfitting. Thus, selecting a moderate value is imperative, taking the learning rate into consideration. In this study, after multiple adjustments and careful consideration of the simulation accuracy, 200 was selected as the n-estimator. The learning rate is the weight-shrinking coefficient for each decision tree model, ranging from 0 to 1. Although a smaller learning rate can reduce overfitting, it requires more iterations of the decision tree model for overall training. After multiple parameter adjustment tests, 0.1 was chosen as the learning rate for training in this study. The “subsample” refers to the proportion of subsampling during training. A small subsample value can prevent overfitting but may increase the sample bias. In this study, subsampling was not used, and the subsample value was set to 1. The parameter Loss was used to select the loss function, encompassing mean squared error (“ls”), absolute loss (“lad”), Huber loss (“huber”), and quantile loss (“quantile”). Due to the small sample size in this study, the “ls” parameter was used to improve the training.
Apart from the hyperparameters of the boosting frameworks, several hyperparameters of each individual decision tree estimator also need to be adjusted to establish the GBDT model. The “max depth” represents the maximum depth of the decision tree. After testing, a value of 2 was chosen as the max depth to optimize the model accuracy. The parameter “min-sample-split” denotes the minimum number of samples required for internal node splitting. If the number of the node samples is less than this parameter, no attempt is made to split the node further. Owing to the limited number of samples in this study, this parameter was set to 2. The parameter “min-sample-leaf” signifies the minimum number of samples for a leaf node. If the number of leaf nodes is smaller than the number of samples, it may be pruned along with the sibling nodes. To improve the precision of the model, the value was set to 1.
5. Discussion
In order to further investigate the intrinsic relationship between the solar radiation shading rates and the terrain shading factor, this study conducted a comparison between ML models and traditional curve-fitting models. Based on the analysis results in the form of Pearson correlation coefficients, it was evident that the direct and diffuse radiation shading rates were most closely related to
Ssolar. Thus, this study set
Ssolar as the independent variable to perform univariate curve fitting. During the fitting process, eight different curve equations were selected, and error statistics were calculated, with the analysis results shown in
Table 2. From the table, it is evident that for the estimation of the annual direct and diffuse radiation shading rates, the power-function equation performed the best, with R
2 values of 0.887 and 0.961, respectively. The power-function equations of the annual direct solar radiation shading rate (
Rdirect) and the annual diffuse solar radiation shading rate (
Rdirect) are as follows:
After that analysis, a residual comparison analysis was conducted. By comparing the residuals of the solar radiation shading rate models trained by the curve-fitting, OLS, and GBDT algorithms, a comprehensive analysis was conducted to assess the accuracy of the models. The residual comparison of the direct radiation shading rate simulated by models using these three algorithms is illustrated in
Figure 8. For the direct solar radiation shading rate, the R
2 of the GBDT-based model exceeded that of the OLS-based model by 0.081 and exceeded that of the curve-fitting model by 0.094. The standard deviations of the residuals (SD) for the curve-fitting model, OLS model, and GBDT model were 1.317%, 1.260%, and 0.330%. The residual comparison indicated that the predictions of the GBDT-based model were more stable than those of the other two models. The residual values of the GBDT model consistently remained no greater than 1%, with only a few above 1%. The predicted results of the OLS-based models were influenced by the reference values. When the reference value exceeded 12%, the absolute value of the residual might also exceed 2%. For the curve-fitting model, the error was relatively even across the entire range of reference values, and the number of residual values greater than 2% was higher with this model than with the other two types of ML models.
Figure 9 displays a residual comparison of the diffuse radiation shading rates simulated by models using the curve-fitting, OLS, and GBDT algorithms. For the diffuse radiation shading rates, the GBDT-based model outperformed the OLS-based model and the curve-fitting model, presenting a higher R
2 value by 0.023 and 0.028, respectively. The difference in accuracy among the three algorithms for predicting the diffuse radiation shading rate was smaller than that for predicting the direct solar radiation shading rate. The standard deviations of the residuals for the curve-fitting model, OLS model, and GBDT model were 1.313%, 1.000%, and 0.336%. The SD of the GBDT-based model was still below 0.5%, and the SDs of the OLS and curve fitting models were larger than 1%. The residual values of the predicted diffuse solar radiation shading rates using the GBDT-based model consistently remained no greater than 1%, with only a few above 1%. The predicted diffuse radiation shading rate of the OLS-based models was also affected by the reference values. When the reference value was greater than 15% or close to 0%, the absolute value of the residuals could be greater than 2%. For the curve-fitting model, the error was similarly uniform across the entire range of reference values, and the quantity of residual values exceeding 2% for this model was more numerous than for the other two types of ML models.
From the aforementioned error comparisons, it can be seen that the direct and diffuse radiation shading rate models based on the GBDT algorithm perform best. The computational precision of the direct and diffuse radiation shading rate models based on the OLS algorithm is only slightly higher than that of the curve fitting equation. Thus, in practical applications, an appropriate algorithm for estimating solar radiation shading rates can be selected according to the actual precision requirement.
Although using the SVF concept to analyze the shading effects on solar radiation is a commonly used method, it only contains information regarding the shading percentage, without giving the precise shading location details [
17]. In instances of severe shading, the calculation of solar radiation shading using SVF would cause great errors [
15]. Based on the calculation principle of radiance [
38] or the concept of the viewshed [
31], shading effects can also be quantitatively analyzed. In order to estimate the solar radiation data of the research point under shading, Rutten [
39] developed a Grasshopper plugin in Rhinoceros3D 7.5 software based on the principle of radiance calculation. Subsequently, Roudsari and Pak [
40] further developed the related complementary plugins for Grasshopper. When calculating the shading effects on solar radiation by the Grasshopper plugin, the sky hemisphere was divided into 145 parts [
41]. Zhang et al. [
42] developed a model for calculating instantaneous solar radiation under mountainous terrain shading based on the viewshed by dividing the viewshed grid resolution into 16 azimuth and altitude angle parts. However, the finite number of sky hemisphere divisions restricts the calculation accuracy.
The solar radiation shading rate of the training set of this study is calculated based on the model of Xu et al. [
33]. It divides the viewshed grid resolution into 360 parts in the azimuth and 90 parts in the altitude angle. The calculation of diffuse solar radiation data under shading effects takes place through double integration on the unblocked surface of the sky dome [
33]. Compared with the typical measured annual meteorological data, the R
2 of the hourly solar radiation calculation errors of the model of Xu et al. [
33] exceeds 0.97. Therefore, the method presented in this study is not only precise in the ML process but also has accurate training and test sets. In summary, the solar radiation shading rate estimation model proposed by the research not only has a fast calculation speed but also has satisfactory calculation accuracy compared with the existing shading quantification analysis models.
However, there are also some limitations to this study. Specifically, the focus was only on the annual solar radiation shading rates, without considering variations across different seasons. In addition, the solar radiation shading rates of surfaces with varying orientations have not been involved. In future work, the solar radiation shading rates of surfaces with varying orientations during different time periods need to be further studied.
6. Conclusions
Based on mountainous terrain factors, this study proposed an ML method for solar radiation shading rate prediction in mountainous areas with complex terrain by using the OLS and GBDT algorithms. Error analysis was conducted to select the optimal models, enabling accurate and rapid predictions of both the direct radiation shading rate and the diffuse radiation shading rate.
The Western Sichuan Plateau was chosen as a representative case to establish a rapid estimation model of solar radiation shading rates. The complex terrain in western Sichuan has an obvious shading impact on solar radiation, and the average direct radiation shading rate of the 139 towns in western Sichuan is 4.6%, while the average diffuse radiation shading rate is 8.3%. According to the correlation analysis between various terrain factors and solar radiation shading rates, it was revealed that the annual direct and diffuse radiation shading rates in the western Sichuan are most correlated with the average terrain shading angle within the solar azimuth range, with Pearson correlation coefficients of 0.901 and 0.971, respectively. The annual direct radiation shading rate and the diffuse solar radiation shading rate have the lowest correlation with the average shading angle in the north direction, with Pearson coefficients of 0.517 and 0.786, respectively.
During the model development process, a comparative analysis was performed using five sets of input variables. For western Sichuan, the R2 values of the optimal OLS-based models for direct solar radiation shading rate and diffuse radiation shading rate are 0.900 and 0.967, respectively. However, the R2 values for the optimal GBDT-based models are higher, at 0.982 and 0.989, respectively. Furthermore, the study made a comparison between the classic curve-fitting model and the ML model. Since the direct and diffuse radiation shading rates are most closely related to Ssolar, this study set Ssolar as the independent variable and conducted a single-factor curve fitting. The resulting equations for the annual shading rates of direct and diffuse radiation yielded R2 values of 0.887 and 0.961, respectively. It is found that for the direct solar radiation shading rate prediction, the standard deviations of residuals for the curve-fitting model, OLS model, and GBDT model are 1.317%, 1.260%, and 0.330%. And for the diffuse solar radiation shading rate prediction, the standard deviations of residuals for the curve-fitting model, OLS model, and GBDT model are 1.313%, 1.000%, and 0.336%. Therefore, no matter whether it is used for the direct radiation shading rate prediction or the diffuse radiation shading rate prediction, the GBDT-based models always perform best, and the OLS-based models perform slightly better than the curve-fitting models. In practical applications, an appropriate algorithm for estimating solar radiation shading rates can be selected according to the actual precision requirements.
In summary, the solar radiation shading rate estimation model proposed by the research not only has a fast calculation speed but also has satisfactory calculation accuracy compared with the existing shading quantification analysis models. Based on the solar radiation shading rates predicted by this method, solar radiation data obtained by conventional models that do not consider terrain shading effects can be corrected to obtain precise solar radiation data in mountainous areas. This study could effectively address the issue of the insufficient solar radiation data in mountainous areas, thereby providing crucial fundamental data for the field of urban site selection and rooftop solar energy utilization.