Data-Driven Approaches for State-of-Charge Estimation in Battery Electric Vehicles Using Machine and Deep Learning Techniques

Abstract

One of the most important functions of the battery management system (BMS) in battery electric vehicle (BEV) applications is to estimate the state of charge (SOC). In this study, several machine and deep learning techniques, such as linear regression, support vector regressors (SVRs), k-nearest neighbor, random forest, extra trees regressor, extreme gradient boosting, random forest combined with gradient boosting, artificial neural networks (ANNs), convolutional neural networks, and long short-term memory (LSTM) networks, are investigated to develop a modeling framework for SOC estimation. The purpose of this study is to improve overall battery performance by examining how BEV operation affects battery deterioration. By using dynamic response simulation of lithium battery electric vehicles (BEVs) and lithium battery packs (LIBs), the proposed research provides realistic training data, enabling more accurate prediction of SOC using data-driven methods, which will have a crucial and effective impact on the safe operation of electric vehicles. The paper evaluates the performance of machine and deep learning algorithms using various metrics, including the R2 Score, median absolute error, mean square error, mean absolute error, and max error. All the simulation tests were performed using MATLAB 2023, Anaconda platform, and COMSOL Multiphysics.

1. Introduction

Global warming has been regarded as one of the most pressing issues of our day. One of the most dangerous forms of environmental pollution in metropolitan areas is the CO₂ gas released while internal combustion engine automobiles are operating. The automobile industry is paying greater attention to electric vehicles [1], which can use electric motors as propulsion systems, to overcome these issues. What makes battery electric vehicles (BEVs) so attractive is that they forgo combustion engines entirely and rely on a battery pack to power the car [2]. Automotive manufacturing often adopts battery technologies such as nickel–metal hybrid (NiMH), nickel–cadmium (NiCd), lead–acid, and lithium-ion (LIB) technologies. Specifically, LIBs can deliver high energy density, depending on the chemistry. They also have a longer lifespan and are less expensive than other technologies [3,4]. The battery management system (BMS) controls how LIBs operate in BEVs. The BMS, which fits the battery pack in BEVs, is a combination of hardware (such as sensors, controllers, actuators, etc.) and software that works to improve safety, shield individual cells from damage, increase battery efficiency, and prolong battery life.

2. Related Works

There are many ways to estimate a battery charge level, from simple methods like tracking voltage changes to more advanced techniques using artificial intelligence. Ultimately, the BMS aims to keep the battery safe and efficient and make it last as long as possible [5]. The BMS plays a critical role in maintaining the battery’s temperature within safe and optimal limits, ensuring its long-term performance and safety. Temperature significantly affects battery performance, safety, and lifespan. There are a variety of methods that exist for temperature estimation, including electrochemical modeling, equivalent circuit modeling, machine learning, and direct impedance measurement [6]. Electric vehicle batteries rely heavily on the battery management system. This system acts like a watchful guardian, constantly monitoring the battery’s state of health (SOH), charge level (known as SOC), and state of function (SOF). SOF, SOC, and SOH are interconnected metrics that provide a comprehensive understanding of a battery’s performance. It is a complex task because batteries behave differently depending on various factors.

Monitoring the battery pack’s state of health (SOH) and state of charge (SOC) and acting quickly to correct aberrant behavior are two of the BMS’s primary responsibilities. Due to the non-linearities of the processes that define the battery’s electrochemical activity, evaluating the online SOC is a difficult operation [7]. Several methodologies have been invested in to identify the state of charge (SOC) in battery electric vehicles (BEVs). These methods can be divided into many categories, including nonlinear observers, adaptive filtering techniques, model-based estimation techniques, traditional techniques, and learning algorithms. Common approaches include electromotive force (EMF), Coulomb counting, and internal resistance measurements [8,9,10,11,12,13,14]. Model-based estimation methods often rely on equivalent circuit models (ECM), reduced-order models (ROM), state–space models, electrochemical models (EM), and electrochemical impedance spectroscopy models (EISM). Adaptive filter algorithms, also known as Bayesian frameworks, encompass Kalman filters (KF), extended Kalman filters (EKF), unscented Kalman filters (UKF), and adaptive unscented Kalman filters (AUKF). Other approaches include nonlinear observers, bi-linear interpolation (BI) techniques, and particle filter (PF) methods [15,16,17,18,19,20,21,22]. Learning techniques, including machine learning (ML), fuzzy logic (FL), and genetic algorithms (GA), for SOC estimation [12,23,24,25,26,27,28] belong to a distinctive class of techniques since they do not include modeling the battery’s dynamic states or physical processes, let alone the parameter estimation. Essentially, they only use trained data that are readily available and include battery properties (such as temperature, voltage, and current) gathered from laboratory experiments to understand the non-linearities of the processes taking place within a cell.

Currently, many researchers are using artificial intelligence models for battery state-of-charge calculation. Lab experiments often use single cells or a few cells, while BEVs have entire battery packs with multiple modules connected in series and parallel. This limited setup does not reflect the complex discharge patterns of a full BEV battery. When a lab battery is fully discharged, it can only run for a certain number of hours. As a result, its driving range is lowered in comparison to the range of BEVs that are presently available for purchase. For instance, according to estimates from the Environmental Protection Agency (EPA), the Tesla S vehicle can travel 391 miles (630 km) at a time [29]. Additionally, lab tests typically only consider the battery itself, ignoring other vehicle components like the motor, powertrain, and external factors like air resistance. These all influence battery discharges in real-world driving. Models trained using data from a specific battery chemistry cannot accurately predict SOC for batteries with different chemistries. The internal electrochemical processes occurring inside the battery have a major influence on the connection between SOC and battery properties. These limitations call for more comprehensive data collection methods that consider real-world BEV operation and diverse battery chemistries to create accurate data-driven SOC estimation models. This investigation introduces a simulating form designed to create reliable training data for learning-based procedures that are utilized to estimate the BEV state of charge. To overcome these issues, the developed BEV model is used to compute the battery characteristics and SOC with a high degree of realism to actual driving conditions.

In addition to the commonly used electric current, voltage, and temperature, power losses from aerodynamic drag and variations in the mechanical power output of the electric motor are other elements taken into account for SOC prediction. The technique has been applied to Tesla S models available on the BEV market to gather information for practical uses. Building a larger extensive dataset is feasible for a data-driven model by simulating the distinct chemistries of the battery packs’ cells (which are made of nickel, manganese, and cobalt minerals) as well as the many ways in which the powertrain and electric motors operate. This research tackles key challenges in improving battery performance for electric vehicles (BEVs) with more accurate SOC estimation. This research simulates various driving conditions, as follows: the US06, Federal Test Procedure 75 (FTP75); the Heavy-Duty Urban Dynamometer Driving Schedule (HDUDDS); the Highway Fuel Economy Test (HWFET); Los Angeles 92 (LA92); the Supplementary Federal Test Procedure (SC03); and the Worldwide Harmonized Light Vehicles Test Procedure (WLTP) to develop a realistic dataset for training SOC estimation models. The models, including linear regression, support vector regressors (SVRs), k-nearest neighbor, random forest, extra trees regressor, extreme gradient boosting, random forest combined with gradient boosting, artificial neural networks (ANNs), convolutional neural networks, long short-term memory (LSTM) networks, are renowned for being efficient at SOC prediction. This research offers a new approach for generating training data for accurate SOC estimation and investigates the impact of BEV operation on battery degradation, aiming to improve overall battery performance. The automotive simulations were performed using seven EPA drive cycles, with two cases for the testing and prediction of the SOC to determine the results more accurately than other models.

Employing machine and deep learning (DL) algorithms for state-of-charge forecasting of BEVs, such as linear regression, SVRs, K-NN, RF, EXR, XGB, random forest combined with gradient boosting, ANNs, CNN, and LSTM for this research made the results of the prediction more accurate with fewer errors than the results presented in [30]. In this research, several machine learning and deep learning algorithms were used, thus supporting the reliability of the model over others. In this research, the use of optimal parameters for machine learning and deep learning algorithms was investigated to obtain an accurate estimation of SOC. For example, our research used a genetic algorithm to obtain the optimum parameters of the LSTM network.

The contributions of this paper are as follows: (i) we provide a modeling framework for generating accurate training data for algorithms based on learning used in BEV SOC estimation; (ii) the battery properties and state of charge are accurately determined according to real-world driving parameters; (iii) machine and deep learning algorithms are employed for the state-of-charge forecasting of BEVs; (iv) machine learning and deep learning algorithms are parameterized to obtain a precise estimation of SOC; (v) a genetic algorithm is combined with LSTM to determine the optimal parameter of LSTM units. The article is arranged as follows. The model description is presented in Section 2. Machine and deep learning algorithms are discussed in Section 3. The modeling findings are discussed in Section 4. Lastly, Section 5 presents the conclusions of the research.

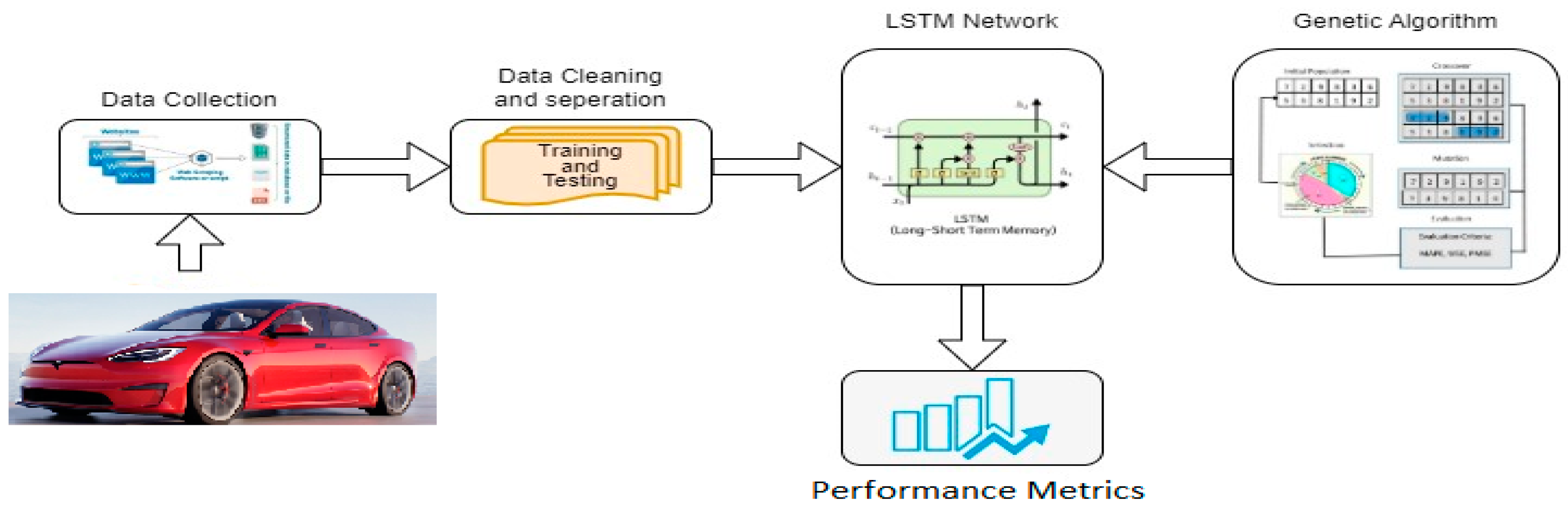
3. Model Description

This study provides a deep learning and machine learning algorithm-based computational method for studying the battery state of charge in electric vehicles (BEVs). The electrochemical and thermal data of the LIB model are integrated with machine learning techniques and automotive simulations in the BEV model. The MATLAB platform was used to execute the automotive simulations [31]. Data-driven models of vehicle powertrains, including gasoline, diesel, and electric systems, are made using the Powertrain blockset [32] MATLAB/Simulink software (2023a). Primarily, using the blocks in the Powertrain blockset library allows one to change the settings of the different parts of the vehicle by providing the appropriate look-up tables. The technical specifications of the Tesla S vehicle were used to parameterize the model’s blocks [29]. Utilizing the LIB modeling in COMSOL Multiphysics served as the foundation for the lookup tables implemented in the battery block parametrization of the BEV’s model [33]. Then, using our informed dataset that included the characteristics of the BEV’s components, we trained and evaluated ANN, CNN, LSTM, extreme gradient boosting, ensemble, K-NN, SVR, extra trees regressor, linear regression, and a random forest utilizing the data generated by the automotive simulations of BEVs. The learning methods were developed using the packages TensorFlow, Scikit-Learn keras, pytorch, and seaborn for ML and DL model construction [34,35,36]. Figure 1 illustrates the layout of the BEV model.

Utilizing specific blocks from the powertrain block set library, the test model replicates the dynamic behavior of the battery pack, electric motor, differential, wheels, braking system, and vehicle structure. The battery pack is constructed using the information sheet battery block [33], which makes use of an ECM whose factors can be predicted using look-up tables constructed by introducing the cell discharge curves at constant temperatures and C-rates. In particular, the created electrochemical–thermal model in COMSOL Multiphysics was used to simulate the discharge curves at various C-rates from 1C, 2C, 3C, 4C, and 5C with a constant temperature of 293 K, and at various temperatures of 263 K, 273 K, 29K, and 313 K at the constant 1C. We considered the many features of the batteries used in the Tesla S, specifically the cylindrical NMC 18,650 cell with a nominal capacity of 2.86 Ah. The information sheet of the battery block is designed to account for the connections that define the Tesla S battery packs (96 series 86 parallel). This makes it feasible to replicate the 100 kWh total energy discharge of the vehicles’ complete battery packs. The Coulomb counting method is used by the block to determine the SOC. The Mapped Motor block is used to imitate the Tesla S’s permanent magnet synchronous motor (PMSM) [37]. To meet the reference torque need, the block regulates the output shaft torque.

The motor’s characteristic curves at a certain angular speed are used to calculate the shaft torque. The reference torque considers the breaking torque that recovers the SOC during deceleration as well as the positive torque required for the vehicle to accelerate. To fit the demands of the driving cycle, the acceleration torque is calculated by multiplying the percentual acceleration [%] that the proportional integral (PI) controller computes from the motor’s characteristic curve at the angular speed. The limited slip differential [38] and the longitudinal wheel [39] blocks replicate the vehicle’s powertrain system by calculating the torque associated with the left and right axles as well as the net longitudinal forces applied to the front and back wheels. In addition, the tarmac and wheel friction are taken into account. Utilizing the vehicle body 1DOF longitudinal [40] block, the dynamics of the vehicle are simulated. The block considers the net longitudinal forces provided to the wheels and the aerodynamic drag force utilized by the windshield owing to the aerodynamic resistance of air, modeling the vehicle as a rigid body with one degree of freedom moving longitudinally parallel to the ground. We can calculate the acceleration and subsequent speed thanks to the balance of forces acting on the vehicle’s mass. The PI controller dynamically adjusts the feedback speed so that it coincides with the applied DC’s reference speed. The Mathworks webpages devoted to the powertrain blockset modules offer a more thorough description of how the look-up tables and differential equations that characterize each block were constructed [32]. The driving cycle that determines the vehicle’s reference speed is fed into the model, which then simulates the dynamics of BEV driving and determines the related SOC variation.

Several machine learning approaches for the estimate of the battery’s SOC have been trained and tested with the data created using the integrated automotive and electrochemical models of BEVs and LIBs, as discussed in this section. Here, we begin by introducing the input variables (features). Subsequently, we present a summary of the selected learning models for estimating the SOC. The battery block of the BEV model computes the current, voltage, and SOC fluctuation, whereas the cell’s thermal model computes the temperature profile. The dataset includes the system’s powertrain and the mechanical power flow from the electric motor to the wheels. It contains information on the power that the motor produces, the power that is transmitted via the differential, the power that is delivered to the wheels, the power that is lost as a result of rolling resistance, and the power needed for braking. Lastly, we considered the power loss brought on by the wind’s aerodynamic resistance. Consequently, the SOC was estimated by combining the nine variables that describe the vehicle performance. (I cell, V cell, T cell, Wmotor, W differential, W wheels, W rolling resistance, W breaks, W drag). We examined the learning algorithms that are included within the numerous categories mentioned in Section 1—linear regression, support vector regressors (SVRs), k-nearest neighbor, random forest, extra trees regressor, extreme gradient boosting, random forest combined with gradient boosting, ANNs, CNN, and LSTM networks [41,42,43,44,45,46,47,48,49,50,51]. All models will be illustrated in the next section.

4. Machine Learning Model

The integrated automotive and electrochemical models of BEVs and LIBs discussed in the preceding sections generated modeling data that were utilized to train and test numerous ML and DL models for the estimation of the battery’s state of charge (SOC). Here, we start by outlining the input variables, or features. Next, we provide a brief overview of the learning models that we have chosen to estimate the SOC. Then, we give a brief description of the learning models that we selected to compute the SOC. The discharge current, voltage, temperature, and SOC are the factors that define the battery. The system’s powertrain is taken into consideration in the dataset. Training and estimating are the two main stages of utilizing machine learning (ML) technology to estimate the state of health (SOH). While the estimating process can be carried out online or offline, the training process is usually carried out offline. Gathering an appropriate dataset is the initial step in the training process. From the raw data, pertinent characteristics that record aging information are then extracted. The training dataset is made up of these characteristics as well as the real SOH values. Then, to suit the training data, the ML algorithms learn and modify their weights and biases. Through this process, a nonlinear connection is established between the input characteristics, which represent the SOH, and the output, which is usually the capacity or SOH. Consequently, the SOC is estimated by combining nine variables that describe the vehicle’s performance. The proposed approach for the estimation of the SOC is divided into the following three modules: input parameters; feature extraction; and ML and DL algorithms. Ten different algorithms are implemented in this study, as shown in Figure 2.

4.1. Linear Regression

One of the most popular prediction models in statistics and machine learning is linear regression. Linear regression is an effective and practical technique for examining the relationship between two or more variables. To use this tool, the variables must be divided into independent input variables and a single dependent output variable. The objective is to identify the best linear function or a set of coefficients to accurately estimate the value of the reliant variable. The linear regression model is formally expressed as follows [52]:

$$Y={\beta }_0+{\beta }_1{X}_1+{\beta }_2{X}_2+\dots \dots ..+{\beta }_n{X}_n+\epsilon$$

(1)

where X₁ to X_n represents the independent variable, ε is the error term, β₀ is the intercept, and β₁ to β_n is the regression coefficient.

4.2. Support Vector Regression (SVR)

SVR is a machine learning approach based on the ideas of statistical learning [17]. The main idea of this method is to find a hyperplane by transforming a nonlinear input space into a higher-dimensional space using nonlinear mapping. Support vector regression (SVR) is a type of SVM used for function approximation and regression. Numerous kernel functions are used in SVM models, including polynomial, exponential, radial basis function, sigmoid, and linear. The kernel utilized in SVR forecasting and optimization is provided. The regression model can be formulated as presented in the following equation [53]:

$$\mathsf{\gamma }={\mathsf{\omega }}^{\mathrm{T}}\theta \left(\chi \right)+b$$

(2)

To find the weight vector ω, we need to minimize the following regularized expression, subject to the constraints given in Equations (4)–(6). In this expression, ω is the weight vector, b is the bias term, and θ(χ) is a nonlinear mapping function that transforms χ into a higher-dimensional feature space, as follows:

$$\mathrm{m}\mathrm{i}\mathrm{n}\left\{{\displaystyle \frac{1}{2}}{\mathsf{\omega }}^2+C {\sum }_{i=1}^N\left(\left\{{\xi }_i+{{\xi }_i}^{(\ast )}\right\}\right)\right\}$$

(3)

$${\mathsf{\gamma }}_i-\left\{\left({\mathsf{\omega }}^{\mathrm{T}}\theta \left(\chi \right)+b\right)\right\}\le \psi +{\xi }_i \mathrm{i}=1,2,\dots ,\mathrm{N}$$

(4)

$${\xi }_i.{{\xi }_i}^{(\ast )}\ge 0 \mathrm{i}=1,2,\dots ,\mathrm{N}$$

(5)

$\psi$ represents the desired level of accuracy in the function approximation on the training data. The variables ${\xi }_i$ and ${{\xi }_i}^{(\ast )}$ represent the positive slack variables, while C is a penalty parameter that controls the balance between regularization and empirical risk. The SVR is solved using the Lagrange multipliers ${\delta }_i$ and ${{\delta }_i}^{(\ast )}$ by incorporating the following constraints:

$$\mathrm{f}\left(\mathsf{\chi }\right)={\sum }_{\mathrm{i}=1}^{\mathrm{N}}\left({\mathsf{\delta }}_{\mathrm{i}}-{{\mathsf{\delta }}_{\mathrm{i}}}^{\left(\ast \right)}\right)\mathrm{K}\left(\mathsf{\chi }.{\mathsf{\chi }}_{\mathrm{i}}\right)+\mathrm{b}$$

(6)

Data that are not linearly separable can be handled well by kernel functions. One valuable tool for solving non-linear regression issues is a kernel function, which is essentially a measure of pattern similarity. The following RBF kernels are used in our study:

$$\mathrm{K}\left(\mathsf{\chi }.{\mathsf{\chi }}^{\prime }\right)=\exp \left(-{\displaystyle \frac{‖\mathsf{\chi }-{\mathsf{\chi }}^{\prime }‖}{2{\mathsf{\sigma }}^2}}\right)=\exp \left(-{\mathsf{\gamma }‖\mathsf{\chi }-{\mathsf{\chi }}^{\prime }‖}^2\right)$$

(7)

Here, $\mathsf{\gamma }$ > 0

4.3. K-Nearest Neighbor (K-NN)

Depending on the dataset parameter, the k-NN regression technique was employed in this work to forecast the SOC battery values. When k-NN is used in regression, as described in this article, it first uses a distance measure to determine the k nearest points, ${\mathrm{m}}_1$, ${\mathrm{m}}_2$, …, ${\mathrm{m}}_{\mathrm{k}}$, of a new point, ${\mathrm{m}}_{\mathrm{n}\mathrm{e}\mathrm{w}}$. It then computes the weighted average of their response to forecast a future outcome of ${\mathrm{x}}_{\mathrm{n}\mathrm{e}\mathrm{w}}$. Given a training dataset of N points M = {${\mathrm{m}}_1$, ${\mathrm{m}}_2$, …, ${\mathrm{m}}_{\mathrm{N}}$}, where each point has d features, k-NN may estimate the response of a new data point ${\mathrm{m}}_{\mathrm{n}\mathrm{e}\mathrm{w}}$ as follows. First, the weighted Euclidean distance between each training point ${\mathrm{m}}_{\mathrm{i}}$ and the testing point ${\mathrm{m}}_{\mathrm{n}\mathrm{e}\mathrm{w}}$, is determined and may be represented as in [54] to explain how near each is to the other, as follows:

$$\mathrm{d} ({\mathrm{m}}_{\mathrm{i}}, {\mathrm{m}}_{\mathrm{n}\mathrm{e}\mathrm{w}})=\sqrt{{\sum }_{j=1}^d{\mathrm{w}}_{\mathrm{j}}({M_{new}^j-m_i^j)}^2}$$

(8)

where ${\mathrm{M}}_{\mathrm{n}\mathrm{e}\mathrm{w},\mathrm{j}}$ and ${\mathrm{m}}_{\mathrm{i},\mathrm{j}}$ are the j-th characteristic of the new point ${\mathrm{m}}_{\mathrm{n}\mathrm{e}\mathrm{w}}$ and the training points ${\mathrm{m}}_{\mathrm{i}}$, consequently. In addition, w_j is the weight of jth feature, with the weights being exposed to the restriction $\sum _{j=1}^d{\mathrm{w}}_{\mathrm{j}}$ = 1. According to the distance d, the k training points ${\mathrm{m}}_1$, ${\mathrm{m}}_2$, …, ${\mathrm{m}}_{\mathrm{k}}$ arranged from the closest to furthest are determined. These are referred to as the k nearest neighbors of ${\mathrm{m}}_{\mathrm{n}\mathrm{e}\mathrm{w}}$. to each neighbor is given a weight using a kernel function (which is often based on the determined distance); an estimate for the new sample ${\mathrm{m}}_{\mathrm{n}\mathrm{e}\mathrm{w}}$ may be produced by

$$\widehat{n_{new}}={\displaystyle \frac{\sum _{i=1}^{k}k({\mathrm{m}}_{\mathrm{n}\mathrm{e}\mathrm{w}},{\mathrm{m}}_{\mathrm{i}}){\mathrm{n}}_{\mathrm{i}}}{\sum _{i=1}^{k}k({\mathrm{m}}_{\mathrm{n}\mathrm{e}\mathrm{w}},{\mathrm{m}}_{\mathrm{i}})}}$$

(9)

where the letter k indicates the number of nearest neighbors and represents the resilience of the model (the smoother the model, the higher k), ${\mathrm{n}}_{\mathrm{i}}$ symbolizes the recognized response of ${\mathrm{m}}_{\mathrm{i}}$, $\widehat{n_{new}}$, the predicted response of ${\mathrm{m}}_{\mathrm{n}\mathrm{e}\mathrm{w}}$, and K (${\mathrm{m}}_{\mathrm{n}\mathrm{e}\mathrm{w}}$, ${\mathrm{m}}_{\mathrm{i}}$), indicates the kernel function.

4.4. Random Forest

Random forest is a general-purpose machine learning approach that is used extensively for regression and classification applications. In this work, the remarkable regression capacity of the RF model is utilized to precisely predict the SOC of batteries used in electric vehicles. Leo Breiman introduced random forest regression [55]. Regression trees, $\overline{h}\left(x\right)$,${\theta }_k$, k = 1, …, K}, where X is the noticed input vector, X and ${\theta }_k$ are independent and similarity distributed random vectors, establish the random forest for regression. The output forecasting values of the random forest regression are numerical. Y is the output’s actual value. It is intended that the training data are chosen independently from the joint distribution of (X, Y). The RF estimate is the unweighted average of all regression tree forecasts, and it may be computed using [47], as follows:

$$\overline{\mathrm{h}}(\mathrm{x})=({\displaystyle \frac{1}{\mathrm{k}}}){\sum }_1^{\mathrm{k}}\mathrm{h}(\mathrm{x},{\mathsf{\theta }}_{\mathrm{k}})$$

(10)

4.5. Extra Trees Regressor

Developed from the random forest (RF) model, the extra tree regressor (ETR) explains a notable increase in ensemble learning. The ETR method makes use of a collection of unpruned regression trees, each of which is produced via a traditional top-down approach. The method presented is different from the RF model, which uses a two-step process for regression analysis that includes bootstrapping and bagging. The ETR model employs a deterministic splitting strategy to create individual trees. RF utilizes a chosen technique to find the best split from a random collection of properties at each node. On the other hand, ETR determines a split point at random for every characteristic before selecting the most suitable split among these options. This process can be expressed mathematically as follows [48]:

$${\mathrm{S}\mathrm{p}\mathrm{l}\mathrm{i}\mathrm{t}}_{\mathrm{E}\mathrm{T}\mathrm{R}}={\mathrm{a}\mathrm{r}\mathrm{g}}_{\mathrm{f},\mathrm{s}}\mathrm{m}\mathrm{i}\mathrm{n}\left[\mathrm{e}\mathrm{r}\mathrm{r}\mathrm{o}\mathrm{r}\left(\mathrm{f},\mathrm{s}\right)\right]$$

(11)

In this case, the chosen split in the ETR algorithm is indicated by the variable SplitETR. To represent a feature, we use the symbol “f”. A random split point for this feature is denoted by “s.” The function Error (f, s) measures how much the error is reduced by splitting the data based on f and s. The technique selects the f and s combination that reduces this error. In the RF algorithm’s bagging phase, each tree in the ensemble contributes a prediction. The final estimation is typically decided by averaging these individual predictions. A similar approach is used by the ETR technique, but with a more varied ensemble of unpruned trees. Mathematically, the result of the final ETR model is represented briefly in Equation (12), as follows:

$$Y_{ETR}=({\displaystyle \frac{1}{N}}){\sum }_{i=1}^N{T}_i(x)$$

(12)

The ensemble’s total number of trees, represented as N, the i-th tree in the ensemble, represented as $T_i$, and the input feature vector, represented as X, all contribute to the expected output, defined as $Y_{ETR}$. The ETR technique generates a unique regression approach that incorporates mathematical elements to strike a balance between accuracy and unpredictability.

4.6. Extreme Gradient Boosting

Using the gradient boosting framework, XGBoost is an ensemble machine learning approach built on decision trees. A supervised learning approach called gradient boosting fits new models successively to make up for the shortcomings of older models. The models are then linearly combined to create new models. However, in the presence of noise, gradient boosting may result in overfitting. XGBoost provides the values of γ and λ to avoid the overfitting issue caused by gradient boosting. A classification and regression tree (CART) model is used by XGBoost. With each node representing a dataset, CART represents a single value. The XGBoost algorithm starts by initializing the model as a constant, as defined in the next equation [56], as follows:

$$\widehat{y_i}=\varphi (o_i)={\sum }_{k=1}^k{f}_k\left(o_i\right),f_k\in \mathcal{F}$$

(13)

$o_i$ is the TCN layer’s output, $y_i$ is the predicted number of $o_i$, K is the number of CARTs, and F is the space of the regression trees. The formula that follows is an objective function that directs each CART model’s training:

$$obj(\theta )={\sum }_i^{n}l\left(y_i,{\hat{y}}_i\right)+{\sum }_{k=1}^k\mathsf{\Omega }(f_k)$$

(14)

To limit the intricacy of the tree structure and avoid overfitting, the right side of the equation acts as a regularization parameter. The gap between the actual and anticipated values is the training loss, which is shown on the left-hand side. W is a normalizing function that is used to prevent overfitting, and $\left(y_i,{\hat{y}}_i\right)$ is the objective function that is generated based on the desired value $y_i$ and the expected value ${\hat{y}}_i$.The values assigned to the leaf nodes are denoted as $\theta$ = $f_1$, $f_2$, …$f_k$. XGBoost iteratively adds models that predict the unexpected parts at each step, leading to a new objective function that can be expressed as an expansion. The layout of each tree are the variables that need to be learned, as follows:

$${obj}^{(t)}={\sum }_{i=1}^n[g_i{f}_t(o_i)+{\displaystyle \frac{1}{2}}{h}_i{f}_t^2(o_i)+\mathsf{\Omega }(f_t)]$$

(15)

4.7. Ensemble (Random Forest Combined Gradient Boost)

By combining the predictions of many machine learning models, ensemble learning is a potent approach that enhances the precision and resilience of SoC estimates in electric vehicles. It uses the combined knowledge of several models to provide more accurate forecasts [28,55,57], as follows:

$$F(x)=({\displaystyle \frac{1}{N}}){\sum }_{i=1}^N{f}_i(x)$$

(16)

where $F\left(x\right)$ represents the ensemble forecast for input x, N is the number of decision trees in the ensemble, and $f_i(x$) is the estimate of the i-th decision tree. The random forest regressor and its variations, such as gradient boosting regressor, have shown impressive performances in the scope of SOC estimation.

4.8. Artificial Neural Network

An artificial neural network (ANN) is formed of multiple active variables arranged in a deep architecture known as hidden layers; it breaks down the correlations between the input variables and a goal via a series of algebraic linear combinations. The input and output layers of the network are represented by the input variables and the target. In networks, there is a static mapping between the input and the output, where the input signal travels forward, layer by layer, from the input layer, via the hidden layers, to the output. Let k be the total number of input and output layers that are concealed. The ith node in the nth layer is stated by node(n, i), and the overall number of nodes in the nth layer is Nn − 1. Figure 3 illustrates how node (n + 1, i) assesses the following formula [58]:

$${\mathrm{x}}_{\mathrm{i}}^{\mathrm{n}+1}(\mathrm{t})=\mathsf{\phi }{\sum }_{\mathrm{j}=1}^{{\mathrm{N}}_{\mathrm{n}-1}}{\mathrm{w}}_{\mathrm{i},\mathrm{j}}^{\mathrm{n}}{\mathrm{x}}_{\mathrm{j}}^{\mathrm{n}}(\mathrm{t})+{\mathrm{b}}_{\mathrm{i}}^{\mathrm{n}+1}$$

(17)

The weighted and biased mathematical functions for the ANN are produced and shown as follows:

$${\mathrm{a}}^2={\mathrm{f}}^2({\mathrm{w}}^2{\mathrm{f}}^1\left({\mathrm{w}}^1\mathrm{p}+{\mathrm{b}}^1\right)+{\mathrm{b}}^2)$$

(18)

where W represents weight and b and P represent bias and input.

Nine neurons in the input layer of ANN that we utilized to solve this issue reflect the values of the nine input variables at time t. The rectified linear unit (ReLu) activation process drives the neurons in the hidden layer, while the output layer has just one neuron that represents the final SOC forecasting, as seen in Figure 4.

4.9. Convolutional Neural Network

Another DL method for estimating battery SOH is CNN [54]. As can be seen in Figure 5a, the CNN with a 2D input consists of one or more stacks of convolutional and pooling layers, layers that are completely connected, and the output layer. Each convolutional layer output is linked to a portion of the inputs, as opposed to being entirely connected. The sparse connectivity is obtained by sliding a filter (the weights matrix) across the input space. As can be noted in Figure 5b, “convolution” describes the computation that occurs between the subset of input and the filter (i.e., the weights matrix).

Because of their ability to automate and identify the significant attribute in the input data, CNNs are a pattern of neural networks especially good at reducing the number of parameters in data processing. This is because CNNs will take out the most significant features and search for correlations between the various input factors [59]. The CNN architecture is illustrated in Figure 6

4.10. Long Short-Term Memory

To solve the RNN’s gradient vanishing issue, the LSTM [30,59,60] develops a novel activation function to reduce the gradient vanishing incidence and preserve long-term associations. Cell memory, the core idea of the long short-term memory (LSTM), is unpacked and moves down the whole chain by an affine transformation. The construction of a typical LSTM unit is shown in Figure 7, where $c_k$ represents the unit memory at time t equals k, as follows:

$$c_k=f_k·c_{k-1}+i_k·{\tilde{c}}_k$$

(19)

The three types of gates that the LSTM unit uses to calculate the effects of cell memory on node output, the forgetting rate of cell memory upon current input, and the percentage of current cell memory merging into the old cell memory are the input gate I, forget gate F, and output gate O. At time k, an LSTM unit makes a forward pass in the manner described below:

$${\mathrm{f}}_{\mathrm{k}}={\mathsf{\sigma }}_{\mathrm{g}}({\mathrm{w}}_{\mathrm{f}}{\mathrm{x}}_{\mathrm{k}}+{\mathrm{U}}_{\mathrm{f}}{\mathrm{h}}_{\mathrm{k}-1}+{\mathrm{b}}_{\mathrm{f}})$$

(20)

$${\mathrm{i}}_{\mathrm{k}}={\mathsf{\sigma }}_{\mathrm{g}}({\mathrm{w}}_{\mathrm{i}}{\mathrm{x}}_{\mathrm{k}}+{\mathrm{U}}_{\mathrm{i}}{\mathrm{h}}_{\mathrm{k}-1}+{\mathrm{b}}_{\mathrm{i}})$$

(21)

$${\mathrm{o}}_{\mathrm{k}}={\mathsf{\sigma }}_{\mathrm{g}}({\mathrm{w}}_{\mathrm{o}}{\mathrm{x}}_{\mathrm{k}}+{\mathrm{U}}_{\mathrm{o}}{\mathrm{h}}_{\mathrm{k}-1}+{\mathrm{b}}_{\mathrm{o}})$$

(22)

$${\mathrm{c}}_{\mathrm{k}}={\mathrm{f}}_{\mathrm{k}}\circ {\mathrm{c}}_{\mathrm{k}-1}+{\mathrm{i}}_{\mathrm{k}}\circ {\mathsf{\sigma }}_{\mathrm{c}}({\mathrm{w}}_{\mathrm{c}}{\mathrm{x}}_{\mathrm{k}}+{\mathrm{U}}_{\mathrm{c}}{\mathrm{h}}_{\mathrm{k}-1}+{\mathrm{b}}_{\mathrm{c}})$$

(23)

$${\mathrm{h}}_{\mathrm{k}}={\mathrm{o}}_{\mathrm{k}}\circ {\mathsf{\sigma }}_{\mathrm{h}}\left({\mathrm{c}}_{\mathrm{k}}\right)$$

(24)

where $x_k$ and $h_k$ are the unit input and referring output at time k, consequently; $c_k$ indicates the hidden cell memory; w, u, and b are weight matrices and bias vectors to be learned during training; o signifies the element-wise product of the vectors. The activation vectors of the input gate, forget gate, and output gate are denoted by the symbols ${\mathrm{f}}_{\mathrm{k}}$, ${\mathrm{i}}_{\mathrm{k}}$, and ${\mathrm{o}}_{\mathrm{k}}$, respectively, while ${\sigma }_g,{\sigma }_h,{\sigma }_c$ are the associated activation functions; precisely, ${\sigma }_g$ is a logistic sigmoid function while ${\sigma }_c$ and ${\sigma }_h$ are both hyperbolic tangent functions.

Nine distinct input factors were taken into consideration when developing the cell SOC estimate method. The cell’s SOC was the algorithm’s output. In this work, we suggest combining LSTM with GA to determine the ideal number of LSTM units for battery state-of-charge estimation, as observed in Figure 8.

Natural evolution serves as the inspiration for GA, a metaheuristic stochastic optimization algorithm [61]. They are often employed to identify nearly ideal solutions for optimization issues involving sizable search areas. Lastly, the performance metrices—a statistic commonly employed in regression problems—between the estimated and the true SOC were taken into consideration to evaluate the effectiveness of the models. The performance metrics involve the R2 score, median absolute error, mean square error, mean absolute error, and max error [62,63].

5. Result and Discussion

This section begins by displaying the simulated data’s progression. The simulations of the SOC deterioration brought on by the BEV degradation are then shown. Finally, we provide the SOC prediction produced by machine and deep learning models that used modeling data for training and testing data.

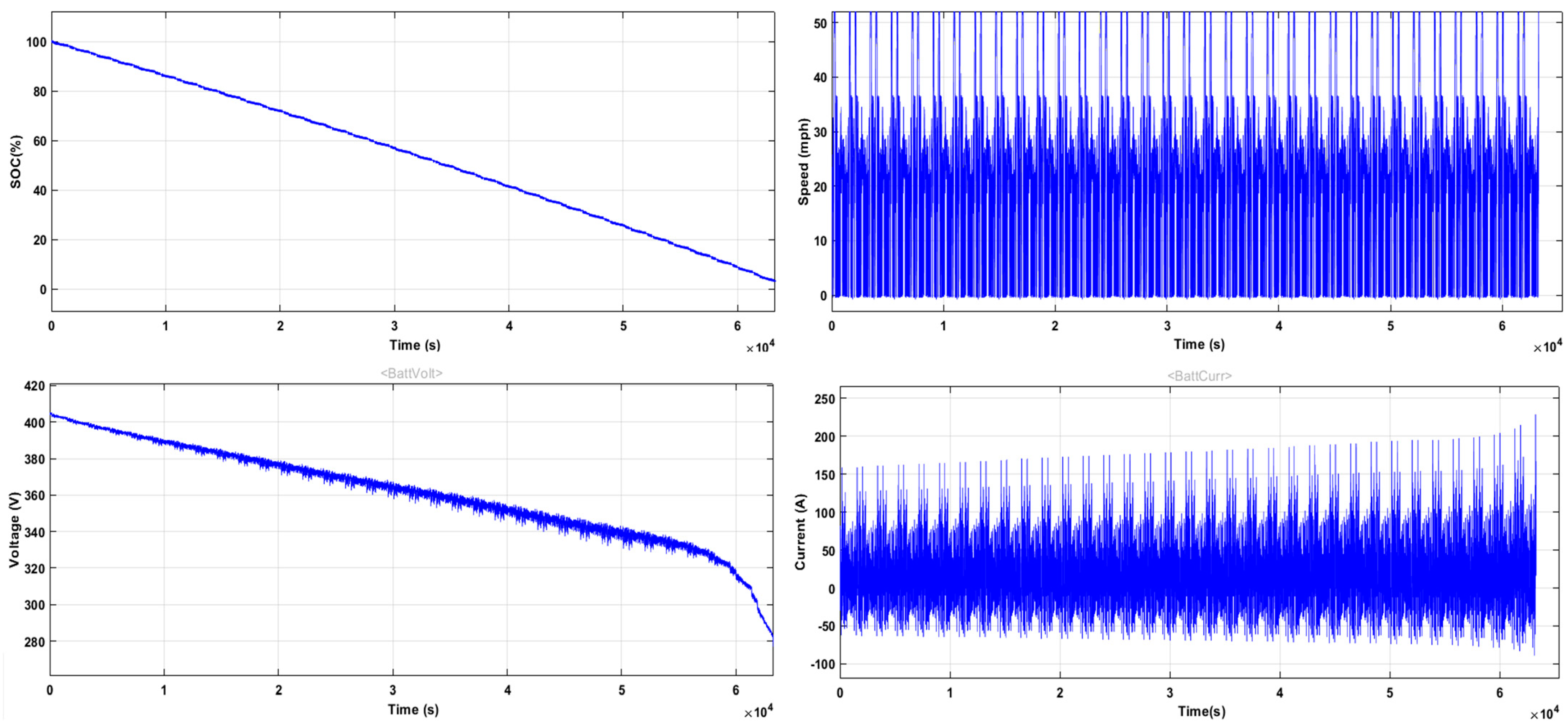
5.1. Simulations of Battery Electric Vehicles and Generation of Datasets

The BEV simulations consider many iterations of the seven DCs for Tesla S models: US06, FTP75, HDUDDS, HWFET, SC03, WLTP, and LA92. We simulate various driving patterns and offer a wider range of setups for a data-driven model by utilizing several DCs. The US06 driving cycle illustrates a fast-paced, aggressive driving style characterized by sharp acceleration and deceleration. However, FTP75 evaluates emissions in urban areas. The HWFET was created to predict the highway fuel economy rating, and the WLTP driving cycle is used to calculate light-duty car emissions and fuel consumption. The number of repetitions for each driving cycle is determined by taking the EPA driving range into account. This allows for the simulation of a full driving cycle before the battery pack needs to be recharged. The decrease in battery SOC is used to verify the dependability of our vehicle modeling; if the battery is consistently empty (SOC < 10%) after the simulation, when the maximum driving range is reached, the automotive model is considered reliable. The SOC fell to acceptable values for every driving cycle conducted; therefore, we believe that our BEV model accurately simulates the Tesla S. The computational model was run at a constant 298 K (25 °C ) ambient temperature for each condition. For the FTP75 and HDUDDS driving cycle, the simulated discharge profiles are displayed in Figure 9 and Figure 10. The discharge curves for the Tesla S model are shown. According to the FTP75 speed profile, Figure 9 and Figure 10 illustrate how long it takes for the Tesla S model battery pack to lose its charge, taking about 18 h, and 17 h for driving cycle HDUDDS. The figure depicts the forms of the voltage profiles and discharge current.

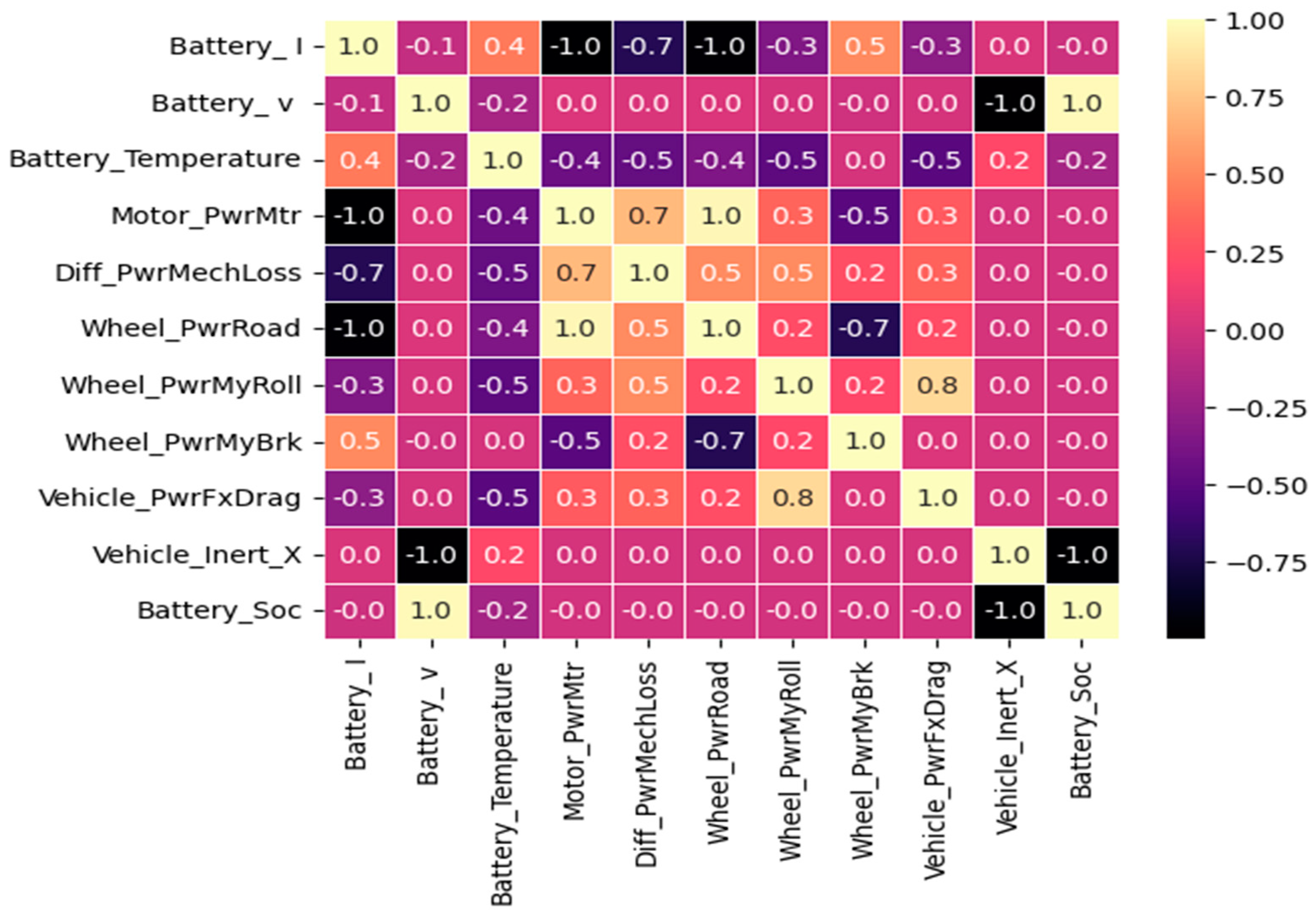
5.2. The Preparation of Data

Before feeding the simulated data into machine learning models, it is necessary to properly preprocess the data using the modeling technique covered in the preceding section. Any machine learning project must begin with data collecting, which also happens to be the initial stage in the data preparation process. Importing the libraries required for machine learning projects, such as NumPy, panda, matplotlib, and seaborn, is the next step. A library is a set of functions that may be called and used by an algorithm. Loading the data that the machine learning algorithm will use is the next crucial step. This is the most important preprocessing step for machine learning. Next, it is time to assess the information and search for any missing values. For non-distance-based algorithms (like the decision tree), scaling is not required. Conversely, all features in distance-based models must be scaled. Lastly, the dataset is divided into sets for training, evaluation, and validation, after which the data preparation stages come to an end. The training and testing datasets can be produced using several methods with the simulated data that represent the seven driving cycles of the Tesla S. A specific approach is to take the datasets and divide them into 30% for testing and 70% for training, at random. These ratios are commonly used in machine learning to choose the training and test datasets. There are several ways to investigate the relevance of features. As seen in Figure 11, correlations may be easily studied using correlation graphs.

The training and test datasets in this work are first created using different DCs. For training and testing, FTP75, HDUDDS, HWFET, LA92, SC03, US06, and WLTP are utilized in Case 1, as shown in

Table 1. Two different cases used to produce the training and test datasets from the thirteen simulated datasets of the Tesla s model for ten different machine and deep learning algorithms.

Case 1	Train	Test	Case 2	Train	Test
1.	FTP75	FTP75	1.	FTP75	HDUDDS
2.	HDUDDS	HDUDDS	2.	FTP75	HWFET
3.	HWFET	HWFET	3.	FTP75	LA92
4.	LA92	LA92	4.	FTP75	SC03
5.	SC03	SC03	5.	FTP75	US06
6.	US06	US06	6.	HDUDDS	HWFET
7.	WLTP	WLTP

. In case 2, FTP75, HDUDDS, and WLTP are used for training, with different driving cycles, such as HDUDDS, HWFET, LA92, SC03, US06, WLTP, HWFET, and SC03, used for testing, as shown in Table 1.

All the simulation tests were executed on a 2.6 GHz i7 PC with 16 GB of RAM using MATLAB 2023, Anaconda platform and COMSOL Multiphysics.

5.3. State-of-Charge Estimation Using Machine Learning Models

In this section, we provide the SOC estimate findings utilizing the suggested learning algorithms on datasets generated by our suggested modeling framework. It was found that a radial basis kernel with values for the regularization parameter C, the polynomial kernel function’s degree, gamma equal to 1, 3, and scale, respectively, provides the best configuration for the SVR. Similarly, the highest accurate SOC estimation is obtained from the ANN constructed with two hidden layers and trained for 500 epochs with a batch size of 32 samples. The artificial neural network (ANN) that we have used for this problem is composed of nine neurons in the input layer that represent the values of the nine input variables at a given time, U. The output layer has just one neuron that represents the final SOC forecasting, whereas the neurons in the hidden layer are stimiulated by the rectified linear unit (ReLu) activation function. The ANN model was built using the Adam optimizer and the mean squared error (MSE) loss function.

The LSTM network consists of three LSTM layers between the input and output layers. The LSTM is trained for 30 epochs, with a 312 batch size, a 0.01258 learning rate with 289 neurons for layer 1 and 226 for other layers, and a 0.2 dropout. The neurons are activated by the rectified linear unit (ReLu) activation function. The LSTM model was built using the Adam optimizer and the mean squared error (MSE) loss function. The optimum parameters of the LSTM network were found using the GA algorithm. The CNN model was built using the Adam optimizer and the mean squared error (MSE) loss function and the model was activated by the rectified linear unit (ReLu) activation function. The CNN model was constructed from 64 filter maps, 2 kernel sizes, and a pool size equal to 2. The CNN Model was trained for 300 epochs with a 32 batch size. Other types of machine learning algorithms were parametrized to obtain an accurate estimation for the state of charge, including random forest, KNN, extra trees regressor, extreme gradient boosting, gradient boosting and ensemble (RF with GB), where the number of estimators and number of neighbors equaled 100 and 5 and the learning rate of extreme gradient boosting equaled 0.1. Figure 12 and Figure 13 show the analysis performance of Tesla’s model including the prediction of the state of charge, R2 prediction, error difference between the testing and prediction, and the distribution plot between testing and forecasting of the model. SOC estimation for Tesla S using SVR was obtained by training and testing the models based on the datasets produced by BEV selection, with FTP75 for training, and HWFET for testing of the model (Case 2).

Estimation is expressed by the SVR (MSE = 1.2501, MAE = 1.0784, R2 = 0.9982, MAE = 1.00155, and max error = 1.8699).

Table 2. The values of performance indicators for the entire training dataset and test datasets built for different cases.

Case 1
Type of Algorithm	Trian Dataset	Test Dataset	R2 Score	Median Absolute Error	Mean Square Error	Mean Absolute Error	Max Error
Linear regression	FTP75	FTP75	0.99998	0.0612	0.0089	0.0707	1.460
	HDUDDS	HDUDDS	0.9980	0.7333	1.9425	0.9710	6.5360
	HWFET	HWFET	0.99935	0.591957	0.474047	0.59087	1.8216
	LA92	LA92	0.976006	1.52719	27.2247	3.460357	17.72459
	SC03	SC03	0.999334	0.66808	0.568693	0.655949	1.867656
	US06	US06	0.9103820	7.2366	101.523	8.21324	28.1134
	WLTP	WLTP	0.913368	3.06668	91.8504	6.53385	32.1179
Support Vector Regression	FTP75	FTP75	0.99935	0.6169	0.5044	0.614	1.8937
	HDUDDS	HDUDDS	0.9995	0.10298	0.4321	0.3134	3.7902
	HWFET	HWFET	0.999983	0.064704	0.012069	0.07859	1.270478
	LA92	LA92	0.999069	0.174527	1.056293	0.557747	5.950100
	SC03	SC03	0.999978	0.055714	0.018425	0.080015	1.529122
	US06	US06	0.99716	0.72306	3.20669	1.11650	9.45919
	WLTP	WLTP	0.99378	0.7538	6.58511	1.46518	12.409794
Random Forest	FTP75	FTP75	0.999964	0.0582	0.0282	0.0944	4.4583
	HDUDDS	HDUDDS	0.99998	0.03008	0.0165	0.0664	2.8850
	HWFET	HWFET	0.999946	0.08380	0.039434	0.1252609	3.103030
	LA92	LA92	0.999963	0.05827	0.02823	0.09447	4.45839
	SC03	SC03	0.999970	0.056700	0.025054	0.091281	6.06554
	US06	US06	0.999946	0.019099	0.061078	0.103797	6.66501
	WLTP	WLTP	0.999952	0.002651	0.05036	0.083293	5.29603
Extreme Gradient Boosting	FTP75	FTP75	0.873154	8.276	99.168	8.512	20.921
	HDUDDS	HDUDDS	0.87419	9.46737	122.7047	9.5353	21.5351
	HWFET	HWFET	0.872993	8.056079	93.00832	8.231521	20.03072
	LA92	LA92	0.873153	8.276448	99.16822	8.512329	20.92114
	SC03	SC03	0.872998	8.761017	108.56696	8.90020	20.6904
	US06	US06	0.87556	10.4652	140.970	10.51034	28.2937
	WLTP	WLTP	0.8764740	7.68849	130.968	9.6904	28.9420
Extra Trees Regressor	FTP75	FTP75	1.000000	0.00082	5.728 × 10−5	0.00315	0.2094
	HDUDDS	HDUDDS	0.99999	0.000141	5.811423	0.002861	0.186819
	HWFET	HWFET	0.99999	0.002870	0.000132	0.005407	0.27410
	LA92	LA92	0.99999	0.000829	5.7289508	0.003154	0.209430
	SC03	SC03	0.9999998	0.0010600	8.629643	0.003780	0.241631
	US06	US06	0.999999	9.999999	0.0007	0.00622	1.363720
	WLTP	WLTP	0.9999996	9.602449	0.00036	0.00511	0.4739
Ensemble (RF with GB)	FTP75	FTP75	0.999980	0.0463	0.00778	0.0642	0.3897
	HDUDDS	HDUDDS	0.999993	0.030020	0.0065654	0.053399	0.45445
	HWFET	HWFET	0.99998	0.05331	0.008968	0.071215	0.301687
	LA92	LA92	0.99999	0.046358	0.007789	0.064200	0.389765
	SC03	SC03	0.999990	0.045019	0.008424	0.065976	0.366817
	US06	US06	0.999996	0.007836	0.004461	0.03516	0.41210
	WLTP	WLTP	0.999997	0.004389	0.002716	0.022973	0.57122
K-nearest neighbor	FTP75	FTP75	0.999991	0.0114	0.0066	0.0407	1.3161
	HDUDDS	HDUDDS	0.99999	0.003399	0.00659	0.03927	1.35447
	HWFET	HWFET	0.999986	0.041400	0.010085	0.06573	0.903299
	LA92	LA92	0.999991	0.011439	0.006697	0.040734	1.3161399
	SC03	SC03	0.999992	0.013199	0.006774	0.043429	0.971580
	US06	US06	0.999953	0.000238	0.05320	0.10091	3.4197
	WLTP	WLTP	0.99988	0.00988	0.12142	0.117660	6.2537
ANN	FTP75	FTP75	0.99985	0.1746	0.1107	0.2406	1.978
	HDUDDS	HDUDDS	0.9999	0.145	0.054	0.179	2.010
	HWFET	HWFET	0.999630	0.336691	0.270569	0.396638	4.898849
	LA92	LA92	0.999873	0.17537	0.14429	0.26360	3.049926
	SC03	SC03	0.999924	0.136437	0.064440	0.18170	3.068916
	US06	US06	0.999824	0.10959	0.19770	0.26190	3.46083
	WLTP	WLTP	0.999665	0.12033	0.35039	0.31387	5.4461
CNN	FTP75	FTP75	0.999774	0.23263	0.17658	0.29018	2.2751403
	HDUDDS	HDUDDS	0.99985	0.162385	0.14232	0.23188	3.1975
	HWFET	HWFET	0.99961	0.32728	0.28412	0.37938	3.7948
	LA92	LA92	0.999501	0.331912	0.565357	0.481458	4.55720
	SC03	SC03	0.99973744	0.413400	0.224447	0.4105519	3.729085
	US06	US06	0.99877	0.189017	1.389862	0.565429	28.8286
	WLTP	WLTP	0.9989	0.1977	1.06597	0.5781	11.9990
LSTM	FTP75	FTP75	0.717	0.012	0.0029	0.034	0.376
	HDUDDS	HDUDDS	0.382	0.009	0.005	0.041	0.687
	HWFET	HWFET	0.728503	0.0111	0.00282	0.03346	0.34197
	LA92	LA92	0.684113	0.015159	0.00333	0.03514	0.38417
	SC03	SC03	0.672582	0.0109	0.0028	0.03007	0.56159
	US06	US06	0.47407	0.019239	0.00731	0.05235	0.61644
	WLTP	WLTP	0.936237	0.012	0.0017	0.02538	0.3248
Case 2
Type of Algorithm	Trian Dataset	Test Dataset	R2 Score	Median Absolute Error	Mean Square Error	Mean Absolute Error	Max Error
Linear regression	FTP75	HDUDDS	0.944688	6.169268	54.16576	6.305490	14.43820
	FTP75	HWFET	0.998891	0.7232199	0.8128205	0.7626440	1.765566
	FTP75	LA92	0.774558	13.45566	255.0127	13.77310	29.498517
	FTP75	SC03	0.9745107	3.7387369	21.62759	3.9347557	10.30854
	FTP75	US06	0.352077	23.38893	733.0006	23.550809	47.32595
	HDUDDS	HWFET	0.911297	7.03832	65.06346	6.974459	13.086
Support Vector Regression	FTP75	HDUDDS	0.963806	4.31045	35.44409	5.071590	11.16512
	FTP75	HWFET	0.9982956	1.078491	1.25011	1.00155	1.869941
	FTP75	LA92	0.849690	10.55599	170.0255	11.16816	24.02100
	FTP75	SC03	0.981634	2.64432	15.58340	3.37026	7.966165
	FTP75	US06	0.55024	18.9719	508.810	19.339	41.12291
	HDUDDS	HWFET	0.90524	8.02890	69.505387	7.309812	12.88882
Random Forest	FTP75	HDUDDS	0.978099	3.70687	21.44641	3.950920	14.15999
	FTP75	HWFET	0.999090	0.4518000	0.666783	0.570178	8.5648099
	FTP75	LA92	0.908637	8.179610	103.3460	8.60731	25.4749
	FTP75	SC03	0.990841	2.225249	7.77122	2.3749767	10.19230
	FTP75	US06	0.706681	13.973060	331.83435	15.52745	34.25831
	HDUDDS	HWFET	0.9734	3.47196	19.4669	3.78535	10.16846
Extreme Gradient Boosting	FTP75	HDUDDS	0.7777579	11.54962	217.638	12.4800	27.47621
	FTP75	HWFET	0.881164	7.857725	87.165907	7.988959	19.01007
	FTP75	LA92	0.600633	17.8110	451.7514	18.12876	37.51642
	FTP75	SC03	0.8230246	10.1676035	150.163561	10.40730	24.513339
	FTP75	US06	0.20522	27.476217	899.1345	26.40807	49.25548
	HDUDDS	HWFET	0.8572260	8.425267	104.7245	8.72540	21.52842
Extra Trees Regressor	FTP75	HDUDDS	0.963924	5.427150	35.32862	5.199840	10.253589
	FTP75	HWFET	0.999159	0.6366099	0.616186	0.667019	1.538449
	FTP75	LA92	0.85903	10.25706	159.4529	10.80695	23.73962
	FTP75	SC03	0.9826334	3.2892749	14.73552	3.3156945	6.8823999
	FTP75	US06	0.639784	17.363779	407.51493	17.54104	36.695768
	HDUDDS	HWFET	0.95132	5.26737	35.70235	5.205165	11.26198
Ensemble(RF with GB)	FTP75	HDUDDS	0.945076	6.054256	53.78597	6.27432	13.9758
	FTP75	HWFET	0.9990030	0.6596117	0.731296	0.707902	1.900086
	FTP75	LA92	0.7756410	13.53782	253.7879	13.73583	29.11365
	FTP75	SC03	0.9748041	3.6784266	21.37864	3.899275	9.452009
	FTP75	US06	0.3509593	23.666262	734.2655	23.592165	47.57728
	HDUDDS	HWFET	0.9122273	6.783993	64.38115	6.888871	14.283523
K-nearest neighbor	FTP75	HDUDDS	0.944292	6.165199	54.55361	6.34278	14.6457
	FTP75	HWFET	0.998831	0.7013999	0.857278	0.770161	2.579159
	FTP75	LA92	0.774033	13.5274	255.60627	13.798035	29.30851
	FTP75	SC03	0.974361	3.736400	21.75384	3.944995	9.55501
	FTP75	US06	0.348802	23.66719	736.70599	23.630257	48.21114
	HDUDDS	HWFET	0.90758	6.9487	67.7888	7.060678	15.74
ANN	FTP75	HDUDDS	0.9680461	4.206541	31.2918	4.68868	10.51939
	FTP75	HWFET	0.9991923	0.655842	0.59239	0.671977	3.167894
	FTP75	LA92	0.964415	4.18107	40.252	5.41403	22.7257
	FTP75	SC03	0.9925348	2.00708	6.33421	2.122339	8.924430
	FTP75	US06	0.8989102	5.731417	114.3637	7.8901	67.6631
	HDUDDS	HWFET	0.973266	4.11192	19.6090	3.95599	8.738533
CNN	FTP75	HDUDDS	0.9724	4.8353	26.952	4.6266	9.5065
	FTP75	HWFET	0.9986	0.80965	0.96155	0.82544	19.833
	FTP75	LA92	0.91045	6.4213	101.294	8.5106	27.1870
	FTP75	SC03	0.98693	2.67879	11.0837	2.72809	8.33125
	FTP75	US06	0.75188	11.02597	280.6934	13.6859	89.38482
	HDUDDS	HWFET	0.9205194	6.82924	58.2989	6.75236	12.5695
LSTM	FTP75	HDUDDS	0.7253989	0.01123	0.002859	0.03239	0.3777
	FTP75	HWFET	0.7917078	0.0262392	0.002318	0.035580	0.237059
	FTP75	LA92	0.6838248	0.014541	0.0031163	0.034588	0.3867878
	FTP75	SC03	0.672904	0.01269	0.003392	0.035063	0.524022
	FTP75	US06	0.4734503	0.016042	0.00584	0.044111	0.590704
	HDUDDS	HWFET	0.73224	0.025603	0.002849	0.03742	0.337044

reports the values of performance indicators for the entire training dataset and the test datasets built.

6. Conclusions

This work investigates the integration of machine learning approaches with electrochemical and thermal data of the LIB model, together with automotive simulations in the BEV model, for estimating the SOC of batteries. Seven driving cycles of automotive simulations (FTP75, US06, HWFET, HDUDDS, SCO3, WLTP, and LA92) were presented to simulate the fluctuation of the discharge current flowing in the NMC cylindrical cells of the Tesla S. Two different cases were provided to generate the training and test datasets from the thirteen simulated datasets of the Tesla s model for ten different machines and deep learning algorithms. Linear regression, (SVRs), K-NN, RF, EXR, XGB, random forest combined with gradient boosting, ANNs, CNN, and LSTM were trained and tested to predict the SOC using modeling data that accurately reflects the behavior of BEVs in real life. Mostly, when comparing the same algorithm in the first case, the results were better than the second case; this is normal because the model was trained and tested on the same drive cycle while the second case was trained on the drive cycle and tested on another drive cycle. This is one of the reasons that led us to use the second case to accurately evaluate the model. The suggested modeling framework may accommodate several BEVs with distinct battery structures. Future articles will take into account the applications of the diverse chemistry and the challenge of implementing the computation of running complex models for real-time applications.