Review of Bridge Structure Damping Model and Identification Method
Abstract
:1. Introduction
2. Damping Model and Damping Characteristics of Bridge Structure
2.1. Viscous Damping Model
2.1.1. Rayleigh Damping Model
2.1.2. Caughey Damping Model
2.1.3. Wilson–Penzien Damping Model
2.1.4. Clough Damping Model
2.2. Hysteretic Damping Model
2.3. Complex Damping Model
2.4. Coulomb Damping Model
2.5. Convolution Damping Model
- Exponential function
- 2.
- Gaussian function
- 3.
- Double exponential function
2.6. Aerodynamic Damping Model
2.7. Damping Characteristics of Bridge Structure
3. Modal Damping Ratio Identification Method of Bridge Structure
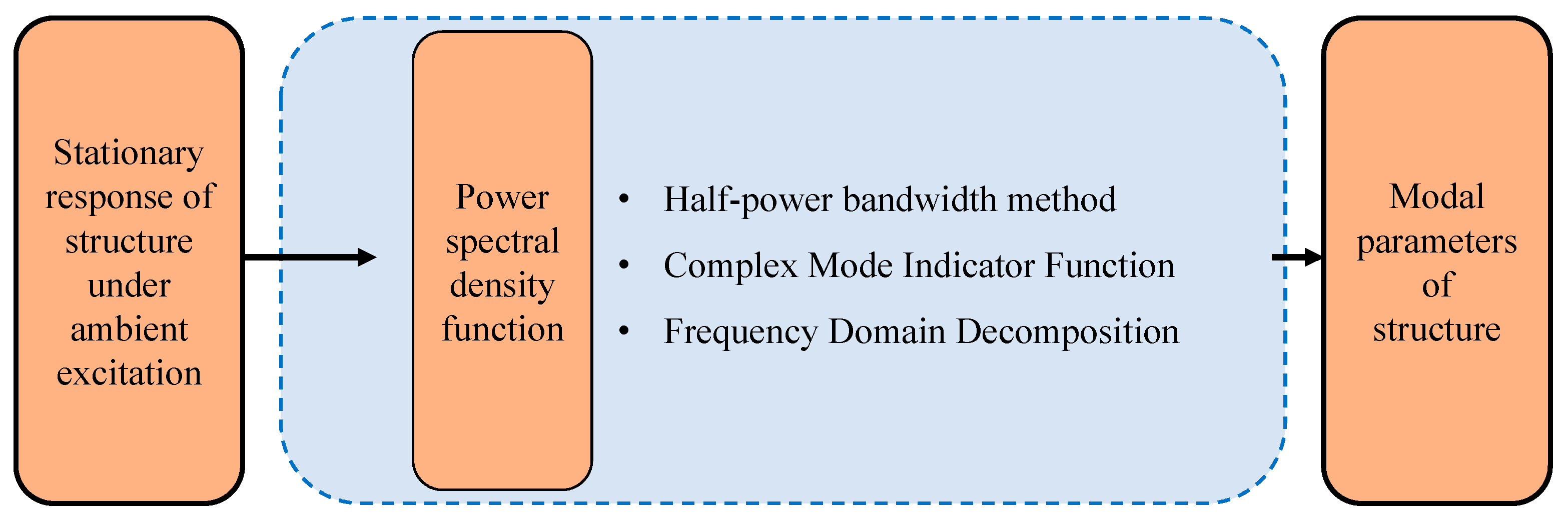
3.1. Modal Damping Ratio Identification of Bridge Structure Based on Response Under Ambient Excitation
3.1.1. Time Domain Identification Method
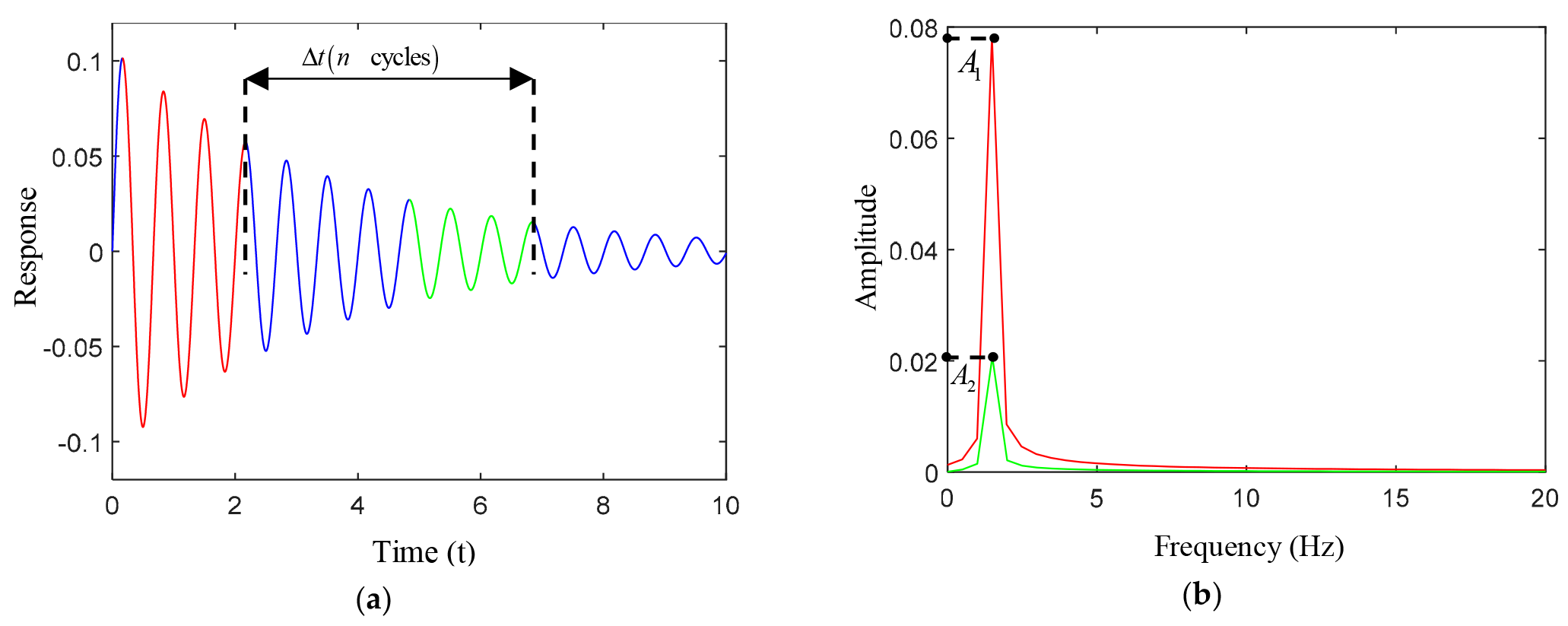
- Logarithmic decrement method
- 2.
- Eigensystem realization algorithm (ERA)
- 3.
- Stochastic subspace identification (SSI)
- 4.
- Ibrahim time domain method (ITD)
- 5.
- ARMA time series model analysis method
- 6.
- Least squares complex exponential (LSCE)
- 7.
- Empirical Mode Decomposition (EMD)
- 8.
- Recursive digital technique (RDT)
3.1.2. Frequency Domain Identification Method
- Half-power bandwidth method
- 2.
- Complex mode indicator function (CMIF)
- 3.
- Frequency domain decomposition (FDD)
3.1.3. Time-Frequency Domain Identification Method
- Wavelet analysis (WA)
- 2.
- Hilbert–Huang transform (HHT)
3.2. Modal Damping Ratio Identification of Bridge Structure Based on Response Under Artificial Excitation
3.2.1. Polynomial Fitting Method
3.2.2. Least Square Complex Frequency Domain (LSCF)
3.3. Abnormal Data Processing and Modal Verification
3.3.1. Abnormal Data Processing
3.3.2. Modal Verification
- Mathematical indication verification method
- (1)
- Modal assurance criterion (MAC)
- (2)
- Mode Phase Collinearity (MPC)
- 2.
- Stabilization Diagram (SD)
4. Summary and Outlook
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Qin, S.; Gao, Z. Developments and Prospects of Long-Span High-Speed Railway Bridge Technologies in China. Engineering 2017, 3, 787–794. [Google Scholar] [CrossRef]
- Zhou, X.; Zhang, X. Thoughts on the Development of Bridge Technology in China. Engineering 2019, 5, 1120–1130. [Google Scholar] [CrossRef]
- Liu, J.P.; Chen, B.C.; Li, C.; Zhang, M.J.; Mou, T.M.; Tabatabai, H. Recent Application of and Research on Concrete Arch Bridges in China. Struct. Eng. Int. 2023, 33, 394–398. [Google Scholar] [CrossRef]
- Liu, J.; Li, X.; Liu, H.; Chen, B. Recent Application and Development of Concrete-Filled Steel Tube Arch Bridges in China. In Advances in Civil Engineering Materials; Nia, E.M., Ling, L., Awang, M., Emamian, S.S., Eds.; Lecture Notes in Civil Engineering; Springer Nature Singapore: Singapore, 2023; Volume 310, pp. 263–272. ISBN 978-981-19802-3-7. [Google Scholar]
- Xie, Y.; Li, X. Influence of the Coupling Effect of Ocean Currents and Waves on the Durability of Pier Structure of Cross-Sea Bridges. J. Coast. Res. 2020, 110, 87–90. [Google Scholar] [CrossRef]
- Zhou, M.; Liao, J.; An, L. Effect of Multiple Environmental Factors on the Adhesion and Diffusion Behaviors of Chlorides in a Bridge with Coastal Exposure: Long-Term Experimental Study. J. Bridge Eng. 2020, 25, 04020081. [Google Scholar] [CrossRef]
- Ma, K.-C.; Yi, T.-H.; Yang, D.-H.; Li, H.-N.; Liu, H. Nonlinear Uncertainty Modeling between Bridge Frequencies and Multiple Environmental Factors Based on Monitoring Data. J. Perform. Constr. Facil. 2021, 35, 04021056. [Google Scholar] [CrossRef]
- Kashani, M.M.; Maddocks, J.; Dizaj, E.A. Residual Capacity of Corroded Reinforced Concrete Bridge Components: State-of-the-Art Review. J. Bridge Eng. 2019, 24, 03119001. [Google Scholar] [CrossRef]
- Yang, X.-M.; Yi, T.-H.; Qu, C.-X.; Li, H.-N. Modal Identification of Bridges Using Asynchronous Responses through an Enhanced Natural Excitation Technique. J. Eng. Mech. 2021, 147, 04021106. [Google Scholar] [CrossRef]
- Konar, T.; Ghosh, A. (Dey) A Review on Various Configurations of the Passive Tuned Liquid Damper. J. Vib. Control. 2023, 29, 1945–1980. [Google Scholar] [CrossRef]
- Papagiannopoulos, G.A. On the Modal Damping Ratios of Mixed Reinforced Concrete—Steel Buildings. Soil Dyn. Earthq. Eng. 2024, 178, 108481. [Google Scholar] [CrossRef]
- Zahid, F.B.; Ong, Z.C.; Khoo, S.Y. A Review of Operational Modal Analysis Techniques for In-Service Modal Identification. J. Braz. Soc. Mech. Sci. Eng. 2020, 42, 398. [Google Scholar] [CrossRef]
- Prashant, S.W.; Chougule, V.N.; Mitra, A.C. Investigation on Modal Parameters of Rectangular Cantilever Beam Using Experimental Modal Analysis. Mater. Today Proc. 2015, 2, 2121–2130. [Google Scholar] [CrossRef]
- Pereira, S.; Magalhães, F.; Gomes, J.P.; Cunha, Á. Modal Tracking under Large Environmental Influence. J Civ. Struct Health Monit 2022, 12, 179–190. [Google Scholar] [CrossRef]
- Qu, C.-X.; Zhang, H.-M.; Yi, T.-H.; Pang, Z.-Y.; Li, H.-N. Anomaly Detection of Massive Bridge Monitoring Data through Multiple Transfer Learning with Adaptively Setting Hyperparameters. Eng. Struct. 2024, 314, 118404. [Google Scholar] [CrossRef]
- Qu, C.-X.; Jiang, J.-Z.; Yi, T.-H.; Li, H.-N. Computer Vision-Based 3D Coordinate Acquisition of Surface Feature Points of Building Structures. Eng. Struct. 2024, 300, 117212. [Google Scholar] [CrossRef]
- JTG/T3360-01-2018; Code for Wind Resistance Design of Highway Bridges. China Communications Press: Beijing, China, 2018.
- JTG/T2231-01-2020; Code for Seismic Design of Highway Bridges. China Communications Press: Beijing, China, 2020.
- Wang, S.; He, J.; Fan, J.; Sun, P.; Wang, D. A Time-Domain Method for Free Vibration Responses of an Equivalent Viscous Damped System Based on a Complex Damping Model. J. Low Freq. Noise Vib. Act. Control 2023, 42, 1531–1540. [Google Scholar] [CrossRef]
- Šána, V. Different Approaches to Modeling of Proportional Damping. AMM 2015, 769, 166–171. [Google Scholar] [CrossRef]
- Wilson, E.L.; Penzien, J. Evaluation of Orthogonal Damping Matrices. Int. J. Numer. MethodsEng. 1972, 4, 5–10. [Google Scholar] [CrossRef]
- Yang, F.; Zhi, X.; Fan, F. Effect of Complex Damping on Seismic Responses of a Reticulated Dome and Shaking Table Test Validation. Thin-Walled Struct. 2019, 134, 407–418. [Google Scholar] [CrossRef]
- Fay, T.H. Coulomb Damping. Int. J. Math. Educ. Sci. Technol. 2012, 43, 923–936. [Google Scholar] [CrossRef]
- Biot, M.A. Variational Principles in Irreversible Thermodynamics with Application to Viscoelasticity. Phys. Rev. 1955, 97, 1463–1469. [Google Scholar] [CrossRef]
- Puthanpurayil, A.M.; Carr, A.J.; Dhakal, R.P. A Generic Time Domain Implementation Scheme for Non-Classical Convolution Damping Models. Eng. Struct. 2014, 71, 88–98. [Google Scholar] [CrossRef]
- Su, L.; Mei, S.-Q.; Pan, Y.-H.; Wang, Y.-F. Experimental Identification of Exponential Damping for Reinforced Concrete Cantilever Beams. Eng. Struct. 2019, 186, 161–169. [Google Scholar] [CrossRef]
- Quan, Y.; Gu, M.; Tamura, Y. Experimental Evaluation of Aerodynamic Damping of Square Super High-Rise Buildings. Wind Struct. 2005, 8, 309–324. [Google Scholar] [CrossRef]
- Wu, Y.; Chen, X. Identification of Nonlinear Aerodynamic Damping from Stochastic Crosswind Response of Tall Buildings Using Unscented Kalman Filter Technique. Eng. Struct. 2020, 220, 110791. [Google Scholar] [CrossRef]
- Su, C.; Han, D.J.; Yan, Q.S.; Au, F.T.K.; Tham, L.G.; Lee, P.K.K.; Lam, K.M.; Wong, K.Y. Wind-Induced Vibration Analysis of the Hong Kong Ting Kau Bridge. Proc. Inst. Civ. Eng. Struct. Build. 2003, 156, 263–272. [Google Scholar] [CrossRef]
- Jiang, Z.; Kim, S.J.; Plude, S.; Christenson, R. Real-Time Hybrid Simulation of a Complex Bridge Model with MR Dampers Using the Convolution Integral Method. Smart Mater. Struct. 2013, 22, 105008. [Google Scholar] [CrossRef]
- Asadollahi, P.; Li, J. Statistical Analysis of Modal Properties of a Cable-Stayed Bridge through Long-Term Wireless Structural Health Monitoring. J. Bridge Eng. 2017, 22, 04017051. [Google Scholar] [CrossRef]
- Kim, S.; Kim, S.; Kim, H.-K. High-Mode Vortex-Induced Vibration of Stay Cables: Monitoring, Cause Investigation, and Mitigation. J. Sound Vib. 2022, 524, 116758. [Google Scholar] [CrossRef]
- Ni, Y.-C.; Zhang, Q.-W.; Liu, J.-F. Dynamic Property Evaluation of a Long-Span Cable-Stayed Bridge (Sutong Bridge) by a Bayesian Method. Int. J. Struct. Stab. Dyn. 2019, 19, 1940010. [Google Scholar] [CrossRef]
- Chu, X.; Cui, W.; Xu, S.; Zhao, L.; Guan, H.; Ge, Y. Multiscale Time Series Decomposition for Structural Dynamic Properties: Long-Term Trend and Ambient Interference. Struct. Control Health Monit. 2023, 2023, 1–18. [Google Scholar] [CrossRef]
- Hwang, D.; Kim, S.; Kim, H.-K. Long-Term Damping Characteristics of Twin Cable-Stayed Bridge under Environmental and Operational Variations. J. Bridge Eng. 2021, 26, 04021062. [Google Scholar] [CrossRef]
- Dan, D.; Yu, X.; Han, F.; Xu, B. Research on Dynamic Behavior and Traffic Management Decision-Making of Suspension Bridge after Vortex-Induced Vibration Event. Struct. Health Monit. 2022, 21, 872–886. [Google Scholar] [CrossRef]
- Sun, L.; Shang, Z.; Xia, Y.; Bhowmick, S.; Nagarajaiah, S. Review of Bridge Structural Health Monitoring Aided by Big Data and Artificial Intelligence: From Condition Assessment to Damage Detection. J. Struct. Eng. 2020, 146, 04020073. [Google Scholar] [CrossRef]
- Li, H.; Ou, J. The State of the Art in Structural Health Monitoring of Cable-Stayed Bridges. J. Civ. Struct. Health Monit. 2016, 6, 43–67. [Google Scholar] [CrossRef]
- Rao, H.; Zhao, H.; Li, S.; Li, M.Z. Design and Implementation of Bridge Structural Health Monitoring System. AMR 2012, 442, 346–350. [Google Scholar] [CrossRef]
- Desjardins, S.; Lau, D. Advances in Intelligent Long-Term Vibration-Based Structural Health-Monitoring Systems for Bridges. Adv. Struct. Eng. 2022, 25, 1413–1430. [Google Scholar] [CrossRef]
- He, Z.; Li, W.; Salehi, H.; Zhang, H.; Zhou, H.; Jiao, P. Integrated Structural Health Monitoring in Bridge Engineering. Autom. Constr. 2022, 136, 104168. [Google Scholar] [CrossRef]
- Cooper, J.E. Extending the Logarithmic Decrement Method to Analyse Two Degree of Freedom Transient Responses. Mech. Syst. Signal Process. 1996, 10, 497–500. [Google Scholar] [CrossRef]
- Shang, Z.; Xia, Y.; Chen, L.; Sun, L. Damping Ratio Identification Using Attenuation Responses Extracted by Time Series Semantic Segmentation. Mech. Syst. Signal Process. 2022, 180, 109287. [Google Scholar] [CrossRef]
- Magalhães, F.; Cunha, Á.; Caetano, E.; Brincker, R. Damping Estimation Using Free Decays and Ambient Vibration Tests. Mech. Syst. Signal Process. 2010, 24, 1274–1290. [Google Scholar] [CrossRef]
- Lamarque, C.-H.; Pernot, S.; Cuer, A. Damping Identification in Multi-Degree-of-Freedom Systems via a Wavelet-Logarithmic Decrement—Part 1: Theory. J. Sound Vib. 2000, 235, 361–374. [Google Scholar] [CrossRef]
- López-Aragón, J.A.; Puchol, V.; Astiz, M.A. Influence of the Modal Damping Ratio Calculation Method in the Analysis of Dynamic Events Obtained in Structural Health Monitoring of Bridges. J Civ. Struct. Health Monit. 2024, 14, 1191–1213. [Google Scholar] [CrossRef]
- Siringoringo, D.M.; Fujino, Y. System Identification of Suspension Bridge from Ambient Vibration Response. Eng. Struct. 2008, 30, 462–477. [Google Scholar] [CrossRef]
- Zhang, G.; Ma, J.; Chen, Z.; Wang, R. Automated Eigensystem Realisation Algorithm for Operational Modal Analysis. J. Sound Vib. 2014, 333, 3550–3563. [Google Scholar] [CrossRef]
- Shen, R.; Qian, X.; Zhou, J.; Lee, C.-L. An Eigensystem Realization Algorithm for Identification of Modal Parameters of Nonviscous Damping Structure System. Int. J. Struct. Stab. Dyn. 2024, 24, 2450052. [Google Scholar] [CrossRef]
- He, X.; Moaveni, B.; Conte, J.P.; Elgamal, A.; Masri, S.F. System Identification of Alfred Zampa Memorial Bridge Using Dynamic Field Test Data. J. Struct. Eng. 2009, 135, 54–66. [Google Scholar] [CrossRef]
- Qu, C.; Yi, T.; Li, H. Mode Identification by Eigensystem Realization Algorithm through Virtual Frequency Response Function. Struct. Control Health Monit. 2019, 26, e2429. [Google Scholar] [CrossRef]
- Ozcelik, O.; Yormaz, D.; Amaddeo, C.; Girgin, O.; Kahraman, S. System Identification of a Six-Span Steel Railway Bridge Using Ambient Vibration Measurements at Different Temperature Conditions. J. Perform. Constr. Facil. 2019, 33, 04019001. [Google Scholar] [CrossRef]
- Lorenzoni, F.; De Conto, N.; Da Porto, F.; Modena, C. Ambient and Free-Vibration Tests to Improve the Quantification and Estimation of Modal Parameters in Existing Bridges. J. Civ. Struct. Health Monit. 2019, 9, 617–637. [Google Scholar] [CrossRef]
- Zabel, V.; Gössinger, J. Modal Analysis and Numerical Models of a Typical Railway Bridge. In Dynamics of Civil Structures, Volume 4; Catbas, F.N., Ed.; Conference Proceedings of the Society for Experimental Mechanics Series; Springer International Publishing: Cham, Switzerland, 2014; pp. 351–358. ISBN 978-3-319-04545-0. [Google Scholar]
- Xin, J.; Sheng, J.; Sui, W. Study on the Reason for Difference of Data-Driven and Covariance-Driven Stochastic Subspace Identification Method. In Proceedings of the 2012 International Conference on Computer Science and Electronics Engineering, Hangzhou, China, 23–25 March 2012; pp. 356–360. [Google Scholar]
- Brincker, R.; Olsen, P.; Amador, S.; Juul, M.; Malekjafarian, A.; Ashory, M. Modal Participation in Multiple Input Ibrahim Time Domain Identification. Math. Mech. Solids 2019, 24, 168–180. [Google Scholar] [CrossRef]
- Tian, G.; Zhang, Y.; Fan, H.-B.; Wu, D.-H. A New Modal Parameter Identification Method Based on Velocity Response Signals. In Proceedings of the Design, Manufacturing and Mechatronics, Wuhan, China, 17–18 April 2015; pp. 699–705. [Google Scholar]
- Anuar, M.A.; Roslan, L.; Mat Isa, A.A. Dynamic Parameter Identification Using Ambient Response Analysis and Ibrahim Time Domain Approach: A Case Study on a Steel Plate Structure. AMM 2011, 110–116, 2395–2399. [Google Scholar] [CrossRef]
- Cárdenas, E.M.; Castillo-Zúñiga, D.F.; Medina, L.U.; Góes, L.C.S. In-Flight Modal Identification by Operational Modal Analysis. J. Braz. Soc. Mech. Sci. Eng. 2023, 45, 278. [Google Scholar] [CrossRef]
- Pi, Y.L.; Mickleborough, N.C. Modal Identification of Vibrating Structures Using ARMA Model. J. Eng. Mech. 1989, 115, 2232–2250. [Google Scholar] [CrossRef]
- Pei, Q.; Li, L. Structural Modal Parameter Identification Based on ARMA Model. AMM 2013, 477–478, 736–739. [Google Scholar] [CrossRef]
- Chen, W.; Yao, J.; Liu, Y.; Zhou, L.; Mou, Y.; Liu, J.; Zhao, X. A Novel Method for Modal Parameters Estimate Based on RDT—ARMA with Measured Acceleration. In Proceedings of the 2018 5th International Conference on Information Science and Control Engineering (ICISCE), Zhengzhou, China, 20–22 July 2018; pp. 1040–1044. [Google Scholar]
- Chen, D.D.; Wu, L.; Xiang, J.W. The Comparison Investigation of OMA Methods on Time Domain. AMR 2011, 422, 443–447. [Google Scholar] [CrossRef]
- Argentini, T.; Belloli, M.; Rosa, L.; Sabbioni, E.; Villani, M. Modal Identification of Stays and Deck of a Cable-Stayed Bridge. In Proceedings of the International Conference on Noise and Vibration Engineering (ISMA2012), Leuven, Belgium, 17–19 September 2012; Volume 2, pp. 1031–1044. [Google Scholar]
- Huang, N.E.; Shen, Z.; Long, S.R.; Wu, M.C.; Shih, H.H.; Zheng, Q.; Yen, N.-C.; Tung, C.C.; Liu, H.H. The Empirical Mode Decomposition and the Hilbert Spectrum for Nonlinear and Non-Stationary Time Series Analysis. Proc. R. Soc. Lond. A 1998, 454, 903–995. [Google Scholar] [CrossRef]
- Bekara, M.; Van Der Baan, M. Random and Coherent Noise Attenuation by Empirical Mode Decomposition. Geophysics 2009, 74, V89–V98. [Google Scholar] [CrossRef]
- Yeh, J.-R.; Shieh, J.-S.; Huang, N.E. Complementary Ensemble Empirical Mode Decomposition: A Novel Noise Enhanced Data Analysis Method. Adv. Adapt. Data Anal. 2010, 2, 135–156. [Google Scholar] [CrossRef]
- Wang, T.; Zhang, M.; Yu, Q.; Zhang, H. Comparing the Applications of EMD and EEMD on Time–Frequency Analysis of Seismic Signal. J. Appl. Geophys. 2012, 83, 29–34. [Google Scholar] [CrossRef]
- Torres, M.E.; Colominas, M.A.; Schlotthauer, G.; Flandrin, P. A Complete Ensemble Empirical Mode Decomposition with Adaptive Noise. In Proceedings of the 2011 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Prague, Czech Republic, 22–27 May 2011; pp. 4144–4147. [Google Scholar]
- Feng, Z.; Shen, W.; Chen, Z. Consistent Multilevel RDT-ERA for Output-Only Ambient Modal Identification of Structures. Int. J. Str. Stab. Dyn. 2017, 17, 1750106. [Google Scholar] [CrossRef]
- Feng, Z.Q.; Zhao, B.; Hua, X.G.; Chen, Z.Q. Enhanced EMD-RDT Method for Output-Only Ambient Modal Identification of Structures. J. Aerosp. Eng. 2019, 32, 04019046. [Google Scholar] [CrossRef]
- He, X.H.; Hua, X.G.; Chen, Z.Q.; Huang, F.L. EMD-Based Random Decrement Technique for Modal Parameter Identification of an Existing Railway Bridge. Eng. Struct. 2011, 33, 1348–1356. [Google Scholar] [CrossRef]
- Wang, I. An Analysis of Higher Order Effects in the Half Power Method for Calculating Damping. J. Appl. Mech. 2011, 78, 014501. [Google Scholar] [CrossRef]
- Wang, J.-T.; Jin, F.; Zhang, C.-H. Estimation Error of the Half-Power Bandwidth Method in Identifying Damping for Multi-DOF Systems. Soil Dyn. Earthq. Eng. 2012, 39, 138–142. [Google Scholar] [CrossRef]
- Magalhães, F.; Caetano, E.; Cunha, Á. Challenges in the Application of Stochastic Modal Identification Methods to a Cable-Stayed Bridge. J. Bridge Eng. 2007, 12, 746–754. [Google Scholar] [CrossRef]
- Brownjohn, J.; Dumanoglu, A.; Severn, R.; Taylor, C. Ambient Vibration Measurements of the Humber Suspension Bridge and Com Parison with Calculated Characteristics. Proc. Inst. Civ. Eng. 1987, 83, 561–600. [Google Scholar] [CrossRef]
- Wu, B. A Correction of the Half-Power Bandwidth Method for Estimating Damping. Arch. Appl. Mech. 2015, 85, 315–320. [Google Scholar] [CrossRef]
- Papagiannopoulos, G.A.; Hatzigeorgiou, G.D. On the Use of the Half-Power Bandwidth Method to Estimate Damping in Building Structures. Soil Dyn. Earthq. Eng. 2011, 31, 1075–1079. [Google Scholar] [CrossRef]
- Olmos, B.A.; Roesset, J.M. Evaluation of the Half-power Bandwidth Method to Estimate Damping in Systems without Real Modes. Earthq. Eng. Struct. Dyn. 2010, 39, 1671–1686. [Google Scholar] [CrossRef]
- Shih, C.Y.; Tsuei, Y.G.; Allemang, R.J.; Brown, D.L. Complex Mode Indication Function and Its Applications to Spatial Domain Parameter Estimation. Mech. Syst. Signal Process. 1988, 2, 367–377. [Google Scholar] [CrossRef]
- Catbas, F.N.; Brown, D.L.; Aktan, A.E. Parameter Estimation for Multiple-Input Multiple-Output Modal Analysis of Large Structures. J. Eng. Mech. 2004, 130, 921–930. [Google Scholar] [CrossRef]
- Tian, Y.; Zhang, J.; Xia, Q.; Li, P. Flexibility Identification and Deflection Prediction of a Three-Span Concrete Box Girder Bridge Using Impacting Test Data. Eng. Struct. 2017, 146, 158–169. [Google Scholar] [CrossRef]
- Gul, M.; Catbas, F.N. Ambient Vibration Data Analysis for Structural Identification and Global Condition Assessment. J. Eng. Mech. 2008, 134, 650–662. [Google Scholar] [CrossRef]
- Lin, C.-S. System Identification of Structures with Severe Closely Spaced Modes Using Parametric Estimation Algorithms Based on Complex Mode Indicator Function with Singular Value Decomposition. KSCE J. Civ. Eng. 2020, 24, 2716–2730. [Google Scholar] [CrossRef]
- Bakir, P.G.; Eksioglu, E.M.; Alkan, S. Reliability Analysis of the Complex Mode Indicator Function and Hilbert Transform Techniques for Operational Modal Analysis. Expert Syst. Appl. 2012, 39, 13289–13294. [Google Scholar] [CrossRef]
- Shi, W.; Shan, J.; Lu, X. Modal Identification of Shanghai World Financial Center Both from Free and Ambient Vibration Response. Eng. Struct. 2012, 36, 14–26. [Google Scholar] [CrossRef]
- Brincker, R.; Zhang, L.; Andersen, P. Modal Identification of Output-Only Systems Using Frequency Domain Decomposition. Smart Mater. Struct. 2001, 10, 441–445. [Google Scholar] [CrossRef]
- Ghalishooyan, M.; Shooshtari, A.; Abdelghani, M. Output-Only Modal Identification by in-Operation Modal Appropriation for Use with Enhanced Frequency Domain Decomposition Method. J. Mech. Sci. Technol. 2019, 33, 3055–3067. [Google Scholar] [CrossRef]
- Qu, C.-X.; Liu, Y.-F.; Yi, T.-H.; Li, H.-N. Structural Damping Ratio Identification through Iterative Frequency Domain Decomposition. J. Struct. Eng. 2023, 149, 04023042. [Google Scholar] [CrossRef]
- Brincker, R.; Zhang, L.; Andersen, P. Modal Identification from Ambient Responses Using Frequency Domain Decomposition. In Proceedings of the IMAC 18: Proceedings of the International Modal Analysis Conference (IMAC), San Antonio, TX, USA, 7–10 February 2000; pp. 625–630. [Google Scholar]
- Hasan, M.D.A.; Ahmad, Z.A.B.; Salman Leong, M.; Hee, L.M. Enhanced Frequency Domain Decomposition Algorithm: A Review of a Recent Development for Unbiased Damping Ratio Estimates. J. Vibroengineering 2018, 20, 1919–1936. [Google Scholar] [CrossRef]
- Qu, C.-X.; Liu, Y.-F.; Yi, T.-H.; Li, H.-N. Structural Damping Ratio Identification with Iterative Compensation for Spectral Leakage Errors Using Frequency Domain Decomposition. Eng. Struct. 2024, 321, 119027. [Google Scholar] [CrossRef]
- Morlet, J. Sampling Theory and Wave Propagation. In Issues in Acoustic Signal—Image Processing and Recognition; Chen, C.H., Ed.; Springer: Berlin/Heidelberg, Germany, 1983; pp. 233–261. ISBN 978-3-642-82004-5. [Google Scholar]
- Kijewski, T.; Kareem, A. Wavelet Transforms for System Identification in Civil Engineering. Comput. Aided Civ. Eng 2003, 18, 339–355. [Google Scholar] [CrossRef]
- Lardies, J.; Ta, M.N.; Berthillier, M. Modal Parameter Estimation Based on the Wavelet Transform of Output Data. Arch. Appl. Mech. 2004, 73, 718–733. [Google Scholar] [CrossRef]
- Gilles, J. Empirical Wavelet Transform. IEEE Trans. Signal Process. 2013, 61, 3999–4010. [Google Scholar] [CrossRef]
- Yan, B.; Miyamoto, A. A Comparative Study of Modal Parameter Identification Based on Wavelet and Hilbert-Huang Transforms. Comp-Aided Civ. Eng 2006, 21, 9–23. [Google Scholar] [CrossRef]
- Levy, E.C. Complex-Curve Fitting. IRE Trans. Automat. Contr. 1959, AC-4, 37–43. [Google Scholar] [CrossRef]
- Richardson, M.H.; Formenti, D.L. Parameter Estimation from Frequency Response Measurements Using Rational Fraction Polynomials. In Proceedings of the 1st International Modal Analysis Conference, Orlando, FLL, USA, 8–10 November 1982. [Google Scholar]
- Forsythe, G.E. Generation and Use of Orthogonal Polynomials for Data-Fitting with a Digital Computer. J. Soc. Ind. Appl. Math. 1957, 5, 74–88. [Google Scholar] [CrossRef]
- Arruda, J.R.F. Objective Functions for the Nonlinear Curve Fit of Frequency Response Functions. AIAA J. 1992, 30, 855–857. [Google Scholar] [CrossRef]
- Duan, Y.; Zhu, L.; Xiang, Y. Damping Identification Using Weighted Fitting of Frequency-Response-Function (WFF) Method. In Proceedings of the 2011 International Conference on Multimedia Technology, Hangzhou, China, 26–28 July 2011; pp. 5349–5352. [Google Scholar]
- Peeters, B.; Van Der Auweraer, H.; Guillaume, P.; Leuridan, J. The PolyMAX Frequency-Domain Method: A New Standard for Modal Parameter Estimation? Shock Vib. 2004, 11, 395–409. [Google Scholar] [CrossRef]
- Brownjohn, J.M.W.; Magalhaes, F.; Caetano, E.; Cunha, A. Ambient Vibration Re-Testing and Operational Modal Analysis of the Humber Bridge. Eng. Struct. 2010, 32, 2003–2018. [Google Scholar] [CrossRef]
- Verboven, P.; Guillaume, P.; Cauberghe, B.; Parloo, E.; Vanlanduit, S. Frequency-Domain Generalized Total Least-Squares Identification for Modal Analysis. J. Sound Vib. 2004, 278, 21–38. [Google Scholar] [CrossRef]
- Hızal, Ç. Frequency Domain Data Merging in Operational Modal Analysis Based on Least Squares Approach. Measurement 2021, 170, 108742. [Google Scholar] [CrossRef]
- Zhukov, A.O. Recursive Identification of Discrete Dynamical Systems with Single Input and Single Output. J. Automat Inf. Sci. 2009, 41, 44–57. [Google Scholar] [CrossRef]
- Peres, M.; Kallmeyer, C.; Witter, M.; Carneiro, R.; Marques, F.; de Oliveira, L. Advantages of Multiple-Input Multiple-Output Testing. Sound Vib. 2015, 49, 8–12. [Google Scholar]
- Entezami, A.; Sarmadi, H.; Behkamal, B.; De Michele, C. On Continuous Health Monitoring of Bridges under Serious Environmental Variability by an Innovative Multi-Task Unsupervised Learning Method. Struct. Infrastruct. Eng. 2024, 20, 1975–1993. [Google Scholar] [CrossRef]
- Lee, J.S.; Min Kim, H.; Il Kim, S.; Min Lee, H. Evaluation of Structural Integrity of Railway Bridge Using Acceleration Data and Semi-Supervised Learning Approach. Eng. Struct. 2021, 239, 112330. [Google Scholar] [CrossRef]
- Kim, S.-Y.; Mukhiddinov, M. Data Anomaly Detection for Structural Health Monitoring Based on a Convolutional Neural Network. Sensors 2023, 23, 8525. [Google Scholar] [CrossRef]
- Zhang, X.; Zhou, W. Structural Vibration Data Anomaly Detection Based on Multiple Feature Information Using CNN-LSTM Model. Struct. Control. Health Monit. 2023, 2023, 1–19. [Google Scholar] [CrossRef]
- Jana, D.; Patil, J.; Herkal, S.; Nagarajaiah, S.; Duenas-Osorio, L. CNN and Convolutional Autoencoder (CAE) Based Real-Time Sensor Fault Detection, Localization, and Correction. Mech. Syst. Signal Process. 2022, 169, 108723. [Google Scholar] [CrossRef]
- Greś, S.; Döhler, M.; Mevel, L. Uncertainty Quantification of the Modal Assurance Criterion in Operational Modal Analysis. Mech. Syst. Signal Process. 2021, 152, 107457. [Google Scholar] [CrossRef]
- Greś, S.; Döhler, M.; Andersen, P.; Mevel, L. Uncertainty Quantification for the Modal Phase Collinearity of Complex Mode Shapes. Mech. Syst. Signal Process. 2021, 152, 107436. [Google Scholar] [CrossRef]







Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Qu, C.; Tu, G.; Gao, F.; Sun, L.; Pan, S.; Chen, D. Review of Bridge Structure Damping Model and Identification Method. Sustainability 2024, 16, 9410. https://doi.org/10.3390/su16219410
Qu C, Tu G, Gao F, Sun L, Pan S, Chen D. Review of Bridge Structure Damping Model and Identification Method. Sustainability. 2024; 16(21):9410. https://doi.org/10.3390/su16219410
Chicago/Turabian StyleQu, Chunxu, Guikai Tu, Fuzhong Gao, Li Sun, Shengshan Pan, and Dongsheng Chen. 2024. "Review of Bridge Structure Damping Model and Identification Method" Sustainability 16, no. 21: 9410. https://doi.org/10.3390/su16219410
APA StyleQu, C., Tu, G., Gao, F., Sun, L., Pan, S., & Chen, D. (2024). Review of Bridge Structure Damping Model and Identification Method. Sustainability, 16(21), 9410. https://doi.org/10.3390/su16219410





