Intermittent Drip Irrigation Soil Wet Front Prediction Model and Effective Water Storage Analysis
Abstract
1. Introduction
2. Materials and Methods
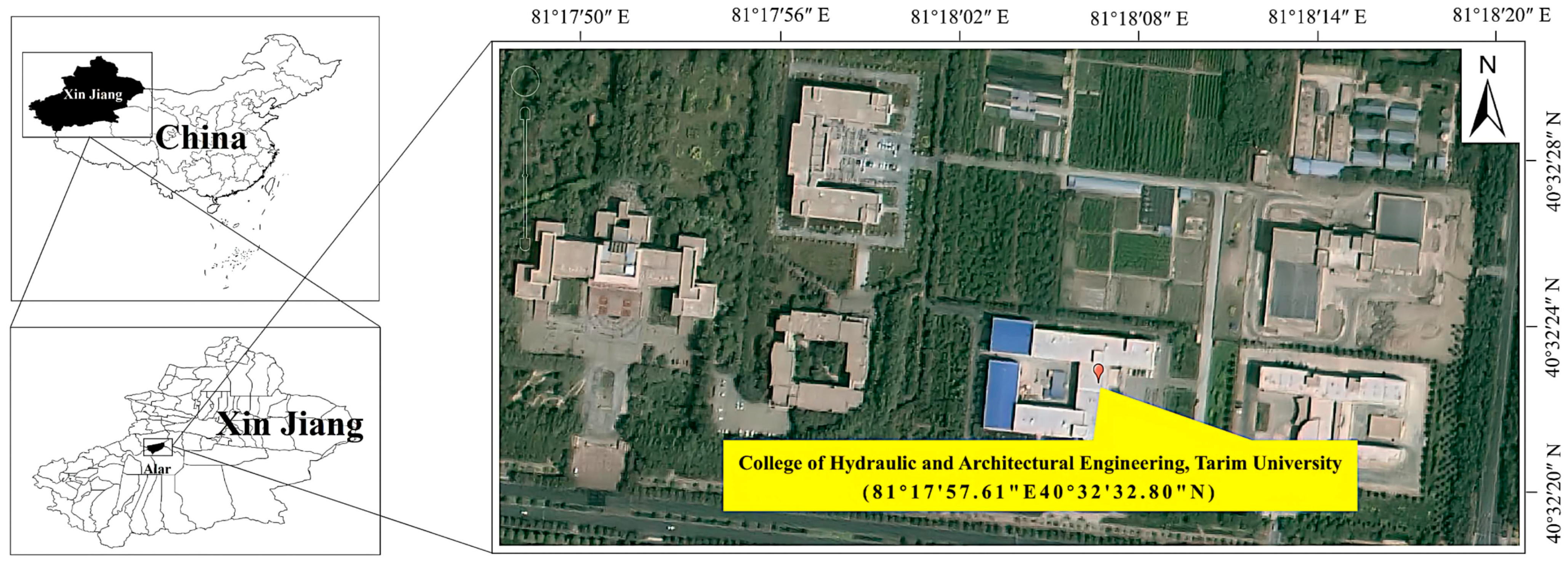
2.1. Study Area
2.2. Soil Characteristics
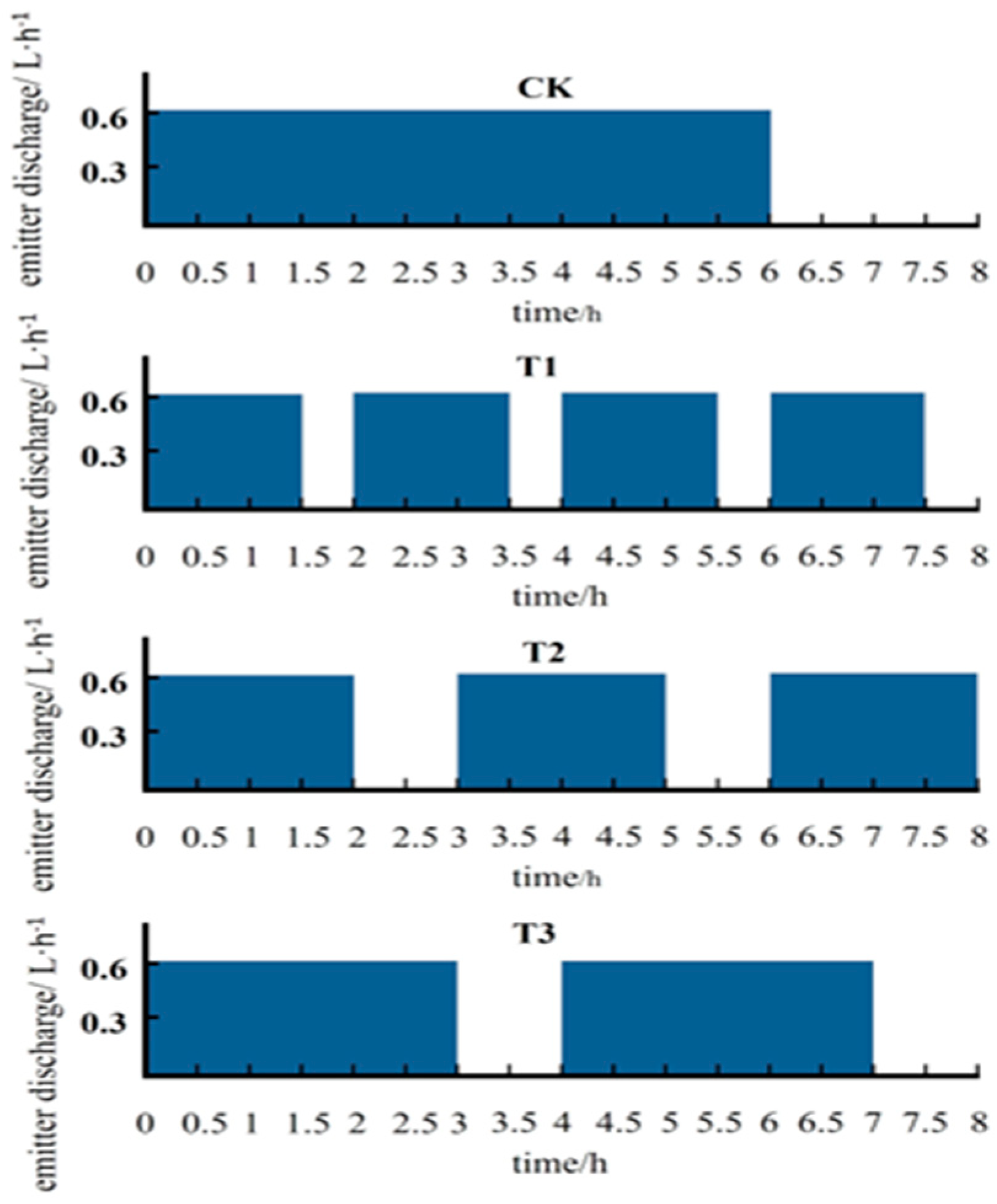
2.3. Experimental Design
2.4. Measurements and Methods
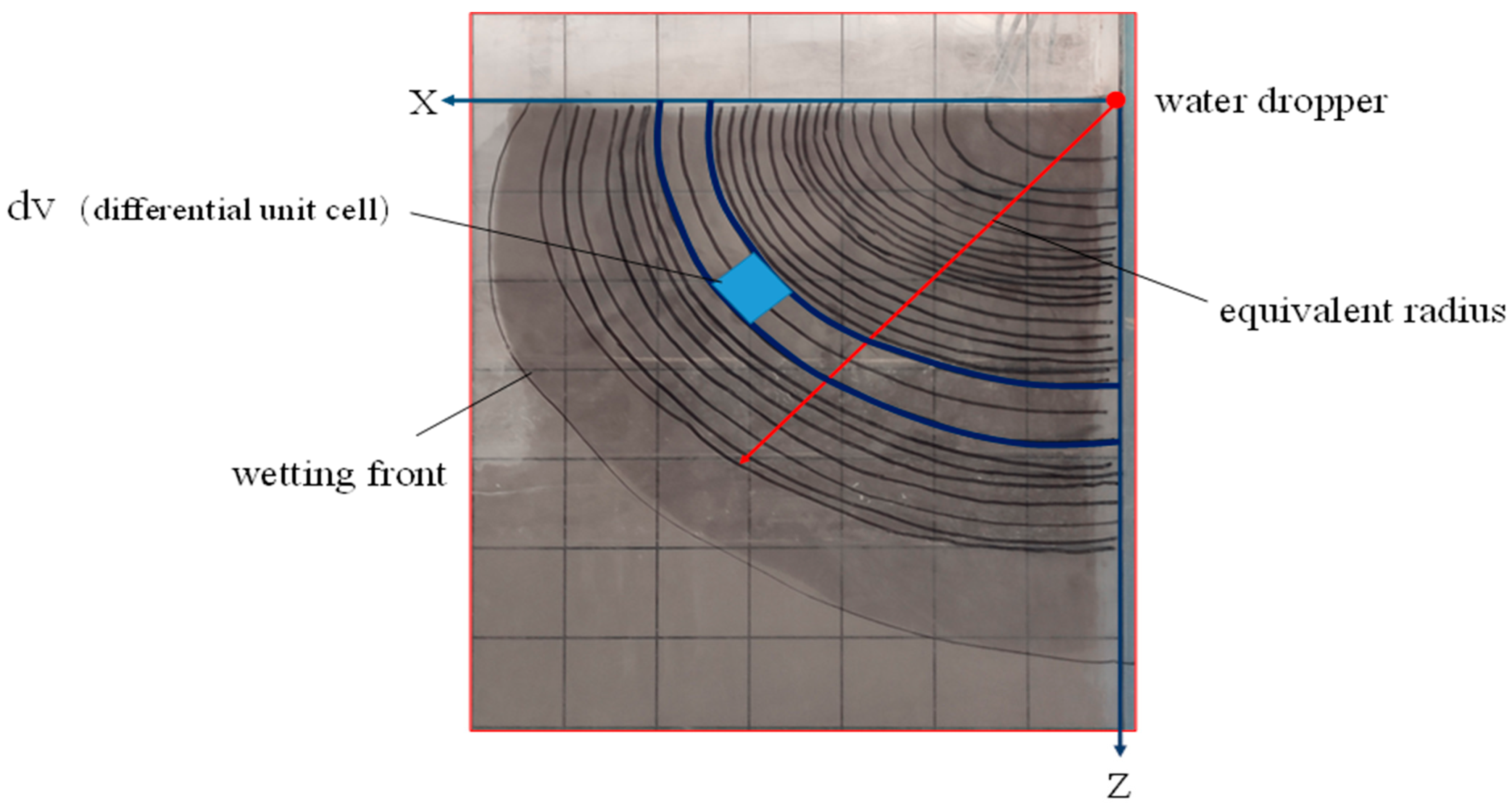
2.4.1. Soil Moisture Front
2.4.2. Soil Moisture
2.4.3. Soil-Saturated Hydraulic Conductivity
2.4.4. Validation of Estimation Model
2.5. Data Processing
3. Results
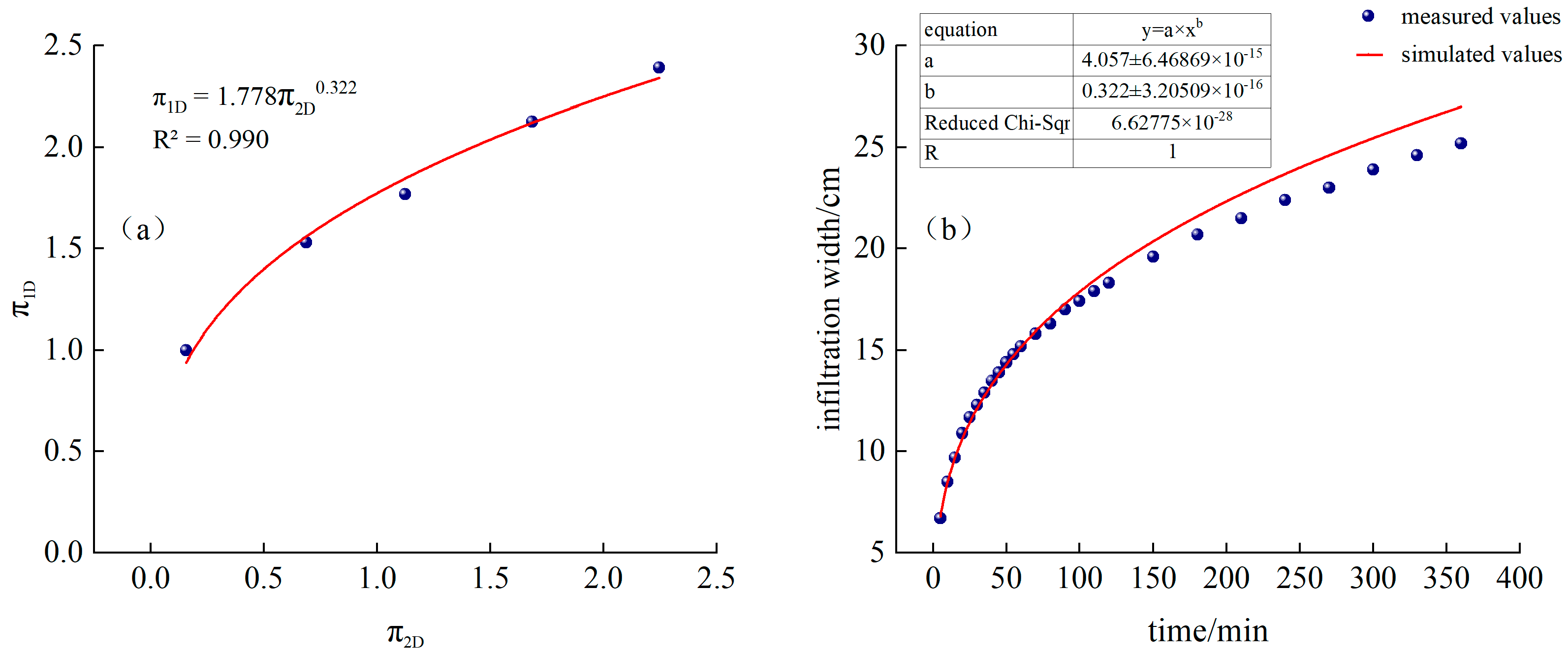
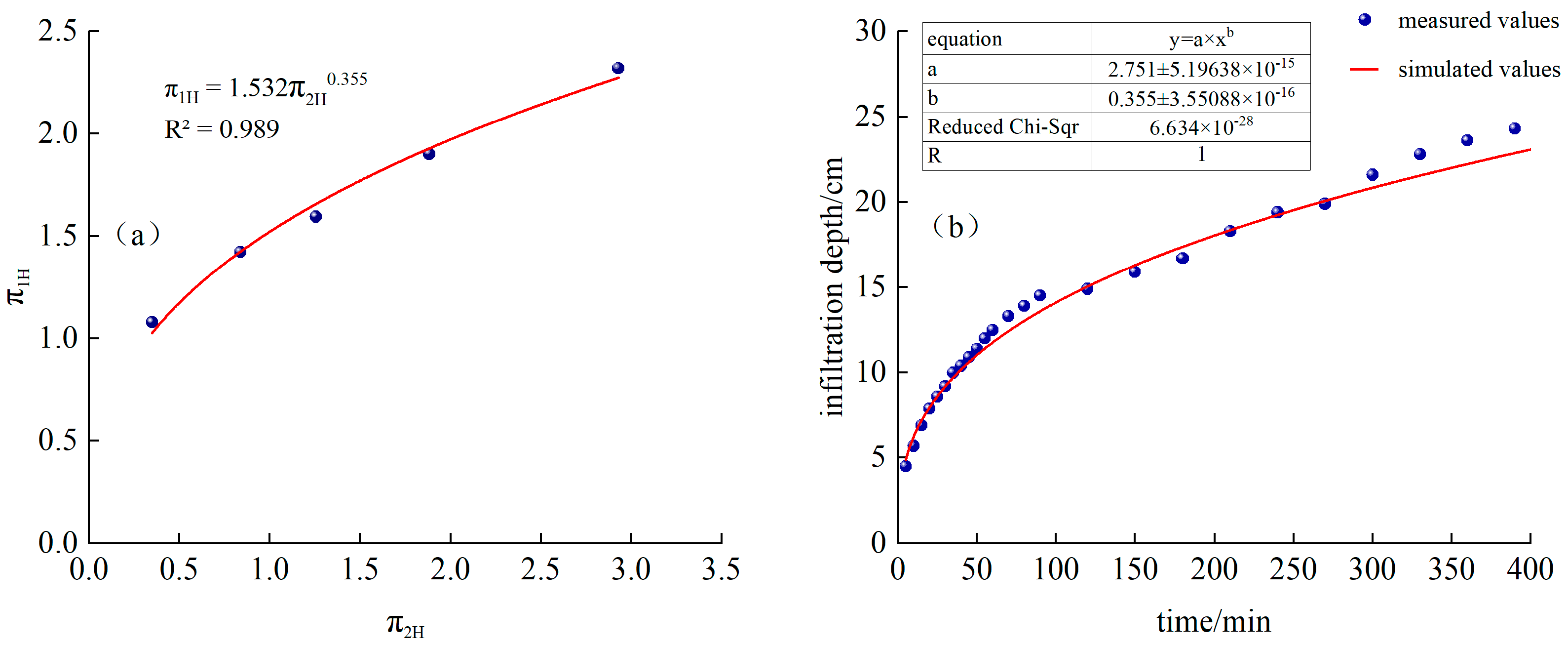
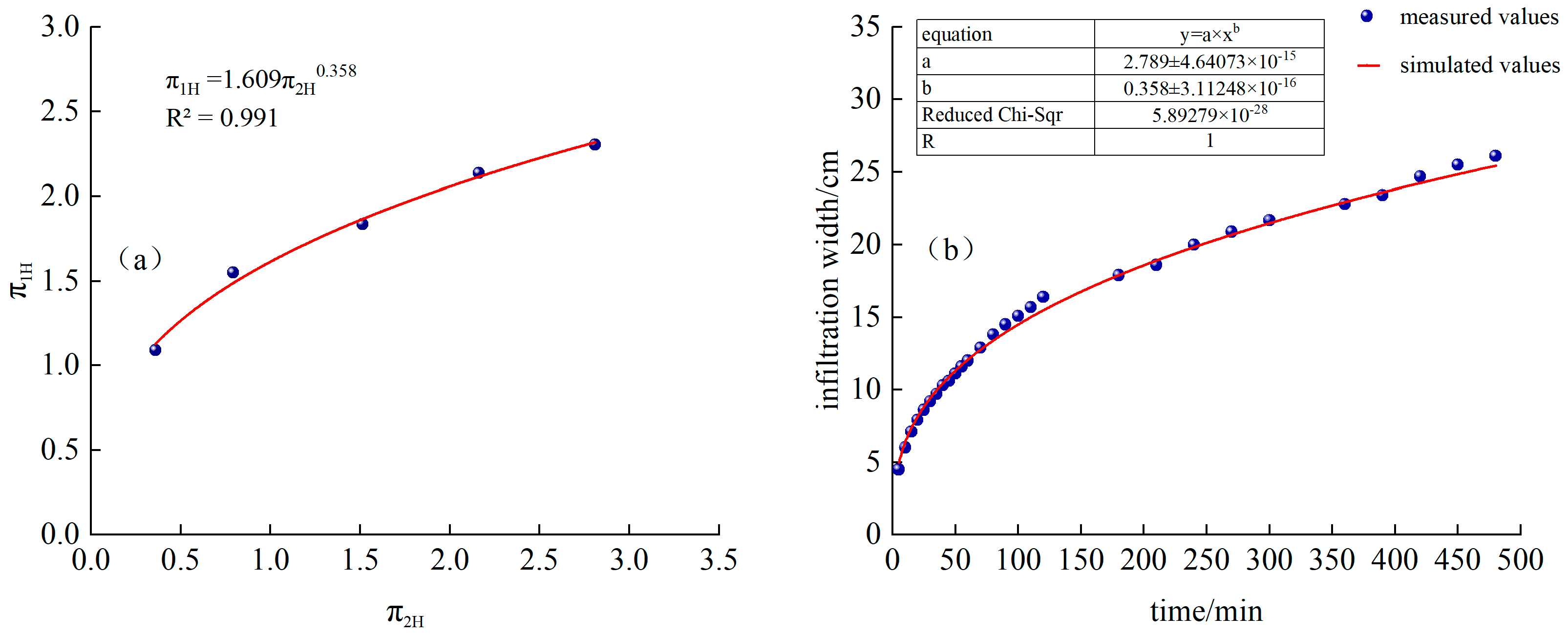
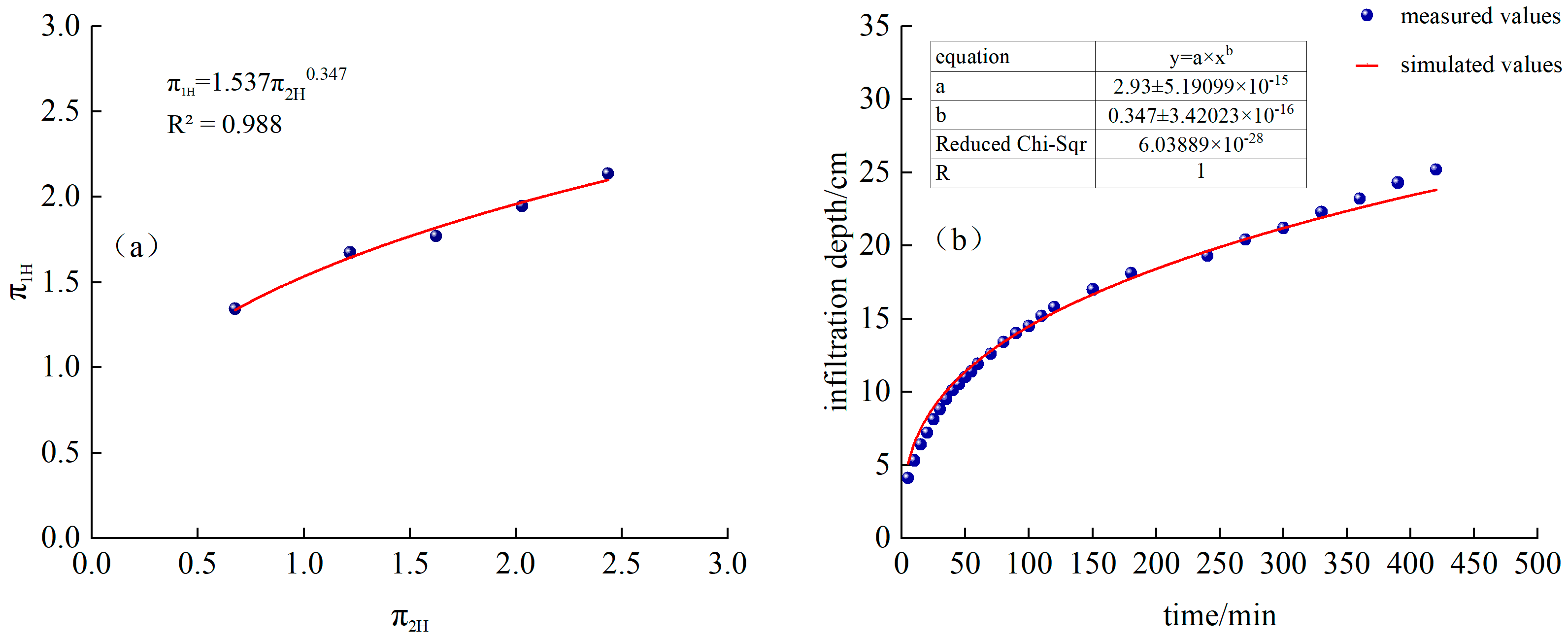
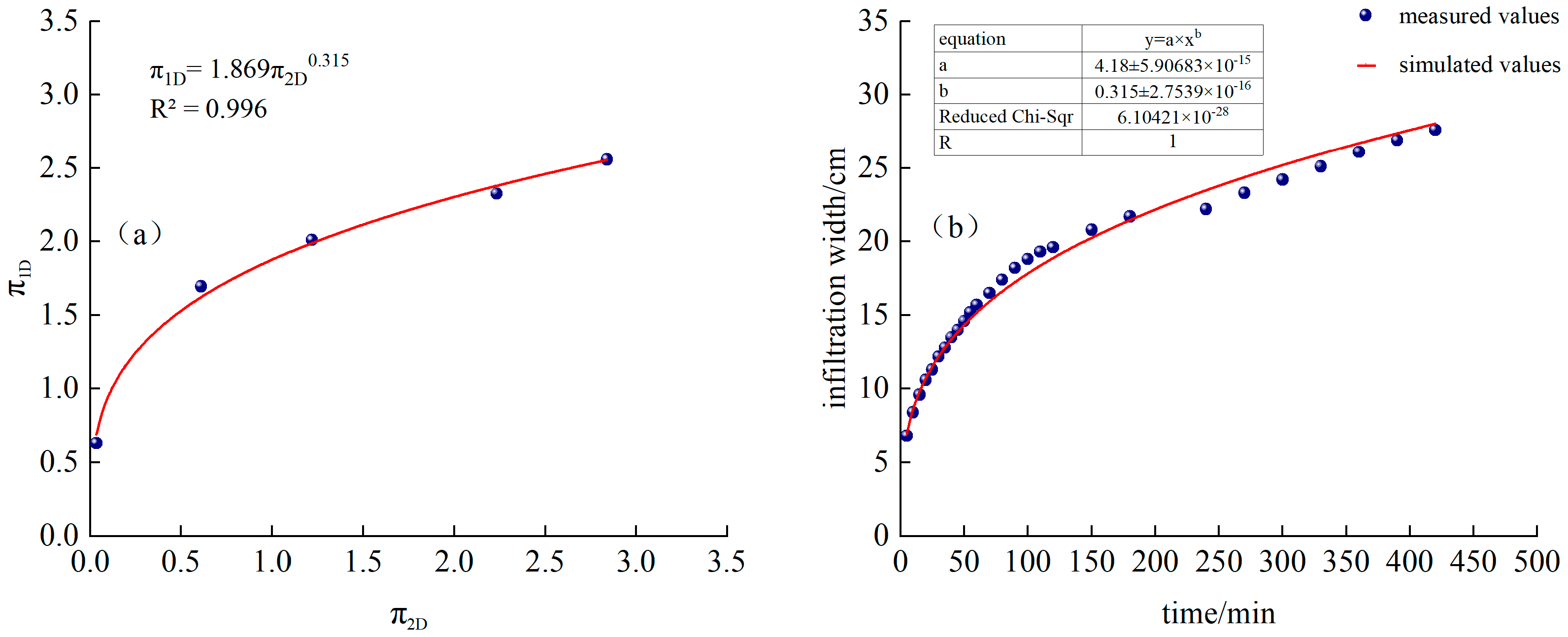
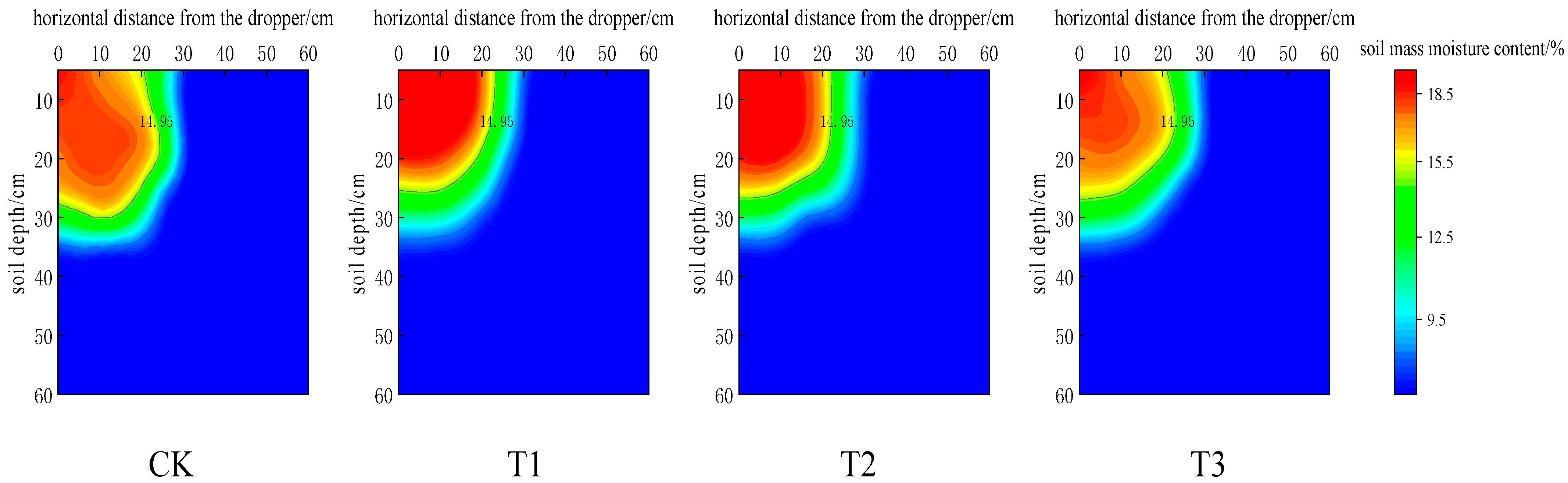
3.1. Estimating the Depth and Width of Wetted Body Penetration
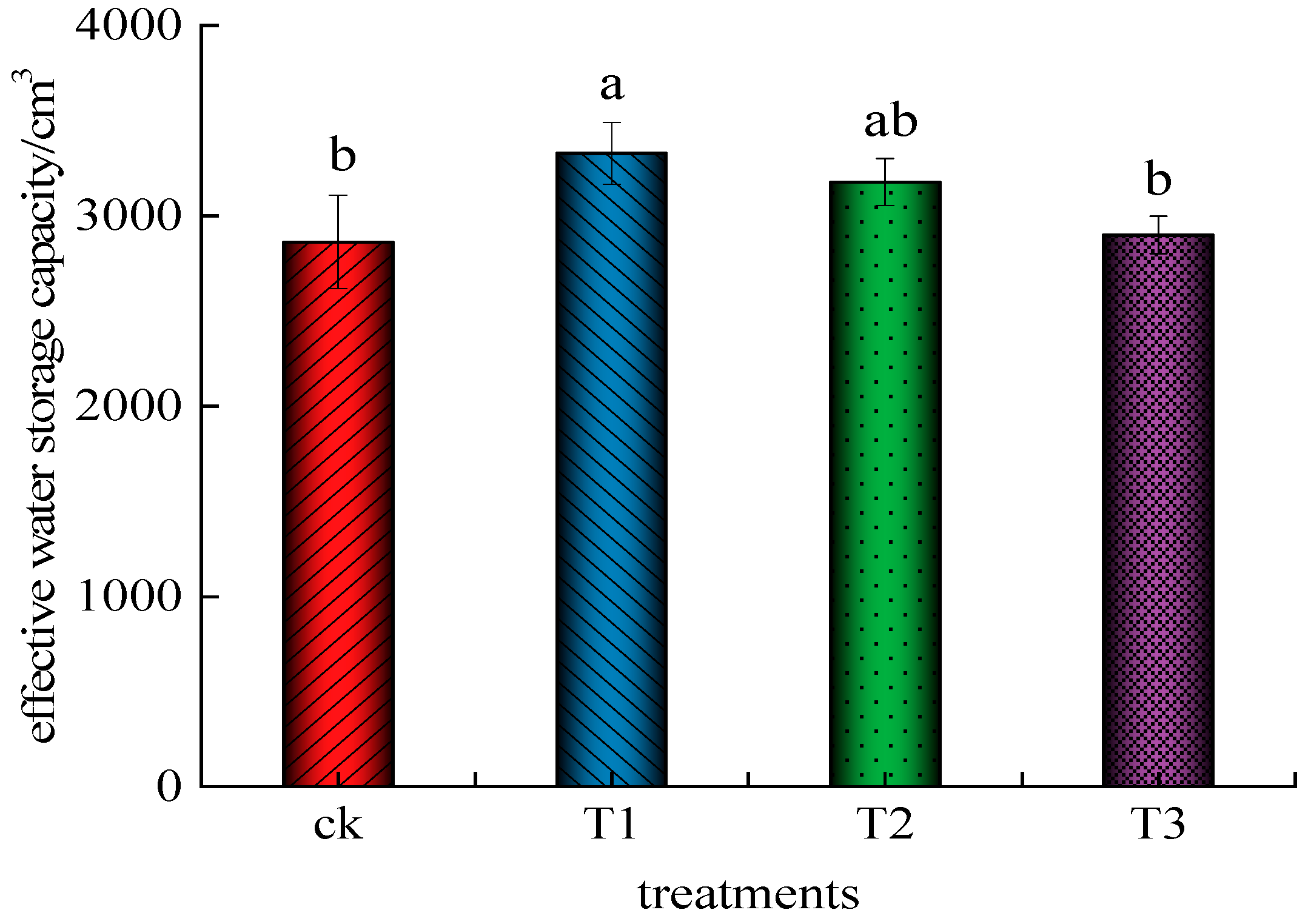
3.2. Estimation of Effective Water Storage Capacity of Wet Bodies
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Fuglie, K.O.; Morgan, S.; Jelliffe, J. World Agricultural Production, Resource Use, and Productivity, 1961–2020. Econ. Inf. Bull.—USDA Econ. Res. Serv. 2024, 54. [Google Scholar] [CrossRef]
- Rasul, F.; Munir, H.; Wajid, A.; Safdar, M.; Salman Ayub, M.; Shahzad, S.; Mehmood, R.; Adnan Shahid, M.; Sarwar, A.; Danish Majeed, M.; et al. Sustainable Irrigation Management for Higher Yield. In Irrigation and Drainage—Recent Advances; Intechopen: London, UK, 2023. [Google Scholar]
- Liu, X.; Gao, P.; Yang, D.; Zhang, Q.; Zhang, Y. Effects of intermittent combined irrigation of brackish and fresh water on soil water and salt transport characteristics in sa-line-alkali cultivated land. J. Soil Sci. 2017, 54, 1404–1413. [Google Scholar]
- Eid, A.R.; Bakry, B.A.; Taha, M.H. Effect of pulse drip irrigation and mulching systems on yield, quality traits and irrigation water use efficiency of soybean under sandy soil conditions. Agric. Sci. 2013, 4, 249–261. [Google Scholar] [CrossRef]
- Li, Y.; Fan, J.; Guan, X.; Liu, H.; Yin, F. Current status and countermeasures of agricultural water-saving development in Xinjiang irrigation areas. J. Huazhong Agric. Univ. 2024, 43, 93–98. [Google Scholar]
- Xu, Q.; Song, Z.; Li, C.; Dong, X.; Huang, T.; Song, Z.; Xiao, F.; Yang, Y. Research on precise nitrogen application in Xinjiang under-film drip irrigation cotton fields based on meta-analysis. J. Cotton 2024, 36, 50–65. [Google Scholar]
- Yan, B.; Xu, Y.; Ma, P.; Gao, Q.; Wang, C.; Zhang, J.; Xue, L.; Sun, L. Effect of sowing date on spring soybean yield and water use efficiency under film drip irrigation in northern Xinjiang. J. China Agric. Univ. 2017, 54, 1404–1413. [Google Scholar]
- Hussein, H.A.; Aldulaimy, S.E. Effect of Surface Drip Irrigation and Polymer Addition on Some Physical Soil Characteristics, Growth and Yield Characteristics of Cauliflower. IOP Conf. Ser. Earth Environ. Sci. 2023, 1222, 12007. [Google Scholar] [CrossRef]
- Rasheed, M.W.; Tang, J.; Sarwar, A.; Shah, S.; Saddique, N.; Khan, M.U.; Imran Khan, M.; Nawaz, S.; Shamshiri, R.R.; Aziz, M.; et al. Soil moisture measuring techniques and factors affecting the moisture dynamics: A comprehensive review. Sustainability 2022, 14, 11538. [Google Scholar] [CrossRef]
- Monjezi, M.S.; Ebrahimian, H.; Liaghat, A.; Moradi, M.A. Soil-wetting front in surface and subsurface drip irrigation. Proc. Inst. Civ. Eng.—Water Manag. 2013, 166, 272–284. [Google Scholar] [CrossRef]
- Wang, J.; Tian, Z.; Yang, T.; Li, X.; He, Q.; Wang, D.; Chen, R. Characteristics of limited flow and soil water infiltration boundary of a subsurface drip irrigation emitter in silty loam soil. Agric. Water Manag. 2024, 291, 108636. [Google Scholar] [CrossRef]
- Rubio, E.; Rubio-Alfaro, M.d.S.; Hernández-Marín, M. Wetting Front Velocity Determination in Soil Infiltration Processes: An Experimental Sensitivity Analysis. Agronomy 2022, 12, 1155. [Google Scholar] [CrossRef]
- Fan, Y.; Shao, X.; Gong, J.; Wang, Y. An empirical model for estimating soil wetting pattern dimensions during film hole irrigation. Arch. Agron. Soil Sci. 2020, 66, 1765–1779. [Google Scholar] [CrossRef]
- Kilic, M. A new analytical method for estimating the 3D volumetric wetting pattern under drip irrigation system. Agric. Water Manag. 2020, 228, 105898. [Google Scholar] [CrossRef]
- Moncef, H.; Khemaies, Z. An analytical approach to predict the moistened bulb volume beneath a surface point source. Agric. Water Manag. 2016, 166, 123–129. [Google Scholar] [CrossRef]
- Li, J.; Jin, H.; Wang, C.; Wang, H. A new method of estimating soil water diffusivity based on variation in the wetting front position and on the principle of stationary action. J. Hydrol. 2022, 612, 128290. [Google Scholar] [CrossRef]
- Karimi, B.; Mohammadi, P.; Sanikhani, H.; Salih, S.Q.; Yaseen, Z.M. Modeling wetted areas of moisture bulb for drip irrigation systems: An enhanced empirical model and artificial neural network. Comput. Electron. Agric. 2020, 178, 105767. [Google Scholar] [CrossRef]
- Fan, Y.; Zhang, C.; Tang, X.; Shi, J.; Liang, J. An Improved Dimensional Model for Calculating the Wetting Pattern in Soil under Drip Irrigation. J. Irrig. Drain. Eng. 2023, 149, 4023020. [Google Scholar] [CrossRef]
- Vishwakarma, D.K.; Kumar, R.; Abed, S.A.; Al-Ansari, N.; Kumar, A.; Kushwaha, N.L.; Yadav, D.; Kumawat, A.; Kuriqi, A.; Alataway, A.; et al. Modeling of soil moisture movement and wetting behavior under point-source trickle irrigation. Sci. Rep. 2023, 13, 14981. [Google Scholar] [CrossRef]
- Vidana Gamage, D.N.; Biswas, A.; Strachan, I.B. Actively heated fiber optics method to monitor three-dimensional wetting patterns under drip irrigation. Agric. Water Manag. 2018, 210, 243–251. [Google Scholar] [CrossRef]
- Al-Ogaidi, A.A.M.; Wayayok, A.; Rowshon, M.K.; Abdullah, A.F. Wetting patterns estimation under drip irrigation systems using an enhanced empirical model. Agric. Water Manag. 2016, 176, 203–213. [Google Scholar] [CrossRef]
- Subbaiah, R. A review of models for predicting soil water dynamics during trickle irrigation. Irrig. Sci. 2013, 31, 225–258. [Google Scholar] [CrossRef]
- Malek, K.; Peters, R.T. Wetting Pattern Models for Drip Irrigation: New Empirical Model. J. Irrig. Drain. Eng. 2011, 137, 530–536. [Google Scholar] [CrossRef]
- Shen, Q.; Liu, Z.; Wang, Z.; Li, H. Simulation of the soil wetting shape under porous pipe sub-irrigation using dimensional analysis. Irrig. Drain. 2007, 56, 389–398. [Google Scholar]
- Solat, S.; Maroufpoor, E.; Karimi, B. Simulation of moisture redistribution pattern on sloping lands under drip irrigation system. J. Water Soil Conserv. 2021, 28, 89–108. [Google Scholar]
- Kisi, O.; Khosravinia, P.; Heddam, S.; Karimi, B.; Karimi, N. Modeling wetting front redistribution of drip irrigation systems using a new machine learning method: Adaptive neuro- fuzzy system improved by hybrid particle swarm optimization—Gravity search algorithm. Agric. Water Manag. 2021, 256, 107067. [Google Scholar] [CrossRef]
- Najib, A.; Orfi, J.; Alansary, H.; Ali, E. Application of the Buckingham π Theorem to Model the Multiple Effect Vacuum Membrane Distillation. J. Therm. Sci. Eng. Appl. 2021, 14, 31003. [Google Scholar] [CrossRef]
- Zamani, S.; Ostad-Ali-Askari, K.; Nafchi, R.F.; Provenzano, G. Assessing a semi-empirical model performance to predict the wetting patterns in subsurface drip irrigation. Clean. Water 2024, 1, 100020. [Google Scholar] [CrossRef]
- Fan, Y.; Yang, Z.; Wei, H. Establishment and verification of the prediction model of soil wetting pattern size in vertical moistube irrigation. Water Supply 2021, 21, 331–343. [Google Scholar] [CrossRef]
- García-Barrachina, L.; Gámez, A.J. Dimensional Analysis of Superplastic Processes with the Buckingham Π Theorem. Metals 2020, 10, 1575. [Google Scholar] [CrossRef]
- Yao, B. Study on Rules and Rugulation of Soil Water-Heat-Salt Spatiotemporal Transfer Under No Winter and Spring Irrigation Cotton Field in Southern Xinjiang. Ph.D. Thesis, China Agricultural University, Beijing, China, 2017. [Google Scholar]
- Zhang, M.; Li, Q.; Shi, X. Soil Science and Agricultural Science; China Water Conservancy and Hydropower Press: Beijing, China, 2007. [Google Scholar]
- Maller, A.; Rezende, R.; Freitas, P.S.L.d.; Seron, C.C.; Hachmann, T.L. Moisture in the soil profile with water applications using pulse drip irrigation. Rev. Ciência Agronômica 2019, 50, 234–241. [Google Scholar] [CrossRef]
- Liu, X.; Yang, D.; Gao, P.; Zhang, Q.; Zhao, Y.; Zhang, Y. Infiltration rules of moderate saline-alkali soil under intermittent combined irrigation. J. Drain. Irrig. Mech. Eng. 2019, 37, 1082–1087. [Google Scholar]
- Wang, C.; Cao, W.; Ma, B.; Li, Z. Analysis and Simulation of Influencing Factors on Soil Saturated Hydraulic Conductivity under Composite Infiltration of Herbaceous Plants with Different Root Architectures and Shrubs. Bull. Soil Water Conserv. 2023, 43, 10–16+43. [Google Scholar]
- Zhong, Y. Study on the Mechanism and Influencing Factors of Infiltration Reduction Under the Border Irrigationand the Film-Hole Irrigation with Muddy Water. Ph.D. Thesis, Xi’an University of Technology, Xi’an, China, 2020. [Google Scholar]
- Liu, J.; Bi, Y.; Sun, X.; Guo, X.; Ma, J.; Yan, Y. Research on infiltration characteristics and soil water-salt distribution under alternate water supply conditions. J. Irrig. Drain. 2015, 34, 55–60. [Google Scholar]
- Chen, S.; Mao, X. Quantitative characterization of soil wetting pattern under surface drip irrigation. J. Agric. Mech. 2018, 49, 285–292. [Google Scholar]
- Su, L.; Lin, S.; Wang, Q.; Wang, K. The impact of soil hydraulic parameters on the wetting pattern shape under point source infiltration. Trans. Chin. Soc. Agric. Eng. 2020, 51, 264–274. [Google Scholar]
- Bai, X.; Ai, D.; Yang, H.; Ge, Y.; Xing, Z.; Hu, X.; Zhou, S. Characteristics of soil wetting pattern and effectiveness evaluation under different initial soil water contents and dripper flow rates in drip irrigation. J. Irrig. Drain. 2019, 38, 73–78. [Google Scholar]
- Wang, H.; Zhang, Y.; Dong, P. The impact of soil compaction on the redistribution of soil water under single point source infiltration. J. Arid Land Resour. Environ. 2019, 33, 146–151. [Google Scholar]
- Li, S. Study of Sandy Soil Drip Irrigation Wetting Characteristic on Different Soil Available Water Boundaries Based on HYDRUS Model. Master’s Thesis, Northwest A&F University, Xianyang, China, 2017. [Google Scholar]
- Assouline, S. Infiltration into soils: Conceptual approaches and solutions. Water Resour. Res. 2013, 49, 1755–1772. [Google Scholar] [CrossRef]
- Castellini, M.; Di Prima, S.; Giglio, L.; Leogrande, R.; Alagna, V.; Autovino, D.; Rinaldi, M.; Iovino, M. Applying a Comprehensive Model for Single-Ring Infiltration: Assessment of Temporal Changes in Saturated Hydraulic Conductivity and Physical Soil Properties. Water 2024, 16, 2950. [Google Scholar] [CrossRef]
- Zhang, Y.; Schaap, M.G. Estimation of saturated hydraulic conductivity with pedotransfer functions: A review. J. Hydrol. 2019, 575, 1011–1030. [Google Scholar] [CrossRef]
- Šimůnek, J.; van Genuchten, M.T.; Šejna, M. Development and Applications of the HYDRUS and STANMOD Software Packages and Related Codes. Vadose Zone J. 2008, 7, 587–600. [Google Scholar] [CrossRef]
- Vigo, Á.D.; Zubelzu, S.; Juana, L. Infiltration models and soil characterisation for hemispherical and disc sources based on Green-Ampt assumptions. J. Hydrol. 2021, 595, 125966. [Google Scholar] [CrossRef]
- del Vigo, Á.; Zubelzu, S.; Juana, L. Numerical routine for soil water dynamics from trickle irrigation. Appl. Math. Model. 2020, 83, 371–385. [Google Scholar] [CrossRef]




| Infiltration Depth | Infiltration Width | |||||||
|---|---|---|---|---|---|---|---|---|
| Deal with | RMSE (cm) | MAE (cm) | PBIAS (%) | EF | RMSE (cm) | MAE(cm) | PBIAS (%) | EF |
| ck | 0.179 | 0.146 | 0.264 | 0.999 | 0.806 | 0.562 | −2.802 | 0.974 |
| T1 | 0.743 | 0.580 | 2.540 | 0.985 | 0.879 | 0.743 | 0.296 | 0.972 |
| T2 | 0.383 | 0.312 | 0.618 | 0.996 | 0.783 | 0.653 | 0.247 | 0.980 |
| T3 | 0.649 | 0.511 | −1.127 | 0.988 | 0.627 | 0.514 | 0.101 | 0.988 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhu, Z.; Rasheed, M.W.; Safdar, M.; Yao, B.; Tumaerbai, H.; Sarwar, A.; Zhu, L. Intermittent Drip Irrigation Soil Wet Front Prediction Model and Effective Water Storage Analysis. Sustainability 2024, 16, 9553. https://doi.org/10.3390/su16219553
Zhu Z, Rasheed MW, Safdar M, Yao B, Tumaerbai H, Sarwar A, Zhu L. Intermittent Drip Irrigation Soil Wet Front Prediction Model and Effective Water Storage Analysis. Sustainability. 2024; 16(21):9553. https://doi.org/10.3390/su16219553
Chicago/Turabian StyleZhu, Zhu, Muhammad Waseem Rasheed, Muhammad Safdar, Baolin Yao, Hudan Tumaerbai, Abid Sarwar, and Lianyong Zhu. 2024. "Intermittent Drip Irrigation Soil Wet Front Prediction Model and Effective Water Storage Analysis" Sustainability 16, no. 21: 9553. https://doi.org/10.3390/su16219553
APA StyleZhu, Z., Rasheed, M. W., Safdar, M., Yao, B., Tumaerbai, H., Sarwar, A., & Zhu, L. (2024). Intermittent Drip Irrigation Soil Wet Front Prediction Model and Effective Water Storage Analysis. Sustainability, 16(21), 9553. https://doi.org/10.3390/su16219553






