Comparative Evaluation of Crop Evapotranspiration Estimation Methods in a Semi-Arid Region
Abstract
:1. Introduction
2. Materials and Methods
2.1. Materials
2.1.1. Research Area and Meteorological Stations
2.1.2. Data Source, Instruments Calibration and Data Validation
2.2. Methods
3. Results
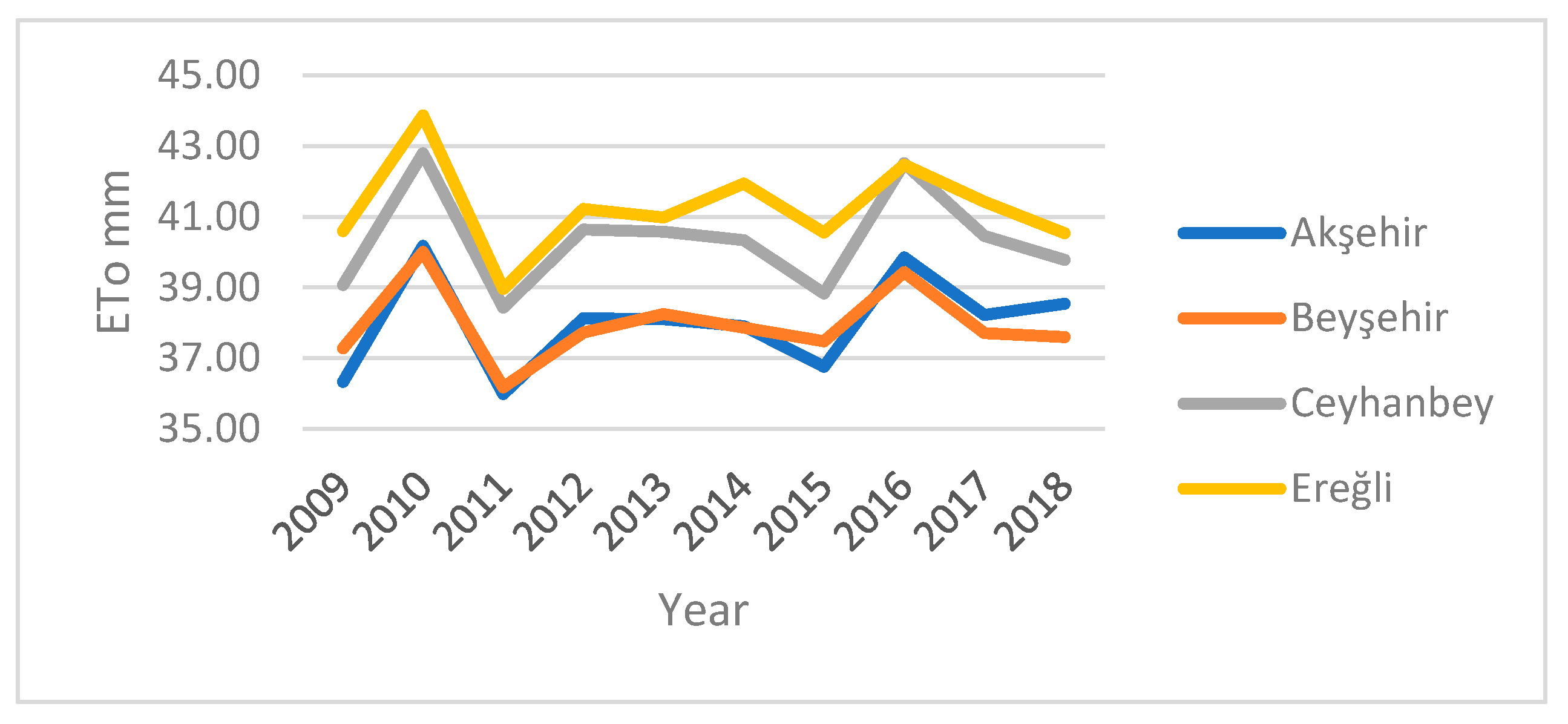
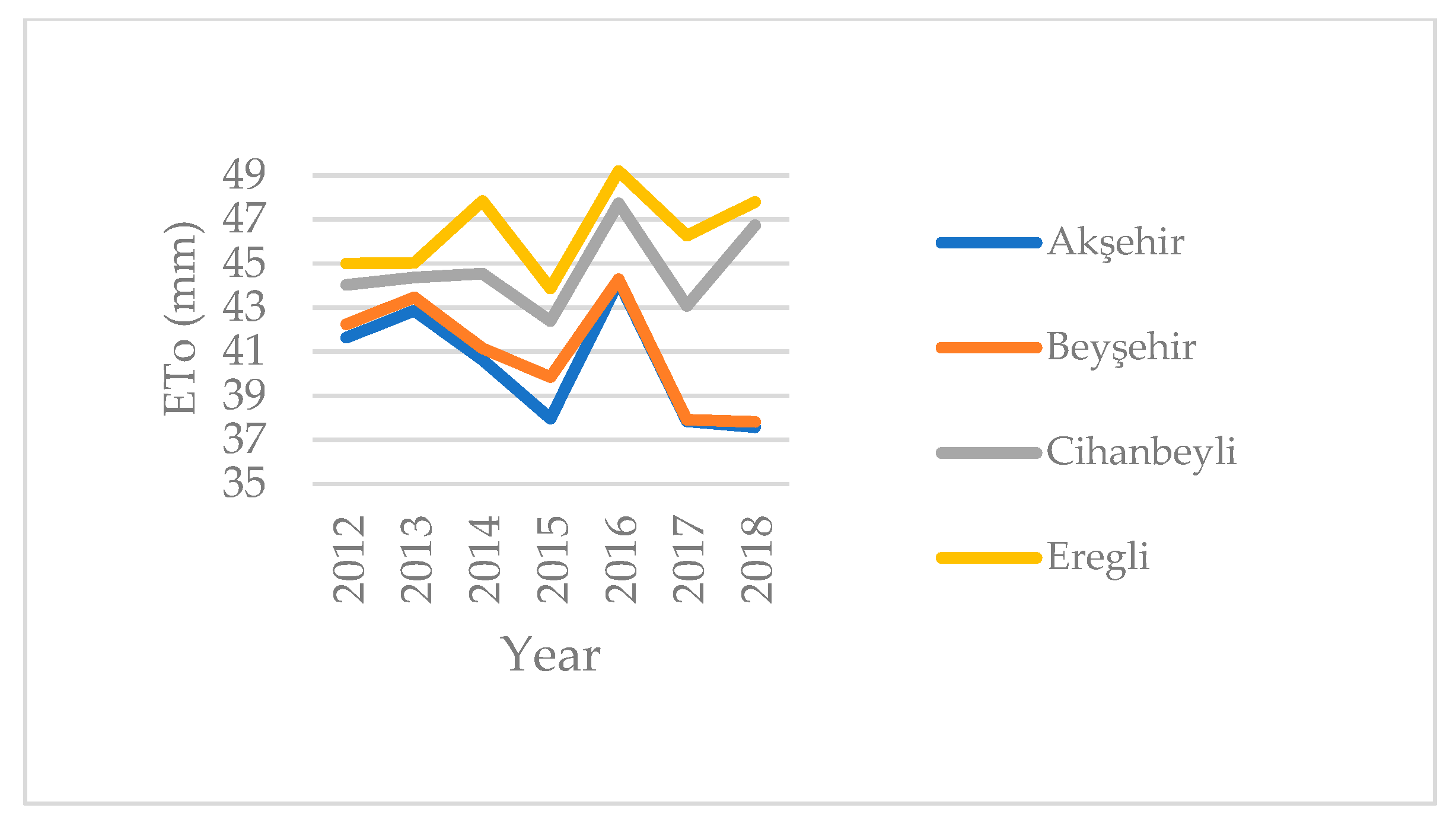
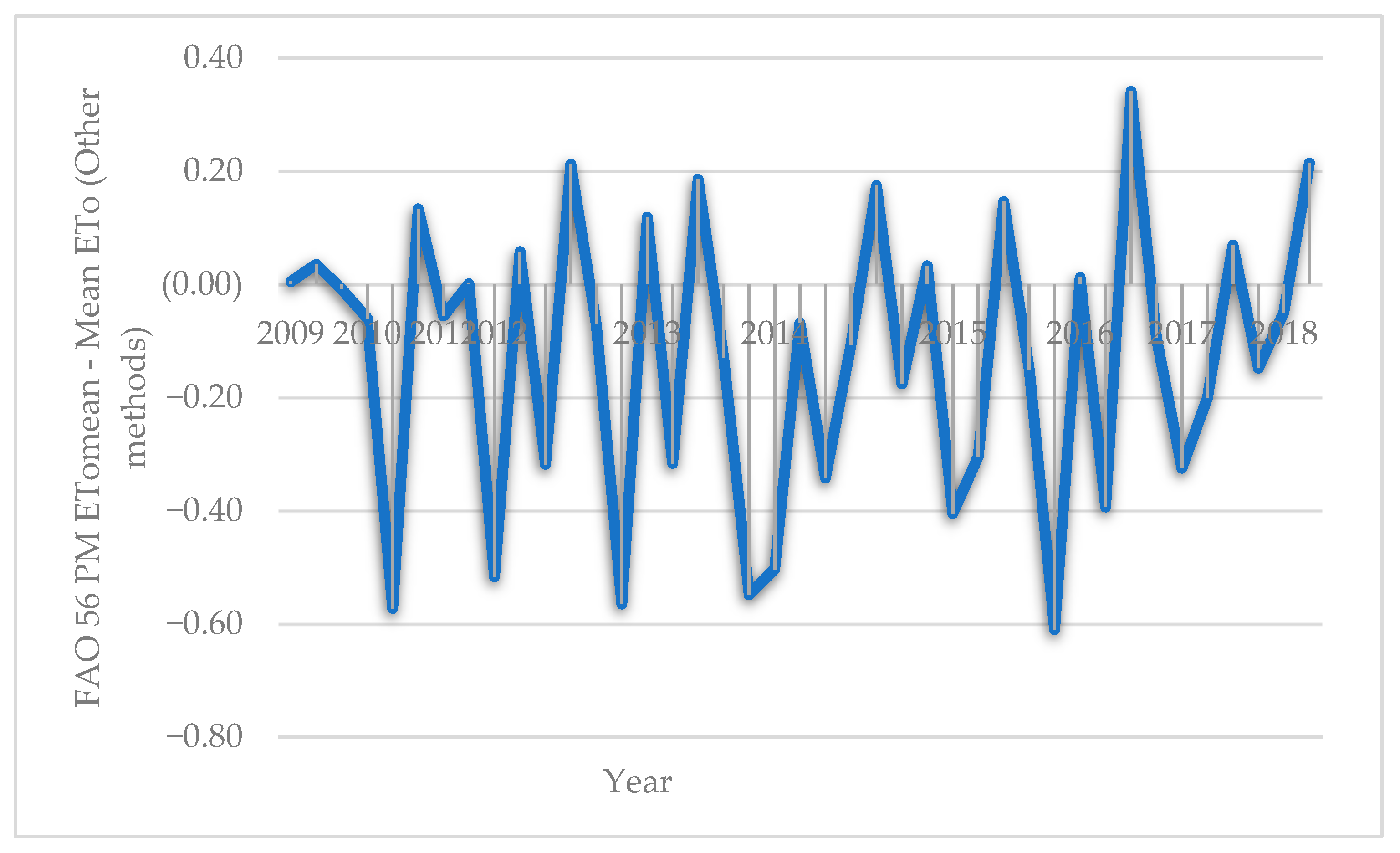
3.1. Reference Crop Evapotranspiration (ETo)
3.2. Crop Evapotranspiration ETc
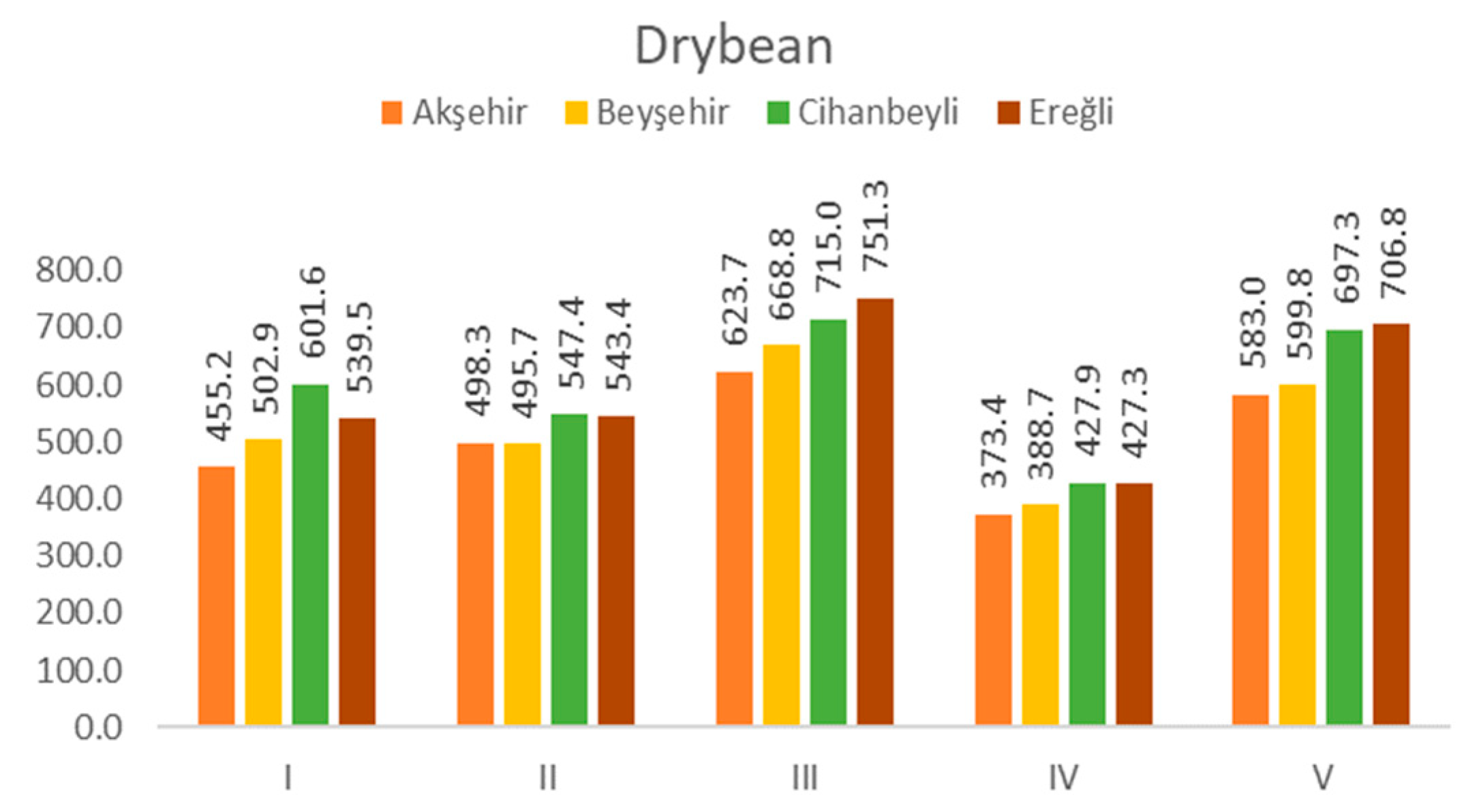
3.2.1. Dry Bean
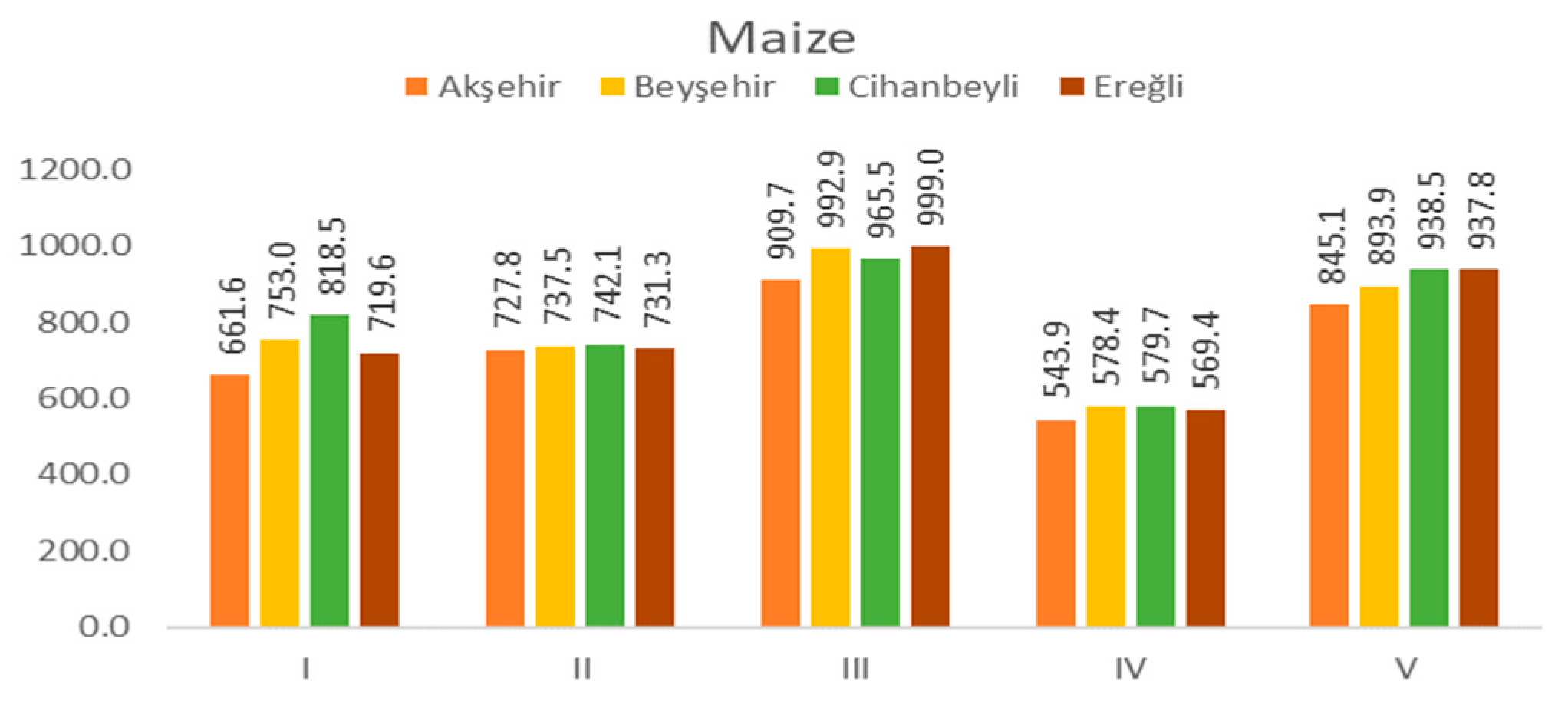
3.2.2. Maize
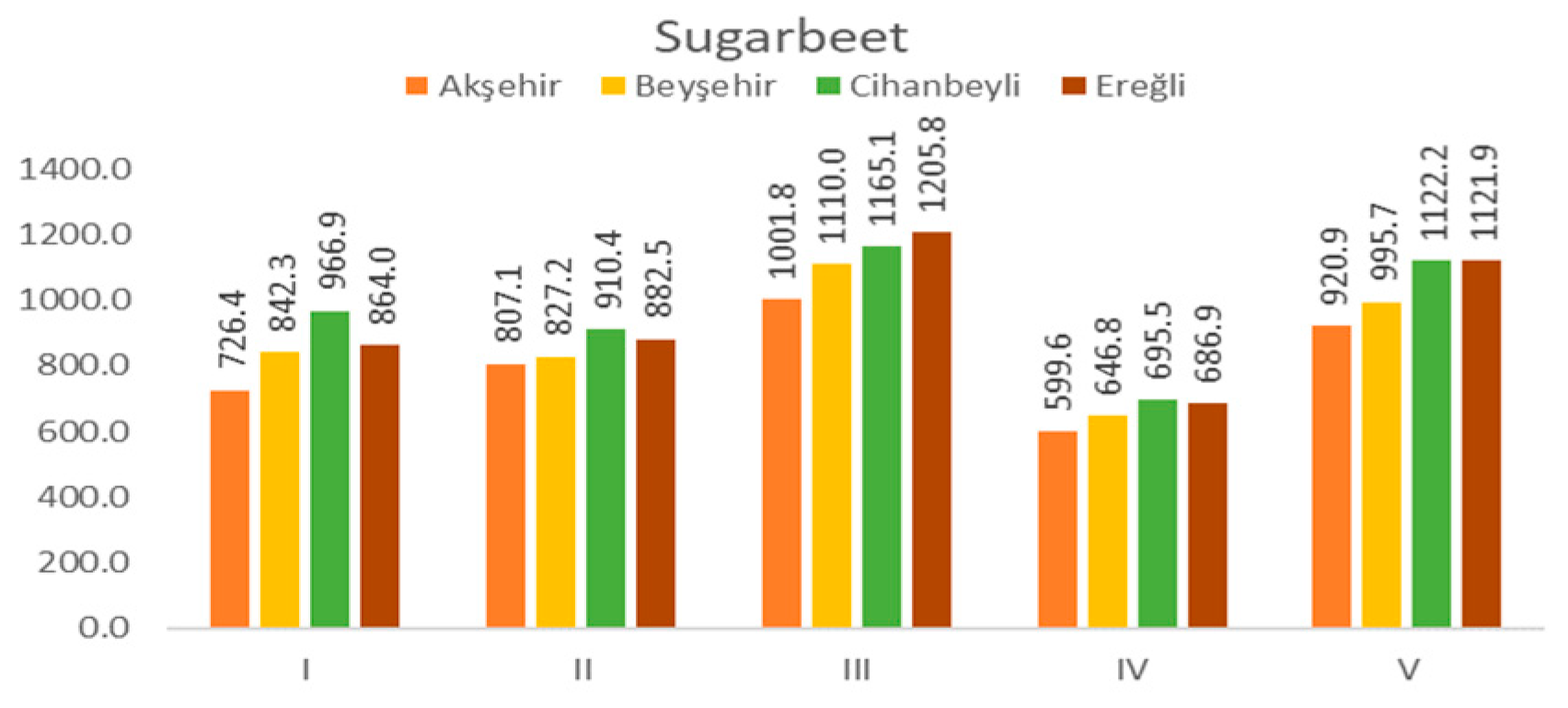
3.2.3. Sugar Beet
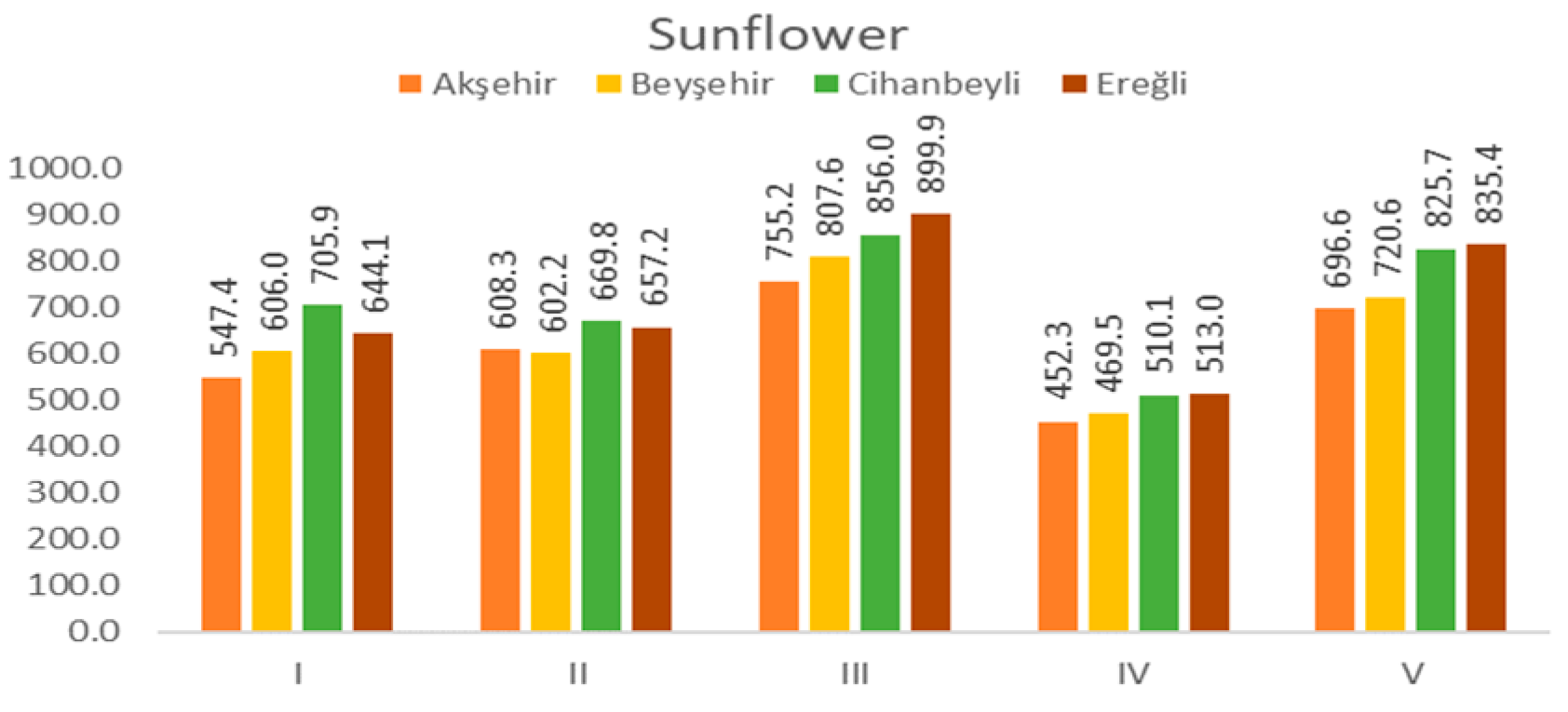
3.2.4. Sunflower
3.2.5. Wheat
4. Discussion
5. Conclusions
Author Contributions
Funding
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Manida, M. The Future of Food and Agriculture—Trends and Challenges; Agriculture & Food E-Newsletter 2022. Available online: https://www.researchgate.net/publication/358402720_The_Future_of_Food_and_Agriculture_Trends_and_Challenges (accessed on 11 September 2024).
- Alexandratos, N.; Bruinsma, J. World Agriculture towards 2030/2050: The 2012 Revision. In ESA Working Paper; FAO: Rome, Italy, 2012. [Google Scholar]
- Rockström, J.; Williams, J.; Daily, G.; Noble, A.; Matthews, N.; Gordon, L.; Wetterstrand, H.; DeClerck, F.; Shah, M.; Steduto, P.; et al. Sustainable Intensification of Agriculture for Human Prosperity and Global Sustainability. Ambio 2017, 46, 4–17. [Google Scholar] [CrossRef]
- Allen, R.G.; Pereira, L.S.; Raes, D.; Smith, M. Crop Evapotranspiration-Guidelines for Computing Crop Water Requirements. FAO Irrig. Drain. Pap. 1998, 56, 60–64. [Google Scholar]
- Fereres, E.; Soriano, M.A. Deficit Irrigation for Reducing Agricultural Water Use. J. Exp. Bot. 2007, 58, 147–159. [Google Scholar] [CrossRef]
- Xiang, K.; Li, Y.; Horton, R.; Feng, H. Similarity and Difference of Potential Evapotranspiration and Reference Crop Evapotranspiration–a Review. Agric. Water Manag. 2020, 232, 106043. [Google Scholar] [CrossRef]
- Hargreaves, G.H.; Samani, Z.A. Reference Crop Evapotranspiration from Temperature. Appl. Eng. Agric. 1985, 1, 96–99. [Google Scholar] [CrossRef]
- Watanabe, K.; Yamamoto, T.; Yamada, T.; Sakuratani, T.; Nawata, E.; Noichana, C.; Sributta, A.; Higuchi, H. Changes in Seasonal Evapotranspiration, Soil Water Content, and Crop Coefficients in Sugarcane, Cassava, and Maize Fields in Northeast Thailand. Agric. Water Manag. 2004, 67, 133–143. [Google Scholar] [CrossRef]
- Makkink, G.F. Testing the Penman Formula by Means of Lysimeters. J. Inst. Water Eng. 1957, 11, 277–288. [Google Scholar]
- Doorenbos, J.; Pruitt, W. Crop Water Requirements. In Land and Water Development Division; FAO: Rome, Italy, 1977. [Google Scholar]
- Blaney, H.F.; Criddle, W.D. Determining Consumptive Use and Irrigation Water Requirements; United State Department of Agriculture Technical Bullettin, 1275: Washington, DC, USA, 1962. [Google Scholar]
- Howell, T.A.; Evett, S.R. The Penman-Monteith Method; USDA-Agricultural Research Service, Conservation & Production Research Laboratory: Washington, DC, USA, 2004; Volume 14. [Google Scholar]
- Awal, R.; Habibi, H.; Fares, A.; Deb, S. Estimating Reference Crop Evapotranspiration under Limited Climate Data in West Texas. J. Hydrol. Reg. Stud. 2020, 28, 100677. [Google Scholar] [CrossRef]
- Tabari, H.; Grismer, M.E.; Trajkovic, S. Comparative Analysis of 31 Reference Evapotranspiration Methods under Humid Conditions. Irrig. Sci. 2013, 31, 107–117. [Google Scholar] [CrossRef]
- Gao, F.; Fen, G.; Ouyang, Y.; Wang, H.; Fisher, D.; Adeli, A.; Jenkins, J. Evaluation of Reference Evapotranspiration Methods in Arid, Semiarid, and Humid Regions. J. Am. Water Resour Assoc. 2017, 53, 791–808. [Google Scholar] [CrossRef]
- Yıldırım, Y.E.; Kodal, S. Ankara Koşullarında Mısır Su Tüketiminin Tahmininde Kullanılabilecek Yöntemler. J. Agric. Sci. 1996, 2, 13–18. [Google Scholar] [CrossRef]
- Djaman, K.; Balde, A.B.; Sow, A.; Muller, B.; Irmak, S.; N’Diaye, M.K.; Saito, K. Evaluation of Sixteen Reference Evapotranspiration Methods under Sahelian Conditions in the Senegal River Valley. J. Hydrol. Reg. Stud. 2015, 3, 139–159. [Google Scholar] [CrossRef]
- Ampas, V.; Baltas, E.; Papamichail, D. Comparison of Different Methods for the Estimation of the Reference Crop Evapotranspiration in the Florina Region. WSEAS Trans. Environ. Dev. 2007, 2, 1449–1454. [Google Scholar]
- Liu, X.; Xu, C.; Zhong, X.; Li, Y.; Yuan, X.; Cao, J. Comparison of 16 Models for Reference Crop Evapotranspiration against Weighing Lysimeter Measurement. Agric. Water Manag. 2017, 184, 145–155. [Google Scholar] [CrossRef]
- Mohan, S. Intercomparison of Evapotranspiration Estimates. Hydrol. Sci. J. 1991, 36, 447–460. [Google Scholar] [CrossRef]
- Şahin, M.; Kara, M. Konya Kent Merkezinde Farkli Sulama Uygulamalarinda Çim Su Tüketimi ve Bitki Katsayilarinin Belirlenmesi. Selcuk J. Agric. Food Sci. 2005, 19, 135–145. [Google Scholar]
- Süheri, S.; Amarkai, P.A.; Yavuz, D. A Comparative Study of Crop Evapotranspiration Estimation by Three Methods with Measured Crop Evapotranspiration in Konya Plain. Selcuk J. Agric. Food Sci. 2019, 33, 1–6. [Google Scholar] [CrossRef]
- Taş, İ.; Kirnak, H. Yari Kurak İklim Bölgelerinde Bitki Su Tüketiminin Tahmininde Kullanilabilecek Ampirik Modeller. Adnan Menderes Üniversitesi Ziraat Fakültesi Derg. 2011, 8, 57–66. [Google Scholar]
- Yassen, A.N.; Nam, W.H.; Hong, E.M. Impact of Climate Change on Reference Evapotranspiration in Egypt. Catena 2020, 194, 104711. [Google Scholar] [CrossRef]
- Dinpashoh, Y.; Jhajharia, D.; Fakheri-Fard, A.; Singh, V.P.; Kahya, E. Trends in Reference Crop Evapotranspiration over Iran. J. Hydrol. 2011, 399, 422–433. [Google Scholar] [CrossRef]
- Harmsen, E.W.; Miller, N.L.; Schlegel, N.J.; Gonzalez, J.E. Seasonal Climate Change Impacts on Evapotranspiration, Precipitation Deficit and Crop Yield in Puerto Rico. Agric. Water Manag. 2009, 96, 1085–1095. [Google Scholar] [CrossRef]
- Katerji, N.; Rana, G.; Ferrara, R.M. Actual Evapotranspiration for a Reference Crop within Measured and Future Changing Climate Periods in the Mediterranean Region. Theor. Appl. Climatol. 2017, 129, 923–938. [Google Scholar] [CrossRef]
- Nistor, M.M.; Cheval, S.; Gualtieri, A.F.; Dumitrescu, A.; Boţan, V.E.; Berni, A.; Hognogi, G.; Irimuş, I.A.; Porumb-Ghiurco, C.G. Crop Evapotranspiration Assessment under Climate Change in the Pannonian Basin during 1991–2050. Meteorol. Appl. 2017, 24, 84–91. [Google Scholar] [CrossRef]
- Lang, D.; Zheng, J.; Shi, J.; Liao, F.; Ma, X.; Wang, W.; Zhang, M. A Comparative Study of Potential Evapotranspiration Estimation by Eight Methods with FAO Penman–Monteith Method in Southwestern China. Water 2017, 9, 734. [Google Scholar] [CrossRef]
- Arabi, C.; Candoğan, B.N. Marmara Bölgesinde Referans Bitki Su Tüketiminin Alansal ve Zamansal Değişimi. Uluslararası Tarım Ve Yaban Hayatı Bilim. Derg. 2022, 8, 268–281. [Google Scholar] [CrossRef]
- Bayramoğlu, E. Trabzon Ilinde Iklim Değişikliğinin Mevsimsel Bitki Su Tüketimine Etkisi: Penman-Monteith Yöntemi. Kastamonu Univ. J. For. Fac. 2013, 13, 300–306. [Google Scholar]
- Dadaser-Celik, F.; Cengiz, E.; Guzel, O. Trends in Reference Evapotranspiration in Turkey: 1975–2006. Int. J. Climatol. 2016, 36, 1733–1743. [Google Scholar] [CrossRef]
- Ünlükara, A.; Yürekli, K.; Aküzüm, T.; Örs, İ.; Safi, S. Konya ve Karaman İllerinde Bitki Su Tüketimi (ETo) Değişiminin Analizi. Tarım Bilim. Araştırma Derg. 2011, 4, 1–5. [Google Scholar]
- Yürekli, K.; Ünlükara, A.; Cömert, M.M. Holt Yaklaşımı Ile Referans Bitki Su Tüketiminin Mevsimsel Değişiminin Saptanması. Gaziosmanpaşa Bilimsel Araştırma Derg. 2017, 6, 75–81. [Google Scholar]
- Ünlü, M.; Koç, M.; Barutçular, C.; Koç, L.; Kapur, B.; Tekin, S.; Kanber, R. Effect of Climate Change for Evapotranspiration and Crop Growth under the Çukurova Condition. Turkey. ICCAP Workshop 2007, 30–31. Available online: https://www.researchgate.net/profile/Servet-Tekin/publication/283784442_EFFECT_OF_CLIMATE_CHANGE_FOR_EVAPOTRANSPIRATION_AND_CROP_GROWTH_UNDER_THE_CUKUROVA_CONDITIONS_TURKEY/links/5647061d08aef646e6cf29cc/EFFECT-OF-CLIMATE-CHANGE-FOR-EVAPOTRANSPIRATION-AND-CROP-GROWTH-UNDER-THE-CUKUROVA-CONDITIONS-TURKEY.pdf (accessed on 11 September 2024).
- Nistor, M.M.; Mîndrescu, M.; Petrea, D.; Nicula, A.S.; Rai, P.K.; Benzaghta, M.A.; Dezsi, Ş.; Hognogi, G.; Porumb-Ghiurco, C.G. Climate Change Impact on Crop Evapotranspiration in Turkey during the 21st Century. Meteorol. Appl. 2019, 26, 442–453. [Google Scholar] [CrossRef]
- Saadi, S.; Todorovic, M.; Tanasijevic, L.; Pereira, L.S.; Pizzigalli, C.; Lionello, P. Climate Change and Mediterranean Agriculture: Impacts on Winter Wheat and Tomato Crop Evapotranspiration, Irrigation Requirements and Yield. Agric. Water Manag. 2015, 147, 103–115. [Google Scholar] [CrossRef]
- Yıldırım, A.İ.; Demir, S.K.; Yayla, U. Konya İl Gıda Tarım ve Hayvancılık Müdürlüğü.Şube ve İlçe Müdürlükleri 2017 Yılı Değerlendirme ve Koordinasyon Toplantısı: Sonuç Raporu; Konya Tarım İl Müdürlüğü: Ankara, Türkiye, 2017; pp. 12–14. [Google Scholar]
- ISO/IEC 17025; International Organization for Standardization & International Electrotechnical Commission. General Requirements for the Competence of Testing and Calibration Laboratories. 2017. Available online: https://www.iso.org/obp/ui/en/#iso:std:66912:en (accessed on 11 September 2024).
- Allen, R.G.; Pruitt, W.O. FAO-24 Reference Evapotranspiration Factors. J. Irrig. Drain. Eng. 1991, 117, 758–773. [Google Scholar] [CrossRef]
- Ward, A.D.; Trimble, S.W.; Burckhard, S.R.; Lyon, J.G. Environmental Hydrology, 3rd ed.; CRC Press: Boca Raton, FL, USA, 2015. [Google Scholar]
- Allen, R.G.; Pruitt, W.O. Rational Use of the FAO Blaney-Criddle Formula. J. Irrig. Drain. Eng. 1986, 12, 139–155. [Google Scholar] [CrossRef]
- Ferro, C.A.; Hannachi, A.; Stephenson, D.B. Simple Nonparametric Techniques for Exploring Changing Probability Distributions of Weather. J. Clim. 2005, 18, 4344–4354. [Google Scholar] [CrossRef]
- Anonymous Türkiye’de Sulanan Bitkilerin Bitki Su Tüketimi Rehberi. Tarımsal Araştırmalar Ve Politakalar Genel Müdürlüğü; 2016. Available online: https://www.almaatatarim.net/icerik/uploads/turkiyede-sulanan-Bitkilerin-Su-Tuuketimi-Rehberi-5-9-2016.pdf (accessed on 11 September 2024).
- Lum, M.; Bateni, S.; Shiri, J.; Keshavarzi, A. Estimation of Reference Evapotranspiration from Climatic Data. Int. J. Hydrol. 2017, 1, 25–30. [Google Scholar]
- Farias, V.D.D.S.; Lima, M.J.A.D.; Nunes, H.G.G.C.; Sousa, D.D.P.; Souza, P.J.D.O.P. Water Demand, Crop Coefficient and Uncoupling Factor of Cowpea in The Eastern Amazon1. Rev. Caatinga 2017, 30, 190–200. [Google Scholar] [CrossRef]
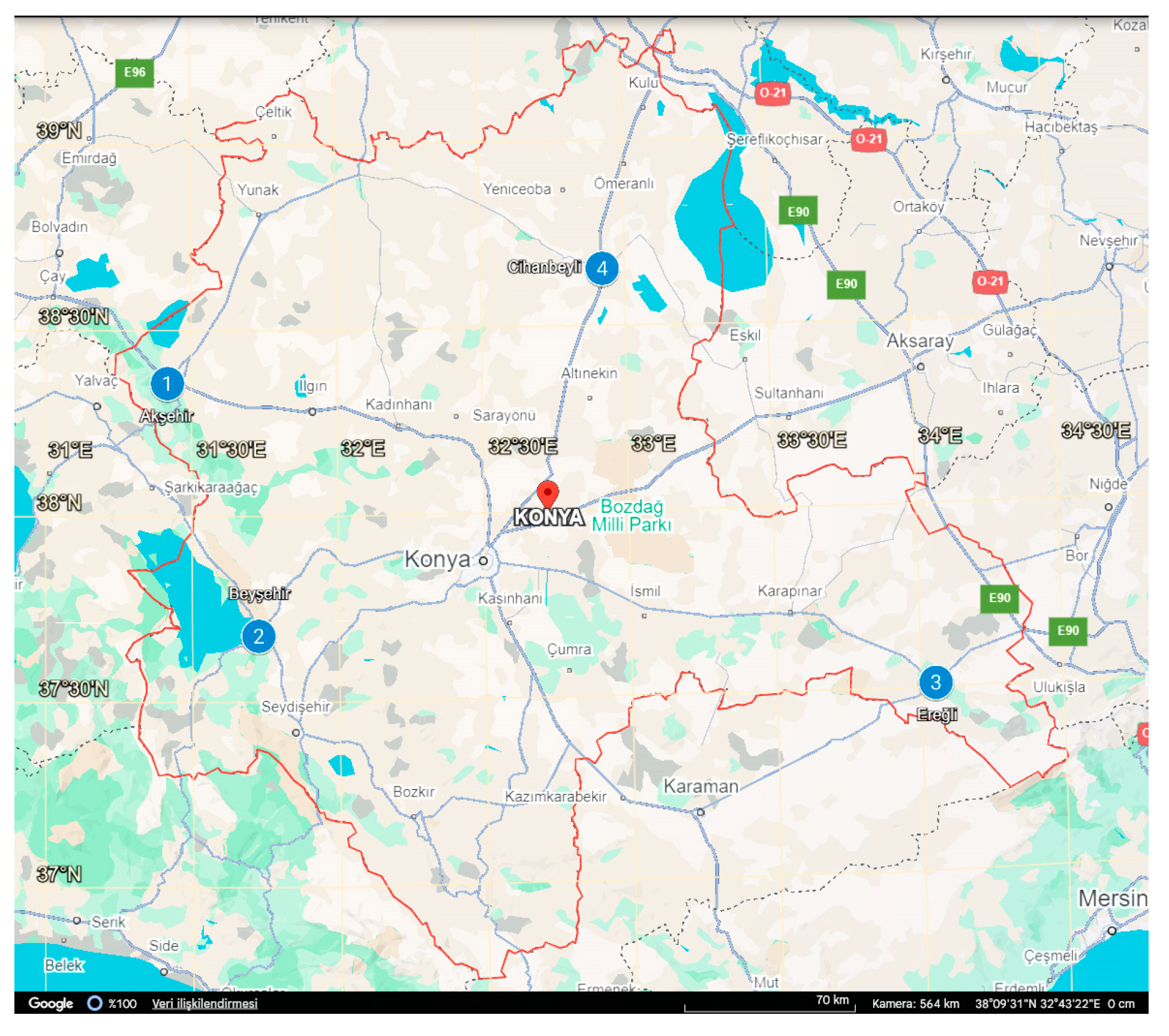
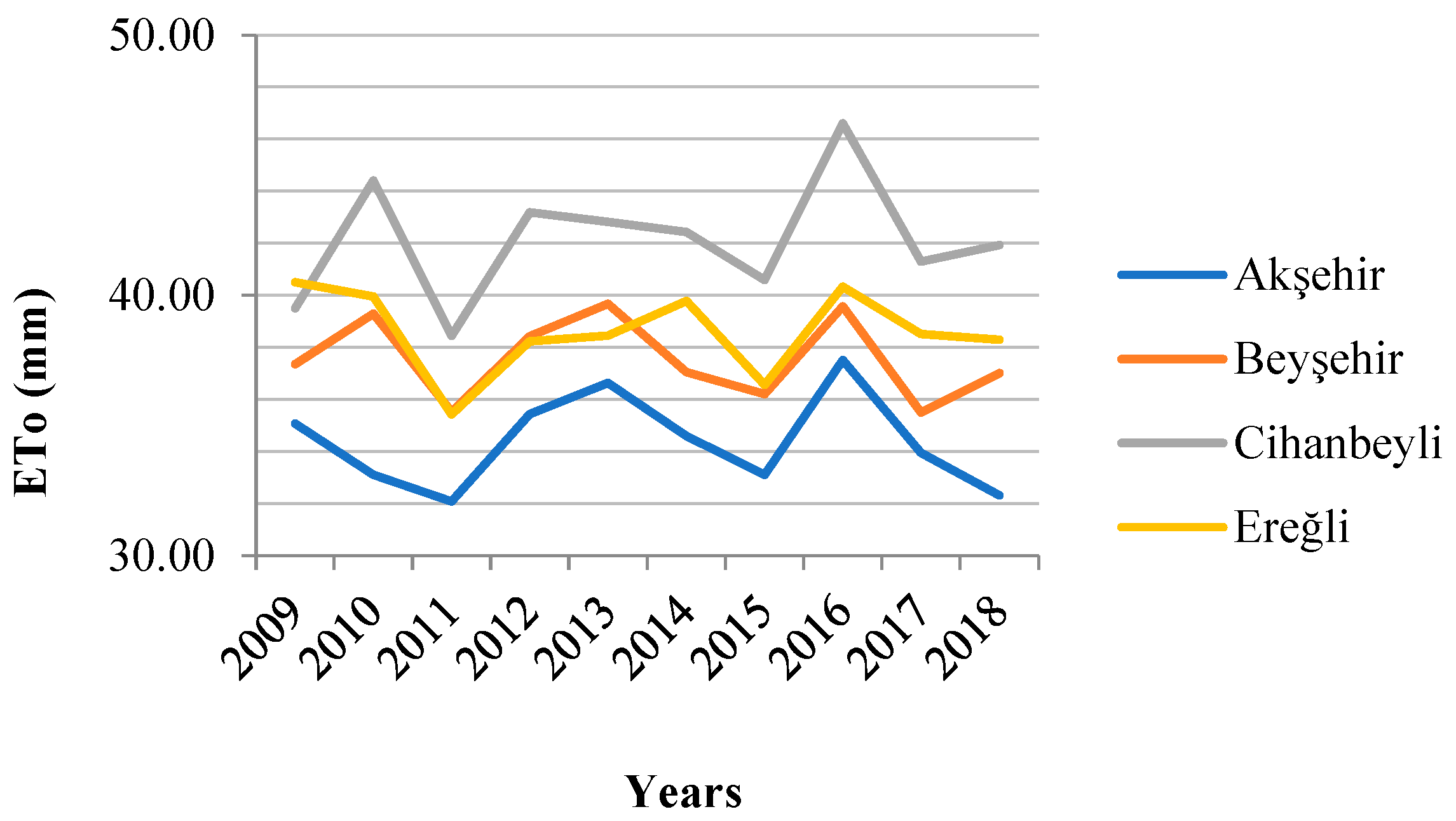
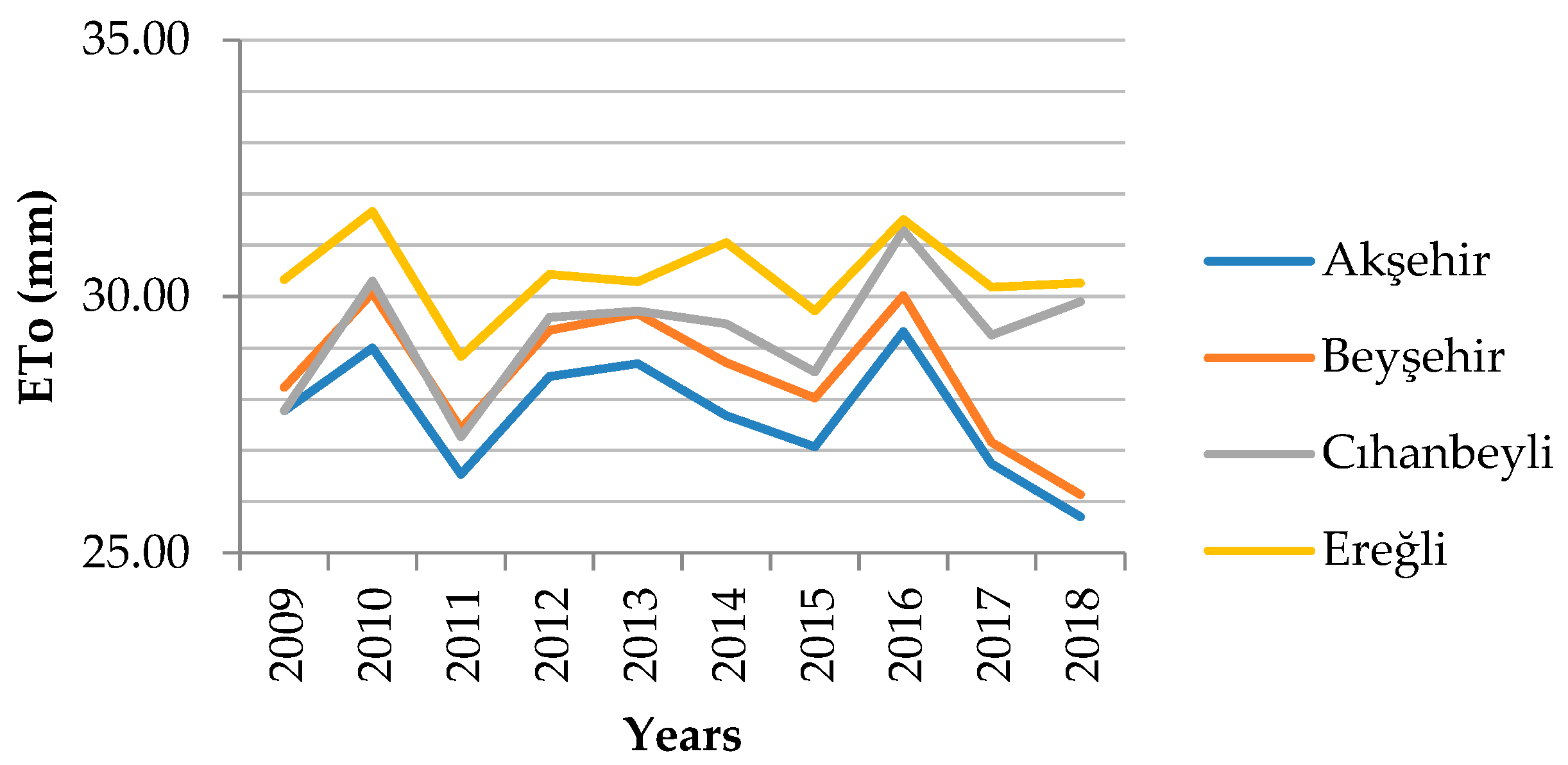
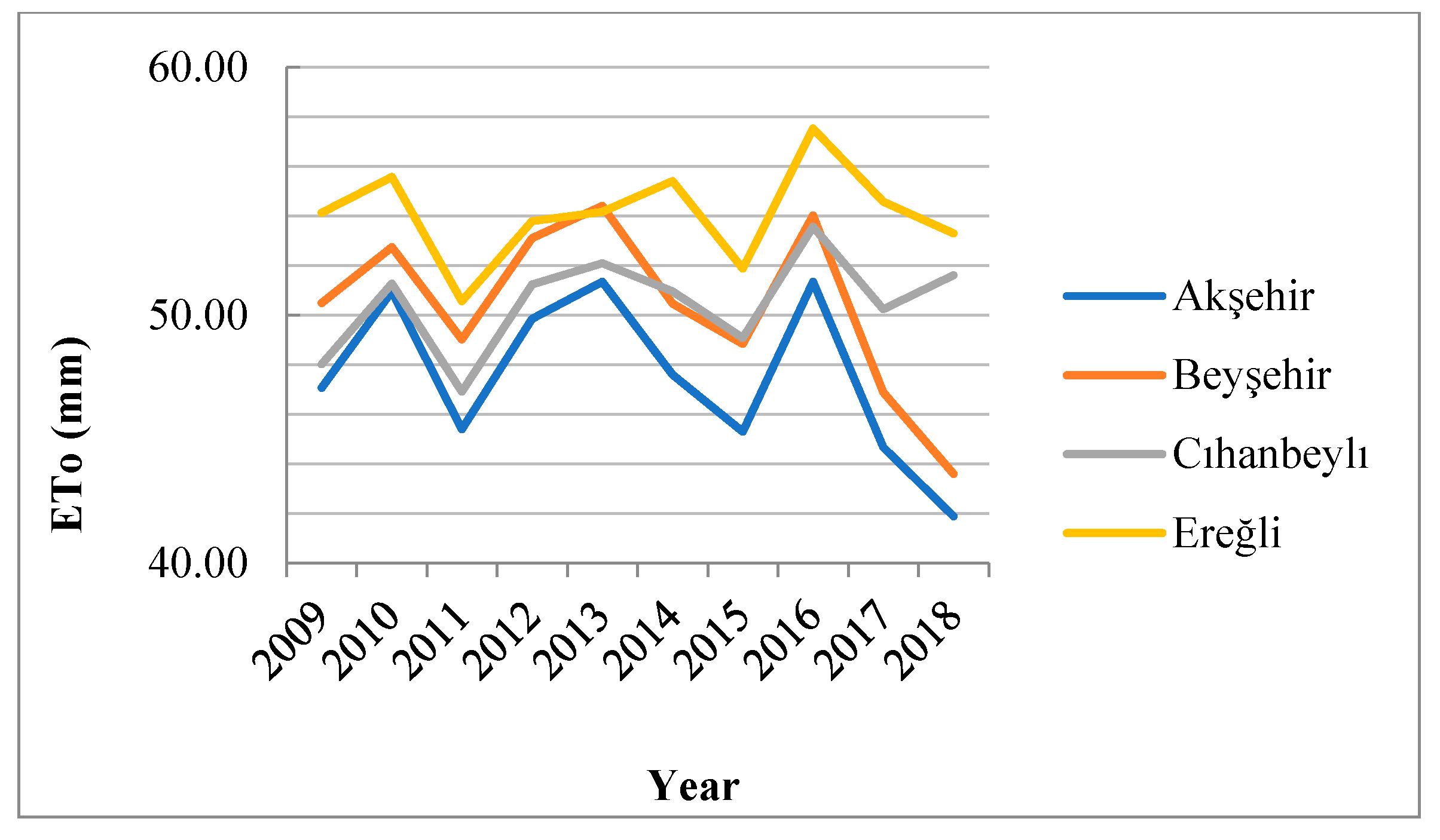


| Meteorological Station | Latitude (N) | Longitude (E) | Elevation (m) | Climate Type |
|---|---|---|---|---|
| Akşehir | 38.3688 | 31.4297 | 1002 | Cool |
| Beyşehir | 37.6777 | 31.7463 | 1141 | Mountain Slope |
| Cihanbeyli | 38.6503 | 32.9226 | 969 | Central Anatolia |
| Ereğli | 37.5255 | 34.0485 | 1046 | Central Anatolia |
| Meteorological Station | Crops | Planting Date | Vegetations Period (Days) | Kc Coefficients | Length of Growth Stages (Days) | |||||
|---|---|---|---|---|---|---|---|---|---|---|
| Kcini | Kcmid | Kcend | I | II | III | IV | ||||
| Akşehir | Dry bean | 20/05 | 120 | 0.24 | 1.06 | 0.92 | 20 | 35 | 45 | 20 |
| Maize | 20/04 | 160 | 0.28 | 1.17 | 1.06 | 30 | 40 | 55 | 35 | |
| Sugar beet | 20/03 | 185 | 0.44 | 1.20 | 0.70 | 30 | 50 | 70 | 35 | |
| Sunflower | 20/04 | 144 | 0.36 | 1.07 | 0.36 | 25 | 30 | 59 | 30 | |
| Wheat | 10/10 | 264 | 0.78 | 1.16 | 0.26 | 30 | 162 | 42 | 30 | |
| Beyşehir | Dry bean | 1/05 | 124 | 0.25 | 1.05 | 0.36 | 23 | 33 | 44 | 24 |
| Maize | 20/04 | 158 | 0.27 | 1.21 | 1.07 | 30 | 40 | 54 | 34 | |
| Sugar beet | 20/03 | 185 | 0.45 | 1.21 | 0.71 | 30 | 50 | 70 | 35 | |
| Sunflower | 20/04 | 145 | 0.34 | 1.06 | 0.36 | 25 | 30 | 60 | 30 | |
| Wheat | 10/10 | 267 | 0.80 | 1.18 | 0.26 | 159 | 37 | 41 | 30 | |
| Cihanbeyli | Dry bean | 20/05 | 125 | 0.16 | 1.10 | 0.39 | 20 | 35 | 50 | 20 |
| Maize | 10/05 | 160 | 0.18 | 1.23 | 1.11 | 30 | 40 | 50 | 40 | |
| Sugar beet | 1/04 | 185 | 0.30 | 1.25 | 0.74 | 30 | 50 | 70 | 35 | |
| Sunflower | 20/04 | 145 | 0.20 | 1.12 | 0.42 | 25 | 30 | 60 | 30 | |
| Wheat | 20/10 | 270 | 0.67 | 1.18 | 0.30 | 170 | 30 | 40 | 30 | |
| Ereğli | Dry bean | 20/05 | 125 | 0.21 | 1.07 | 0.36 | 20 | 35 | 50 | 20 |
| Maize | 10/05 | 160 | 0.23 | 1.18 | 1.07 | 30 | 40 | 50 | 40 | |
| Sugar beet | 1/04 | 185 | 0.26 | 1.22 | 0.71 | 30 | 50 | 70 | 35 | |
| Sunflower | 20/04 | 145 | 0.29 | 1.08 | 0.37 | 25 | 30 | 60 | 30 | |
| Wheat | 20/10 | 270 | 0.62 | 1.16 | 0.27 | 170 | 30 | 40 | 30 | |
| 2009 | 2010 | 2011 | 2012 | 2013 | 2014 | 2015 | 2016 | 2017 | 2018 | Mean | |
|---|---|---|---|---|---|---|---|---|---|---|---|
| Akşehir | |||||||||||
| FAO 56 Penman–Monteith | 456.7 | 466.1 | 459.0 | 477.0 | 470.2 | 462.3 | 441.2 | 471.8 | 442.1 | 405.8 | 455.2 |
| Hargreaves–Samani | 471.9 | 528.9 | 490.6 | 505.5 | 482.0 | 501.3 | 482.9 | 507.8 | 503.9 | 508.3 | 498.3 |
| Radiation Equation | 610.0 | 678.5 | 648.3 | 670.7 | 655.8 | 634.2 | 610.2 | 643.6 | 585.3 | 500.8 | 623.7 |
| ASCE Penman–Monteith | 370.2 | 407.7 | 378.7 | 388.0 | 376.3 | 375.0 | 368.0 | 383.2 | 361.1 | 325.3 | 373.4 |
| Blaney–Criddle | - | - | - | 633.5 | 606.7 | 608.6 | 575.3 | 615.3 | 565.2 | 476.2 | 583.0 |
| Re | 66.7 | 68.8 | 84.4 | 60.4 | 53 | 166.1 | 173.1 | 48.6 | 128.5 | 147.9 | 99.8 |
| Beyşehir | |||||||||||
| FAO 56 Penman–Monteith | 520.0 | 505.4 | 498.3 | 542.2 | 540.0 | 505.8 | 468.2 | 519.5 | 478.6 | 451.3 | 502.9 |
| Hargreaves–Samani | 495.2 | 510.2 | 489.0 | 499.5 | 493.5 | 491.6 | 481.3 | 505.6 | 493.4 | 497.5 | 495.7 |
| Radiation Equation | 690.7 | 679.0 | 679.7 | 726.9 | 725.1 | 683.6 | 633.5 | 700.6 | 625.2 | 543.5 | 668.8 |
| ASCE Penman–Monteith | 391.7 | 398.8 | 389.1 | 412.6 | 405.4 | 394.5 | 373.4 | 404.3 | 373.0 | 344.1 | 388.7 |
| Blaney–Criddle | - | - | - | 652.6 | 642.7 | 620.1 | 570.5 | 638.0 | 572.0 | 502.4 | 599.8 |
| Re | 70.8 | 111.9 | 53.8 | 77.5 | 63.3 | 141.4 | 110.3 | 136.5 | 145.9 | 122.9 | 103.4 |
| Cihanbeyli | |||||||||||
| FAO 56 Penman–Monteith | 553.8 | 620.3 | 577.9 | 624.3 | 603.3 | 595.0 | 581.7 | 638.1 | 598.5 | 623.4 | 601.6 |
| Hargreaves–Samani | 521.2 | 580.8 | 540.4 | 557.1 | 533.1 | 543.4 | 536.2 | 561.3 | 556.2 | 544.3 | 547.4 |
| Radiation Equation | 678.8 | 722.5 | 701.4 | 737.5 | 727.0 | 710.6 | 696.1 | 733.4 | 715.1 | 727.9 | 715.0 |
| ASCE Penman–Monteith | 401.9 | 441.0 | 417.4 | 437.0 | 424.7 | 425.7 | 416.1 | 448.9 | 431.2 | 435.3 | 427.9 |
| Blaney–Criddle | - | - | - | 713.8 | 684.0 | 693.8 | 680.2 | 722.7 | 693.2 | 693.5 | 697.3 |
| Re | 79.1 | 85 | 143.5 | 38.7 | 31.2 | 152.6 | 196.7 | 68.4 | 58.2 | 99 | 95.2 |
| Ereğli | |||||||||||
| FAO 56 Penman–Monteith | 554.4 | 549.1 | 517.2 | 543.1 | 543.9 | 549.2 | 512.8 | 539.3 | 540.0 | 546.3 | 539.5 |
| Hargreaves–Samani | 524.6 | 571.7 | 532.3 | 549.9 | 529.0 | 544.0 | 541.5 | 544.9 | 551.1 | 545.0 | 543.4 |
| Radiation Equation | 729.9 | 761.8 | 732.6 | 757.3 | 762.0 | 766.8 | 725.0 | 764.5 | 751.0 | 761.8 | 751.3 |
| ASCE Penman–Monteith | 420.1 | 438.6 | 420.9 | 430.2 | 425.0 | 433.0 | 417.0 | 429.5 | 426.1 | 432.3 | 427.3 |
| Blaney–Criddle | - | - | - | 705.4 | 693.4 | 723.8 | 685.4 | 717.3 | 709.1 | 713.0 | 706.8 |
| Re | 17.6 | 5.6 | 16.7 | 26.5 | 13.8 | 75.9 | 19.8 | 50.0 | 24.3 | 24.0 | 27.4 |
| 2009 | 2010 | 2011 | 2012 | 2013 | 2014 | 2015 | 2016 | 2017 | 2018 | Mean | |
|---|---|---|---|---|---|---|---|---|---|---|---|
| Akşehir | |||||||||||
| FAO 56 Penman–Monteith | 667.1 | 666.9 | 656.8 | 696.3 | 694.7 | 662.6 | 636.2 | 688.9 | 642.1 | 603.9 | 661.6 |
| Hargreaves–Samani | 691.6 | 763.9 | 712.2 | 744.5 | 714.0 | 722.7 | 705.3 | 741.4 | 736.3 | 746.4 | 727.8 |
| Radiation Equation | 898.8 | 976.6 | 926.9 | 985.8 | 969.5 | 907.8 | 877.9 | 941.0 | 850.5 | 761.9 | 909.7 |
| ASCE Penman–Monteith | 542.0 | 585.8 | 544.6 | 568.3 | 555.2 | 539.5 | 532.4 | 558.0 | 524.9 | 488.5 | 543.9 |
| Blaney–Criddle | - | - | - | 924.0 | 891.2 | 858.2 | 822.3 | 890.4 | 810.8 | 719.1 | 845.1 |
| Re | 165.1 | 117.3 | 170.6 | 121.1 | 112.9 | 290.2 | 292.3 | 142.0 | 224.4 | 258.3 | 189.4 |
| Beyşehir | |||||||||||
| FAO 56 Penman–Monteith | 755.9 | 770.2 | 752.0 | 808.6 | 803.4 | 746.1 | 720.6 | 767.5 | 723.9 | 681.4 | 753.0 |
| Hargreaves–Samani | 722.6 | 766.1 | 727.2 | 744.6 | 729.1 | 723.7 | 731.5 | 744.6 | 744.4 | 741.2 | 737.5 |
| Radiation Equation | 1002.0 | 1023.6 | 1012.9 | 1081.8 | 1073.2 | 994.0 | 964.4 | 1027.6 | 928.7 | 821.2 | 992.9 |
| ASCE Penman–Monteith | 571.1 | 601.9 | 579.6 | 611.2 | 601.0 | 580.6 | 568.3 | 595.2 | 558.0 | 517.5 | 578.4 |
| Blaney–Criddle | - | - | - | 972.9 | 950.0 | 905.2 | 881.5 | 934.1 | 855.4 | 758.1 | 893.9 |
| Re | 119.6 | 168.5 | 84.1 | 106.3 | 91.6 | 189.9 | 160.4 | 167.4 | 213.1 | 134.6 | 143.5 |
| Cihanbeyli | |||||||||||
| FAO 56 Penman–Monteith | 752.6 | 850.1 | 785.6 | 843.0 | 813.8 | 791.6 | 803.8 | 864.8 | 831.4 | 848.6 | 818.5 |
| Hargreaves–Samani | 712.7 | 780.4 | 728.2 | 759.1 | 720.8 | 725.1 | 738.3 | 756.0 | 759.5 | 741.3 | 742.1 |
| Radiation Equation | 911.2 | 969.9 | 945.0 | 996.4 | 977.8 | 942.5 | 952.7 | 993.3 | 981.7 | 984.6 | 965.5 |
| ASCE Penman–Monteith | 543.3 | 597.0 | 564.3 | 591.5 | 570.5 | 568.6 | 573.4 | 605.2 | 590.9 | 592.2 | 579.7 |
| Blaney–Criddle | - | - | - | 964.2 | 909.5 | 913.1 | 933.9 | 971.6 | 940.5 | 936.6 | 938.5 |
| Re | 82.7 | 85.4 | 141.6 | 42.2 | 29.3 | 180.0 | 236.1 | 65.4 | 69.4 | 89.2 | 102.1 |
| Ereğli | |||||||||||
| FAO 56 Penman–Monteith | 737.7 | 733.9 | 691.1 | 720.0 | 717.0 | 725.9 | 691.7 | 719.2 | 729.1 | 730.2 | 719.6 |
| Hargreaves–Samani | 708.5 | 765.5 | 712.8 | 742.9 | 708.7 | 720.3 | 738.0 | 732.5 | 748.3 | 735.3 | 731.3 |
| Radiation Equation | 969.0 | 1009.7 | 975.0 | 1007.9 | 1005.5 | 1008.7 | 973.2 | 1019.3 | 1010.2 | 1011.4 | 999.0 |
| ASCE Penman–Monteith | 558.1 | 584.7 | 560.0 | 573.1 | 560.9 | 575.7 | 561.4 | 571.4 | 570.7 | 578.1 | 569.4 |
| Blaney–Criddle | - | - | - | 939.1 | 907.9 | 944.5 | 925.1 | 952.1 | 949.6 | 946.0 | 937.8 |
| Re | 83.1 | 82.7 | 73.2 | 126.1 | 58.9 | 35.3 | 158.5 | 111.6 | 77.4 | 43.8 | 85.1 |
| 2009 | 2010 | 2011 | 2012 | 2013 | 2014 | 2015 | 2016 | 2017 | 2018 | Mean | |
|---|---|---|---|---|---|---|---|---|---|---|---|
| Akşehir | |||||||||||
| FAO 56 Penman–Monteith | 746.3 | 725.0 | 706.0 | 760.6 | 778.3 | 733.7 | 688.1 | 761.1 | 698.6 | 665.9 | 726.4 |
| Hargreaves–Samani | 773.7 | 843.0 | 781.6 | 822.3 | 806.2 | 803.5 | 774.9 | 824.0 | 805.0 | 836.8 | 807.1 |
| Radiation Equation | 1014.2 | 1072.3 | 994.0 | 1074.5 | 1086.6 | 1012.4 | 950.7 | 1038.7 | 929.9 | 844.3 | 1001.8 |
| ASCE Penman–Monteith | 607.7 | 640.0 | 590.7 | 624.9 | 622.0 | 597.7 | 580.1 | 616.3 | 573.6 | 542.5 | 599.6 |
| Blaney–Criddle | - | - | - | 994.9 | 991.7 | 942.6 | 872.9 | 971.5 | 870.9 | 801.6 | 920.9 |
| Re | 234.0 | 176.1 | 218.1 | 143.4 | 139.0 | 294.3 | 359.7 | 177.7 | 256.3 | 336.7 | 233.5 |
| Beyşehir | |||||||||||
| FAO 56 Penman–Monteith | 845.8 | 860.1 | 838.4 | 895.9 | 896.2 | 828.9 | 813.5 | 861.4 | 814.6 | 768.5 | 842.3 |
| Hargreaves–Samani | 813.4 | 856.3 | 810.5 | 835.4 | 816.9 | 807.5 | 825.4 | 837.1 | 835.3 | 834.4 | 827.2 |
| Radiation Equation | 1119.4 | 1139.1 | 1126.4 | 1199.2 | 1199.1 | 1102.0 | 1085.4 | 1154.0 | 1039.9 | 935.2 | 1110.0 |
| ASCE Penman–Monteith | 639.1 | 670.7 | 644.8 | 679.6 | 669.4 | 645.7 | 640.2 | 665.8 | 624.8 | 587.4 | 646.8 |
| Blaney–Criddle | - | - | - | 1075.9 | 1053.1 | 996.9 | 990.5 | 1044.7 | 950.7 | 857.8 | 995.7 |
| Re | 171.2 | 201.6 | 131.7 | 142.2 | 117.8 | 218.9 | 223.8 | 221.4 | 264.9 | 171.8 | 186.5 |
| Cihanbeyli | |||||||||||
| FAO 56 Penman–Monteith | 900.7 | 1005.4 | 911.0 | 1008.6 | 994.1 | 945.8 | 925.2 | 1025.8 | 943.9 | 1008.2 | 966.9 |
| Hargreaves–Samani | 876.1 | 960.9 | 887.1 | 931.6 | 904.6 | 892.5 | 887.4 | 928.2 | 923.2 | 912.8 | 910.4 |
| Radiation Equation | 1119.3 | 1179.3 | 1120.3 | 1211.0 | 1208.1 | 1146.4 | 1123.4 | 1190.7 | 1151.7 | 1200.5 | 1165.1 |
| ASCE Penman–Monteith | 659.8 | 716.6 | 667.0 | 714.0 | 704.5 | 685.2 | 671.2 | 723.9 | 697.0 | 715.7 | 695.5 |
| Blaney–Criddle | - | - | - | 1159.0 | 1128.2 | 1098.1 | 1081.7 | 1157.0 | 1095.7 | 1135.8 | 1122.2 |
| Re | 179.5 | 132.3 | 210.6 | 71.0 | 93.4 | 231.5 | 290.4 | 117.3 | 103.3 | 175.7 | 160.5 |
| Ereğli | |||||||||||
| FAO 56 Penman–Monteith | 898.3 | 879.4 | 818.0 | 871.2 | 876.4 | 878.0 | 817.0 | 864.2 | 860.9 | 876.3 | 864.0 |
| Hargreaves–Samani | 859.4 | 923.6 | 855.1 | 898.5 | 870.2 | 876.5 | 877.3 | 880.0 | 893.4 | 890.8 | 882.5 |
| Radiation Equation | 1193.2 | 1224.2 | 1160.8 | 1220.5 | 1230.0 | 1225.5 | 1156.4 | 1224.2 | 1200.7 | 1222.9 | 1205.8 |
| ASCE Penman–Monteith | 680.3 | 705.5 | 669.0 | 693.5 | 688.3 | 694.4 | 669.0 | 689.9 | 680.8 | 698.3 | 686.9 |
| Blaney–Criddle | - | - | - | 1128.1 | 1111.6 | 1138.9 | 1079.3 | 1135.3 | 1118.9 | 1141.1 | 1121.9 |
| Re | 127.4 | 110.8 | 187.1 | 88.9 | 128.6 | 166.9 | 143.6 | 131.3 | 122.0 | 91.6 | 129.8 |
| 2009 | 2010 | 2011 | 2012 | 2013 | 2014 | 2015 | 2016 | 2017 | 2018 | Mean | |
|---|---|---|---|---|---|---|---|---|---|---|---|
| Akşehir | |||||||||||
| FAO 56 Penman–Monteith | 568.4 | 541.9 | 534.4 | 576.2 | 585.3 | 557.7 | 510.3 | 576.6 | 524.3 | 499.0 | 547.4 |
| Hargreaves–Samani | 586.8 | 632.9 | 590.2 | 620.8 | 606.4 | 611.3 | 576.8 | 625.0 | 603.4 | 628.9 | 608.3 |
| Radiation Equation | 769.5 | 801.4 | 753.1 | 813.3 | 815.3 | 773.6 | 704.7 | 787.1 | 702.4 | 631.3 | 755.2 |
| ASCE Penman–Monteith | 461.9 | 479.8 | 447.6 | 474.0 | 467.7 | 453.8 | 432.2 | 467.0 | 432.8 | 406.4 | 452.3 |
| Blaney–Criddle | - | - | - | 755.3 | 746.9 | 724.6 | 646.0 | 740.8 | 659.0 | 603.7 | 696.6 |
| Re | 155.3 | 116.9 | 165.2 | 118.7 | 95.4 | 225.1 | 290.3 | 132.7 | 219.1 | 258.2 | 177.7 |
| Beyşehir | |||||||||||
| FAO 56 Penman–Monteith | 625.7 | 612.4 | 596.0 | 650.4 | 653.9 | 607.0 | 568.8 | 623.2 | 576.1 | 546.5 | 606.0 |
| Hargreaves–Samani | 600.1 | 620.7 | 590.6 | 606.2 | 603.3 | 594.8 | 587.7 | 611.8 | 599.1 | 607.3 | 602.2 |
| Radiation Equation | 835.7 | 823.7 | 812.6 | 876.1 | 880.4 | 820.6 | 770.0 | 841.5 | 751.8 | 663.3 | 807.6 |
| ASCE Penman–Monteith | 472.8 | 483.2 | 465.9 | 496.9 | 492.4 | 474.9 | 453.7 | 486.3 | 449.4 | 419.0 | 469.5 |
| Blaney–Criddle | - | - | - | 781.5 | 776.9 | 739.0 | 690.9 | 761.0 | 684.2 | 610.5 | 720.6 |
| Re | 110.9 | 165.0 | 83.1 | 106.3 | 88.0 | 163.5 | 149.2 | 159.1 | 202.4 | 126.9 | 135.4 |
| Cihanbeyli | |||||||||||
| FAO 56 Penman–Monteith | 671.1 | 715.8 | 662.7 | 743.1 | 732.3 | 699.9 | 661.4 | 761.1 | 675.4 | 735.8 | 705.9 |
| Hargreaves–Samani | 649.1 | 704.0 | 653.8 | 686.9 | 667.2 | 662.6 | 641.1 | 689.2 | 673.0 | 670.8 | 669.8 |
| Radiation Equation | 834.2 | 856.4 | 820.9 | 892.6 | 891.4 | 853.7 | 808.6 | 883.4 | 834.7 | 884.5 | 856.0 |
| ASCE Penman–Monteith | 490.9 | 518.3 | 488.4 | 526.8 | 519.2 | 506.7 | 482.4 | 536.7 | 505.7 | 525.4 | 510.1 |
| Blaney–Criddle | - | - | - | 855.2 | 836.4 | 819.2 | 775.0 | 861.3 | 796.5 | 836.3 | 825.7 |
| Re | 145.7 | 116.7 | 195.6 | 66.6 | 73.4 | 170.5 | 265.5 | 104.5 | 98.9 | 170.2 | 140.8 |
| Ereğli | |||||||||||
| FAO 56 Penman–Monteith | 678.4 | 648.9 | 609.3 | 651.0 | 659.1 | 655.9 | 600.3 | 649.4 | 637.0 | 651.9 | 644.1 |
| Hargreaves–Samani | 645.8 | 685.0 | 637.5 | 668.8 | 652.0 | 659.7 | 643.1 | 658.6 | 658.8 | 662.4 | 657.2 |
| Radiation Equation | 900.9 | 908.2 | 865.0 | 907.4 | 925.8 | 920.0 | 850.3 | 920.4 | 890.2 | 910.7 | 899.9 |
| ASCE Penman–Monteith | 513.5 | 523.3 | 499.5 | 518.2 | 517.4 | 517.9 | 494.3 | 518.3 | 506.3 | 521.5 | 513.0 |
| Blaney–Criddle | - | - | - | 838.1 | 837.9 | 854.9 | 785.7 | 854.7 | 827.4 | 849.3 | 835.4 |
| Re | 112.7 | 109.5 | 172.4 | 88.7 | 128.6 | 69.1 | 141.7 | 107.8 | 118.3 | 87.4 | 113.6 |
| 2009 | 2010 | 2011 | 2012 | 2013 | 2014 | 2015 | 2016 | 2017 | 2018 | Mean | |
|---|---|---|---|---|---|---|---|---|---|---|---|
| Akşehir | |||||||||||
| FAO 56 Penman–Monteith | 545.5 | 503.0 | 456.7 | 530.1 | 597.0 | 550.6 | 495.3 | 608.8 | 515.6 | 590.5 | 539.3 |
| Hargreaves–Samani | 561.8 | 628.1 | 567.7 | 580.5 | 626.4 | 604.3 | 565.6 | 648.2 | 586.2 | 680.5 | 604.9 |
| Radiation Equation | 751.0 | 793.8 | 660.9 | 759.1 | 827.1 | 789.2 | 661.8 | 844.9 | 694.1 | 781.3 | 756.3 |
| ASCE Penman–Monteith | 428.0 | 434.4 | 388.4 | 419.5 | 461.7 | 431.9 | 401.6 | 464.5 | 401.9 | 455.2 | 428.7 |
| Blaney–Criddle | - | - | 565.1 | 640.6 | 588.5 | 480.4 | 658.5 | 498.7 | 669.6 | 585.9 | |
| Re | 520.1 | 522.9 | 472.0 | 349.6 | 381.0 | 312.4 | 595.0 | 284.8 | 445.0 | 539.8 | 442.2 |
| Beyşehir | |||||||||||
| FAO 56 Penman–Monteith | 553.6 | 594.0 | 509.6 | 556.6 | 605.2 | 570.2 | 524.0 | 607.2 | 534.1 | 584.6 | 563.9 |
| Hargreaves–Samani | 590.3 | 633.9 | 573.4 | 581.5 | 637.4 | 611.5 | 575.1 | 641.1 | 588.6 | 659.4 | 609.2 |
| Radiation Equation | 794.4 | 824.5 | 717.9 | 809.9 | 848.9 | 825.1 | 710.7 | 860.3 | 737.4 | 782.6 | 791.2 |
| ASCE Penman–Monteith | 431.8 | 456.7 | 401.5 | 432.9 | 464.2 | 443.1 | 410.1 | 464.3 | 410.1 | 447.7 | 436.2 |
| Blaney–Criddle | - | - | - | 597.3 | 641.5 | 591.4 | 511.1 | 645.3 | 518.2 | 635.0 | 591.4 |
| Re | 492.2 | 540.9 | 434.1 | 530.4 | 498.2 | 434.0 | 479.2 | 340.0 | 500.6 | 382.5 | 463.2 |
| Cihanbeyli | |||||||||||
| FAO 56 Penman–Monteith | 379.7 | 467.3 | 378.8 | 440.5 | 458.0 | 478.8 | 415.7 | 507.8 | 427.4 | 511.8 | 446.6 |
| Hargreaves–Samani | 444.7 | 524.1 | 460.7 | 479.0 | 512.7 | 505.9 | 454.4 | 535.6 | 480.8 | 536.5 | 493.4 |
| Radiation Equation | 536.6 | 607.8 | 504.6 | 581.4 | 601.7 | 636.1 | 571.1 | 635.2 | 583.9 | 677.8 | 593.6 |
| ASCE Penman–Monteith | 294.2 | 341.3 | 288.5 | 317.0 | 341.8 | 345.8 | 312.7 | 356.8 | 326.3 | 372.4 | 329.7 |
| Blaney–Criddle | - | - | - | 412.3 | 471.8 | 484.0 | 411.7 | 510.9 | 414.3 | 568.2 | 467.6 |
| Re | 378.9 | 323.6 | 397.5 | 240.6 | 260.9 | 244.4 | 444.7 | 192.7 | 258.8 | 328.5 | 307.1 |
| Ereğli | |||||||||||
| FAO 56 Penman–Monteith | 573.8 | 575.4 | 499.6 | 552.7 | 562.4 | 582.3 | 510.9 | 592.0 | 540.7 | 593.8 | 558.4 |
| Hargreaves–Samani | 581.5 | 650.4 | 586.1 | 611.8 | 635.6 | 635.1 | 589.2 | 640.5 | 601.5 | 662.1 | 619.4 |
| Radiation Equation | 791.1 | 806.1 | 716.6 | 787.6 | 791.0 | 817.3 | 725.6 | 843.4 | 780.6 | 835.9 | 789.5 |
| ASCE Penman–Monteith | 430.9 | 459.6 | 412.5 | 438.0 | 451.3 | 450.7 | 421.8 | 465.3 | 430.0 | 471.5 | 443.2 |
| Blaney–Criddle | - | - | - | 637.3 | 641.5 | 658.8 | 562.7 | 689.7 | 604.2 | 722.8 | 645.3 |
| Re | 328.2 | 309.1 | 395.4 | 268.4 | 374.9 | 195.6 | 367.2 | 224.5 | 301.9 | 250.3 | 301.5 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Amarkai, P.A.; Süheri, S. Comparative Evaluation of Crop Evapotranspiration Estimation Methods in a Semi-Arid Region. Sustainability 2024, 16, 11133. https://doi.org/10.3390/su162411133
Amarkai PA, Süheri S. Comparative Evaluation of Crop Evapotranspiration Estimation Methods in a Semi-Arid Region. Sustainability. 2024; 16(24):11133. https://doi.org/10.3390/su162411133
Chicago/Turabian StyleAmarkai, Peter Addo, and Sinan Süheri. 2024. "Comparative Evaluation of Crop Evapotranspiration Estimation Methods in a Semi-Arid Region" Sustainability 16, no. 24: 11133. https://doi.org/10.3390/su162411133
APA StyleAmarkai, P. A., & Süheri, S. (2024). Comparative Evaluation of Crop Evapotranspiration Estimation Methods in a Semi-Arid Region. Sustainability, 16(24), 11133. https://doi.org/10.3390/su162411133






