Operational Optimization of Regional Integrated Energy Systems with Heat Pumps and Hydrogen Renewable Energy under Integrated Demand Response
Abstract
:1. Introduction
- (1)
- Introducing an IDR into RIES that considers the human body’s delayed and subjective temperature perception, proposing an optimization method for the operation of the RIES that includes IDR.
- (2)
- Incorporating a refined P2G electric hydrogen production model with an adjustable thermoelectric ratio to support the RIES’s transition from traditional fossil fuels to RESs.
- (3)
- Including the ground-source HP as conversion equipment in the traditional RIES and conducting a comparative analysis to confirm the model’s economic and energy-saving benefits.
2. The RIES’ Structure and IDR Model
2.1. The RIES Framework
- (1)
- Renewable energy units: these include wind turbines (WT) and PV panels, which harness wind and solar energy for generating power.
- (2)
- Energy conversion devices: this category encompasses a suite of technologies such as gas turbines (GT), ground-source HP units, waste heat boilers (WHB), absorption refrigerators (AR), EC, and HFC, each contributing to the system’s ability to convert energy from one form to another.
- (3)
- Energy storage devices: the system incorporates a hydrogen storage tank (HST) for hydrogen retention and a combined heat and cold storage tank (HS/CS) to maintain thermal energy reserves.
- (4)
- Load side components: the demand side includes the electrical load (EL), the heat load (HL), and the cold load (CL), all of which are integral to the IDR strategy.
2.2. IDR Model
2.2.1. Power Load IDR
2.2.2. HL Demand Response
2.2.3. CL Demand Response
3. Output and Constraint Modeling of Equipment in the RIES
3.1. Scenery Output Model
3.2. Mathematical Model of CCHP
3.3. Mathematical Model of Ground-Source HPs
3.4. Mathematical Model of Electric Hydrogen Production Equipment
3.5. Mathematical Model of the Energy Storage Device
3.6. Constraints on the Equipment’s Start-Up and Shutdown
4. The RIES Optimization Model under IDR
4.1. Objective Function
- (1)
- Cost of gas of the unit:
- (2)
- Operation and maintenance cost of the unit:
- (3)
- Equipment start-up and shutdown costs:
- (4)
- Electric energy interaction cost:
4.2. Constraints of the Balance of the RIES
- (1)
- Electrical power balance constraints:
- (2)
- Thermal power balance constraints:
- (3)
- Cold power balance constraints:
- (4)
- Hydrogen power balance constraints:
4.3. Solution Method
5. Results and Discussion
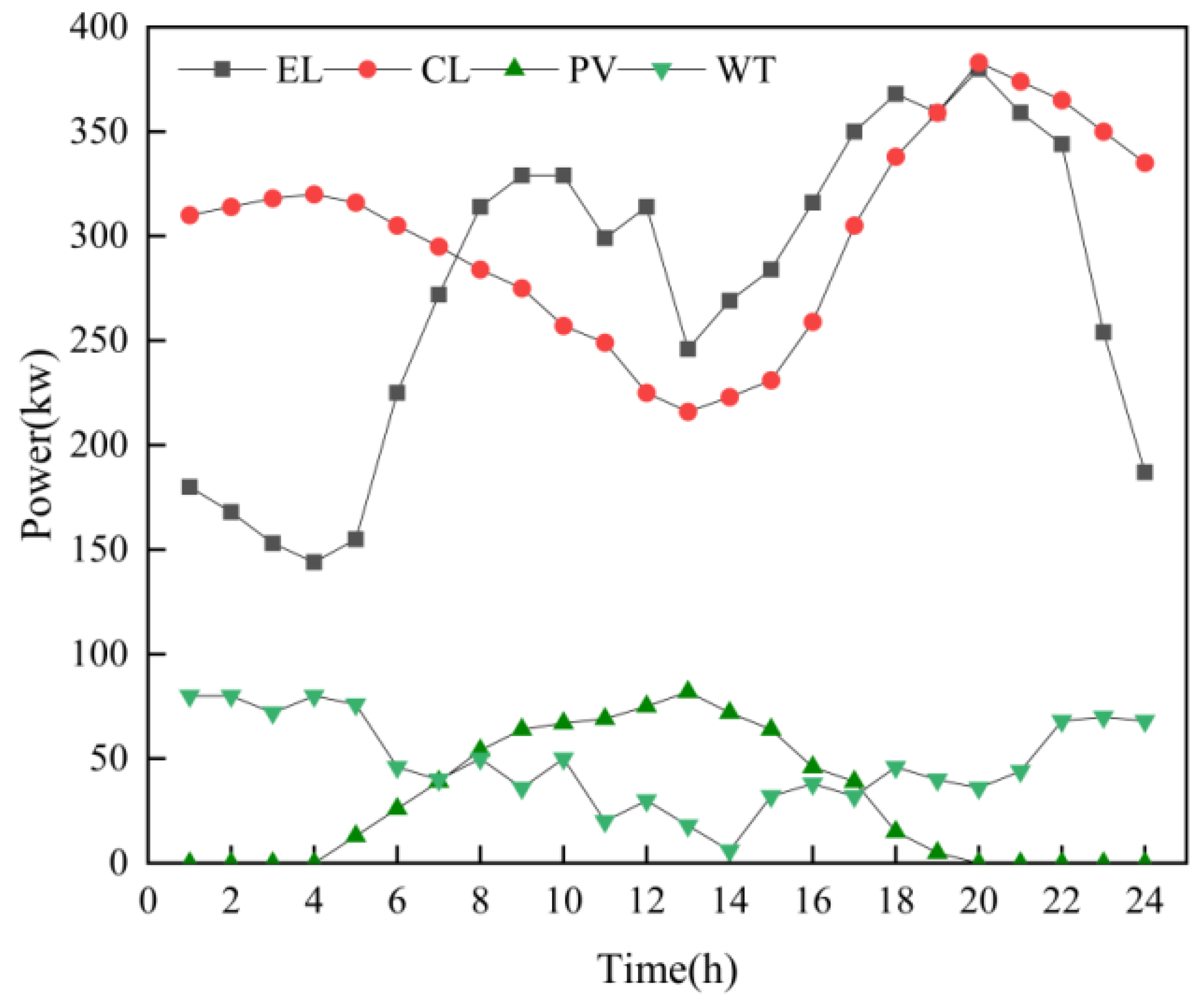
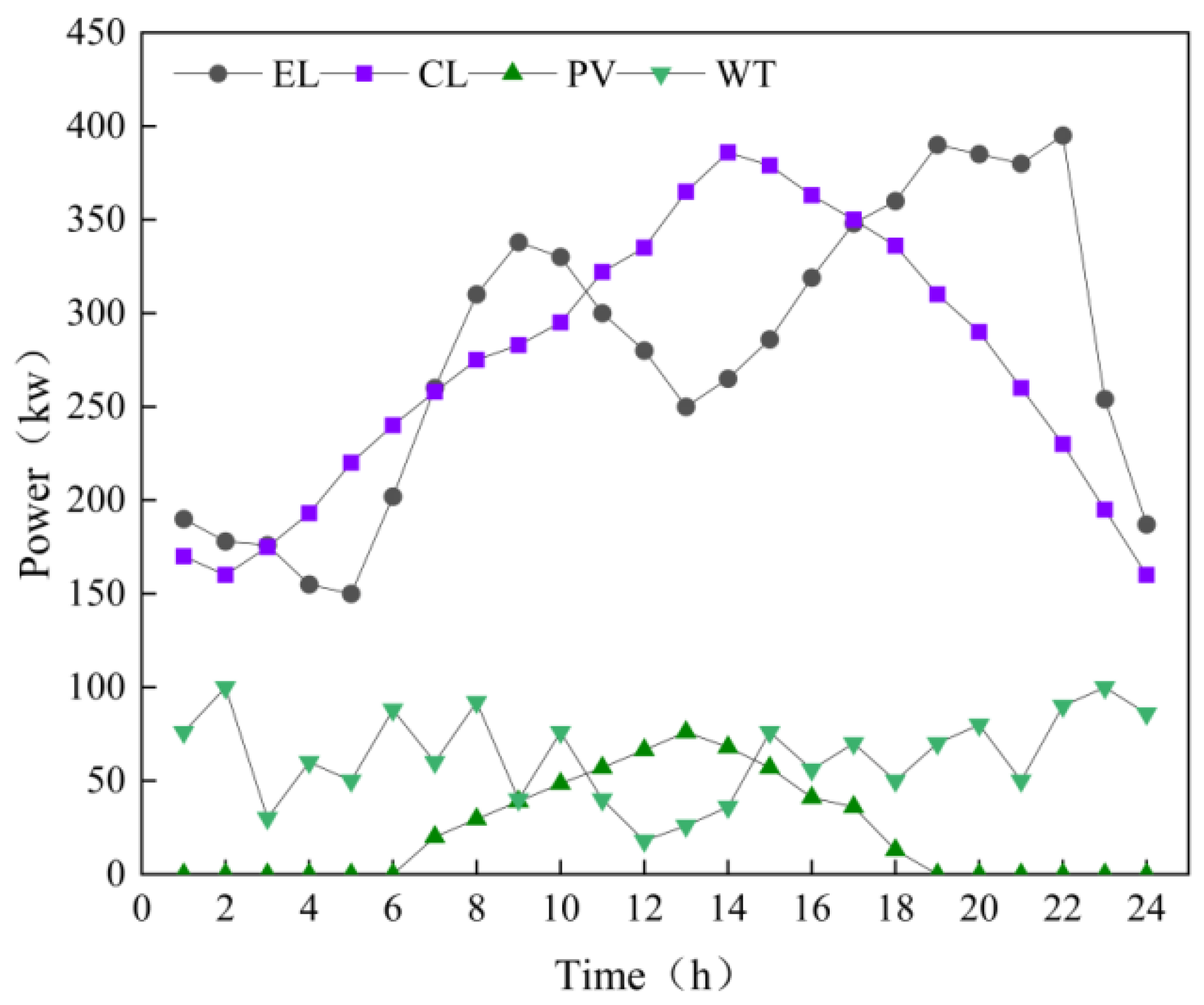
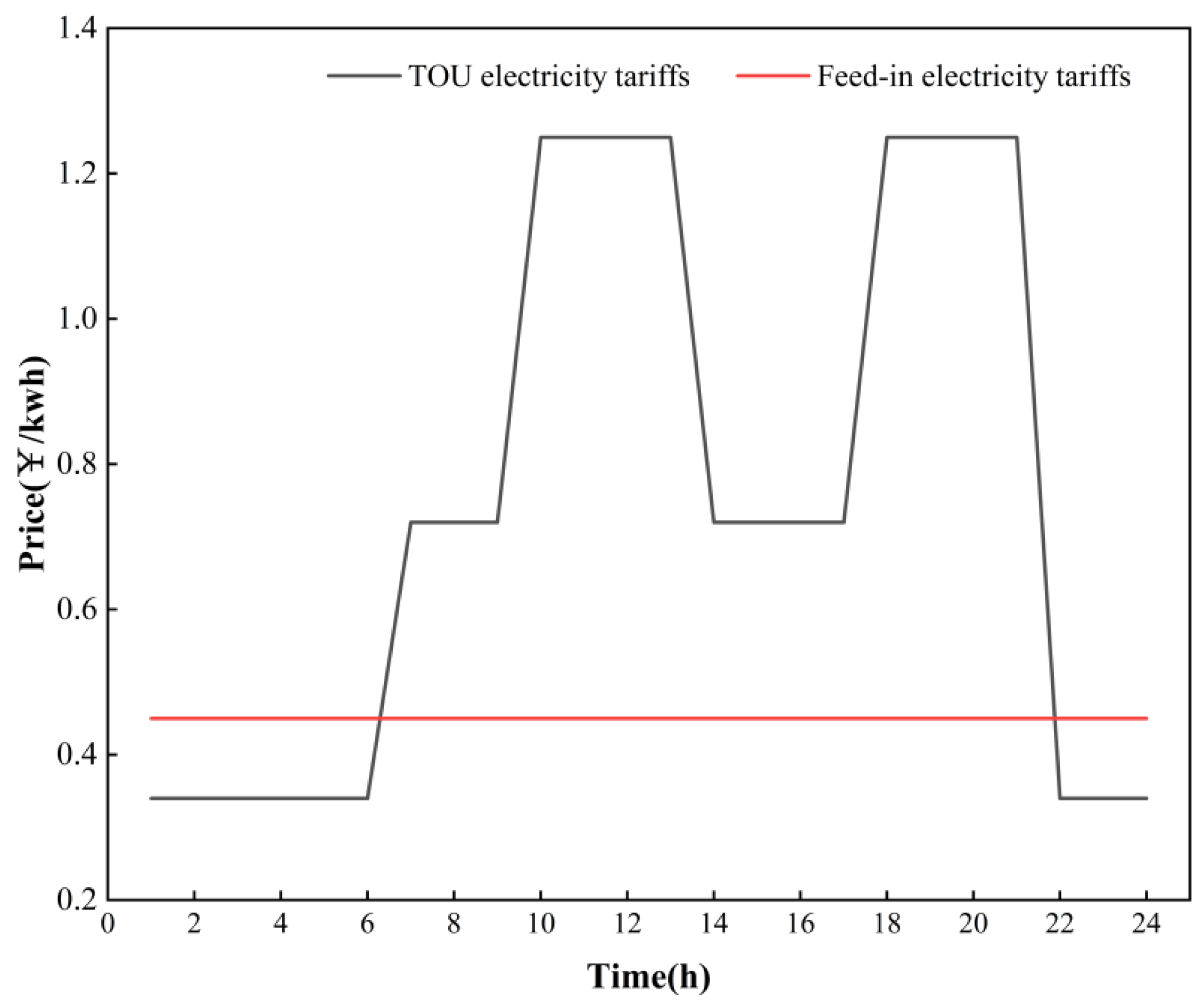
5.1. Baseline Data
5.2. Analysis of the Influence of Different Scheduling Models on the Simulation’s Results
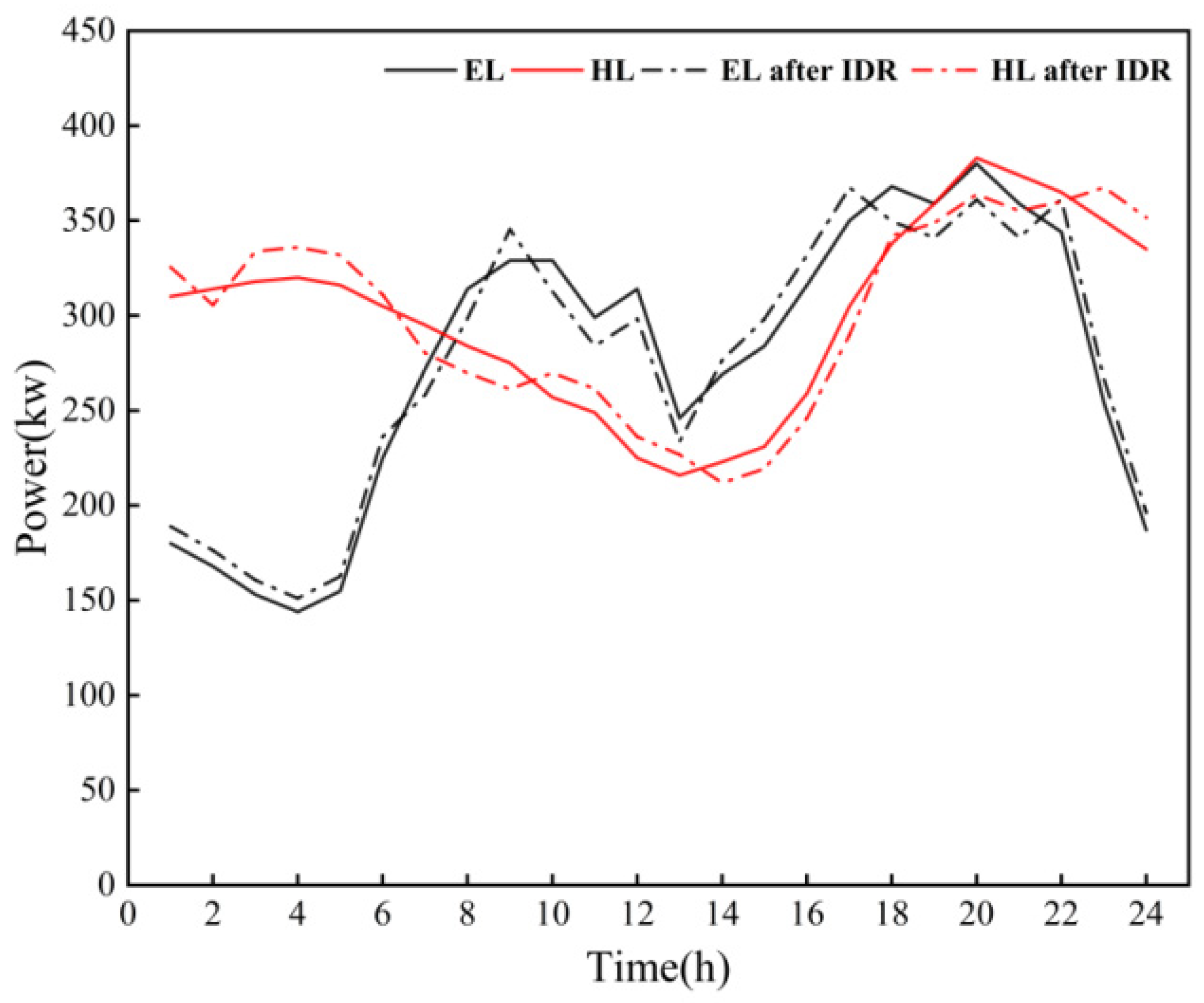
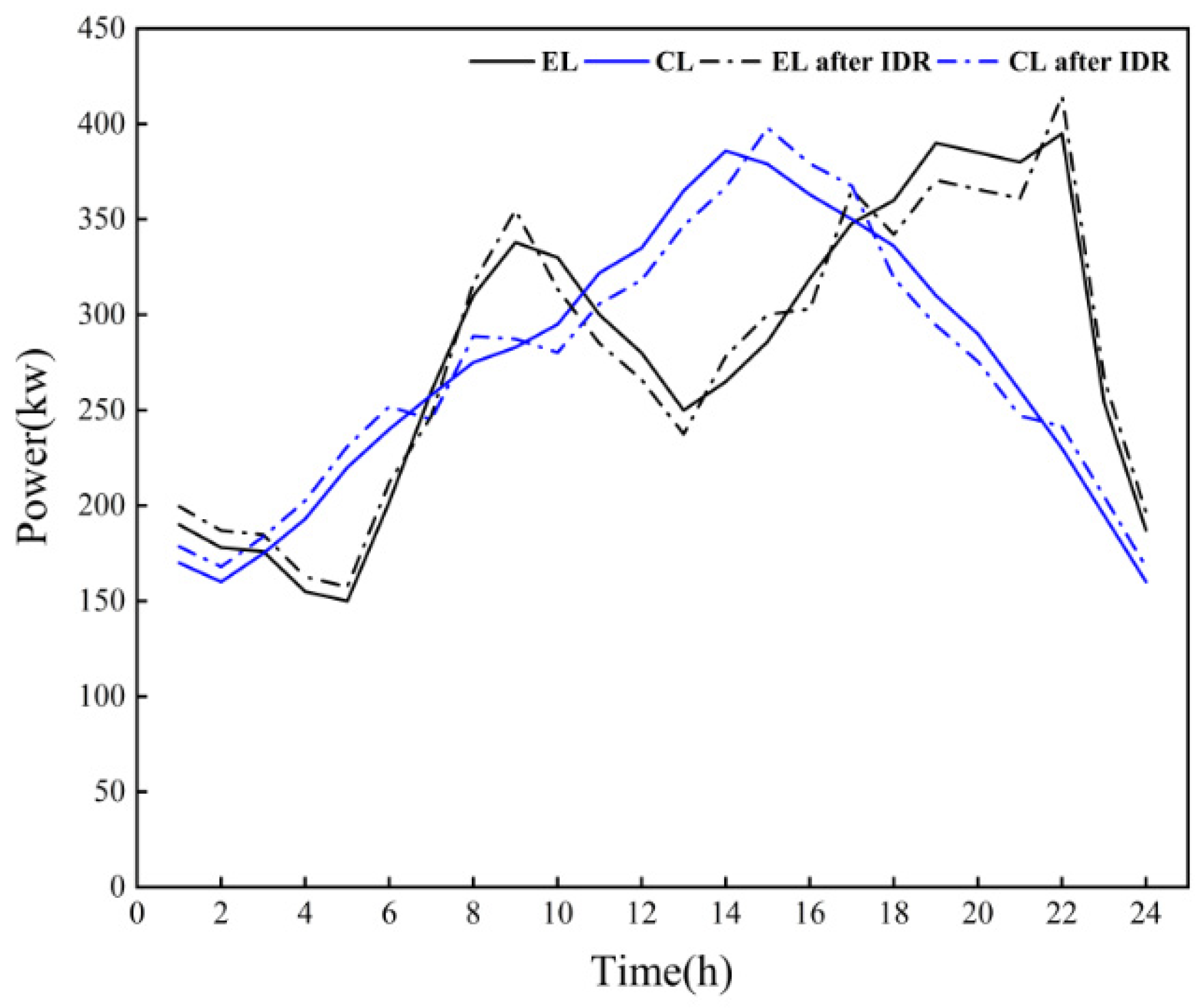
5.2.1. Influence of IDR on the RIES’s Operation
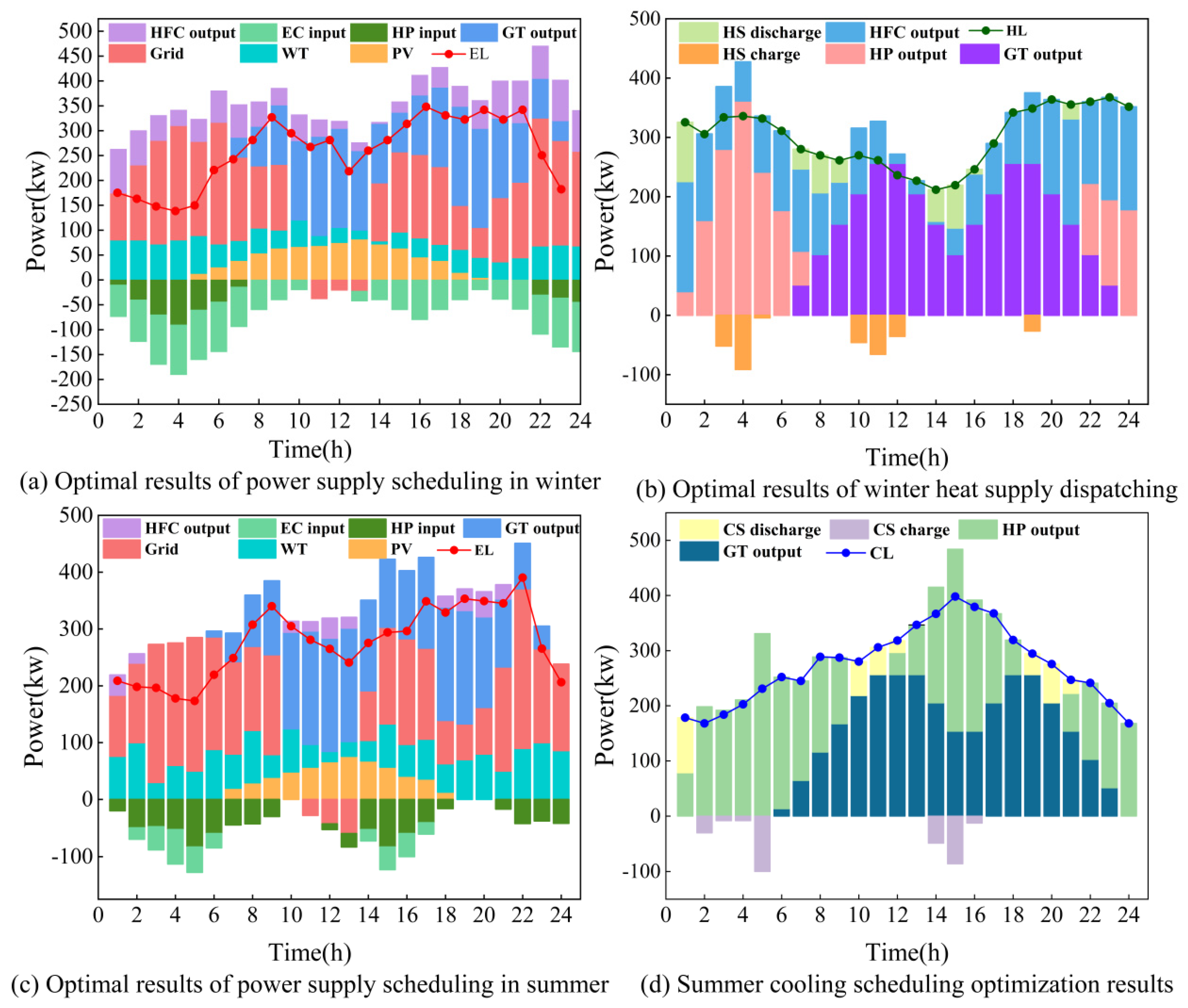
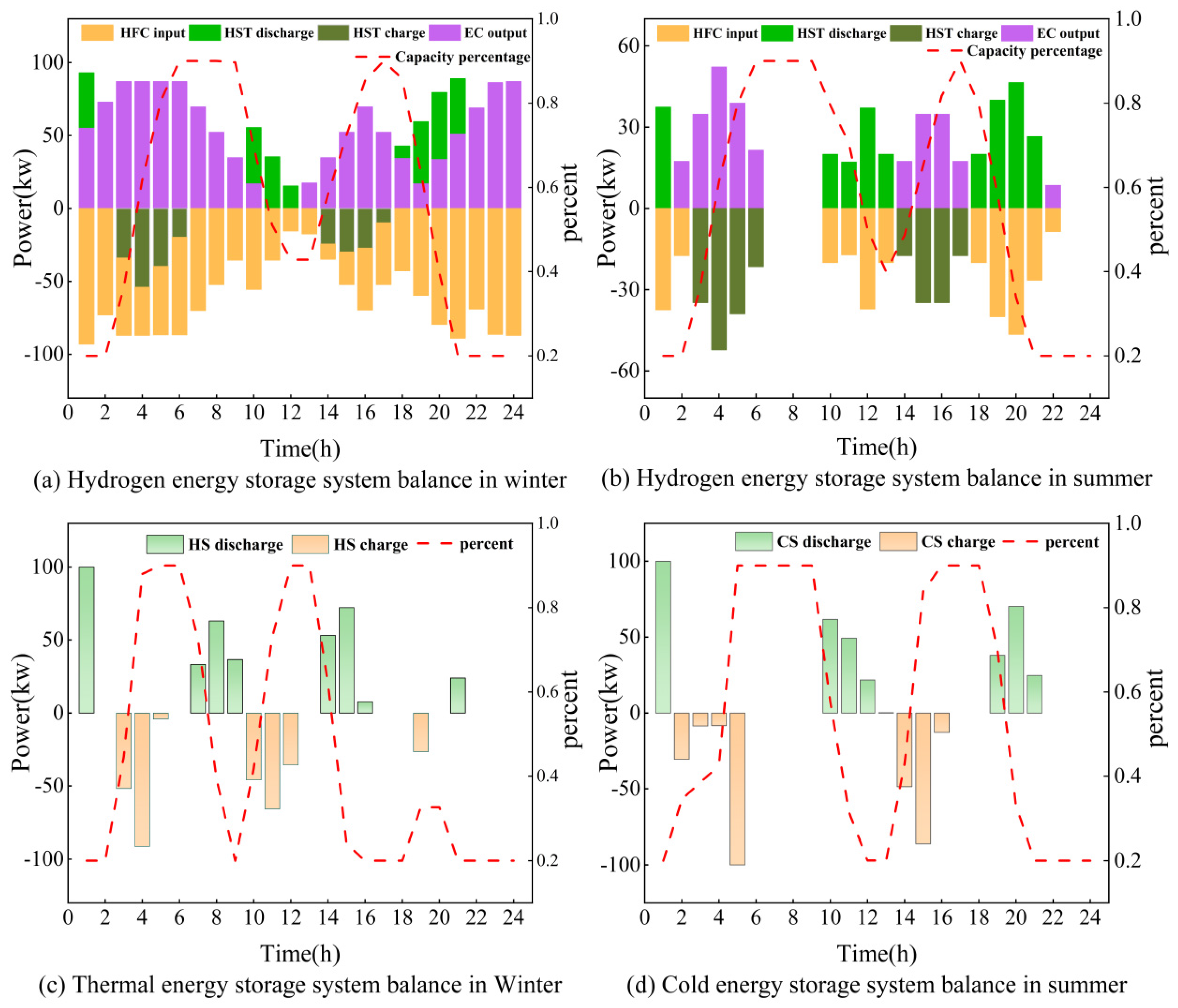
5.2.2. Analysis of Supply–Demand Balance
Results of Optimization of Typical Winter Days
Results of Optimization of Typical Summer Days
5.2.3. Simulation and Comparative Analysis of the Optimization Schemes
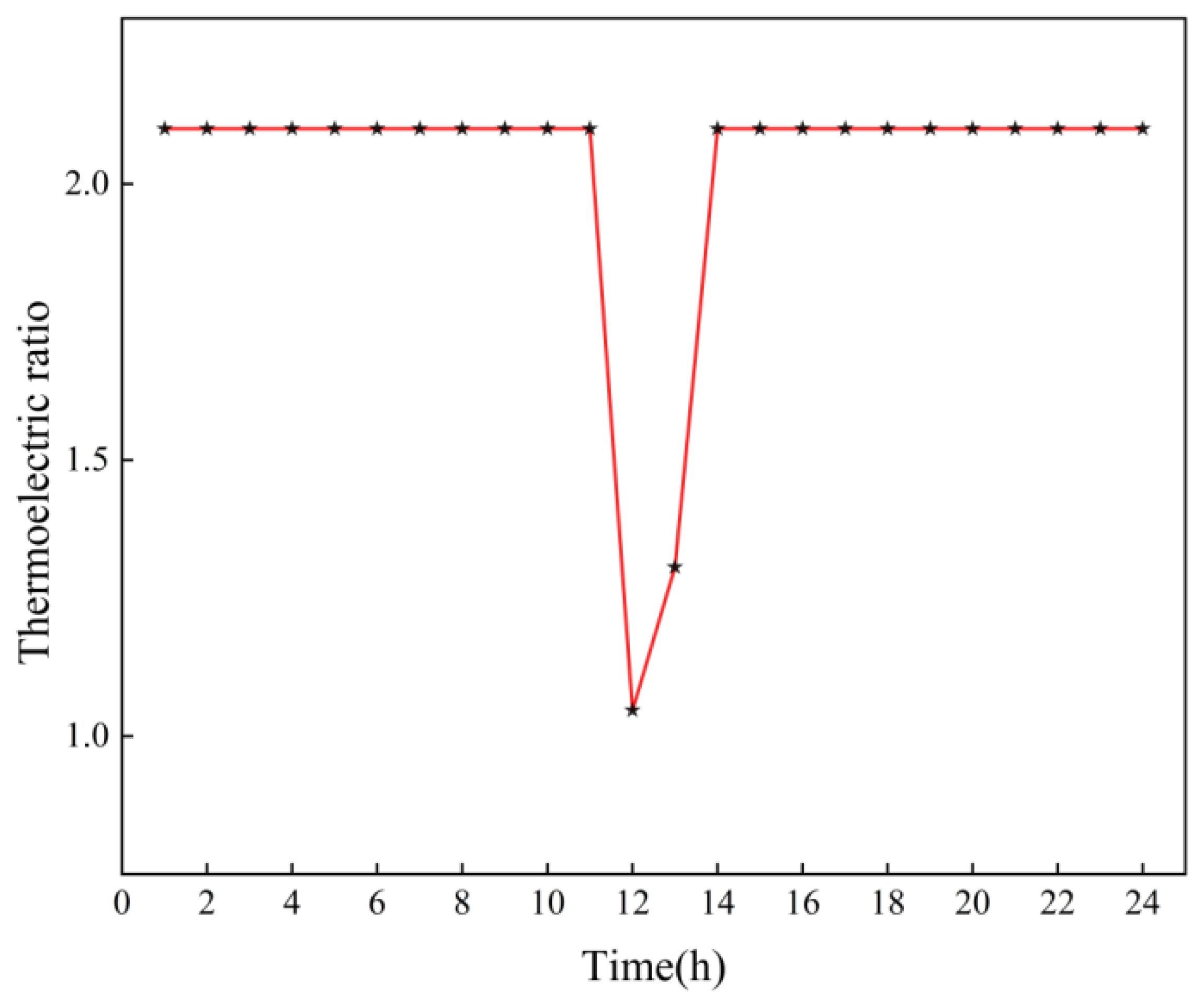
5.2.4. Influence of the HFC’s Adjustable Thermoelectric Ratio System
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Wang, Y.; Huang, F.; Tao, S.; Ma, Y.; Ma, Y.; Liu, L.; Dong, F. Multi-objective planning of regional integrated energy system aiming at exergy efficiency and economy. Appl. Energy 2022, 306, 118120. [Google Scholar] [CrossRef]
- Yan, R.; Wang, J.; Lu, S.; Ma, Z.; Zhou, Y.; Zhang, L.; Cheng, Y. Multi-objective two-stage adaptive robust planning method for an integrated energy system considering load uncertainty. Energy Build. 2021, prepublish. [Google Scholar] [CrossRef]
- Duan, P.; Zhao, B.; Zhang, X.; Fen, M. A day-ahead optimal operation strategy for integrated energy systems in multi-public buildings based on cooperative game. Energy 2023, 275, 127395. [Google Scholar] [CrossRef]
- Xu, J.; Wang, X.; Gu, Y.; Ma, S. A data-based day-ahead scheduling optimization approach for regional integrated energy systems with varying operating conditions. Energy 2023, 283, 128534. [Google Scholar] [CrossRef]
- González-Delgado, Á.D.; Vargas-Mira, A.; Zuluaga-García, C. Economic Evaluation and Technoeconomic Resilience Analysis of Two Routes for Hydrogen Production via Indirect Gasification in North Colombia. Sustainability 2023, 15, 16371. [Google Scholar] [CrossRef]
- Ahern, E.P.; Deane, P.; Persson, T.; Gallachóir, B.; Murphy, J.D. A perspective on the potential role of renewable gas in a smart energy island system. Renew. Energy 2015, 78, 648–656. [Google Scholar] [CrossRef]
- Nazari-Heris, M.; Mirzaei, M.A.; Mohammadi-Ivatloo, B.; Marzband, M.; Asadi, S. Economic-environmental effect of power to gas technology in coupled electricity and gas systems with price-responsive shiftable loads. J. Clean. Prod. 2019, 244, 118769. [Google Scholar] [CrossRef]
- Luo, Z.; Wang, J.; Xiao, N.; Yang, L.; Zhao, W.; Geng, J.; Lu, T.; Luo, M.; Dong, C. Low Carbon Economic Dispatch Optimization of Regional Integrated Energy Systems Considering Heating Network and P2G. Energies 2022, 15, 5494. [Google Scholar] [CrossRef]
- Khalili, R.; Khaledi, A.; Marzband, M.; Nematollahi, A.F.; Vahidi, B.; Siano, P. Robust multi-objective optimization for the Iranian electricity market considering green hydrogen and analyzing the performance of different demand response programs. Appl. Energy 2023, 334, 120737. [Google Scholar] [CrossRef]
- Zhang, X.; Zhang, Y. Environment-friendly and economical scheduling optimization for integrated energy system considering power-to-gas technology and carbon capture power plant. J. Clean. Prod. 2020, 276, 123348. [Google Scholar] [CrossRef]
- Ancona, M.A.; Antonucci, V.; Branchini, L.; Catena, F.; De Pascale, A.; Di Blasi, A.; Ferraro, M.; Italiano, C.; Melino, F.; Vita, A. Parametric Thermo-Economic Analysis of a Power-to-Gas Energy System with Renewable Input, High Temperature Co-Electrolysis and Methanation. Energies 2022, 15, 1791. [Google Scholar] [CrossRef]
- Li, X.; Li, T.; Liu, L.; Wang, Z.; Li, X.; Huang, J.; Huang, J.; Guo, P.; Xiong, W. Operation optimization for integrated energy system based on hybrid CSP-CHP considering power-to-gas technology and carbon capture system. J. Clean. Prod. 2023, 391, 136119. [Google Scholar] [CrossRef]
- Xu, L.; Wang, S.; Wang, Z.; Qi, X. Dual-layer self-healing strategy for standalone building energy systems: A case study of a tropical island. Energy Build. 2023, 283, 112827. [Google Scholar] [CrossRef]
- Yun, Y.; Zhang, D.; Yang, S.; Li, Y.; Yan, J. Low-carbon optimal dispatch of integrated energy system considering the operation of oxy-fuel combustion coupled with power-to-gas and hydrogen-doped gas equipment. Energy 2023, 283, 129127. [Google Scholar] [CrossRef]
- Mansour-Saatloo, A.; Pezhmani, Y.; Mirzaei, M.A.; Mohammadi-Ivatloo, B.; Zare, K.; Marzband, M.; Anvari-Moghaddam, A. Robust decentralized optimization of Multi-Microgrids integrated with Power-to-X technologies. Appl. Energy 2021, 304, 117635. [Google Scholar] [CrossRef]
- Nojavan, S.; Nourollahi, R.; Pashaei-Didani, H.; Zare, K. Uncertainty-based electricity procurement by retailer using robust optimization approach in the presence of demand response exchange. Int. J. Electr. Power Energy Syst. 2019, 105, 237–248. [Google Scholar] [CrossRef]
- Ali, P.; Mahdi, S. A system dynamics investigation on the long-term impacts of demand response in generation investment planning incorporating renewables. Renew. Sustain. Energy Rev. 2023, 171, 113003. [Google Scholar]
- Jordehi, A.R.; Mansouri, S.A.; Tostado-Véliz, M.; Hossain, M.J.; Nasir, M.; Jurado, F. Optimal placement of hydrogen fuel stations in power systems with high photovoltaic penetration and responsive electric demands in presence of local hydrogen markets. Int. J. Hydrogen Energy 2023, 360, 62–76. [Google Scholar]
- Jeseok, R.; Jinho, K. A prospect-theoretic game approach to demand response market participation through energy sharing in energy storage systems under uncertainty. Energy Rep. 2023, 9, 1093–1103. [Google Scholar]
- Zhang, S.; Wen, M.; Cheng, H.; Hu, X.; Xu, G. Reliability evaluation of electricity-heat integrated energy system with heat pump. CSEE J. Power Energy Syst. 2018, 4, 425–433. [Google Scholar] [CrossRef]
- Yin, L.; Tao, M. Balanced broad learning prediction model for carbon emissions of integrated energy systems considering distributed ground source heat pump heat storage systems and carbon capture & storage. Appl. Energy 2023, 329, 120269. [Google Scholar]
- Yin, L.; Tao, M. Correlational broad learning for optimal scheduling of integrated energy systems considering distributed ground source heat pump heat storage systems. Energy 2022, 239, 122531. [Google Scholar] [CrossRef]
- Chen, L.; Tang, H.; Wu, J.; Li, C.; Wang, Y. A robust optimization framework for energy management of CCHP users with integrated demand response in electricity market. Int. J. Electr. Power Energy Syst. 2022, 141, 108181. [Google Scholar] [CrossRef]
- Lu, Q.; Guo, Q.; Zeng, W. Optimal dispatch of community integrated energy system based on Stackelberg game and integrated demand response under carbon trading mechanism. Appl. Therm. Eng. 2023, 219, 119508. [Google Scholar] [CrossRef]
- Zeng, L.; Xu, J.; Wang, Y.; Liu, Y.; Tang, J.; Jiang, Z.; Wen, M. Day-ahead interval optimization of combined cooling and power microgrid based on interval measurement. Energy Build. 2022, 273, 112383. [Google Scholar] [CrossRef]
- Zhu, X.; Sun, Y.; Yang, J.; Dou, Z.; Li, G.; Xu, C.; Wen, Y. Day-ahead energy pricing and management method for regional integrated energy systems considering multi-energy demand responses. Energy 2022, 251, 123914. [Google Scholar] [CrossRef]
- Bin, Q.; Shaoxin, S.; Kai, W.; Zhen, Y. Optimal operation of regional integrated energy systems, including demand response and tiered carbon trading mechanisms. J. Power Syst. Autom. 2022, 34, 88–101. [Google Scholar]
- Smith, M.; Bevacqua, A.; Tembe, S.; Lal, P. Life cycle analysis (LCA) of residential ground source heat pump systems: A comparative analysis of energy efficiency in New Jersey. Sustain. Energy Technol. Assess. 2021, 47, 101364. [Google Scholar] [CrossRef]
- Alessandro, F.; Caterina, G. Recent and Future Advances in Water Electrolysis for Green Hydrogen Generation: Critical Analysis and Perspectives. Sustainability 2023, 15, 16917. [Google Scholar]
- Zhao, J.; Chen, J.; Liu, P. Simulation Study on Heating Stability of PV/T-GSHP Automatic Control Heating System Based on TRNSYS. Energies 2023, 16, 4341. [Google Scholar] [CrossRef]
- Xiao, H.; Long, F.; Zeng, L.; Zhao, W.; Wang, J.; Li, Y. Optimal scheduling of regional integrated energy system considering multiple uncertainties and integrated demand response. Electr. Power Syst. Res. 2023, 217, 109169. [Google Scholar] [CrossRef]

| Ref. | System | Objective Function | P2G | HP | DR | |||
|---|---|---|---|---|---|---|---|---|
| Electric Natural Gas | Electric Hydrogen Production | Thermoelectric Ratio Adjustability | CDR and HDR | EDR | ||||
| [6] | P2G system | Minimal operating cost | √ | √ | ||||
| [7] | Electric power system | Minimal operating costs and minimal environmental costs | √ | √ | ||||
| [8] | P2G system, heating system | Minimal operating costs and minimal carbon trading costs | √ | |||||
| [9] | RIES | Minimal operating costs | √ | √ | ||||
| [10] | IES | Minimal operating costs and minimal environmental costs | √ | |||||
| [11] | P2G system | Minimal operating costs and reductions in CO2 | √ | |||||
| [12] | P2G system, CHP | Minimal operating costs and CO2 reduction | √ | |||||
| [18] | P2G system, electric power system | Minimal operating costs | √ | |||||
| [20] | CHP | Minimal operating costs | √ | |||||
| [21] | IES | Minimal operating costs | √ | |||||
| [22] | IES | Minimal operating cost and stability | √ | |||||
| Proposed method | RIES | Minimal operating costs | √ | √ | √ | √ | √ | |
| Abbreviation | Photovoltaic Output Value | ||
|---|---|---|---|
| AR | Absorption refrigerator | Photovoltaic output value | |
| CS | Cooling storage | Solar irradiance | |
| DR | Demand response | GT’s remaining heat at time t | |
| EC | Electrolytic cell | Cooling capacity of the AR at time t | |
| E/H/CL | Electrical/heating/cooling load | Input power of the AR at time t | |
| GT | Gas turbine | Heat production of the WHB at time t | |
| HFC | Hydrogen fuel cell | GT output power at time t | |
| HP | Geothermal heat pump | Input power of the WHB at time t | |
| HST | Hydrogen storage tank | Fixed load at time t | |
| HS | Heating storage | The load can be transferred at time t | |
| IDR | Integrated demand response | Hydrogen energy output by the EC | |
| PV | Photovoltaic | HFC’s output of electricity and heat | |
| RIES | Regional integrated energy system | HP’s cooling, heat production at | |
| WHB | Waste heat boiler | time t | |
| WT | Gas turbine | HP’s cooling and heat consumption at | |
| Variables | time t | ||
| Wind field’s output value | Indices | ||
| Field speed | T | Index for a typical day | |
| Rated power of the wind farm | t | Index for time periods in a typical day | |
| Wind field’s cut wind speed | Index of scenarios | ||
| Wind field’s cutting wind speed |
| Case | Multi-Energy Coupling | Heat Pump System | Energy Storage System | IDR |
|---|---|---|---|---|
| 1 | √ | × | × | √ |
| 2 | √ | × | √ | √ |
| 3 | √ | √ | × | √ |
| 4 | √ | √ | √ | × |
| 5 | √ | √ | √ | √ |
| Microsource Type | Lower Power Limit (kW) | Upper Power Limit (kW) | Lower Limit of Climbing Speed (kW/h) | Upper Limit of Climbing Speed (kW/h) | Minimum Boot Time (h) | Minimum Shutdown Time (h) |
|---|---|---|---|---|---|---|
| GT | 20 | 220 | 7 | 14 | 3 | 2 |
| AR | 30 | 280 | 6 | 12 | 3 | 2 |
| WHB | 30 | 280 | 6 | 12 | 3 | 2 |
| HP | 10 | 150 | 10 | 30 | 2 | 2 |
| EC | 10 | 100 | 8 | 20 | 2 | 2 |
| HFC | 10 | 100 | 8 | 20 | 2 | 2 |
| Power grid | −300 | 300 | - | - | - | - |
| Type of Energy Storage | Charge and Discharge Rate | Consumption Rate | Minimum State | Maximum State | Capacity (kW·h) |
|---|---|---|---|---|---|
| Hydrogen energy storage | 0.92 | 0.009 | 0.2 | 0.9 | 200 |
| Thermal energy storage | 0.90 | 0.01 | 0.2 | 0.9 | 200 |
| Cold energy storage | 0.90 | 0.01 | 0.2 | 0.9 | 200 |
| Microsource Type | Unit Price (RMB/kW) | Microsource Type | Unit Price (RMB/kW) |
|---|---|---|---|
| WT | 0.029 | HP | 0.023 |
| PV | 0.025 | WHB | 0.021 |
| GT | 0.025 | EC | 0.012 |
| AR | 0.021 | HFC | 0.028 |
| HST | 0.0018 | HS/CS | 0.0014 |
| Case | RIES’s Running Cost (RMB) | Interaction Cost (RMB) | Start–Stop Cost (RMB) | Fuel Cost (RMB) | RIES’s Total Cost (RMB) |
|---|---|---|---|---|---|
| 1 | 377.18 | −422.38 | 5.68 | 10,242.15 | 10,202.63 |
| 2 | 401.47 | 183.99 | 23.74 | 8907.47 | 9516.67 |
| 3 | 275.26 | 3868.00 | 7.7 | 4701.18 | 8852.15 |
| 4 | 330.23 | 3650.29 | 31.54 | 4635.87 | 8647.94 |
| 5 | 321.75 | 3526.33 | 28.01 | 4442.3 | 8318.47 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Duan, P.; Feng, M.; Zhao, B.; Xue, Q.; Li, K.; Chen, J. Operational Optimization of Regional Integrated Energy Systems with Heat Pumps and Hydrogen Renewable Energy under Integrated Demand Response. Sustainability 2024, 16, 1217. https://doi.org/10.3390/su16031217
Duan P, Feng M, Zhao B, Xue Q, Li K, Chen J. Operational Optimization of Regional Integrated Energy Systems with Heat Pumps and Hydrogen Renewable Energy under Integrated Demand Response. Sustainability. 2024; 16(3):1217. https://doi.org/10.3390/su16031217
Chicago/Turabian StyleDuan, Pengfei, Mengdan Feng, Bingxu Zhao, Qingwen Xue, Kang Li, and Jinglei Chen. 2024. "Operational Optimization of Regional Integrated Energy Systems with Heat Pumps and Hydrogen Renewable Energy under Integrated Demand Response" Sustainability 16, no. 3: 1217. https://doi.org/10.3390/su16031217
APA StyleDuan, P., Feng, M., Zhao, B., Xue, Q., Li, K., & Chen, J. (2024). Operational Optimization of Regional Integrated Energy Systems with Heat Pumps and Hydrogen Renewable Energy under Integrated Demand Response. Sustainability, 16(3), 1217. https://doi.org/10.3390/su16031217






