Research on Efficiency of Permanent-Magnet Synchronous Motor Based on Adaptive Algorithm of Fuzzy Control
Abstract
1. Introduction
- (1)
- An algorithm is proposed to improve the PMSM’s online magnet chain values by adjusting the forgetting factors based on fuzzy self-adaption;
- (2)
- The recursive least-squares parameter estimation algorithm is adopted to identify the parameters of the PMSM; this ensures that the parameter estimation values can be dynamically updated with data changes, adapting to the time-varying parameters;
- (3)
- A control algorithm based on the fuzzy control adaptive forgetting factor algorithm is constructed on a physical experimental platform.
2. PMSM Control Model Building
2.1. Building Field-Oriented Control (FOC) for PMSM
2.2. Improved PMSM Control Model’s Linearization
2.3. The Influence of the PMSM’s Winding Temperature Changes
2.3.1. Motor Stator Resistance and Motor Winding Temperature Changes
2.3.2. Magnetic Chain Observation and Temperature Changes
2.3.3. Electromagnetic Torque and Temperature Change
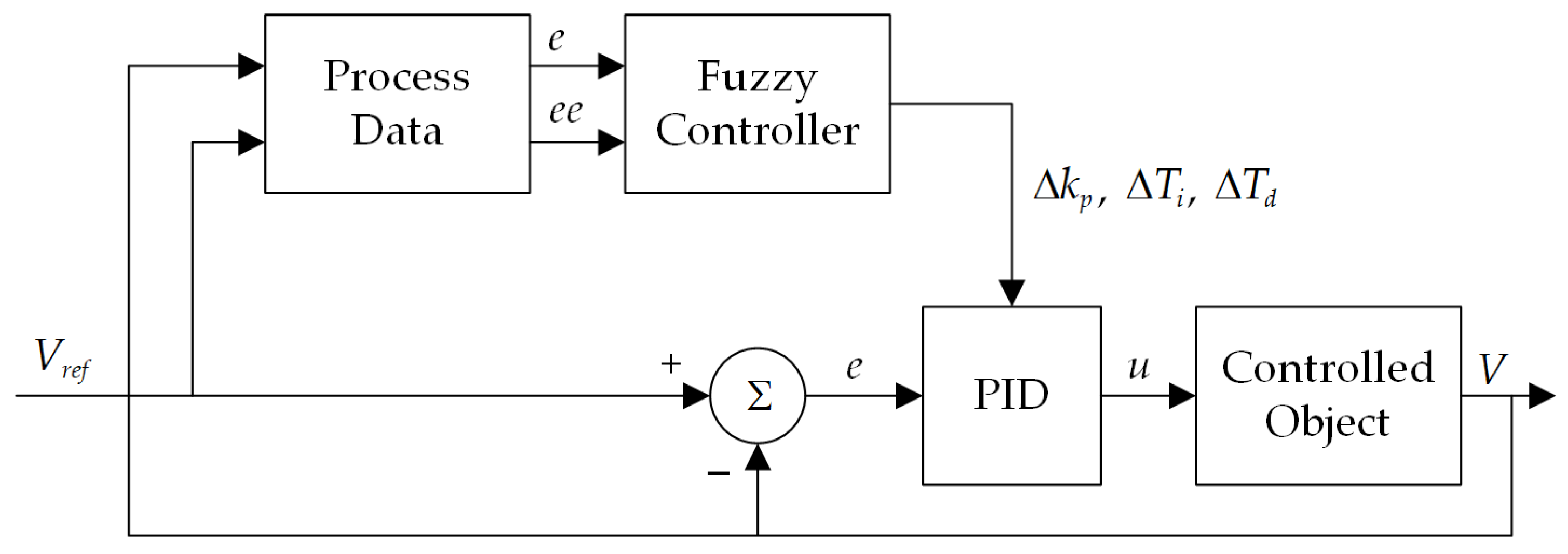
3. Design of the Fuzzy Controller
3.1. Structure of the Fuzzy Controller
3.2. Establishment of Fuzzy Control Rules
3.3. Algorithm Design of the Fuzzy PID Controller
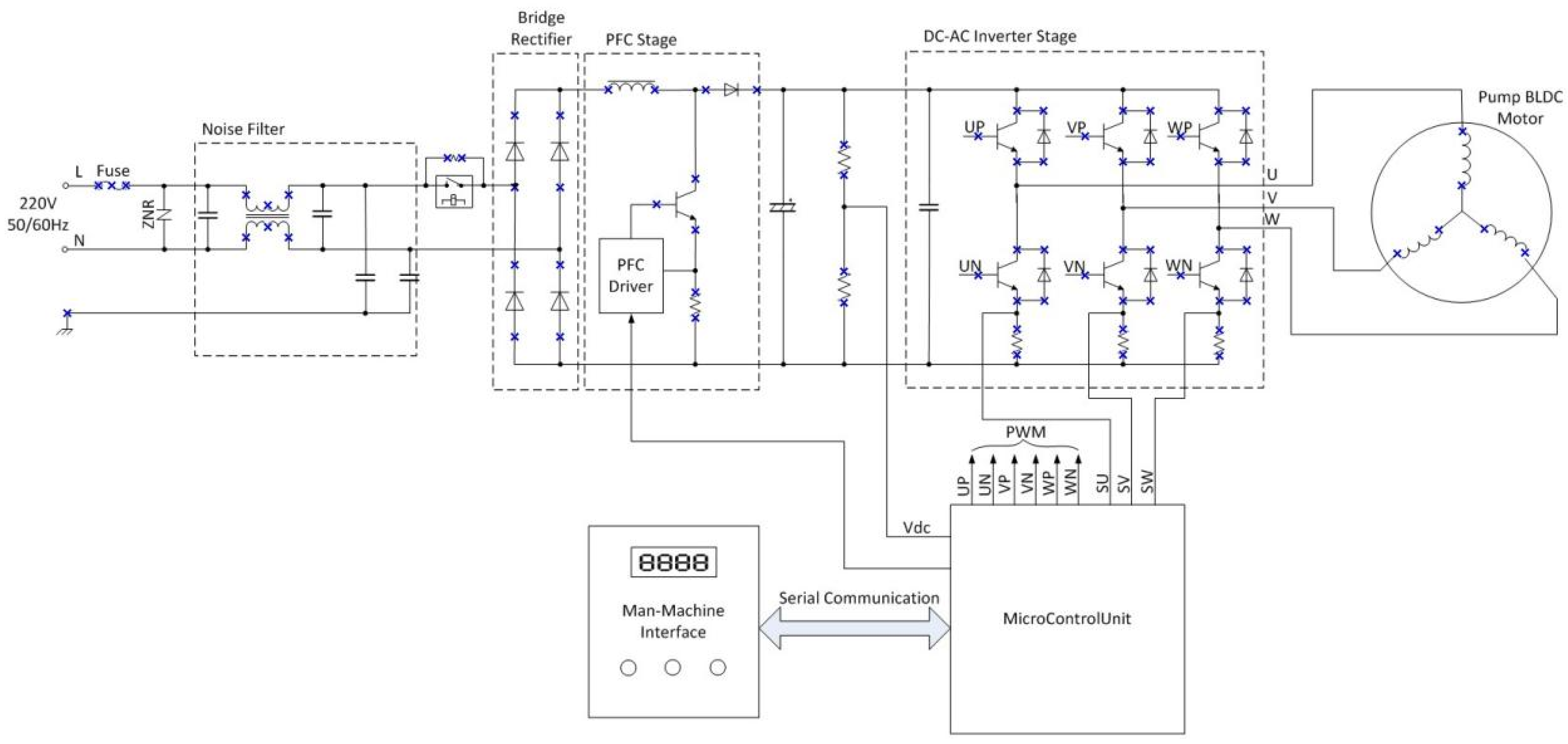
4. Design of the Experimental Set-Up
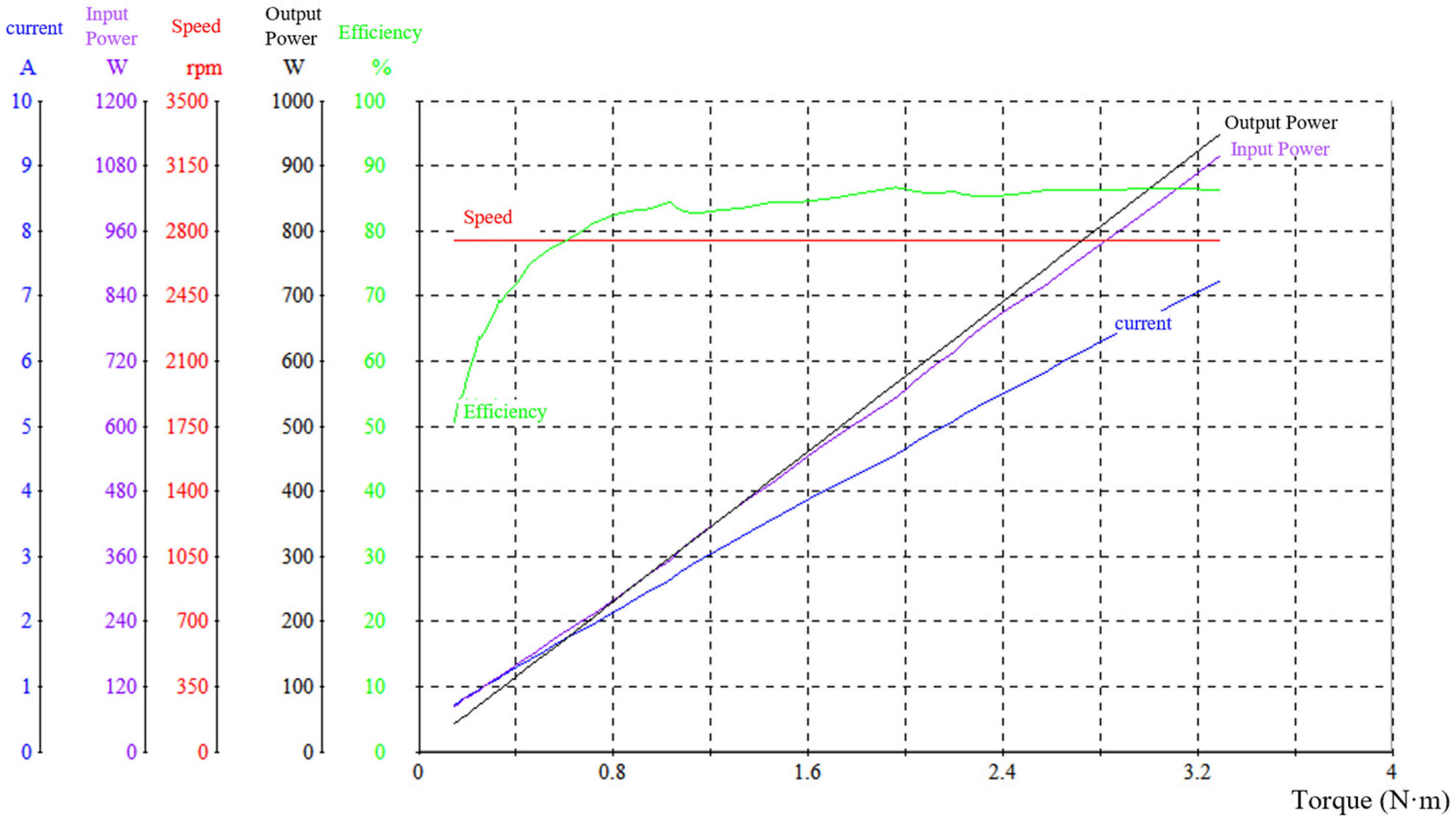
4.1. PMSM Experimental Sample Preparation
4.2. Production of the Motor Drive Circuit Board and Control Circuit Board with the Fuzzy Adaptive Algorithm
4.3. Comparison of the Test with the Inverter Used in the Experiment
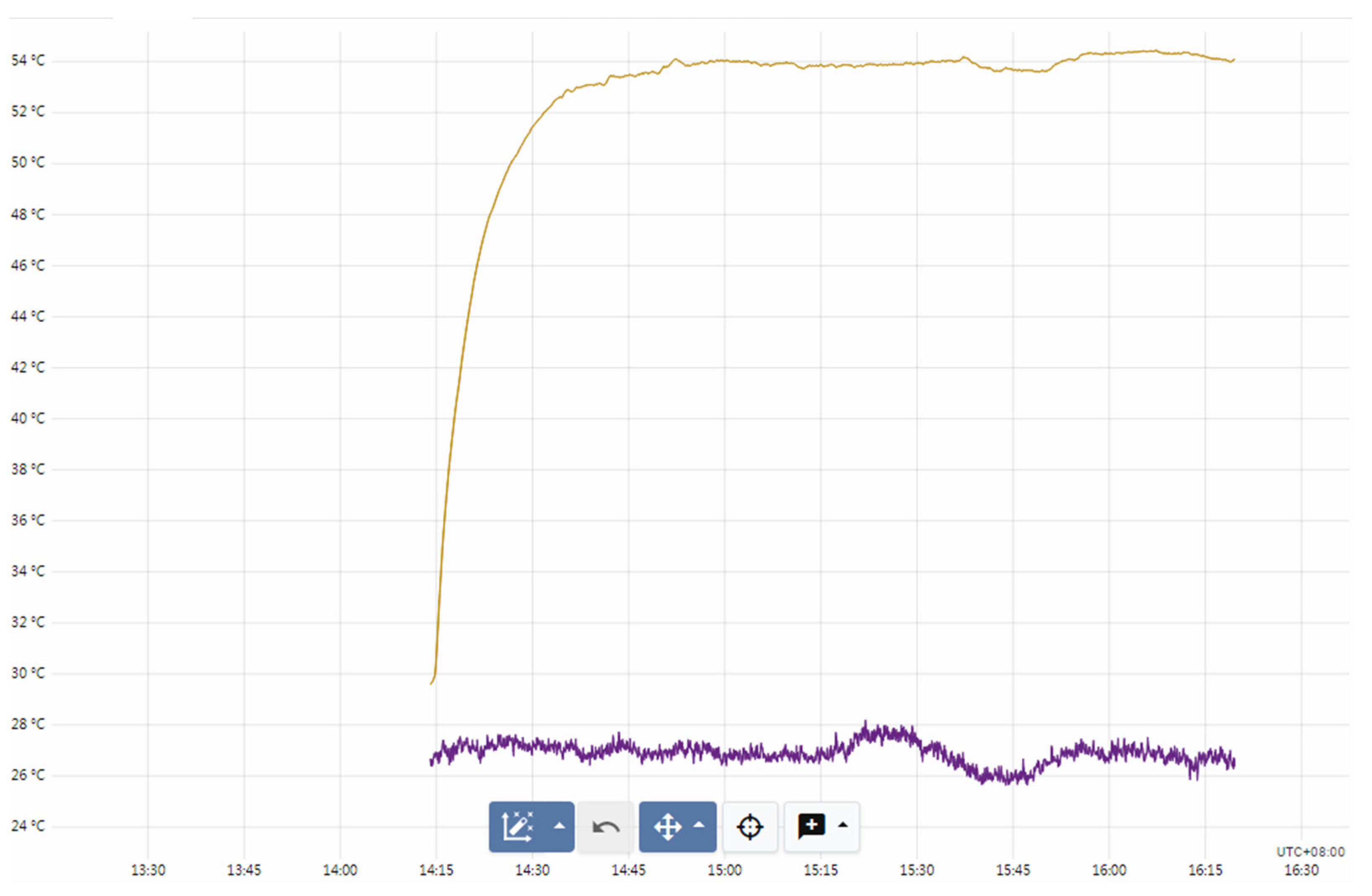
4.4. Testing of the Equipment
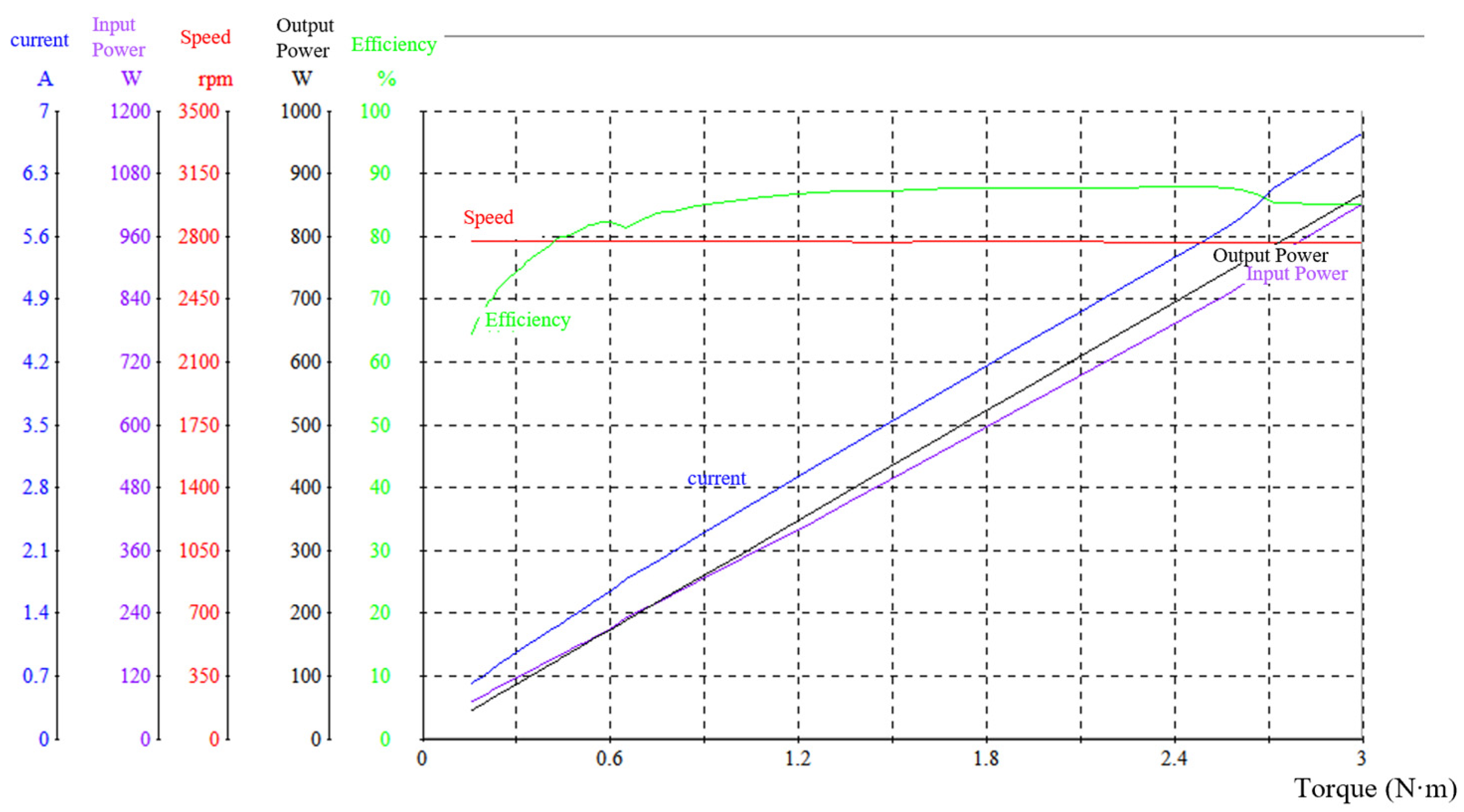
4.5. Comparison of the Experimental Results
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Mi, C.; Slemon, G.R.; Bonert, R. Modeling of Iron Losses of Permanent-Magnet Synchronous Motors. IEEE Trans. Ind. Appl. 2003, 39, 734–742. [Google Scholar] [CrossRef]
- Slemon, G.R.; Liu, X. Core Losses in Permanent Magnet Motors. IEEE Trans. Magn. 1990, 26, 1653–1655. [Google Scholar] [CrossRef]
- Gao, S. Vector Control of PMSM Based on Compensating Iron Loss Influence. Electrotech. Appl. 2007, 88–92. [Google Scholar]
- Liu, L.; Liu, W.; Tian, J. Optimal-efficiency Control of Asynchronous Motor Taking Core Loss into Account. Micromotors 2001, 50–53. [Google Scholar] [CrossRef]
- Xu, Y.; Zhong, Y. Simulation of Minimum Loss Control for PMSM. J. Syst. Simul. 2007, 19, 5283–5286. [Google Scholar] [CrossRef]
- Xu, J.; Feng, J.; Xu, J. Direct Torque Control of Permanent Magnet Synchronous Machine Considering Loss Model. Power Electron. 2005, 39, 24–25+28. [Google Scholar]
- Song, J.; Su, Y. Study of efficiency-optimized control based on accurate modeling for PMSM. Adv. Technol. Electr. Eng. Energy 2004, 23, 22–25. [Google Scholar]
- Giorgos, M.; Manolis, M. Default Nudge and Street Lightning Conservation: Towards a Policy Proposal for the Current Energy Crisis. J. Knowl. Econ. 2023, 15, 1–10. [Google Scholar] [CrossRef]
- Abdulrasheed, Z.; Fatai, A.; Festus, B. The effect of energy consumption on the environment in the OECD countries: Economic policy uncertainty perspectives. Environ. Sci. Pollut. Res. 2021, 28, 52295–52305. [Google Scholar]
- Ma, X.; Liu, J.; Li, H.; Zhang, H. Research on Efficiency Optimization Control of Induction Motor Based on Genetic Algorithm. Micromotors 2013, 46, 36–40. [Google Scholar] [CrossRef]
- Sun, X.; Shi, Z.; Lei, G.; Guo, Y.; Zhu, J. Multi-Objective Design Optimization of an IPMSM Based on Multilevel Strategy. IEEE Trans. Ind. Electron. 2021, 68, 139–148. [Google Scholar] [CrossRef]
- Zhang, K. Study on Energy Efficiency Optimization for Electric Vehicles. Ph.D. Thesis, Tsinghua University, Beijing, China, 2014. [Google Scholar]
- Gautam, A.K.; Tariq, M.; Pandey, J.P.; Verma, K.S. Optimal Power Management Strategy by Using Fuzzy Logic Controller for BLDC Motor-Driven E-Rickshaw. J. Intell. Fuzzy Syst. 2022, 42, 1089–1098. [Google Scholar] [CrossRef]
- Zhang, L. Research on Efficiency Optimization Control of Asynchronous Motor Systems for Electric Vehicles. Ph.D. Thesis, Institute of Electrical Engineering, Chinese Academy of Sciences, Beijing, China, 2006. [Google Scholar]
- Sheng, Y. Efficiency Optimization Control Methods of Interior Permanent Magnet Synchronous Motors Drive System for Urban Rail Traction. Ph.D. Thesis, Central South University, Changsha, China, 2012. [Google Scholar]
- Liu, K.; Zhang, Q.; Chen, J.; Zhu, Z.Q.; Zhang, J. Online Multiparameter Estimation of Nonsalient-Pole PM Synchronous Machines with Temperature Variation Tracking. IEEE Trans. Ind. Electron. 2011, 58, 1776–1788. [Google Scholar] [CrossRef]
- Kong, X.; Liu, X. Efficient Nonlinear Model Predictive Control for Permanent Magnet Synchronous Motor. Acta Autom. Sin. 2014, 40, 1958–1966. [Google Scholar]
- Yang, L.; Peng, X.; Li, Z. Induction Motor Electrical Parameters Identification Using RLS Estimation. In Proceedings of the 2010 International Conference on Mechanic Automation and Control Engineering, Wuhan, China, 26–28 June 2010; pp. 3294–3297. [Google Scholar]
- Nahid-Mobarakeh, B.; Meibody-Tabar, F.; Sargos, F.-M. Mechanical Sensorless Control of PMSM with Online Estimation of Stator Resistance. IEEE Trans. Ind. Appl. 2004, 40, 457–471. [Google Scholar] [CrossRef]
- Xiao, X.; Xu, Q.; Wang, Y.; Shi, Y. Parameter Identification of Interior Permanent Magnet Synchronous Motors Based on Genetic Algorithm. Trans. China Electrotech. Soc. 2014, 29, 21–26. [Google Scholar] [CrossRef]
- Li, Q.; Wang, Y.; Zhang, X. Analysis and Simulation of a Variable Forgetting Factor RLS Algorithm. Mod. Electron. Tech. 2008, 17, 45–47. [Google Scholar] [CrossRef]
- Huang, Z.; Duan, X.; Zou, J.; Wan, H. Fault Current Parameter Estimation Based on Adaptive RLS Algorithm. Proc. CSEE 2014, 34, 2460–2469. [Google Scholar] [CrossRef]
- Zhang, H.; Gong, S.; Dong, Z. On-Line Parameter Identification of Induction Motor Based on RLS Algorithm. In Proceedings of the 2013 International Conference on Electrical Machines and Systems (ICEMS), Busan, Republic of Korea, 26–29 October 2013; pp. 2132–2137. [Google Scholar]
- Caponio, A.; Cascella, G.L.; Neri, F.; Salvatore, N.; Sumner, M. A Fast Adaptive Memetic Algorithm for Online and Offline Control Design of PMSM Drives. IEEE Trans. Syst. Man. Cybern. Syst. 2007, 37, 28–41. [Google Scholar] [CrossRef]
- Underwood, S.J.; Husain, I. Online Parameter Estimation and Adaptive Control of Permanent-Magnet Synchronous Machines. IEEE Trans. Ind. Electron. 2010, 57, 2435–2443. [Google Scholar] [CrossRef]
- Hamida, M.A.; De Leon, J.; Glumineau, A.; Boisliveau, R. An Adaptive Interconnected Observer for Sensorless Control of PM Synchronous Motors with Online Parameter Identification. IEEE Trans. Ind. Electron. 2013, 60, 739–748. [Google Scholar] [CrossRef]
- Noel Hernandez Perez, J.; Sandre Hernandez, O.; Morales Caporal, R.; Rangel Magdaleno, J.d.J.; Peregrina Barreto, H. Parameter Identification of a Permanent Magnet Synchronous Machine Based on Current Decay Test and Particle Swarm Optimization. IEEE Latin Am. Trans. 2013, 11, 1176–1181. [Google Scholar] [CrossRef]
- Wang, G.; Qu, L.; Zhan, H.; Xu, J.; Ding, L.; Zhang, G.; Xu, D. Self-Commissioning of Permanent Magnet Synchronous Machine Drives at Standstill Considering Inverter Nonlinearities. IEEE Trans. Power Electron. 2014, 29, 6615–6627. [Google Scholar] [CrossRef]
- Ying, H. Deriving Analytical Input–Output Relationship for Fuzzy Controllers Using Arbitrary Input Fuzzy Sets and Zadeh Fuzzy AND Operator. IEEE Trans. Fuzzy Syst. 2006, 14, 654–662. [Google Scholar] [CrossRef]
- Hashemzadeh, M.; Golzari Oskouei, A.; Farajzadeh, N. New Fuzzy C-Means Clustering Method Based on Feature-Weight and Cluster-Weight Learning. Appl. Soft. Comput. 2019, 78, 324–345. [Google Scholar] [CrossRef]
- Zhang, R.; Song, L.; Yang, J.; Hoffman, T. DC Motor Speed Control System Simulation Based on Fuzzy Self-Tuning PID. In Proceedings of the Fuzzy Information and Engineering Volume 2; Cao, B., Li, T.-F., Zhang, C.-Y., Eds.; Springer: Berlin/Heidelberg, Germany; Chongqing, China, 2009; Volume 62, pp. 967–975. [Google Scholar]
- Chung, I.-F.; Chen, Y.-C.; Pal, N.R. Feature Selection with Controlled Redundancy in a Fuzzy Rule Based Framework. IEEE Trans. Fuzzy Syst. 2018, 26, 734–748. [Google Scholar] [CrossRef]
- Stetco, A.; Zeng, X.-J.; Keane, J. Fuzzy C-Means++: Fuzzy C-Means with Effective Seeding Initialization. Expert. Syst. Appl. 2015, 42, 7541–7548. [Google Scholar] [CrossRef]
- Han, M.; Zhong, K.; Qiu, T.; Han, B. Interval Type-2 Fuzzy Neural Networks for Chaotic Time Series Prediction: A Concise Overview. IEEE T. Cybern. 2019, 49, 2720–2731. [Google Scholar] [CrossRef]
- Xie, B.-K.; Lee, S.-J. An Extended Type-Reduction Method for General Type-2 Fuzzy Sets. IEEE Trans. Fuzzy Syst. 2017, 25, 715–724. [Google Scholar] [CrossRef]
- Juang, C.-F.; Hung, C.-W.; Hsu, C.-H. Rule-Based Cooperative Continuous Ant Colony Optimization to Improve the Accuracy of Fuzzy System Design. IEEE Trans. Fuzzy Syst. 2014, 22, 723–735. [Google Scholar] [CrossRef]
- Terziyska, M.; Todorov, Y.; Dobreva, M. Efficient Error Based Metrics for Fuzzy-Neural Network Performance Evaluation. In Proceedings of the Advanced Computing in Industrial Mathematics; Georgiev, K., Todorov, M., Georgiev, I., Eds.; Springer International Publishing: Sofia, Bulgaria, 2018; pp. 185–201. [Google Scholar]
- Na, R.; Wang, X. An Improved Vector-Control System of PMSM Based on Fuzzy Logic Controller. In Proceedings of the 2014 International Symposium on Computer, Consumer and Control, Taichung, Taiwan, 10–12 June 2014; pp. 326–331. [Google Scholar]
- Zhao, K. Solvability, Approximation and Stability of Periodic Boundary Value Problem for a Nonlinear Hadamard Fractional Differential Equation with 𝓅-Laplacian. Axioms 2023, 12, 733. [Google Scholar] [CrossRef]
- Zhao, K. Generalized UH-stability of a nonlinear fractional coupling (𝓅1, 𝓅2)-Laplacian system concerned with nonsingular Atangana–Baleanu fractional calculus. J. Inequalities Appl. 2023, 2023, 96. [Google Scholar] [CrossRef]














| EC | NB | NM | NS | ZO | PS | PM | PB | ||
|---|---|---|---|---|---|---|---|---|---|
| U | |||||||||
| E | |||||||||
| NB | PB | PB | PB | PB | PM | PM | PS | ||
| NM | PB | PB | PB | PM | PM | PS | ZO | ||
| NS | PM | PM | PM | PS | PS | ZO | NS | ||
| ZO | PM | PM | PS | ZO | NS | NM | NM | ||
| PS | PS | PS | ZO | NS | NS | NM | NB | ||
| PM | ZO | ZO | NS | NM | NM | NB | NB | ||
| PB | ZO | ZO | NM | NB | NB | NB | NB | ||
| Variable | Parameter |
|---|---|
| Number of phases | 3 |
| Number of poles | 8 |
| Rated voltage (VDC) | 300 |
| No load speed (rpm) | 2850 |
| No load current (a) | 0.63 |
| Rated speed (rpm) | 2850 |
| Rated torque (N·m) | 2.5 |
| Rated power (W) | 750 |
| Rated current (A) | 3.8 |
| Max peak torque (N·m) | 2.9 |
| Motor Type | U Phase (Ω) | V Phase (Ω) | W Phase (Ω) |
|---|---|---|---|
| PMSM + Inverter (in 5 min) | 2.347 Ω | 2.353 Ω | 2.351 Ω |
| PMSM + Inverter (in 2 h) | 2.496 Ω | 2.488 Ω | 2.47 Ω |
| PMSM + Fuzzy Controller (in 5 min) | 2.334 Ω | 2.334 Ω | 2.34 Ω |
| PMSM + Fuzzy Controller (in 2 h) | 2.571 Ω | 2.576 Ω | 2.552 Ω |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sun, W.; Si, H.; Qiu, J.; Li, J. Research on Efficiency of Permanent-Magnet Synchronous Motor Based on Adaptive Algorithm of Fuzzy Control. Sustainability 2024, 16, 1253. https://doi.org/10.3390/su16031253
Sun W, Si H, Qiu J, Li J. Research on Efficiency of Permanent-Magnet Synchronous Motor Based on Adaptive Algorithm of Fuzzy Control. Sustainability. 2024; 16(3):1253. https://doi.org/10.3390/su16031253
Chicago/Turabian StyleSun, Wangsheng, Haiqing Si, Jingxuan Qiu, and Jiayi Li. 2024. "Research on Efficiency of Permanent-Magnet Synchronous Motor Based on Adaptive Algorithm of Fuzzy Control" Sustainability 16, no. 3: 1253. https://doi.org/10.3390/su16031253
APA StyleSun, W., Si, H., Qiu, J., & Li, J. (2024). Research on Efficiency of Permanent-Magnet Synchronous Motor Based on Adaptive Algorithm of Fuzzy Control. Sustainability, 16(3), 1253. https://doi.org/10.3390/su16031253






