A Novel Parts-to-Picker System with Buffer Racks and Access Racks in Flexible Warehousing Systems
Abstract
:1. Introduction
- (1)
- High space utilization and storage capacity. Flexible warehousing systems can quickly pick up goods on ultra-high racks, fully utilize vertical space, and save at least 90% of storage space. Due to the reasonable layout of warehouses and the support of numerous intelligent devices, the actual storage capacity is much larger than that of traditional single-layer warehouses (less than eight meters). In [4], the authors study the storage utilization of a compact robotic automated parking system (CRAPS) and use a queuing network model to estimate its performance by minimizing car retrieval time. The space utilization increased by over 32% and the car retrieval time was reduced by at least 29.7%.
- (2)
- Operational efficiency. The application of intelligent equipment, such as automatic guided vehicles (AGVs), mobile racks, shuttles, lifters, stackers, and other automatic storage and retrieval robots in flexible warehousing, can achieve fast picking and loading processes. They save time and effort and greatly improve the efficiency of warehousing operations. Parts-to-picker systems can complete 1000 order lines per hour per person, which is eight to fifteen times more than traditional systems [5]. The racks are moved by AGVs to the pickers, and the pickers manually select the items from the racks. This manual method generates picker fatigue and leads to selection errors. In addition, the movable racks are not suitable for storing parts, components, or products, because as a result of their various sizes, shapes, and weights, they cannot be placed in narrow spaces like cookie boxes or candy bags.
2. Related Research
2.1. Storage and Retrieval Operations
2.2. Picking
2.3. Transportation
2.4. Operation Integration
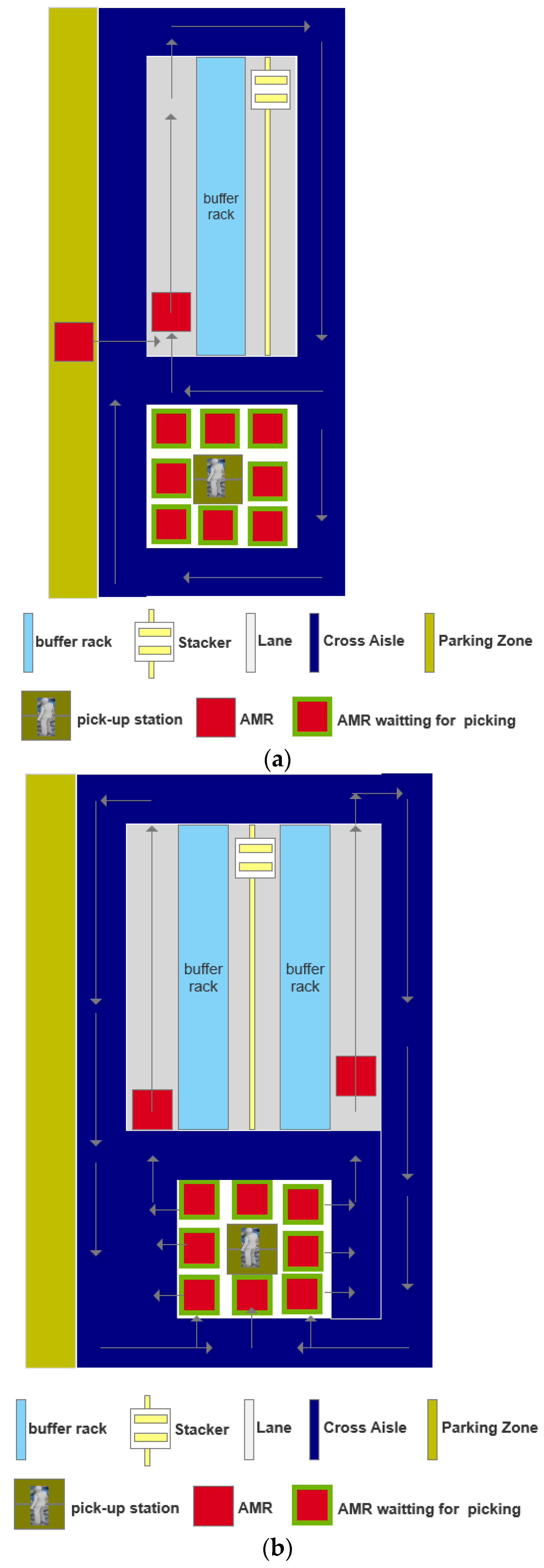
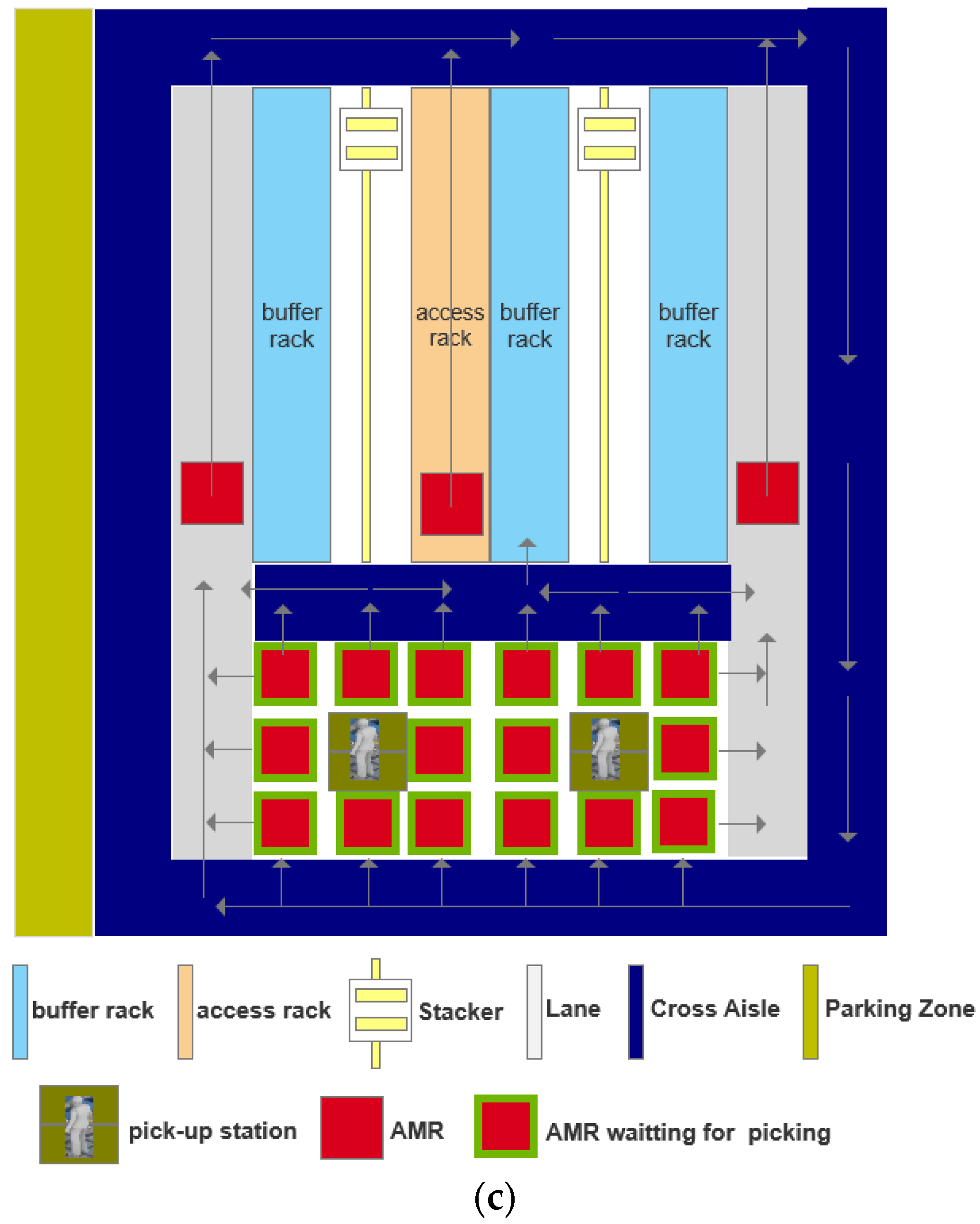
3. System Description and Problem Analysis
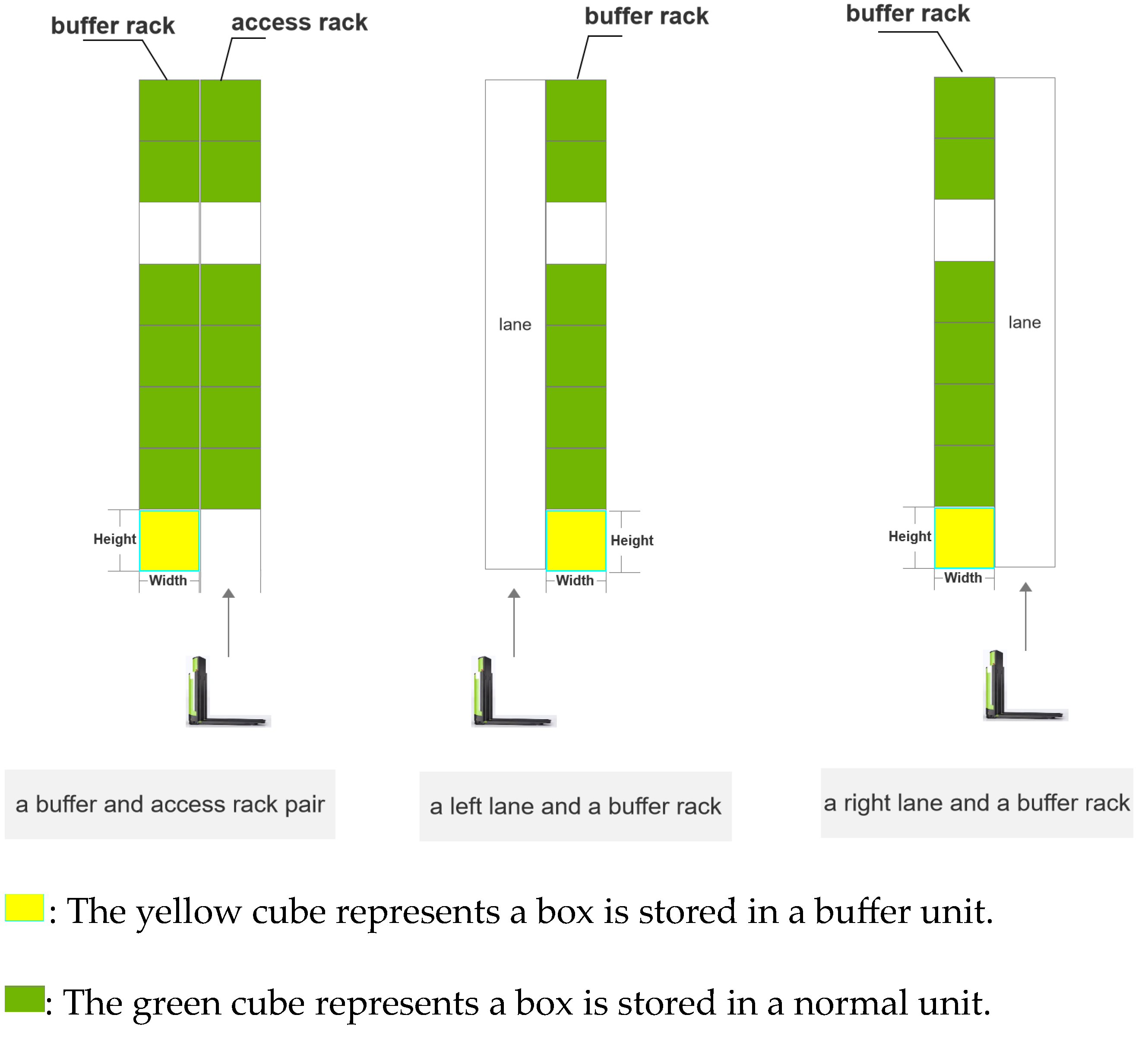
3.1. Buffer Racks and Access Racks
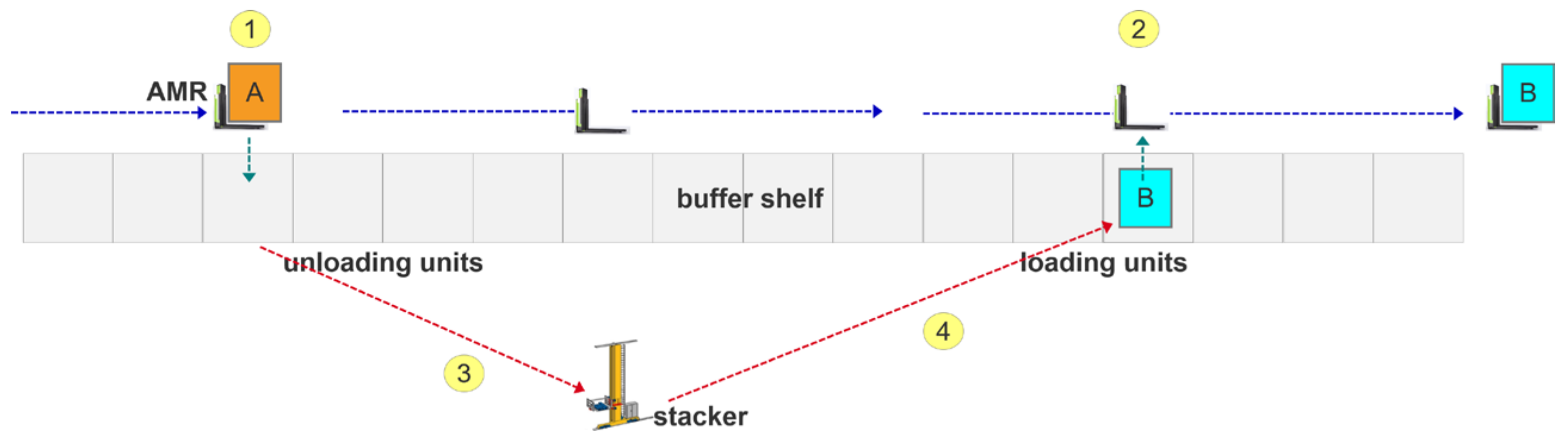
3.2. AMR Loading and Unloading
3.3. Different Unit Sizes
3.4. Stacker Picking and Loading
4. Numerical Experiments
- (1)
- The units in buffer shelves are big enough to load all kinds of items, and all sizes of items are equally convenient to be loaded or unloaded by AMRs.
- (2)
- Small items are allowed to be stored in small-, medium-, or big-sized units; medium items are allowed to be stored in medium- or big-sized units; and big items are only allowed to be stored in big-sized units.
- (3)
- All AMRs move with the same speed mode, including constant speed, acceleration, and deceleration.
- (4)
- Stackers and AMRs are both of single depth.
- (5)
- There is no collision throughout the entire process, and AMRs move along the established route. By default, existing technologies (such as a camera [44]) avoid conflicts when AMRs meet, some priority rules avoid congestion, and the processes proceed smoothly.
4.1. Storage Capacity and Space Utilization
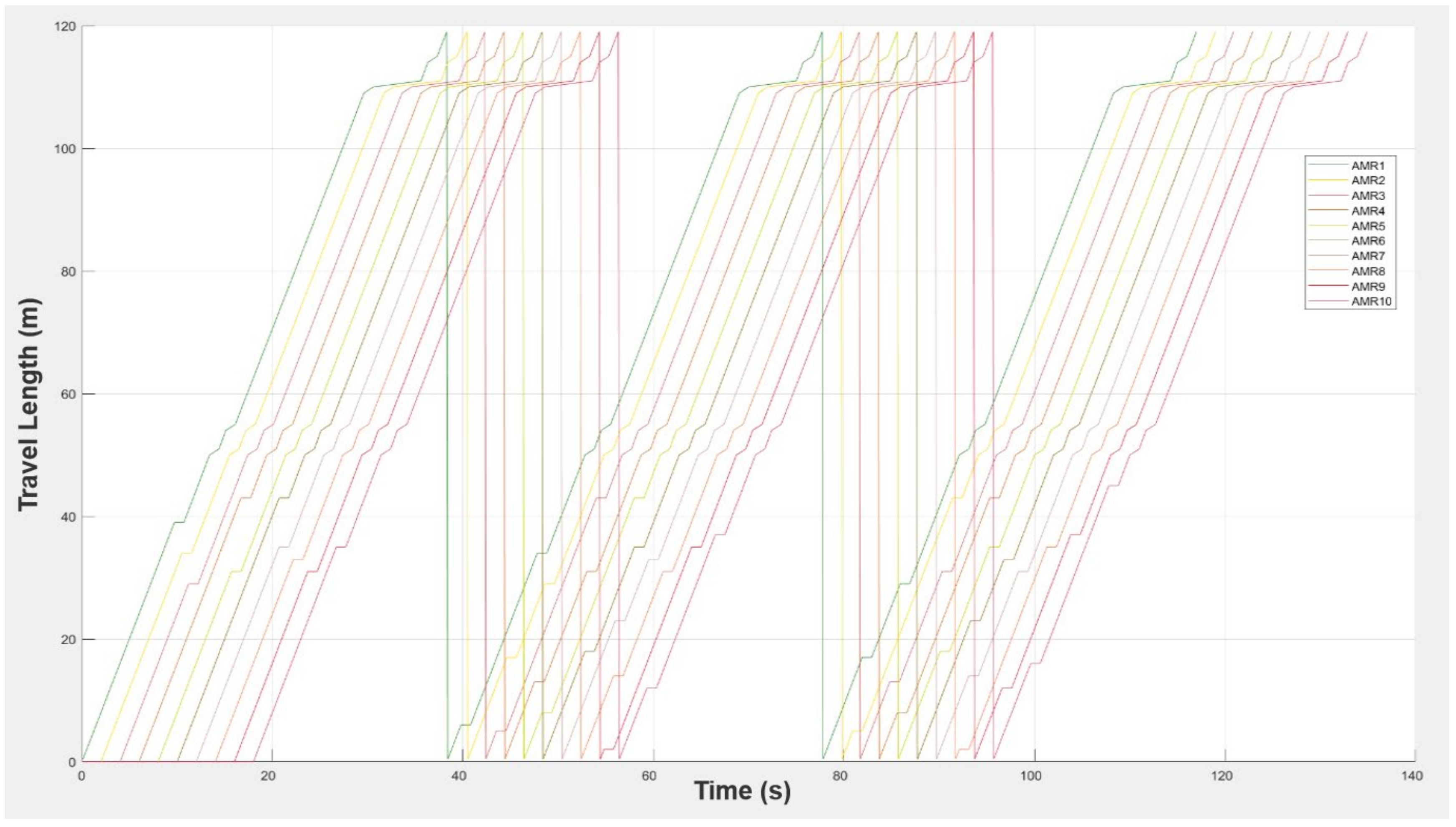
4.2. Picking Efficiency
- (1)
- The distances between adjacent AMRs may be less than 1 m.
- (2)
- There is no more space for new AMRs.
5. Conclusions and Further Research Opportunities
- (1)
- High storage capacity and picking efficiency. The proposed parts-to-picker system is flexible and efficient compared with the existing systems. The storage capacity (in the large-scale model, the storage capacity is 13440, as listed in Table 7) is significantly bigger than the KIVA system (2000 to 4000, [5,6]). At the same time, the picking efficiency (in the large-scale model, the picking efficiency can reach 2430 boxes per hour, as listed in Table 7) is significantly better than the SBS/RS (between 500 and 800 boxes per hour, [1]) and the miniload AS/RS (less than 300 boxes per hour, [22]). Furthermore, when the number of AMRs reaches the max, the picking efficiency (2430 in the large-scale model, as listed in Table 7) is no less than the KIVA system (nearly 2000 per hour, [5,6]). This integration operation demonstrates its various advantages and can meet the needs of enterprises in reducing costs and improving efficiency, and it shows great practical value.
- (2)
- Sustainable transformation and upgrading. The novel design shows a small and efficient structural transformation in manufacturing warehousing systems, such as changing the bottom shelves to access shelves, and the rest of the racks are basically unchanged. The renovation cost is low, but the improvement in storage capacity and picking efficiency is great. For example, in the Min-3 Model, there are 80 buffer units, and the capacity can reach 2240 when the warehouse is 860 square meters, and the picking efficiency can reach 2044 boxes per hour. More importantly, this sustainable improvement for existing warehouses realizes the efficient utilization of spatial resources [54,55] and provides important support for the construction of green supply chains.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Volling, T.; Matzke, A.; Grunewald, M.; Spengler, T.S. Planning of capacities and orders in build-to-order automobile production: A review. Eur. J. Oper. Res. 2013, 224, 240–260. [Google Scholar] [CrossRef]
- Brabazon, P.G.; MacCarthy, B. Fundamental behaviour of virtual-build-to-order systems. Int. J. Prod. Econ. 2006, 104, 514–524. [Google Scholar] [CrossRef]
- Peng, G.; Wu, Y.; Zhang, C.; Shen, W. Integrated optimization of storage location assignment and crane scheduling in an unmanned slab yard. Comput. Ind. Eng. 2021, 161, 107623. [Google Scholar] [CrossRef]
- Wu, G.; Xu, X.; Lu, X. Considering the influence of queue length on performance improvement for a new compact robotic automated parking system. Int. J. Inf. Manag. 2020, 50, 487–497. [Google Scholar] [CrossRef]
- Yang, X.; Hua, G.; Hu, L.; Cheng, T.C.E.; Huang, A. Joint optimization of order sequencing and rack scheduling in the robotic mobile fulfilment system. Comput. Oper. Res. 2021, 135, 105467. [Google Scholar] [CrossRef]
- Guan, C.; Zhang, Z.; Liu, S.; Gong, J. Multi-objective particle swarm optimization for multi-workshop facility layout problem. J. Manuf. Syst. 2019, 53, 32–48. [Google Scholar] [CrossRef]
- Bortolini, M.; Faccio, M.; Ferrari, E.; Gamberi, M.; Pilati, F. Time and energy optimal unit-load assignment for automatic S/R warehouses. Int. J. Prod. Econ. 2017, 190, 133–145. [Google Scholar] [CrossRef]
- Sato, Y.; Tan, K.H.; Tse, Y.K. An integrated marginal analysis approach for build-to-order products. Int. J. Prod. Econ. 2015, 170, 422–428. [Google Scholar] [CrossRef]
- Chen, X.; Yang, P.; Shao, Z. Simulation-based time-efficient and energy-efficient performance analysis of an overhead robotic compact storage and retrieval system. Simul. Model. Pract. Theory 2022, 119, 102560. [Google Scholar] [CrossRef]
- Roodbergen, K.J.; Vis, I.F.A. A survey of literature on automated storage and retrieval systems. Eur. J. Oper. Res. 2009, 194, 343–362. [Google Scholar] [CrossRef]
- Chow, W.M. Development of an automated storage and retrieval system for manufacturing assembly lines. In Proceedings of the International Conference on Robotics and Automation, San Francisco, CA, USA, 7–10 April 1986; IEEE: Piscataway, NJ, USA, 1986; pp. 490–495. [Google Scholar]
- Liu, S.; Wang, Q.; Sun, J. Integrated optimization of storage allocations in automated storage and retrieval system of bearings. In Proceedings of the 25th Chinese Control and Decision Conference (CCDC), Guiyang, China, 25–27 May 2013; IEEE: Piscataway, NJ, USA, 2013; pp. 4267–4271. [Google Scholar]
- Boywitz, D.; Boysen, N. Robust storage assignment in stack- and queue-based storage systems. Comput. Oper. Res. 2018, 100, 189–200. [Google Scholar] [CrossRef]
- Yang, P.; Qi, M.; Miao, L. Optimal Boundaries for Class-based Automated Storage/retrieval Systems Considering the Acceleration/deceleration of the Storage and Retrieval Machine. In Proceedings of the International Conference on Logistics Systems and Intelligent Management, Harbin, China, 9–10 January 2010; IEEE: Piscataway, NJ, USA, 2010; pp. 1400–1404. [Google Scholar]
- Polten, L.; Emde, S. Multi-shuttle crane scheduling in automated storage and retrieval systems. Eur. J. Oper. Res. 2022, 302, 892–908. [Google Scholar] [CrossRef]
- Keung, K.L.; Lee, C.K.M.; Ji, P. Data-driven order correlation pattern and storage location assignment in robotic mobile fulfillment and process automation system. Adv. Eng. Inform. 2021, 50, 101369. [Google Scholar] [CrossRef]
- Ma, Y.; Chen, H.; Yu, Y. An efficient heuristic for minimizing the number of moves for the retrieval of a single item in a puzzle-based storage system with multiple escorts. Eur. J. Oper. Res. 2022, 301, 51–66. [Google Scholar] [CrossRef]
- Dukic, G.; Opetuk, T.; Lerher, T. A throughput model for a dual-tray Vertical Lift Module with a human order-picker. Int. J. Prod. Econ. 2015, 170, 874–881. [Google Scholar] [CrossRef]
- Durasevic, M.; Dumic, M. Automated design of heuristics for the container relocation problem using genetic programming. Appl. Soft Comput. 2022, 130, 109696. [Google Scholar] [CrossRef]
- Rehman, S. A parallel and silent emerging pandemic: Antimicrobial resistance (AMR) amid COVID-19 pandemic. J. Infect. Public Health 2023, 16, 611–617. [Google Scholar] [CrossRef] [PubMed]
- Sarker, B.R.; Babu, P.S. Travel time models in automated storage/retrieval systems: A critical review. Int. J. Prod. Econ. 1995, 40, 173–184. [Google Scholar] [CrossRef]
- He, M.; Guan, Z.; Wang, C.; Hou, G. Multiple-Rack Strategies Using Optimization of Location Assignment Based on MRCGA in Miniload Automated Storage and Retrieval System. Processes 2023, 11, 950. [Google Scholar] [CrossRef]
- Pan, J.C.H.; Shih, P.H.; Wu, M.H. Storage assignment problem with travel distance and blocking considerations for a picker-to-part order picking system. Comput. Ind. Eng. 2012, 62, 527–535. [Google Scholar] [CrossRef]
- Parsa, N.R.; Karimi, B.; Husseini, S.M.M. Minimizing total flow time on a batch processing machine using a hybrid max-min ant system. Comput. Ind. Eng. 2016, 99, 372–381. [Google Scholar] [CrossRef]
- Lee, I.G.; Chung, S.H.; Yoon, S.W. Two-stage storage assignment to minimize travel time and congestion for warehouse order picking operations. Comput. Ind. Eng. 2020, 139, 106129. [Google Scholar] [CrossRef]
- Dijkstra, A.S.; Roodbergen, K.J. Exact route-length formulas and a storage location assignment heuristic for picker-to-parts warehouses. Transp. Res. Part E 2017, 102, 38–59. [Google Scholar] [CrossRef]
- Manzini, R.; Accorsi, R.; Gamberi, M.; Penazzi, S. Modeling class-based storage assignment over life cycle picking patterns. Int. J. Prod. Econ. 2015, 170, 790–800. [Google Scholar] [CrossRef]
- Srinivas, S.; Yu, S. Collaborative order picking with multiple pickers and robots: Integrated approach for order batching, sequencing and picker-robot routing. Int. J. Prod. Econ. 2022, 254, 108634. [Google Scholar] [CrossRef]
- Li, X.; Yang, X.; Zhang, C.; Qi, M. A simulation study on the robotic mobile fulfillment system in high-density storage warehouses. Simul. Model. Pract. Theory 2021, 112, 102366. [Google Scholar] [CrossRef]
- Zhang, J.; Zhang, X.; Zhang, N. Considering pickers’ learning effects in selecting between batch picking and batch-synchronized zone picking for online-to-offline groceries. Appl. Math. Model. 2023, 113, 358–375. [Google Scholar] [CrossRef]
- Roy, D.; Nigam, S.; de Koster, R.; Adan, I.; Resing, J. Robot-storage zone assignment strategies in mobile fulfillment systems. Transp. Res. Part E 2019, 122, 119–142. [Google Scholar] [CrossRef]
- Li, X.; Hua, G.; Huang, A.; Sheu, J.B.; Cheng, T.C.E.; Huang, F. Storage assignment policy with awareness of energy consumption in the Kiva mobile fulfilment system. Transp. Res. Part E 2020, 144, 102158. [Google Scholar] [CrossRef]
- Zhuang, Y.; Zhou, Y.; Hassini, E.; Yuan, Y.; Hu, X. Rack retrieval and repositioning optimization problem in robotic mobile fulfillment systems. Transp. Res. Part E 2022, 167, 102920. [Google Scholar] [CrossRef]
- Kuhn, H.; Schubert, D.; Holzapfel, A. Integrated order batching and vehicle routing operations in grocery Retail—A General Adaptive Large Neighborhood Search algorithm. Eur. J. Oper. Res. 2021, 294, 1003–1021. [Google Scholar] [CrossRef]
- Žulj, I.; Salewski, H.; Goeke, D.; Schneider, M. Order batching and batch sequencing in an AMR-assisted picker-to-parts system. Eur. J. Oper. Res. 2022, 298, 182–201. [Google Scholar] [CrossRef]
- van Geest, M.; Tekinerdogan, B.; Catal, C. Design of a reference architecture for developing smart warehouses in industry 4.0. Comput. Ind. 2021, 124, 103343. [Google Scholar] [CrossRef]
- Vis, I.F.A. Survey of research in the design and control of automated guided vehicle systems. Eur. J. Oper. Res. 2006, 170, 677–709. [Google Scholar] [CrossRef]
- Roodbergen, K.J.; de Koster, R. Routing order pickers in a warehouse with a middle aisle. Eur. J. Oper. Res. 2001, 133, 32–43. [Google Scholar] [CrossRef]
- Lau, H.Y.K.; Zhao, Y. Integrated scheduling of handling equipment at automated container terminals. Int. J. Prod. Econ. 2008, 112, 665–682. [Google Scholar] [CrossRef]
- Zhong, M.; Yang, Y.; Dessouky, Y.; Postolache, O. Multi-AGV scheduling for conflict-free path planning in automated container terminals. Comput. Ind. Eng. 2020, 142, 106371. [Google Scholar] [CrossRef]
- Fan, X.; He, Q.; Zhang, Y. Zone Design of Tandem Loop AGVs Path with Hybrid Algorithm. IFAC-Pap. 2015, 48, 869–874. [Google Scholar] [CrossRef]
- Miyamoto, T.; Inoue, K. Local and random searches for dispatch and conflict-free routing problem of capacitated AGV systems. Comput. Ind. Eng. 2016, 91, 1–9. [Google Scholar] [CrossRef]
- Qi, M.; Li, X.; Yan, X.; Zhang, C. On the evaluation of AGVS-based warehouse operation performance. Simul. Model. Pract. Theory 2018, 87, 379–394. [Google Scholar] [CrossRef]
- Yang, Q.; Lian, Y.; Xie, W. Hierarchical planning for multiple AGVs in warehouse based on global vision. Simul. Model. Pract. Theory 2020, 104, 102124. [Google Scholar] [CrossRef]
- Drótos, M.; Györgyi, P.; Horváth, M.; Kis, T. Suboptimal and conflict-free control of a fleet of AGVs to serve online requests. Comput. Ind. Eng. 2021, 152, 106999. [Google Scholar] [CrossRef]
- Zhai, D.; Wang, C.; Cao, H.; Garg, S.; Hassan, M.M.; AlQahtani, S.A. Deep neural network based UAV deployment and dynamic power control for 6G-Envisioned intelligent warehouse logistics system. Future Gener. Comput. Syst. 2022, 137, 164–172. [Google Scholar] [CrossRef]
- Ho, Y.C.; Liao, T.W. Zone design and control for vehicle collision prevention and load balancing in a zone control AGV system. Comput. Ind. Eng. 2009, 56, 417–432. [Google Scholar] [CrossRef]
- Zhong, S.; Giannikas, V.; Merino, J.; McFarlane, D.; Cheng, J.; Shao, W. Evaluating the benefits of picking and packing planning integration in e-commerce warehouses. Eur. J. Oper. Res. 2022, 301, 67–81. [Google Scholar] [CrossRef]
- Zhang, G.; Shang, X.; Alawneh, F.; Yang, Y.; Nishi, T. Integrated production planning and warehouse storage assignment problem: An IoT assisted case. Int. J. Prod. Econ. 2021, 234, 108058. [Google Scholar] [CrossRef]
- Fu, X.; Zhang, B.; Yu, H. Vehicles routing and scheduling algorithm for an automated storage and retrieval system of a warehouse. In Proceedings of the International Conference on Logistics, Barcelona, Spain, 27–29 July 2015; IEEE: Piscataway, NJ, USA, 2015. [Google Scholar]
- Xu, X.; Shen, Y.; Chen, W.; Gong, Y.; Wang, H. Data-driven decision and analytics of collection and delivery point location problems for online retailers. Omega 2021, 100, 102280. [Google Scholar] [CrossRef]
- Sun, J.; Zhang, F.; Lu, P.; Yee, J. Optimized modeling and opportunity cost analysis for overloaded interconnected dangerous goods in warehouse operations. Appl. Math. Model. 2021, 90, 151–164. [Google Scholar] [CrossRef]
- Yener, F.; Yazgan, H.R. Optimal warehouse design: Literature review and case study application. Comput. Ind. Eng. 2019, 129, 1–13. [Google Scholar] [CrossRef]
- Pavlov, N.; Durdjevic, D.; Andrejic, M. A Novel Two-Stage Methodological Approach for Storage Technology Selection: An Engineering–FAHP–WASPAS Approach. Sustainability 2023, 15, 13037. [Google Scholar] [CrossRef]
- Czerniachowska, K.; Wichniarek, R.; Zywicki, K. A Model for an Order-Picking Problem with a One-Directional Conveyor and Buffer. Sustainability 2023, 15, 13731. [Google Scholar] [CrossRef]












| Paper | System | Method | Improvement |
|---|---|---|---|
| [11] | AS/RS | Dispatching rules | Material handling delay |
| [12] | AS/RS | Storage allocation | Energy consumption |
| [8] | Warehouse and yard management | Relocation rules | Crane operation time |
| [16] | Robotic mobile fulfillment system | Zone clustering and storage location assignment classification | Total travel cost |
| [15] | Multi-shuttle AS/RS | Multiple unit load crane | Average makespan |
| [22] | Miniload RS/AS | Rack design strategies | Capacities Space utilization |
| Paper | System | Model | Task Assignment | Path Planning | Traffic Control |
|---|---|---|---|---|---|
| [26] | Traditional warehouse | picker-to-parts | √ | √ | - |
| [31] | RMFS | parts-to-picker | √ | √ | √ |
| [32] | KIVA mobile fulfillment system | parts-to-picker | √ | √ | √ |
| [29] | Combination of the traditional RMFS and the puzzle-based storage system | parts-to-picker | √ | √ | √ |
| [34] | distribution center (DC) | picker-to-parts | √ | √ | - |
| [5] | RMFS | parts-to-picker | √ | √ | - |
| [28] | Collaborative human–robot order-picking system (CHR-OPS) | picker-to-parts | √ | √ | - |
| [35] | Autonomous mobile robot-assisted (AMR-assisted) order picking system | picker-to-parts | √ | √ | - |
| [33] | RMFS | parts-to-picker | √ | - | √ |
| [23] | Traditional warehouse | picker-to-parts | √ | √ | √ |
| System | Integrated Strategy | |
|---|---|---|
| [52] | Dangerous goods warehouse | Adding temporary positions |
| [13] | Stack- and queue-based compact storage systems | Adding buffer lanes |
| [38] | Basic warehouse | Adding a middle aisle |
| [9] | Overhead robotic compact storage and retrieval system | The length-to-height ratio should be set to around 5;The storage depth should be 6 or 7; The optimal trade-off point is around 0.7. |
| [37] | AGVs system | the number of pick-up and delivery points |
| [7] | Single-deep rack automatic warehouses | A belt conveyor to carry the bins from the pick-up and delivery point to the load/unload position |
| [47] | AGV system | Dynamic zone strategy |
| [41] | AGV system | Tandem loop AGVs Path |
| [48] | Picking and packing planning integration | Mixed-integer nonlinear programming model |
| [34] | Grocery retailers | General ALNS (GALNS) |
| [49] | Food manufacturing company | IoT-enabled tracking systems |
| [50] | Pallet shuttle high-density storage system | Offline vehicle routing and online vehicle scheduling |
| [51] | Online retailers | Use customer behavior data to evaluate location of collection and delivery points |
| Disadvantages | Advantages | |
|---|---|---|
| SBS/RS + conveyor belt | The conveyor belt design is complex. The picking rate is over 500 per hour but less than 800 per hour. | High storage capacity. |
| SBS/RS + AGV | AGVs have low efficiency in R/S stations. The picking rate is under 500 per hour | High storage capacity. |
| Miniload AS/RS + AGV | The picking rate is under 300 per hour. | High storage capacity. |
| KIVA system | The racks are less than two meters, and there is low utilization of vertical space. The storage units are not suitable for manufacturing materials, which are various sizes and weights. | High picking efficiency, which can reach 1000 per hour. |
| This paper | - | High storage capacity. High picking efficiency (support robot or manual picking). |
| Label | Definition |
|---|---|
| number of buffer racks | |
| number of access racks | |
| length of rack | |
| width of rack | |
| number of rows in a rack | |
| number of columns in a rack | |
| number of lanes | |
| length of lane | |
| width of lane | |
| number of stackers | |
| number of AMRs | |
| number of aisles | |
| length of aisle | |
| width of aisle | |
| number of pick-up stations | |
| length of pick-up station | |
| width of pick-up station | |
| number of waiting points at pick-up stations | |
| speed of AMR | |
| speed of stacker | |
| time cost for picking once | |
| time costs for loading, AMR and stacker are equal | |
| time costs for unloading, AMR and stacker are equal | |
| buffer capacity, the number of buffer bins | |
| storage capacity, the number of storage bins | |
| area occupancy, multiplying the length and width | |
| storage utilization rate | |
| picking efficiency index |
| Layout | |||||||
|---|---|---|---|---|---|---|---|
| Min-1 | 1 | 0 | 20 | 20 | 140 | 130 | 107.69% |
| Min-1 | 1 | 0 | 30 | 30 | 210 | 180 | 116.67% |
| Min-1 | 1 | 0 | 40 | 40 | 280 | 230 | 121.74% |
| Min-1 | 1 | 0 | 50 | 50 | 350 | 280 | 125.00% |
| Min-1 | 1 | 0 | 60 | 60 | 420 | 330 | 127.27% |
| Min-1 | 1 | 0 | 70 | 70 | 490 | 380 | 128.95% |
| Min-1 | 1 | 0 | 80 | 80 | 560 | 430 | 130.23% |
| Min-3 | 3 | 1 | 20 | 60 | 560 | 260 | 215.38% |
| Min-3 | 3 | 1 | 30 | 90 | 840 | 360 | 233.33% |
| Min-3 | 3 | 1 | 40 | 120 | 1120 | 460 | 243.48% |
| Min-3 | 3 | 1 | 50 | 150 | 1400 | 560 | 250.00% |
| Min-3 | 3 | 1 | 60 | 180 | 1680 | 660 | 254.55% |
| Min-3 | 3 | 1 | 70 | 210 | 1960 | 760 | 257.89% |
| Min-3 | 3 | 1 | 80 | 240 | 2240 | 860 | 260.47% |
| medium | 7 | 5 | 20 | 140 | 1680 | 832 | 201.92% |
| medium | 7 | 5 | 30 | 210 | 2520 | 1092 | 230.77% |
| medium | 7 | 5 | 40 | 280 | 3360 | 1352 | 248.52% |
| medium | 7 | 5 | 50 | 350 | 4200 | 1612 | 260.55% |
| medium | 7 | 5 | 60 | 420 | 5040 | 1872 | 269.23% |
| medium | 7 | 5 | 70 | 490 | 5880 | 2132 | 275.80% |
| medium | 7 | 5 | 80 | 560 | 6720 | 2392 | 280.94% |
| large | 13 | 11 | 20 | 260 | 3360 | 1769 | 189.94% |
| large | 13 | 11 | 30 | 390 | 5040 | 2349 | 214.56% |
| large | 13 | 11 | 40 | 520 | 6720 | 2929 | 229.43% |
| large | 13 | 11 | 50 | 650 | 8400 | 3509 | 239.38% |
| large | 13 | 11 | 60 | 780 | 10080 | 4089 | 246.52% |
| large | 13 | 11 | 70 | 910 | 11760 | 4669 | 251.87% |
| large | 13 | 11 | 80 | 1040 | 13440 | 5249 | 256.05% |
| Layout | (/h) | ||||||
|---|---|---|---|---|---|---|---|
| Min-1 | 30 | 1 | 1 | 30 | 210 | 10 | 284 |
| Min-1 | 50 | 1 | 1 | 50 | 350 | 15 | 577 |
| Min-1 | 80 | 1 | 1 | 80 | 560 | 22 | 1174 |
| Min-3 | 30 | 2 | 2 | 90 | 840 | 40 | 620 |
| Min-3 | 50 | 2 | 2 | 150 | 1400 | 51 | 1045 |
| Min-3 | 80 | 2 | 2 | 240 | 2240 | 73 | 2044 |
| Medium | 30 | 6 | 6 | 210 | 2520 | 130 | 927 |
| Medium | 50 | 6 | 6 | 350 | 4200 | 160 | 1408 |
| Medium | 80 | 6 | 6 | 560 | 6720 | 206 | 2327 |
| Large | 30 | 12 | 14 | 390 | 5040 | 312 | 1000 |
| Large | 50 | 12 | 14 | 650 | 8400 | 382 | 1500 |
| Large | 80 | 12 | 14 | 1040 | 13440 | 486 | 2430 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
He, M.; Guan, Z.; Hou, G.; Wang, X. A Novel Parts-to-Picker System with Buffer Racks and Access Racks in Flexible Warehousing Systems. Sustainability 2024, 16, 1388. https://doi.org/10.3390/su16041388
He M, Guan Z, Hou G, Wang X. A Novel Parts-to-Picker System with Buffer Racks and Access Racks in Flexible Warehousing Systems. Sustainability. 2024; 16(4):1388. https://doi.org/10.3390/su16041388
Chicago/Turabian StyleHe, Miao, Zailin Guan, Guoxiang Hou, and Xiaofen Wang. 2024. "A Novel Parts-to-Picker System with Buffer Racks and Access Racks in Flexible Warehousing Systems" Sustainability 16, no. 4: 1388. https://doi.org/10.3390/su16041388
APA StyleHe, M., Guan, Z., Hou, G., & Wang, X. (2024). A Novel Parts-to-Picker System with Buffer Racks and Access Racks in Flexible Warehousing Systems. Sustainability, 16(4), 1388. https://doi.org/10.3390/su16041388





