Multi-Objective Battery Coordination in Distribution Networks to Simultaneously Minimize CO2 Emissions and Energy Losses
Abstract
1. Introduction
1.1. General Context
1.2. Motivation
1.3. Literature Review
1.4. Contributions and Scope
- i.
- The proposal employs a convex-based optimization model based on semi-definite programming (SDP) theory to efficiently coordinate BESUs and REUs in distribution networks. This approach considers technical and environmental objective functions within a multi-objective optimization method.
- ii.
- This work assesses the impact of incorporating the reactive power control capabilities of the power electronic converters that connect BESUs and REUs. This allows operation with variable power factors, in contrast to conventional unitary power factor operation.
1.5. Document Structure
2. Mathematical Modeling
2.1. Objective Functions
2.2. Set of Constraints
3. Proposed Convexification Approach
3.1. Semi-Definite Programming Approximation
3.2. Approximated Convex Model
3.3. Weighting-Based Optimization Approach
4. Studied Test System
- The BESUs are located at buses 6, 14, and 31 and have nominal sizes of 2000, 1000, and 1500 kWh, respectively. In addition, the BESU connected to bus 6 has charging and discharging times of 5 h, whereas the remaining BESUs have times of 4 h.
- The PV sources are located at nodes 13, 25, and 30 and have installed capacities of about 1125, 1320, and 999 kW, respectively.
5. Numerical Validations
5.1. Computational Validation against Literature Reports
- i.
- The proposed SDP approximation outperforms the proposal made by [22] that uses the PVSA for both objective functions. In the case of the expected daily energy losses, the improvement is about 4.3975 kWh/day. As for the CO2 emissions, the improvement is about kgh/day. Even though both reductions may seem like minor improvements, they demonstrate that the proposed SDP approximation effectively finds the best possible solution for the studied problem. At the same time, metaheuristic optimizers may become trapped in local optima.
- ii.
- With respect to the benchmark case (i.e., operation with solar sources and without BESUs), the improvement in daily energy losses is approximately 4.4743%, while the reduction in the expected CO2 emissions is about 0.1848%. This confirms that the optimal coordination of BESUs in electrical distribution networks can improve both technical and environmental objective functions, implying that efficient energy management systems must be designed for utilities to take full advantage of their potential.
5.2. Multi-Objective Analysis
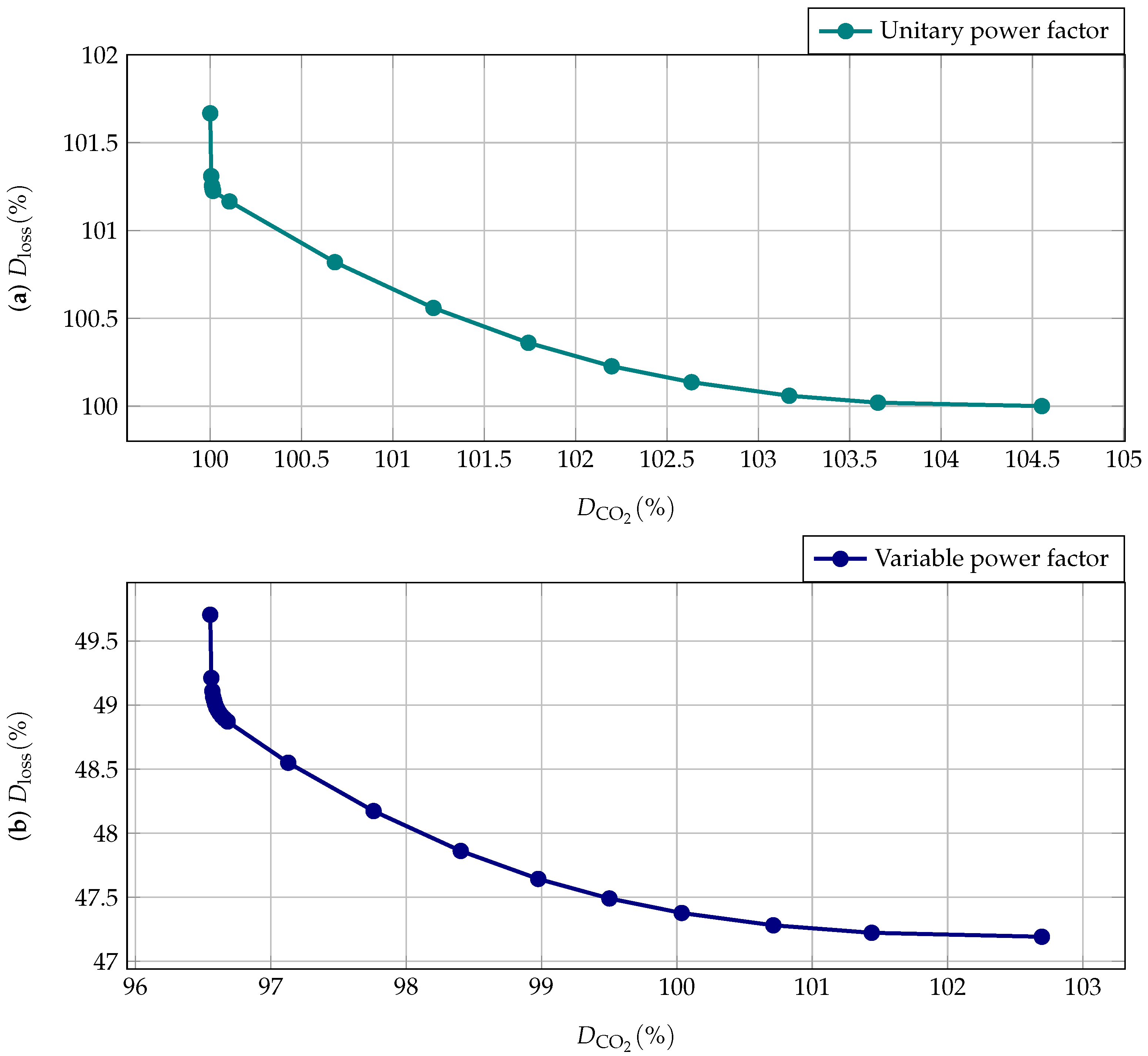
- i
- Regarding unitary power factor operation (see Figure 3a), when the optimal solution is reached for the objective function (see vertical axis with 100% of the value), the emissions level is shown to be higher than , i.e., exactly . This means that, concerning the reference value assigned to the coefficient, the CO2 emissions level is higher, which corresponds to about kgh/day of additional emissions when minimizing the energy losses. In the case of CO2 emissions minimization (see horizontal axis with 100% of the value), the energy losses increase by about with respect to the reference value in . This means that minimizing generates about of additional energy losses in a typical day of operation.
- ii
- The results regarding variable power factor operation (see Figure 3b) show the behavior of the energy losses to be between and with respect to the reference case, i.e., the value for unitary power factor operation. In other words, consideration of the reactive power control capabilities of the BESUs and solar generation sources allows for improvements greater than 50% for the energy losses indicator in comparison with the unitary power factor scenario. Moreover, the Pareto front in Figure 3b shows that the CO2 emissions index varies between and with respect to the reference case associated with the coefficient. This implies that when considering variable power factor operation, a wider range of possibilities is obtained. This means that the distribution company has more options to decide on for the daily operation of its DERs as a function of its interests and policies.
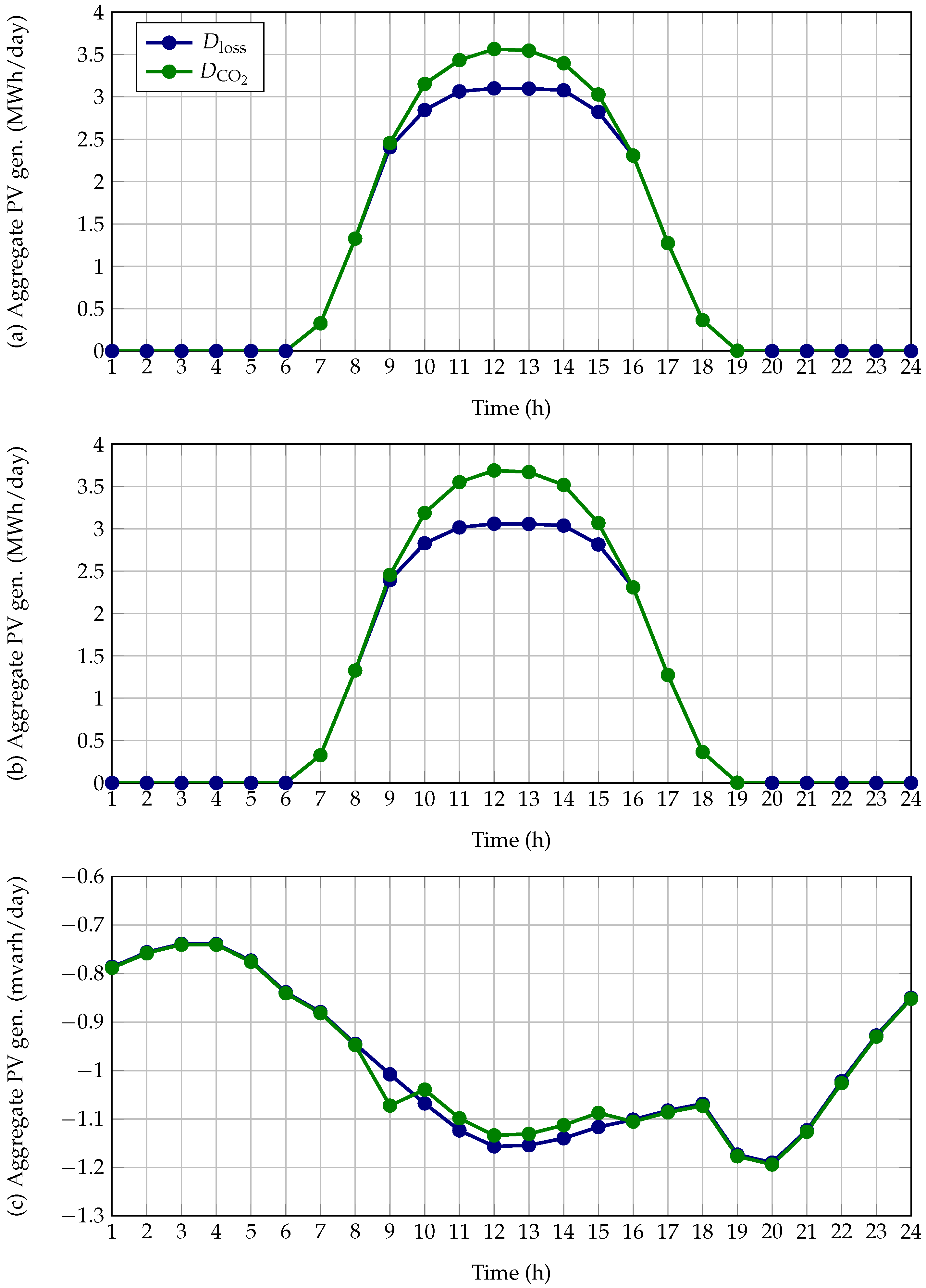
5.3. Complementary Analysis
- i.
- Active power generation in unitary and variable power factor operation is always greater in the case of minimizing CO2 emissions, which is an expected result since carbon dioxide emissions are directly a function of the power injections in the equivalent substation bus, which implies that, if possible, all the available renewable generation will be injected into the grid to minimize the total power generation in the substation terminals.
- ii.
- In the case of variable power factor operation, the main result, as expected, is reactive power injection in all operating periods for both objective functions, which implies that with reactive power, energy losses are reduced. In the case of energy loss minimization, the expected results are evident. On the other hand, in the case of CO2 emissions, the reduction in energy losses implies a reduction in the power injections of the substations, i.e., a reduction in the total CO2 emissions. In both objective function analyses, the expected level of reactive power injection shows similar demand behavior (compared to Figure 2), which is the expected behavior since energy losses are a quadratic function of the demanded current variations.
5.4. Stochastic Analysis
- i.
- When considering the reduction of the expected daily emissions of CO2 as the objective function, the minimum possible value corresponds to kg/day under the most favorable demand and generation conditions, i.e., the high availability and low demand profile. In contrast, the worst case exhibits a value of about kg/day and is associated with a high demand value and low PV generation potential. In addition, the most likely value for a daily operation scenario corresponds to the average emissions profile, with about kg/day and a standard deviation of about .
- ii.
- The stochastic scenario has reduced effects on the expected energy losses profile. Under the worst operating conditions, the value of the expected losses is about kWh/day. In contrast, in the most favorable scenario, the minimum possible value is about kWh/day. In this case, the standard deviation is only 2.13%, and the mean value is kWh/day.
- iii.
- In a general analysis, for the IEEE 33-bus network under the studied operating conditions, there are possible variations of about kWh/day and kg/day regarding energy losses and CO2 emissions, respectively. This shows the potential effect of variations in the expected demand and PV generation curves with respect to the deterministic case, allowing distribution companies to define the adequate dispatch of REUs and BESUs as a function of their operating plans and interests.
6. Conclusions and Future Work
- i.
- Single-objective function analysis considering unitary power factor operation for BESUs and REUs shows that the proposed SDP approach outperforms the metaheuristic methods reported in the literature regarding optimal values for and . It is worth mentioning that the optimizers used for comparison were the CGA, the PPSO, and the PVSA.
- ii.
- The results obtained with multi-objective operation that takes into consideration the expected daily energy losses and CO2 emissions shows that with high renewable energy availability, the objective functions are effectively in conflict, i.e., minimizing one of them implies compromising the other. In addition, when comparing the variable and unitary power factor approaches, it is observed that the expected energy losses can be improved by more than 50%. At the same time, the Pareto front for the CO2 emissions level varies by about 6%, which means that the distribution company has more options to define the operation of its electrical network and its DERs.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Nomenclature
| Indices | |
| b | Superscript associated with battery. |
| g | Superscript associated with conventional source. |
| Superscript associated with renewable source. | |
| Subscript associated with nodes. | |
| h | Subscript associated with period. |
| Parameters and Variables | |
| Objective function value regarding the expected daily energy losses (Wh/day). | |
| Objective function value regarding the daily CO2 emissions (kg/day). | |
| CO2 emission rates associated with conventional source (kg/W). | |
| CO2 emission rates associated with renewable source (kg/W). | |
| Complex voltage variables associated with node k at time h (V). | |
| Nodal admittance parameter relating nodes k and m (S). | |
| Length of time discretization (h). | |
| Complex power generation of the conventional source connected at bus k during period h (VA). | |
| Complex power generation of the renewable source connected at bus k during period h. | |
| Complex power injected/absorbed by the BESU connected at node k during period h (VA). | |
| Complex power consumption at bus k and time h (VA). | |
| State of charge of the BESU connected at node k during period h (%). | |
| State of charge of the BESU connected at node k during period (%). | |
| Efficiency of the absorbed/injected power of the BESU connected at bus k (%/Wh). | |
| Initial state of charge of the BESU connected at bus k (%). | |
| Final state of charge of the BESU connected at bus k (%). | |
| Impedance of the branch connected between nodes k and m (). | |
| Complex current flow through the branch connected between nodes k and m during period h (A). | |
| Maximum complex power generation limits for a conventional source connected at node k (VA). | |
| Maximum complex power generation limits for a renewable source connected at node k (VA). | |
| Complex power capacity of the BESU connected at bus k (VA). | |
| Maximum active power absorption of the BESU connected at bus k (W). | |
| Maximum active power injection of the BESU connected at bus k (W). | |
| Minimum allowable voltage (V). | |
| Maximum allowable voltage (V). | |
| Maximum current flow through the branch connected between nodes k and m (A). | |
| Initial analysis period (h). | |
| Final analysis period (h). | |
| Complex Hermitian semi-definite matrix during period h (V2). | |
| Complex square voltage results product between during period h (V2). | |
| Magnitude of current flow squared through the branch between nodes k and m during period h (A2). | |
| Weighting factor. | |
| Sets | |
| Set that contains all branches of the network. | |
| Set that contains all nodes in the network. | |
| Set that contains all analysis periods. | |
References
- Bose, B.K. Global Warming: Energy, Environmental Pollution, and the Impact of Power Electronics. IEEE Ind. Electron. Mag. 2010, 4, 6–17. [Google Scholar] [CrossRef]
- Harris, M.A. Confronting Global Climate Change: Experiments and Applications in the Tropics; CRC Press: Boca Raton, FL, USA, 2019. [Google Scholar] [CrossRef]
- Godde, C.; Mason-D’Croz, D.; Mayberry, D.; Thornton, P.; Herrero, M. Impacts of climate change on the livestock food supply chain; a review of the evidence. Glob. Food Secur. 2021, 28, 100488. [Google Scholar] [CrossRef]
- Thaker, S.; Oni, A.O.; Gemechu, E.; Kumar, A. Evaluating energy and greenhouse gas emission footprints of thermal energy storage systems for concentrated solar power applications. J. Energy Storage 2019, 26, 100992. [Google Scholar] [CrossRef]
- It’s too soon to call this the anthropocene. IEEE Spectr. 2015, 52, 28. [CrossRef]
- Ekardt, F.; Wieding, J.; Zorn, A. Paris Agreement, Precautionary Principle and Human Rights: Zero Emissions in Two Decades? Sustainability 2018, 10, 2812. [Google Scholar] [CrossRef]
- Banerjee, A. Financing the Climate Change through Green (Climate Sustainable) Bonds. In Proceedings of the 2019 Advances in Science and Engineering Technology International Conferences (ASET), Dubai, United Arab Emirates, 26–28 March 2019; IEEE: Piscataway, NJ, USA, 2019. [Google Scholar] [CrossRef]
- Sher, F.; Curnick, O.; Azizan, M.T. Sustainable Conversion of Renewable Energy Sources. Sustainability 2021, 13, 2940. [Google Scholar] [CrossRef]
- Szetela, B.; Majewska, A.; Jamroz, P.; Djalilov, B.; Salahodjaev, R. Renewable Energy and CO2 Emissions in Top Natural Resource Rents Depending Countries: The Role of Governance. Front. Energy Res. 2022, 10, 872941. [Google Scholar] [CrossRef]
- Roga, S.; Bardhan, S.; Kumar, Y.; Dubey, S.K. Recent technology and challenges of wind energy generation: A review. Sustain. Energy Technol. Assess. 2022, 52, 102239. [Google Scholar] [CrossRef]
- Hamed, T.A.; Alshare, A. Environmental Impact of Solar and Wind energy—A Review. J. Sustain. Dev. Energy Water Environ. Syst. 2022, 10, 1090387. [Google Scholar] [CrossRef]
- Wang, J.; Chen, L.; Tan, Z.; Du, E.; Liu, N.; Ma, J.; Sun, M.; Li, C.; Song, J.; Lu, X.; et al. Inherent spatiotemporal uncertainty of renewable power in China. Nat. Commun. 2023, 14, 5379. [Google Scholar] [CrossRef]
- Stevens, K.A.; Tang, T.; Hittinger, E. Innovation in complementary energy technologies from renewable energy policies. Renew. Energy 2023, 209, 431–441. [Google Scholar] [CrossRef]
- Casals, L.C.; Amante García, B.; Canal, C. Second life batteries lifespan: Rest of useful life and environmental analysis. J. Environ. Manag. 2019, 232, 354–363. [Google Scholar] [CrossRef]
- Saboori, H.; Jadid, S. Optimal scheduling of mobile utility-scale battery energy storage systems in electric power distribution networks. J. Energy Storage 2020, 31, 101615. [Google Scholar] [CrossRef]
- Saboori, H.; Jadid, S. Mobile and self-powered battery energy storage system in distribution networks–Modeling, operation optimization, and comparison with stationary counterpart. J. Energy Storage 2021, 42, 103068. [Google Scholar] [CrossRef]
- Valencia, A.; Hincapie, R.A.; Gallego, R.A. Optimal location, selection, and operation of battery energy storage systems and renewable distributed generation in medium–low voltage distribution networks. J. Energy Storage 2021, 34, 102158. [Google Scholar] [CrossRef]
- Lazzeroni, P.; Repetto, M. Optimal planning of battery systems for power losses reduction in distribution grids. Electr. Power Syst. Res. 2019, 167, 94–112. [Google Scholar] [CrossRef]
- Montoya, O.D.; Gil-González, W. Dynamic active and reactive power compensation in distribution networks with batteries: A day-ahead economic dispatch approach. Comput. Electr. Eng. 2020, 85, 106710. [Google Scholar] [CrossRef]
- Grover-Silva, E.; Girard, R.; Kariniotakis, G. Optimal sizing and placement of distribution grid connected battery systems through an SOCP optimal power flow algorithm. Appl. Energy 2018, 219, 385–393. [Google Scholar] [CrossRef]
- Li, Z.; Su, S.; Jin, X.; Xia, M.; Chen, Q.; Yamashita, K. Stochastic and distributed optimal energy management of active distribution network with integrated office buildings. CSEE J. Power Energy Syst. 2022, 1–12. [Google Scholar] [CrossRef]
- Grisales-Noreña, L.; Cortés-Caicedo, B.; Montoya, O.D.; Hernandéz, J.; Alcalá, G. A battery energy management system to improve the financial, technical, and environmental indicators of Colombian urban and rural networks. J. Energy Storage 2023, 65, 107199. [Google Scholar] [CrossRef]
- Alzahrani, A.; Alharthi, H.; Khalid, M. Minimization of Power Losses through Optimal Battery Placement in a Distributed Network with High Penetration of Photovoltaics. Energies 2019, 13, 140. [Google Scholar] [CrossRef]
- Eid, A.; Mohammed, O.; El-Kishky, H. Efficient operation of battery energy storage systems, electric-vehicle charging stations and renewable energy sources linked to distribution systems. J. Energy Storage 2022, 55, 105644. [Google Scholar] [CrossRef]
- Helling, F.; Glück, J.; Singer, A.; Pfisterer, H.J.; Weyh, T. The AC battery—A novel approach for integrating batteries into AC systems. Int. J. Electr. Power Energy Syst. 2019, 104, 150–158. [Google Scholar] [CrossRef]
- Gonzales-Calienes, G.; Kannangara, M.; Bensebaa, F. Economic and Environmental Viability of Lithium-Ion Battery Recycling—Case Study in Two Canadian Regions with Different Energy Mixes. Batteries 2023, 9, 375. [Google Scholar] [CrossRef]
- Andrić, M. Jensen-Type Inequalities for (h, g; m)-Convex Functions. Mathematics 2021, 9, 3312. [Google Scholar] [CrossRef]
- Chen, L.; Wemhoff, A.P. Predicting embodied carbon emissions from purchased electricity for United States counties. Appl. Energy 2021, 292, 116898. [Google Scholar] [CrossRef]
- González-Dumar, A.; Arango-Aramburo, S.; Correa-Posada, C.M. Quantifying power system flexibility for the energy transition in Colombia. Int. J. Electr. Power Energy Syst. 2024, 155, 109614. [Google Scholar] [CrossRef]
- Zorin, I.A.; Gryazina, E.N. An Overview of Semidefinite Relaxations for Optimal Power Flow Problem. Autom. Remote Control 2019, 80, 813–833. [Google Scholar] [CrossRef]
- Manshadi, S.D.; LIU, G.; Khodayar, M.E.; Wang, J.; Dai, R. A convex relaxation approach for power flow problem. J. Mod. Power Syst. Clean Energy 2019, 7, 1399–1410. [Google Scholar] [CrossRef]
- Grant, M.; Boyd, S. CVX: Matlab Software for Disciplined Convex Programming; Version 2.1; CVX Research, Inc.: Austin, TX, USA, 2014; Available online: http://cvxr.com/cvx (accessed on 1 December 2023).
- Grant, M.; Boyd, S. Graph implementations for nonsmooth convex programs. In Recent Advances in Learning and Control; Blondel, V., Boyd, S., Kimura, H., Eds.; Lecture Notes in Control and Information Sciences; Springer: Berlin/Heidelberg, Germany, 2008; pp. 95–110. Available online: https://link.springer.com/chapter/10.1007/978-1-84800-155-8_7 (accessed on 9 November 2023).
- Sadiq, R.; Wang, Z.; Chung, C.; Zhou, C.; Wang, C. A review of STATCOM control for stability enhancement of power systems with wind/PV penetration: Existing research and future scope. Int. Trans. Electr. Energy Syst. 2021, 31, e13079. [Google Scholar] [CrossRef]
- Mallem, A.; Boudebbouz, O. Economic Dispatch on a Power System Network Interconnected With Solar Farm. In Proceedings of the 2019 1st International Conference on Sustainable Renewable Energy Systems and Applications (ICSRESA), Tébessa, Algeria, 4–5 December 2019; IEEE: Piscataway, NJ, USA, 2019; pp. 1–6. [Google Scholar]
- Forsati, R.; Mahdavi, M.; Shamsfard, M.; Meybodi, M.R. Efficient stochastic algorithms for document clustering. Inf. Sci. 2013, 220, 269–291. [Google Scholar] [CrossRef]
- Keutchayan, J.; Ortmann, J.; Rei, W. Problem-driven scenario clustering in stochastic optimization. Comput. Manag. Sci. 2023, 20, 13. [Google Scholar] [CrossRef]
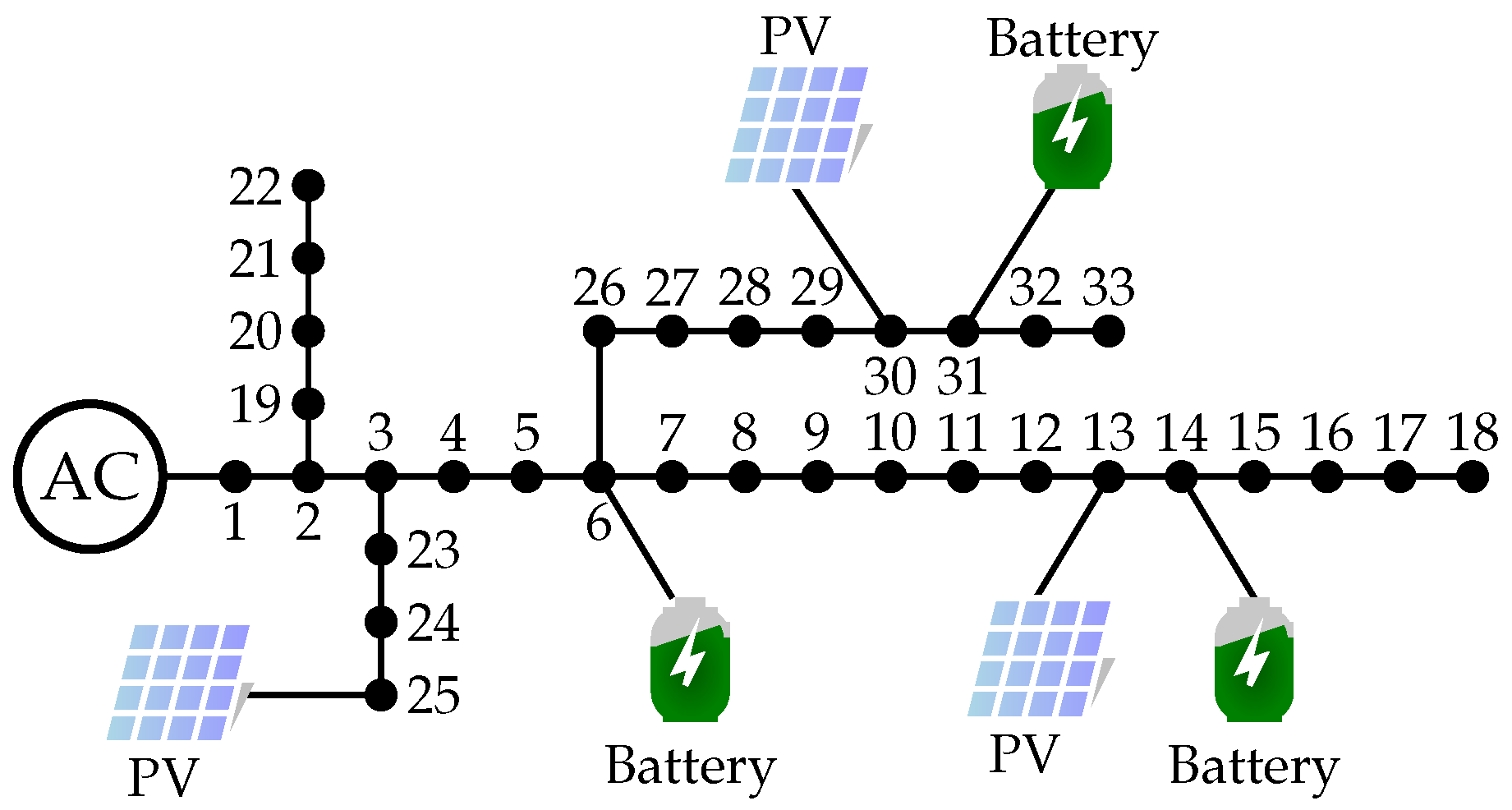



| Line l | Node i | Node j | (kW) | (kvar) | (A) | ||
|---|---|---|---|---|---|---|---|
| 1 | 1 | 2 | 0.0922 | 0.0477 | 100 | 60 | 385 |
| 2 | 2 | 3 | 0.4930 | 0.2511 | 90 | 40 | 355 |
| 3 | 3 | 4 | 0.3660 | 0.1864 | 120 | 80 | 240 |
| 4 | 4 | 5 | 0.3811 | 0.1941 | 60 | 30 | 240 |
| 5 | 5 | 6 | 0.8190 | 0.7070 | 60 | 20 | 240 |
| 6 | 6 | 7 | 0.1872 | 0.6188 | 200 | 100 | 110 |
| 7 | 7 | 8 | 1.7114 | 1.2351 | 200 | 100 | 85 |
| 8 | 8 | 9 | 1.0300 | 0.7400 | 60 | 20 | 70 |
| 9 | 9 | 10 | 1.0400 | 0.7400 | 60 | 20 | 70 |
| 10 | 10 | 11 | 0.1966 | 0.0650 | 45 | 30 | 55 |
| 11 | 11 | 12 | 0.3744 | 0.1238 | 60 | 35 | 55 |
| 12 | 12 | 13 | 1.4680 | 1.1550 | 60 | 35 | 55 |
| 13 | 13 | 14 | 0.5416 | 0.7129 | 120 | 80 | 40 |
| 14 | 14 | 15 | 0.5910 | 0.5260 | 60 | 10 | 25 |
| 15 | 15 | 16 | 0.7463 | 0.5450 | 60 | 20 | 20 |
| 16 | 16 | 17 | 1.2890 | 1.7210 | 60 | 20 | 20 |
| 17 | 17 | 18 | 0.7320 | 0.5740 | 90 | 40 | 20 |
| 18 | 2 | 19 | 0.1640 | 0.1565 | 90 | 40 | 40 |
| 19 | 19 | 20 | 1.5042 | 1.3554 | 90 | 40 | 25 |
| 20 | 20 | 21 | 0.4095 | 0.4784 | 90 | 40 | 20 |
| 21 | 21 | 22 | 0.7089 | 0.9373 | 90 | 40 | 20 |
| 22 | 3 | 23 | 0.4512 | 0.3083 | 90 | 50 | 85 |
| 23 | 23 | 24 | 0.8980 | 0.7091 | 420 | 200 | 85 |
| 24 | 24 | 25 | 0.8960 | 0.7011 | 420 | 200 | 40 |
| 25 | 6 | 26 | 0.2030 | 0.1034 | 60 | 25 | 125 |
| 26 | 26 | 27 | 0.2842 | 0.1447 | 60 | 25 | 110 |
| 27 | 27 | 28 | 1.0590 | 0.9337 | 60 | 20 | 110 |
| 28 | 28 | 29 | 0.8042 | 0.7006 | 120 | 70 | 110 |
| 29 | 29 | 30 | 0.5075 | 0.2585 | 200 | 600 | 95 |
| 30 | 30 | 31 | 0.9744 | 0.9630 | 150 | 70 | 55 |
| 31 | 31 | 32 | 0.3105 | 0.3619 | 210 | 100 | 30 |
| 32 | 32 | 33 | 0.3410 | 0.5302 | 60 | 40 | 20 |
| Method | (kg/day) | (kWh/day) |
|---|---|---|
| Benchmark case | 9887.4082 | 2484.5747 |
| CGA | 9878.0207 | 2431.4745 |
| PPSO | 9869.6348 | 2380.8336 |
| PVSA | 9869.5623 | 2377.8028 |
| SDP | 9869.1339 | 2373.4053 |
| Objective Function | Minimum | Average | Maximum | Standard Deviation |
|---|---|---|---|---|
| (kg/day) | 8539.1511 | 8808.8502 | 9053.1053 | 13.49% (1188.7166) |
| (kWh/day) | 1089.8598 | 1135.8386 | 1163.5758 | 2.13% (24.2202) |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Montoya, O.D.; Grisales-Noreña, L.F.; Gil-González, W. Multi-Objective Battery Coordination in Distribution Networks to Simultaneously Minimize CO2 Emissions and Energy Losses. Sustainability 2024, 16, 2019. https://doi.org/10.3390/su16052019
Montoya OD, Grisales-Noreña LF, Gil-González W. Multi-Objective Battery Coordination in Distribution Networks to Simultaneously Minimize CO2 Emissions and Energy Losses. Sustainability. 2024; 16(5):2019. https://doi.org/10.3390/su16052019
Chicago/Turabian StyleMontoya, Oscar Danilo, Luis Fernando Grisales-Noreña, and Walter Gil-González. 2024. "Multi-Objective Battery Coordination in Distribution Networks to Simultaneously Minimize CO2 Emissions and Energy Losses" Sustainability 16, no. 5: 2019. https://doi.org/10.3390/su16052019
APA StyleMontoya, O. D., Grisales-Noreña, L. F., & Gil-González, W. (2024). Multi-Objective Battery Coordination in Distribution Networks to Simultaneously Minimize CO2 Emissions and Energy Losses. Sustainability, 16(5), 2019. https://doi.org/10.3390/su16052019








