Analysis of Grid-Forming Inverter Controls for Grid-Connected and Islanded Microgrid Integration
Abstract
:1. Introduction
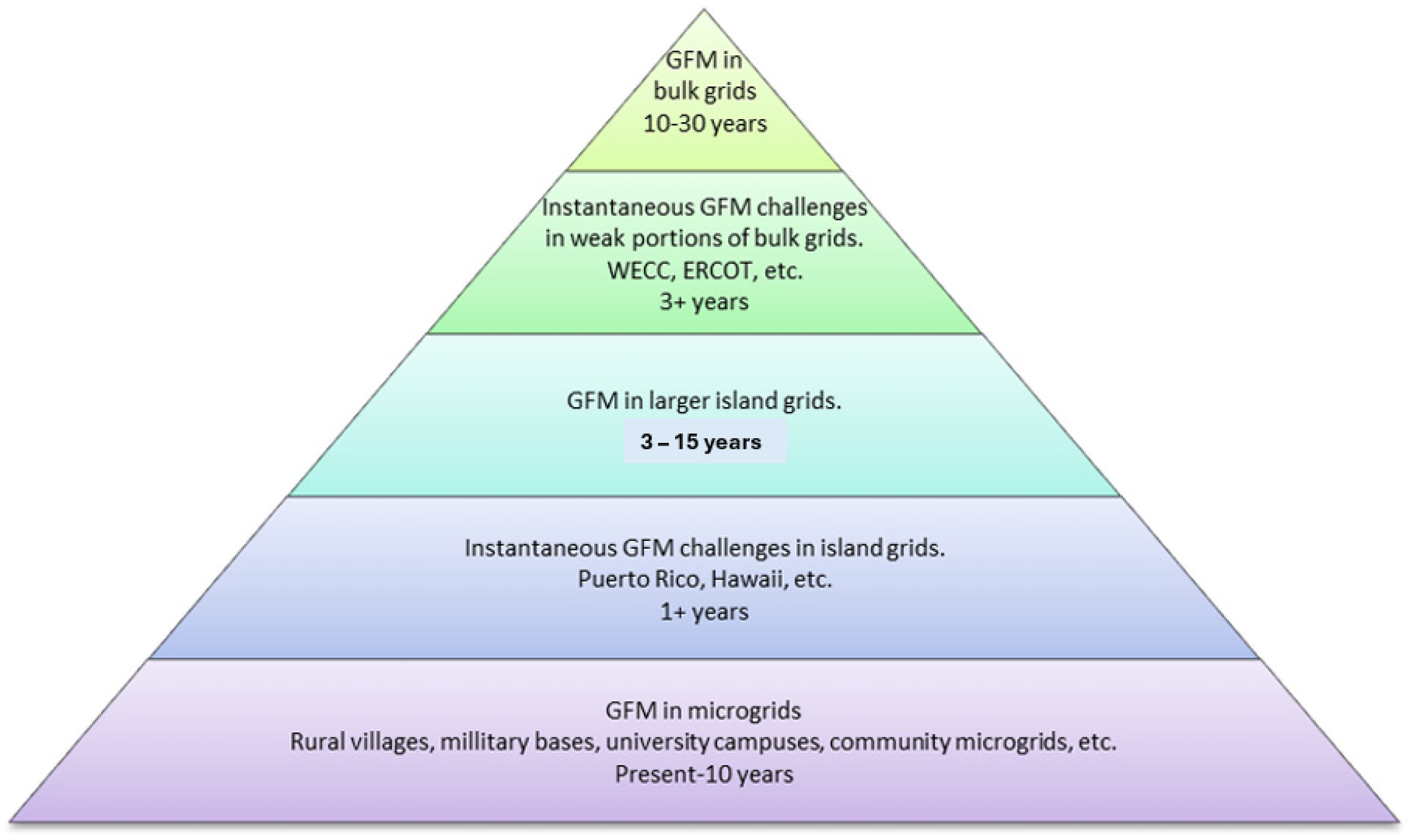
2. Overview of the Support Framework
2.1. GFM Inverter Control Characteristics
2.2. Microgrids in Operation in West Texas
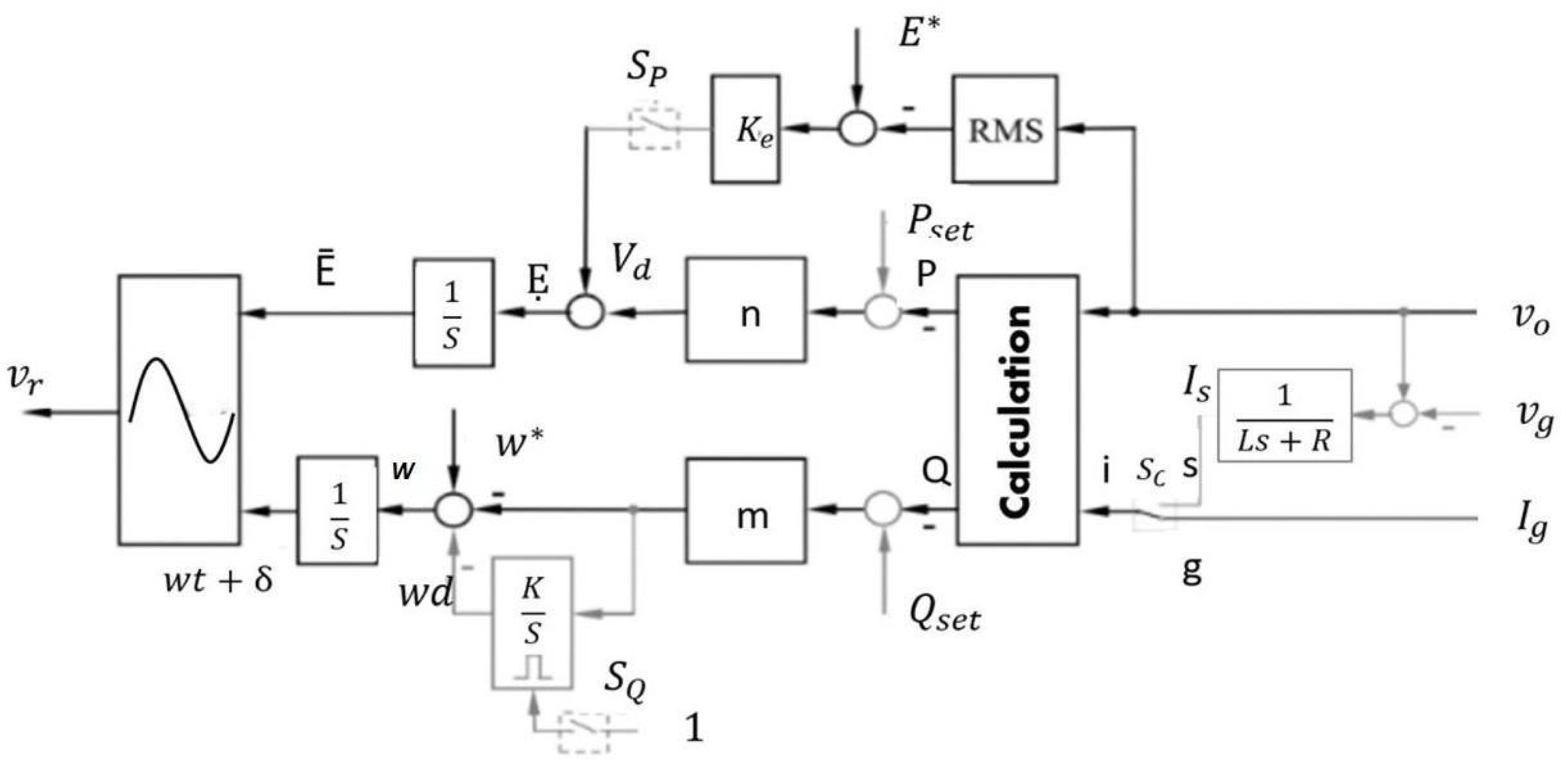
3. Proposed GFM Inverter Control
3.1. GFM Inverter Controller Structure
3.2. GFM Inverter Control Operation Modes
3.2.1. Self—Synchronized Mode
3.2.2. Droop Mode
3.3. Parameter Design Guideline for the GFM Inverter Control Strategy
3.4. Black Start Capability
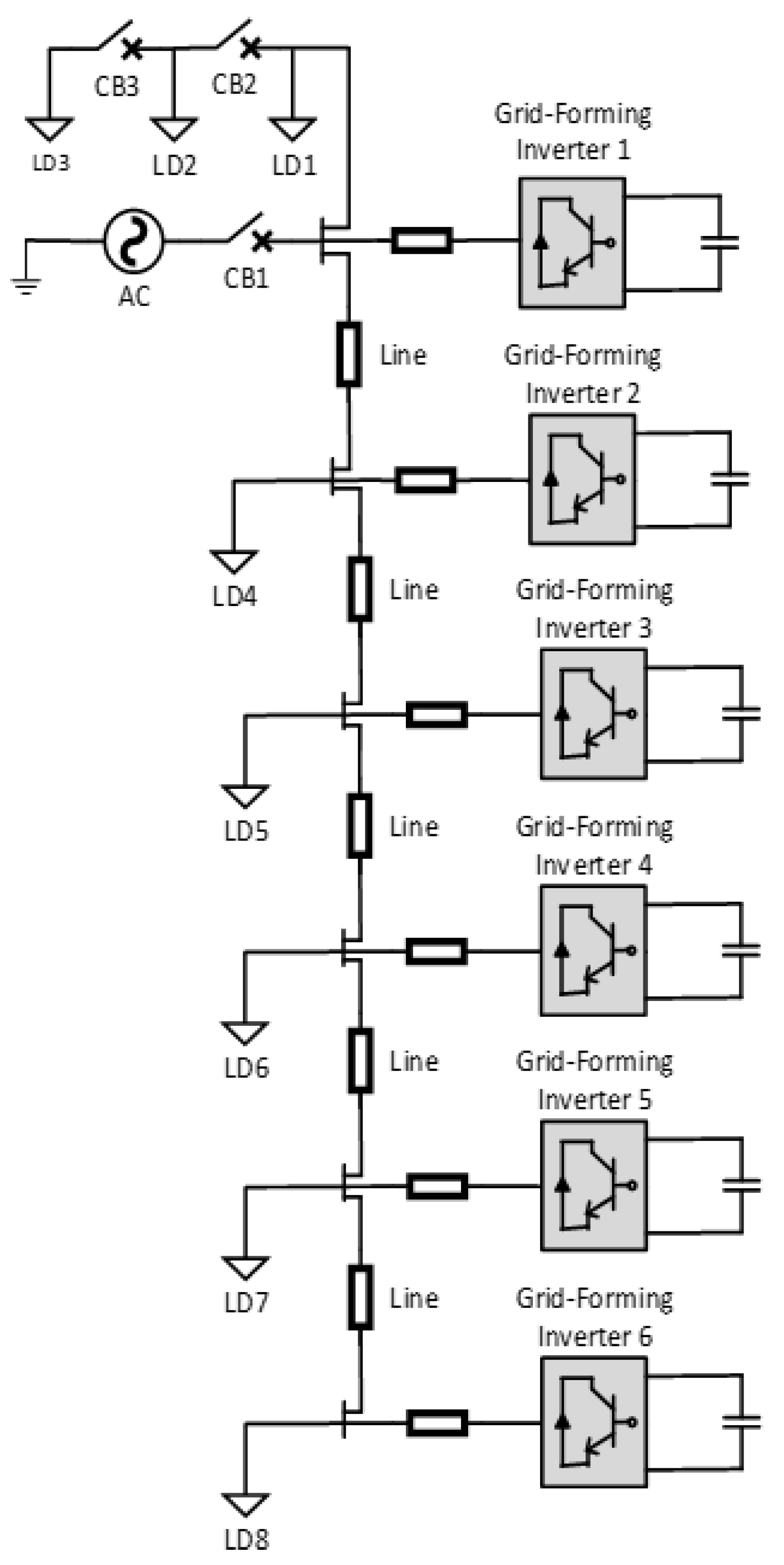
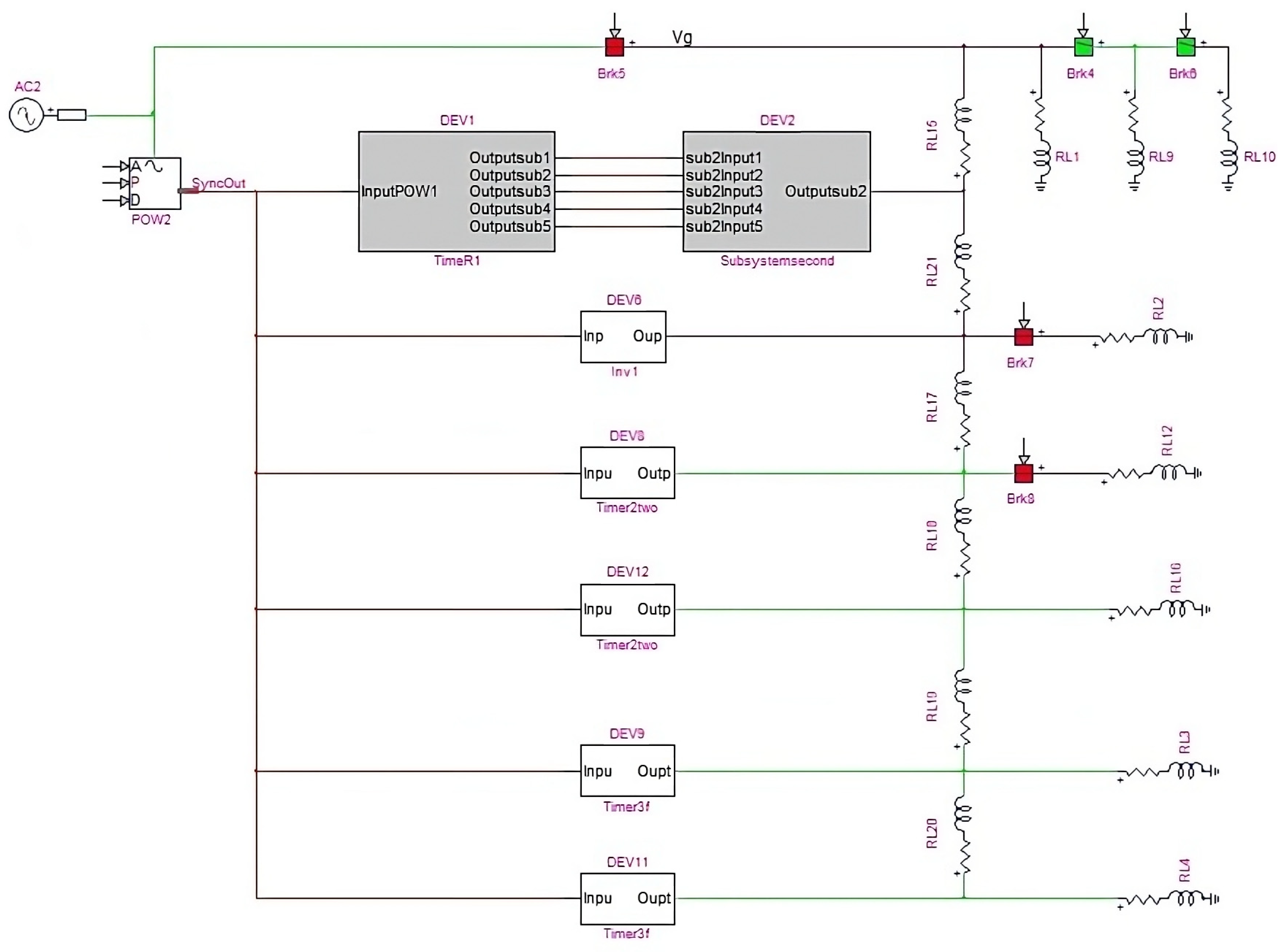
4. Case Study
Modeling and Analysis
5. Case Studies Results
5.1. Results for Case Study I
5.1.1. Grid-Connected and Islanded Mode
5.1.2. Black Start Capability on Grid-Disconnected Mode
5.2. Results for Case Study II
5.2.1. Performance of Six GFM Inverter Controllers in Grid-Connected and Islanded Modes in the Test Feeder
5.2.2. Black Start Capability of Six GFM Inverter Controllers in the IEEE 123 Test Feeder
6. Discussion
7. Conclusions
- Dependency Pattern Analysis:
- Proposed and systematically evaluated the current state of an electrical grid with a focus on decarbonization using GFM power inverters.
- Quantified the dependency pattern of GFL inverters, providing a clear understanding of their role within the grid.
- Voltage and Frequency Regulation:
- Implemented and assessed a novel adoption model incorporating the latest GFM inverter controller in both small electrical networks and large-scale test feeders.
- Quantitatively demonstrated the model’s efficacy in regulating voltage and frequency in grid-connected and islanded photovoltaic microgrids.
- Fossil Fuel Dependence Reduction:
- Quantified the tangible impact of adopting GFM power inverter controller, showcasing a measurable reduction in dependence on fossil fuels.
- Established the paper’s contribution in steering the grid towards cleaner and more sustainable energy sources.
- Enhanced DER Penetration Index:
- Evaluated, in quantitative terms, how the GFM power inverter controller enhances the penetration index of DERs into the grid.
- Provided numerical insights into the scalability of the adoption model, determining the optimal number of GFM inverters for effective DER integration.
- Future Scaling Plans:
- Outlined a concrete plan for future work, involving the application of the proposed adoption model using 60 GFM power inverter controller.
- Anticipated quantitative outcomes from an additional test feeder grid with more electrical nodes, promising a deeper understanding of scalability and performance.
- Advanced Control Strategies:
- Investigate and implement more advanced control strategies for GFM power inverter controllers beyond the current technology. Explore predictive control methods or artificial intelligence-based approaches to further enhance grid stability and performance.
- Cybersecurity Considerations:
- Address the growing importance of cybersecurity in the context of GFM power inverters. Assess vulnerabilities and propose robust security measures to protect against potential cyberthreats, ensuring the resilience of the grid.
- Integration of Energy Storage:
- Explore the integration of energy storage systems in conjunction with GFM power inverters. Investigate how energy storage technologies can be synergistically employed to enhance grid reliability, mitigate intermittency issues, and support continuous power supply during fluctuations.
- Resilience to Extreme Events:
- Evaluate the resilience of GFM power inverter systems to extreme weather events, natural disasters, and other unforeseen challenges. Develop strategies to ensure grid continuity and rapid recovery in the face of adverse conditions.
- GFM in Hybrid Systems:
- Investigate the role of GFM power inverters in hybrid energy systems, where multiple energy sources (renewable and conventional) coexist. Analyze their performance in complex grid architectures and assess the potential for improved hybrid system optimization.
- Economic Viability and Cost–Benefit Analysis:
- Conduct a comprehensive economic analysis to assess the cost-effectiveness of widespread GFM power inverter adoption. Explore potential incentives, subsidies, and cost savings associated with reduced reliance on traditional power generation methods.
- Real-World Implementation and Case Studies:
- Collaborate with utility providers or relevant stakeholders to implement GFM power inverter systems in real-world scenarios. Conduct case studies to validate the scalability, reliability, and performance under actual grid conditions.
- Policy and Regulatory Considerations:
- Examine the existing policy and regulatory frameworks governing the integration of GFM power inverters. Propose recommendations for policy adjustments or regulatory updates to encourage and facilitate their widespread deployment.
- Quantification of Environmental Impact:
- Quantify the environmental impact of adopting GFM power inverters compared to traditional grid configurations. Assess the reduction in carbon emissions and other environmental benefits associated with the transition to cleaner energy sources.
- Public Awareness and Stakeholder Engagement:
- Develop strategies to enhance public awareness and engage relevant stakeholders in the adoption of GFM power inverters. Investigate public perception, potential barriers, and methods to promote acceptance and collaboration.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Breyer, C.; Khalili, S.; Bogdanov, D.; Ram, M.; Oyewo, A.S.; Aghahosseini, A.; Gulagi, A.; Solomon, A.A.; Keiner, D.; Lopez, G.; et al. On the History and Future of 100% Renewable Energy Systems Research. IEEE Access 2022, 10, 78176–78218. [Google Scholar] [CrossRef]
- Shen, B.; Kahrl, F.; Satchwell, A.J. Facilitating Power Grid Decarbonization with Distributed Energy Resources: Lessons from the United States. Annu. Rev. Environ. Resour. 2021, 46, 349–375. [Google Scholar] [CrossRef]
- Hossain, M.B.; Islam, M.R.; Muttaqi, K.M.; Sutanto, D.; Agalgaonkar, A.P. Modeling and performance analysis of renewable hydrogen energy hub connected to an ac/dc hybrid microgrid. Int. J. Hydrogen Energy 2022, 47, 28626–28644. [Google Scholar] [CrossRef]
- Satymov, R.; Bogdanov, D.; Breyer, C. The Value of Fast Transitioning to a Fully Sustainable Energy System: The Case of Turkmenistan. IEEE Access 2021, 9, 13590–13611. [Google Scholar] [CrossRef]
- Burton, R.; Baggu, M.; Rhodes, J.; Blair, N.; Harris, T.; Sengupta, M.; Barrows, C.; Sky, H.; Yang, J.; Elsworth, J.; et al. Puerto Rico Grid Resilience and Transitions to 100% Renewable Energy Study (pr100): Six-Month Progress Update; Technical Report; National Renewable Energy Lab (NREL): Golden, CO, USA, 2022.
- U.S. Energy Information Administration. Us Energy Information Administration Annual Energy Outlook 2020; US Department of Energy: Washington, DC, USA, 2020.
- Barrueto, A.; Díaz, M.; Chávez, H. An Overview of Challenges related to Power-Electronics Based Power Systems. In Proceedings of the 2021 IEEE International Conference on Automation/XXIV Congress of the Chilean Association of Automatic Control (ICA-ACCA), Valparaíso, Chile, 22–26 March 2021; pp. 1–7. [Google Scholar] [CrossRef]
- Multnomah County-Sustainability, “100% Renewable by 2050”. 2017. Available online: https://www.multco.us/sustainability/100-renewable-2050 (accessed on 12 July 2023).
- Bassey, O.; Butler-Purry, K.L.; Chen, B. Dynamic Modeling of Sequential Service Restoration in Islanded Single Master Microgrids. IEEE Trans. Power Syst. 2020, 35, 202–214. [Google Scholar] [CrossRef]
- Saadatmand, S. Advanced Control Techniques for Modern Inertia-Based Inverters. Ph.D. Dissertation, Missouri University of Science and Technology, Rolla, MO, USA, 2021. [Google Scholar]
- Zhong, Q.-C. Power-Electronics-Enabled Autonomous Power Systems: Architecture and Technical Routes. IEEE Trans. Ind. Electron. 2017, 64, 5907–5918. [Google Scholar] [CrossRef]
- Rathnayake, D.B.; Akrami, M.; Phurailatpam, C.; Me, S.P.; Hadavi, S.; Jayasinghe, G.; Zabihi, S.; Bahrani, B. Grid forming inverter modeling, control, and applications. IEEE Access 2021, 9, 114781–114807. [Google Scholar] [CrossRef]
- Pattabiraman, D. Impact of Inverter Control on the Dynamic Performance of Power Systems with High Penetration of Inverter-Based Resources; The University of Wisconsin-Madison: Madison, WI, USA, 2020. [Google Scholar]
- Zhong, Q.-C.; Nguyen, P.-L. Sinusoid-locked loops based on the principles of synchronous machines. In Proceedings of the 2012 24th Chinese Control and Decision Conference (CCDC), Taiyuan, China, 23–25 May 2012; pp. 1518–1523. [Google Scholar] [CrossRef]
- Zhong, Q.-C.; Nguyen, P.-L.; Ma, Z.; Sheng, W. Self-Synchronized Synchronverters: Inverters Without a Dedicated Synchronization Unit. IEEE Trans. Power Electron. 2013, 29, 617–630. [Google Scholar] [CrossRef]
- Tuckey, A.; Round, S. Grid-forming inverters for grid-connected microgrids: Developing “good citizens” to ensure the continued flow of stable, reliable power. IEEE Electrif. Mag. 2022, 10, 39–51. [Google Scholar] [CrossRef]
- Yap, K.Y.; Sarimuthu, C.R.; Lim, J.M.-Y. Virtual Inertia-Based Inverters for Mitigating Frequency Instability in Grid-Connected Renewable Energy System: A Review. Appl. Sci. 2019, 9, 5300. [Google Scholar] [CrossRef]
- U. D. of Energy, O. o. S. Information, and Technical. Large-Scale Adoption of Self-Synchronized Universal Droop Controller Based Inverters to Enable Ancillary Services for Different Modes of Distribution System Operations. 2020. Available online: https://www.osti.gov/biblio/1733353 (accessed on 6 February 2024).
- Lasseter, R.H.; Chen, Z.; Pattabiraman, D. Grid-forming inverters: A critical asset for the power grid. IEEE J. Emerg. Sel. Top. Power Electron. 2020, 8, 925–935. [Google Scholar] [CrossRef]
- Rampokanyo, M.; Dattaray, P.; Kamera, P.; Beerten, J.; Aronovich, I.; Corcoran, D.; Bos, J.; Modi, N.; Rahimi, I.; Quint, R.; et al. Impact of high penetration of inverter-based generation on system inertia of networks. Electra 2021, 319, 1–13. [Google Scholar]
- Du, W.; Tuffner, F.K.; Schneider, K.P.; Lasseter, R.H.; Xie, J.; Chen, Z.; Bhattarai, B. Modeling of grid-forming and grid-following inverters for dynamic simulation of large-scale distribution systems. IEEE Trans. Power Deliv. 2020, 36, 2035–2045. [Google Scholar] [CrossRef]
- Zuo, Y.; Yuan, Z.; Sossan, F.; Zecchino, A.; Cherkaoui, R.; Paolone, M. Performance assessment of grid-forming and grid-following converter-interfaced battery energy storage systems on frequency regulation in low-inertia power grids. Sustain. Energy Grids Netw. 2021, 27, 100496. [Google Scholar] [CrossRef]
- Lu, M. Virtual oscillator grid-forming inverters: State of the art, modeling, and stability. IEEE Trans. Power Electron. 2022, 37, 11579–11591. [Google Scholar] [CrossRef]
- Quedan, D.A.; Ramasubramanian, D.; Farantatos, E. Virtual Oscillator Controlled Grid Forming Inverters Modelling and Testing in Phasor Domain. In Proceedings of the 2021 IEEE 12th Energy Conversion Congress & Exposition—Asia (ECCE-Asia), Singapore, 24–27 May 2021; pp. 2375–2380. [Google Scholar] [CrossRef]
- Hadjileonidas, A.; Li, Y.; Green, T.C. Comparative analysis of transient stability of grid-forming and grid-following inverters. In Proceedings of the 2022 IEEE International Power Electronics and Application Conference and Exposition (PEAC), Guangzhou, China, 4–7 November 2022; pp. 296–301. [Google Scholar]
- Song, G.; Cao, B.; Chang, L. Review of Grid-forming Inverters in Support of Power System Operation. Chin. J. Electr. Eng. 2022, 8, 1–15. [Google Scholar] [CrossRef]
- Lin, Y.; Eto, J.H.; Johnson, B.B.; Flicker, J.D.; Lasseter, R.H.; Villegas Pico, H.N.; Seo, G.S.; Pierre, B.J.; Ellis, A. Research Roadmap on Grid-Forming Inverters; Technical Report; National Renewable Energy Lab. (NREL): Golden, CO, USA, 2020.
- Du, W.; Singhal, A.; Tuffner, F.K.; Schneider, K.P. Comparison of Electromagnetic Transient and Phasor-based Simulation for the Stability of Grid-Forming-Inverter-based Microgrids. In Proceedings of the 2021 IEEE Power & Energy Society Innovative Smart Grid Technologies Conference (ISGT), Washington, DC, USA, 16–18 February 2021; pp. 1–5. [Google Scholar] [CrossRef]
- Aghdam, S.A.; Agamy, M. Virtual oscillator-based methods for grid-forming inverter control: A review. IET Renew. Power Gener. 2022, 16, 835–855. [Google Scholar] [CrossRef]
- Muhanji, S.O.; Muzhikyan, A.; Farid, A.M. Distributed Control for Distributed Energy Resources: Long-Term Challenges and Lessons Learned. IEEE Access 2018, 6, 32737–32753. [Google Scholar] [CrossRef]
- Photovoltaics, D.G.; Storage, E. IEEE standard for interconnection and interoperability of distributed energy resources with associated electric power systems interfaces. IEEE Stand. 2018, 1547, 1547–2018. [Google Scholar]
- Zhong, Q.C.; Ming, W.L.; Zeng, Y. Self-Synchronized Universal Droop Controller. IEEE Access 2016, 4, 7145–7153. [Google Scholar] [CrossRef]
- Ruan, Y.; Zhong, Q.-C. Wind power system control based on the self- synchronized universal droop controller. In Proceedings of the 2019 IEEE Energy Conversion Congress and Exposition (ECCE), Baltimore, MD, USA, 29 September–3 October 2019; pp. 4654–4659. [Google Scholar]
- Arce, L.; Chamana, M.; Osman, I.; Ren, B.; Zhong, Q.C.; Bayne, S. Large-Scale Adoption of Self-Synchronized Universal Droop Controller-Based Inverters to Enable Ancillary Services for Different Modes of Distribution System Operations. In Proceedings of the 2020 5th IEEE Workshop on the Electronic Grid (eGRID), Aachen, Germany, 2–4 November 2020; pp. 1–6. [Google Scholar] [CrossRef]
- Çelik, Ö.; Teke, A.; Tan, A. Overview of micro-inverters as a challenging technology in photovoltaic applications. Renew. Sustain. Energy Rev. 2018, 82, 3191–3206. [Google Scholar] [CrossRef]
- Nguyen, Q.; Vallem, M.R.; Vyakaranam, B.; Tbaileh, A.; Ke, X.; Samaan, N. Control and simulation of a grid-forming inverter for hybrid pv-battery plants in power system black start. In Proceedings of the 2021 IEEE Power & Energy Society General Meeting (PESGM), Washington, DC, USA, 26–29 July 2021; pp. 1–5. [Google Scholar] [CrossRef]
- Ansari, S.; Chandel, A.; Tariq, M. A Comprehensive Review on Power Converters Control and Control Strategies of AC/DC Microgrid. IEEE Access 2021, 9, 17998–18015. [Google Scholar] [CrossRef]
- Wang, S.; Qi, R.; Li, Y. Fuzzy Control Scheme of Virtual Inertia for Synchronverter in Micro-Grid. In Proceedings of the 2018 21st International Conference on Electrical Machines and Systems (ICEMS), Jeju, Republic of Korea, 7–10 October 2018; pp. 2028–2032. [Google Scholar] [CrossRef]
- Laaksonen, H. Universal Grid-Forming Method for Future Power Systems. IEEE Access 2022, 10, 133109–133125. [Google Scholar] [CrossRef]
- Qoria, T.; Rokrok, E.; Bruyere, A.; François, B.; Guillaud, X. A pll-free grid-forming control with decoupled functionalities for high-power transmission system applications. IEEE Access 2020, 8, 197363–197378. [Google Scholar] [CrossRef]
- Kjaer, S.; Pedersen, J.; Blaabjerg, F. A Review of Single-Phase Grid-Connected Inverters for Photovoltaic Modules. IEEE Trans. Ind. Appl. 2005, 41, 1292–1306. [Google Scholar] [CrossRef]
- Bahrani, B. Power-Synchronized Grid-Following Inverter Without a Phase-Locked Loop. IEEE Access 2021, 9, 112163–112176. [Google Scholar] [CrossRef]
- Ellis, A. Grid Forming Inverters in Interconnected Systems. 2019. Available online: https://der-lab.net/wp-content/uploads/2018/11/Ellis_GFI-Vienna.pdf (accessed on 1 June 2023).
- Butt, O.M.; Zulqarnain, M.; Butt, T.M. Recent advancement in smart grid technology: Future prospects in the electrical power network. Ain Shams Eng. J. 2021, 12, 687–695. [Google Scholar] [CrossRef]
- Lasseter, B. Microgrids [distributed power generation]. In Proceedings of the 2001 IEEE Power Engineering Society Winter Meeting. Conference Proceedings (Cat. No. 01CH37194), Columbus, OH, USA, 28 January–1 February 2001; Volume 1, pp. 146–149. [Google Scholar]
- Stadler, M.; Cardoso, G.; Mashayekh, S.; Forget, T.; DeForest, N.; Agarwal, A.; Schönbein, A. Value streams in microgrids: A literature review. Appl. Energy 2016, 162, 980–989. [Google Scholar] [CrossRef]
- Ton, D.T.; Smith, M.A. The us department of energy’s microgrid initiative. Electr. J. 2012, 25, 84–94. [Google Scholar]
- Hoff, S. US electric system is made up of interconnections and balancing authorities. In US Energy Information Administration: Today in Energy; U.S. Energy Information Administration: Washington, DC, USA, 2016. [Google Scholar]
- Negri, C.A.; Daneshvardehnavi, S.; Schmitt, K.E.K.; Nezhad, A.E.; Nardelli, P.H.J.; Bayne, S.; Giesselmann, M.G. Centralized Control Topology for PV Farms Shading Detection and GMPP Searching Restarting Condition. IEEE Access 2022, 10, 28991–29008. [Google Scholar] [CrossRef]
- Daneshvardehnavi, S.; Negri, C.A.; Schmitt, K.E.K.; Bayne, S.; Giesselmann, M. A case study for connecting bidirectional pev station for reactive power support to the GLEAMM prototype microgrid. In Proceedings of the 2021 IEEE Green Technologies Conference (GreenTech), Denver, CO, USA, 7–9 April 2021; pp. 19–25. [Google Scholar] [CrossRef]
- Demir, A.; Gutiérrez, L.F.; Namin, A.S.; Bayne, S. Solar irradiance prediction using transformer-based machine learning models. In Proceedings of the 2022 IEEE International Conference on Big Data (Big Data), Osaka, Japan, 17–20 December 2022; pp. 2833–2840. [Google Scholar]
- Younis, T.; Ismeil, M.; Hussain, E.; Orabi, M. Single-phase self-synchronized synchronverter with current-limiting capability. In Proceedings of the 2016 Eighteenth International Middle East Power Systems Conference (MEPCON), Cairo, Egypt, 27–29 December 2016; pp. 848–853. [Google Scholar]
- Paspatis, A.G.; Konstantopoulos, G.C. Current-limiting droop control with virtual inertia and self-synchronization properties. In Proceedings of the IECON 2017—43rd Annual Conference of the IEEE Industrial Electronics Society, Beijing, China, 29 October–1 November 2017; pp. 196–201. [Google Scholar]
- Hsieh, G.-C.; Hung, J. Phase-locked loop techniques. a survey. IEEE Trans. Ind. Electron. 1996, 43, 609–615. [Google Scholar] [CrossRef]
- Ma, Y.; Cao, W.; Yang, L.; Wang, F.; Tolbert, L.M. Virtual Synchronous Generator Control of Full Converter Wind Turbines with Short-Term Energy Storage. IEEE Trans. Ind. Electron. 2017, 64, 8821–8831. [Google Scholar] [CrossRef]
- Mohammed, N.; Ravanji, M.H.; Zhou, W.; Bahrani, B. Online Grid Impedance Estimation-Based Adaptive Control of Virtual Synchronous Generators Considering Strong and Weak Grid Conditions. IEEE Trans. Sustain. Energy 2022, 14, 673–687. [Google Scholar] [CrossRef]
- Soni, K.A.; Jaiswal, N.K.; Lokhandwala, M.A. Phase locked loop for single phase grid synchronization. In Proceedings of the 2018 2nd International Conference on Trends in Electronics and Informatics (ICOEI), Tirunelveli, India, 11–12 May 2018; pp. 1058–1063. [Google Scholar] [CrossRef]
- Jain, P.; Agarwal, V.; Muni, B.P. Hybrid Phase Locked Loop for Controlling Master-Slave Configured Centralized Inverters in Large Solar Photovoltaic Power Plants. IEEE Trans. Ind. Appl. 2018, 54, 3566–3574. [Google Scholar] [CrossRef]
- Schmitt, K.E.K.; Osman, I.; Bhatta, R.; Murshed, M.; Chamana, M.; Bayne, S. A dynamic load control strategy for an efficient building demand response. In Proceedings of the 2021 IEEE Energy Conversion Congress and Exposition (ECCE), Vancouver, BC, Canada, 10–14 October 2021; pp. 819–826. [Google Scholar]
- Rocabert, J.; Luna, F.A. Blaabjerg, and P. Rodriguez, Control of power converters in ac microgrids. IEEE Trans. Power Electron. 2012, 27, 4734–4749. [Google Scholar] [CrossRef]
- Grid Deployment Office. Puerto Rico Grid Resilience and Transitions to 100. Available online: https://www.energy.gov/gdo/puerto-rico-grid-resilience-and-transitions-100-renewable-energy-study-pr100 (accessed on 1 June 2023).
- Aguero, J.R.; Khodaei, A. Grid modernization, der integration & utility business models-trends & challenges. IEEE Power Energy Mag. 2018, 16, 112–121. [Google Scholar]
- Adibi, M.; Clelland, P.; Fink, L.; Happ, H.; Kafka, R.; Raine, J.; Scheurer, D.; Trefny, F. Power System Restoration—A Task Force Report. IEEE Trans. Power Syst. 1987, 2, 271–277. [Google Scholar] [CrossRef]
- Li, Z.; Cheng, Z.; Li, S.; Si, J.; Gao, J.; Dong, W.; Das, H.S. Virtual Synchronous Generator and SMC-Based Cascaded Control for Voltage-Source Grid-Supporting Inverters. IEEE J. Emerg. Sel. Top. Power Electron. 2021, 10, 2722–2736. [Google Scholar] [CrossRef]
- Awal, M.A.; Yu, H.; Tu, H.; Lukic, S.M.; Husain, I. Hierarchical Control for Virtual Oscillator Based Grid-Connected and Islanded Microgrids. IEEE Trans. Power Electron. 2019, 35, 988–1001. [Google Scholar] [CrossRef]
- De Raul, A.T.G.; Maldonado, A.E.; Javier, P.R.; Jose, A.B.J. Grid-forming type converter decoupling and resynchronization for an ac microgrid. In Proceedings of the 2022 IEEE International Autumn Meeting on Power, Electronics and Computing (ROPEC), Ixtapa, Mexico, 9–11 November 2022; Volume 6, pp. 1–6. [Google Scholar]
- Dong, Y.; Ren, B.; Zhong, Q.-C. Bounded Universal Droop Control to Enable the Operation of Power Inverters Under Some Abnormal Conditions and Maintain Voltage and Frequency Within Predetermined Ranges. IEEE Trans. Ind. Electron. 2021, 69, 11633–11643. [Google Scholar] [CrossRef]
- IEEE. Electronics and Computing (ROPEC); IEEE: Piscataway, NJ, USA, 2022; Volume 6, pp. 1–6. [Google Scholar]
- Gracia, J.R.; O’Connor, P.W.; Markel, L.C.; Shan, R.; Rizy, D.T.; Tarditi, A. Hydropower Plants as Black Start Resources; U.S. Department of Energy: Washington, DC, USA, 2019.
- Bassey, O.; Butler-Purry, K.L. Black Start Restoration of Islanded Droop-Controlled Microgrids. Energies 2020, 13, 5996. [Google Scholar] [CrossRef]
- Shamim, N.; Subburaj, A.; Bayne, S. Model predictive control analysis for the battery energy storage system. In Proceedings of the 2017 Ninth Annual IEEE Green Technologies Conference (GreenTech), Denver, CO, USA, 29–31 March 2017; pp. 34–38. [Google Scholar] [CrossRef]
- Romero-Cadaval, E.; Francois, B.; Malinowski, M.; Zhong, Q.-C. Grid-connected photovoltaic plants: An alternative energy source, replacing conventional sources. IEEE Ind. Electron. Mag. 2015, 9, 18–32. [Google Scholar] [CrossRef]
- Bharati, A.K.; Ajjarapu, V.; Du, W.; Liu, Y. Role of distributed inverter-based resources in bulk grid primary frequency response through helics based smtd co-simulation. IEEE Syst. J. 2022, 17, 1071–1082. [Google Scholar] [CrossRef]
- Arce, P.L.; Bayne, S. Analysis of Offshore Wind Energy in Colombia: Current Status and Future Opportunities. Int. J. Eng. Res. Technol. IJERT 2020, 9, 1–10. [Google Scholar]

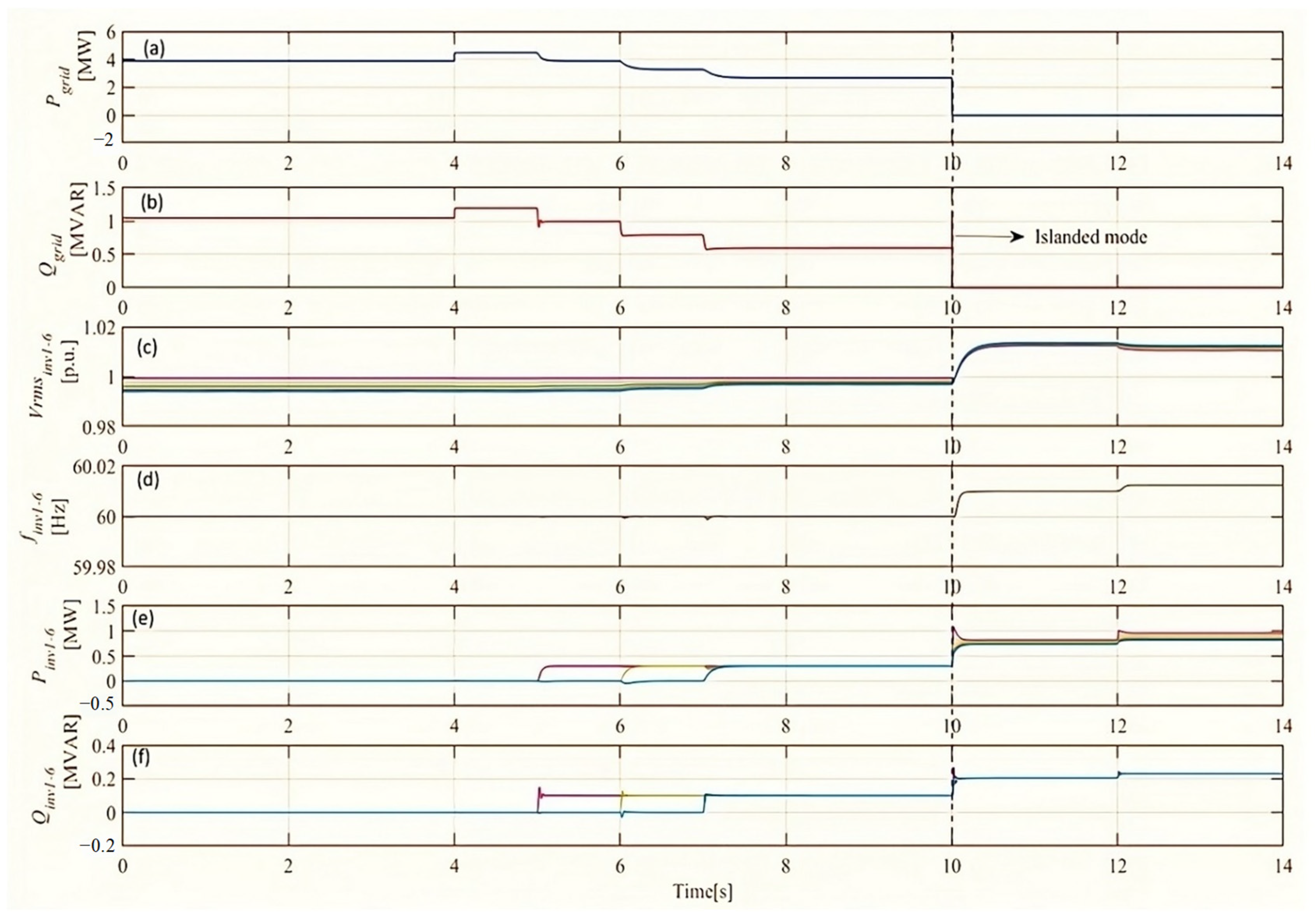
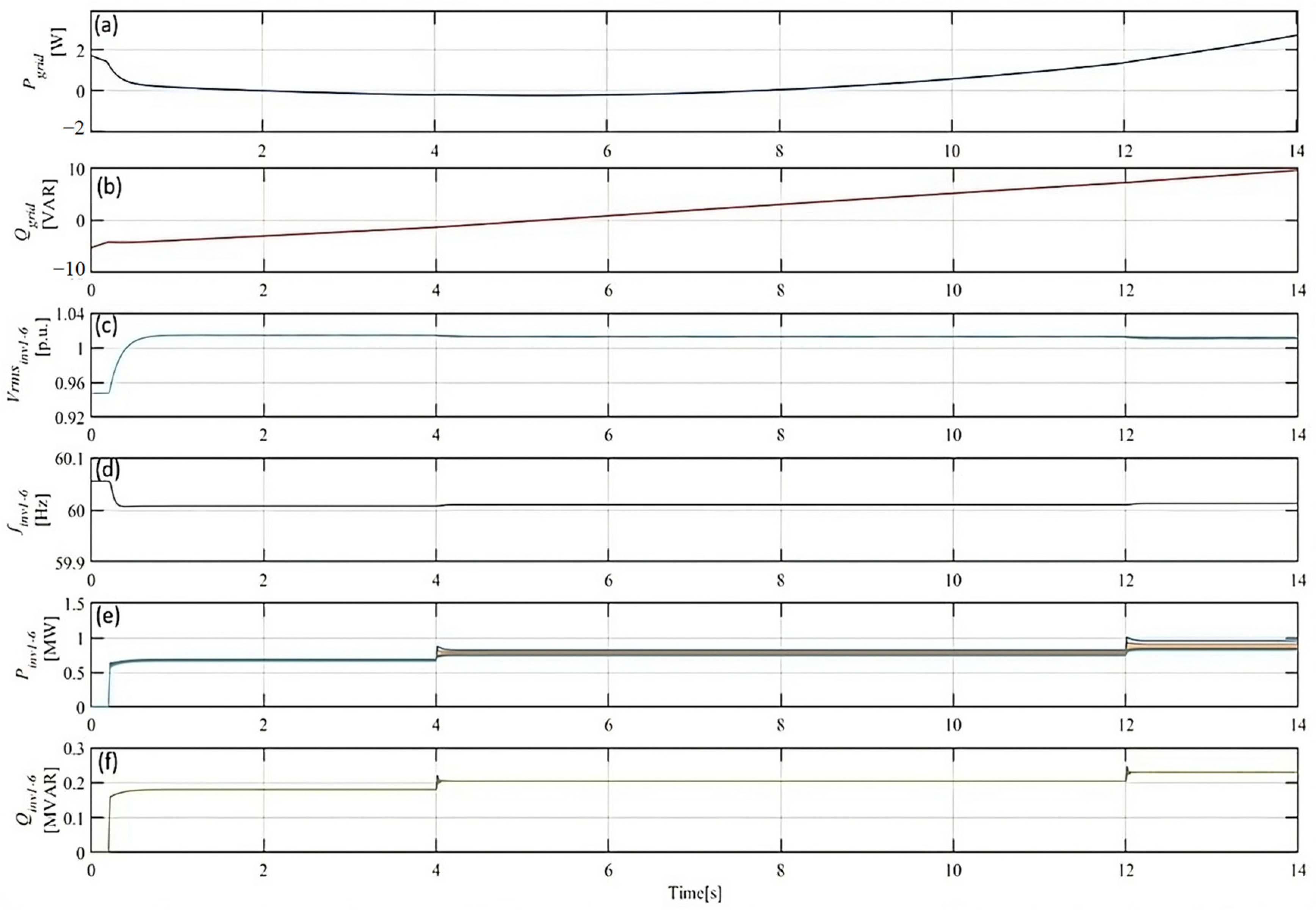
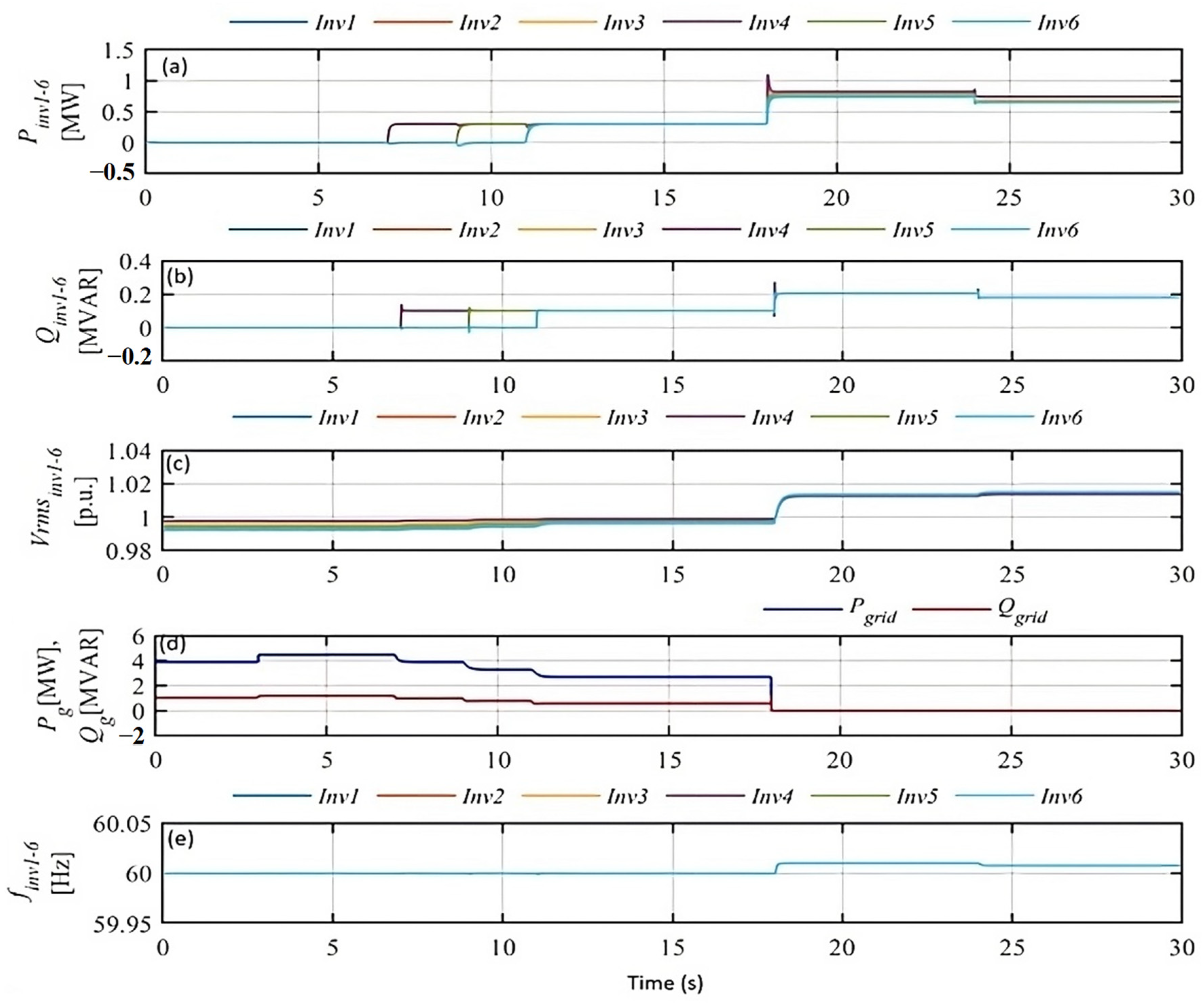
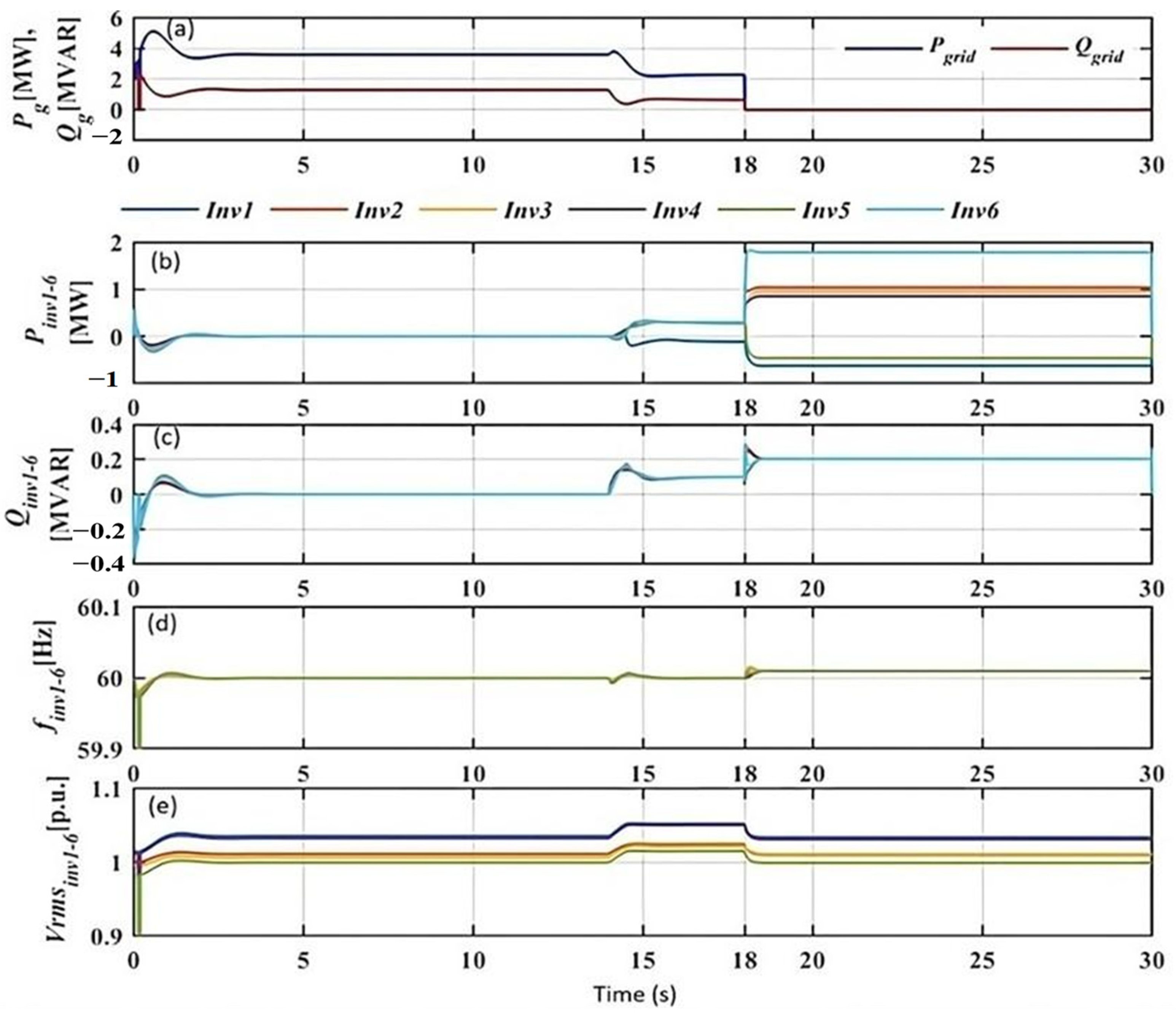
| Parameters | Values |
|---|---|
| Voltage (V) | 1 |
| ω* (angular frequency) | 377 |
| IMAX (maximum current) (A) | 0.5 |
| IMIN (minimum current) (A) | 0.033 |
| Ke (constant) | 20 |
| ω | 5 |
| Kω | 5 |
| Ksyn (synchronization gain) | 5 |
| mi (constant) | 3 |
| ni (constant) | 2 |
| Apparent power (VA) | 1 |
| Aspects | Small Network | IEEE 123 |
|---|---|---|
| Network size | Small | Large |
| Number of inverter controls | 6 | 6 |
| Grid complexity | Small network | IEEE 123 |
| Available generation resources | Simple | Complex |
| Voltage stability | Easy to maintain | More challenging |
| System protection | Simplified | Extensive |
| Fault analysis | Easier | Comprehensive |
| Power flow management | Simpler | Demanding |
| Integration with existing systems | Easier | Complex |
| System modeling and simulation | Detailed | Extensive |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ward, L.; Subburaj, A.; Demir, A.; Chamana, M.; Bayne, S.B. Analysis of Grid-Forming Inverter Controls for Grid-Connected and Islanded Microgrid Integration. Sustainability 2024, 16, 2148. https://doi.org/10.3390/su16052148
Ward L, Subburaj A, Demir A, Chamana M, Bayne SB. Analysis of Grid-Forming Inverter Controls for Grid-Connected and Islanded Microgrid Integration. Sustainability. 2024; 16(5):2148. https://doi.org/10.3390/su16052148
Chicago/Turabian StyleWard, Laura, Anitha Subburaj, Ayda Demir, Manohar Chamana, and Stephen B. Bayne. 2024. "Analysis of Grid-Forming Inverter Controls for Grid-Connected and Islanded Microgrid Integration" Sustainability 16, no. 5: 2148. https://doi.org/10.3390/su16052148
APA StyleWard, L., Subburaj, A., Demir, A., Chamana, M., & Bayne, S. B. (2024). Analysis of Grid-Forming Inverter Controls for Grid-Connected and Islanded Microgrid Integration. Sustainability, 16(5), 2148. https://doi.org/10.3390/su16052148








