A Joint Electricity Market-Clearing Mechanism for Flexible Ramping Products with a Convex Spot Market Model
Abstract
1. Introduction
- We propose a novel FCESMJC model that reduces spikes in electricity prices and dramatic electricity price volatility. The model’s clearing price can more accurately represent the relationship between the active output and the value of electricity in market clearing. The FCESMJC model reduces the system’s spikes in electricity price, contributing to the electricity market’s stable operation.
- We design a FOLP method that provides better economic benefits to FRP market participants. The FOLP method offers positive incentives for DPG to participate in the FRP market by reasonably compensating market participants. Meanwhile, the price obtained by the FOLP method is more intuitive, facilitating FRP market participants in making market decisions.
- We conduct economic analyses which improve the economic efficiency of the electricity market. The FCESMJC model brings significant ramping capabilities to the system. At the same time, the unexpected costs that arise from net load fluctuations are reduced, and the economic efficiency of the electricity market is improved prominently.
2. Convex Electricity Spot Market Clearing
2.1. Convex Electricity Spot Market Clearing Model
2.2. CESM Vectorized Structure and Solution Methods
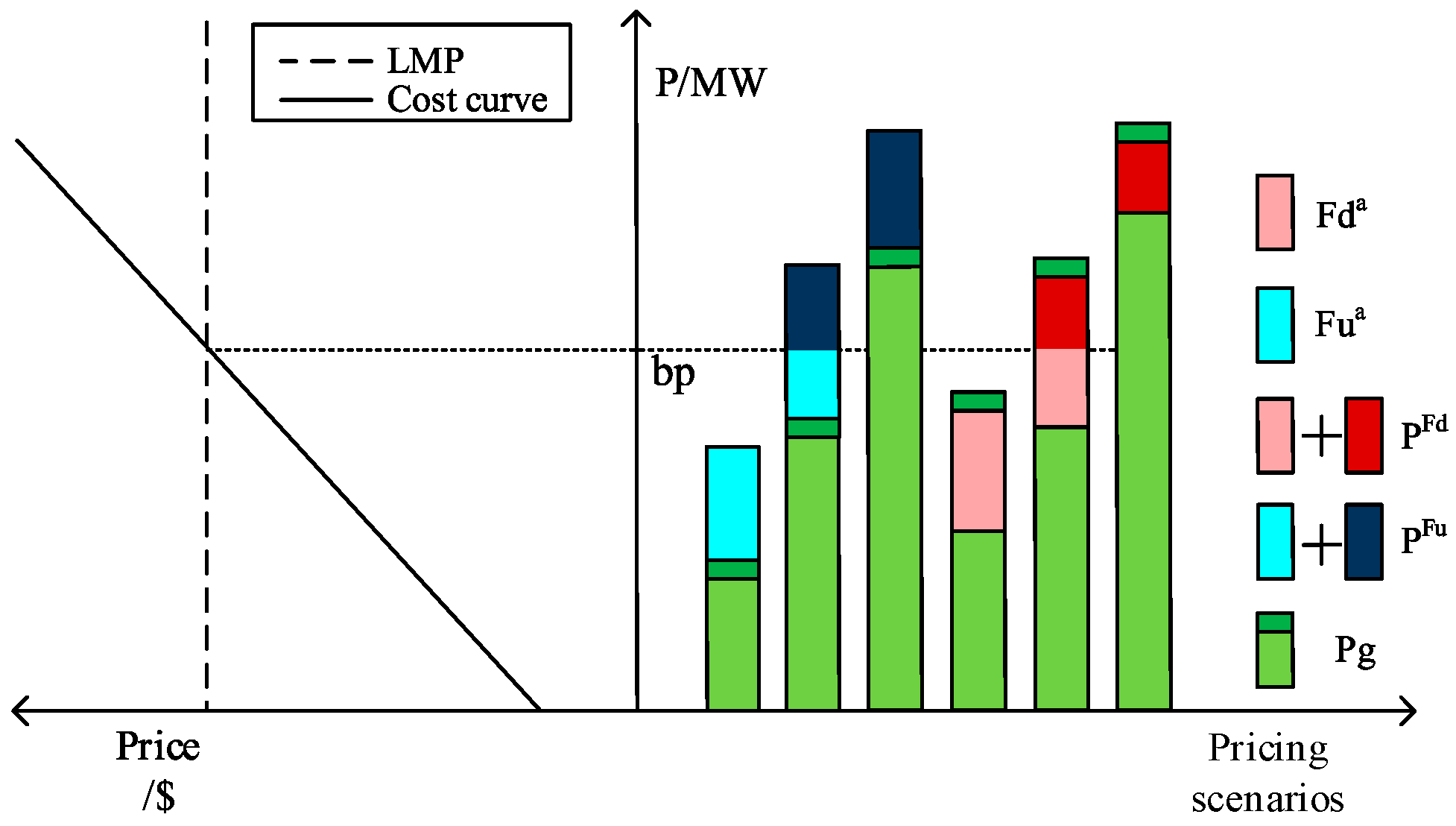
3. FCESMJC Model
3.1. Assessment of FRP Demand
3.2. Mathematical Model of the FOLP Method
3.3. Mathematical Modeling of Joint FRP and Convex Electricity Spot Market Clearing
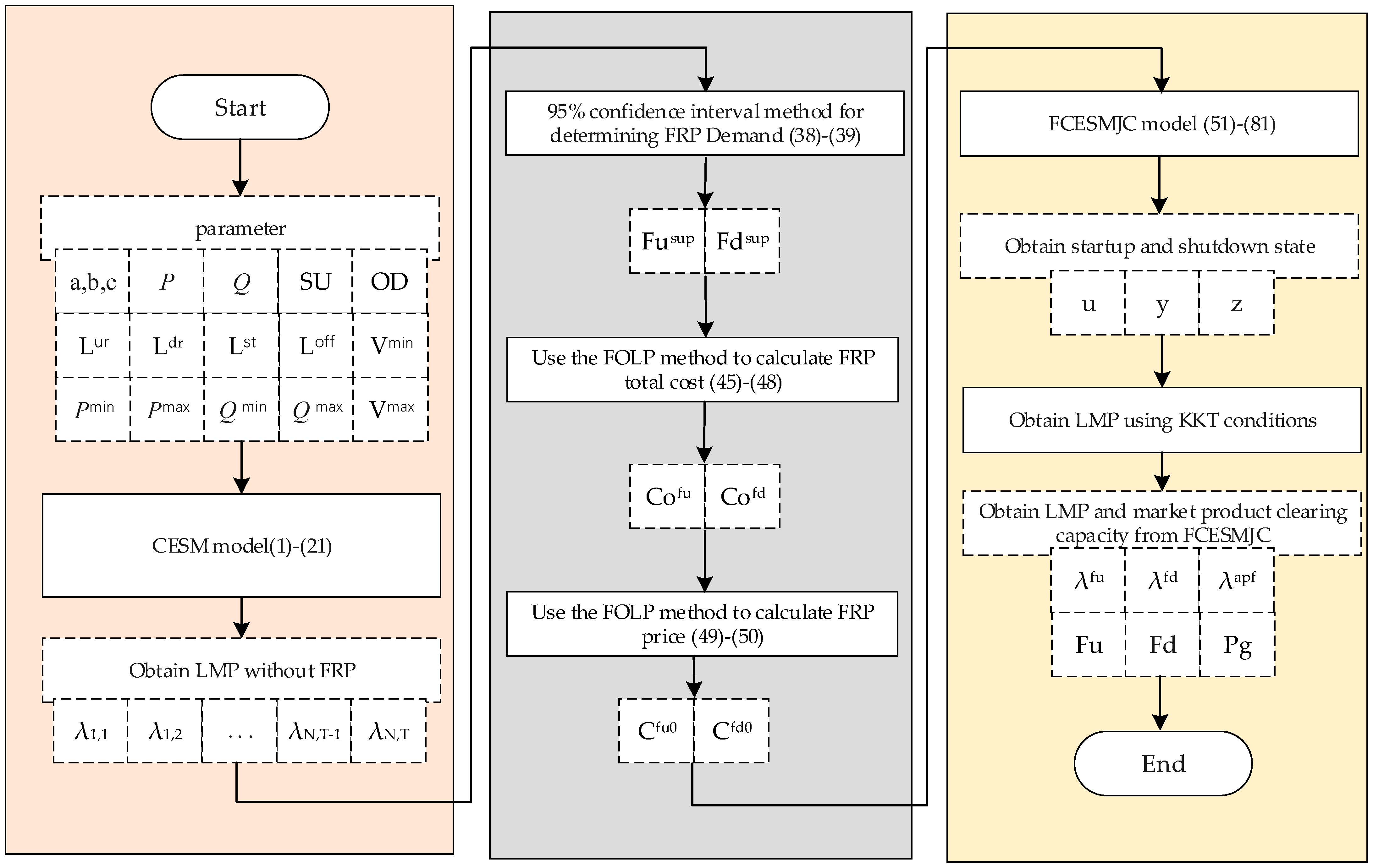
4. Numerical Experiments
4.1. Assumptions
- (1)
- LESM: linear electricity spot markets without FRP and net load fluctuations;
- (2)
- LESM-F: linear electricity spot markets without FRP but with net load fluctuations;
- (3)
- FCESMJC: convex electricity spot markets with FRP and net load fluctuations;
- (4)
- FCESMJC-F: convex electricity spot markets without FRP but with net load fluctuations;
- (5)
- NP-FCE: model of joint clearing of FRP and convex electricity spot markets without FOLP.
4.2. Simulation Results
4.2.1. Market Clearing Price Analysis
4.2.2. Economic Analysis of Market Participants
4.2.3. Markets Economics Analysis
4.3. Discussion
- In the traditional LESM model, the LMP at t = 7 of bus 13 was USD 60/MW, as shown in Figure 6, which far exceeded the generation cost of the DPG and made the electricity price fluctuate drastically. In the proposed FCESMJC model, the LMP at t = 7 of bus 13 was USD 3.29/MW, as shown in Figure 6. In contrast, the proposed FCESMJC model reduced the number of spikes in electricity prices and the dramatic fluctuations in the electricity prices.
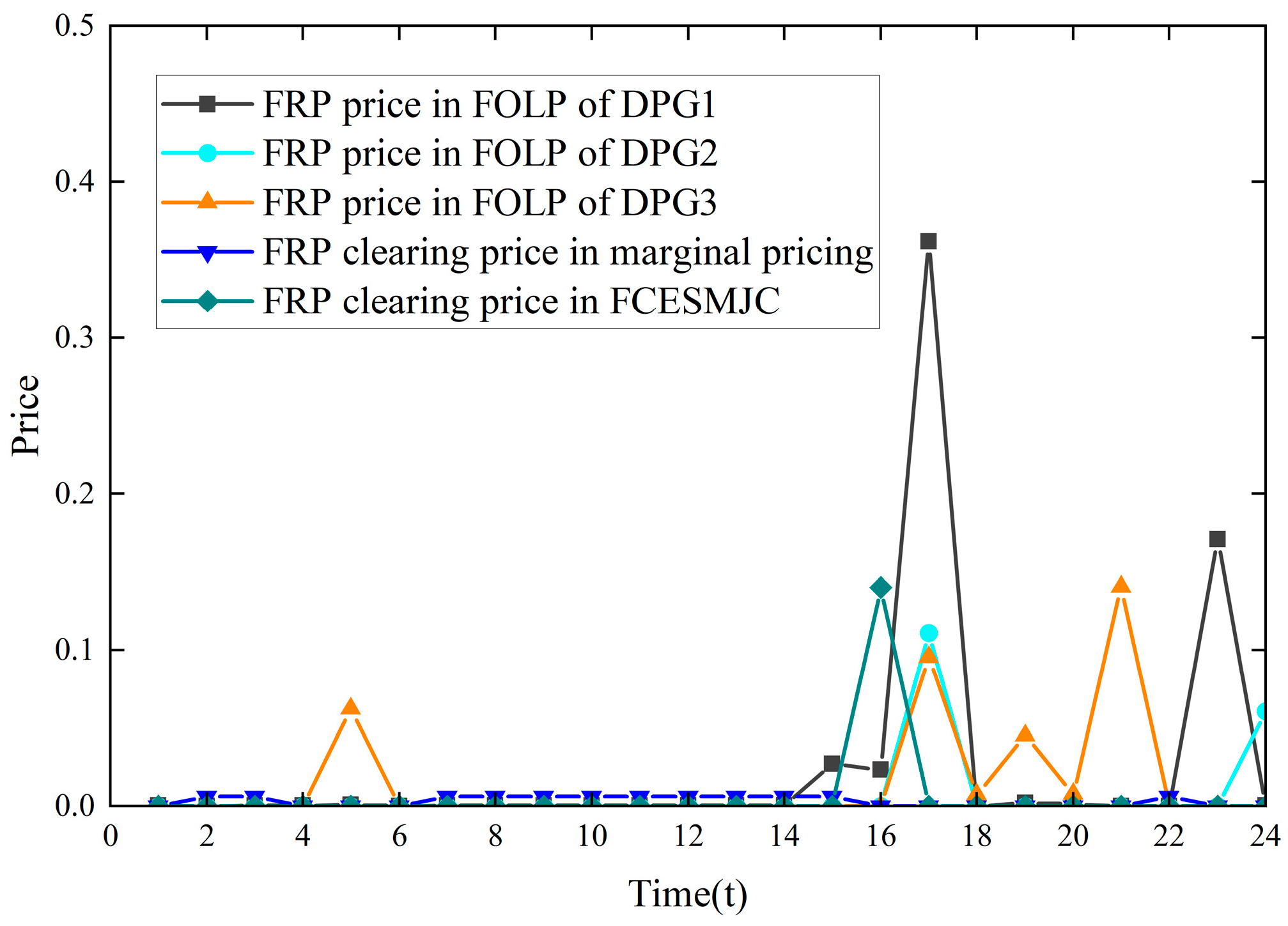
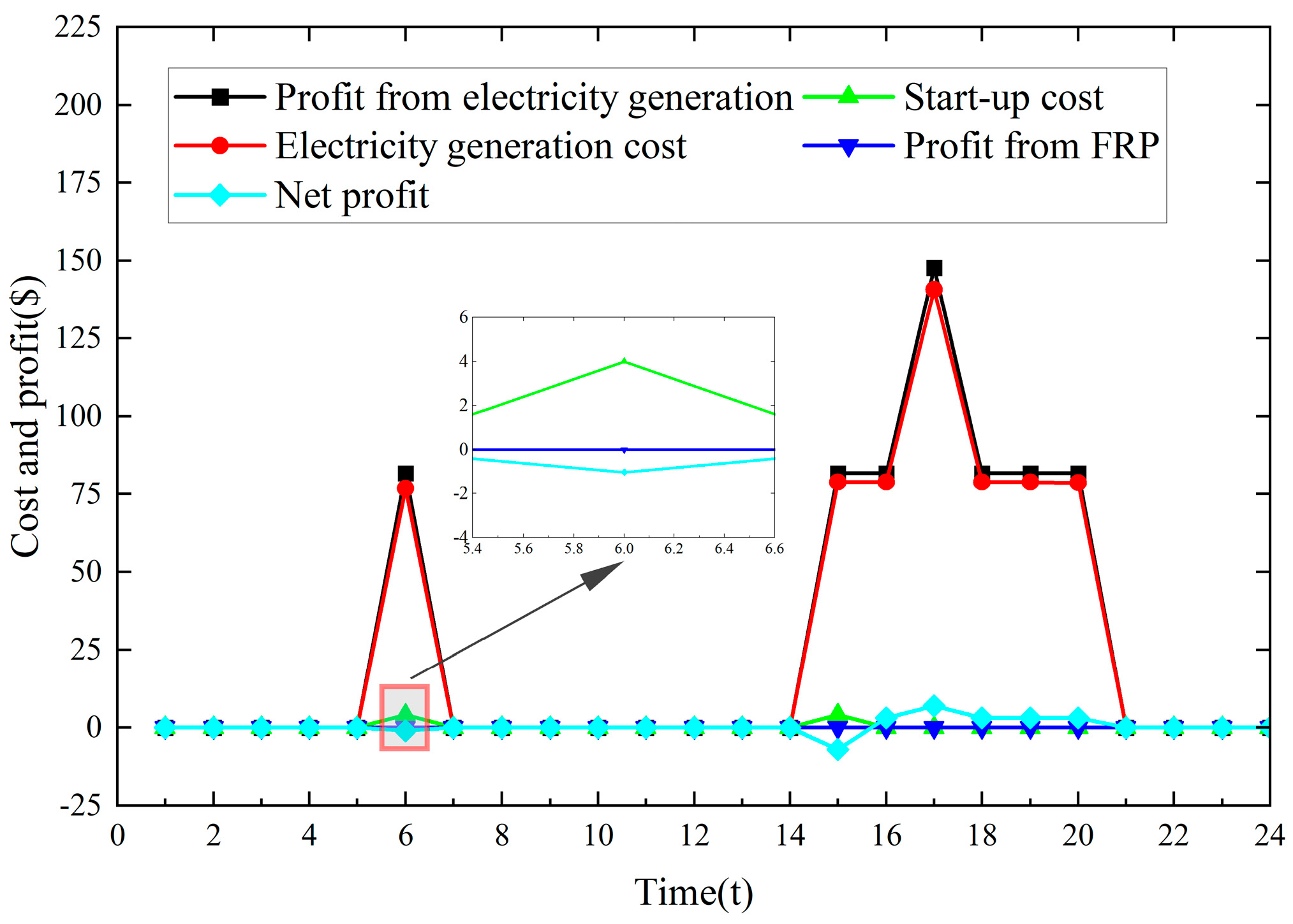
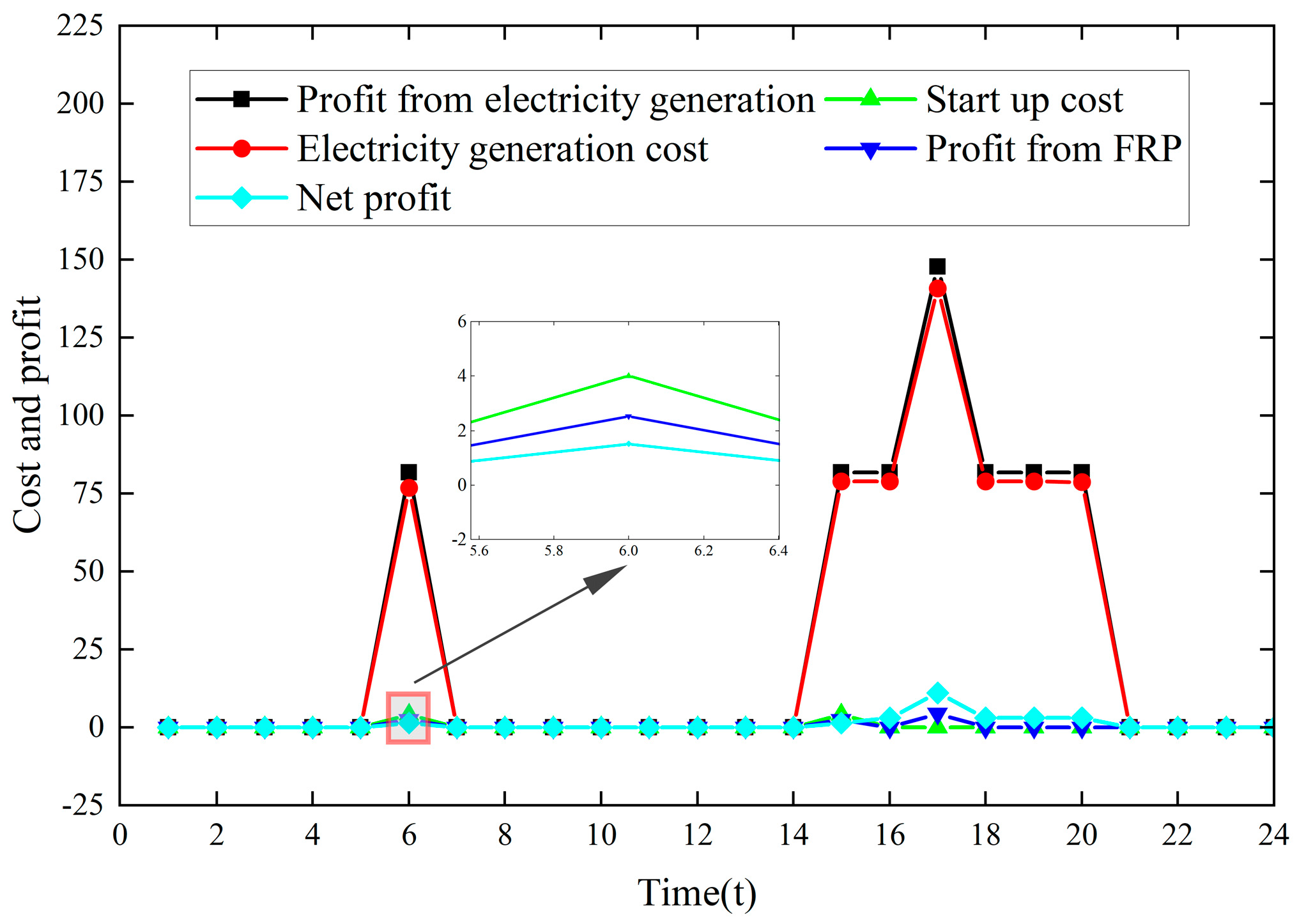
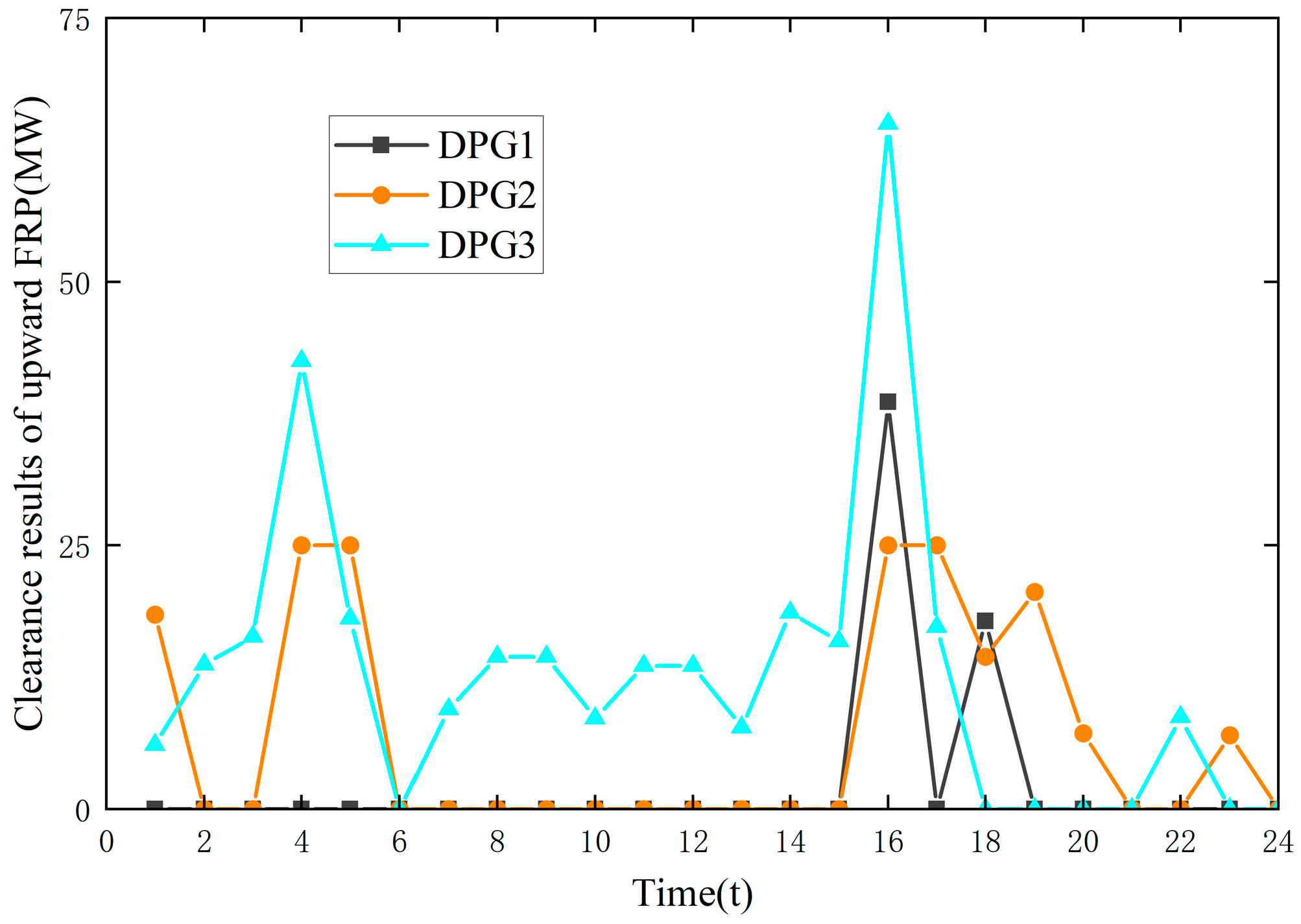
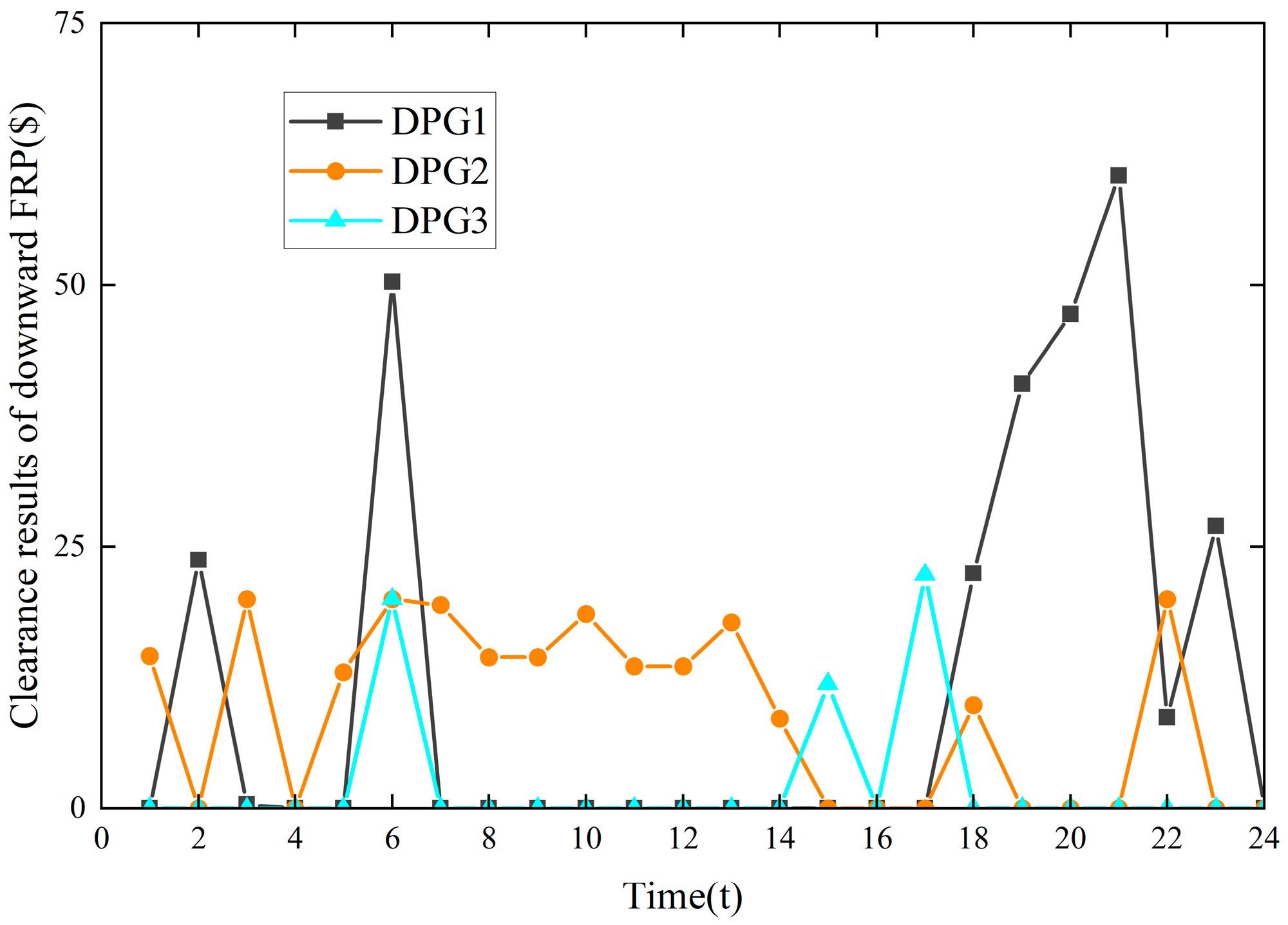
- In the NP-FCE model, the downward FRP price for all DPGs at t = 6 was USD 8 × 10−6/MW, as shown in Figure 9, and the net profit of DPG3 was USD −1.001, as shown in Figure 10. In the FCESMJC model, using the FOLP method, the downward FRP prices for DPG1, DPG2, and DPG3 at t = 6 were USD 0.114/MW, 0.21514/MW, and 0/MW, respectively, as shown in Figure 9, and the net profit of DPG3 was USD 1.530, as shown in Figure 11. The FRP price for all DPGs in the NP-FCE model at t = 6 was close to 0, and DPG3 operated at a negative net profit. This was not enough to cover the lost opportunity cost of DPG3. In contrast, DPG3 had better economic profit in the FCESMJC model. The proposed FCESMJC model could calculate the FRP price based on the power output of the DPG and LMP and better compensate for the FRP cost of the FRP market participants.
- In the conventional LESM-F model, the generation cost was USD 9092.1337, the FRP cost was USD 0, the accidental cost was USD 2209.1099, and the system cost was USD 11,301.2436, as shown in Table 6. In the proposed FCESMJC-F model, the generation cost was USD 9175.3727, the FRP cost was USD 20.9244, the unexpected cost was USD 0, and the system cost was USD 9196.2971, as shown in Table 6. Compared with the LESM model, although the generation cost and FRP cost of the FCESMJC model increased by 0.68%, the unexpected cost of the system was reduced by improving the ramping capacity of the system, which resulted in a decrease in the system cost by 18.6%. This improved the economic efficiency of the system.
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Nomenclature
| Indices and set | |
| Set, index of thermal DPGs | |
| Set, index of periods | |
| Set, index of buses | |
| Set of DPGs on bus | |
| Parameters | |
| Quadratic term factor, primary term factor, and constant term factor for generation costs | |
| Startup cost factor | |
| Conductance and conductivity matrix | |
| Active power load of DPG bus at period | |
| Reactive power load of DPG at bus period | |
| Maximum and minimum values of bus voltage at bus | |
| Maximum and minimum values of active power by DPG | |
| Maximum and minimum values of reactive power by DPG | |
| Upward and downward ramping rate of DPG | |
| Startup and shutdown rate of DPG | |
| Minimum continuous startup time of DPG | |
| Maximum continuous startup time of DPG | |
| Number of periods of DPG that still need to run continuously at the initial time point | |
| Number of consecutive periods of DPG that still need to be closed at the initial point in time | |
| Coefficient matrix of quadratic inequality constraint | |
| b, c, d, a, h, | Constant coefficient column vectors in the CESM |
| The number of inequality constraints and linear equivalence constraints in CESM | |
| Dimension of the unit diagonal matrix (varies with the correlation matrix) | |
| Upward FRP cost factor | |
| Downward FRP cost factor | |
| The unexpected cost factor for load curtailment of bus at period | |
| The unexpected cost factor for power surplus of bus at period | |
| Cost of electricity per unit of capacity in the cost offer curve when the active power is of DPG | |
| Variables | |
| Secondary cost of DPG at period | |
| Active power of DPG at period | |
| Reactive power of DPG at period | |
| ∊ {0, 1}, commitment status of DPG at period | |
| ∊ {0, 1}, startup status of DPG at period | |
| ∊ {0, 1}, shutdown status of DPG at period | |
| Two variables related to the real and imaginary parts of the voltage of each bus in the SOCP- OPF | |
| Uncertainty and variability fluctuations | |
| Upward FRP demand at period | |
| Downward FRP demand at period | |
| Unit cost of electricity for ancillary products of DPG in the FOLP pricing method | |
| Fixed output in FOLP pricing method | |
| Ramping capacity required for systems participating in FOLP pricing | |
| The total cost of ancillary products in the FOLP pricing method for DPG at period | |
| Unit cost of ancillary products in the FOLP pricing method for DPG at period ($/M.W.) | |
| Active power corresponding to the intersection between the LMP and the DPG cost offer curve | |
| The upward ramping capacity of participating FOLP of DPG at period | |
| The downward ramping capacity of participating FOLP of DPG at period | |
| Upward FRP capacity with nonzero cost of DPG at period . | |
| Downward FRP capacity with nonzero cost of DPG at period | |
| The total cost of upward FRP of DPG at period | |
| LMP obtained by market clearing at the period in the bus where DPG is located | |
| LMP in CESM model of bus at period | |
| LMP in FCESMJC model of bus at period | |
| Upward FRP clearing price at the period in the bus where DPG is located | |
| Downward FRP clearing price at the period in the bus where DPG is located | |
| The total cost of downward FRP of DPG at period | |
| Unit capacity cost of upward FRP of DPG at period | |
| Unit capacity cost of upward FRP of DPG at period | |
| Upward FRP clearing capacity of DPG at period | |
| Downward FRP clearing capacity of DPG at period | |
| Unexpected capacity for load curtailment of bus at period | |
| Unexpected capacity for power surplus of bus at period |
References
- CAISO. 2018 Annual Report on Market Issues & Performance. May 2019. Available online: http://www.caiso.com/Documents/2018AnnualReportonMarketIssuesandPerformance.pdf (accessed on 26 January 2024).
- Haegel, N.M.; Kurtz, S.R. Global Progress Toward Renewable Electricity: Tracking the Role of Solar. IEEE J. Photovolt. 2021, 11, 1335–1342. [Google Scholar] [CrossRef]
- Tseng, M.-L.; Eshaghi, N.; Gassoumi, A.; Dehkalani, M.M.; Gorji, N.E. Experimental Measurements of Soiling Impact on Current and Power Output of Photovoltaic Panels. Mod. Phys. Lett. B 2023, 37, 2350182. [Google Scholar] [CrossRef]
- Wang, Q.; Hodge, B.-M. Enhancing Power System Operational Flexibility With Flexible Ramping Products: A Review. IEEE Trans. Ind. Inform. 2017, 13, 1652–1664. [Google Scholar] [CrossRef]
- Riaz, S.; Mancarella, P. Modelling and Characterisation of Flexibility From Distributed Energy Resources. IEEE Trans. Power Syst. 2022, 37, 38–50. [Google Scholar] [CrossRef]
- Mladenov, V.; Chobanov, V.; Georgiev, A. Impact of Renewable Energy Sources on Power System Flexibility Requirements. Energies 2021, 14, 2813. [Google Scholar] [CrossRef]
- Min, C. Investigating the Effect of Uncertainty Characteristics of Renewable Energy Resources on Power System Flexibility. Appl. Sci. 2021, 11, 5381. [Google Scholar] [CrossRef]
- Steriotis, K.; Šepetanc, K.; Smpoukis, K.; Efthymiopoulos, N.; Makris, P.; Varvarigos, E.; Pandžić, H. Stacked Revenues Maximization of Distributed Battery Storage Units Via Emerging Flexibility Markets. IEEE Trans. Sustain. Energy 2022, 13, 464–478. [Google Scholar] [CrossRef]
- Badanjak, D.; Pandžić, H. Battery Storage Participation in Reactive and Proactive Distribution-Level Flexibility Markets. IEEE Access 2021, 9, 122322–122334. [Google Scholar] [CrossRef]
- California Independent System Operator. Addendum-Draft Final Technical Appendix-Flexible Ramping Product. 2016. Available online: https://www.caiso.com/Documents/Addendum-DraftFinalTechnicalAppendix-FlexibleRampingProduct.pdf (accessed on 26 January 2024).
- Sreekumar, S.; Sharma, K.C.; Bhakar, R. Multi-Interval Solar Ramp Product to Enhance Power System Flexibility. IEEE Syst. J. 2021, 15, 170–179. [Google Scholar] [CrossRef]
- Varghese, S.; Dalvi, S.; Narula, A.; Webster, M. The Impacts of Distinct Flexibility Enhancements on the Value and Dynamics of Natural Gas Power Plant Operations. IEEE Trans. Power Syst. 2021, 36, 5803–5813. [Google Scholar] [CrossRef]
- Khatami, R.; Parvania, M.; Narayan, A. Flexibility Reserve in Power Systems: Definition and Stochastic Multi-Fidelity Optimization. IEEE Trans. Smart Grid 2020, 11, 644–654. [Google Scholar] [CrossRef]
- Wang, B.; Hobbs, B.F. Real-Time Markets for Flexiramp: A Stochastic Unit Commitment-Based Analysis. IEEE Trans. Power Syst. 2016, 31, 846–860. [Google Scholar] [CrossRef]
- Pan, H.; Chen, X.; Jin, T.; Bai, Y.; Chen, Z.; Wen, J.; Wu, Q. Real-Time Power Market Clearing Model With Improved Network Constraints Considering PTDF Correction and Fast-Calculated Dynamic Line Rating. IEEE Trans. Ind. Appl. 2023, 59, 2130–2139. [Google Scholar] [CrossRef]
- Howdhury, M.M.-U.-T.; Biswas, B.D.; Kamalasadan, S. Second-Order Cone Programming (SOCP) Model for Three Phase Optimal Power Flow (OPF) in Active Distribution Networks. IEEE Trans. Smart Grid 2023, 14, 3732–3743. [Google Scholar] [CrossRef]
- Garifi, K.; Johnson, E.S.; Arguello, B.; Pierre, B.J. Transmission Grid Resiliency Investment Optimization Model with SOCP Recovery Planning. IEEE Trans. Power Syst. 2022, 37, 26–37. [Google Scholar] [CrossRef]
- Bai, X.; Wei, H.; Fujisawa, K.; Wang, Y. Semidefinite Programming for Optimal Power Flow Problems. Int. J. Electr. Power Energy Syst. 2008, 30, 383–392. [Google Scholar] [CrossRef]
- Shin, H.; Baldick, R. Optimal Battery Energy Storage Control for Multi-Service Provision Using a Semidefinite Programming-Based Battery Model. IEEE Trans. Sustain. Energy 2023, 14, 2192–2204. [Google Scholar] [CrossRef]
- Lorca, Á.; Sun, X.A. The Adaptive Robust Multi-Period Alternating Current Optimal Power Flow Problem. IEEE Trans. Power Syst. 2018, 33, 1993–2003. [Google Scholar] [CrossRef]
- Kim, D.; Kwon, K.; Kim, M.-K. Application of Flexible Ramping Products with Allocation Rates in Microgrid Utilizing Electric Vehicles. Int. J. Electr. Power Energy Syst. 2021, 133, 107340. [Google Scholar] [CrossRef]
- Chen, S.; Conejo, A.J.; Wei, Z. Power-Gas Coordination: Making Flexible Ramping Products Feasible. IEEE Trans. Power Syst. 2023, 38, 4697–4707. [Google Scholar] [CrossRef]
- Cha, S.-H.; Kwak, S.-H.; Ko, W. A Robust Optimization Model of Aggregated Resources Considering Serving Ratio for Providing Reserve Power in the Joint Electricity Market. Energies 2023, 16, 7061. [Google Scholar] [CrossRef]
- Zhong, J.; Chen, H.; Chen, W. Real-time power market clearing with flexibility resource trading. Grid Technol. 2021, 45, 1032–1041. [Google Scholar]
- Park, H.; Huang, B.; Baldick, R. Enhanced Flexible Ramping Product Formulation for Alleviating Capacity Shortage in Look-Ahead Commitment. J. Mod. Power Syst. Clean Energy 2022, 10, 850–860. [Google Scholar] [CrossRef]
- Khoshjahan, M.; Dehghanian, P.; Moeini-Aghtaie, M.; Fotuhi-Firuzabad, M. Harnessing Ramp Capability of Spinning Reserve Services for Enhanced Power Grid Flexibility. IEEE Trans. Ind. Appl. 2019, 55, 7103–7112. [Google Scholar] [CrossRef]
- Zhang, X.; Hu, J.; Wang, H.; Wang, G.; Chan, K.W.; Qiu, J. Electric Vehicle Participated Electricity Market Model Considering Flexible Ramping Product Provisions. IEEE Trans. Ind. Appl. 2020, 56, 5868–5879. [Google Scholar] [CrossRef]
- Zhang, Z.; Li, F.; Park, S.-W.; Son, S.-Y. Local Energy and Planned Ramping Product Joint Market Based on a Distributed Optimization Method. CSEE J. Power Energy Syst. 2021, 7, 1357–1368. [Google Scholar]
- PJM Education. Consistency of Energy-Related Opportunity Cost Calculations [EB/OL]. 20 May 2017. Available online: http://citeseerx.ist.psu.edu/viewdoc/download.doi=10.1.1.352.7791&rep=rep1&1&type=pdf (accessed on 26 January 2024).
- Kocuk, B.; Dey, S.S.; Sun, X.A. Strong SOCP Relaxations for the Optimal Power Flow Problem. Oper. Res. 2016, 64, 1177–1196. [Google Scholar] [CrossRef]
- Mezghani, I.; Stevens, N.; Papavasiliou, A.; Chatzigiannis, D.I. Hierarchical Coordination of Transmission and Distribution System Operations in European Balancing Markets. IEEE Trans. Power Syst. 2023, 38, 3990–4002. [Google Scholar] [CrossRef]
- O’Neill, R.P.; Castillo, A.; Eldridge, B.; Hytowitz, R.B. Dual Pricing Algorithm in ISO Markets. IEEE Trans. Power Syst. 2017, 32, 3308–3310. [Google Scholar] [CrossRef]
- Fiacco, A.V.; McCormick, G.P. Nonlinear Programming: Sequential Unconstrained Minimization Techniques; Society for Industrial and Applied Mathematics: Philadelphia, PA, USA, 1990. [Google Scholar]
- Wei, H.; Sasaki, H.; Kubokawa, J.; Yokoyama, R. An Interior Point Nonlinear Programming for Optimal Power Flow Problems with a Novel Data Structure. IEEE Trans. Power Syst. 1998, 13, 870–877. [Google Scholar] [CrossRef]
- California Independent System Operator. Revised Draft Final Proposal-Flexible Ramping Product. 2015. Available online: https://www.caiso.com/Documents/RevisedDraftFinalProposal-FlexibleRampingProduct-2015.pdf (accessed on 26 January 2024).
- MISO. Ramp Product Questions and Answers [EB/OL]. 31 March 2016. Available online: https://www.misoenergy.org/Library/Repository/Communication%20Material/Strategic%20Initiatives/Ramp%20Product%20Questions%20and%20Answers.pdf (accessed on 26 January 2024).
- Cornelius, A.; Bandyopadhyay, R.; Patiño-Echeverri, D. Assessing Environmental, Economic, and Reliability Impacts of Flexible Ramp Products in MISO’s Electricity Market. Renew. Sustain. Energy Rev. 2018, 81, 2291–2298. [Google Scholar] [CrossRef]








| DPG | The Bus Where the DPG Is Located | DPG Cost Parameters | Characteristic Parameters of DPG | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| DPG1 | 1 | 0.005 | 2.45 | 1.0 | 50 | 200 | 1 | 1 | 4 | 4 | 55 | 55 | 50 | 50 | 259.33 |
| DPG2 | 2 | 0.005 | 3.51 | 1.0 | 20 | 100 | 1 | 1 | 2 | 2 | 25 | 25 | 20 | 20 | 34.53 |
| DPG3 | 6 | 0.005 | 3.89 | 1.0 | 20 | 100 | 1 | 1 | 1 | 1 | 65 | 65 | 20 | 20 | 4.01 |
| DPG | Segmental Power Points | Segmental Step Cost | |||||||
|---|---|---|---|---|---|---|---|---|---|
| SPP1 | SPP2 | SPP3 | SPP4 | SPP5 | cost1 | cost2 | cost3 | cost4 | |
| DPG1 | 50 | 90 | 130 | 170 | 200 | 315 | 355 | 395 | 430 |
| DPG2 | 20 | 40 | 60 | 80 | 100 | 381 | 401 | 420 | 442 |
| DPG3 | 20 | 40 | 60 | 80 | 100 | 419 | 439 | 455 | 483 |
| Hours | Buses | |||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| B1 | B2 | B3 | B4 | B5 | B6 | B7 | B8 | B9 | B10 | B11 | B12 | B13 | B14 | |
| h1 | 3.55 | 3.55 | 3.55 | 3.55 | 3.55 | 3.55 | 3.55 | 3.55 | 3.55 | 3.55 | 3.55 | 3.55 | 3.55 | 3.55 |
| h2 | 3.95 | 3.95 | 3.95 | 3.95 | 3.95 | 3.95 | 3.95 | 3.95 | 3.95 | 3.95 | 3.95 | 3.95 | 3.95 | 3.95 |
| h3 | 3.95 | 3.95 | 3.95 | 3.95 | 3.95 | 3.95 | 3.95 | 3.95 | 3.95 | 3.95 | 3.95 | 3.95 | 3.95 | 3.95 |
| h4 | 3.95 | 3.95 | 3.95 | 3.95 | 3.95 | 3.95 | 3.95 | 3.95 | 3.95 | 3.95 | 3.95 | 3.95 | 3.95 | 3.95 |
| h5 | 4.01 | 4.01 | 4.01 | 4.01 | 4.01 | 4.01 | 4.01 | 4.01 | 4.01 | 4.01 | 4.01 | 4.01 | 4.01 | 4.01 |
| h6 | 4.01 | 4.01 | 4.01 | 4.01 | 4.01 | 4.01 | 4.01 | 4.01 | 4.01 | 4.01 | 4.01 | 4.01 | 4.01 | 4.01 |
| h7 | 60.0 | 60.0 | 60.0 | 60.0 | 60.0 | 60.0 | 60.0 | 60.0 | 60.0 | 60.0 | 60.0 | 60.0 | 60.0 | 60.0 |
| h8 | 3.81 | 3.81 | 3.81 | 3.81 | 3.81 | 3.81 | 3.81 | 3.81 | 3.81 | 3.81 | 3.81 | 3.81 | 3.81 | 3.81 |
| h9 | 3.81 | 3.81 | 3.81 | 3.81 | 3.81 | 3.81 | 3.81 | 3.81 | 3.81 | 3.81 | 3.81 | 3.81 | 3.81 | 3.81 |
| h10 | 3.81 | 3.81 | 3.81 | 3.81 | 3.81 | 3.81 | 3.81 | 3.81 | 3.81 | 3.81 | 3.81 | 3.81 | 3.81 | 3.81 |
| h11 | 3.81 | 3.81 | 3.81 | 3.81 | 3.81 | 3.81 | 3.81 | 3.81 | 3.81 | 3.81 | 3.81 | 3.81 | 3.81 | 3.81 |
| h12 | 3.81 | 3.81 | 3.81 | 3.81 | 3.81 | 3.81 | 3.81 | 3.81 | 3.81 | 3.81 | 3.81 | 3.81 | 3.81 | 3.81 |
| h13 | 3.81 | 3.81 | 3.81 | 3.81 | 3.81 | 3.81 | 3.81 | 3.81 | 3.81 | 3.81 | 3.81 | 3.81 | 3.81 | 3.81 |
| h14 | 3.55 | 3.55 | 3.55 | 3.55 | 3.55 | 3.55 | 3.55 | 3.55 | 3.55 | 3.55 | 3.55 | 3.55 | 3.55 | 3.55 |
| h15 | 3.55 | 3.55 | 3.55 | 3.55 | 3.55 | 3.55 | 3.55 | 3.55 | 3.55 | 3.55 | 3.55 | 3.55 | 3.55 | 3.55 |
| h16 | 3.81 | 3.81 | 3.81 | 3.81 | 3.81 | 3.81 | 3.81 | 3.81 | 3.81 | 3.81 | 3.81 | 3.81 | 3.81 | 3.81 |
| h17 | 60.0 | 60.0 | 60.0 | 60.0 | 60.0 | 60.0 | 60.0 | 60.0 | 60.0 | 60.0 | 60.0 | 60.0 | 60.0 | 60.0 |
| h18 | 3.95 | 3.95 | 3.95 | 3.95 | 3.95 | 3.95 | 3.95 | 3.95 | 3.95 | 3.95 | 3.95 | 3.95 | 3.95 | 3.95 |
| h19 | 3.95 | 3.95 | 3.95 | 3.95 | 3.95 | 3.95 | 3.95 | 3.95 | 3.95 | 3.95 | 3.95 | 3.95 | 3.95 | 3.95 |
| h20 | 4.29 | 4.29 | 4.29 | 4.29 | 4.29 | 4.29 | 4.29 | 4.29 | 4.29 | 4.29 | 4.29 | 4.29 | 4.29 | 4.29 |
| h21 | 4.19 | 4.19 | 4.19 | 4.19 | 4.19 | 4.19 | 4.19 | 4.19 | 4.19 | 4.19 | 4.19 | 4.19 | 4.19 | 4.19 |
| h22 | 3.95 | 3.95 | 3.95 | 3.95 | 3.95 | 3.95 | 3.95 | 3.95 | 3.95 | 3.95 | 3.95 | 3.95 | 3.95 | 3.95 |
| h23 | 3.95 | 3.95 | 3.95 | 3.95 | 3.95 | 3.95 | 3.95 | 3.95 | 3.95 | 3.95 | 3.95 | 3.95 | 3.95 | 3.95 |
| h24 | 3.95 | 3.95 | 3.95 | 3.95 | 3.95 | 3.95 | 3.95 | 3.95 | 3.95 | 3.95 | 3.95 | 3.95 | 3.95 | 3.95 |
| Hours | Buses | |||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| B1 | B2 | B3 | B4 | B5 | B6 | B7 | B8 | B9 | B10 | B11 | B12 | B13 | B14 | |
| h1 | 3.24 | 3.3 | 3.43 | 3.38 | 3.36 | 3.36 | 3.38 | 3.38 | 3.38 | 3.38 | 3.38 | 3.39 | 3.39 | 3.42 |
| h2 | 3.43 | 3.51 | 3.65 | 3.59 | 3.56 | 3.56 | 3.59 | 3.59 | 3.59 | 3.59 | 3.59 | 3.61 | 3.61 | 3.64 |
| h3 | 3.38 | 3.45 | 3.59 | 3.53 | 3.5 | 3.5 | 3.53 | 3.53 | 3.53 | 3.53 | 3.52 | 3.53 | 3.54 | 3.57 |
| h4 | 3.36 | 3.43 | 3.56 | 3.5 | 3.48 | 3.48 | 3.5 | 3.5 | 3.5 | 3.51 | 3.5 | 3.51 | 3.52 | 3.55 |
| h5 | 3.7 | 3.81 | 4.01 | 3.92 | 3.88 | 3.88 | 3.92 | 3.92 | 3.92 | 3.93 | 3.92 | 3.93 | 3.95 | 3.99 |
| h6 | 3.51 | 3.6 | 3.8 | 3.7 | 3.66 | 4.09 | 3.7 | 3.7 | 3.7 | 3.71 | 3.70 | 3.71 | 3.72 | 3.78 |
| h7 | 3.17 | 3.22 | 3.32 | 3.28 | 3.26 | 3.26 | 3.28 | 3.28 | 3.28 | 3.28 | 3.28 | 3.29 | 3.29 | 3.32 |
| h8 | 3.11 | 3.17 | 3.26 | 3.22 | 3.2 | 3.2 | 3.22 | 3.22 | 3.22 | 3.22 | 3.22 | 3.22 | 3.23 | 3.25 |
| h9 | 3.11 | 3.17 | 3.26 | 3.22 | 3.2 | 3.2 | 3.22 | 3.22 | 3.22 | 3.22 | 3.22 | 3.22 | 3.23 | 3.25 |
| h10 | 3.11 | 3.17 | 3.26 | 3.22 | 3.2 | 3.2 | 3.22 | 3.22 | 3.22 | 3.22 | 3.22 | 3.22 | 3.23 | 3.25 |
| h11 | 3.06 | 3.11 | 3.2 | 3.16 | 3.14 | 3.14 | 3.16 | 3.16 | 3.16 | 3.16 | 3.16 | 3.16 | 3.17 | 3.19 |
| h12 | 3.06 | 3.11 | 3.2 | 3.16 | 3.14 | 3.14 | 3.16 | 3.16 | 3.16 | 3.16 | 3.16 | 3.16 | 3.17 | 3.19 |
| h13 | 3.06 | 3.11 | 3.2 | 3.16 | 3.14 | 3.14 | 3.16 | 3.16 | 3.16 | 3.16 | 3.16 | 3.16 | 3.17 | 3.19 |
| h14 | 3.01 | 3.05 | 3.13 | 3.1 | 3.08 | 3.08 | 3.10 | 3.10 | 3.10 | 3.10 | 3.10 | 3.10 | 3.11 | 3.13 |
| h15 | 3.01 | 3.05 | 3.13 | 3.09 | 3.08 | 4.09 | 3.09 | 3.09 | 3.09 | 3.10 | 3.09 | 3.10 | 3.10 | 3.12 |
| h16 | 3.01 | 3.04 | 3.12 | 3.08 | 3.07 | 4.09 | 3.08 | 3.08 | 3.08 | 3.09 | 3.08 | 3.09 | 3.09 | 3.11 |
| h17 | 4.07 | 4.18 | 4.43 | 4.29 | 4.24 | 4.24 | 4.29 | 4.29 | 4.29 | 4.31 | 4.29 | 4.30 | 4.32 | 4.39 |
| h18 | 3.74 | 3.86 | 4.1 | 3.97 | 3.92 | 4.09 | 3.97 | 3.97 | 3.97 | 3.98 | 3.96 | 3.98 | 4.02 | 4.06 |
| h19 | 3.81 | 3.93 | 4.18 | 4.05 | 4.00 | 4.09 | 4.05 | 4.05 | 4.05 | 4.07 | 4.05 | 4.06 | 4.08 | 4.15 |
| h20 | 3.75 | 3.87 | 4.11 | 3.99 | 3.94 | 4.09 | 3.99 | 3.99 | 3.99 | 4.00 | 3.98 | 4.02 | 4.01 | 4.07 |
| h21 | 3.71 | 3.81 | 4.03 | 3.93 | 3.89 | 3.89 | 3.93 | 3.93 | 3.93 | 3.94 | 3.93 | 3.94 | 3.96 | 4.01 |
| h22 | 3.48 | 3.57 | 3.72 | 3.65 | 3.62 | 3.62 | 3.65 | 3.65 | 3.65 | 3.66 | 3.65 | 3.66 | 3.67 | 3.7 |
| h23 | 3.58 | 3.69 | 3.83 | 3.76 | 3.73 | 3.73 | 3.76 | 3.76 | 3.76 | 3.77 | 3.76 | 3.76 | 3.77 | 3.81 |
| h24 | 3.48 | 3.57 | 3.69 | 3.63 | 3.61 | 3.61 | 3.63 | 3.63 | 3.63 | 3.64 | 3.63 | 3.64 | 3.65 | 3.68 |
| Model | Load Curtailment (MW) | Power Surplus (MW) |
|---|---|---|
| LESM-F | 26.8 | 10.0 |
| FCESMJC-F | 0 | 0 |
| Model | Generation Costs (USD) | FRP Cost (USD) | Unexpected Costs (USD) | System Costs (USD) |
|---|---|---|---|---|
| LESM-F | 9092.1337 | 0 | 2209.1099 | 11,301.2436 |
| FCESMJC-F | 9175.3727 | 20.9244 | 0 | 9196.2971 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gao, S.; Bai, X.; Shang, Q.; Weng, Z.; Wu, Y. A Joint Electricity Market-Clearing Mechanism for Flexible Ramping Products with a Convex Spot Market Model. Sustainability 2024, 16, 2390. https://doi.org/10.3390/su16062390
Gao S, Bai X, Shang Q, Weng Z, Wu Y. A Joint Electricity Market-Clearing Mechanism for Flexible Ramping Products with a Convex Spot Market Model. Sustainability. 2024; 16(6):2390. https://doi.org/10.3390/su16062390
Chicago/Turabian StyleGao, Senpeng, Xiaoqing Bai, Qinghua Shang, Zonglong Weng, and Yinghe Wu. 2024. "A Joint Electricity Market-Clearing Mechanism for Flexible Ramping Products with a Convex Spot Market Model" Sustainability 16, no. 6: 2390. https://doi.org/10.3390/su16062390
APA StyleGao, S., Bai, X., Shang, Q., Weng, Z., & Wu, Y. (2024). A Joint Electricity Market-Clearing Mechanism for Flexible Ramping Products with a Convex Spot Market Model. Sustainability, 16(6), 2390. https://doi.org/10.3390/su16062390






