Recent Progress in Research on the Design and Use of an Archimedes Screw Turbine: A Review
Abstract
1. Introduction
- Large: higher than 100 MW;
- Medium: 10–100 MW;
- Small: 1–10 MW;
- Mini: 100 kW–1 MW;
- Micro: 5–100 kW;
- Pico: less then 5 kW.
2. Archimedes Screw
3. Operational Advantages
3.1. Environment Impact
- the geometry of turbine cannot cause mechanical damage to fish fauna (the shape of rotor blades and spaces available for fish flow with dimensions characteristic for a given river ecosystem);
- pressures inside the flow device must not damage the gills of fish (pressures causing cavitation are not allowed);
- the design of turbine should ensure that the lubricant does not come into contact with river water (bearings are raised above water level);
- the noise of device should not exceed 80 dB;
- the device should be optimized in terms of vibration emission (installing anti-vibration solutions);
- installation of the device should have the least possible construction interference with the existing water threshold/natural damming;
- the device should enable free fish migration, including upstream (e.g., hydroelevator system);
- ensuring adequate durability of the device (e.g., by applying coatings on the rotor blades);
- the device should ensure the use of a water threshold with natural falls (usually low or ultra-low), which will enable the use of existing, natural dams.
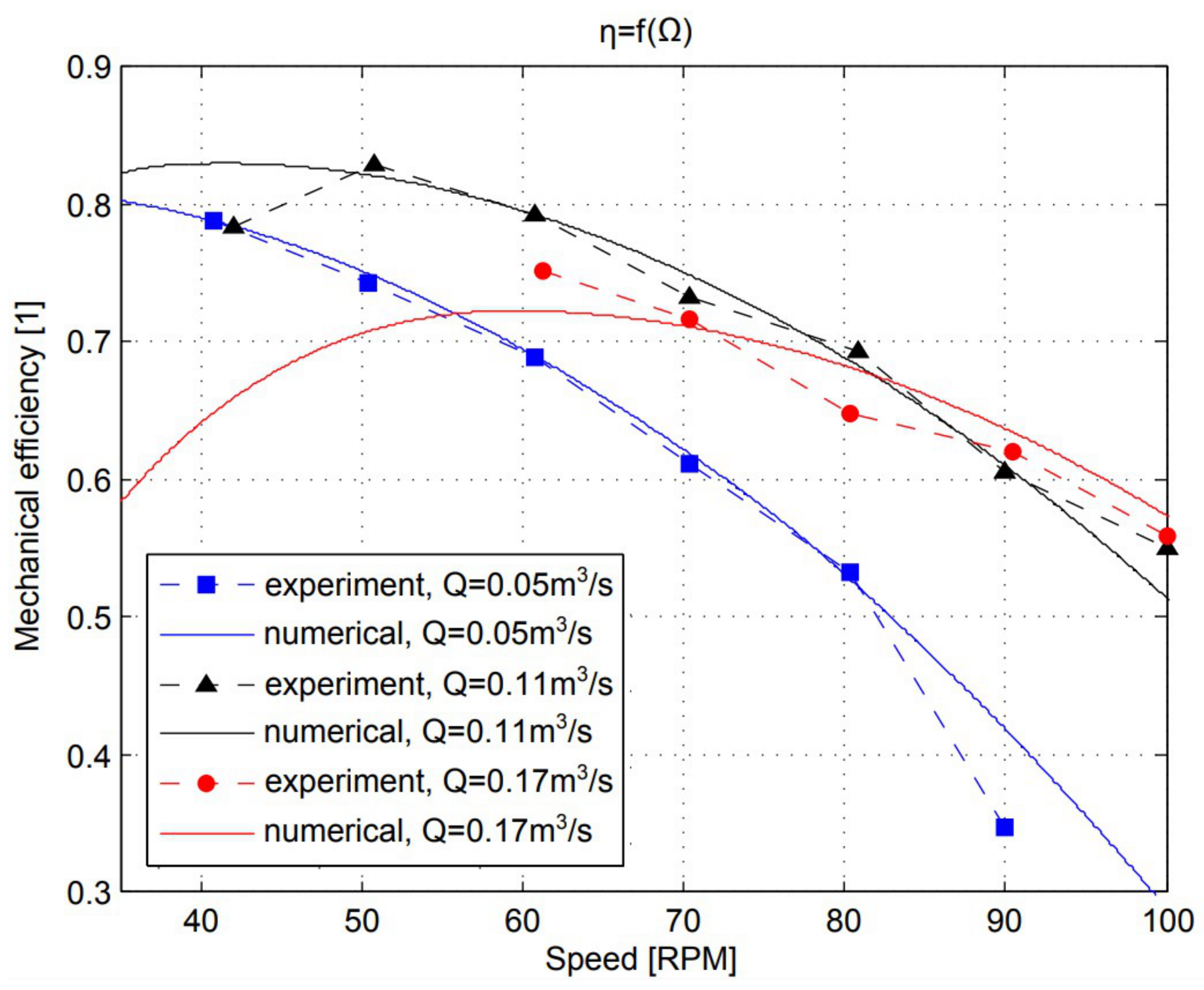
3.2. AST Efficiency
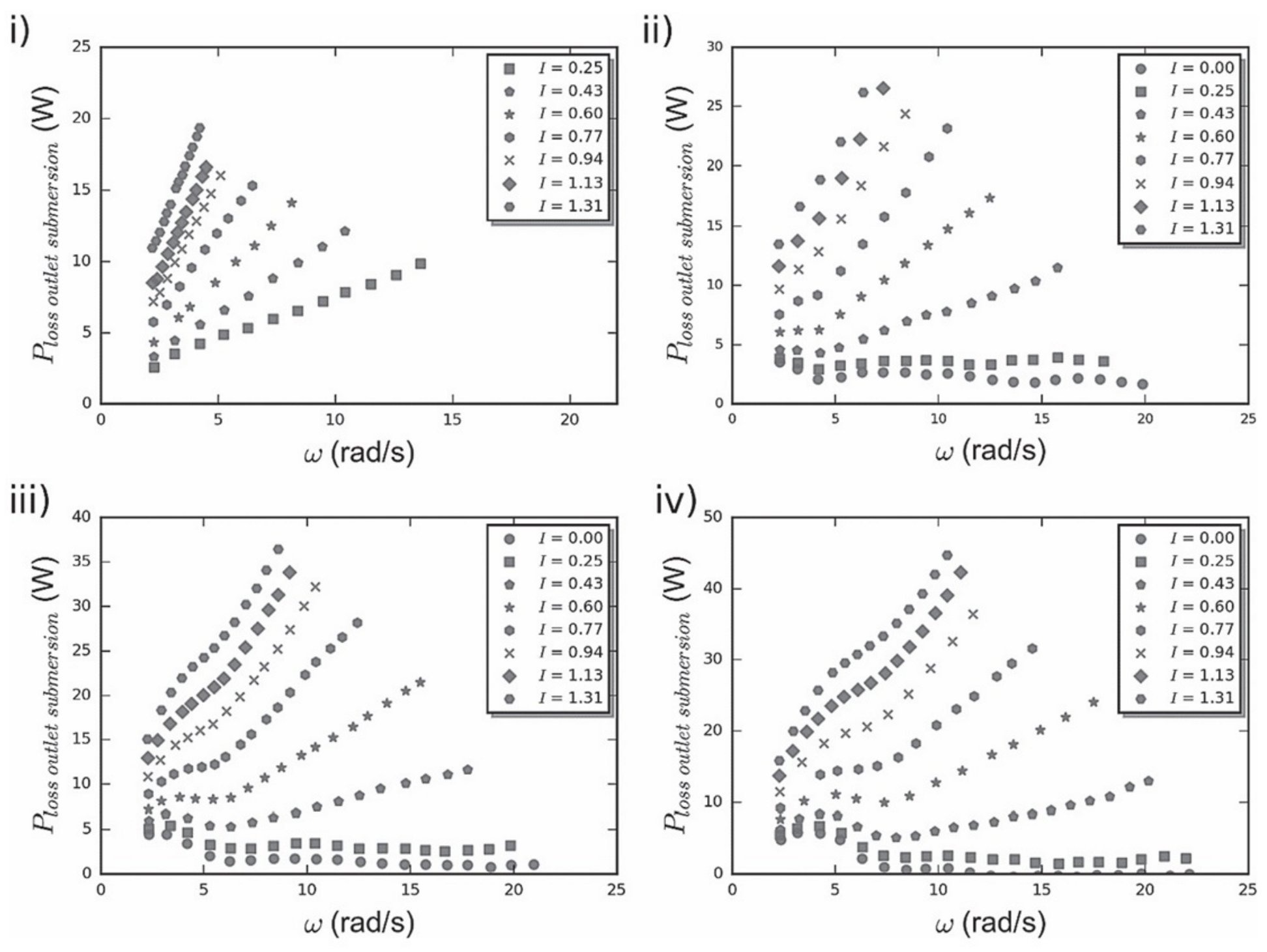
3.3. AST Losses
3.4. Variable Speed Influence
3.5. Length Influence
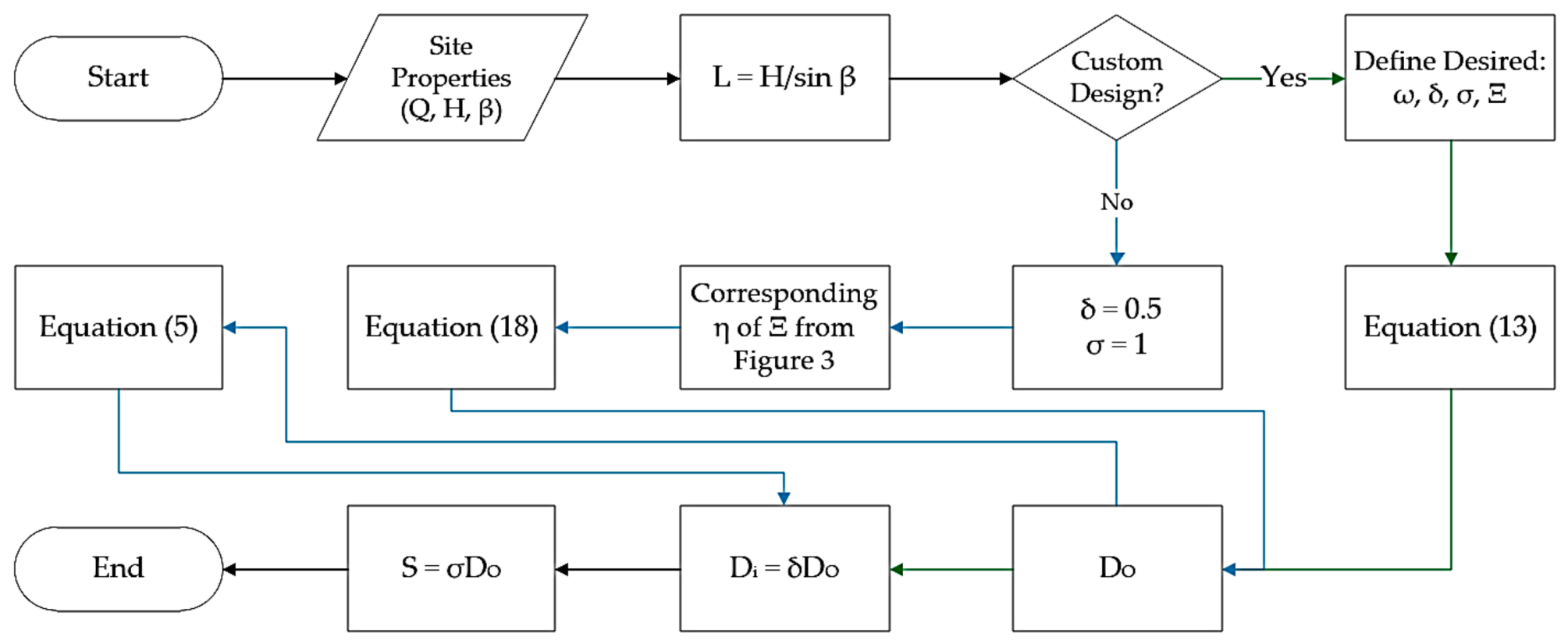
3.6. Selection of Overall Dimensions
- Equation (5): ;
- Equation (13): ;
- Equation (18): ;
- η: the constant accounting for screw geometry, rotation speed, and fill level in the power function form of the diameter equation (s3/7m−2/7);
- Ξ: the dimensionless inlet depth of the screw (-);
- ωM: the maximum rotation speed of the screw (Muysken limit) (rad s−1);
- ω: the rotation speed of the screw (rad s−1);
- σ: the screw’s inner to outer diameter ratio (Di/Do) (-);
- θ: the angle of the sector. Subscript: i—inner; o—outer (rad);
- L: the total length of the screw (m);
- δ: the screw’s pitch to outer diameter ratio (S/Do) (-).
3.7. Tilt Angle Influence
3.8. Rotational Speed Influence
3.9. Diameter Influence
3.10. Degree of Filling Influence
4. Discussion
4.1. New Directions of Research
4.2. Integration with Other Renewable Energy Systems
5. Conclusions
Funding
Conflicts of Interest
References
- Wang, C.H.; Tong, Y.W.; Loh, K.C.; Wang, R.; Li, X. Advanced technologies on sustainable energy and environment: SET2016 virtual special issue. Energy 2017, 137, 350–352. [Google Scholar] [CrossRef]
- The U.S. Environmental Protection Agency (USEPA). Global Greenhouse Gas Emissions Data. Available online: https://www.epa.gov/ghgemissions/global-greenhouse-gas-emissions-data (accessed on 16 February 2024).
- Bioenergy for the Region Cluster. Klaster Bioenergii dla Regionu. Available online: https://www.bioenergiadlaregionu.eu/gfx/baza_wiedzy/98/lik1.pdf (accessed on 24 November 2023).
- REN21. Renewable Energy Policy Network for the 21st Century. Available online: https://www.ren21.net/wp-content/uploads/2019/05/GSR2022_Full_Report.pdf (accessed on 27 December 2024).
- JRC Publications Repository. Drought in Europe March 2023. Available online: https://publications.jrc.ec.europa.eu/repository/handle/JRC133025 (accessed on 16 February 2024).
- Oliveira, P.F.G.; Martins, N.M.C.; Fontes, P.; Covas, D. Hydroenergy Harvesting Assessment: The Case Study of Alviela River. Water 2021, 13, 1764. [Google Scholar] [CrossRef]
- Purece, C.; Corlan, L. Archimedean screw as fish-friendly turbines for harnessing hydropower potential. E3S Web Conf. 2021, 286, 02007. [Google Scholar] [CrossRef]
- Ministry of Infrastructure, Poland. Hydropower Plants: Still a Lot to Do. Available online: https://raport.togetair.eu/water/the-future-of-rivers-seas-and-inland-waterway/hydropower-plants-still-a-lot-to-do (accessed on 27 December 2024).
- Ubando, A.T.; Marfori, I.A.V.; Peradilla, M.S.; Sy, C.L.; Calapatia, A.M.A.; Chen, W.H. Sustainable Manufacturability of Archimedes Screw Turbines: A Critical Review. J. Manuf. Mater. Process. 2022, 6, 161. [Google Scholar] [CrossRef]
- Waters, S.; Aggidis, G.A. Over 2000 years in review: Revival of the Archimedes Screw from Pump to Turbine. Renew. Sustain. Energy Rev. 2015, 51, 497–505. [Google Scholar] [CrossRef]
- Müller, G.; Senior, J. Simplified theory of Archimedean screws. J. Hydraul. Res. 2009, 47, 666–669. [Google Scholar] [CrossRef]
- Simmons, S.; Lubitz, W. Archimedes Screw Generators for Sustainable Energy Development. In Proceedings of the 2017 IEEE Canada International Humanitarian Technology Conference (IHTC), Toronto, ON, Canada, 21–22 July 2017. [Google Scholar] [CrossRef]
- Brada, K. Wasserkraftschnecke Ermoglicht Stromerzeugung Uber Kleinkraftwerke. [Hydraulic screw generates electricity from micro hydropower stations]. Maschinenmarkt Würzbg. 1999, 21, 52–56. [Google Scholar]
- Buysse, D.; Mouton, A.M.; Stevens, M.; Van den Neucker, T.; Coeck, J. Mortality of European eel after downstream migration through two types of pumping stations. Fish. Manag. Ecol. 2014, 21, 13–21. [Google Scholar] [CrossRef]
- Simmons, S.C.; Miller, L.; Lubitz, W.D. Review and Evaluation of Archimedes Screw Pump Design Guidance. In Responsible Engineering and Living. REAL 2022; Ting, D.S.K., Vasel-Be-Hagh, A., Eds.; Springer Proceedings in Energy; Springer: Cham, Switzerland, 2023; pp. 225–243. [Google Scholar] [CrossRef]
- Dellinger, G.; Garambois, P.A.; Dellinger, N.; Dufresne, M.; Terfous, A.; Vazquez, J.; Ghenaim, A. Computational fluid dynamics modeling for the design of Archimedes Screw Generator. Renew. Energy 2018, 118, 847–857. [Google Scholar] [CrossRef]
- Janicka, A.; Molska, J.; Świeściak, J.; Włostowski, R.; Włóka, A.; Zawiślak, M. Designing a Small Water Power Plant in Poland in the Aspect of Minimizing the Impact on River Ecosystem. Rocz. Ochr. Środowiska 2021, 23, 332–345. [Google Scholar] [CrossRef]
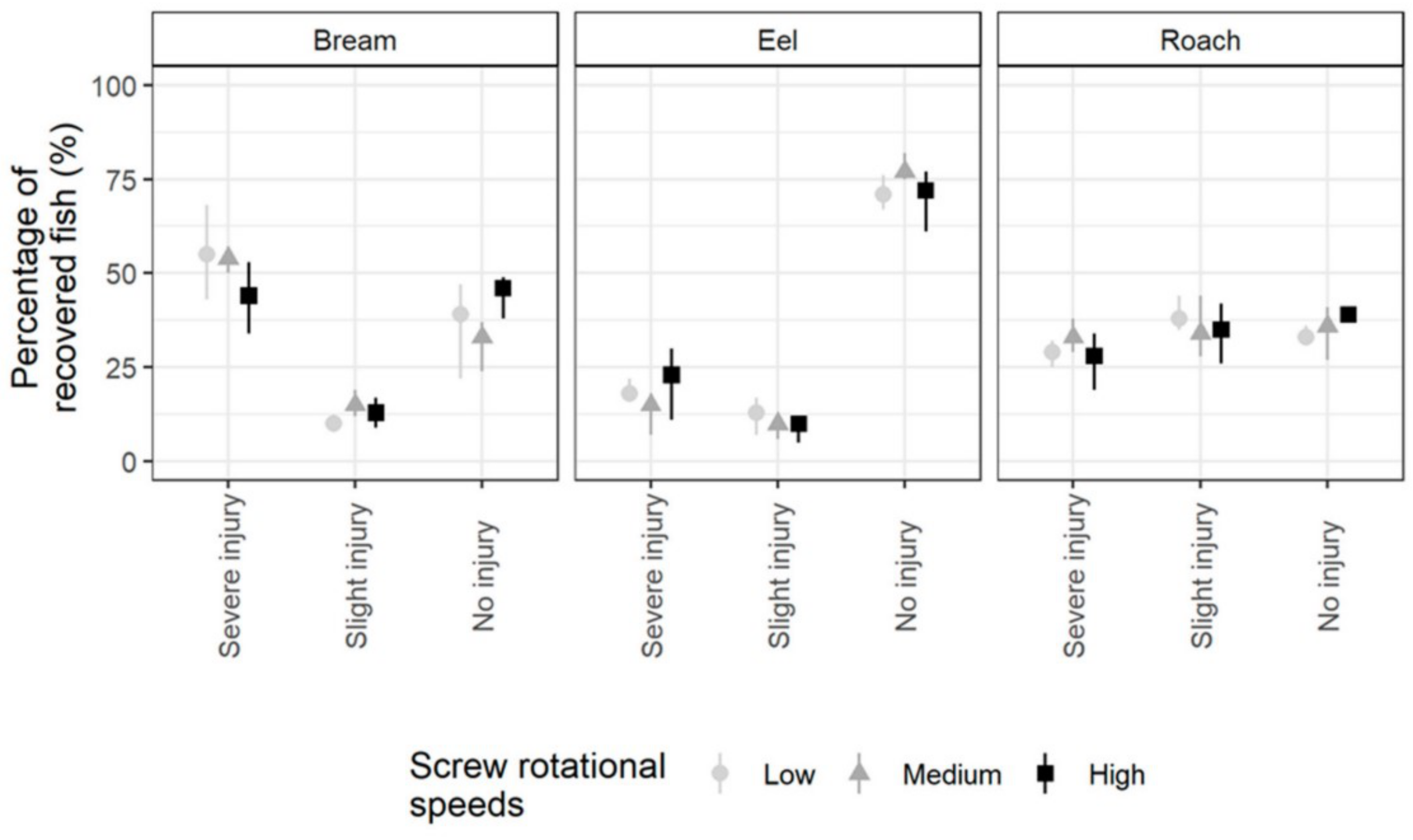
- Mueller, M.; Knott, J.; Pander, J.; Geist, J. Experimental comparison of fish mortality and injuries at innovative and conventional small hydropower plants. J. Appl. Ecol. 2022, 59, 2360–2372. [Google Scholar] [CrossRef]
- Havn, T.; Sæther, S.; Thorstad, E.; Teichert, M.; Heermann, L.; Diserud, O.; Borcherding, J.; Tambets, M.; Økland, F. Downstream migration of Atlantic salmon smolts past a low head hydropower station equippped with Archimedes screw and Francis turbines. Ecol. Eng. 2017, 105, 262–275. [Google Scholar] [CrossRef]
- Pauwels, I.S.; Baeyens, R.; Toming, G.; Schneider, M.; Buysse, D.; Coeck, J.; Tuhtan, J.A. Multi-Species Assessment of Injury, Mortality, and Physical Conditions during Downstream Passage through a Large Archimedes Hydrodynamic Screw (Albert Canal, Belgium). Sustainability 2020, 12, 8722. [Google Scholar] [CrossRef]
- Renardy, S.; Benitez, J.P.; Tauzin, A.; Dierckx, A.; Nzau Matondo, B.; Ovidio, M. How and where to pass? Atlantic salmon smolt’s behaviour at a hydropower station offering multiple migration routes. Hydrobiologia 2020, 847, 469–485. [Google Scholar] [CrossRef]
- Renardy, S.; Ciraane, U.D.; Benitez, J.P.; Dierckx, A.; Archambeau, P.; Pirotton, M.; Erpicum, S.; Ovidio, M. Combining fine-scale telemetry and hydraulic numerical modelling to understand the behavioural tactics and the migration route choice of smolts at a complex hydropower plant. Hydrobiologia 2023, 850, 3091–3111. [Google Scholar] [CrossRef]
- Renardy, S.; Ciraane, U.D.; Benitez, J.P.; Dierckx, A.; Gelder, J.; Silva, A.T.; Archambeau, P.; Dewals, B.; Pirotton, M.; Erpicum, S.; et al. Assessment of the Attractiveness and Passage Efficiency of Different Fish Passage Solutions at a Hydropower Plant by Combining Fine Scale 2D-Telemetry and Hydraulic Numerical Modelling. Environments 2023, 10, 107. [Google Scholar] [CrossRef]
- Knott, J.; Mueller, M.; Pander, J.; Geist, J. Downstream fish passage at small-scale hydropower plants: Turbine or bypass? Front. Environ. Sci. 2023, 11, 1168473. [Google Scholar] [CrossRef]
- YoosefDoost, A.; Lubitz, W.D. Archimedes Screw Turbines: A Sustainable Development Solution for Green and Renewable Energy Generation—A Review of Potential and Design Procedures. Sustainability 2020, 12, 7352. [Google Scholar] [CrossRef]
- Koukouvinis, P.F.; Anagnostopoulos, J. State of the Art in Designing Fish-Friendly Turbines: Concepts and Performance Indicators. Energies 2023, 16, 2661. [Google Scholar] [CrossRef]
- Lichtneger, P.; Sindelar, C.; Habersack, H.; Zeiringer, B.; Lechner, C.; Mayer, G.; Struska, N.; Albrecht, W. Performance tests and evaluation of hydropower plant with double rotating hydropower screw system. Građevinar 2018, 70, 361–368. [Google Scholar] [CrossRef]
- Dellinger, G.; Abdelali Terfous, P.A.G.; Ghenaim, A. Experimental investigation and performance analysis of Archimedes screw generator. J. Hydraul. Res. 2016, 54, 197–209. [Google Scholar] [CrossRef]
- Rohmer, J.; Knittel, D.; Sturtzer, G.; Flieller, D.; Renaud, J. Modeling and experimental results of an Archimedes screw turbine. Renew. Energy 2016, 94, 136–146. [Google Scholar] [CrossRef]
- Kumar Thakur, N.; Thakur, R.; Kashyap, K.; Goel, B. Efficiency enhancement in Archimedes screw turbine by varying different input parameters—An experimental study. Mater. Today Proc. 2022, 52, 1161–1167. [Google Scholar] [CrossRef]
- Shahverdi, K. Modeling for prediction of design parameters for micro-hydro Archimedean screw turbines. Sustain. Energy Technol. Assess. 2021, 47, 101554. [Google Scholar] [CrossRef]
- Saroinsong, T.; Soenoko, R.; Wahyudi, S.; Sasongko, M. Performance of three-bladed Archimedes screw turbine. ARPN J. Eng. Appl. Sci. 2016, 11, 9491–9495. [Google Scholar]
- Siswantara, A.; Warjito, B.; Harmadi, R.; Gumelar, S.M.; Adanta, D. Investigation of the α angle’s effect on the performance of an Archimedes turbine. Energy Procedia 2019, 156, 458–462. [Google Scholar] [CrossRef]
- Lee, M.D.; Lee, P.S. Modelling the Energy Extraction from Low-Velocity Stream Water by Small Scale Archimedes Screw Turbine. J. King Saud Univ. Eng. Sci. 2023, 35, 319–326. [Google Scholar] [CrossRef]
- Shahverdi, K.; Loni, R.; Ghobadian, B.; Gohari, S.; Marofi, S.; Bellos, E. Numerical Optimization Study of Archimedes Screw Turbine (AST): A case study. Renew. Energy 2020, 145, 2130–2143. [Google Scholar] [CrossRef]
- Shahverdi, K.; Loni, R.; Maestre, J.; Najafi, G. CFD numerical simulation of Archimedes screw turbine with power output analysis. Ocean Eng. 2021, 231, 108718. [Google Scholar] [CrossRef]
- Shahverdi, K.; Najafi, G.; Mamat, R.; Ghazali, M.F.; EI-Shafy, A.; Mousa, M. Introducing a design procedure for Archimedes Screw Turbine based on optimization algorithm. Energy Sustain. Dev. 2023, 72, 162–172. [Google Scholar] [CrossRef]
- Erinofiardi, E.; Koirala, R.; Shiwakoti, N.; Date, A. Sustainable Power Generation Using Archimedean Screw Turbine: Influence of Blade Number on Flow and Performance. Sustainability 2022, 14, 15948. [Google Scholar] [CrossRef]
- Alonso-Martinez, M.; Suárez Sierra, J.L.; Coz Díaz, J.J.d.; Martinez-Martinez, J.E. A New Methodology to Design Sustainable Archimedean Screw Turbines as Green Energy Generators. Int. J. Environ. Res. Public Health 2020, 17, 9236. [Google Scholar] [CrossRef] [PubMed]
- Saroinsong, T.; Soenoko, R.; Wahyudi, S.; Sasongko, M. Fluid Flow Phenomenon in a Three-Bladed Power-Generating Archimedes Screw Turbine. J. Eng. Sci. Technol. Rev. 2016, 9, 72–79. [Google Scholar] [CrossRef]
- Eswanto, E.; Hasan, H.; Razlan, Z.M. An Analysis on Performance of Pico-hydro with Archimedes Screw Model Viewed from Turbine Shaft Angle. Int. J. Eng. 2023, 36, 10–18. [Google Scholar] [CrossRef]
- Abbas, Z.; Waqas, M.; Khan, S.S.; Khatoon, R.; Larkin, S.; Zhao, L. Numerical and experimental investigation of an Archimedes screw turbine for open channel water flow application. Energy Sci. Eng. 2024, 12, 1317–1336. [Google Scholar] [CrossRef]
- Paturi, U.M.R.; Cheruku, S.; Reddy, N.S. Artificial neural networks modelling for power coefficient of Archimedes screw turbine for hydropower applications. J. Braz. Soc. Mech. Sci. Eng. 2022, 44, 447. [Google Scholar] [CrossRef]
- Zamani, M.; Shafaghat, R.; Alizadeh Kharkeshi, B. Experimental Investigation on the Effect of Flow Rate and Load on the Hydrodynamic Behavior and Performance of an Archimedes Screw Turbine. Int. J. Eng. 2023, 36, 733–745. [Google Scholar] [CrossRef]
- Zamani, M.; Shafaghat, R.; Alizadeh Kharkeshi, B. Numerical Study of the Hydrodynamic Behavior of an Archimedes Screw Turbine by Experimental Data in order to Optimize Turbine Performance: The Genetic Algorithm. J. Appl. Comput. Mech. 2023, 9, 1060–1075. [Google Scholar] [CrossRef]
- Zamani, M.; Shafaghat, R.; Alizadeh Kharkeshi, B. Enhancing Performance Evaluation of Archimedes Screw Turbines under Optimal Conditions: A Focus on Flow Rate Analysis, Empirical Equations, and Comparative Scaling Methods. Iran. J. Energy Environ. 2024, 15, 123–134. [Google Scholar] [CrossRef]
- Simmons, S.C.; Lubitz, W.D. Analysis of internal fluid motion in an Archimedes screw using computational fluid mechanics. J. Hydraul. Res. 2021, 59, 932–946. [Google Scholar] [CrossRef]
- Kozyn, A.; Lubitz, W.D. A power loss model for Archimedes screw generators. Renew. Energy 2017, 108, 260–273. [Google Scholar] [CrossRef]
- Dellinger, G.; Garambois, P.A.; Dufresne, M.; Terfous, A.; Vazquez, J.; Ghenaim, A. Numerical and experimental study of an Archimedean Screw Generator. IOP Conf. Ser. Earth Environ. Sci. 2016, 49, 102002. [Google Scholar] [CrossRef]
- Lyons, M.; Lubitz, W. Archimedes Screws for Microhydro Power Generation. In Proceedings of the ASME 2013 7th International Conference on Energy Sustainability, Long Beach, CA, USA, 27–31 July 2007. [Google Scholar] [CrossRef]
- Lashofer, A.; Hawle, W.; Kampel, I.; Kaltenberger, F.; Pelikan, B. State of technology and design guidelines for the Archimedes screw turbine. In Proceedings of the Hydro 2012—Innovative Approaches to Global Challenges, Bilbao, Spain, 29–31 October 2012. [Google Scholar]
- YoosefDoost, A.; Lubitz, W.D. Archimedes Screw Design: An Analytical Model for Rapid Estimation of Archimedes Screw Geometry. Energies 2021, 14, 7812. [Google Scholar] [CrossRef]
- YoosefDoost, A.; Lubitz, W.D. Design Guideline for Hydropower Plants Using One or Multiple Archimedes Screws. Processes 2021, 9, 2128. [Google Scholar] [CrossRef]
- Bouvant, M.; Betancour, J.; Velásquez, L.; Rubio-Clemente, A.; Chica, E. Design optimization of an Archimedes screw turbine for hydrokinetic applications using the response surface methodology. Renew. Energy 2021, 172, 941–954. [Google Scholar] [CrossRef]
- Lisicki, M.; Lubitz, W.; Taylor, G.W. Optimal design and operation of Archimedes screw turbines using Bayesian optimization. Appl. Energy 2016, 183, 1404–1417. [Google Scholar] [CrossRef]
- Simmons, S.C.; Elliott, C.; Ford, M.; Clayton, A.; Lubitz, W.D. Archimedes screw generator powerplant assessment and field measurement campaign. Energy Sustain. Dev. 2021, 65, 144–161. [Google Scholar] [CrossRef]
- Simmons, S.; Dellinger, G.; Lubitz, W.D. Effects of Parameter Scaling on Archimedes Screw Generator Performance. Energies 2023, 16, 7331. [Google Scholar] [CrossRef]
- Edirisinghe, D.S.; Yang, H.S.; Kim, M.S.; Kim, B.H.; Gunawardane, S.P.; Lee, Y.H. Computational Flow Analysis on a Real Scale Run-of-River Archimedes Screw Turbine with a High Incline Angle. Energies 2021, 14, 3307. [Google Scholar] [CrossRef]
- Erinofiardi; Nuramal, A.; Bismantolo, P.; Date, A.; Akbarzadeh, A.; Mainil, A.K.; Suryono, A.F. Experimental Study of Screw Turbine Performance based on Different Angle of Inclination. Energy Procedia 2017, 110, 8–13. [Google Scholar] [CrossRef]
- Indarto, B.; Ramazhoni, D.A.; Bustomi, M.A. Characteristics Analysis of Archimedes Screw Turbine Micro Hydro Power Plants with Variations in Water Discharge. J. Phys. Conf. Ser. 2021, 1805, 012029. [Google Scholar] [CrossRef]
- Shahverdi, K.; Maestre, J.M. Holistic Framework for Canal Modernization: Operation Optimization, and Economic and Environmental Analyses. Water Resour. Manag. 2023, 37, 6145–6164. [Google Scholar] [CrossRef]
- Zhang, D.; Guo, P.; Hu, Q.; Li, J. Parametric study and Multi-Objective optimization of a ductless Archimedes screw hydrokinetic Turbine: Experimental and numerical investigation. Energy Convers. Manag. 2022, 273, 116423. [Google Scholar] [CrossRef]
- Zhang, D.; Guo, P.; Wang, Y.; Hu, Q.; Li, J. Performance analysis of a ductless Archimedes screw turbine array for deep-sea power supply. Ocean Eng. 2023, 288, 116113. [Google Scholar] [CrossRef]
- Zitti, G.; Fattore, F.; Brunori, A.; Brunori, B.; Brocchini, M. Efficiency evaluation of a ductless Archimedes turbine: Laboratory experiments and numerical simulations. Renew. Energy 2020, 146, 867–879. [Google Scholar] [CrossRef]
- Maulana, M.; Syuhada, A.; Almas, F. Computational Fluid Dynamic Predictions on Effects of Screw Number on Performance of Single Blade Archimedes Screw Turbine. E3S Web Conf. 2018, 67, 04027. [Google Scholar] [CrossRef]
- Maulana, M.I.; Syuhada, A.; Nawawi, M. Blade number impact on pressure and performance of archimedes screw turbine using CFD. AIP Conf. Proc. 2018, 1931, 030037. [Google Scholar] [CrossRef]
- Cuenca, S.A.; Galeano, W.F.; Zambrano, J.M. Design of a micro-hydraulic generation system based on an Archimedes screw. Ingenius 2023, 29, 98–107. [Google Scholar] [CrossRef]
- Jurasz, J.; Ciapała, B. Solar–hydro hybrid power station as a way to smooth power output and increase water retention. Sol. Energy 2018, 173, 675–690. [Google Scholar] [CrossRef]
- Jurasz, J.; Ciapała, B. Integrating photovoltaics into energy systems by using a run-off-river power plant with pondage to smooth energy exchange with the power gird. Appl. Energy 2017, 198, 21–35. [Google Scholar] [CrossRef]
- Shahverdi, K.; Loni, R.; Ghobadian, B.; Monem, M.; Gohari, S.; Marofi, S.; Najafi, G. Energy harvesting using solar ORC system and Archimedes Screw Turbine (AST) combination with different refrigerant working fluids. Energy Convers. Manag. 2019, 187, 205–220. [Google Scholar] [CrossRef]



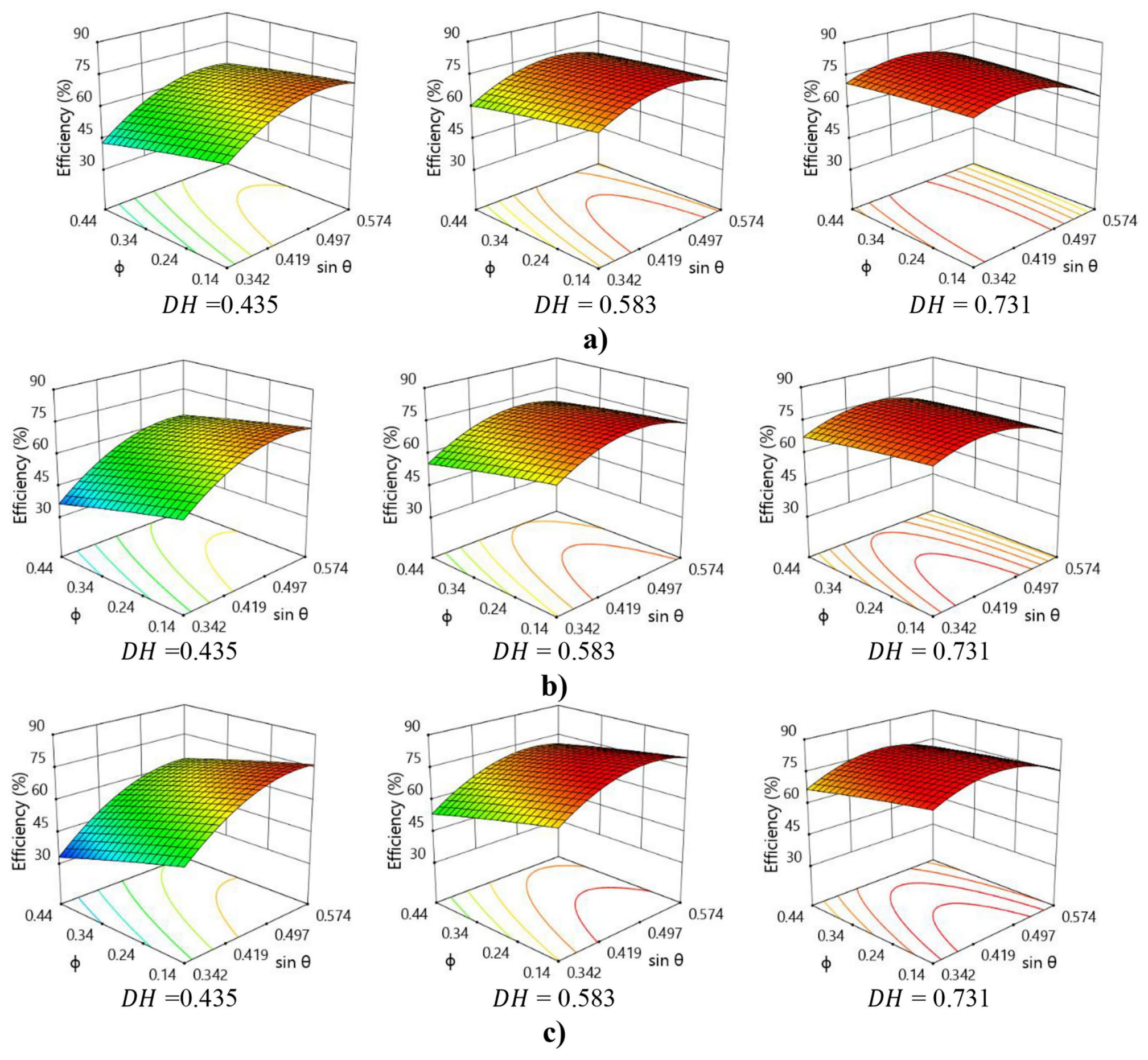
| N | N = 2 | N = 3 | N = 4 | |||||||
|---|---|---|---|---|---|---|---|---|---|---|
| DH | ° | ° | ° | |||||||
| 0.435 | 73.2 | 31.0 | 0.14 | 72.9 | 32.1 | 0.14 | 76.1 | 33.2 | 0.14 | |
| 0.583 | 78.1 | 28.0 | 0.14 | 78.3 | 29.0 | 0.14 | 82.0 | 30.0 | 0.14 | |
| 0.731 | 78.5 | 25.0 | 0.14 | 79.2 | 26.0 | 0.14 | 83.4 | 27.0 | 0.14 | |
| Ref. No. | Who | Type | (%) | (°) | L [m] | Ri [m] | Ro [m] | Q [ ] | S [m] | N | n [rpm] |
|---|---|---|---|---|---|---|---|---|---|---|---|
| [7] | Purece C. and Corlan L. | Simulation | 80.2 | 35 | 1 | 0.035 | 0.065 | 2.5 | 0.07 | 3 | 157 |
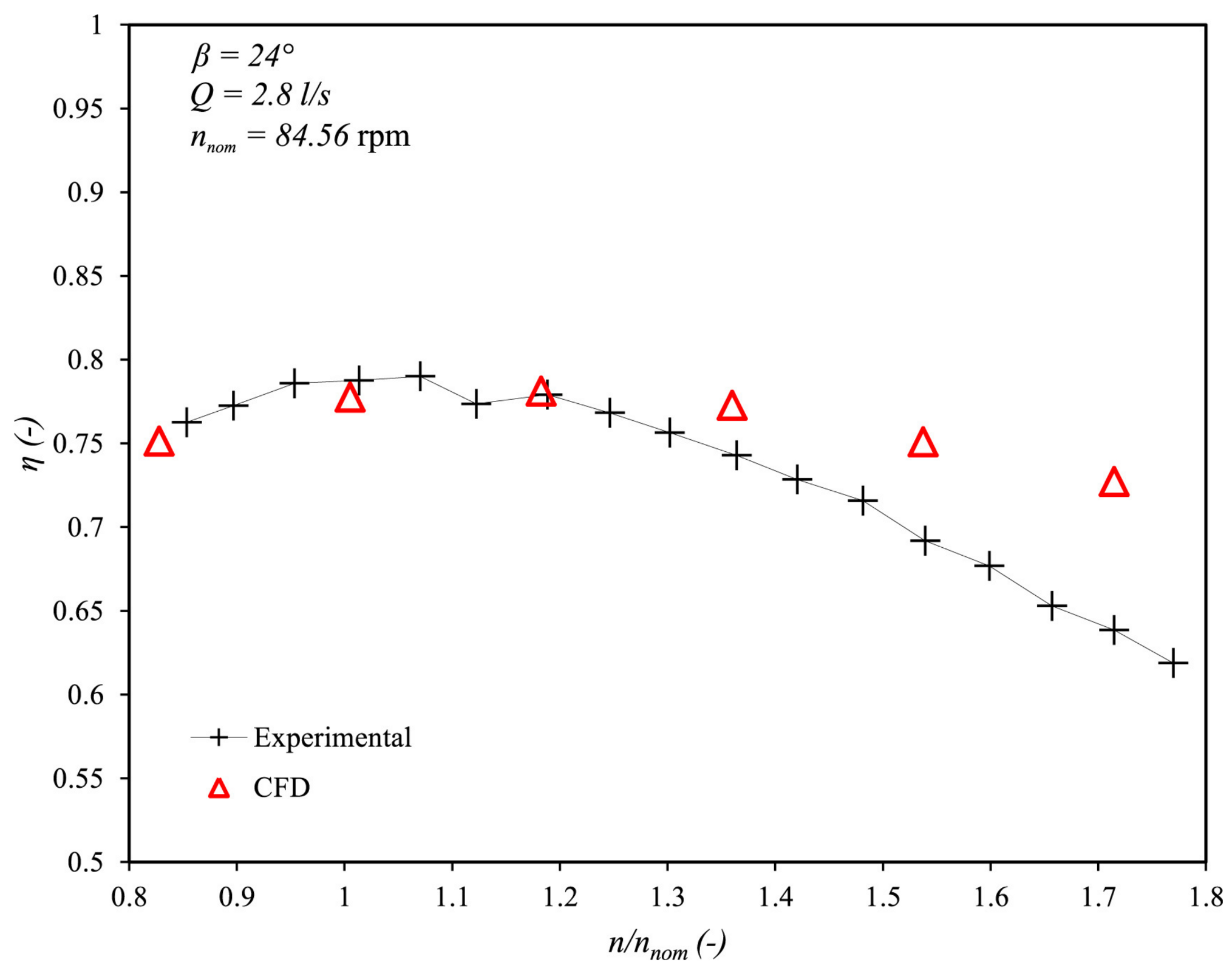
| [16] | Guilhem Dellinger et al. | Experiment | 80 | 24 | 0.4 | 0.052 | 0.096 | 2.8 | 0.192 | 3 | 84.56 |
| [28] | Guilhem Dellinger et al. | Experiment | 82 | 24 | 0.4 | 0.052 | 0.096 | 3 | 0.192 | 3 | 80 |
| [29] | Julien Rohmer et al. | Experiment | 82 | 30 | - | 0.21 | 0.42 | 80 | 0.96 | 3 | 40 |
| [30] | Neeraj Kumar Thakur et al. | Experiment | 74.27 | 22 | 1.626 | 0.04 | 0.1 | 1 | 0.3 | 1 | 115 |
| [31] | Kazem Shahverdi | Simulation | 83.4 | 27 | 0.058 | 0.004 | 0.073 | - | 0.015 | 4 | 100 |
| [32,40] | Tineke Saroinsong et al. | Experiment | 89 | 25 | 0.528 | 0.03 | 0.055 | - | 0.132 | 3 | 50 |
| [33] | A. I. Siswantara et al. | Experiment | 30 | 36 | 2.09 | 0.08 | 0.15 | 1 | 0.251 | 2 | 84.2 |
| [34] | Man Djun Lee and Pui San Lee | Experiment | 94.6 | 45 | 1.56 | 0.03 | 0.06 | - | 0.15 | 1 | 179.8 |
| [35] | K. Shahverdi et al. | Simulation | 90.83 | 20 | 6 | 0.375 | 0.75 | 1220 | 1.5 | 1 | - |
| [36] | Kazem Shahverdi et al. | Simulation | 83 | 24.9 | 0.058 | 0.004 | 0.073 | 1.13 | 0.015 | 3 | 100 |
| [37] | Kazem Shahverdi et al. | Simulation | 91 | 20–22.5 | - | - | - | - | - | 2 | - |
| [38] | Erinofiardi et al. | Experiment | 88 | 24.9 | 0.28 | 0.0085 | 0.0215 | 0.095 | - | 3 | 262 |
| [39] | Mar Alonso-Martinez et al. | Real scale | 88 | 22 | 4.179 | 0.636 | 1.139 | 2500 | 4.54 | 3 | 50 |
| [42] | Zeshan Abbas et al. | Simulation and Experiment | 51 | 60 | 0.48 | 0.02 | 0.06 | 0.76 | 0.13 | 1 | 160 |
| [44] | Zamani M. et al. | Experiment | 77.28 | 25 | 0.17 | 0.05 | 0.1 | 1.2–3.6 | 0.17 | 4 | - |
| [45] | Zamani M. et al. | Simulation | 77.28 | 25 | 0.17 | 0.05 | 0.2 | 1.2–3.7 | 0.17 | 4 | - |
| [58] | Edirisinghe D.S et al. | Simulation | 80 | 45 | 7.3 | 0.643 | 1.2 | 0.232 | - | 3 | 54.58 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sołowiej, P.; Łapiński, K. Recent Progress in Research on the Design and Use of an Archimedes Screw Turbine: A Review. Sustainability 2025, 17, 201. https://doi.org/10.3390/su17010201
Sołowiej P, Łapiński K. Recent Progress in Research on the Design and Use of an Archimedes Screw Turbine: A Review. Sustainability. 2025; 17(1):201. https://doi.org/10.3390/su17010201
Chicago/Turabian StyleSołowiej, Piotr, and Krzysztof Łapiński. 2025. "Recent Progress in Research on the Design and Use of an Archimedes Screw Turbine: A Review" Sustainability 17, no. 1: 201. https://doi.org/10.3390/su17010201
APA StyleSołowiej, P., & Łapiński, K. (2025). Recent Progress in Research on the Design and Use of an Archimedes Screw Turbine: A Review. Sustainability, 17(1), 201. https://doi.org/10.3390/su17010201






