A Multi-Objective Design Optimization of a New-Build Future Homes Standard House in Controlled Conditions
Abstract
:1. Introduction
2. Literature Review
2.1. Multi-Objective Optimization for Building Performance Simulation
2.2. Multi-Objective Optimization Algorithms
2.3. In Situ Performance Measurement Methods
3. Materials and Methods
3.1. Energy House 2.0 and TFH Experimental Study
3.2. TFH and Building Standards Context
3.3. Selection of Variables for Multi-Objective Optimization
3.3.1. External Walls
3.3.2. Loft Ceiling
3.3.3. Windows and French Door
3.3.4. Air Permeability Rate
3.3.5. Ground Floor
3.3.6. Heating Setpoint Temperatures
3.4. Running Multi-Objective Optimization
4. Results and Discussion
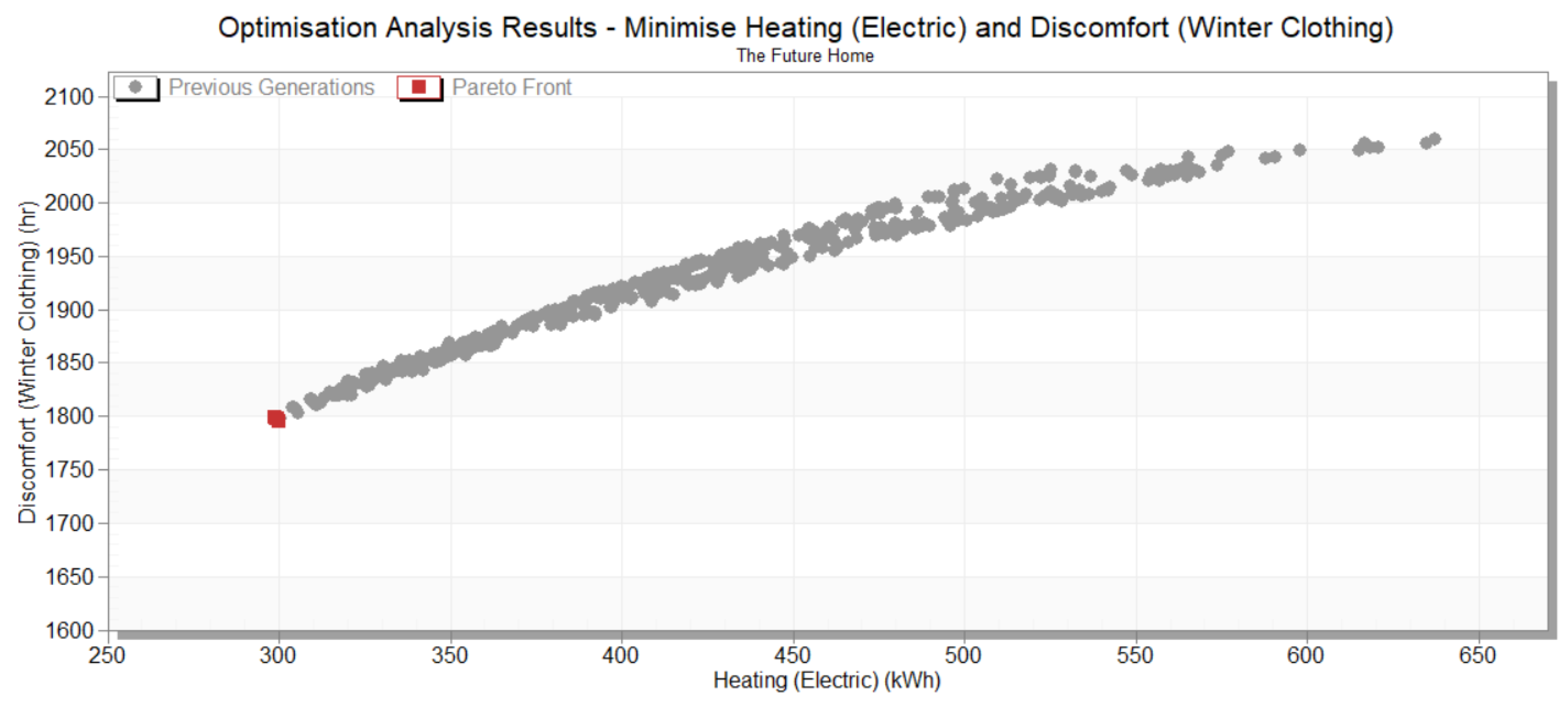
4.1. Fixed Heating Set-Point Optimization Analysis
4.2. Variable Heating Setpoint Optimization Analysis
4.3. Constrained Optimization Analysis with Maximum Discomfort Threshold
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Nomenclature
| FHS | Future Homes Standard |
| HTC | Heat Transfer Coefficient |
| DTS | Dynamic Thermal Simulation |
| MOO | Multi-Objective Optimization |
| HVAC | Heating, Ventilation and Air-Conditioning |
| NZEB | Net-Zero Energy Building |
| NSGA-II | Non-dominated Sorting Genetic Algorithm |
| TFH | The Future Home in Energy House Labs Environmental Chamber 1 developed in collaboration between Bellway Homes and the University of Salford |
| MVHR | Mechanical Ventilation and Heat Recovery |
| PTT | Point Thermal Transmittance |
| eHome2 | Experimental house in Energy House Labs Environmental Chamber 1 developed in collaboration between Barratt Developments, Saint-Gobain, and the University of Salford. |
References
- Hines, J.; Godber, S.; Butcher, B.; Siddall, M.; Jennings, P.; Grant, N.; Clarke, A.; Mead, K.; Parsons, C. How to Build a Passivhaus: Rules of Thumb; Passivhaus Trust: London, UK, 2015. [Google Scholar]
- HM Government. The Future Homes and Buildings Standards: 2023 Consultation; Department for Levelling Up, Housing and Communities: London, UK, 2023. [Google Scholar]
- Kaynakli, O. A Review of the Economical and Optimum Thermal Insulation Thickness for Building Applications. Renew. Sustain. Energy Rev. 2012, 16, 415–425. [Google Scholar] [CrossRef]
- Nematchoua, M.K.; Raminosoa, C.R.R.; Mamiharijaona, R.; René, T.; Orosa, J.A.; Elvis, W.; Meukam, P. Study of the Economical and Optimum Thermal Insulation Thickness for Buildings in a Wet and Hot Tropical Climate: Case of Cameroon. Renew. Sustain. Energy Rev. 2015, 50, 1192–1202. [Google Scholar] [CrossRef]
- Jankovic, L. Lessons Learnt from Design, off-Site Construction and Performance Analysis of Deep Energy Retrofit of Residential Buildings. Energy Build. 2019, 186, 319–338. [Google Scholar] [CrossRef]
- Jankovic, L. Improving Building Energy Efficiency through Measurement of Building Physics Properties Using Dynamic Heating Tests. Energies 2019, 12, 1450. [Google Scholar] [CrossRef]
- Jankovic, L. Designing Zero Carbon Buildings Using Dynamic Simulation Methods, 2nd ed.; Routledge: London, UK, 2017; ISBN 978-1-315-62090-9. [Google Scholar]
- Fitton, R.; Diaz, H.; Farmer, D.; Henshaw, G.; Sitmalidis, A.; Swan, W. Bellway Homes “The Future Home” Baseline Performance Report; ERDF & Innovate: Salford, UK, 2024. [Google Scholar]
- Tsang, C.; Fitton, R.; Hernandez, H.D.; Henshaw, G.; Sitmalidis, A. Pioneering Net Zero Homes: A Study of Bellway “The Future Home” Simulation Calibration; University of Salford: Manchester, UK, 2024. [Google Scholar]
- Nguyen, A.-T.; Reiter, S.; Rigo, P. A Review on Simulation-Based Optimization Methods Applied to Building Performance Analysis. Appl. Energy 2014, 113, 1043–1058. [Google Scholar] [CrossRef]
- Ascione, F.; Bianco, N.; De Stasio, C.; Mauro, G.M.; Vanoli, G.P. Multi-Stage and Multi-Objective Optimization for Energy Retrofitting a Developed Hospital Reference Building: A New Approach to Assess Cost-Optimality. Appl. Energy 2016, 174, 37–68. [Google Scholar] [CrossRef]
- Asadi, E.; da Silva, M.G.; Antunes, C.H.; Dias, L.; Glicksman, L. Multi-Objective Optimization for Building Retrofit: A Model Using Genetic Algorithm and Artificial Neural Network and an Application. Energy Build. 2014, 81, 444–456. [Google Scholar] [CrossRef]
- Wang, B.; Xia, X.; Zhang, J. A Multi-Objective Optimization Model for the Life-Cycle Cost Analysis and Retrofitting Planning of Buildings. Energy Build. 2014, 77, 227–235. [Google Scholar] [CrossRef]
- Asadi, E.; da Silva, M.G.; Antunes, C.H.; Dias, L. Multi-Objective Optimization for Building Retrofit Strategies: A Model and an Application. Energy Build. 2012, 44, 81–87. [Google Scholar] [CrossRef]
- Delgarm, N.; Sajadi, B.; Delgarm, S. Multi-Objective Optimization of Building Energy Performance and Indoor Thermal Comfort: A New Method Using Artificial Bee Colony (ABC). Energy Build. 2016, 131, 42–53. [Google Scholar] [CrossRef]
- Rosso, F.; Ciancio, V.; Dell’Olmo, J.; Salata, F. Multi-Objective Optimization of Building Retrofit in the Mediterranean Climate by Means of Genetic Algorithm Application. Energy Build. 2020, 216, 109945. [Google Scholar] [CrossRef]
- D’Agostino, D.; Minelli, F.; Minichiello, F. New Genetic Algorithm-Based Workflow for Multi-Objective Optimization of Net Zero Energy Buildings Integrating Robustness Assessment. Energy Build. 2023, 284, 112841. [Google Scholar] [CrossRef]
- Benincá, L.; Crespo Sánchez, E.; Passuello, A.; Karini Leitzke, R.; Grala da Cunha, E.; Maria González Barroso, J. Multi-Objective Optimization of the Solar Orientation of Two Residential Multifamily Buildings in South Brazil. Energy Build. 2023, 285, 112838. [Google Scholar] [CrossRef]
- Deb, K.; Pratap, A.; Agarwal, S.; Meyarivan, T. A Fast and Elitist Multiobjective Genetic Algorithm: NSGA-II. IEEE Trans. Evol. Comput. 2002, 6, 182–197. [Google Scholar] [CrossRef]
- DesignBuilder Software Ltd. DesignBuilder, Version 7.0.0.116; DesignBuilder Software Ltd.: Stroud, UK, 2022.
- ISO 7345:2018; Thermal Performance of Buildings and Building Components—Physical Quantities and Definitions. ISO: Geneva, Switzerland, 2018.
- ISO 9869-1:2014; Thermal Insulation—Building Elements—In-Situ Measurement of Thermal Resistance and Thermal Transmittance Part 1: Heat Flow Meter Method. ISO: Geneva, Switzerland, 2014.
- Johnston, D.; Miles-Shenton, D.; Farmer, D. Quantifying the Domestic Building Fabric ‘Performance Gap’. Build. Serv. Eng. Res. Technol. 2015, 36, 614–627. [Google Scholar] [CrossRef]
- ATTMA. ATTMA Technical Standard L1. In Measuring the Air Permeability of Building Envelopes (Dwellings); Air Tightness Testing and Measurement Association: Northampton, UK, 2010. [Google Scholar]
- Kronvall, J. Testing of Houses for Air-Leakage Using a Pressure Method; AIVC: Hanover, Germany, 1978. [Google Scholar]
- HM Government BEIS. SAP 10.2: The Government’s Standard Assessment Procedure for Energy Rating of Dwellings; BRE Garston: Watford, WD, USA, 2023.
- d’Ambrosio Alfano, F.R.; Dell’Isola, M.; Ficco, G.; Tassini, F. Experimental Analysis of Air Tightness in Mediterranean Buildings Using the Fan Pressurization Method. Build. Environ. 2012, 53, 16–25. [Google Scholar] [CrossRef]
- Johnston, D.; Miles-Shenton, D.; Wingfield, J.; Farmer, D.; Bell, M. Whole House Heat Loss Test Method (Coheating); Leeds Metropolitan University: Leeds, UK, 2012. [Google Scholar]
- Alzetto, F.; Pandraud, G.; Fitton, R.; Heusler, I.; Sinnesbichler, H. QUB: A Fast Dynamic Method for in-Situ Measurement of the Whole Building Heat Loss. Energy Build. 2018, 174, 124–133. [Google Scholar] [CrossRef]
- Catapult Energy Systems: Veritherm: Identifying Consumer Routes to Market for Thermal Testing. Available online: https://es.catapult.org.uk/case-study/veritherm-identifying-consumer-routes-to-market-for-thermal-testing/ (accessed on 15 December 2024).
- BSI BS EN ISO 6946; Building Components and Building Elements—Thermal Resistance and Thermal Transmittance—Calculation Methods. British Standards Institution: Milton Keynes, UK, 2007.
- HM Government RIBA Publishing Ltd. UK Building Regulations. Part L1A: Conservation of Fuel and Power in New Dwellings; HM Government RIBA Publishing Ltd.: London, UK, 2023. [Google Scholar]
- Passivhaus Institute Passive House Institute. Criteria for Buildings: Passive House—EnerPHit—PHI Low Energy Building; Passivhaus Institute: Darmstadt, Germany, 2023. [Google Scholar]
- CIBSE. CIBSE Guide A: Environmental Design; CIBSE: London, UK, 2015; ISBN 978-0-240-81224-3. [Google Scholar]
- ASHRAE. ASHRAE Handbook Fundamentals; ASHRAE Standard: Atlanta, GA, USA, 2018. [Google Scholar]
- ASHRAE 55-2004; Thermal Environmental Conditions for Human Occupancy. ASHRAE Standard: Atlanta, GA, USA, 2004.
- De Dear, R.; Brager, G.S. Developing an Adaptive Model of Thermal Comfort and Preference; Center for the Built Environment: Berkeley, CA, USA, 1998. [Google Scholar]
- Wang, W.; Zmeureanu, R.; Rivard, H. Applying Multi-Objective Genetic Algorithms in Green Building Design Optimization. Build. Environ. 2005, 40, 1512–1525. [Google Scholar] [CrossRef]
- Carlucci, S.; Pagliano, L. A Review of Indices for the Long-Term Evaluation of the General Thermal Comfort Conditions in Buildings. Energy Build. 2012, 53, 194–205. [Google Scholar] [CrossRef]
- Fitton, R.; Diaz, H.; Farmer, D.; Henshaw, G.; Sitmalidis, A.; Swan, W. Saint Gobain & Barratt Developments “eHome2” Baseline Performance Report; ERDF & Innovate: Salford, UK, 2024. [Google Scholar]



| Building Fabric Element | Design | As-Built | UK FHS | UK Building Regulations | PassivHaus Standard |
|---|---|---|---|---|---|
| External wall U-value (W/m2K) | 0.18 | 0.17 | 0.18 | 0.26 | 0.15 |
| Loft ceiling U-value (W/m2K) | 0.09 | 0.14 | 0.11 | 0.16 | 0.15 |
| Ground floor PTT-value (W/m2K) | 0.11 | 0.14 | 0.13 | 0.18 | 0.15 |
| Windows U-value (W/m2K) | 1.20 | - | 1.20 | 1.60 | 0.80 |
| French door U-value (W/m2K) | 1.40 | - | 1.20 | - | - |
| External door U-value (W/m2K) | 1.00 | - | 1.00 | 1.60 | 0.80 |
| Air infiltration rate @50 Pa (m3/hm2) | 2.50 | 4.00 | 5.00 | 8.00 | 0.60 |
| Variable | Baseline | Perturbations/Scenarios | Iterations |
|---|---|---|---|
| External wall U-value (W/m2K) | 0.17 | 0.12, 0.13, 0.14, 0.15, 0.16, 0.17 §, 0.18, 0.19, 0.20 | 9 |
| Loft ceiling U-value (W/m2K) | 0.14 | 0.09, 0.10, 0.11, 0.12, 0.13, 0.14, 0.15, 0.16 | 8 |
| Window U-values (W/m2K) | 1.2 | 0.8, 0.9, 1.0, 1.1, 1.2, 1.3, 1.4, 1.5, 1.6 | 9 |
| French door U-value (W/m2K) | 1.4 | 1.0, 1.1, 1.2, 1.3, 1.4, 1.5, 1.6, 1.7, 1.8 | 9 |
| Air permeability rate @50 Pa (m3/hm2) | 4.0 | 2.5, 3.0, 3.5, 4.0, 4.5, 5.0 | 6 |
| Ground floor PTT-value (W/m2K) | 0.14 | 0.11, 0.12, 0.13, 0.14, 0.15, 0.16, 0.17, 0.18 | 8 |
| Living room heating setpoint (°C) | 21 | 19, 20, 21, 22 | 4 |
| Other zone heating setpoint (°C) | 18 | 18, 19, 20, 21 | 4 |
| Pareto Extreme | Heating (Electric) (kWh) | Total Building Cost (GBP) | Discomfort (Winter Clothing) (h) | Air Permeability Rate @50 Pa (m3/hm2) | Glazing U-Value (W/m2K) | Living Room Heating Set-Point Temperature (°C) | Other Rooms Heating Setpoint Temperature (°C) |
|---|---|---|---|---|---|---|---|
| (1) | 672 | 134,357 | 397 | 2.5 | 0.8 | 22 | 22 |
| (2) | 1044 | 134,865 | 276 | 5.0 | 1.6 | 22 (23) * | 22 |
| Difference (2) − (1) | 372 | 508 | −101 | 2.5 | 0.8 | 0 (1) * | 0 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tsang, C.; Jankovic, L.; Fitton, R.; Henshaw, G. A Multi-Objective Design Optimization of a New-Build Future Homes Standard House in Controlled Conditions. Sustainability 2025, 17, 724. https://doi.org/10.3390/su17020724
Tsang C, Jankovic L, Fitton R, Henshaw G. A Multi-Objective Design Optimization of a New-Build Future Homes Standard House in Controlled Conditions. Sustainability. 2025; 17(2):724. https://doi.org/10.3390/su17020724
Chicago/Turabian StyleTsang, Christopher, Ljubomir Jankovic, Richard Fitton, and Grant Henshaw. 2025. "A Multi-Objective Design Optimization of a New-Build Future Homes Standard House in Controlled Conditions" Sustainability 17, no. 2: 724. https://doi.org/10.3390/su17020724
APA StyleTsang, C., Jankovic, L., Fitton, R., & Henshaw, G. (2025). A Multi-Objective Design Optimization of a New-Build Future Homes Standard House in Controlled Conditions. Sustainability, 17(2), 724. https://doi.org/10.3390/su17020724








