Fuel Consumption Prediction for Full Flight Phases Toward Sustainable Aviation: A DMPSO-LSTM Model Using Quick Access Recorder (QAR) Data
Abstract
:1. Introduction
2. Literature Review
2.1. Fuel Consumption Prediction
2.2. Knowledge Gap
3. Methodology
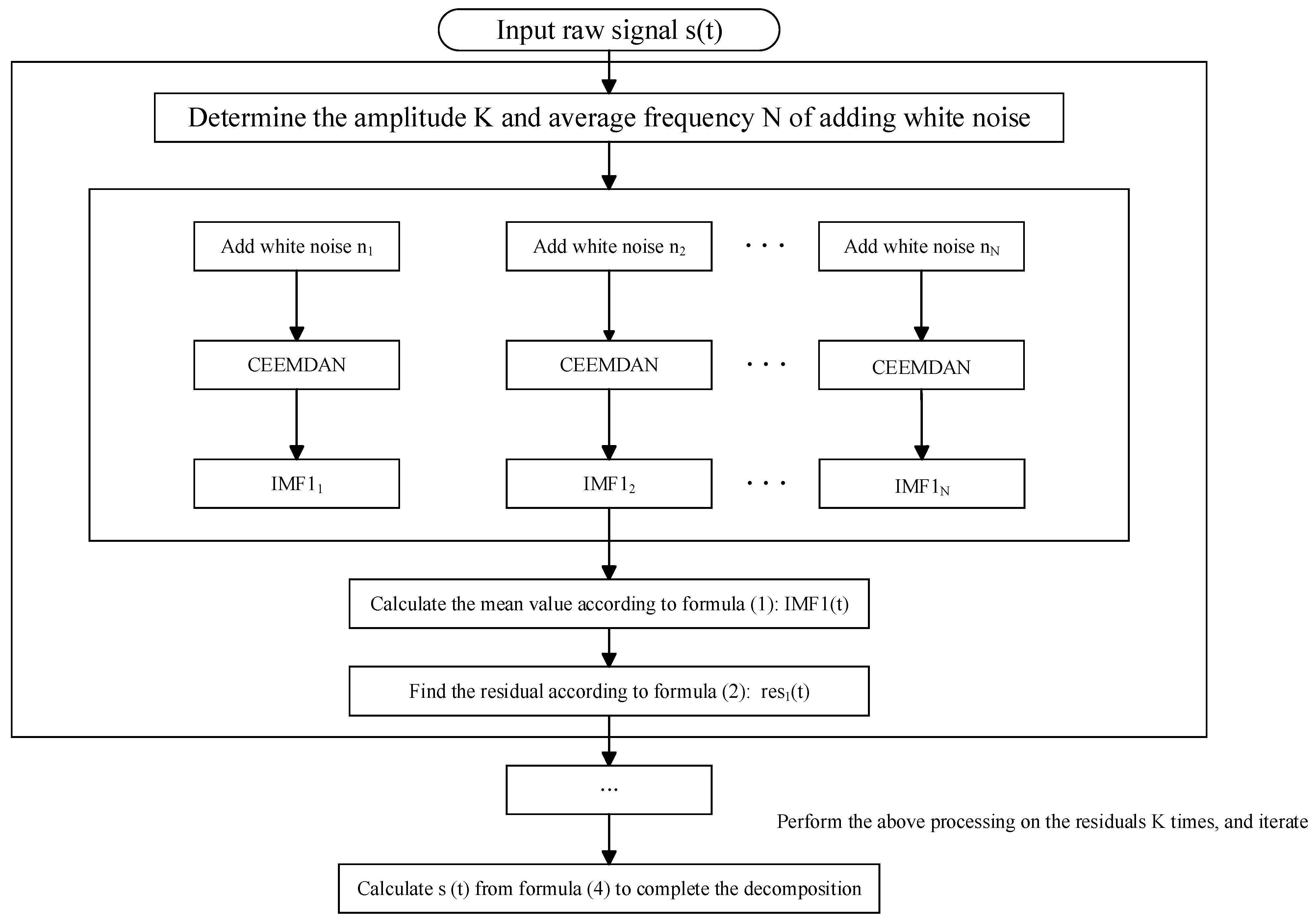
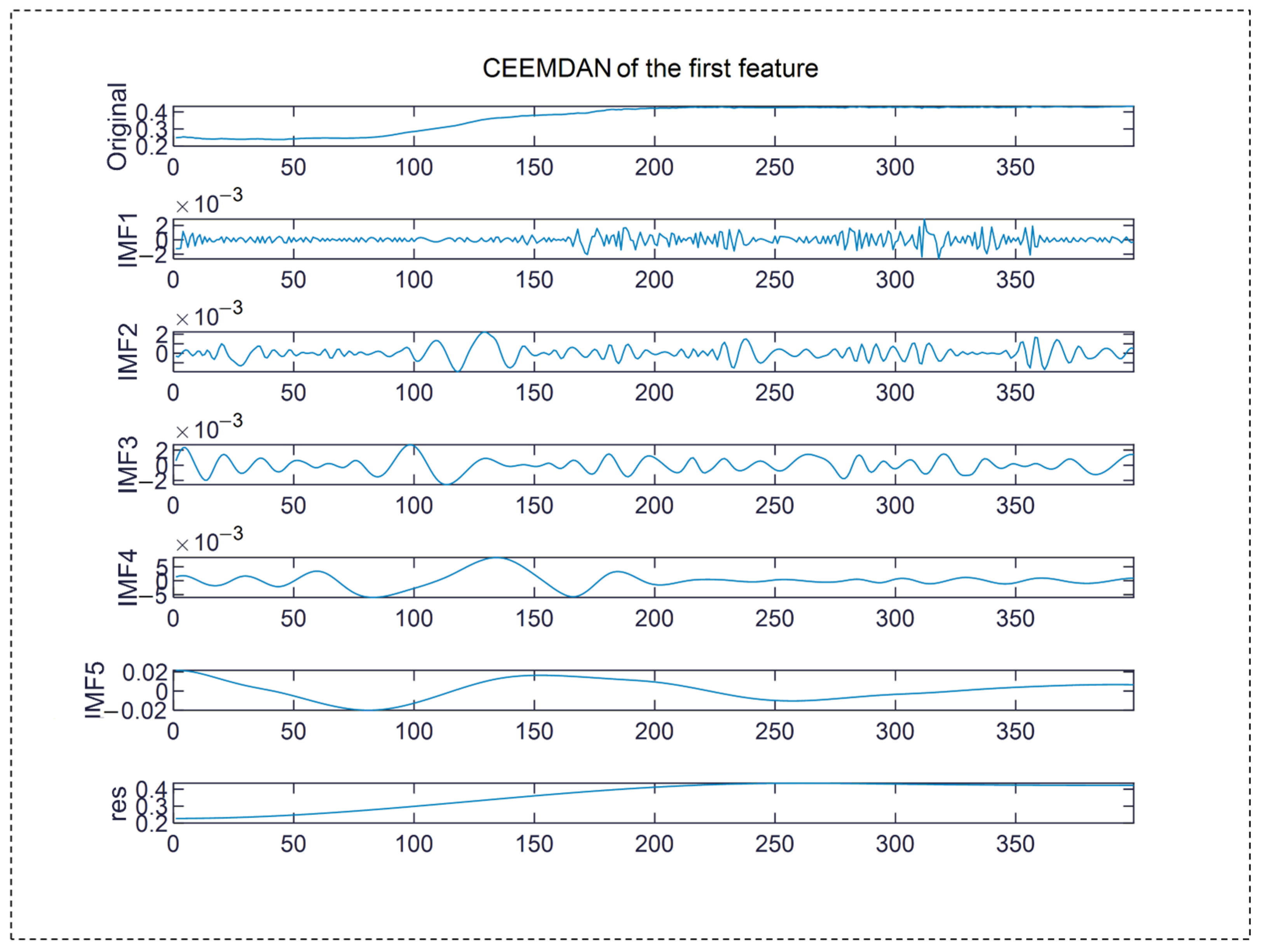
3.1. Decomposition of Fuel Consumption Impact Characteristics Based on CEEMDAN
3.2. Dimension Reduction in Aircraft Fuel Consumption Impact Characteristics Based on KPCA
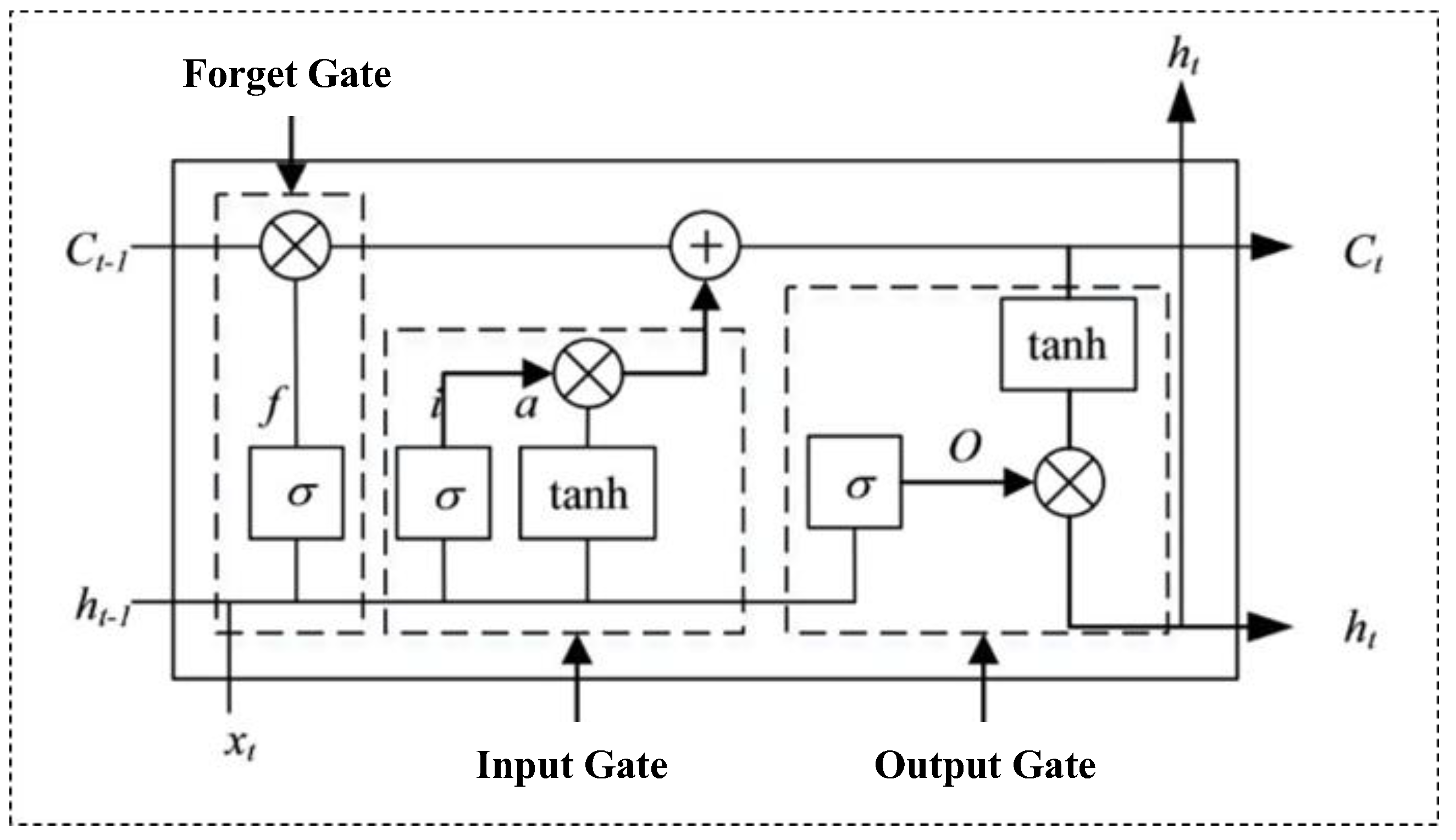
3.3. Aircraft Fuel Consumption Prediction Model Based on Improved PSO-LSTM
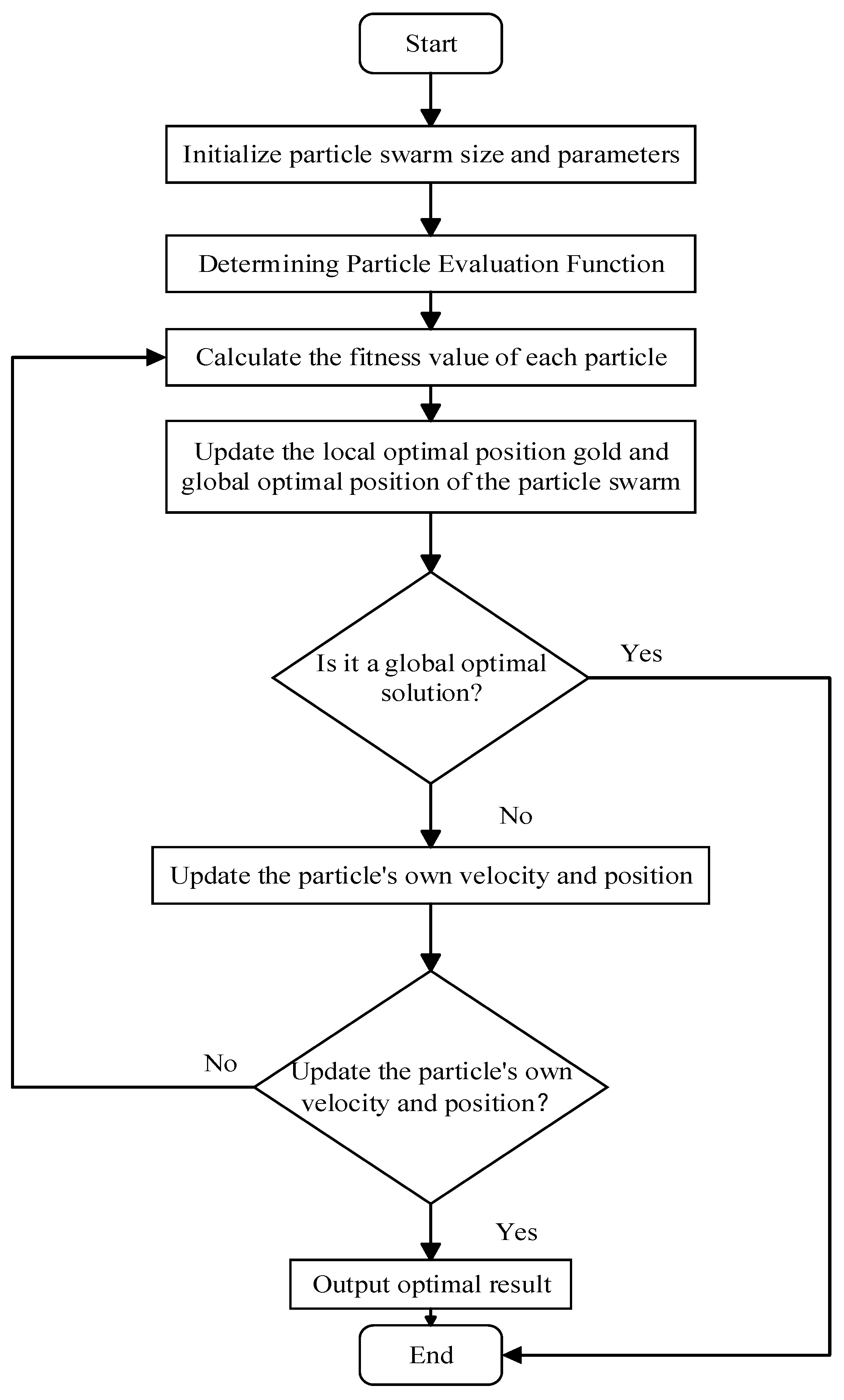
3.3.1. DMPSO Algorithm
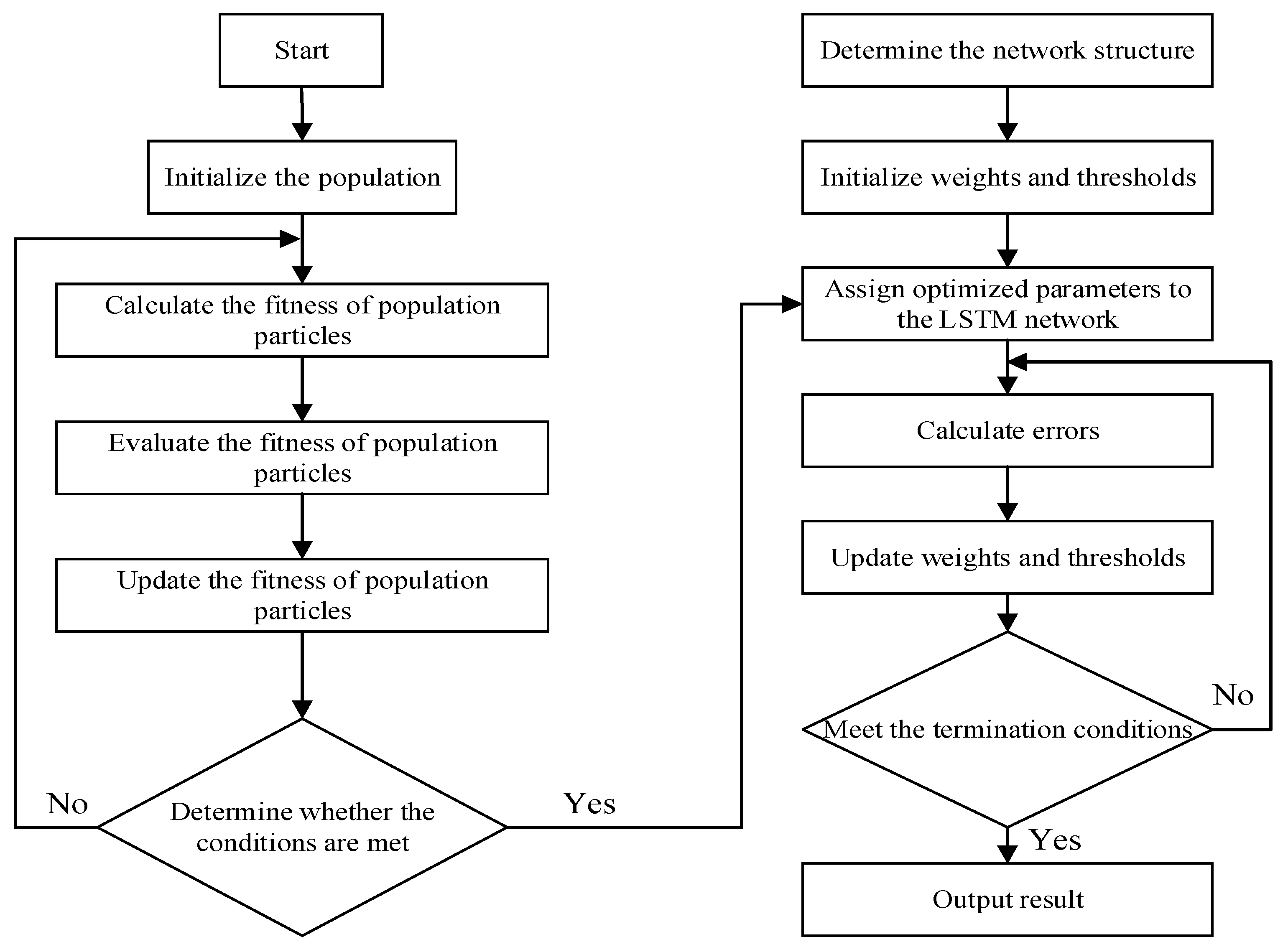
3.3.2. DMPSO-LSTM Model
4. Case Study
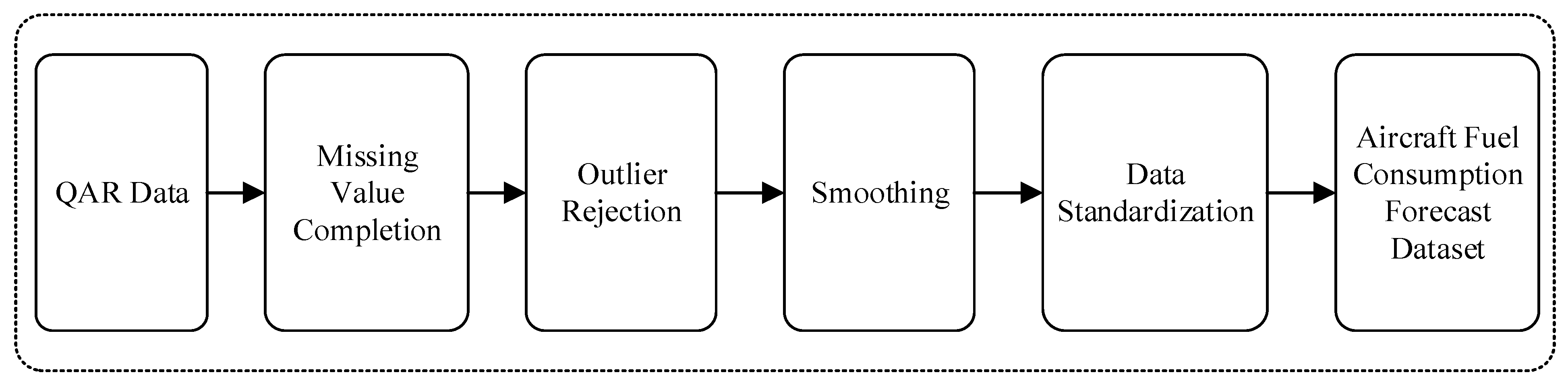
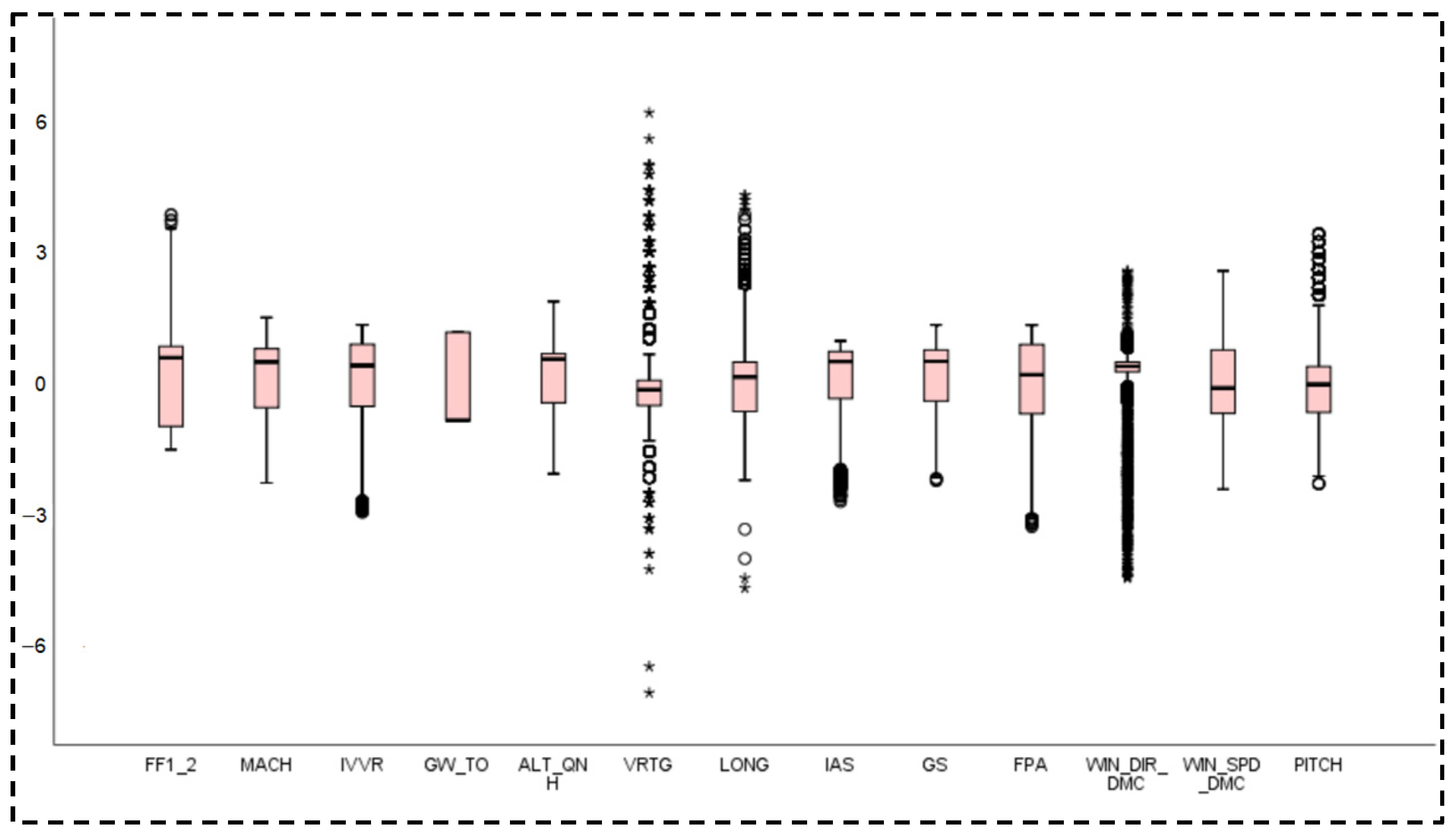
4.1. Data Preprocessing
4.2. Decomposition and Dimensionality Reduction in Factors Affecting Aircraft Fuel Consumption
4.2.1. Decomposition of Factors Influencing Aircraft Fuel Consumption Characteristics
4.2.2. Dimensionality Reduction in Aircraft Fuel Consumption Impact Characteristics
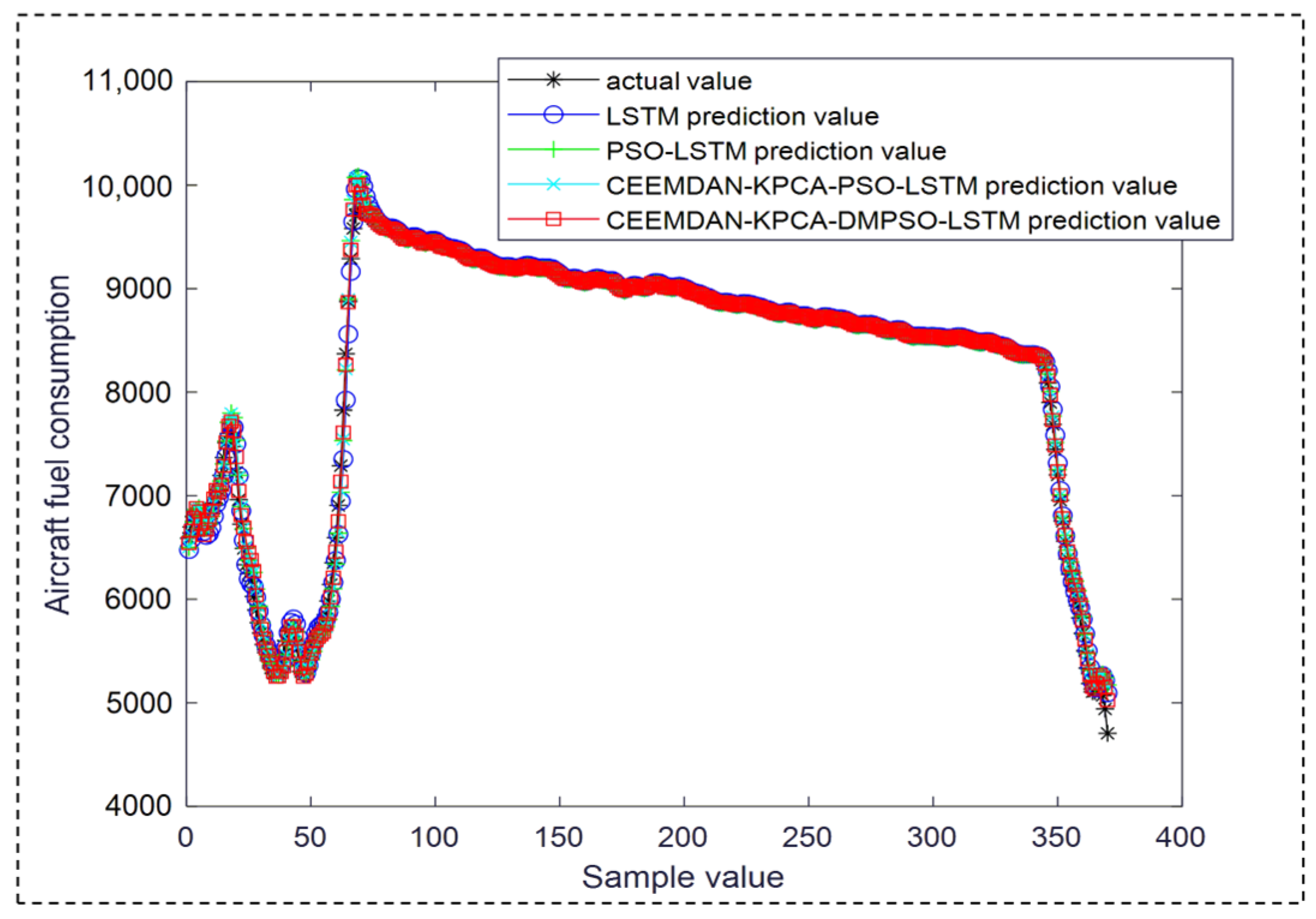
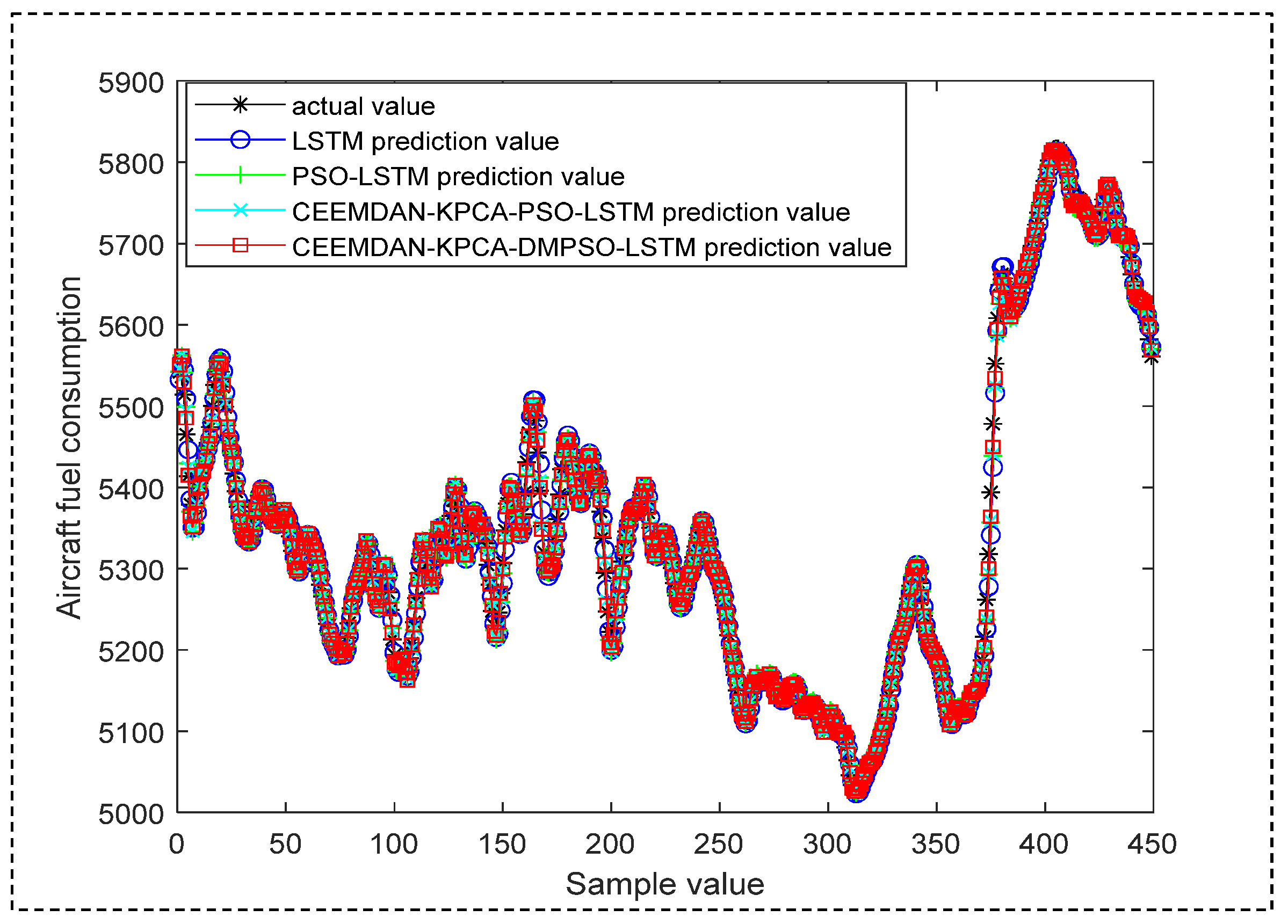
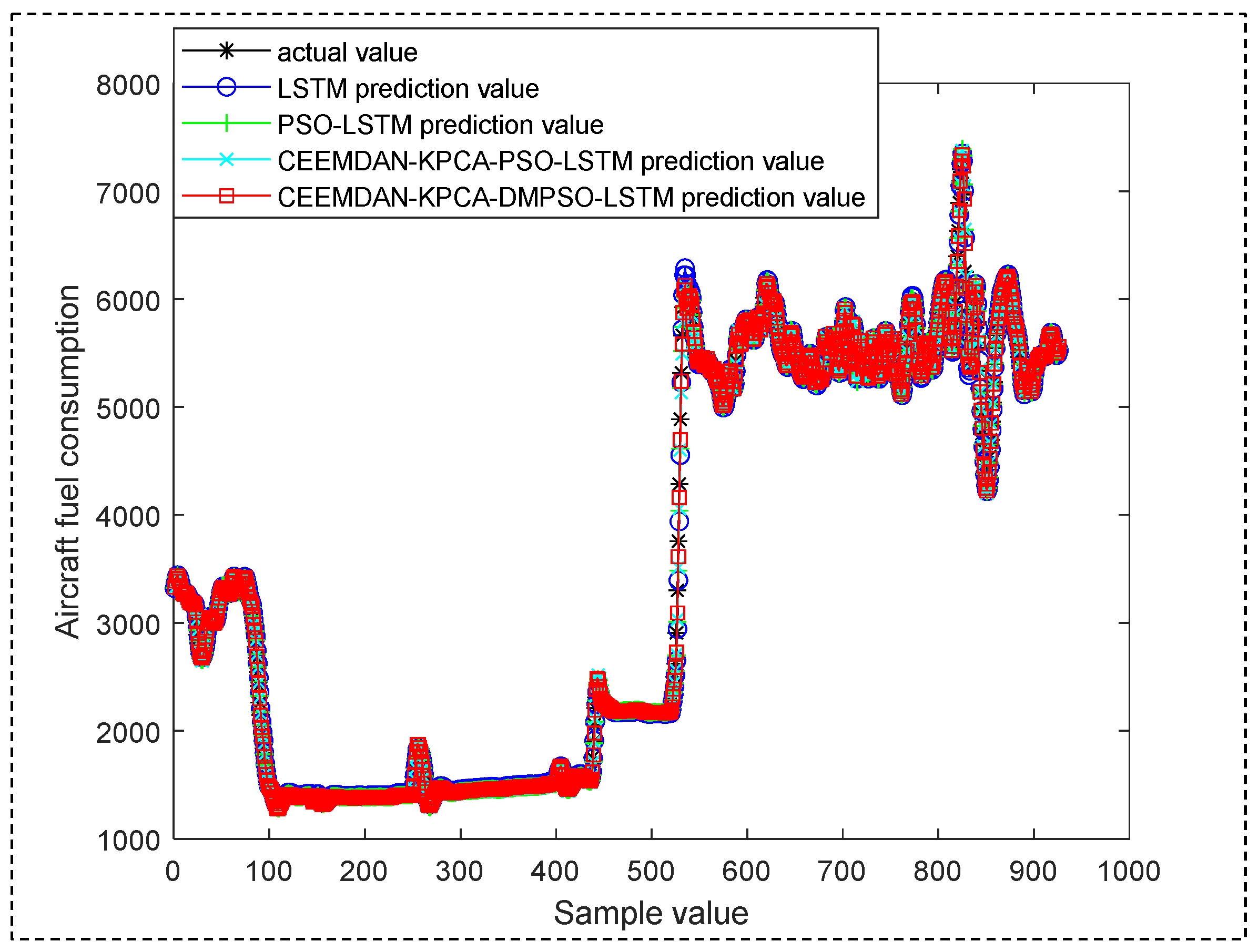
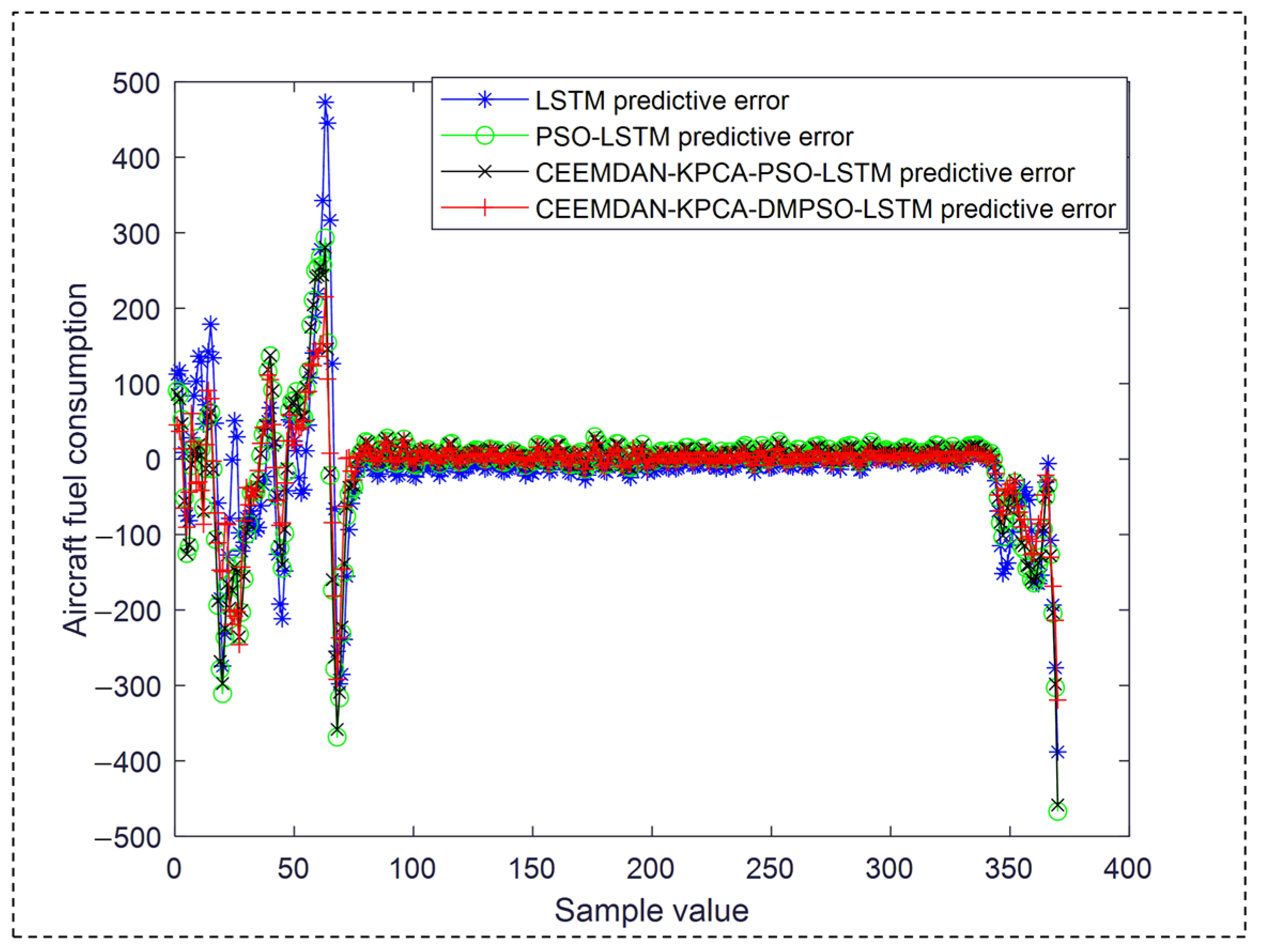
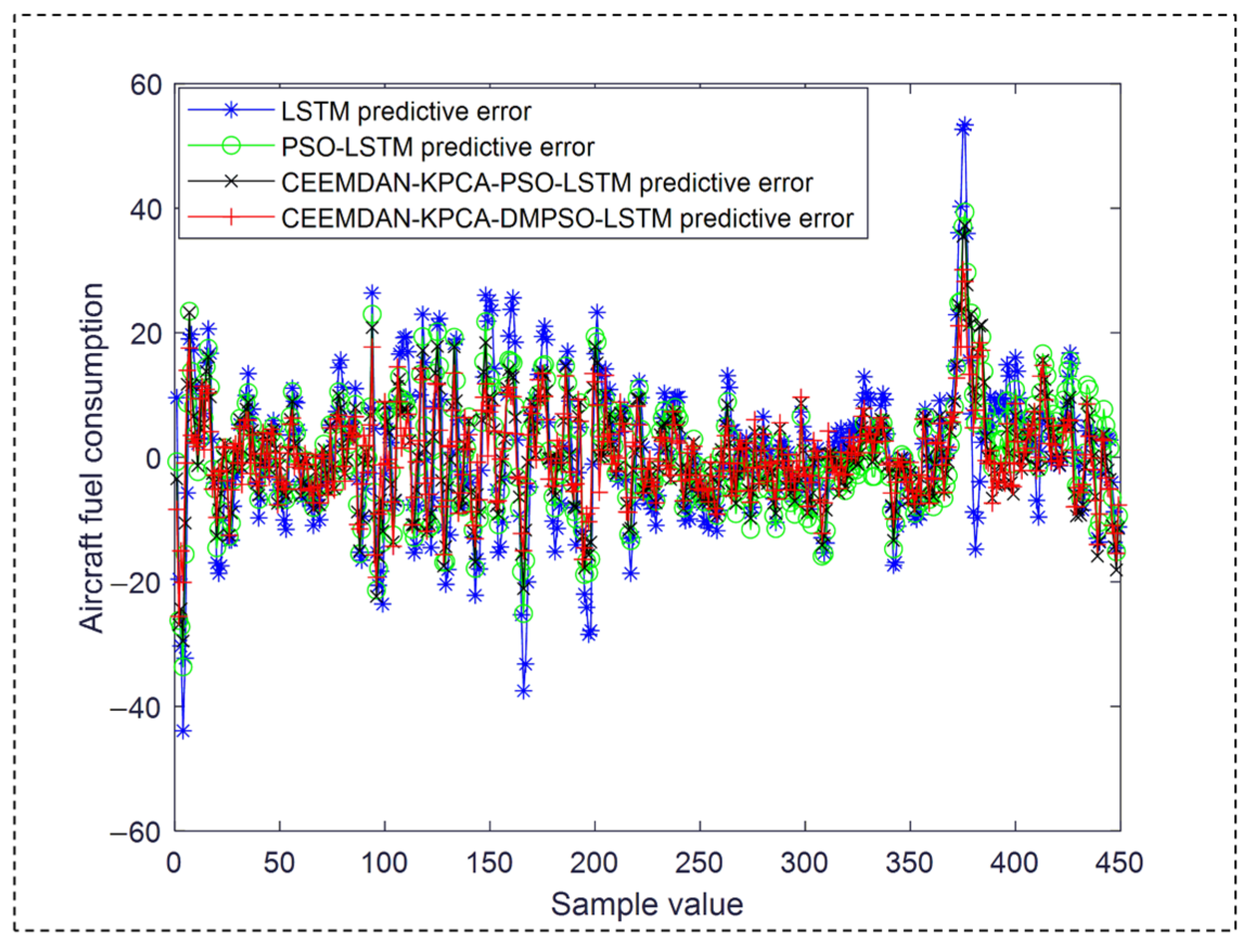
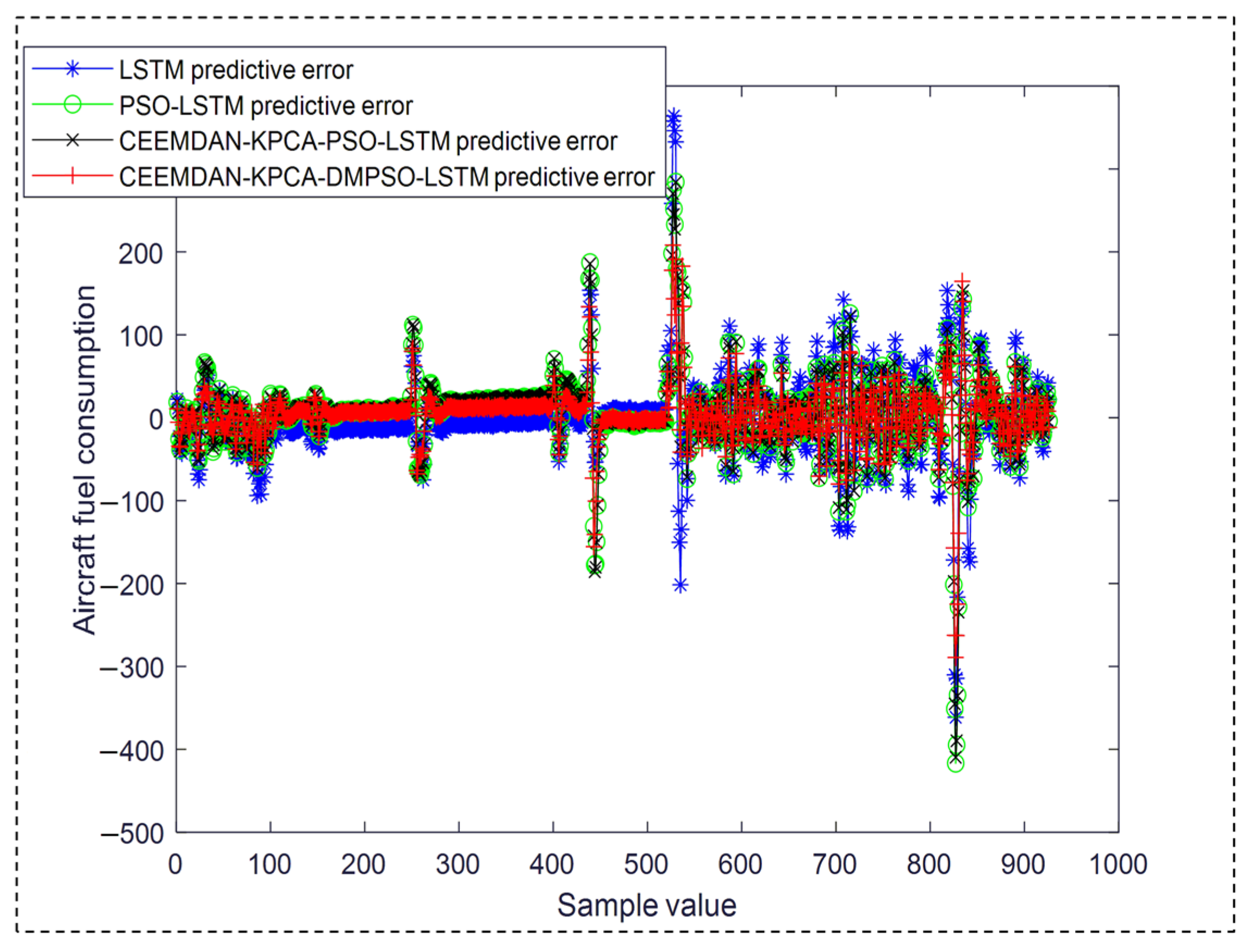
4.3. Experimental Results
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- IEA. CO2 Emissions in 2022; International Energy Agency: Paris, France, 2023. [Google Scholar]
- Siavash, K.; Eetu, R.; Dmitrii, B.; Christian, B. Global Transportation demand development with impacts on the energy demand and greenhouse gas emissions in a climate-constrained world. Energies 2019, 12, 3870. [Google Scholar] [CrossRef]
- ICAO. 2022 Environmental Report: Aviation’s Roadmap to Net-Zero Carbon Emissions by 2050; ICAO: Montreal, QC, Canada, 2022. [Google Scholar]
- Pagoni, I.; Psaraki-Kalouptsidi, V. Calculation of aircraft fuel consumption and CO2 emissions based on path profile estimation by clustering and registration. Transp. Res. Part D Transp. 2017, 54, 172–190. [Google Scholar] [CrossRef]
- Baklacioglu, T. Modeling the fuel flow-rate of transport aircraft during flight phases using genetic algorithm-optimized neural networks. Aerosp. Sci. Technol. 2016, 49, 52–62. [Google Scholar] [CrossRef]
- Nikoleris, T.; Gupta, G.; Kistler, M. Detailed estimation of fuel consumption and emissions during aircraft taxi operations at Dallas/Fort Worth International Airport. Transp. Res. Part D Transp. Environ. 2011, 16, 302–308. [Google Scholar] [CrossRef]
- Yanto, J.; Liem, R.P. Aircraft fuel burn performance study: A data-enhanced modeling approach. Transp. Res. 2018, 65, 574–595. [Google Scholar] [CrossRef]
- Zhang, M.; Huang, Q.; Liu, S.; Zhang, Y. Fuel Consumption Model of the Climbing Phase of Departure Aircraft Based on Flight Data Analysis. Sustainability 2019, 11, 4362. [Google Scholar] [CrossRef]
- Nuic, A.; Poles, D.; Mouillet, V. BADA: An advanced aircraft performance model for present and future ATM systems. Int. J. Adapt. Control Signal Process. 2022, 24, 850–866. [Google Scholar] [CrossRef]
- Khan, W.A.; Ma, H.-L.; Ouyang, X.; Mo, D.Y. Prediction of aircraft trajectory and the associated fuel consumption using covariance bidirectional extreme learning machines. Transp. Res. Part E Logist. Transp. Rev. 2021, 145, 102189. [Google Scholar] [CrossRef]
- Kaiser, M.; Schultz, M.; Fricke, H. Enhanced jet performance model for high precision 4D flight path prediction. In Proceedings of the 1st International Conference on Application and Theory of Automation in Command and Control Systems, Barcelona, Spain, 26–27 May 2011; pp. 33–40. [Google Scholar]
- Dalmau, R.; Prats, X. Fuel and time savings by flying continuous cruise climbs. Transp. Res. Part D Transp. Environ. 2019, 35, 62–71. [Google Scholar] [CrossRef]
- Burzlaff, M. Aircraft Fuel Consumption-Estimation and Visualization. Ph.D. Thesis, Hamburg University of Applied Science, Hamburg, Germany, 2017. [Google Scholar]
- Yutko, B.M. Approaches to Representing Aircraft Fuel Efficiency Performance for the Purpose of a Commercial Aircraft Certification Standard. Ph.D. Thesis, Massachusetts Institute of Technology, Cambridge, MA, USA, 2021. [Google Scholar]
- Jensen, L.; Hansman, R.J.; Venuti, J.C.; Reynolds, T. Commercial airline speed optimization strategies for reduced cruise fuel consumption. In Proceedings of the 2013 Aviation Technology, Integration, and Operations Conference, Los Angeles, CA, USA, 12–14 August 2013; p. 4289. [Google Scholar]
- Trani, A.; Wing-Ho, F.; Schilling, G.; Baik, H.; Seshadri, A. A Neural Network Model to Estimate Aircraft Fuel Consumption. Aiaa J. 2024, 10, 61–68. [Google Scholar]
- Wang, Z.M.; Xue, D.B.; Wu, L.X.; Yan, R. A reliable predict-then-optimize approach for minimizing aircraft fuel consumption. Transp. Res. Part D Transp. 2025, 142, 104693. [Google Scholar] [CrossRef]
- Wang, B.; Zou, R.Y.; Mao, J.F.; Wu, C.L.; Xue, D.B. Developing an aircraft takeoff mass estimation model based on the hybrid KMI-DNN-BI model using quick access recorder (QAR) data. Aerosp. Sci. Technol. 2025, 158, 109918. [Google Scholar] [CrossRef]
- Wang, F.; Li, X.; Zhang, K. Multivariate regression with PCA for aircraft fuel consumption prediction: A case study of QAR data analytics. Transp. Res. Part D Transp. Environ. 2022, 108, 103315. [Google Scholar]
- Smith, T.; Jones, P. Bayesian hierarchical modeling of aircraft fuel burn integrating QAR data and performance benchmarks. Aerospace 2021, 8, 256. [Google Scholar]
- García, M.; Pérez, A.; López, R. Generalized additive models for fuel consumption prediction: A QAR data-driven approach with flight phase segmentation. J. Air Transp. Manag. 2023, 107, 102335. [Google Scholar]
- International Air Transport Association [IATA]. Statistical Methods for Aviation Fuel Efficiency Analysis Using Flight Data; IATA Technical Report No. 2022-ATFR-15; IATA: Montreal, QC, Canada, 2022. [Google Scholar]
- Zhang, Y.; Zhou, M.; Chen, H.; Wang, L. Hybrid CNN-LSTM model for aircraft fuel burn prediction using high-frequency QAR data. Transp. Res. Part C Emerg. Technol. 2021, 132, 103405. [Google Scholar]
- Liu, Y.; Wang, H.; Zhang, T. A transformer-based approach for aircraft fuel consumption prediction with attention to QAR data spatiotemporal features. Expert Syst. Appl. 2022, 207, 117952. [Google Scholar]
- Chen, X.; Li, Z.; Zhang, Q. Graph neural networks for integrated fuel prediction: Combining QAR data, radar tracks, and weather impacts. IEEE Trans. Aerosp. Electron. Syst. 2023, 59, 1450–1463. [Google Scholar]
- Liu, H.; Wang, J. Data-driven fuel efficiency optimization in commercial aviation: A QAR-based anomaly detection framework. Aerosp. Sci. Technol. 2022, 128, 107754. [Google Scholar]
- Chen, X.; Li, Z.; Zhang, Q.; Liu, Y. Spatiotemporal feature fusion for fuel prediction: Integrating QAR data and air traffic control constraints. IEEE Trans. Intell. Transp. Syst. 2023, 24, 2876–2888. [Google Scholar]
- Schäfer, A.W.; Yadav, P.; Stolarski, D.G. Fuel consumption prediction and trajectory optimization for climate-efficient aviation. Transp. Res. Part D Transp. Environ. 2022, 109, 103335. [Google Scholar]
- Zhang, Y.; Li, Q.; Wang, J. A multi-objective deep learning framework for fuel prediction and emission budgeting in sustainable aviation. Appl. Energy 2023, 334, 120678. [Google Scholar]
- IATA. Machine Learning for ESG Reporting in Aviation; IATA: Geneva, Switzerland, 2023. [Google Scholar]
- Airbus. Global Market Forecast: Navigating the Future; Airbus: Leiden, The Netherlands, 2023. [Google Scholar]
- Zhang, Y.; Li, H.; Chen, Z. An enhanced CEEMDAN method with adaptive noise amplitude selection for rotating machinery fault diagnosis. Mech. Syst. Signal Process. 2023, 189, 110432. [Google Scholar] [CrossRef]
- Wang, L.; Liu, J.; Yang, Q. CEEMDAN-based hybrid deep learning model for ECG signal denoising and arrhythmia classification. IEEE Trans. Instrum. Meas. 2022, 71, 1–12. [Google Scholar]
- Li, X.; Zhang, Y.; Wang, H. An adaptive particle swarm optimization with dynamic inertia weight and learning factors for high-dimensional optimization. Expert Syst. Appl. 2023, 213, 119213. [Google Scholar]
- Chen, R.; Li, W.; Zhang, T. A dynamic multi-strategy particle swarm optimizer with adaptive parameters for engineering design optimization. Swarm Intell. 2024, 18, 45–67. [Google Scholar]
- Gupta, S.; Deep, K. A hybrid PSO algorithm with adaptive learning mechanism for complex optimization problems. Swarm Evol. Comput. 2022, 71, 101090. [Google Scholar]
- Fu, W.; Wang, B.; Li, X.; Liu, L.; Wang, Y.l. Particle swarm optimization algorithm of learning factors and time factor adjusting to weights. Appl. Res. Comput. 2014, 31, 3291–3294. [Google Scholar]
- Sudhir-Kumar, P.; Narendra, B.C.; Mukul, B. Long short-term memory. Big Data Min. Anal. 2021, 4, 279–297. [Google Scholar]





| Parameter | Value |
|---|---|
| Population size | 30 |
| Time window | 10 |
| Learning factor | 1.5 |
| Inertia weight | 0.8 |
| Number of iterations | 500 |
| Learning rate | 0.001 |
| Batch size | 60 |
| Number of neurons in the first hidden layer | 12 |
| Number of neurons in the second hidden layer | 22 |
| Fuel Volume | Mach Number | Vertical Velocity | Takeoff Weight | Barometric Altitude | ... | Vertical Acceleration | Longitudinal Acceleration | Airspeed | Ground Speed | Wind Speed | Bank Angle |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 5060 | 0.743 | −128 | 64.084 | 31,196 | … | 0.93 | 0.0195 | 273.75 | 463 | 14 | −0.44 |
| 4812 | 0.743 | −208 | 64.084 | 31,192 | … | 0.93 | 0.0195 | 273.88 | 463 | 89 | −0.09 |
| 4696 | 0.744 | −304 | 64.084 | 31,188 | … | 0.93 | 0.0156 | 273.88 | 463 | 17 | −2.64 |
| 4500 | 0.744 | −400 | 64.084 | 31,188 | … | 0.93 | 0.0156 | 274 | 463 | 53 | −1.58 |
| … | ... | ... | ... | ... | … | ... | ... | ... | ... | 51 | −1.76 |
| 3976 | 0.744 | −576 | 64.084 | 31,168 | … | 0.93 | 0.0078 | 274 | 462 | ... | ... |
| 3816 | 0.744 | −656 | 64.084 | 31,156 | … | 0.93 | 0.0078 | 274.25 | 462 | 6 | −2.72 |
| 3612 | 0.745 | −720 | 64.084 | 31,148 | … | 0.938 | 0.0039 | 274.13 | 462 | 6 | −2.46 |
| 3456 | 0.744 | −784 | 64.084 | 31,128 | … | 0.949 | 0 | 274.63 | 462 | 6 | −1.9 |
| 3380 | 0.744 | −832 | 64.084 | 31,120 | … | 0.949 | 0 | 274.38 | 462 | 5 | −2.72 |
| Flight Segment Name | Influence Factor |
|---|---|
| Climbing phase | Mach number, vertical velocity, barometric altitude, longitudinal acceleration, airspeed, ground speed, tilt angle |
| Cruise phase | Vertical speed, aircraft weight, barometric altitude, longitudinal acceleration, airspeed, tilt angle, wind speed, wind direction |
| Descending phase | Mach number, vertical velocity, barometric altitude, longitudinal acceleration, aircraft weight, tilt angle, wind speed, wind direction |
| Ground Speed | Longitudinal Acceleration | Vertical Acceleration | Wind Speed | ... | Bank Angle | Airspeed | Pressure Altitude | Fuel Volume |
|---|---|---|---|---|---|---|---|---|
| 0.25 | 0.16 | –0.37 | −0.75 | ... | 0.36 | 0.67 | −0.67 | 0.44 |
| 0.92 | 0.29 | −0.53 | 0.98 | ... | 0.53 | 0.99 | 0.99 | −1.00 |
| 0.04 | 0.45 | −0.60 | −0.68 | ... | −0.70 | 0.34 | −0.69 | 0.47 |
| 0.57 | 0.24 | −0.53 | 0.15 | ... | −0.19 | 0.88 | 0.26 | −0.55 |
| 0.58 | 0.22 | −0.53 | 0.10 | ... | −0.28 | 0.88 | 0.24 | −0.54 |
| … | … | … | … | ... | ... | … | … | ... |
| −0.93 | 0.03 | −0.49 | −0.93 | ... | −0.74 | −0.05 | −0.99 | 1.00 |
| −0.93 | 0.24 | −0.49 | −0.93 | ... | −0.62 | −0.08 | −0.99 | 0.99 |
| −0.7 | 0.22 | −0.49 | −0.93 | ... | −0.35 | 0.89 | −0.99 | 0.98 |
| −0.34 | 0.28 | −0.29 | −0.95 | ... | −0.74 | −0.05 | −0.99 | 0.92 |
| Factors Affecting of the Climbing Phase | IMF Number of Components/Piece | Remaining Number of Components/Piece |
|---|---|---|
| Mach number | 10 | 1 |
| Vertical velocity | 11 | 1 |
| Pressure altitude | 10 | 1 |
| Longitudinal acceleration | 10 | 1 |
| Airspeed | 10 | 1 |
| Ground speed | 11 | 1 |
| Bank angle | 9 | 1 |
| Total | 71 | 7 |
| Factors Affecting Cruise Phase | IMF number of Components/Piece | Remaining Number of Components/Piece |
|---|---|---|
| Vertical velocity | 9 | 1 |
| Airplane weight | 8 | 1 |
| Pressure altitude | 9 | 1 |
| Longitudinal acceleration | 10 | 1 |
| Airspeed | 8 | 1 |
| Bank angle | 9 | 1 |
| Wind speed | 10 | 1 |
| Wind direction | 8 | 1 |
| Total | 71 | 8 |
| Factors Influencing the Decline Stage | IMF Number of Components/Piece | Remaining Number of Components/Piece |
|---|---|---|
| Mach number | 7 | 1 |
| Vertical velocity | 8 | 1 |
| Pressure altitude | 7 | 1 |
| Longitudinal acceleration | 8 | 1 |
| Airplane weight | 7 | 1 |
| Bank angle | 8 | 1 |
| Wind speed | 7 | 1 |
| Wind direction | 8 | 1 |
| Total | 60 | 8 |
| Model | MAE | RMSE | R2 |
|---|---|---|---|
| LSTM | 20.9576 | 25.9763 | 0.95001 |
| PSO-LSTM | 20.3879 | 25.3159 | 0.95146 |
| CEEMDAN-KPCA-PSO-LSTM | 17.3672 | 23.6483 | 0.96731 |
| CEEMDAN-KPCA-DMPSO-LSTM | 14.1574 | 17.3145 | 0.97165 |
| Model | MAE | RMSE | R2 |
|---|---|---|---|
| LSTM | 21.9853 | 26.4680 | 0.95942 |
| PSO-LSTM | 20.9731 | 25.8921 | 0.96132 |
| CEEMDAN-KPCA-PSO-LSTM | 18.3626 | 23.6528 | 0.96891 |
| CEEMDAN-KPCA-DMPSO-LSTM | 15.3752 | 18.3682 | 0.97312 |
| Model | MAE | RMSE | R2 |
|---|---|---|---|
| LSTM | 22.9428 | 24.0616 | 0.95998 |
| PSO-LSTM | 22.3781 | 23.7652 | 0.96316 |
| CEEMDAN-KPCA-PSO-LSTM | 20.0219 | 21.8924 | 0.97012 |
| CEEMDAN-KPCA-DMPSO-LSTM | 19.6724 | 19.2792 | 0.97987 |
| Model | MAE | RMSE | R2 |
|---|---|---|---|
| BP | 24.0872 | 31.4789 | 0.89685 |
| RNN | 22.3257 | 28.3695 | 0.91465 |
| CEEMDAN-KPCA-DMPSO-LSTM | 14.1574 | 17.3145 | 0.97165 |
| Model | MAE | RMSE | R2 |
|---|---|---|---|
| BP | 28.1542 | 34.5732 | 0.90347 |
| RNN | 25.4379 | 31.4635 | 0.92578 |
| CEEMDAN-KPCA-DMPSO-LSTM | 15.3752 | 18.3682 | 0.97312 |
| Model | MAE | RMSE | R2 |
|---|---|---|---|
| BP | 26.3580 | 33.4637 | 0.91615 |
| RNN | 24.4732 | 27.3468 | 0.93575 |
| CEEMDAN-KPCA-DMPSO-LSTM | 19.6724 | 19.2792 | 0.97987 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xiong, J.; Zou, C.; Wan, Y.; Sun, Y.; Yu, G. Fuel Consumption Prediction for Full Flight Phases Toward Sustainable Aviation: A DMPSO-LSTM Model Using Quick Access Recorder (QAR) Data. Sustainability 2025, 17, 3358. https://doi.org/10.3390/su17083358
Xiong J, Zou C, Wan Y, Sun Y, Yu G. Fuel Consumption Prediction for Full Flight Phases Toward Sustainable Aviation: A DMPSO-LSTM Model Using Quick Access Recorder (QAR) Data. Sustainability. 2025; 17(8):3358. https://doi.org/10.3390/su17083358
Chicago/Turabian StyleXiong, Jing, Chunling Zou, Yongbing Wan, Youchao Sun, and Gang Yu. 2025. "Fuel Consumption Prediction for Full Flight Phases Toward Sustainable Aviation: A DMPSO-LSTM Model Using Quick Access Recorder (QAR) Data" Sustainability 17, no. 8: 3358. https://doi.org/10.3390/su17083358
APA StyleXiong, J., Zou, C., Wan, Y., Sun, Y., & Yu, G. (2025). Fuel Consumption Prediction for Full Flight Phases Toward Sustainable Aviation: A DMPSO-LSTM Model Using Quick Access Recorder (QAR) Data. Sustainability, 17(8), 3358. https://doi.org/10.3390/su17083358






