A Novel Method for Estimating Soil Organic Carbon Density Using Soil Organic Carbon and Gravel Content Data

Abstract

Soil organic carbon density (SOCD) is crucial for assessing soil organic carbon (SOC) storage, but its estimation remains challenging when bulk density (BD) data are unavailable. Traditional methods for substituting missing BD data, including using the mean, median, and pedotransfer functions (PTFs), introduce varying degrees of uncertainty in SOCD estimation: (1) The mean and median methods ignore the effects of soil type, environmental conditions, and land use changes on BD. They also heavily rely on the representativeness of soil samples, which may lead to systematic bias. (2) The accuracy of PTFs depends on modeling approaches, variable selection, and dataset characteristics, and differences among PTFs may introduce estimation biases in SOCD. To overcome this challenge, we analyzed 443 soil profiles from the Yangtze River Delta region of China and developed an innovative approach that estimates SOCD using only SOC and gravel content data. By formulating linear, polynomial, and power function regression models, we directly estimated SOCD per centimeter of soil horizon i (SOCD_icm) under conditions with and without available gravel content data, followed by SOCD calculation. The results indicated a strong correlation between SOC and SOCD_icm, with the three function models for direct SOC-based SOCD_icm estimation yielding consistently high accuracy. Neglecting gravel content overall resulted in the overestimation of SOCD_icm by 7.01–9.45%. After incorporating gravel content as a correction factor, the accuracy of the new method for estimating SOCD was improved, with the prediction set achieving R² values of 0.927–0.945, an RMSE of 0.819–0.949 kg m⁻², and an RPIQ of 4.773–5.533. The accuracy of estimating SOCD surpassed that of the BD mean and median methods and was comparable to that of the PTF method, thus enabling reliable SOCD estimation. This study introduces an innovative approach by developing regional models to estimate SOCD_icm, enabling rapid SOCD estimation for samples with missing BD information in historical data, and provides a new methodology for calculating regional and global SOC stocks. This study contributes to improving the accuracy of soil carbon stock estimation, supporting land management and carbon cycle research, and providing scientific evidence for sustainable agricultural development and climate change mitigation strategies.

1. Introduction

Soil organic carbon (SOC) is one of the most crucial components of soil resources [1]. The global stock of SOC within the top 1 m of soil is 2–3 times greater than that of atmospheric and vegetation carbon stocks. Consequently, even minor fluctuations in SOC can substantially influence the global carbon cycle [2]. Soil organic carbon density (SOCD) is a standard metric for characterizing SOC stocks [3]. Precisely estimating SOCD is crucial in effectively depicting regional carbon cycling processes. SOCD estimations can act as a valuable dataset for land management decisions, holding substantial importance in regulating soil carbon sequestration and rational soil resource utilization [4,5]. Additionally, statistical data on SOCD are crucial for studying greenhouse gas fluxes between soil and the atmosphere, the impacts of different land use practices on soil quality, and the evolution of land quality [6]. Therefore, accurately estimating SOCD, as the primary challenge in determining SOC stocks, has become a crucial foundation and key aspect of contemporary global terrestrial carbon cycling research [7]. Soil bulk density (BD) is a pivotal parameter for accurately calculating SOCD. However, extensive measurements of BD are labor-intensive, time-consuming, and often impractical [8], leading to the widespread absence of soil BD data in most global soil databases [9], engendering significant challenges to research on SOCD, SOC stocks, and related investigations. BD has been considered one of the critical sources of error in estimating large-scale SOC stocks [10]. Soil gravel, typically referring to mineral particles with a diameter between 2 and 75 mm, is an important element in the calculation of SOCD. Variations in gravel content over time and space, even small changes, can have a significant impact on the accurate estimation of soil carbon stocks [11]. The accurate measurement of BD is crucial for the sustainable management of soil resources [12], while gravel, by occupying soil volume and owing to its low-density characteristics, affects the precision of BD measurement, thereby influencing the accuracy of SOCD estimation. As the gravel content increases, the number of fine soil particles per unit volume decreases, and the continuous input of low-density organic matter and moisture into fine soil leads to a reduction in soil BD [13].

To overcome the challenges arising from the absence of BD data, it is customary to substitute measured BD values with the mean or median BD values from databases [14,15,16] or to utilize pedotransfer functions (PTFs) for indirect BD predictions [17,18,19,20,21]. However, these substitution methods also introduce uncertainties in the estimation of SOCD and SOC stocks, and the accuracy of these PTFs is not consistently satisfactory. Traditional PTF methods require predicting BD first and then calculating SOCD based on the predicted BD, which may lead to error accumulation and propagation. Khalil [22], Khan [23], and Xu [24] successfully employed BD PTFs to estimate SOCD or SOC stocks with high accuracy. Nonetheless, these studies did not systematically compare the precision of different BD PTFs and the accuracy of SOCD estimation. Additionally, the underlying factors for the successful application of BD PTFs in SOCD estimation remain unexplored. Meanwhile, traditional PTF methods rarely specifically consider the impact of gravel content on SOCD. Contemporary research indicates that SOC is the most critical and frequently employed attribute for constructing PTFs [9,25]. Consequently, utilizing SOC to establish BD PTFs for SOCD estimation essentially involves estimating SOCD through SOC and gravel content. Moreover, when the gravel content of the majority of soil samples in a study is low, the impact of gravel content on SOCD is minimal [26]. Hence, we present a novel inquiry: can SOC and gravel content be utilized as predictor variables to directly and accurately estimate SOCD in the absence of BD data? Compared to PTF methods, this approach eliminates the need for additional BD prediction, simplifies the calculation process, reduces potential sources of error, and explicitly considers the impact of gravel content on SOCD.

To our knowledge, no research has directly employed SOC and gravel content to estimate SOCD. In light of this, we utilized data from Chinese soil surveys and collected soil profile samples (0–100 cm) from Jiangsu, Zhejiang, and Anhui provinces and Shanghai Municipality in the Yangtze River Delta region of China. Models were established based on traditional BD substitution methods (BD mean and median methods, PTF method), as well as SOC and gravel content, to estimate SOCD per centimeter of soil horizon i (SOCD_icm). The specific objectives of this study are as follows: (1) To propose a new method for estimating SOCD that achieves high precision without the need for predicted BD data; (2) To evaluate the estimation accuracy of the new method under two different conditions and validate the estimation capabilities of three direct SOCD_icm estimation models utilizing SOC, as well as models with gravel content as a correction factor; and (3) To compare the novel method with traditional BD substitution methods, analyzing its advantages in estimation accuracy and applicability.

2. Materials and Methods

2.1. Study Area and Data Sources

The study area is located in the entirety of Jiangsu Province, Anhui Province, Zhejiang Province, and Shanghai Municipality in the Yangtze River Delta region of China (27°02′–35°20′ N, 114°54′–123°10′ E) (Figure 1). Situated in the subtropical monsoon climate and temperate monsoon climate zone, with an average annual temperature ranging from 13.6 to 18.1 °C, the area experiences distinct seasonal variations with concurrent rainfall and heat. The terrain is predominantly low and flat and crisscrossed by numerous rivers and supports a thriving agricultural sector primarily focused on crops such as rice, cotton, rapeseed, sugarcane, and tea.

The data for this study originate from the systematic survey results of soil taxa and soil series based on the Chinese Soil Taxonomy system. Specifically, the data were sourced from the volumes of the “Soil Series of China” series dedicated to Jiangsu Province [27], Zhejiang Province [28], Anhui Province [29], and Shanghai Municipality [30]. The soil profile surveys were conducted from 2009 to 2013. The “Soil Series of China” was compiled through a decade-long systematic investigation conducted by the Institute of Soil Science, Chinese Academy of Sciences (ISSCAS), in collaboration with numerous universities and research institutions across China. The data were collected by the research team following a unified sampling protocol and field investigation standards and were complemented by laboratory soil sample analyses. The data also took into account soil types, distribution area, spatial uniformity, and intensively sampled points in typical regions, ensuring high data quality and strong representativeness. The database’s high reliability and systematic nature make it the most important source of soil survey information in China since the second national soil survey, and it has been widely applied in soil science and related fields of research [31,32,33]. The collected data provide detailed information about the soil conditions in the study area, including soil types, geographic locations, horizon divisions, organic matter content, texture, BD, pH, and the >2 mm gravel content of the soil profiles. After screening and processing, a total of 443 representative soil profiles were selected for analysis, comprising 143 profiles from Jiangsu Province, 114 from Anhui Province, 47 from Shanghai Municipality, and 139 from Zhejiang Province (Figure 1). These profiles cover nine soil orders according to the Chinese Soil Taxonomy [34], including Vertosols, Cambosols, Ferrosols, Isohumosols, Argosols, Gleyosols, Anthrosols, Primosols, and Halosols. Additionally, we provided a cross-reference table (Table S1) for the classification units of the sampled profiles in both the Chinese Soil Taxonomy (CST) and the World Reference Base for Soil Resources (WRB) [35]. A total of 1929 soil horizon samples were collected from the 443 profiles.

At each sampling site, undisturbed soil cores were collected from the center of each soil horizon using standard sharpened steel cylinders of 100 cm³ volume (5.05 cm diameter, 5 cm height), with three replicates taken from each soil horizon to measure soil BD. At the same time, disturbed soil samples weighing approximately 2–3 kg were collected from each horizon using individual plastic or cloth bags to determine soil particle composition and organic carbon content.

The undisturbed soil core samples were weighed in the field and then brought back to the laboratory for drying in a 105 °C oven until constant weight (>48 h). The dried soil blocks inside the steel cylinders were weighed, and then they were sieved through a 2 mm mesh, after which the portion > 2 mm was weighed. The soil BD values were calculated, i.e., the mass of an oven-dried sample of undisturbed soil per unit bulk volume [36], using the following formula [37]:

$$BD={\displaystyle \frac{W_c-W_g}{V-W_g/2.65}}$$

(1)

where $BD$ represents the bulk density of the soil (<2 mm fine earth fraction) (g cm⁻³); $W_c$ represents the oven-dry weight of the soil block inside the steel cylinder (g); $W_g$ represents the dry weight of the gravel inside the steel cylinder (g); $V$ represents the volume of the steel cylinder (cm³); $W_g/2.65$ denotes the volume of the gravel inside the steel cylinder (cm³), where 2.65 is the specific gravity of gravel (g cm⁻³) [38].

Before the analysis of soil chemical properties, disturbed soil samples were spread out on trays to remove plant roots, stems, and other intrusive materials such as bricks and tiles. The samples were air-dried at 30–35 °C and then crushed and sieved. Soil particle composition was determined using the pipette method, and according to the USDA soil classification system, soil texture is classified into three fractions: clay (<0.002 mm), silt (0.002–0.05 mm), and sand (0.05–2 mm). SOC content was measured using the potassium dichromate–sulfuric acid digestion method [39].

2.2. SOCD Calculation

SOCD refers to the stock of SOC in a unit area (1 m² or 1 hm²) and a specific depth (typically 1 m) of the soil horizon. Equation (2) is used to compute SOCD_icm (kg m⁻²) for each horizon within a soil profile, representing the stock of SOC within a 1 cm thick layer per unit area:

$${SOCD}_{icm}={SOC}_i\times {BD}_i\times (1 - C_i/100)/100$$

(2)

The SOCD of soil horizon i (SOCD_i) (kg m⁻²) can be calculated using Equation (3) (assuming that the SOCD_icm value per centimeter is consistent within the soil horizon):

$${SOCD}_i=D_i\times {SOCD}_{icm}$$

(3)

The SOCD within a soil profile (kg m⁻²) can be calculated using Equation (4):

$$SOCD =\sum _{i=1}^n{SOCD}_i$$

(4)

where n represents the number of soil horizons, SOC_i denotes the SOC content (g kg⁻¹) of soil horizon i, BD_i is the soil bulk density (g cm⁻³) of soil horizon i, D_i stands for the thickness (cm) of soil horizon i, C_i represents the content of gravel (>2 mm) in the soil sample for that horizon (%), and 100 is a unit conversion factor.

2.3. SOCD Estimation

2.3.1. The Novel Method Proposed in This Paper

Considering the availability of gravel content data, two new methods were employed in this study to estimate SOCD.

Method one: When gravel content data were missing, linear, polynomial, and power function regression models were separately established for SOC and SOCD_icm. The specific formulas are as follows:

$${SOCD}_{icm}=\mathrm{a}\times {SOC}_i+\mathrm{b}$$

(5)

$${SOCD}_{icm}=\mathrm{a}\times {{SOC}_i}^2+\mathrm{b}\times {SOC}_i+\mathrm{c}$$

(6)

$${SOCD}_{icm}=\mathrm{a}\times {{SOC}_i}^{\mathrm{b}}$$

(7)

Method two: When gravel content data were available, they were utilized as a correction factor. Linear, polynomial, and power function regression models were separately established for SOC, gravel content, and SOCD_icm. The specific formulas are as follows:

$${SOCD}_{icm}=(\mathrm{a}\times {SOC}_i+\mathrm{b})\times (1 - Ci/100)$$

(8)

$${SOCD}_{icm}=(\mathrm{a}\times {{SOC}_i}^2+\mathrm{b}\times {SOC}_i+\mathrm{c})\times (1 - Ci/100)$$

(9)

$${SOCD}_{icm}=(\mathrm{a}\times {{SOC}_i}^{\mathrm{b}})\times (1 - Ci/100)$$

(10)

where a, b, and c are calibration coefficients.

These regression models intuitively describe the mathematical relationships between SOC, gravel content, and SOCD_icm. The linear regression model is the most basic, making it suitable for simple linear relationships. The polynomial regression model can capture potential nonlinear relationships, making it suitable for more complex data distributions. The power function regression model is particularly useful for describing power law relationships between variables, especially in cases of nonlinear growth or decay trends. These three models are easy to interpret, computationally efficient, and capable of covering a range of relationships from simple linear to complex nonlinear. They provide a reliable mathematical foundation for SOCD estimation, with parameters that are easy to calibrate, offering high practicality and operability.

SOCD_i can be obtained by multiplying SOCD_icm by the thickness of soil horizon i, denoted as D_i (Equation (3)).

In a soil profile with n soil horizons, the total SOCD of the profile is obtained by summing the SOCD_i of each horizon (Equation (4)).

Equations (3)–(10) demonstrate that if SOC can be used to estimate SOCD_icm accurately, it would enable the calculation of precise SOCD.

2.3.2. Traditional BD Substitution Methods

To validate the accuracy advantage of the proposed method in SOCD estimation, we designed a comparative experiment using eight traditional BD substitution methods (including a mean method, a median method, and six PTFs) as references (

Table 1. Methods used to estimate soil BD.

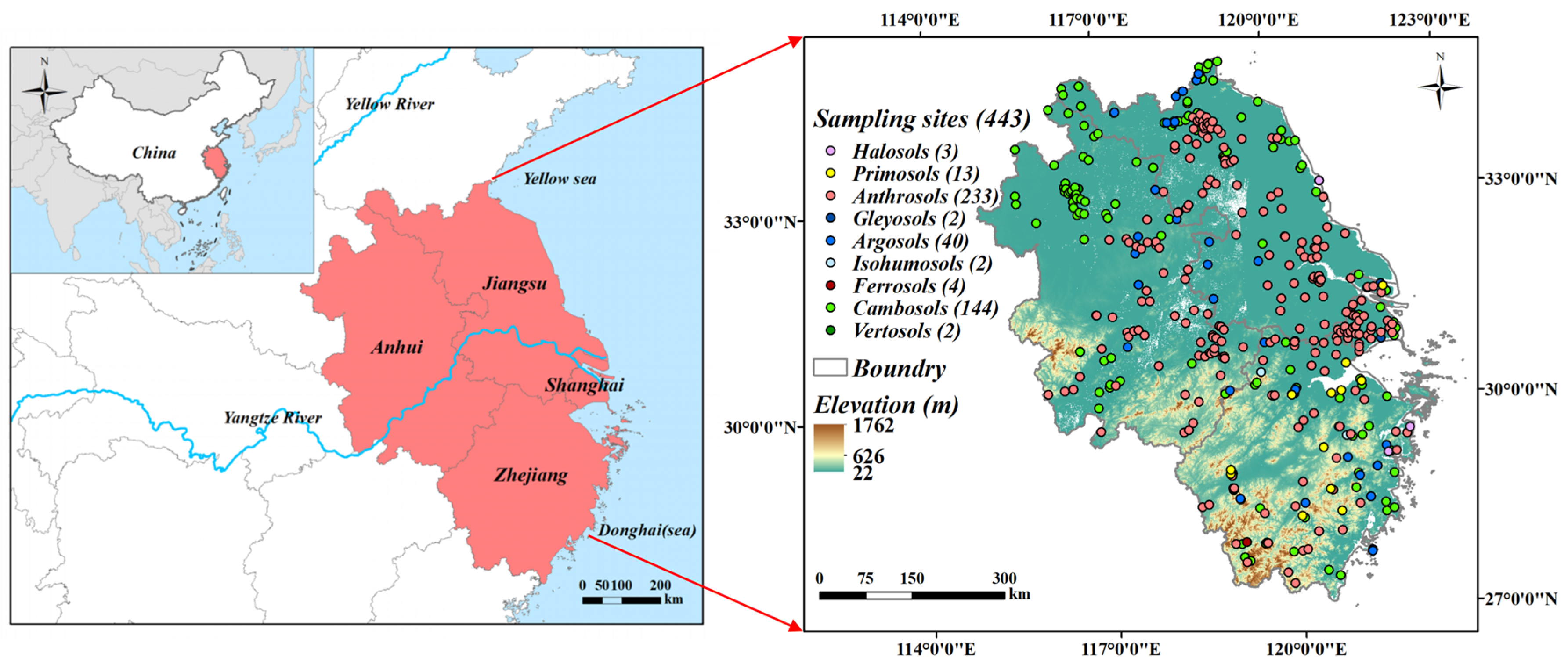
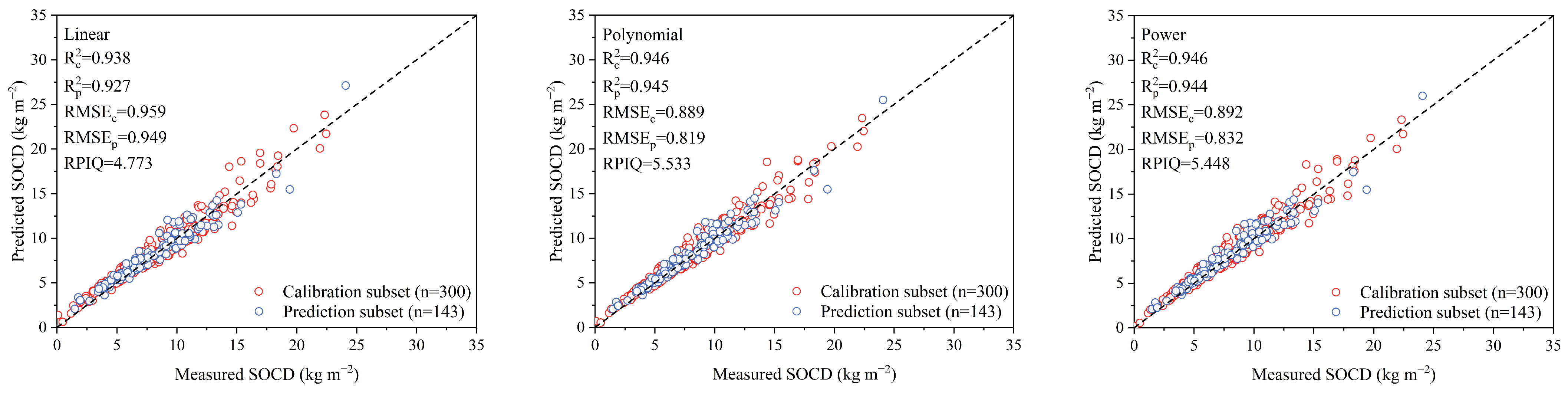
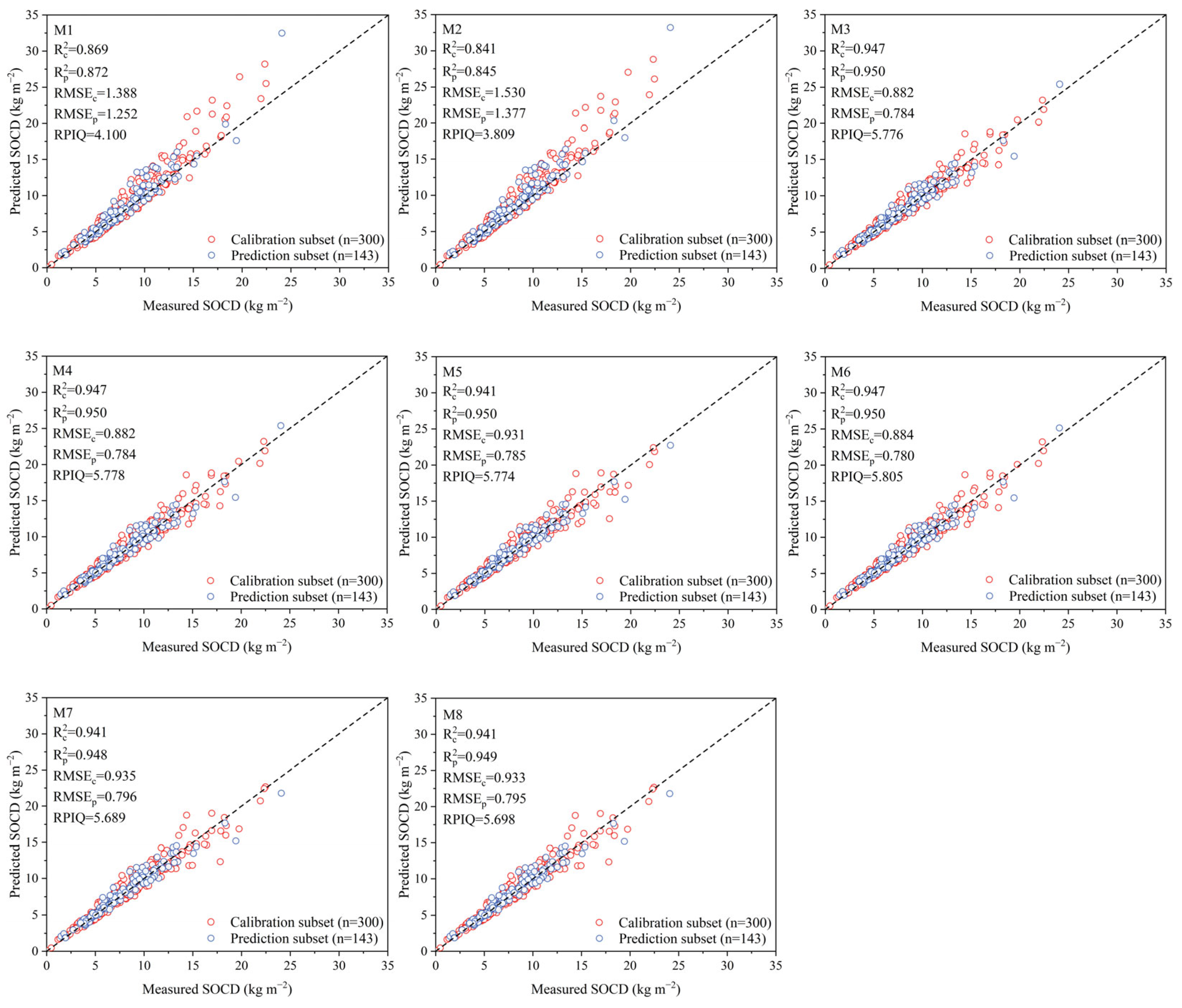
Method No.	Method Description			Reference
	Approaches	Investigated Soils	Estimating Bulk Density (BD, g cm−3)
M1	Mean method	varying soils in this study area	Mean value of horizon samples in this study
M2	Median method	varying soils in this study area	Median value of horizon samples in this study
M3	PTFs	forest soils in New Hampshire	$\ln \left(\mathrm{BD}\right)=\mathrm{a}+\mathrm{bln}\left(\mathrm{SOM}\right)+\mathrm{c}{[\ln \left(\mathrm{SOM}\right)]}^2$	[41]
M4	PTFs	forest soils in New Hampshire	$\ln \left(\mathrm{BD}\right) =\mathrm{a}+\mathrm{bln}\left(\mathrm{SOC}\right)+\mathrm{c}{[\ln \left(\mathrm{SOC}\right)]}^2$	[41]
M5	PTFs	varying soils in continental USA, Hawaii, Puerto Rico, and some foreign countries	$\mathrm{BD}=\mathrm{a}+\mathrm{b}(\mathrm{SOC})$	[42]
M6	PTFs	varying soils in continental USA, Hawaii, Puerto Rico, and some foreign countries	$\mathrm{BD}=\mathrm{a}+\mathrm{b}{(\mathrm{SOC}}^{0.5})$	[42]
M7	PTFs	varying soils in Hebei Province	$\mathrm{BD}=\mathrm{a}+\mathrm{b}\left(\mathrm{SOC}\right)+\mathrm{c}\left(\mathrm{silt}\right)+\mathrm{d}(\mathrm{clay})$	[43]
M8	PTFs	arid soils in Amman–Zarqa basin	$\mathrm{BD}=\mathrm{a}+\mathrm{b}\left(\mathrm{SOC}\right)+\mathrm{c}\left(\mathrm{clay}\right)+\mathrm{d}\left(\mathrm{silt}\right)+\mathrm{e}(\mathrm{sand})$	[44]

Note: M1 to M8 is an abbreviation for Method 1 to Method 8.

). M1 and M2, respectively, used the mean and median of measured BD values for estimation. Experience has shown that SOC or soil organic matter (SOM) and soil texture are the main factors determining soil BD. Based on SOC or SOM and texture data, numerous attempts have been made to estimate soil BD using PTFs [40]. We selected six commonly used PTFs for estimating BD, denoted as M3, M4, M5, M6, M7, and M8. Among them, M3 to M6 were established based on the relationship between BD and SOC/SOM to estimate BD, while M7 and M8 used SOC and soil texture as independent variables for BD estimation. Subsequently, the estimated BD values obtained above were used in Equation (2) to calculate the SOCD_icm values, which were further calculated from Equations (3) and (4) to obtain SOCD values. By comparing the estimation results of these traditional methods with those of the proposed method, we comprehensively assessed the applicability and accuracy of the new approach, highlighting its advantages in SOCD estimation.

2.4. Data Splitting

The dataset was divided on a complete profile basis, with 300 profiles (approximately 67.72%) randomly selected as the calibration set (including 1309 soil horizon samples), while the remaining 143 profiles (approximately 32.28%) were allocated as the prediction set (including 620 soil horizon samples). Within the profiles of the calibration set, models were established using all soil horizon samples. Subsequently, the constructed models were validated for their predictive capability on independent samples from the soil horizons of the prediction set profiles. All calibration and prediction processes were carried out in MATLAB 2022a (MathWorks Inc., Natick, MA, USA).

2.5. Evaluation of Model Performance

In this article, the predictive models were evaluated through three statistical metrics calculated between the predicted values and the measured values: the root mean square error (RMSE), coefficient of determination (R²), and the ratio of performance to interquartile distance (RPIQ).

The lower the RMSE, the closer the R² is to 1, and the higher the RPIQ, the better the model. The coefficient of determination and root mean square error for the calibration set are denoted as R_c² and RMSE_C, respectively, while for the prediction set, they are R_p² and RMSE_P. The RPIQ is the ratio of IQ to RMSE_P, where IQ represents the interquartile range (IQR) of the measured values, which is the difference between the third quartile (Q₇₅) and the first quartile (Q₂₅) of the sample values; in other words, it is the range where values fall between 25% and 75% of the ordered data. The RPIQ, an improvement over RPD in model evaluation, overcomes the bias from non-normal data distributions by considering quartile differences [45,46,47].

2.6. Statistical Analysis

The correlations between soil properties were discerned using Spearman correlation analysis and partial correlation analysis. The assumption of normality in the data was tested using the Kolmogorov–Smirnov (K–S) test. For non-normally distributed original data, the Kruskal–Wallis H test was employed to test for significant differences (p < 0.05). Further intergroup differences were analyzed using the Bonferroni multiple mean comparison method (p < 0.05). The aforementioned data analysis procedures were performed using OriginPRO 2021, SPSS (IBM Version 21, Chicago, IL, USA), and R version 4.3.1 [48]. The partial correlation coefficients were computed using the R package ppcor [49]. The relative deviation of SOCD_icm obtained from the measured method and the new method proposed in this study was calculated to explore the impact of gravel content on SOCD. The relative deviation was calculated by taking the absolute difference between the two sets of data, dividing it by the sum of the two sets of data, and then multiplying by 100%. This calculation process was performed in MATLAB 2022a (MathWorks Inc., MA, USA).

3. Results

3.1. The Basic Statistics of the Dataset

Descriptive statistics were calculated for soil properties on all samples and the calibration and prediction sets (

Table 2. Descriptive statistics for soil properties.

Variables	Min	Max	Mean	SD	CV	Skew	Kurt
Whole set (m = 1929)
BD	0.58	1.80	1.37	0.19	14	−0.48	−0.23
SOC	0.06	52.37	7.87	6.76	86	1.87	5.02
SOCDicm	0.0009	0.4926	0.0967	0.0720	74	1.40	2.50
SOCD (n = 443)	0.08	24.07	8.21	3.75	46	0.93	1.57
Sand	1.00	950.00	298.81	200.63	67	0.70	−0.33
Silt	17.05	913.00	466.48	182.70	39	−0.08	−0.79
Clay	10.00	666.00	234.75	119.99	51	0.53	−0.10
Calibration subset (m = 1309)
BD	0.58	1.80	1.37	0.19	14	−0.44	−0.39
SOC	0.06	52.37	8.09	6.96	86	1.86	5.04
SOCDicm	0.0009	0.4926	0.0993	0.0740	75	1.40	2.42
SOCD (n = 300)	0.08	22.44	8.43	3.84	46	0.81	1.12
Sand	1.00	918.00	292.84	198.41	68	0.71	−0.31
Silt	21.00	913.00	469.63	184.25	39	−0.05	−0.84
Clay	10.00	659.00	237.60	120.20	51	0.42	−0.36
Prediction subset (m = 620)
BD	0.62	1.76	1.36	0.18	13	−0.59	0.20
SOC	0.12	43.66	7.40	6.31	85	1.87	4.67
SOCDicm	0.0018	0.4295	0.0911	0.0672	74	1.38	2.52
SOCD (n = 143)	1.48	24.07	7.75	3.51	45	1.21	3.12
Sand	20.00	950.00	311.42	204.81	66	0.68	−0.37
Silt	17.00	895.00	459.83	179.36	39	−0.16	−0.68
Clay	21.00	666.00	228.74	119.42	52	0.77	0.55

Note: Min: minimum; Max: maximum; SD: standard deviation; CV: coefficient of variation, %; Skew: skewness; Kurt: kurtosis; BD: bulk density, g cm⁻³; SOC: soil organic carbon, g kg⁻¹; SOCD_icm: SOC density per centimeter of soil horizon i, kg m⁻²; SOCD: SOC density, kg m⁻²; Sand: 0.05–2 mm, g kg⁻¹; Silt: 0.002–0.05 mm, g kg⁻¹; Clay: <0.002 mm, g kg⁻¹; m: the number of soil horizon samples; n: the number of soil profiles.

). Overall, BD ranged from 0.58 to 1.80 g cm⁻³, with a mean of 1.37 g cm⁻³ and a standard deviation of 0.19 g cm⁻³. BD exhibited the lowest variation (14%) compared to other soil variables. The SOC content was relatively low, with an average of 7.87 g kg⁻¹ and the highest variation (CV = 86%), ranging from 0.06 to 52.37 g kg⁻¹. The heterogeneity of SOCD_icm, calculated based on measured BD values, was 74%, second only to that of SOC. The profile SOCD was calculated using Equation (4), ranging from a maximum of 24.07 kg m⁻² to a minimum of only 0.08 kg m⁻², with a standard deviation of 3.75 kg m⁻². Data follow a normal distribution when skewness and kurtosis are both 0. However, SOC, SOCD_icm, SOCD, sand, and clay exhibited positive skewness and either leptokurtic or platykurtic distributions, while BD and silt displayed negative skewness. This suggests that the soil property data have a non-normal distribution. Similar statistical values were observed for various soil properties in the calibration, prediction, and overall datasets, indicating a fairly even data distribution between the two sets.

3.2. Correlation Analysis

The correlation analysis results indicated that BD was significantly correlated with SOC, SOCD_icm, sand, and clay at the 0.001 level while showing a weak correlation with silt (p > 0.05). The relationship between BD and SOC was the closest, and BD was also closely associated with soil texture. SOCD_icm was significantly negatively correlated with BD and sand but significantly positively correlated with SOC, silt, and clay. The highest correlation was observed between SOC and SOCD_icm (r = 0.976), followed by that between sand and silt (r = −0.799), BD and SOC (r = −0.553), sand and clay (r = −0.431), and BD and SOCD_icm (r = −0.410). From the correlation analysis results, it is evident that the correlation between SOC and SOCD_icm is more robust than that between BD and SOC, as well as soil texture. This suggests that predictive models established based on SOC and SOCD_icm might exhibit higher accuracy than BD PTFs developed with SOC and soil texture as independent variables.

Due to the significant correlation between SOC and BD (r = −0.553), it was necessary to compute the partial correlation coefficients of SOCD_icm with both SOC and BD. After removing the influence of SOC, the correlation between BD and SOCD_icm underwent a significant change. The correlation coefficient between BD and SOCD_icm shifted from −0.410 to 0.715, indicating that the correlation was enhanced and changed from negative to positive. After eliminating the effects of BD, the correlation between SOC and SOCD_icm remained significantly positive, and the correlation coefficient increased from 0.976 to 0.986.

3.3. The Direct Estimation of SOCD Based on the Novel Method

3.3.1. Estimation Results of SOCD_icm Without Considering Gravel Content

We generated a scatter plot of SOC against the measured SOCD_icm using the calibration set and performed separate fittings using linear, polynomial, and power functions (Figure 2). All three function fittings resulted in R² values surpassing 0.91, indicating a robust functional relationship between SOC and SOCD_icm. Interestingly, the results demonstrated that the outcomes of the nonlinear fitting slightly outperformed those of the linear fitting.

The prediction set SOC values were employed to generate predicted SOCD_icm values using the three models above. A scatter plot (Figure 3) was constructed to compare the predicted SOCD_icm values from the prediction set with the actual measured SOCD_icm values. The SOCD_icm predictions from all three regression models exhibited favorable alignment with the actual measured values (R_p² > 0.9), albeit demonstrating a certain degree of underestimation for low values and overestimation for high values. The polynomial regression model showed the highest prediction accuracy, with R_p² and RMSE_P values of 0.919 and 0.019 kg m⁻², respectively, and an RPIQ value of 4.357. Comparatively, the predictive accuracy of the linear regression model and power function regression model was inferior to that of the polynomial regression model. Furthermore, the results of these two models were comparable, with R_p² values of 0.901 and 0.911 and RPIQ values of 3.929 and 3.942, respectively. The above results indicated that utilizing SOC enables a highly effective direct prediction of SOCD_icm.

A thorough analysis of the significance of differences was conducted on the predicted outcomes of the three fitting methods to assess whether significant differences exist in the predictive capabilities of the three distinct fitting models. The results (Figure 4) indicated that there were no statistically significant differences (p > 0.05) in the estimated SOCD_icm values obtained from the three fitting methods, implying comparable predictive accuracy across the models. Moreover, the estimated SOCD_icm values from all three models aligned closely with the measured values, demonstrating high prediction accuracy and reliability.

3.3.2. Estimation Results of SOCD Without Considering Gravel Content

The profile SOCD was calculated from the SOCD_icm estimated by the three models in the calibration and prediction sets (Equations (3) and (4)). Scatter plots (Figure 5) were generated to compare the estimated SOCD with the actual measured SOCD. The three established models could all be employed for SOCD estimation, with R_c² ranging from 0.860 to 0.877; R_p² ranging from 0.869 to 0.893; RMSE_C and RMSE_P varying between 1.346 and 1.434 kg m⁻² and 1.147 and 1.270 kg m⁻², respectively; and RPIQ ranging from 3.568 to 3.948. The polynomial regression model exhibited superior results (the highest R_c², R_p², and RPIQ values, as well as the smallest RMSE_C and RMSE_P). The linear regression model demonstrated higher modeling precision than the power function regression model, although its validation accuracy was relatively lower. While the calibration set results tended to underestimate lower values, this phenomenon was less pronounced in the prediction set. These outcomes suggest that the SOCD_icm predictions derived from SOC can be effectively utilized for profile SOCD calculations, yielding favorable results.

The significance analysis of the differences indicated no significant variation in estimated SOCD among different models (p > 0.05). The SOCD values estimated from the three models were not significantly higher or lower than the measured SOCD values; thus, these models demonstrated similar accuracy in SOCD estimation (Figure 6).

3.3.3. The Impact of Gravel Content on the Estimation of SOCD_icm

Dividing soil sample data based on gravel content, the discrepancies between the measured values of SOCD_icm and the estimated values obtained from three modeling methods generally increased with an increase in gravel content (Figure 7). When the gravel content was less than 5%, there was no significant difference among the methods, and all three models slightly underestimated SOCD_icm. When the gravel content was between 5% and 30%, the differences between the measured values of SOCD_icm and the estimates from the three models were not significant, and the underestimation phenomenon transitioned to overestimation. Conversely, when the gravel content was greater than or equal to 30%, the discrepancies between the results of the three modeling methods and the measured values were considerable (Figure 7).

The systematic errors of the three new models in estimating SOCD_icm are represented by the relative deviation between the estimated values and the measured results. In the highest gravel content category (≥30% gravel content) of soil samples, the linear regression model exhibited the largest deviation, with an average overestimation of SOCD_icm by 34.77%, while the polynomial and power function regression models overestimated by 32.84% and 33.78%, respectively (

Table 3. Proportion of different gravel content levels and average relative deviation of SOCD_icm estimated by different modeling methods compared to measured SOCD_icm values.

Gravel Content (%)	Frequency (%)	Average Relative Deviation from Measured SOCDicm Values
	0–100 cm	Linear	Polynomial	Power
<5	76.72	7.34	5.19	4.93
5–10	9.49	9.12	6.96	6.95
10–15	5.39	15.12	11.41	10.46
15–20	2.38	14.74	12.79	13.24
20–25	1.56	19.57	16.49	17.06
25–30	0.88	27.18	23.39	24.50
≥30	3.58	34.77	32.84	33.78
total		9.45	7.20	7.01

). In this study, the gravel content of most soil horizons (76.72%) was less than 5%, with those without gravel content accounting for 62.52% of the total. Overall, disregarding gravel content resulted in an overestimation of SOCD_icm by 7.01–9.45% (Table 3).

3.3.4. The Estimation Results of SOCD_icm with Gravel Content as a Correction Factor

Linear, polynomial, and power function regression models were separately established with SOC and gravel content as predictor variables, and the estimation ability of these models was verified. The results (

Table 4. The specific models and prediction results for estimating SOCD_icm based on SOC and gravel content.

Model	Function	Calibration Subset (m = 1309)		Prediction Subset (m = 620)
		Rc2	RMSEC (kg m−2)	Rp2	RMSEP (kg m−2)	RPIQ
Linear	${SOCD}_{icm}=(0.011{SOC}_i+0.016)\times (1 - C_i/100)$	0.950	0.017	0.935	0.017	4.852
Polynomial	${SOCD}_{icm}=(-7.312\times {10}^{-5}{{SOC}_i}^2+0.013{SOC}_i+0.008)\times (1-C_i/100)$	0.957	0.015	0.947	0.016	5.381
Power	${SOCD}_{icm}=(0.019{{SOC}_i}^{0.841})\times (1-C_i/100)$	0.958	0.015	0.947	0.015	5.397

Note: m represents the number of soil horizon samples.

, Figure 2 and Figure 3) indicated that considering gravel content improved the accuracy of the SOCD_icm estimation models, with an increase in R² ranging from 0.028 to 0.036 and RPIQ reaching 4.852 to 5.397. The power function regression model exhibited the strongest estimation capability for SOCD_icm, followed by the polynomial regression model, while the linear regression model had the poorest estimation capability. There were minimal differences in the SOCD_icm estimation results among different modeling methods (Figure 8), and no significant discrepancies were observed compared to the measured values, indicating that the model predictions are reasonably reliable.

3.3.5. The Estimation Results of SOCD with Gravel Content as a Correction Factor

The SOCD_icm values estimated by the three models using the calibration and prediction subsets were used to calculate the profile SOCD (Equations (3) and (4)). Scatter plots of the estimated SOCD against the measured SOCD were drawn (Figure 9). The SOCD estimation values obtained from all three models demonstrated good agreement with the measured values. The inclusion of gravel content data resulted in the predicted values being more concentrated and symmetrically distributed around the 1:1 line. Among the models, the polynomial regression model exhibited the best performance. The values of R_c² ranged from 0.938 to 0.946; R_p² ranged from 0.927 to 0.945; RMSE_C and RMSE_P varied between 0.889 and 0.959 kg m⁻² and 0.819 and 0.949 kg m⁻², respectively; and RPIQ ranged from 4.773 to 5.533. These results indicated that considering gravel content as a correction factor for estimating SOCD results in high precision and good performance. The SOCD estimation results from the three models were close to the true values, with no significant differences observed, demonstrating their ability to accurately estimate SOCD values (Figure 10).

3.4. Estimating SOCD Based on Traditional BD Substitution Methods

3.4.1. Estimation Results of BD Based on PTFs

The parameters of the six published PTFs in Table 1 were calibrated (

Table 5. Summary of revised PTFs defined in previous research.

Method No.	Function	Refitted Coefficients		Reference
		Estimate	s.e. of Estimate
M3	$\ln \left(\mathrm{BD}\right)=\mathrm{a}+\mathrm{bln}\left(\mathrm{SOM}\right)+\mathrm{c}{[\ln \left(\mathrm{SOM}\right)]}^2$	a = 1.5254	0.0159	[41]
		b = 0.0277	0.0138
		c = −0.0359	0.0031
M4	$\ln \left(\mathrm{BD}\right) =\mathrm{a}+\mathrm{bln}\left(\mathrm{SOC}\right)+\mathrm{c}{[\ln \left(\mathrm{SOC}\right)]}^2$	a = 1.5291	0.0104	[41]
		b = −0.0103	0.0107
		c = −0.0362	0.0032
M5	$\mathrm{BD}=\mathrm{a}+\mathrm{b}(\mathrm{SOC})$	a = 1.5059	0.0066	[42]
		b = −0.0165	0.0006
M6	$\mathrm{BD}=\mathrm{a}+\mathrm{b}{(\mathrm{SOC}}^{0.5})$	a = 1.6473	0.0109	[42]
		b = −0.1048	0.0038
M7	$\mathrm{BD}=\mathrm{a}+\mathrm{b}\left(\mathrm{SOC}\right)+\mathrm{c}\left(\mathrm{silt}\right)+\mathrm{d}(\mathrm{clay})$	a = 1.4343	0.0163	[43]
		b = −0.0165	0.0006
		c = 4.7978 × 10−5	2.3422 × 10−5
		d = 0.0002	3.5868 × 10−5
M8	$\mathrm{BD}=\mathrm{a}+\mathrm{b}\left(\mathrm{SOC}\right)+\mathrm{c}\left(\mathrm{clay}\right)$ $+\mathrm{d}\left(\mathrm{silt}\right)+\mathrm{e}(\mathrm{sand})$	a = −2.6847	2.9931	[44]
		b = −0.0165	0.0006
		c = 0.0043	0.0030
		d = 0.0042	0.0030
		e = 0.0041	0.0030

Note: M3 to M8 is an abbreviation for Method 3 to Method 8. “s.e. of estimate” represents the standard error of the coefficient.

) to predict BD values. The R² values of the PTFs ranged from 0.332 to 0.372, RMSE values ranged from 0.143 to 0.154 g cm⁻³, and RPIQ values ranged from 1.786 to 1.822 (

Table 6. The accuracy of PTFs for BD estimation.

No. Method	Calibration Subset (m = 1309)		Prediction Subset (m = 620)
	Rc2	RMSEC (g cm−3)	Rp2	RMSEP (g cm−3)	RPIQ
M3	0.370	0.153	0.332	0.146	1.786
M4	0.370	0.153	0.332	0.146	1.786
M5	0.354	0.154	0.349	0.144	1.810
M6	0.364	0.153	0.344	0.144	1.802
M7	0.371	0.152	0.358	0.143	1.822
M8	0.372	0.152	0.358	0.143	1.822

Note: M3 to M8 is an abbreviation for Method 3 to Method 8; m represents the number of soil horizon samples.

). The performance of M7 and M8 was slightly better than that of other PTFs, with the highest R_p² and RPIQ values and the lowest RMSE values. The validation accuracy of M3 and M4 was slightly lower, and the predictive accuracy of all models showed little difference. These results suggest that considering soil texture along with SOC can improve the predictive accuracy of the model to some extent.

3.4.2. Results of SOCD_icm Based on Estimated BD

Based on the soil sample data from the study area, the mean and median values of BD were calculated to be 1.37 and 1.40 g cm⁻³, respectively. The BD values obtained from the mean, median, and the six PTFs were individually incorporated into Equation (2) to compute the predicted values of SOCD_icm, which were then compared with the measured SOCD_icm. As shown in

Table 7. The predicted SOCD_icm results of the eight traditional methods.

No. Method	Calibration Subset (m = 1309)		Prediction Subset (m = 620)
	Rc2	RMSEC (kg m−2)	Rp2	RMSEP (kg m−2)	RPIQ
M1	0.872	0.026	0.852	0.026	3.602
M2	0.851	0.029	0.830	0.028	3.429
M3	0.958	0.015	0.950	0.015	5.520
M4	0.958	0.015	0.950	0.015	5.523
M5	0.944	0.018	0.949	0.015	5.481
M6	0.957	0.015	0.950	0.015	5.522
M7	0.942	0.018	0.947	0.015	5.400
M8	0.941	0.018	0.948	0.015	5.402

Note: M1 to M8 is an abbreviation for Method 1 to Method 8; m represents the number of soil horizon samples.

, the predicted SOCD_icm values from the six PTF models were closely aligned and demonstrated high precision. The values of R_c² and R_p² ranged from 0.941 to 0.958 and 0.947 to 0.950, respectively. The RMSE_C and RMSE_P values fell between 0.015 and 0.018 kg m⁻², while the RPIQ ranged from a minimum of 5.400 to a maximum of 5.523. Despite the relatively low predictive accuracy of BD PTFs (Table 6), the precision of SOCD_icm was high. In comparison, while the accuracy of estimating SOCD_icm using the mean and median values of BD was relatively low, it still yielded satisfactory results (R² ≥ 0.830).

3.4.3. Results of SOCD Based on Estimated BD

The predicted SOCD_icm was multiplied by the respective thickness of each soil horizon to calculate SOCD_i (Equation (3)), and then the profile SOCD was calculated from SOCD_i (Equation (4)). The predicted SOCD was plotted against the measured SOCD in a scatter plot (Figure 11). It can be observed that the accuracy of the SOCD predicted based on BD PTFs is quite similar to that of SOCD_icm. The values of R_p² were greater than 0.948, the RMSE_P values were less than 0.796 kg m⁻², and the RPIQ values ranged from 5.689 to 5.805. Although M7 and M8 exhibited the strongest predictive capability for BD, their predictive results for SOCD were not optimal, probably because M3 to M6 more effectively captured the relationship between SOC/SOM and SOCD, while M7 and M8 did not fully consider the complex relationship between SOC and BD when predicting SOCD. Therefore, the predictive accuracy of SOCD is not directly correlated with the predictive accuracy of the PTFs. The SOCD prediction accuracy of M1 and M2 was relatively low.

4. Discussion

4.1. Correlation Between SOC, BD, and SOCD_icm

Soil BD is primarily determined by the respective specific gravity and relative proportion of solid organic and inorganic particles, as well as the soil porosity. Due to the significantly lower density of organic matter compared to mineral particles, and its aggregation effect on soil structure, organic matter predominantly influences soil BD. Generally, an increase in organic matter content results in a decrease in BD and vice versa [50]. Therefore, soils rich in organic matter with a loose porous structure tend to have lower BD, while those with lower organic matter content and more compact structures have higher BD. SOC, SOM, and their correlation with BD are commonly used for carbon sink estimation [51]. Typically, SOC exhibits a negative correlation with BD [12,23,52], with higher SOC content leading to lower BD. This is because SOC reflects the organic matter content in the soil, which increases the interstitial space between soil solid particles due to its low density, enhancing soil aggregation and resulting in a decrease in soil BD [44]. Based on these factors, SOC becomes a crucial variable for constructing BD PTFs [9,25]. However, it is important to note that SOC is not always strongly correlated with BD. In soils with low SOC content, factors such as soil texture or other variables might primarily contribute to BD [41,42,53,54]. Research has shown that despite employing various simulation methods, predicting BD through PTFs remains challenging and often falls short of achieving satisfactory predictive levels [17].

According to Equation (2), theoretically, SOCD_icm should exhibit a positive correlation with both SOC and BD. However, Spearman’s correlation coefficient revealed a negative correlation between SOCD_icm and BD, which stems from the negative correlation between SOC and BD. Specifically, while SOC is positively correlated with SOCD_icm, it is negatively correlated with BD, resulting in a negative correlation between BD and SOCD_icm. Upon controlling for the influence of SOC, the relationship between BD and SOCD_icm transitioned from negative to positive, and the correlation strengthened significantly. Interestingly, even after removing the influence of BD, the correlation between SOC and SOCD_icm remained significantly positive, with a slight increase in the correlation coefficient. This suggests that SOC is the primary driving factor affecting SOCD_icm, and the robust correlation between SOC and SOCD_icm underlies the mechanism of directly estimating SOCD_icm using SOC.

4.2. The Selection and Accuracy of BD PTFs

Many studies have indicated that BD is closely related to SOC or SOM and soil texture [40,55], and SOC or SOM and soil texture (sand, silt, and clay contents) were the most commonly used predictors in the literature when developing PTFs [56]. In our dataset, SOC, SOM, and soil texture are easily measurable and obtainable, whereas factors such as pH [17,57], CaCO₃, cation exchange capacity [17,58], moisture content [52,59], and terrain features (elevation, slope, aspect) have been less frequently applied in previous PTFs and are not consistently available. The results of correlation analysis further confirm that BD is significantly correlated with SOC and is influenced by soil texture. Therefore, PTFs containing SOC and soil texture perform better than those containing only SOC. This is consistent with the findings of Bernoux et al. [54], Kaur et al. [40], and Tomasella and Hodnett [60]. Several studies recommended using SOC or SOM as the sole predictor for BD to avoid collinearity risks with other predictors [9,25,61,62,63]. Based on this, our study selected two categories of published PTFs (the first category using only SOC or SOM as a predictor and the second category incorporating SOC and soil texture together) and revised these PTFs to better fit the local soil data for estimating BD values.

Previous studies on BD PTFs have often been limited to analyzing the accuracy of predicting BD, with the determination coefficients (R²) of the established PTFs typically being less than 0.8. In addition, research regarding the further use of these PTFs for estimating SOCD is scarce. For instance, Chen et al. [9] utilized the generalized boosted model (GBM) algorithm to establish BD PTFs with an R² less than 0.648. Similarly, the BD PTFs developed by Zheng et al. [21] exhibited accuracies below 0.775. The accuracy of BD PTFs is influenced by various factors, including modeling methods, the number of variables, and the composition of the modeling dataset [64]. For example, Al-Qinna and Jaber [44] suggested that incorporating nonlinear models or machine learning methods, as well as increasing the number of variables such as SOC, could potentially enhance the accuracy of prediction models. However, certain studies have indicated that increasing model complexity cannot effectively improve the precision of BD prediction models [21,65]. Developing BD PTFs based on regional or soil-type subdivisions could potentially enhance predictive accuracy to some extent [66,67]. In this study, the accuracy of the six PTFs for predicting BD was not high (R_p² ≤ 0.358) (Table 6). This might be attributed to the diverse range of soil types covered by the samples and the use of traditional modeling methods. Additionally, other factors, such as sampling depth and pH, can also influence BD values. If these factors were incorporated as predictive variables, the performance of the PTFs could potentially be enhanced [20].

4.3. Model Accuracy Validation

Some studies utilized PTFs to estimate BD for calculating SOCD or SOC stocks, yet they did not provide the precision of the constructed PTFs. For instance, Xu et al. [10] developed three PTFs to estimate SOCD, with R² values ranging from 0.850 to 0.917, which is lower than the accuracy achieved by the BD PTFs used in this study. Wiesmeier et al. [68] reported that applying BD PTFs led to an overestimation of SOC stocks by 20–50%. Xu et al. [24] highlighted the variability in PTFs as a significant source of uncertainty in SOC stock estimation, and this uncertainty was exceptionally high for soils with low or high SOC content. In this study, a systematic comparison of the accuracy of BD PTFs and their estimated SOCD was conducted. The results showed that the R² values for the BD PTFs were lower than 0.4 (Table 6). However, when these BD PTFs were used to calculate SOCD_icm and then aggregated to SOCD, the determination coefficients for SOCD_icm and SOCD were greater than 0.93 (Table 7 and Figure 11). This discrepancy can be attributed to the fact that when the BD PTF models built solely based on the single variable SOC are applied to Equation (2), they essentially embody the relationship between SOC, gravel content, and SOCD_icm. Particularly for samples without gravel content, SOCD_icm is solely determined by SOC. The strong correlation between SOC and SOCD_icm determines the high accuracy of SOCD_icm estimation. Although M7 and M8 include texture data, the correlation between texture and SOCD_icm is relatively weak, and the contribution of texture data in the model is minor (Table 6). The incorporation of texture data did not significantly enhance the accuracy of SOCD estimation. This suggests that the computation of SOCD is intricate, and the superior performance of BD PTFs does not necessarily guarantee the highest accuracy in predicting SOCD.

This study found that in estimating SOCD, the accuracy of the BD PTF method surpassed that of the mean and median methods (Figure 12). For certain soil types, changes in the natural environment and land use can significantly influence their physicochemical properties [12,69,70,71,72]. Additionally, the mean and median methods are greatly affected by the representativeness of soil sampling [10]. Therefore, the mean and median methods overlook external factors’ impacts on BD, leading to higher uncertainty in SOCD estimation. In contrast, PTFs consider the relationship between BD and soil physicochemical properties, thus offering higher accuracy. Furthermore, this study found that directly estimating SOCD_icm from SOC was less accurate than the BD PTF method (Figure 12). Part of the reason for this is that the process of calculating SOCD_icm by substituting BD PTFs into Equation (2) considers the gravel content factor, whereas the calculation process of directly estimating SOCD_icm from SOC ignores this factor (Equations (5)–(7)), leading to increased errors. Gravel content is one of the primary parameters for estimating SOCD and soil carbon pools. However, gravel content information is not always available, and rock fragment components are often overlooked in regional-scale studies or national soil surveys [68], making it a significant limiting factor for carbon stocks and concentration [73,74]. The presence of gravel in soil occupies the volume originally composed of fine earth [75], altering soil physicochemical properties such as BD [76,77,78,79] and carbon stocks. Additionally, the content, porosity, and distribution of gravel in soil further alter its physical properties (such as BD and pore distribution). These changes, by affecting soil’s hydrological processes, heat transfer, and other intermediary processes, indirectly or directly alter the soil carbon cycle and SOCD [80]. Therefore, the relationship between gravel content and SOCD is multidimensional, reflecting both its direct impact on soil physical properties and its effect on the dynamics of SOCD through the regulation of carbon cycling processes. Previous studies have shown that neglecting gravel content led to the overestimation of measured soil carbon pools [11,26,75], especially for soils rich in gravel content [12]. The results of this study are consistent with this finding, indicating that ignoring the influence of gravel content resulted in an overall overestimation of SOCD_icm by 7.01–9.45%. Particularly, for soils with a gravel content ≥ 30%, gravel content is particularly important for accurately determining SOCD. The soils in the Yangtze River Delta region are mainly formed by sedimentation from rivers, lakes, and seas, and they are also influenced by other parent materials such as loess, quaternary red soil, weathered residual materials, and colluvium. Due to these specific parent materials, the gravel content in the soils of this region is relatively low. Therefore, even without considering gravel content, the impact on SOCD is not significant. In cases of missing gravel content data, we can still estimate SOCD quickly and accurately. By introducing gravel content data into Equations (8)–(10), the accuracy of SOCD_icm estimation was improved, making this correction comparable to the BD PTF method in terms of SOCD estimation ability and exhibiting higher precision compared to using the BD mean and median substitution methods (Figure 12). The inclusion of gravel content as a correction factor significantly improved the estimation accuracy of SOCD. Specifically, the model’s R_c² and R_p² increased from 0.860–0.877 to 0.938–0.946 and from 0.869–0.893 to 0.927–0.945, respectively, while RMSE_C and RMSE_P decreased by 0.457–0.542 kg m⁻² and 0.321–0.387 kg m⁻², respectively. The RPIQ increased from 3.568–3.948 to 4.773–5.533 (Figure 5 and Figure 9). When gravel content is not considered, directly estimating SOCD from SOC may lead to the overestimation of carbon density, especially in soils with high gravel content. After incorporating the gravel content factor, the model automatically corrected this error, enhancing estimation accuracy. Gravel content varies significantly across different pedogenic environments and land use types. Without correction, it is assumed that the influence of SOC on SOCD is consistent across all soils, whereas the correction allows the model to adjust SOCD based on gravel content, thus improving its applicability to different soil types. This study recommends using the gravel correction factor method to estimate SOCD, avoiding the overestimation of the SOC pool and enabling a more scientific assessment of soil carbon sequestration function. This improvement is especially applicable to soils with higher gravel content, highlighting the importance of determining gravel content and incorporating it into the model in future studies, particularly in regions with high gravel content, to enhance SOCD estimation accuracy. However, when gravel content data are difficult to obtain, the method proposed in this study, which directly estimates SOCD_icm based on SOC, still holds significant potential for application, providing a feasible solution for SOCD estimation in the absence of gravel data and broadening the applicability of the method. It is worth noting that this study did not actually measure gravel density but used 2.65 g cm⁻³ as a substitute, which may introduce biases in estimating fine earth BD and organic carbon pools [81].

Other methods for directly estimating SOCD without requiring SOC data have also been explored. For example, Song et al. [82] and Sun et al. [83], respectively, utilized environmental variables such as terrain and annual average precipitation to directly estimate SOCD. However, these methods are complex and have lower R² values compared to the results of this study (R² = 0.87). Liu et al. [4] employed soil spectra combined with deep neural network technology to estimate SOCD, with the best R² being less than 0.81. While this method can be used for small-scale spatial mapping, it still requires the measurement of soil spectral data. The new method proposed in this study effectively captures the strong correlation between SOC and SOCD_icm. Although the precision of the results is slightly lower than that of the BD PTF method, the new method’s advantage lies in its clear and simple mechanism, making it suitable for the rapid estimation of SOCD for a large number of soil samples.

4.4. Comparison and Limitations of Soil Organic Carbon Measurement Methods

SOC is a major component of SOM. It includes microbial cells, plant and animal residues at various stages of decomposition, stable “humus” synthesized from these residues, and nearly inert, highly carbonized compounds such as charcoal, graphite, and coal [84]. Because it can be measured simply and efficiently, SOC is commonly employed as a key proxy indicator for determining SOM content [85].

Currently, SOC determination primarily utilizes two techniques: the wet digestion and dry combustion methods. The Walkley–Black (WB) wet digestion method has been widely adopted as the standard procedure in most soil testing laboratories due to its operational simplicity, low cost, and minimal equipment requirements [84]. The SOC data used in this study were obtained using this method from the “Soil Series of China”. However, extensive research has demonstrated that the WB method significantly underestimates SOC content [86,87,88,89,90,91,92], with marked spatial variability in organic carbon recovery rates. For instance, Krishan et al. [91] found that the WB method underestimated SOC by an average of 45% in Himalayan soils and 33% in central Indian soils. The lower recovery rate of SOC in soil may be attributed to the incomplete oxidation of organic carbon by the WB method. While a standard correction factor of 1.32 (assuming a 76% SOC recovery rate) is conventionally applied to convert Walkley–Black carbon (WBC) to total organic carbon (TOC), the assumed 76% recovery rate is generally overestimated. Actual recovery rates vary considerably depending on land use patterns, soil types, sampling depths, soil textures, organic matter characteristics, management practices, and climatic conditions [92,93,94]. Therefore, it is recommended to apply a differentiated recovery correction factor that accounts for the above factors to improve the accuracy of SOC estimation using the WB method.

In contrast, dry combustion methods (including the use of an elemental analyzer, TOC analyzer, and gas chromatograph) achieve nearly 100% carbon recovery and are internationally recognized as the most reliable standard for SOC determination [93]. Although minor variations exist among different dry combustion systems, their measurement precision significantly surpasses that of the wet digestion method [95]. Nevertheless, their widespread adoption in developing countries faces challenges including high equipment costs, specialized technical requirements, and environmental compliance issues [96]. This underscores the importance of developing universal conversion models that account for soil type, land use, and climate to accurately translate WBC to true TOC. Although strong correlations have been observed between WB and dry combustion results [93,97,98,99], the systematic bias of the WB method cannot be overlooked. Therefore, for applications requiring high precision (e.g., carbon sequestration accounting), dry combustion methods should be prioritized. If WB method data are used, it is recommended to apply soil-specific correction factors considering parameters such as texture, land use, and depth.

Loss on ignition (LOI) represents another simple method for SOM determination. One of the PTFs developed by Huntington et al. [41] was based on LOI-measured SOM [84]. However, LOI lacks a unified standard protocol, and its accuracy is influenced by factors such as furnace type, sample mass, duration, and the temperature of ignition and clay content of samples [100], potentially leading to SOM overestimation (due to water loss or mineral decomposition) or underestimation (from incomplete combustion) [92]. Davies [101] reported good consistency between SOM content determined by the WB and LOI methods. Therefore, in this study, SOM content was derived by multiplying WB-measured SOC values by 1.724.

Given that our SOC data were obtained using the Walkley–Black method, potential systematic underestimation should be acknowledged. Future research should prioritize dry combustion methods or develop context-specific correction models incorporating soil type, texture, and land use patterns to enhance SOC estimation accuracy.

4.5. The Applicability and Limitations of the Models

Geographical phenomena often exhibit regional characteristics, and statistical models constructed based on soil properties are more applicable within the specific regions covered by the modeling samples, making it challenging to generalize the model beyond the specific area or soil types [66,102,103]. The SOCD_icm model developed in this study, based on SOC and incorporating gravel content as a correction factor, is suitable only for a limited geographical area. In this particular study area, the variation in the BD of soil samples is relatively small, which may contribute to the good results obtained by the new method. When the study scope extends to regions with more extensive variations in BD, the results may not meet expectations. In addition, this study’s SOCD_icm model construction only considered SOC and gravel content and did not account for other factors that may influence SOCD estimation, such as soil type, land use type, climatic factors (e.g., temperature and precipitation), vegetation, soil microorganisms, parent material, topographical factors, soil physicochemical properties, and human activities [104]. The spatial variability in these factors may affect the model’s accuracy. Our decision to use only SOC and gravel content was based on two main considerations. First, to ensure the model’s generalizability and practicality, we prioritized the most reliable and widely available variables in the dataset. Additionally, to develop a simple and easily applicable method, we intentionally streamlined the model structure, focusing on SOC and gravel content as the two most explanatory variables. Incorporating too many variables could increase model complexity and reduce its applicability, particularly in regions where data acquisition is challenging. Second, factors such as climate, parent material, and topography require extensive data collection, making it difficult to obtain complete datasets, which limits their application in this study. To enhance the regional applicability and generalizability of the model, future research could incorporate these variables into the model and optimize relevant parameters. Moreover, refining variable selection strategies and optimizing model structures would further enhance the model’s interpretability and predictive accuracy. Constructing statistical models based on specific soil types can somewhat enhance accuracy [22,68], especially for larger study areas, where grouping by major soil types should be considered. In future research, national- or global-scale data can be used to establish estimation models for each soil type and evaluate their accuracy based on dividing the dataset according to soil type, thus providing high-precision estimation formulas for the SOCD estimation of various soil types and further verifying the reliability of the new method. With the development of computers and machine learning algorithms, SOCD estimation methods have evolved from basic linear and nonlinear regression models to data mining approaches. Simple and multiple linear regression models have been widely used and are often employed as benchmarks for comparison with other advanced methods. Some data mining methods, such as artificial neural networks, extreme gradient boosting, random forests, and support vector machines, have been used in recent SOCD-related studies [83]. However, machine learning methods typically require a large amount of training data, and their “black box” nature may reduce the interpretability of the results. Therefore, this study prioritizes traditional regression models, providing a transparent and easily interpretable computational framework. Future research can further explore the potential of machine learning methods in SOCD estimation.

5. Conclusions

This study proposed a novel method for estimating SOCD in the 0–100 cm soil profile of the Yangtze River Delta region in China, providing a feasible solution for SOCD estimation in the absence of BD data. Based on the availability of gravel content data, linear regression, polynomial regression, and power function regression were used to establish SOCD_icm estimation models based on SOC and gravel content, and SOCD values were further calculated. This method has a clear mechanism and simple computation and avoids excessive reliance on BD data, effectively addressing the potential impact of incomplete gravel content data.

The results showed that in the absence of gravel content data, by leveraging the robust correlation between SOC and SOCD_icm, SOC could be used to directly estimate SOCD_icm with high accuracy and calculate the profile SOCD. The three function models demonstrated excellent predictive performance, with prediction set coefficients of determination (R_p²) exceeding 0.90, RMSE_P below 0.021 kg m⁻², and an RPIQ reaching up to 4.357.

Neglecting the effect of gravel content led to the overestimation of SOCD_icm, with an overall overestimation range of 7.01–9.45%. In soils with a gravel content ≥ 30%, this overestimation was particularly significant, reaching 32.84–34.77%. By incorporating gravel content as a correction factor, the SOCD prediction accuracy of the model was further improved, with R_p² increasing to 0.927–0.945, RMSE_P decreasing to 0.819–0.949 kg m⁻², and the RPIQ improving to 4.773–5.533. This highlights that gravel content is a critical factor influencing SOCD estimation accuracy, especially in high-gravel-content soils, where its correction effect plays a key role in enhancing model precision.

Compared to traditional BD substitution methods (BD mean method, BD median method, and BD PTF method), the proposed method exhibited significant advantages in SOCD estimation accuracy. The BD mean and median methods yielded an R_p² ≤ 0.872, RMSE_P ≥ 1.252 kg m⁻², and an RPIQ between 3.809 and 4.100. The proposed method outperformed the BD mean and median methods in terms of SOCD estimation accuracy and was comparable to the BD PTF method, enabling reasonably accurate SOCD estimation.

The models developed in this study are based on soil data from the Yangtze River Delta region and are suitable for SOCD estimation in this area. However, due to differences in soil types, climatic conditions, and land use, the applicability of these models in other regions requires further validation. Future research could improve model applicability and scalability by incorporating additional variables such as climate, topography, soil types, and parent material. Additionally, region-specific estimation models could be developed for different soil types, and the potential of machine learning methods in SOCD estimation could be further explored.

The proposed method provides a novel approach to SOCD estimation in the absence of BD data. It offers new insights for calculating regional or global SOC stocks, contributing to the advancement of soil carbon estimation methodologies.