A Future Scenario Prediction for the Arid Inland River Basins in China Under Climate Change: A Case Study of the Manas River Basin
Abstract
1. Introduction
2. Data and Methods
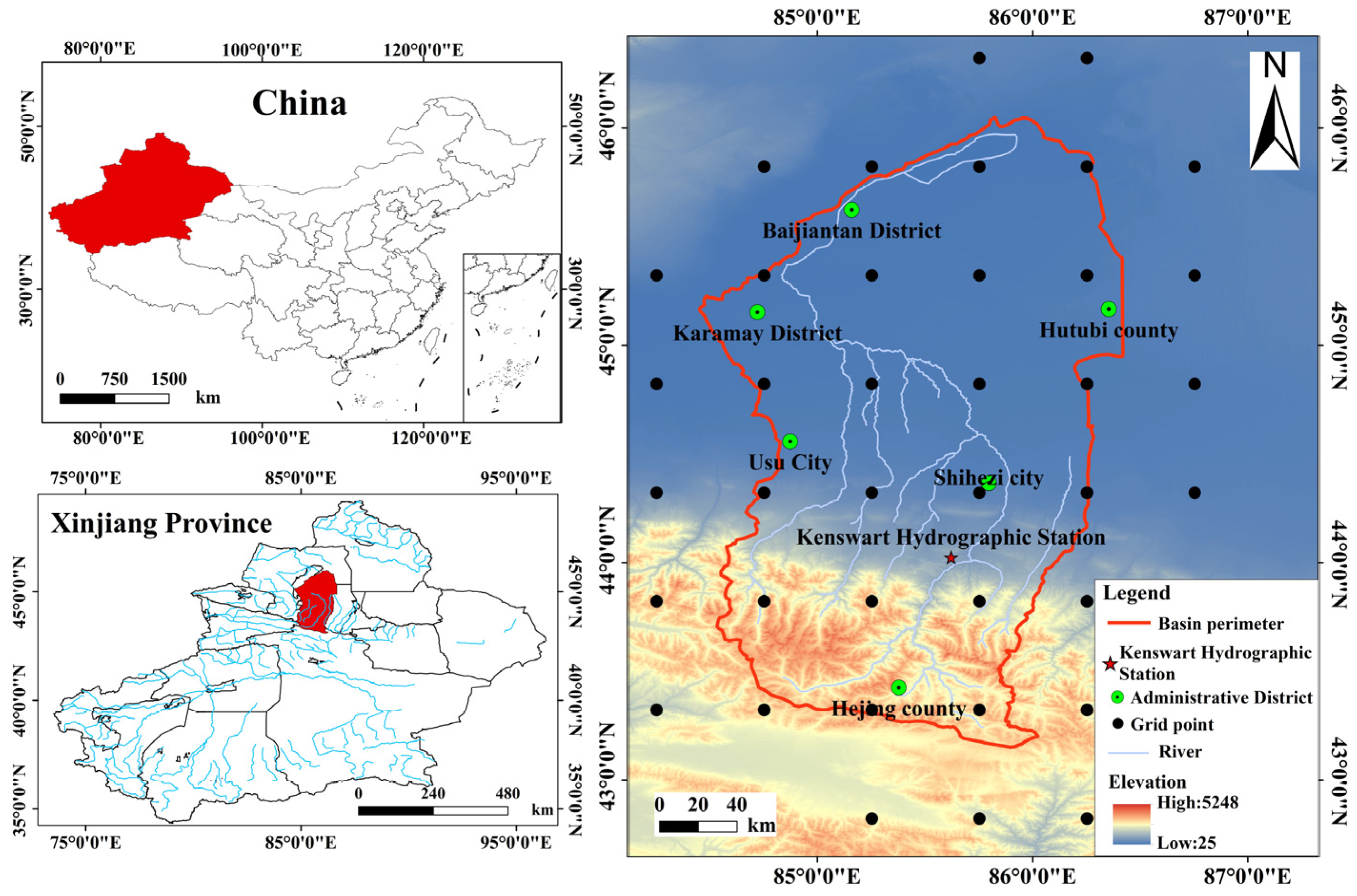
2.1. An Overview of the Study Area
2.2. Data Sources
2.2.1. HRLT
2.2.2. GCM Data
2.3. Research Method
2.3.1. Downscaling and Bias Correction
2.3.2. MME Method
- SCM and WSM
- 2.
- RF
- 3.
- ANN
- 4.
- SVM
2.3.3. Cross-Validation and Skill Metrics
- Taylor diagram and TSS
- 2.
- SS
- 3.
- IVS
- 4.
- KGE
- 5.
- CRI
3. Results and Discussion
3.1. Model Simulation Ability Evaluation
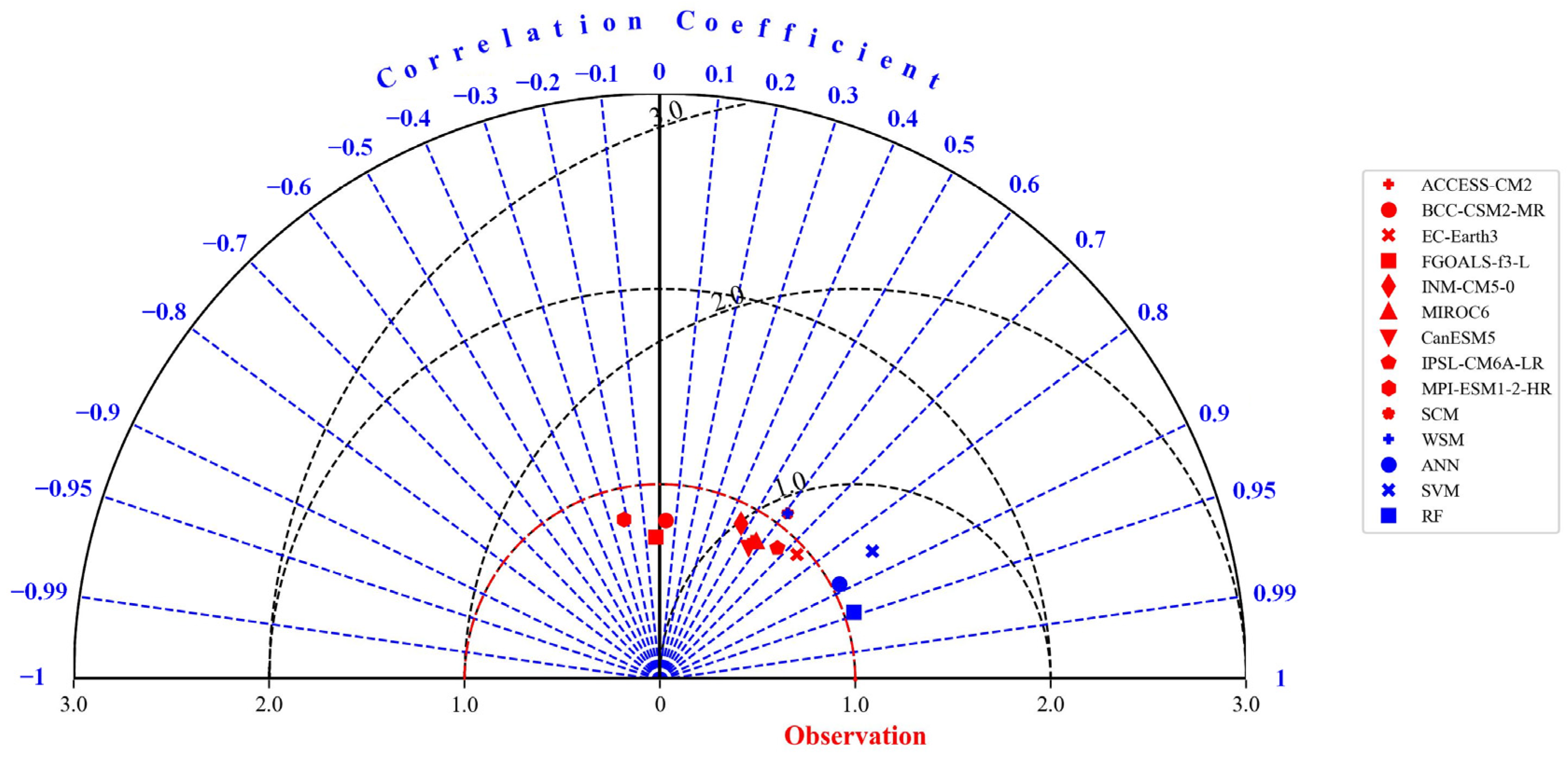
3.1.1. Taylor Diagram and Linear Trend Analysis
- Taylor diagram and trend analysis of temperature
- 2.
- Taylor diagram and trend analysis of precipitation
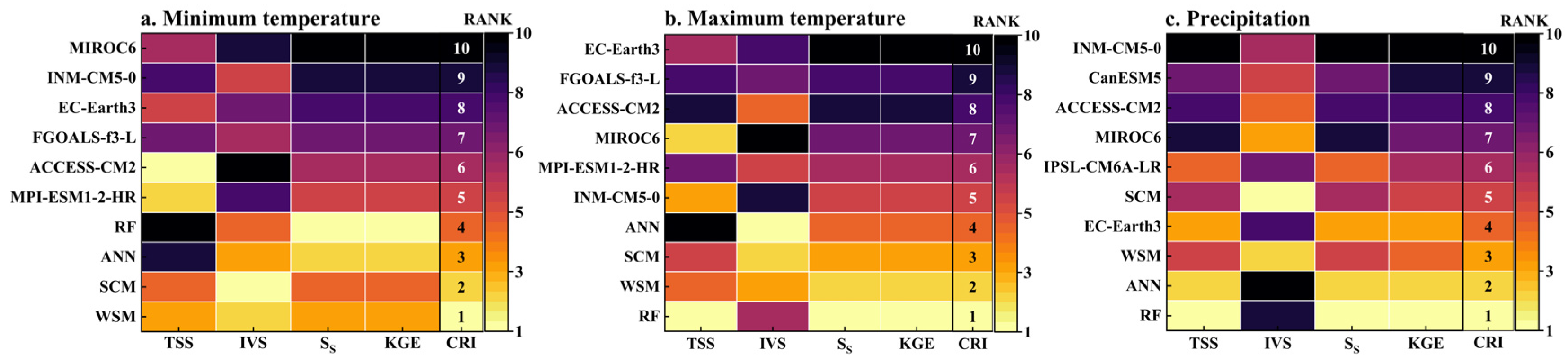
3.1.2. Quantitative Evaluation of GCM Simulation Ability
3.2. Spatiotemporal Changes in Temperature in Future Climate Scenarios
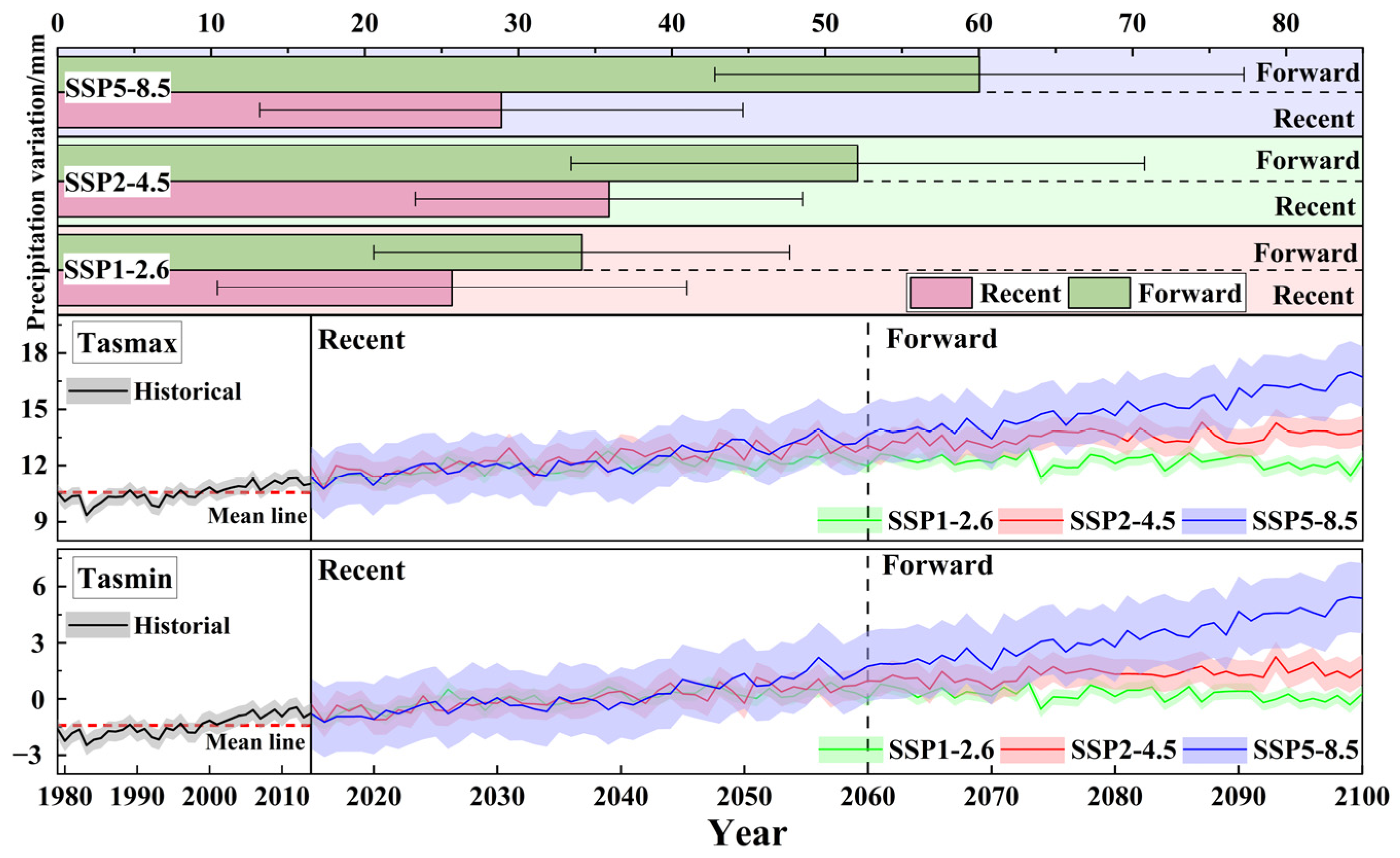
3.2.1. Temperature Time Variation
3.2.2. Temperature Spatiotemporal Distribution Change
3.3. Temporal and Spatial Changes in Precipitation in Future Climate Scenarios
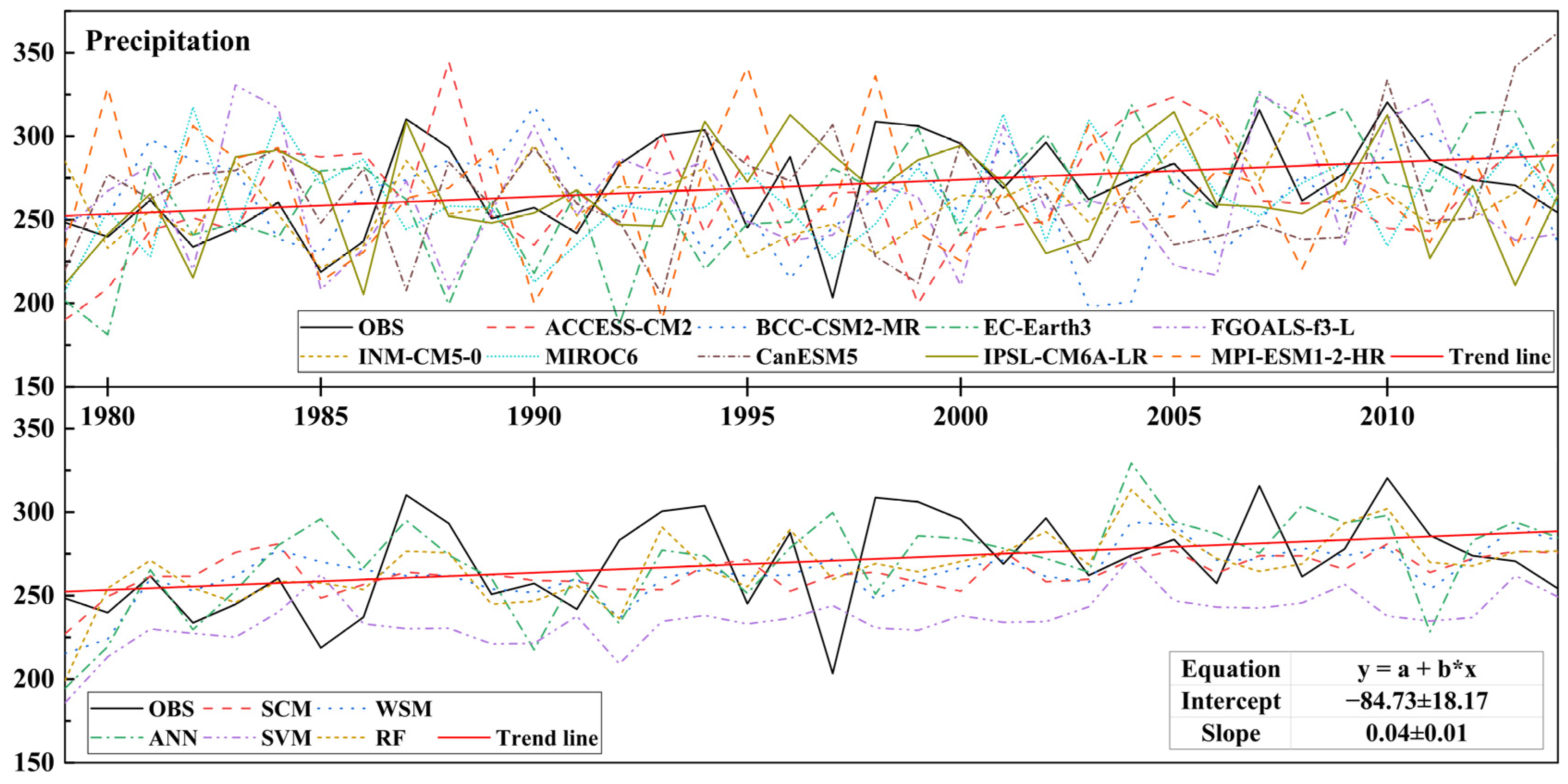
3.3.1. Precipitation Time Variation
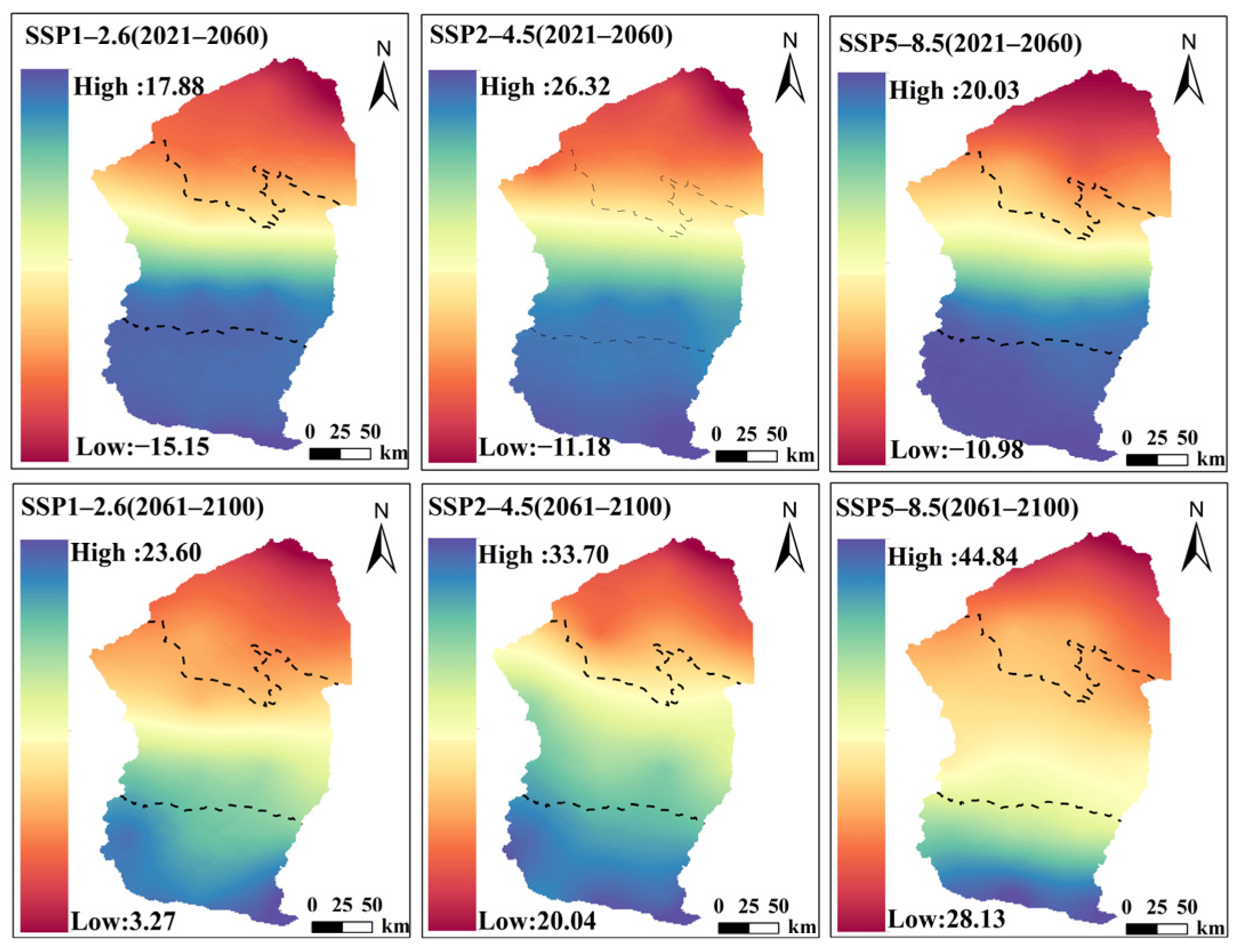
3.3.2. Precipitation Spatiotemporal Distribution Change
3.4. Comparison with Other Inland River Basins in Northwest China
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Wang, Y.; Wang, J.; Zhang, Q. Analysis of ecological drought risk characteristics and leading factors in the Yellow River Basin. Theor. Appl. Climatol. 2023, 155, 1739–1757. [Google Scholar] [CrossRef]
- Sun, F. Analysis of Short-Term Heavy Rainfall-Based Urban Flood Disaster Risk Assessment Using Integrated Learning Approach. Sustainability 2024, 16, 8249. [Google Scholar] [CrossRef]
- Singh, H.V.; Joshi, N.; Suryavanshi, S. Projected climate extremes over agro-climatic zones of Ganga River Basin under 1.5, 2, and 3° global warming levels. Environ. Monit. Assess. 2023, 195, 1062. [Google Scholar] [CrossRef] [PubMed]
- Potopová, V.; Trifan, T.; Trnka, M.; De Michele, C.; Semerádová, D.; Fischer, M.; Meitner, J.; Musiolková, M.; Muntean, N.; Clothier, B. Copulas modelling of maize yield losses—Drought compound events using the multiple remote sensing indices over the Danube River Basin. Agric. Water Manag. 2023, 280, 108217. [Google Scholar] [CrossRef]
- Pawankar, R.; Akdis, C.A. Climate change and the epithelial barrier theory in allergic diseases: A One Health approach to a green environment. Allergy 2023, 78, 2829–2834. [Google Scholar] [CrossRef]
- Wang, J.; Chen, G.; Yuan, Y.; Fei, Y.; Xiong, J.; Yang, J.; Yang, Y.; Li, H. Spatiotemporal changes of ecological environment quality and climate drivers in Zoige Plateau. Environ. Monit. Assess. 2023, 195, 912. [Google Scholar] [CrossRef]
- Zhou, T.; Zou, L.; Chen, X. Commentary on the Coupled Model Intercomparison Project Phase 6 (CMIP6). Clim. Chang. Res. 2019, 15, 445–456. [Google Scholar]
- Salehie, O.; Hamed, M.M.; Ismail, T.b.; Tam, T.H.; Shahid, S. Selection of CMIP6 GCM with projection of climate over the Amu Darya River Basin. Theor. Appl. Climatol. 2022, 151, 1185–1203. [Google Scholar] [CrossRef]
- Crévolin, V.; Hassanzadeh, E.; Bourdeau-Goulet, S.-C. Updating the intensity-duration-frequency curves in major Canadian cities under changing climate using CMIP5 and CMIP6 model projections. Sustain. Cities Soc. 2023, 92, 104473–104489. [Google Scholar] [CrossRef]
- Song, Y.H.; Chung, E.-S.; Shahid, S. Spatiotemporal differences and uncertainties in projections of precipitation and temperature in South Korea from CMIP6 and CMIP5 general circulation models. Int. J. Climatol. 2021, 15, 215–229. [Google Scholar] [CrossRef]
- Jiang, Z.; Li, W.; Xu, J.; Li, L. Extreme Precipitation Indices over China in CMIP5 Models. Part I: Model Evaluation. Am. Meteorol. Soc. 2015, 10, 1–44. [Google Scholar] [CrossRef]
- Ghaemi, A.; Monfared, S.A.H.; Bahrpeyma, A.; Mahmoudi, P.; Zounemat-Kermani, M. Exploitation of the ensemble-based machine learning strategies to elevate the precision of CORDEX regional simulations in precipitation projection. Earth Sci. Inform. 2024, 17, 1373–1392. [Google Scholar] [CrossRef]
- Dawkins, L.C.; Bernie, D.J.; Lowe, J.A.; Economou, T. Assessing climate risk using ensembles: A novel framework for applying and extending open-source climate risk assessment platforms. Clim. Risk Manag. 2023, 40, 100510. [Google Scholar] [CrossRef]
- Shiva, J.S.; Chandler, D.G. Projection of Future Heat Waves in the United States. Part I: Selecting a Climate Model Subset. Atmosphere 2020, 11, 587. [Google Scholar] [CrossRef]
- Sanderson, B.M.; Knutti, R.; Caldwell, P. Addressing interdependency in a multimodel ensemble by interpolation of model properties. Am. Meteorol. Soc. 2015, 28, 5150–5170. [Google Scholar] [CrossRef]
- Salcedo-Sanz, S.; Pérez-Aracil, J.; Ascenso, G.; Ser, J.D.; Casillas-Pérez, D.; Kadow, C.; Fister, D.; Barriopedro, D.; García-Herrera, R.; Giuliani, M.; et al. Analysis, characterization, prediction, and attribution of extreme atmospheric events with machine learning and deep learning techniques: A review. Theor. Appl. Climatol. 2024, 155, 1–44. [Google Scholar] [CrossRef]
- Chen, Y.; Wang, N.; Jiao, J.; Li, J.; Bai, L.; Liang, Y.; Wei, Y.; Zhang, Z.; Xu, Q.; Zhang, Z.; et al. Predicting soil loss in small watersheds under different emission scenarios from CMIP6 using random forests. Earth Surf. Process. Landf. 2024, 49, 4469–4484. [Google Scholar] [CrossRef]
- Dey, A.; Sahoo, D.P.; Kumar, R.; Remesan, R. A multimodel ensemble machine learning approach for CMIP6 climate model projections in an Indian River basin. Int. J. Climatol. 2022, 42, 9215–9236. [Google Scholar] [CrossRef]
- Karimizadeh, K.; Yi, J. Modeling Hydrological Responses of Watershed Under Climate Change Scenarios Using Machine Learning Techniques. Water Resour. Manag. 2023, 37, 5235–5254. [Google Scholar] [CrossRef]
- O’Gorman, P.A.; Dwyer, J.G. Using Machine Learning to Parameterize Moist Convection: Potential for Modeling of Climate, Climate Change, and Extreme Events. J. Adv. Model. Earth Syst. 2018, 10, 2548–2563. [Google Scholar] [CrossRef]
- Sachindra, D.A.; Ahmed, K.; Rashid, M.M.; Shahid, S.; Perera, B.J.C. Statistical downscaling of precipitation using machine learning techniques downscaling with machine learning techniques. Atmos. Res. 2018, 212, 240–258. [Google Scholar] [CrossRef]
- Gumus, V.; El Moçayd, N.; Seker, M.; Seaid, M. Evaluation of future temperature and precipitation projections in Morocco using the ANN-based multi-model ensemble from CMIP6. Atmos. Res. 2023, 292, 106880. [Google Scholar] [CrossRef]
- Yu, P.; Xu, H.; Liu, S.; Qiao, M.; Zhang, Q.; An, H.; Fu, J. Spatial distribution pattern changes of oasis soil types in Manasi River Basin, arid northwestern China. Catena 2011, 87, 253–259. [Google Scholar] [CrossRef]
- Shang, H.; Wang, W.; Dai, Z.; Duan, L.; Zhao, Y.; Zhang, J. An ecology-oriented exploitation mode of groundwater resources in the northern Tianshan Mountains, China. J. Hydrol. 2016, 54, 386–394. [Google Scholar] [CrossRef]
- Qin, R.; Zhang, F. HRLT: A high-resolution (1 day, 1 km) and long-term (1961–2019) gridded dataset for temperature and precipitation across China. Earth Syst. Sci. Data 2022, 14, 4793–4810. [Google Scholar] [CrossRef]
- Feng, M.; Sexton, J.O.; Channan, S.; Townshend, J.R. A global, high-resolution (30-m) inland water body dataset for 2000: First results of a topographic–spectral classification algorithm. Int. J. Digit. Earth 2015, 9, 113–133. [Google Scholar] [CrossRef]
- He, J.; Yang, K.; Tang, W.; Lu, H.; Qin, J.; Chen, Y.; Li, X. The first high-resolution meteorological forcing dataset for land process studies over China. Sci. Data 2020, 7, 25. [Google Scholar] [CrossRef]
- Qian, Y.; Zou, H.; Hong, M. Evaluating the evolution of wind energy resource in the Northwest Passage under climate change based on CMIP5 models. Mar. Forecast. 2021, 38, 76–86. [Google Scholar]
- Li, X.; Li, Z. Evaluation of bias correction techniques for generating high-resolution daily temperature projections from CMIP6 models. Clim. Dyn. 2023, 61, 3893–3910. [Google Scholar] [CrossRef]
- Xue, P.; Zhang, C.; Wen, Z.; Park, E.; Jakada, H. Climate variability impacts on runoff projection under quantile mapping bias correction in the support CMIP6: An investigation in Lushi basin of China. J. Hydrol. 2022, 614, 128550. [Google Scholar] [CrossRef]
- Tadase, A.T. Climate trend analysis in the ramis catchment, upper wabi shebelle basin, Ethiopia, using the CMIP6 dataset. J. Afr. Earth Sci. 2024, 217, 105347. [Google Scholar] [CrossRef]
- Niranjan Kumar, K.; Thota, M.S.; Ashrit, R.; Mitra, A.K.; Rajeevan, M.N. Quantile mapping bias correction methods to IMDAA reanalysis for calibrating NCMRWF unified model operational forecasts. Hydrol. Sci. J. 2022, 67, 870–885. [Google Scholar] [CrossRef]
- Zhang, Q.; Gan, Y.; Zhang, L.; She, D.; Wang, G.; Wang, S. Piecewise-quantile mapping improves bias correction of global climate model daily precipitation towards preserving quantiles and extremes. Int. J. Climatol. 2022, 42, 7968–7986. [Google Scholar] [CrossRef]
- Wang, Z.; Gong, H.; Huang, M.; Gu, F.; Wei, J.; Guo, Q.; Song, W. A multimodel random forest ensemble method for an improved assessment of Chinese terrestrial vegetation carbon density. Methods Ecol. Evol. 2021, 14, 117–132. [Google Scholar] [CrossRef]
- Costache, R.; Arabameri, A.; Elkhrachy, I.; Ghorbanzadeh, O.; Pham, Q.B. Detection of areas prone to flood risk using state-of-the-art machine learning models. Geomat. Nat. Hazards Risk 2021, 12, 1488–1507. [Google Scholar] [CrossRef]
- Than, N.H.; Ly, C.D.; Tat, P.V. The performance of classification and forecasting Dong Nai River water quality for sustainable water resources management using neural network techniques. J. Hydrol. 2021, 596, 126099. [Google Scholar] [CrossRef]
- Jalili, A.A.; Najarchi, M.; Shabanlou, S.; Jafarinia, R. Multi-objective Optimization of water resources in real time based on integration of NSGA-II and support vector machines. Environ. Sci. Pollut. Res. 2023, 30, 16464–16475. [Google Scholar] [CrossRef]
- Li, T.; Jiang, Z.; Treut, H.L.; Li, L.; Zhao, L.; Ge, L. Machine learning to optimize climate projection over China with multi-model ensemble simulations. Environ. Res. Lett. 2021, 16, 28–44. [Google Scholar] [CrossRef]
- Fan, X.; Miao, C.; Duan, Q.; Shen, C.; Wu, Y. The Performance of CMIP6 Versus CMIP5 in Simulating Temperature Extremes Over the Global Land Surface. J. Geophys. Res. Atmos. 2020, 125, 1–16. [Google Scholar] [CrossRef]
- Yang, X.; Zhou, B.; Xu, Y.; Han, Z. CMIP6 Evaluation and Projection of Temperature and Precipitation over China. Adv. Atmos. Sci. 2021, 38, 817–830. [Google Scholar] [CrossRef]
- Hamed, M.M.; Nashwan, M.S.; Shahid, S.; Ismail, T.b.; Wang, X.; Dewan, A.; Asaduzzaman, M. Inconsistency in historical simulations and future projections of temperature and rainfall: A comparison of CMIP5 and CMIP6 models over Southeast Asia. Atmos. Res. 2022, 265, 105927–105940. [Google Scholar] [CrossRef]
- Zhang, Y.; You, Q.; Chen, C.; Ge, J.; Adnan, M. Evaluation of Downscaled CMIP5 Coupled with VIC Model for Flash Drought Simulation in a Humid Subtropical Basin, China. J. Clim. 2018, 31, 31. [Google Scholar] [CrossRef]
- Taylor, K.E. Summarizing multiple aspects of model perform-ance in a single diagram. J. Geophys. Res. Atmos. 2001, 106, 7183–7192. [Google Scholar] [CrossRef]
- de Souza, L.S.; da Silva, M.S.; de Almeida, V.A.; Moraes, N.O.; de Souza, E.P.; Senna, M.C.; França, G.B.; Frota, M.N.; de Almeida, M.V.; Viana, L.Q. Evaluation of Cumulus and Microphysical Parameterization Schemes of the WRF Model for Precipitation Prediction in the Paraíba do Sul River Basin, Southeastern Brazil. Pure Appl. Geophys. 2024, 181, 679–700. [Google Scholar] [CrossRef]
- Luo, N.; Guo, Y.; Chou, J.; Gao, Z. Added value of CMIP6 models over CMIP5 models in simulating the climatological precipitation extremes in China. Int. J. Climatol. 2021, 42, 1148–1164. [Google Scholar] [CrossRef]
- Sun, L.; Lan, Y.; Jiang, R. Using CNN framework to improve multi-GCM ensemble predictions of monthly precipitation at local areas: An application over China and comparison with other methods. J. Hydrol. 2023, 623, 129866. [Google Scholar] [CrossRef]
- Ma, S.; Chen, C.; Zhi, X.; He, H.; Wu, D. The assessment and verification of convection-allowing ensemble forecast based on spatial-temporal uncertainties. Acta Meteorol. Sin. 2018, 76, 578–589. [Google Scholar]
- Maghrebi, M.F.; Vatanchi, S.M.; Kawanisi, K. Investigation of stage-discharge model performance for streamflow estimating: A case study of the Gono River, Japan. River Res. Appl. 2023, 39, 805–818. [Google Scholar] [CrossRef]
- Mo, C.; Liu, G.; Lei, X.; Zhang, M.; Ruan, Y.; Lai, S.; Xing, Z. Study on the Optimization and Stability of Machine Learning Runoff Prediction Models in the Karst Area. Appl. Sci. 2022, 12, 4979. [Google Scholar] [CrossRef]
- Jiang, F.; Hu, R.; Yang, Y. Abrupt Change in the Time Sequences of Flood Disastersin Xinjiang and Its Possible Climatic Reasons. J. Glaciol. Geocryol. 2004, 26, 674–681. [Google Scholar]
- Zou, Q.; Wang, G.; He, B.; Shen, Y. Responding of Summer Runoff and Flood Processes to Extreme Climate Events in Manas River Basin, Tianshan Mountains during 1957–2010. J. Glaciol. Geocryol. 2013, 35, 733–740. [Google Scholar]
- He, C.; Luo, C.; Chen, F.; Long, A.; Tang, H. Prediction of future climate change in Hetian River Basin based on CMIP6 multi-model. Earth Sci. Front. 2023, 30, 515–528. [Google Scholar]
- Jun, D.A.; Haizhu, H.U.; Xiaomin, M.A.; Ji, Z.H. Future climate change trends in the Shiyang River Basin based on the CMIP6 multi-model estimation data. Arid Zone Res. 2023, 40, 1547–1562. [Google Scholar]
- Ma, F.; Yuan, X.; Liu, X. Intensification of drought propagation over the Yangtze River basin under climate warming. Int. J. Climatol. 2023, 43, 5640–5661. [Google Scholar] [CrossRef]
- Reder, A.; Raffa, M.; Montesarchio, M.; Mercogliano, P. Performance evaluation of regional climate model simulations at different spatial and temporal scales over the complex orography area of the Alpine region. Nat. Hazards 2020, 102, 151–177. [Google Scholar] [CrossRef]
- Gu, X. Response of Runoff to Climate Change in Runoff Producing area of Manasi River Basin. Master Thesis, Shihezi University, Shihezi, China, 2021. [Google Scholar]
- Donk, P.; Van Uytven, E.; Willems, P.; Taylor, M.A. Assessment of the potential implications of a 1.5 °C versus higher global temperature rise for the Afobaka hydropower scheme in Suriname. Reg. Environ. Chang. 2018, 18, 2283–2295. [Google Scholar] [CrossRef]
- Niroumand Fard, F.; Khashei Siuki, A.; Hashemi, S.R.; Ghorbani, K. Evaluation of the effect of scenarios in the 6th report of IPCC on the prediction groundwater level using the non-linear model of the input-output time series. Environ. Monit. Assess. 2023, 195, 1359. [Google Scholar] [CrossRef]
- Li, C.; Hao, J.; Zhang, G.; Fang, H.; Wang, Y.; Lu, H. Runoff variations affected by climate change and human activities in Yarlung Zangbo River, southeastern Tibetan Plateau. Catena 2023, 230, 107184. [Google Scholar] [CrossRef]





| Data Type | Data Name | Data Description | Source | |
|---|---|---|---|---|
| Observation Data | HRLT precipitation, maximum/minimum temperature daily value 0.5° × 0.5° grid dataset | The period is from 1979 to 2014. | https://doi.pangaea.de/10.1594/PANGAEA.941329?format=html#download (Accessed on 10 October 2024) | |
| CMIP6 Mode Data | Pattern history data | The period is from 1979 to 2014. | Lawrence Livermore National Laboratory, LLNL | |
| Future scenarios | SSP1-2.6 | Future scenario data: low forcing scenario radiative forcing stabilizes at 2.6 W/m2 in 2100. | ||
| SSP2-4.5 | Future scenario data: medium forcing scenario, radiative forcing stabilizes at 4.5 W/m2 in 2100. | |||
| SSP5-8.5 | Future scenario data: high forcing scenario, radiative forcing stabilizes at 8.5 W/m2 in 2100. | |||
| Pattern Name | Home Country | R&D Organizations | Grid Data | Native Resolution |
|---|---|---|---|---|
| ACCESS-CM2 | Australia | Commonwealth Scientific and Industrial Research Organisation (CSIRO), Bureau of Meteorology (BoM) | 192 × 144 | 1.875° × 2.5° |
| BCC-CSM2-MR | China | Beijing Climate Center (BCC), Chinese Academy of Meteorological Sciences (CAMS) | 288 × 192 | 1.125° × 1.125° |
| CanESM5 | Canada | Canadian Centre for Climate Modelling and Analysis (CCCma), Environment, and Climate Change Canada | 128 × 64 | 2.8125° × 2.8125° |
| EC-Earth3 | Europe | European Centre for Medium-Range Weather Forecasts (ECMWF), several European institutions | 320 × 160 | 1.125° × 1.125° |
| FGOALS-f3-L | China | Institute of Atmospheric Physics (IAP), Chinese Academy of Sciences (CAS) | 80 × 180 | 1.25° × 1.25° |
| INM-CM5-0 | Russia | Institute for Numerical Mathematics (INM), Russian Academy of Sciences (RAS) | 180 × 120 | 2.0° × 2.5° |
| MIROC6 | Japan | Japan Agency for Marine-Earth Science and Technology (JAMSTEC), National Institute for Environmental Studies (NIES), and Atmosphere and Ocean Research Institute (AORI) | 256 × 128 | 1.4° × 1.4° |
| MPI-ESM1-2-HR | Germany | Max Planck Institute for Meteorology (MPI-M) | 192 × 96 | 1.125° × 1.125° |
| IPSL-CM6A-LR | France | Institute Pierre-Simon Laplace (IPSL), several French institutions | 144 × 143 | 1.9° × 2.5° |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, F.; He, X.; Yang, G.; Li, X. A Future Scenario Prediction for the Arid Inland River Basins in China Under Climate Change: A Case Study of the Manas River Basin. Sustainability 2025, 17, 3658. https://doi.org/10.3390/su17083658
Zhang F, He X, Yang G, Li X. A Future Scenario Prediction for the Arid Inland River Basins in China Under Climate Change: A Case Study of the Manas River Basin. Sustainability. 2025; 17(8):3658. https://doi.org/10.3390/su17083658
Chicago/Turabian StyleZhang, Fuchu, Xinlin He, Guang Yang, and Xiaolong Li. 2025. "A Future Scenario Prediction for the Arid Inland River Basins in China Under Climate Change: A Case Study of the Manas River Basin" Sustainability 17, no. 8: 3658. https://doi.org/10.3390/su17083658
APA StyleZhang, F., He, X., Yang, G., & Li, X. (2025). A Future Scenario Prediction for the Arid Inland River Basins in China Under Climate Change: A Case Study of the Manas River Basin. Sustainability, 17(8), 3658. https://doi.org/10.3390/su17083658









