Synergistic Coordination Between PWM Inverters and DC-DC Converters for Power Quality Improvement of Three-Phase Grid-Connected PV Systems
Abstract
:1. Introduction
1.1. Sliding Mode Control
1.2. Key Contributions of the Paper
- Enhanced DC-link voltage stability under varying solar irradiance, improving overall system reliability.
- Improved power quality using a synergistic control approach leads to better power quality by reducing voltage fluctuations and harmonics.
- Reduced system cost and size by enhancing DC-link voltage stability.
- Increasing the resiliency of the system against disturbances and uncertainties by the coordination of the boost converter and VSI controllers.
1.3. Study Outlines
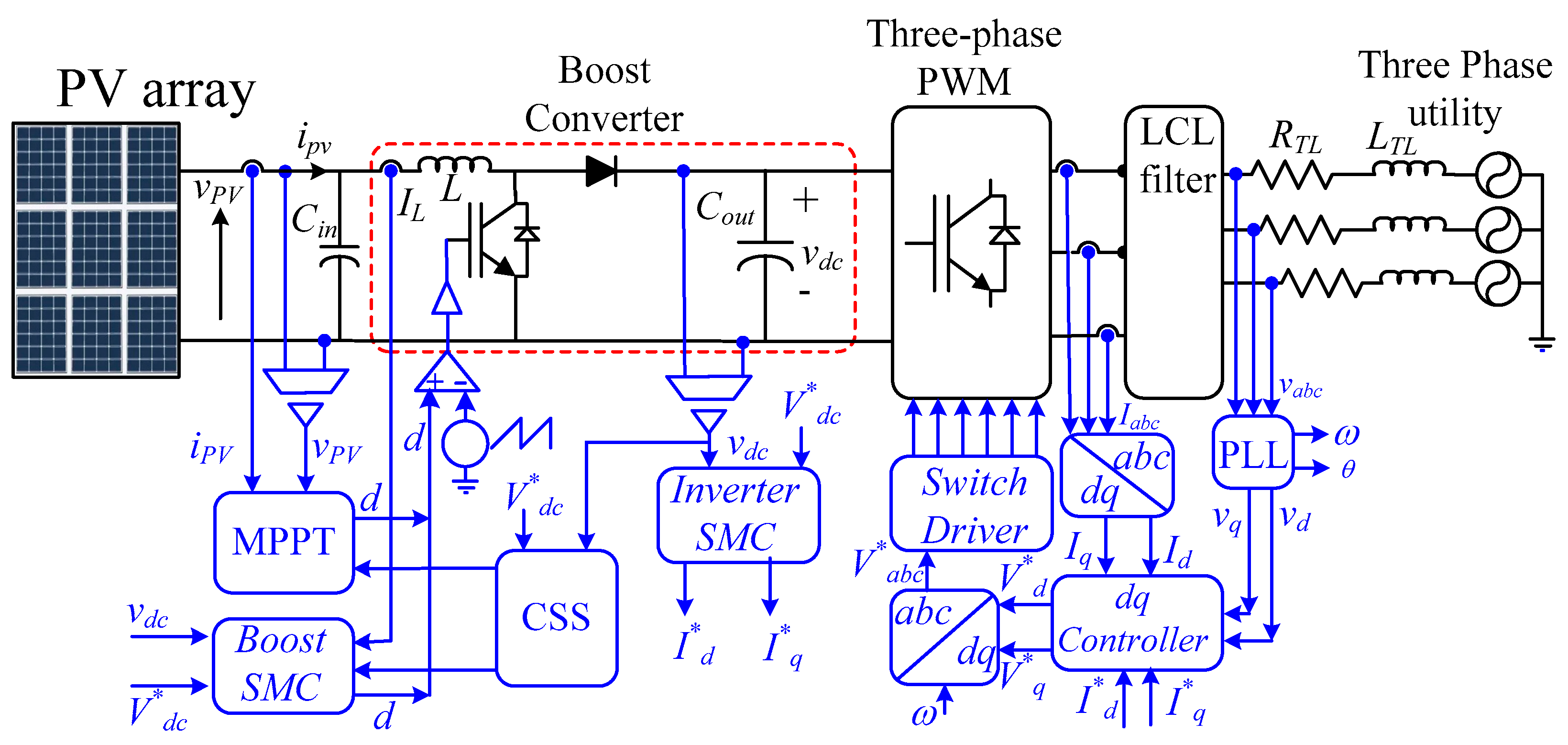
2. System Description
3. System Modeling
3.1. Mathematical Model of the Boost Converter
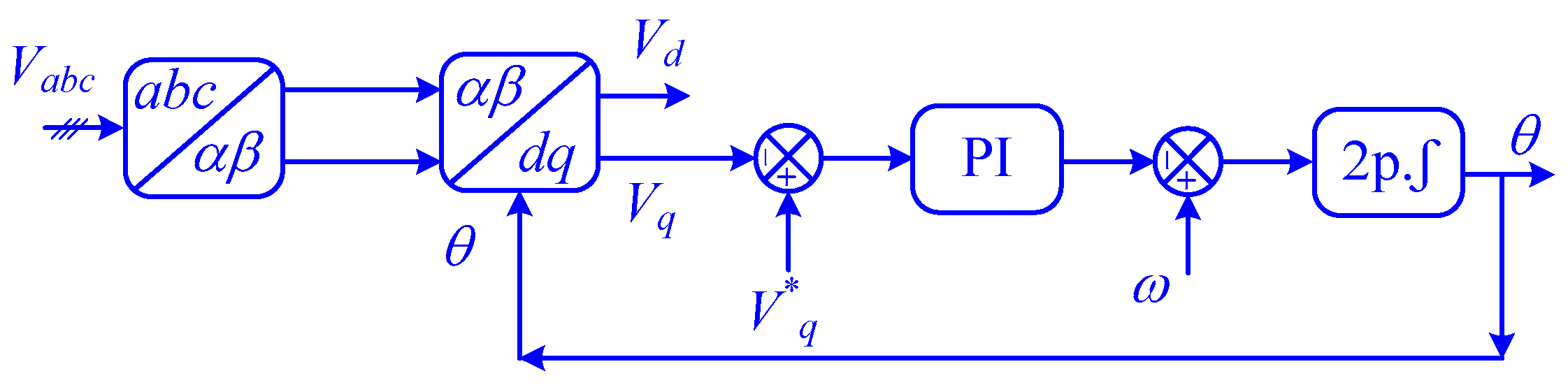
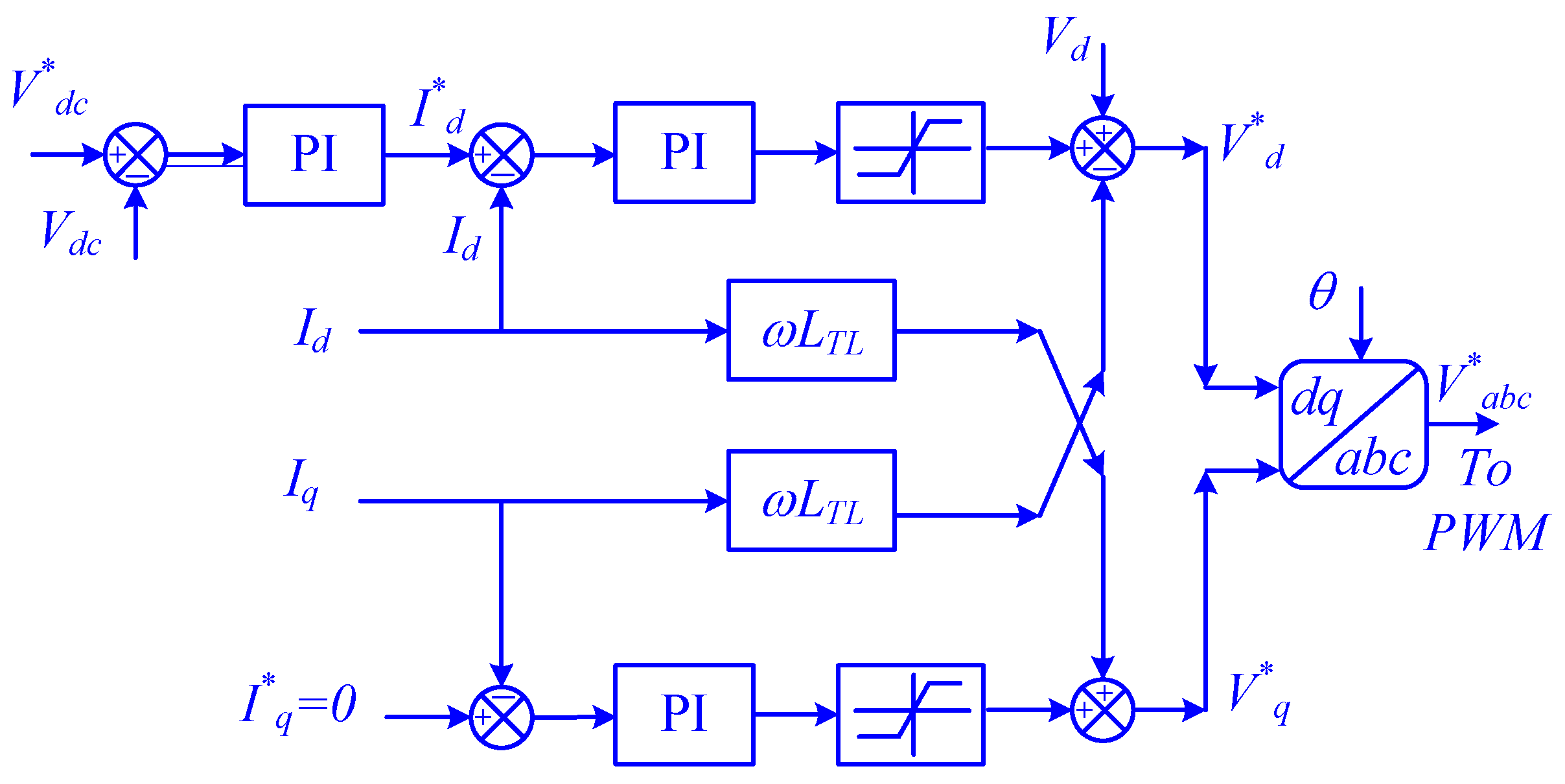
3.2. Mathematical Model of the Three-Phase VSI
4. Simulation Work
4.1. System Parameters
4.2. Simulation Results
- i.
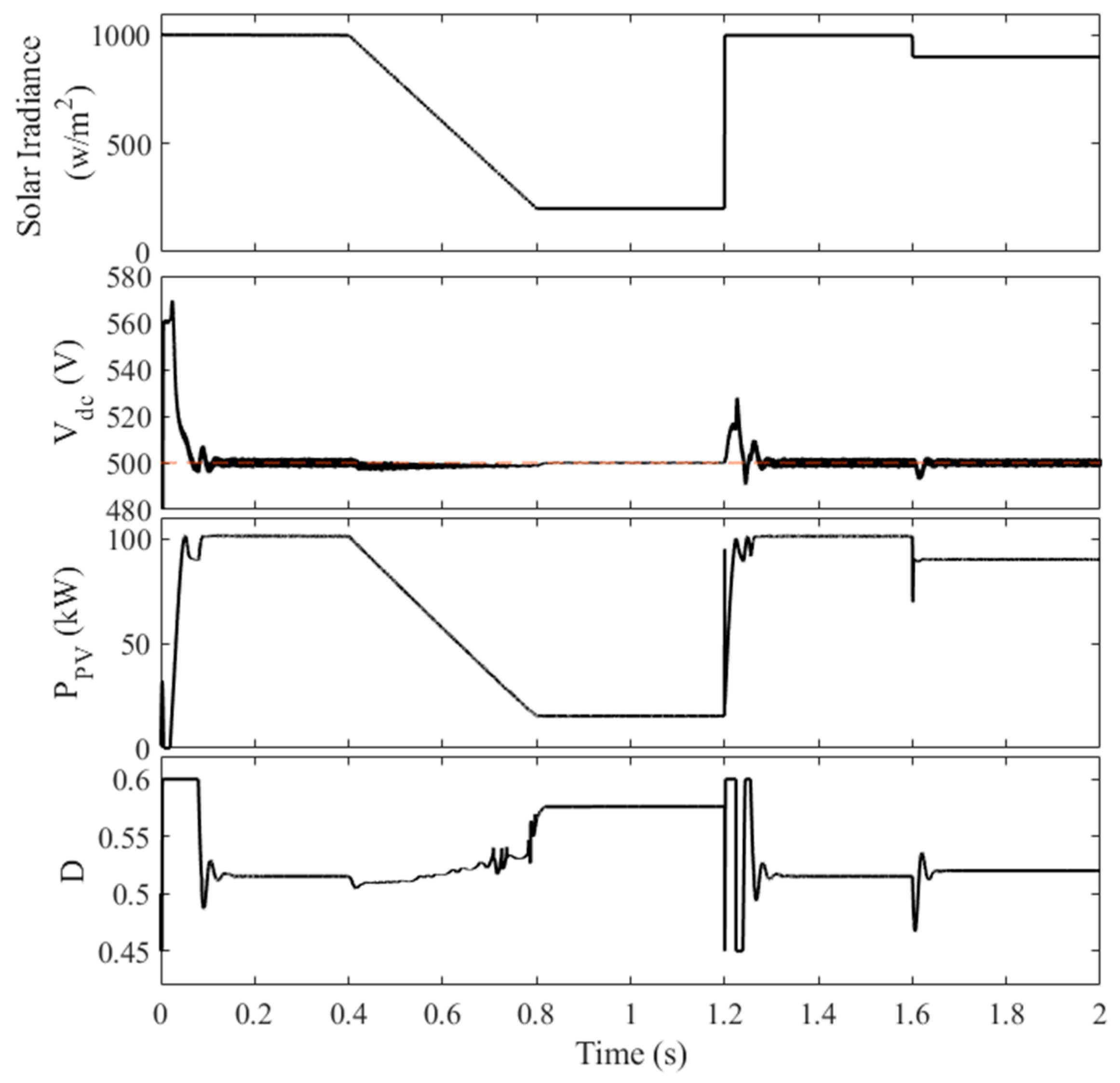
- Without DC-Link Coordination (Without CSS)
- 0–0.4 s: Constant irradiance of 1000 W/m2
- 0.4–0.8 s: decrease in irradiance from 1000 W/m2 to 200 W/m2
- 0.8–1.2 s: Constant irradiance of 200 W/m2
- 1.2–1.6 s: Constant irradiance of 1000 W/m2
- 1.6–2.0 s: Constant irradiance of 900 W/m2
- ii.
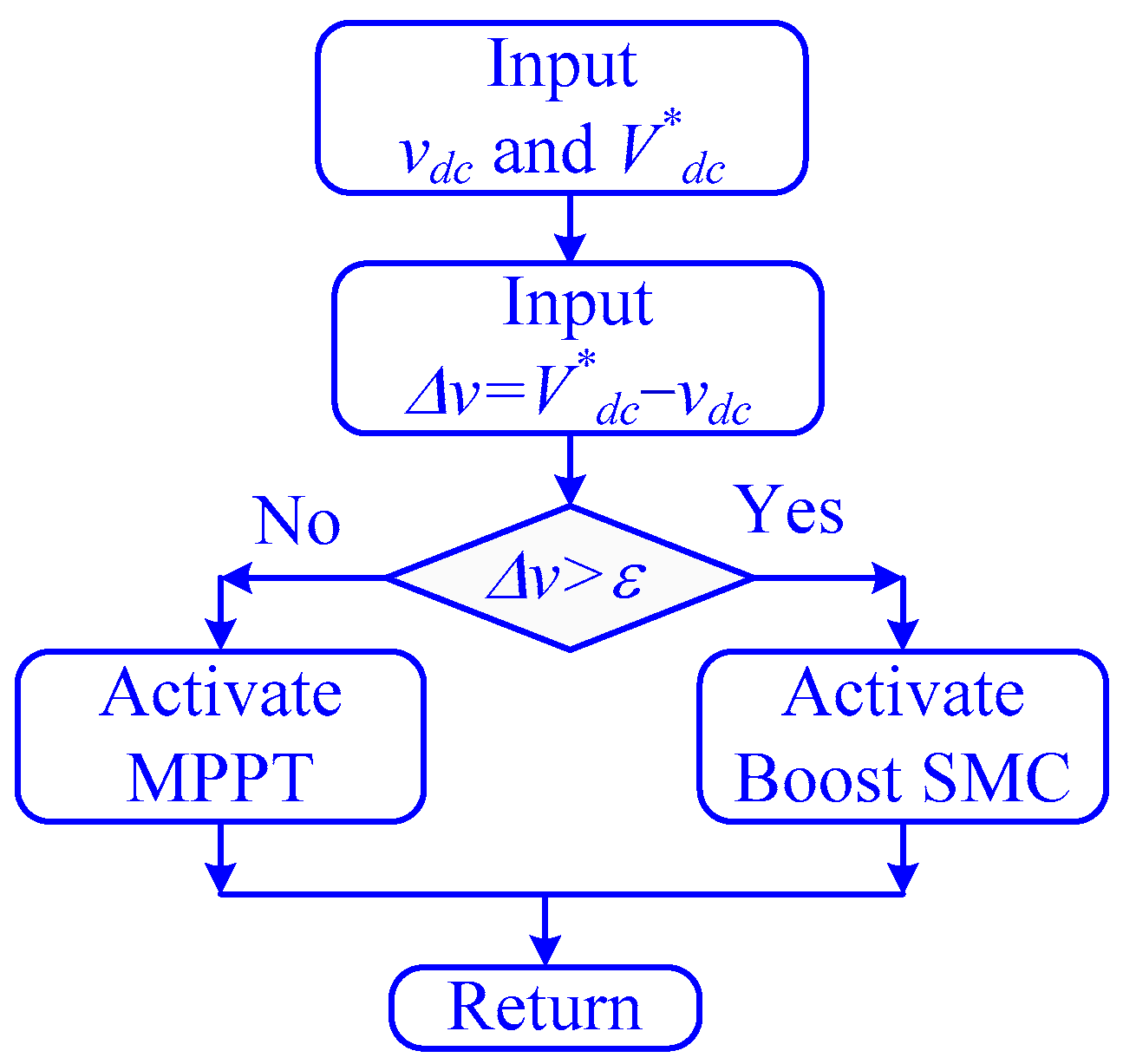
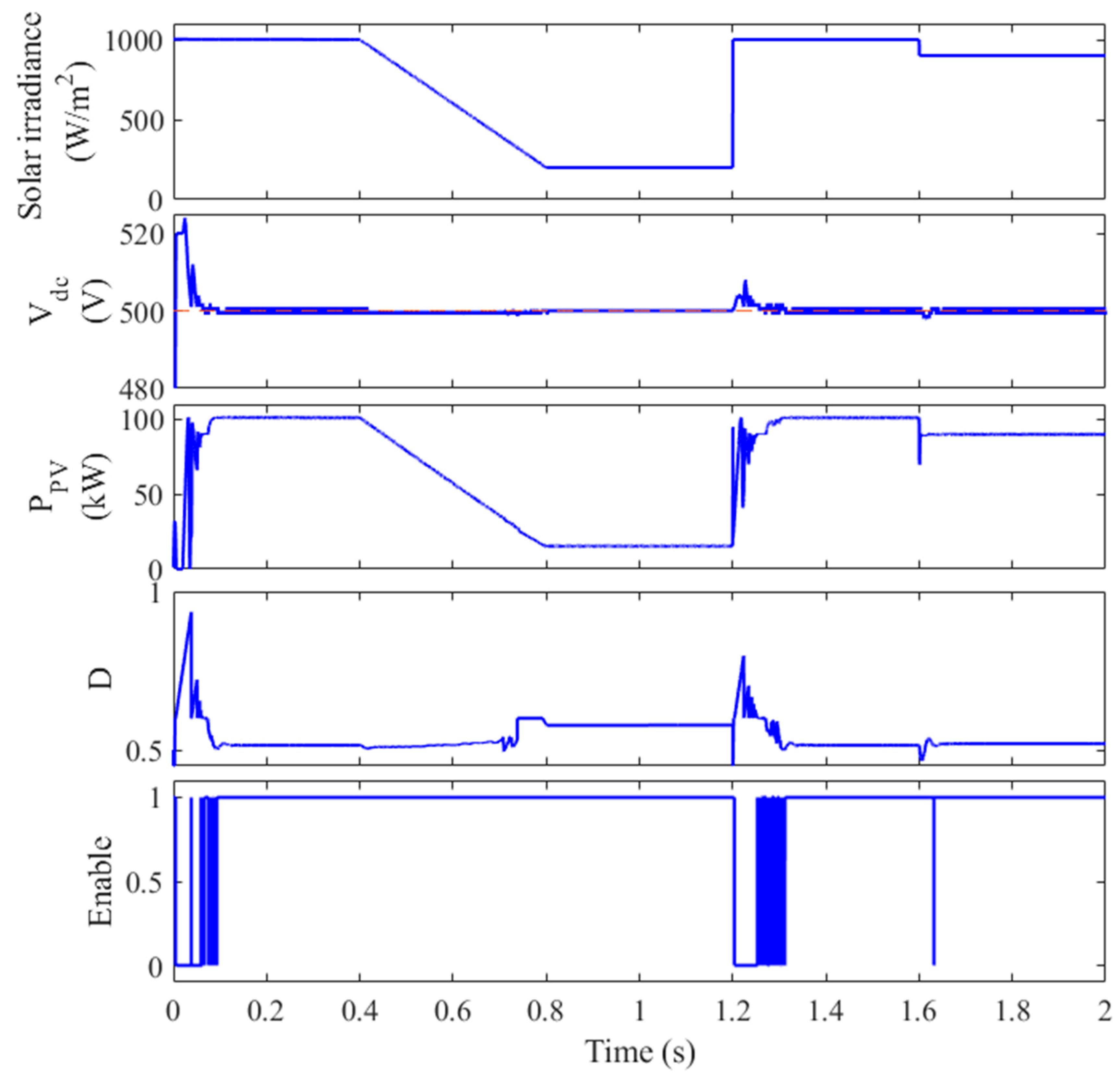
- With DC-Link Coordination (with CSS)
- iii.
- Comparison between with and without CSS
- iv.
- Comparison between SMC, Droop Power Control, and Predictive Control
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| Abb. | Full Form | Abb. | Full Form |
| CPG | Constant Power Generation | P&O | Perturb and Observe |
| CSS | Control Selection Strategy | PI | Proportional-Integral |
| DSMC | Direct SMC | PLL | Phase-Locked Loop |
| ESR | Equivalent Series Resistance | PSCs | Partial Shading Conditions |
| FLC | Fuzzy Logic Controller | PSO | Particle Swarm Optimization |
| GWO | Grey Wolf Optimization | PV | Photovoltaic |
| LVRT | Low-Voltage Ride-Through | PWM | Pulse Width Modulation |
| MCA | Musical Chairs Algorithm | SMC | Sliding Mode Control |
| MPPT | Maximum Power Point Tracker | SMCI | SMC with Integral action |
| OBSMC | Observer-based Backstepping SMC | VSI | Voltage Source Inverter |
| Symbol | Definition | Symbol | Definition |
| vPV | Terminal PV voltage | ed, eq | Park’s transformation of the grid voltages |
| iPV | PV current | va, vb, vc | Inverter output voltages |
| Cin | Input capacitor | ia, ib, ic | Three-phase output currents |
| Cout | DC-link capacitor | ea, eb, ec | Grid three phase voltages |
| vdc | DC-link voltage | Reference of d and q voltages | |
| L | Inductance of boost inductor | Reference of d and q currents | |
| RTL | Transmission line resistance | Parks transformation of the voltages at the output of the three-phase inverter. | |
| LTL | Transmission line inductance | Parks transformation of the grid currents | |
| d | Duty ratio of boost converter | idco | Output current from the DC-link capacitor |
| Reference DC-link voltage | iL | Inductor current of boost converter | |
| Three-phase grid voltages | fs | Switching frequency of the boost converter | |
| Three-phase grid currents | u | Switching state of the boost converter | |
| Reference of the grid voltages | Dmin, Dmax | Minimum and maximum allowable duty ratio of the boost converter | |
| ω | Angular velocity | VI | Vector of the inverter output voltage |
| θ | Phase angle | I | Inverter output current vector |
| ε | Predefined tolerance for change in the DC voltage | E | Vector of electric utility vector |
| ev | Error in DC-link voltage | x1, x2, x3 | State space variables of the SMC |
| ei | Error in PV current | σ | Sliding surface of the SMC |
References
- Raimi, D.; Zhu, Y.; Newell, R.G.; Prest, B.C.; Bergman, A. Global energy outlook 2023: Sowing the seeds of an energy transition. Resour. Future 2023, 1, 1–44. [Google Scholar]
- Baatiah, A.O.; Eltamaly, A.M.; Alotaibi, M.A. Improving photovoltaic MPPT performance through PSO dynamic swarm size reduction. Energies 2023, 16, 6433. [Google Scholar] [CrossRef]
- Guo, K.; Cui, L.; Mao, M.; Zhou, L.; Zhang, Q. An improved gray wolf optimizer MPPT algorithm for PV system with BFBIC converter under partial shading. IEEE Access 2020, 8, 103476–103490. [Google Scholar] [CrossRef]
- Eltamaly, A.M. A novel musical chairs algorithm applied for MPPT of PV systems. Renew. Sustain. Energy Rev. 2021, 146, 111135. [Google Scholar] [CrossRef]
- Rezk, H.; Eltamaly, A.M. A comprehensive comparison of different MPPT techniques for photovoltaic systems. Sol. Energy 2015, 112, 1–11. [Google Scholar] [CrossRef]
- Femia, N.; Petrone, G.; Spagnuolo, G.; Vitelli, M. Optimization of perturb and observe maximum power point tracking method. IEEE Trans. Power Electron. 2005, 20, 963–973. [Google Scholar] [CrossRef]
- Al-Wesabi, I.; Fang, Z.; Wei, Z.; Dong, H. Direct sliding mode control for dynamic instabilities in DC-link voltage of standalone photovoltaic systems with a small capacitor. Electronics 2022, 11, 133. [Google Scholar] [CrossRef]
- Memon, M.A.; Bhutto, G.M.; Buriro, E.A. Sizing of dc-link capacitor for a grid connected solar photovoltaic inverter. Indian J. Sci. Technol 2020, 13, 2272–2281. [Google Scholar] [CrossRef]
- Sangwongwanich, A.; Shen, Y.; Chub, A.; Liivik, E.; Vinnikov, D.; Wang, H.; Blaabjerg, F. Design for accelerated testing of DC-link capacitors in photovoltaic inverters based on mission profiles. IEEE Trans. Ind. Appl. 2020, 57, 741–753. [Google Scholar] [CrossRef]
- Kumar, N.B.; Urundady, V. Sliding mode controller with integral action for dc-link voltage control of grid-integrated domestic photovoltaic systems. Arab. J. Sci. Eng. 2020, 45, 6583–6600. [Google Scholar] [CrossRef]
- Bhattacharyya, S.; Samanta, S. DC link voltage control based power management scheme for standalone PV systems. In Proceedings of the 2018 IEEE International Conference on Power Electronics, Drives and Energy Systems (PEDES), Chennai, India, 18–21 December 2018; pp. 1–5. [Google Scholar]
- Thammasiriroj, W.; Nuchkrua, T.; Ruayariyasub, S. Sliding mode control for stabilizing DC-link of DC-DC converter in photovoltaic systems. In Proceedings of the The 2nd International Symposium on Power Electronics for Distributed Generation Systems, Hefei, China, 16–18 June 2010; pp. 347–351. [Google Scholar]
- Messo, T.; Jokipii, J.; Puukko, J.; Suntio, T. Determining the value of DC-link capacitance to ensure stable operation of a three-phase photovoltaic inverter. IEEE Trans. Power Electron. 2013, 29, 665–673. [Google Scholar] [CrossRef]
- Mohamed, S.R.; Jeyanthy, P.A.; Devaraj, D.; Shwehdi, M.H.; Aldalbahi, A. DC-link voltage control of a grid-connected solar photovoltaic system for fault ride-through capability enhancement. Appl. Sci. 2019, 9, 952. [Google Scholar] [CrossRef]
- Kermadi, M.; Salam, Z.; Eltamaly, A.M.; Ahmed, J.; Mekhilef, S.; Larbes, C.; Berkouk, E. Recent developments of MPPT techniques for PV systems under partial shading conditions: A critical review and performance evaluation. IET Renew. Power Gener. 2020, 14, 3401–3417. [Google Scholar] [CrossRef]
- Eltamaly, A.M. Performance of MPPT techniques of photovoltaic systems under normal and partial shading conditions. In Advances in Renewable Energies and Power Technologies; Elsevier: Amsterdam, The Netherlands, 2018; pp. 115–161. [Google Scholar]
- Laabidi, H.; Jouini, H.; Mami, A. Sliding mode control for PV-wind hybrid system connected to grid. In Proceedings of the International Conference on Green Energy & Environmental Engineering (GEEE-2018), Proceeding of Engineering and technology-PET, Sousse, Tunisia, 28–30 April 2018; pp. 39–44. [Google Scholar]
- Snoussi, J.; Elghali, S.B.; Outbib, R.; Mimouni, M.F. Sliding mode control for frequency-based energy management strategy of hybrid storage system in vehicular application. In Proceedings of the International Symposium on Power Electronics, Electrical Drives, Automation and Motion (SPEEDAM), Capri, Italy, 22–24 June 2016; pp. 1109–1114. [Google Scholar]
- Benadli, R.; Sellami, A. Sliding mode control of a photovoltaic-wind hybrid system. In Proceedings of the 2014 International Conference on Electrical Sciences and Technologies in Maghreb (CISTEM), Tunis, Tunisia, 3–6 November 2014; pp. 1–8. [Google Scholar]
- Anto, E.K.; Asumadu, J.A.; Okyere, P.Y. PID control for improving P&O-MPPT performance of a grid-connected solar PV system with Ziegler-Nichols tuning method. In Proceedings of the IEEE 11th Conference on Industrial Electronics and Applications (ICIEA), Hefei, China, 5–7 June 2016; pp. 1847–1852. [Google Scholar]
- Guo, L.; Hung, J.Y.; Nelms, R.M. Comparative evaluation of sliding mode fuzzy controller and PID controller for a boost converter. Electr. Power Syst. Res. 2011, 81, 99–106. [Google Scholar] [CrossRef]
- Eltamaly, A.M. Modeling of fuzzy logic controller for photovoltaic maximum power point tracker. In Proceedings of the Solar Future 2010 Conference, Istanbul, Turkey, 11–12 February 2010. [Google Scholar]
- Chakraborty, S.; Weiss, M.D.; Simoes, M.G. Distributed intelligent energy management system for a single-phase high-frequency AC microgrid. IEEE Trans. Ind. Electron. 2007, 54, 97–109. [Google Scholar] [CrossRef]
- Sira-Ramírez, H.; Silva-Ortigoza, R. Sliding Mode∑-Δ Modulation Control of the Boost Converter. Asian J. Control 2005, 7, 349–355. [Google Scholar] [CrossRef]
- Viswambharan, A.; Errouissi, R.; Debouza, M.; Shareef, H. Experimental Verification of Disturbance Observer-Based Backstepping Control for DC–DC Boost Converter. IEEE Trans. Circuits Syst. I Regul. Pap. 2023, 70, 5520–5533. [Google Scholar] [CrossRef]
- Nizami, T.K.; Chakravarty, A. Neural network integrated adaptive backstepping control of DC-DC boost converter. IFAC-PapersOnLine 2020, 53, 549–554. [Google Scholar] [CrossRef]
- Abouda, S.; Essounbouli, N.; Chaari, A.; Koubaa, Y. PID and Sliding Mode Control-SMC for a Motor-pump Voltage in a Photovoltaic-PV System based on MPPT Controller. Int. J. Comput. Appl. 2013, 73, 44–49. [Google Scholar] [CrossRef]
- Khan, R.; Khan, L.; Ullah, S.; Sami, I.; Ro, J.-S. Backstepping based super-twisting sliding mode MPPT control with differential flatness oriented observer design for photovoltaic system. Electronics 2020, 9, 1543. [Google Scholar] [CrossRef]
- Idrissi, R.E.; Abbou, A.; Mokhlis, M. Backstepping Integral Sliding Mode Control Method for Maximum Power Point Tracking for Optimization of PV System Operation Based on High-Gain Observer. Int. J. Intell. Eng. Syst. 2020, 13, 133–144. [Google Scholar] [CrossRef]
- Seo, S.-W.; Choi, H.H. Digital implementation of fractional order PID-type controller for boost DC–DC converter. IEEE Access 2019, 7, 142652–142662. [Google Scholar] [CrossRef]
- Johnson, R.S.; Altin, B.; Sanfelice, R.G. Hybrid Adaptive Control for the DC-DC Boost Converter. IFAC-PapersOnLine 2021, 54, 73–78. [Google Scholar] [CrossRef]
- Kobaku, T.; Jeyasenthil, R.; Sahoo, S.; Ramchand, R.; Dragicevic, T. Quantitative feedback design-based robust PID control of voltage mode controlled DC-DC boost converter. IEEE Trans. Circuits Syst. II Express Briefs 2020, 68, 286–290. [Google Scholar] [CrossRef]
- Van, T.H.; Le Van, T.; Thi, T.M.N.; Duong, M.Q.; Sava, G.N. Improving the output of DC-DC converter by phase shift full bridge applied to renewable energy. Rev. Roum. Des Sci. Tech.—Sér. Électrotech. Énerg. 2021, 66, 175–180. [Google Scholar]
- Muktiadji, R.F.; Ramli, M.A.M.; Bouchekara, H.R.E.H.; Milyani, A.H.; Rawa, M.; Seedahmed, M.M.A.; Budiman, F.N. Control of boost converter using observer-based backstepping sliding mode control for DC microgrid. Front. Energy Res. 2022, 10, 828978. [Google Scholar] [CrossRef]
- Ahmed, M.; Harbi, I.; Kennel, R.; Rodriguez, J.; Abdelrahem, M. Model-based maximum power point tracking algorithm with constant power generation capability and fast DC-link dynamics for two-stage PV systems. IEEE Access 2022, 10, 48551–48568. [Google Scholar] [CrossRef]
- Gohar Ali, H.; Vilanova Arbos, R.; Herrera, J.; Tobón, A.; Peláez-Restrepo, J. Non-linear sliding mode controller for photovoltaic panels with maximum power point tracking. Processes 2020, 8, 108. [Google Scholar] [CrossRef]
- Montoya, D.G.; Paja, C.A.R.; Giral, R. A new solution of maximum power point tracking based on sliding mode control. In Proceedings of the IECON 2013-39th Annual Conference of the IEEE Industrial Electronics Society, Vienna, Austria, 10–13 November 2013; pp. 8350–8355. [Google Scholar]
- Montoya, D.G.; Ramos-Paja, C.A.; Giral, R. Improved design of sliding-mode controllers based on the requirements of MPPT techniques. IEEE Trans. Power Electron. 2015, 31, 235–247. [Google Scholar] [CrossRef]
- Noureldeen, O.; Ibrahim, A.M.A. Low-voltage ride-through capability enhancement of a grid-connected photovoltaic/wind hybrid power system. In Proceedings of the Nineteenth International Middle East Power Systems Conference (MEPCON), Cairo, Egypt, 19–21 December 2017; pp. 786–795. [Google Scholar]
- Kumar, V.; Singh, M. Sensorless DC-link control approach for three-phase grid integrated PV system. Int. J. Electr. Power Energy Syst. 2019, 112, 309–318. [Google Scholar] [CrossRef]
- Dhouib, B.; Zdiri, M.A.; Alaas, Z.; Hadj Abdallah, H. Fault Analysis of a Small PV/Wind Farm Hybrid System Connected to the Grid. Appl. Sci. 2023, 13, 1743. [Google Scholar] [CrossRef]
- Trejos, A.; Gonzalez, D.; Ramos-Paja, C.A. Modeling of step-up grid-connected photovoltaic systems for control purposes. Energies 2012, 5, 1900–1926. [Google Scholar] [CrossRef]
- Bianconi, E.; Calvente, J.; Giral, R.; Mamarelis, E.; Petrone, G.; Ramos-Paja, C.A.; Spagnuolo, G.; Vitelli, M. Perturb and observe MPPT algorithm with a current controller based on the sliding mode. Int. J. Electr. Power Energy Syst. 2013, 44, 346–356. [Google Scholar] [CrossRef]
- Bianconi, E.; Calvente, J.; Giral, R.; Mamarelis, E.; Petrone, G.; Ramos-Paja, C.A.; Spagnuolo, G.; Vitelli, M. A fast current-based MPPT technique employing sliding mode control. IEEE Trans. Ind. Electron. 2012, 60, 1168–1178. [Google Scholar] [CrossRef]
- Spiazzi, G.; Mattavelli, P. Sliding-mode control of switched-mode power supplies. In The Power Electronics Handbook; CRC Press: Boca Raton, FL, USA, 2018; pp. 8-1–8-24. [Google Scholar]
- Touil, S.A.; Boudjerda, N.; Boubakir, A.; El Khamlichi Drissi, K. A sliding mode control and artificial neural network based MPPT for a direct grid-connected photovoltaic source. Asian J. Control 2019, 21, 1892–1905. [Google Scholar] [CrossRef]
- Chen, Y.-M.; Chang, C.-H.; Wu, H.-C. DC-link capacitor selections for the single-phase grid-connected PV system. In Proceedings of the International Conference on Power Electronics and Drive Systems (PEDS), Taipei, Taiwan, 2–5 November 2009; pp. 72–77. [Google Scholar]
- Solar, C. CS5P-220M. Available online: https://www.pvxchange.com/Solar-Modules/Canadian-Solar/CS5P-220M_1-2103721 (accessed on 10 December 2024).
- Paspatis, A.G.; Konstantopoulos, G.C. Voltage support under grid faults with inherent current limitation for three-phase droop-controlled inverters. Energies 2019, 12, 997. [Google Scholar] [CrossRef]

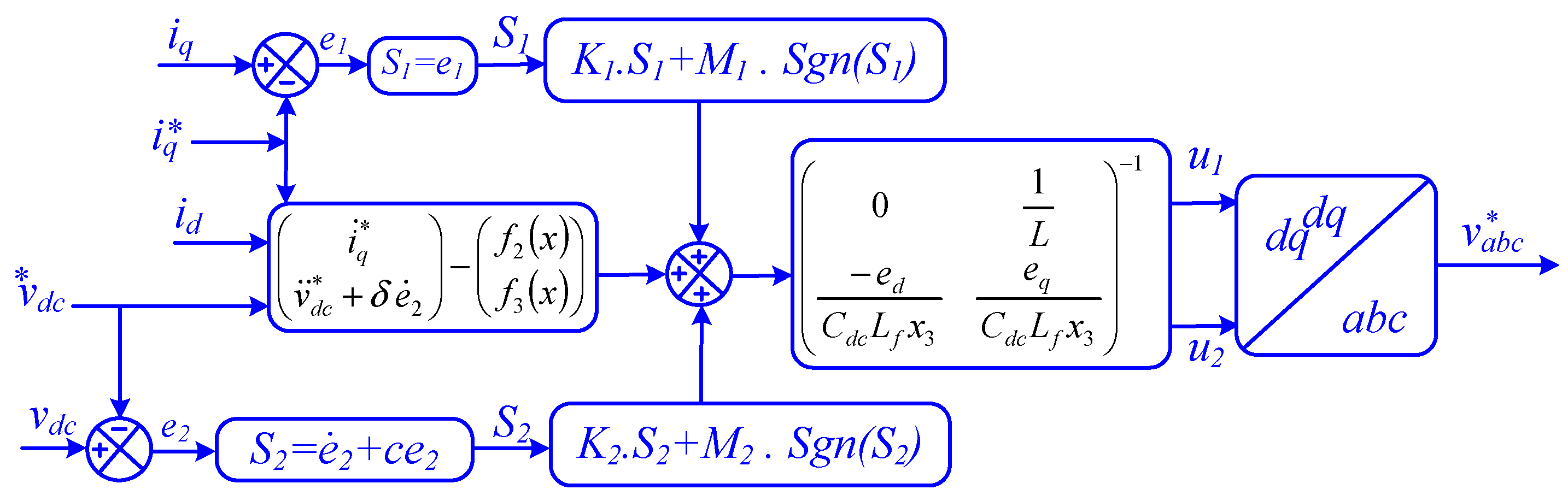
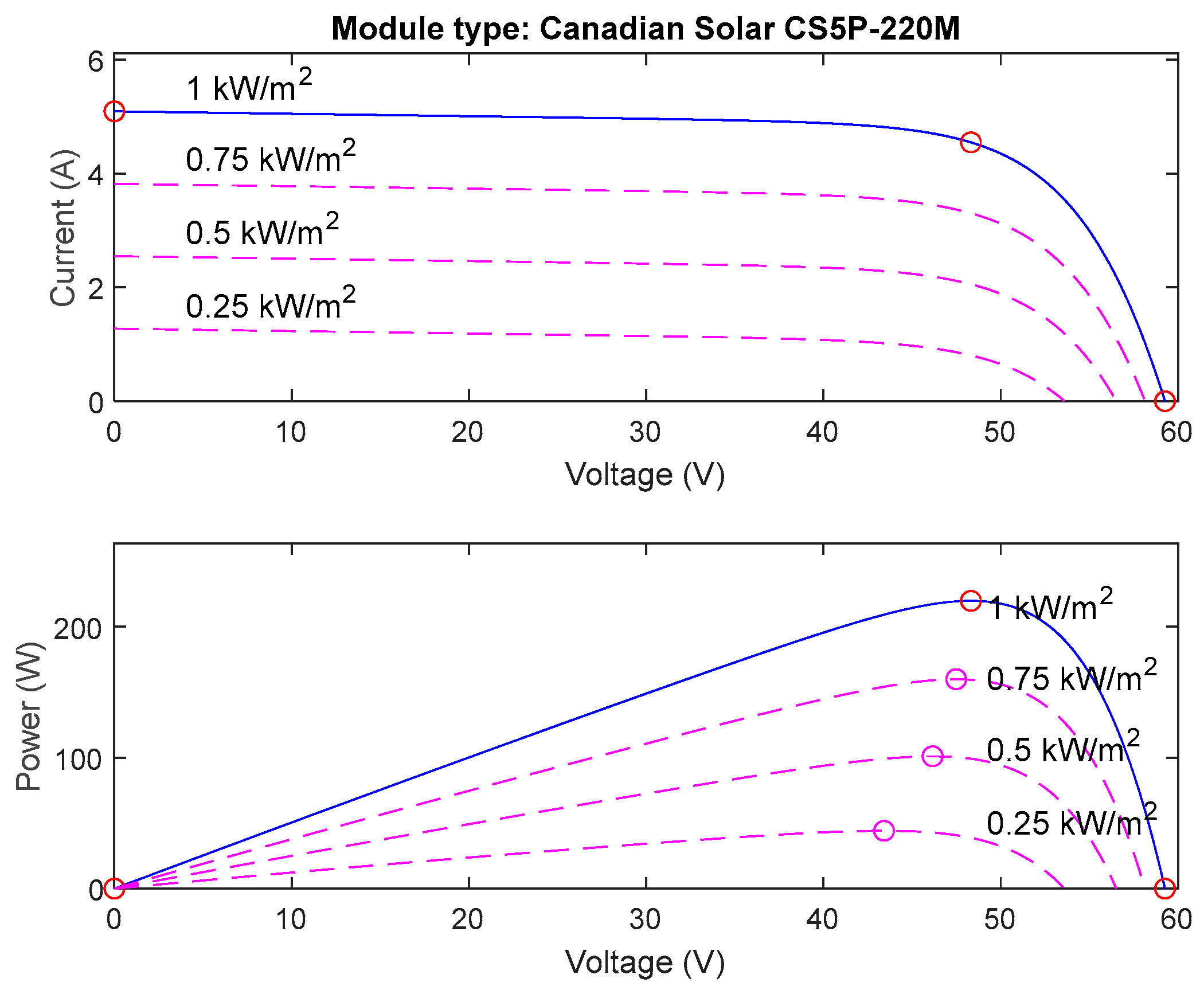

| Study | Integration | MPPT | DC-DC Converter | DC-Link Control | BESS Control | Inverter Control | Coordination |
|---|---|---|---|---|---|---|---|
| [7] | OFF-Grid | P&O | Boost | DSMC | Yes | No | No |
| [10] | ON-Grid | SMC | Boost | SMCI | No | d-q | No |
| [12] | OFF-Grid | SMC | Boost | SMC | No | No | No |
| [14] | ON-Grid | IC | Boost | PI | No | d-q | Yes |
| [35] | ON-Grid | P&O | Boost | CPG | No | d-q | Yes |
| [36] | OFF-Grid | SMC | Boost | No | No | No | No |
| [38] | ON-Grid | SMC | Boost | PI | No | d-q | No |
| [37] | ON-Grid | P&O | Boost | SMC | No | d-q | Yes |
| [39] | ON-Grid | IC | Boost | PI | No | d-q | Yes |
| [40] | ON-Grid | IC | Boost | PI | No | d-q | No |
| Proposed | ON-Grid | MCA | Boost | SMC | No | d-q | Yes |
| Nominal Power (Wp): | Nominal Power (Wp): | Nominal Power (Wp): | Nominal Power (Wp): |
|---|---|---|---|
| 220 | 220 | 220 | 220 |
| Current at MPP (A): | Current at MPP (A): | Current at MPP (A): | Current at MPP (A): |
| 4.68 | 4.68 | 4.68 | 4.68 |
| Parameter | Value | Parameter | Value |
|---|---|---|---|
| Cin | 94 uF | L | 5 mH |
| Cout | 20 mF | LTL | 0.2 mH |
| fs | 10 kHz | RTL | 2 m W |
| Sampling time | 10 ms | Grid | 3-phase 220 V, 60 Hz |
| Items | Without CSS | With CSS | ||
|---|---|---|---|---|
| SMC | DPC | MPC | ||
| Overshooting DC-link voltage (V) | 570 | 523 | 537 | 526 |
| DC-link voltage at t = 1.2 s | 525 | 504.3 | 509.6 | 507.4 |
| Standard deviation of DC-link voltage | 17.93 | 5.92 | 10.2 | 8.17 |
| Average power (kW) | 70.07 | 70.3 | 70.15 | 70.23 |
| Highest THD % | 3.4 | 2.43 | 2.73 | 2.48 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Eltamaly, A.M.; Almutairi, Z.A. Synergistic Coordination Between PWM Inverters and DC-DC Converters for Power Quality Improvement of Three-Phase Grid-Connected PV Systems. Sustainability 2025, 17, 3748. https://doi.org/10.3390/su17083748
Eltamaly AM, Almutairi ZA. Synergistic Coordination Between PWM Inverters and DC-DC Converters for Power Quality Improvement of Three-Phase Grid-Connected PV Systems. Sustainability. 2025; 17(8):3748. https://doi.org/10.3390/su17083748
Chicago/Turabian StyleEltamaly, Ali M., and Zeyad A. Almutairi. 2025. "Synergistic Coordination Between PWM Inverters and DC-DC Converters for Power Quality Improvement of Three-Phase Grid-Connected PV Systems" Sustainability 17, no. 8: 3748. https://doi.org/10.3390/su17083748
APA StyleEltamaly, A. M., & Almutairi, Z. A. (2025). Synergistic Coordination Between PWM Inverters and DC-DC Converters for Power Quality Improvement of Three-Phase Grid-Connected PV Systems. Sustainability, 17(8), 3748. https://doi.org/10.3390/su17083748







