A Hybrid Inexact Optimization Method for Land-Use Allocation in Association with Environmental/Ecological Requirements at a Watershed Level

Abstract

In this study, an inexact stochastic fuzzy programming (ISFP) model is proposed for land-use allocation (LUA) and environmental/ecological planning at a watershed level, where uncertainties associated with land-use parameters, benefit functions, and environmental/ecological requirements are described as discrete intervals, probabilities and fuzzy sets. In this model, an interval stochastic fuzzy programming model is used to support quantitative optimization under uncertainty. Complexities in land-use planning systems can be systematically reflected, thus applicability of the modeling process can be highly enhanced. The proposed method is applied to planning land use/ecological balance in Poyang Lake watershed, China. The objective of the ISFP is maximizing net benefit from the LUA system and the constraints including economic constraints, social constraints, land suitability constraints, environmental constraints, ecological constraints and technical constraints. Modeling results indicate that the desired system benefit will be between [15.17, 18.29] × 10¹² yuan under the minimum violating probabilities; the optimized areas of commercial land, industrial land, agricultural land, transportation land, residential land, water land, green land, landfill land and unused land will be optimized cultivated land, forest land, grass land, water land, urban land, unused land and landfill will be [228234, 237844] ha, [47228, 58451] ha, [20982, 23718] ha, [33897, 35280] ha, [15215, 15907] ha, [528, 879] ha and [1023, 1260] ha. These data can be used for generating decision alternatives under different scenarios and thus help decision makers identify desired policies under various system-reliability constraints of ecological requirement and environmental capacity. Tradeoffs between system benefits and constraint-violation risks can be tackled. They are helpful for supporting (a) decision of land-use allocation and government investment; (b) formulation of local policies regarding ecological protection, environment protection and economic development; (c) analysis of interactions among economic benefits, system reliability and ecological requirements.

1. Introduction

Land-use allocation (LUA) in a watershed has attracted much attention from the scientific community, as there are some particular characteristics of a watershed [1]. For example, the ecological condition and environmental aspect have a marked impact on land cover change at a watershed level. There is no doubt that systems analysis techniques can be employed to assist in LUA, which will be helpful for analyzing tradeoffs among various socio-economic and eco-environmental objectives in a watershed [2].

For decades, various models have been proposed to support LUA [3,4,5,6,7,8,9,10,11,12]. These models can be divided into three categories: mathematical models, intelligent models, and GIS-based spatial models. For instance, Carsjens and van der Knaap (2002) used GIS technology to deal with strategic spatial land-use allocation [13]. Sharawi (2006) proposed a cost–benefit analysis method which based a Little–Mirrlees–Squire–van der Tak (LMST) approach for LUA in Sudan [14]. Liu et al. (2007) developed an integrated GIS-based analysis system (IGAS) for LUA of lake areas in urban fringes [15]. Ligmann-Zielinska et al. (2008) presented a spatial multi-objective optimization model for urban land-use planning [16]. Kamusoko et al. (2009) provided a coupled Markov-CA model for simulating land use/cover change [17]. Zhang et al. (2010) proposed a hybrid intelligent model which integrated multi-agent system and genetic algorithm for multi-objective LUA [18]. Han et al. (2011) applied an interval-parameter linear model with stochastic vertices for land-use allocation and water allocation [19]. Mitsova et al. (2011) used the Cellular Automata (CA) model to simulate land cover change and support LUA [20]. Wang et al. (2011) studied a hybrid model which integrated system dynamics model and CA model, and used it to simulate the changes of land-use patterns in drought areas [21]. Wang and Li (2011) developed a coupled Cellular Automata (CA) and Radial Basis Function Neural (RBFN) Network model, which combines Geographic Information Systems (GIS) to contribute to the understanding of the complex land use/cover change process [22]. Zhang et al. (2012) used a GIS-based spatial optimization model and a linear programming model for regional LUA [23]. Haque and Asami (2014) used a multi-objective function and genetic algorithm for LUA [24]. Stewart and Janssen (2014) purposed a genetic algorithm and GIS-based optimization method for LUA [25]. Zhou et al. (2014) proposed an interval fuzzy national-scale land-use model (IFNLM) for China [26].

The above models play an important role in supporting LUA at urban, watershed, regional and country levels. However, they have two shortcomings: first, these models do not give full consideration to uncertain factors in the land use system. In fact, in a typical land-use system, there are many sections which may produce various uncertain parameters [11,12,27,28,29,30,31,32]. For example, Wang et al. (2004) developed an integrated GIS-based optimization model for land-use allocation at a watershed level. However, this model did not consider uncertainties expressed as probabilities [29]. Liu et al. (2007) proposed an inexact chance-constraint linear programming model for LUA of lake areas in urban fringes. However, this model did not consider uncertainties expressed as fuzzy sets [30]. Wang et al. (2010) used a multi-objective interval linear programming model for LUA, which did not consider uncertainties expressed as probabilities and fuzzy sets [31]. Lu et al. (2014) developed a multi-objective interval stochastic LUA model for Suzhou, China. This model also did not consider uncertainties expressed as fuzzy sets [32].

Second, most existing land-use planning models have little consideration of ecological and environmental factors which have a significant influence on land-use system particularly in a watershed [33,34]. In a watershed, some ecological factors, such as habitat quality, habitat heterogeneity, biodiversity, are very important and have a significant impact on land-use system. Svoray et al. (2005) integrated an ecological model which called Habitat Heterogeneity Model (HHM) into GIS framework and used this model to support urban land-use allocation. This model considers some important ecological factors in the land-use system. However, the quant optimization for land-use allocation was neglected and the model was not suitable for land-use problem at a watershed level [35]. Gong et al. (2012) proposed agenetic algorithm based multi-objective model which considered economic benefits and ecological effectiveness, and a performance evaluation and sensitivity analysis were conducted in this model using Pareto optimality. This model considers the ecological effectiveness of LUA, but did not consider any ecological constraints [36]. Chakir and Gallo (2013) used a spatial panel data analysis method to operate LUA, which considered some ecological factors such as biodiversity, soil erosion, and climate change. However, this method did not integrate these ecological factors into the modeling process [37]. Zhang et al. (2014) proposed a Primary Development and Secondary Optimization Model for LUA which analyzed the tradeoff between socio-economic development and ecological stability. This model did not consider uncertain factors in the model [38].

Thus, the objective of this study is to propose a new model which considers uncertainties and ecological/environmental factors to support LUA at a watershed level. The proposed model is based on an inexact stochastic fuzzy programming (ISFP) method which can handle three uncertainties (discrete intervals, probability distribution and fuzzy sets) in the land-use system. Furthermore, the model comprehensively considers two environmental factors (i.e. wastewater; solid-waste) and three ecological factors (i.e., soil erosion; forest and grass cover rate; fertilizer consumption) which are very important in the land-use system. The proposed model is applied to the land-use planning of Poyang Lake watershed, China. The results can be used to support LUA and ecological/environmental planning in the study area.

2. Inexact Stochastic Fuzzy Programming (ISFP) Model

According to the inexact stochastic programming (ISP) model studied by [6,39] and the inexact fuzzy programming (IFP) model studied by [7], an ISFP model can be generated through coupling ISP and IFP:

$$Max{f}^{\pm }\cong C^{\pm }{x}^{\pm }$$

(1a)

subject to:

$$C^{\pm }{x}^{\pm }\gtrsim b_{opt}^{\pm }$$

(1b)

$$A_i^{\pm }x\lesssim b_i^{\pm } i=1, 2, \dots , m\text{.,} i \ne s$$

(1c)

$$A_s^{\pm }x\lesssim b_s^{(p_s)} s=1, 2, \dots , n\text{.,} s \ne i$$

(1d)

where x is a n × 1 alternative set; C is a 1 × n coefficients of an objective function; A_i is a m × n matrix of coefficients of constraints and b_i is a m × 1 matrix; $b_{opt}^{\pm }$ is the aspiration level of the objective values which is set beforehand; p_s denotes the probability that the constraints s are violated. $b_s^{(p_s)}$ represents corresponding values given the cumulative distribution function of $b_s$ and the probability of violating constraint s (p_s). The solution method of model (1) is expressed as follows: on the basis of the principle of fuzzy flexible programming [40], we let λ^± value correspond to the membership grade of satisfaction for a fuzzy decision; specifically, the flexibility in the constraints and fuzziness in the system objective (which are represented by fuzzy sets and denoted as “fuzzy constraints” and a “fuzzy goal”) are expressed as membership grades λ^±. The λ^± corresponds to the degrees of overall satisfaction for the constraints/objective. Model (1) can be converted to:

$$Max{\lambda }^{\pm }$$

(2a)

subject to

$$C^{\pm }{X}^{\pm }\le f_{opt}^{-}+(1-{\lambda }^{\pm })(f_{opt}^{+}-f_{opt}^{-})$$

(2b)

$$A_i^{\pm }{X}^{\pm }\le b_i^{-}+(1-{\lambda }^{\pm })(b_i^{+}-b_i^{-}), i=1, 2, \dots , m\text{.,} i \ne s$$

(2c)

$$A_s^{\pm }x\le b_s^{(p_s)} s=1, 2, \dots , n\text{.,} s \ne i$$

(2d)

$$X^{\pm }\ge 0$$

(2e)

$$0\le {\lambda }^{\pm }\le 1$$

(2f)

where $f_{opt}^{+}$ and $f_{opt}^{-}$ denote the upper and lower bounds of the objective’s aspiration level as designated by decision makers; ${\lambda }^{\pm }$ denote control decision variables corresponding to the degree (membership grade) $X^{\pm }$ solutions fulfilling the fuzzy objective or constraints. Model (2) can be solved through a two-step method: a sub-model corresponding to ${\lambda }^{-}$ is first formulated and solved [40]:

$$Max{\lambda }^{-}$$

(3a)

subject to:

$${\displaystyle \sum _{j=1}^{k_1}{c}_j^{+}}{x}_j^{+}+{\displaystyle \sum _{j=k_1+1}^n{c}_j^{+}}{x}_j^{-}\le f_{opt}^{-}+(1-{\lambda }^{-})(f_{opt}^{+}-f_{opt}^{-})$$

(3b)

$${\displaystyle \sum _{j=1}^{k_1}{\left|a_{ij}\right|}^{-}}Sign(a_{ij}^{-})x_j^{+}+{\displaystyle \sum _{j=k_1+1}^n{\left|a_{ij}\right|}^{+}}Sign(a_{ij}^{+})x_j^{-}\le b_i^{-}+(1-{\lambda }^{-})(b_i^{+}-b_i^{-}),\forall i$$

(3c)

$${\displaystyle \sum _{j=1}^{k_1}{\left|a_{sj}\right|}^{-}}Sign(a_{sj}^{-})x_j^{+}+{\displaystyle \sum _{j=k_1+1}^n{\left|a_{sj}\right|}^{+}}Sign(a_{sj}^{+})x_j^{-}\le b_s^{p_s},\forall s,s\ne i$$

(3d)

$$0\le {\lambda }^{-}\le 1$$

(3e)

$$x_j^{-}\ge 0,j=1,2,\mathrm{...},k_1$$

(3f)

$$x_j^{+}\ge 0,j=k_1+1,k_1+2,\mathrm{...},n$$

(3g)

where sign function means:

$$Sign(x^{\pm })\text{=}\{\begin{array}{c}1，\text{if }{x}^{\pm }\ge 0\\ -1，\text{if }{x}^{\pm }\le 0\end{array}$$

Let $x_{jopt}^{+}$ (j = 1, 2, …, k₁) and $x_{jopt}^{-}$ (j = k₁ + 1, k₁ + 2, …, n) be solutions of sub-model (3). Then, the second sub-model corresponding to ${\lambda }^{+}$ can be formulated supported by the solution of sub-model (4):

$$Max{\lambda }^{+}$$

(4a)

subject to:

$${\displaystyle \sum _{j=1}^{k_1}{c}_j^{-}}{x}_j^{-}+{\displaystyle \sum _{j=k_1+1}^n{c}_j^{-}}{x}_j^{+}\le f_{opt}^{-}+(1-{\lambda }^{-})(f_{opt}^{+}-f_{opt}^{-})$$

(4b)

$${\displaystyle \sum _{j=1}^{k_1}{\left|a_{ij}\right|}^{+}}Sign(a_{ij}^{+})x_j^{-}+{\displaystyle \sum _{j=k_1+1}^n{\left|a_{ij}\right|}^{-}}Sign(a_{ij}^{-})x_j^{+}\le b_i^{-}+(1-{\lambda }^{-})(b_i^{+}-b_i^{-}),\forall i$$

(4c)

$${\displaystyle \sum _{j=1}^{k_1}{\left|a_{ij}\right|}^{+}}Sign(a_{ij}^{+})x_j^{-}+{\displaystyle \sum _{j=k_1+1}^n{\left|a_{ij}\right|}^{-}}Sign(a_{ij}^{-})x_j^{+}\le b_s^{p_s},\forall s,s\ne i$$

(4d)

$$0\le {\lambda }^{+}\le 1$$

(4e)

$$x_{jopt}^{+}\ge x_j^{-}\ge 0,j=1,2,\mathrm{...},k_1$$

(4f)

$$x_j^{+}\ge x_{jopt}^{-},j=k_1+1,k_1+2,\mathrm{...},n$$

(4g)

Let $x_{jopt}^{-}$ (j = 1, 2, …, k₁) and $x_{jopt}^{+}$ (j = k₁ + 1, k₁ + 2, …, n) be solutions of sub-model (4). Thus, we can obtain the interval solutions as follows:

$${\lambda }_{opt}^{\pm }=[{\lambda }_{opt}^{-},{\lambda }_{opt}^{+}]$$

(5a)

$$x_{jopt}^{\pm }=[x_{jopt}^{-},x_{jopt}^{+}],\forall j$$

(5b)

Then, the optimized objective $f_{opt\text{'}}^{-}$ and $f_{opt\text{'}}^{+}$ can be calculated as follows:

$$f_{opt\text{'}}^{-}={\displaystyle \sum _{j=1}^{k_1}{c}_j^{-}}{x}_j^{-}+{\displaystyle \sum _{j=k_1+1}^n{c}_j^{-}}{x}_j^{+}$$

(6a)

$$f_{opt\text{'}}^{+}={\displaystyle \sum _{j=1}^{k_1}{c}_j^{+}}{x}_j^{+}+{\displaystyle \sum _{j=k_1+1}^n{c}_j^{+}}{x}_j^{-}$$

(6b)

Thus, we have

$$f_{jopt}^{\pm }=[f_{opt}^{-},f_{opt}^{+}],\forall j$$

(7)

The ISFP model can effectively handle system uncertainties expressed as discrete intervals, probability distribution and fuzzy sets. Interval linear programming is a good tool to deal with uncertainties expressed as interval values; Probabilistic programming is an effective method for to handling uncertainties expressed as probability distributions existing in the decision making problems; where fuzzy programming (FP) can effectively handle uncertainties expressed as fuzzy sets. The ISFP model, which incorporates the three methods within a general optimization framework, is a good tool to handle uncertainties expressed as discrete interval values, probability distribution and fuzzy sets in a land-use system.

3. ISFP Model for Land-Use Planning of Poyang Lake Watershed

3.1. The Study Area

The Poyang Lake watershed locates in 115°47′~116°45′E, 28°22′~29°45′N, China (Figure 1). The watershed area is 162 × 10³ km², accounting for 9% of the Yangtze River basin. The Poyang Lake watershed is one of the most important flood control libraries in the middle reaches of Yangtze River basin, and the water storage capacity can reach 19.2 × 10⁹–20.9 × 10⁹ m³. Poyang Lake is the biggest freshwater lake in China. The watershed contains 11 districts and the population is approximately 44,228,000 (2012). The watershed’s gross domestic product (GDP) increased rapidly from 0.32 × 10¹² RMB in 2003 to 6.45× 10¹² RMB in 2012, in concert with a population increase from 38,729,000 million to 44,228,000 million.

As a result of fast economic development and urbanization, Poyang Lake watershed suffered from serious environmental and ecological problems in the past a few years. For example, according to reports from environmental monitoring station of Poyang Lake watershed, in 2012, the total wastewater discharge quantity was 13.89 × 10⁹ ton, accounting for 6.59% of China. The discharge quantity of chemical oxygen demand (COD) and ammonia nitrogen (NH₃-N) were 445.3 × 10³ ton and 34.3 × 10³ ton. The discharge quantity of living sewage was 3.56 billion ton, which increased by 9.31% over 2011. Field investigations and monitoring data indicated that water pollution was mostly discharged from both point sources and non-point sources. In addition, pollution from solid wastes was also serious. In 2012, the output quantity of solid wastes in the Poyang Lake watershed was 128.39 million ton, increasing 18.7% comparing with 2011. Specially, the output quantity of hazardous solid wastes was 2.69 million ton, increasing 20.64% comparing with 2011. These wastewater and solid wastes hadn’t been disposed properly and posed a threat to the safety of residents’ healthy.

Figure 1. The study area.

Figure 1. The study area.

According to Poyang Lake watershed land-use planning (2006–2020), authorized by the Chinese Central Government in 2006, Poyang Lake watershed will become a new focus of urbanization center of Central China in the next several years. Currently, the Poyang Lake watershed is suffering from problems of disordered land use, deteriorating water quality and degraded aquatic ecosystems. The land-use structure in this area has changed rapidly since 2000. In the watershed, industrial land, commercial land, traffic land and residential land occupies 3.15%, 2.57%, 6.38% and 15.87%; while agriculture land, green land, water land, landfill and unused land occupies 24.39%, 5.28%, 36.97%, 0.99% and 4.30%. Around 61.36% of the watershed’s entire territory is made up of agricultural land and water land, and there is still much room to accommodate urban development. However, in the urban area, the proportion of green land, residential land and traffic land is too low; this situation leads to a low living condition and ecological level in this area. The characteristics of Poyang watershed can be summarized by one sentence: a prosperous development prospect of the economy, many serious environmental problems and a low ecological level. Effective land-use allocation techniques are needed for this watershed to help solving above problems. The ISFP-LUAM in Section 3.2 is proposed in this study as a response to above challenges.

3.2. Modeling Framework

Characteristics of the study area can be summarized as follows:

(i)

Multiple processes. A number of processes (e.g., environment protection and ecosystem service), as well as their interactions, are contained in Wuhan’s land-use system. Competitions and interactions may exist not only in each individual process but also between each other. For example, more allocation to industry land will result in more system benefit but lead to more pollutant, thus demand more landfill to tackle the solid wastes; more allocation to green land will be propitious to ecological stability but will obtain less system benefit. These competitions are further intensified by varying social-economic, geographical, ecological and environmental conditions, as well as spatial and temporal distributions of land sources.

(ii)

Complexities and uncertainties. Normally, land market, environment capacity and government policies of Wuhan are unstable and variable, which are subject to spatial and/or temporal fluctuations. For example, investment to build incinerators and waste water treatment plants are statistically uncertain, which can be expressed as probabilistic distributions. In addition, these uncertainties are further complicated by a variety of imprecise information such as land-quality characteristics, land prices, and demand projections. Thus, uncertainties may exist in multiple formats, leading to complexities in the relevant decision-making process.

(iii)

Dynamic. For the planning horizon, social, economic, legislational and resources conditions will vary with time. Reflection of such variations would be important for generating effective planning alternatives.

Consider a LUA problem that the planner will allocate all types of land-use to relevant stockholders. As the land-use system at a watershed level is related to economic, social, environmental and ecological factors, the conceptual model of land-use allocation for a watershed can be established as follows:

Objective: maximize the net benefit of the land-use system

• constraint 1: economic constraints
• constraint 2: social constraints
• constraint 3: land suitability constraints
• constraint 4: environmental constraints
• constraint 5: ecological constraints
• constraint 6: technical constraints

Based on system analysis (Figure 2), the detail conceptual model can be formulated as follows:

Objective: maximize the net benefit of the land-use system

• constraint 1: government investment constraint
• constraint 2: agricultural production input-output constraint
• constraint 3: water production input-output constraint
• constraint 4: available water consumption constraint
• constraint 5: available electricity power consumption constraint
• constraint 6: maximum people in a unit land area constraint
• constraint 7: available labor constraint
• constraint 8: land suitability constraints
• constraint 9: wastewater treatment capacity constraint
• constraint 10: solid-waste treatment capacity constraint
• constraint 11: available soil erosion constraint
• constraint 12: forest and grass cover rate constraints
• constraint 13: fertilizer consumption constraints
• constraint 14: total land areas constraint
• constraint 15: non-negative constraints

Based on the above conceptual model, consider a situation of multi-area land-use planning, we propose an ISFP based land-use allocation model (ISFP-LUAM) of Poyang Lake watershed as follows:

Figure 2. The framework of ISFP-LUAM.

Figure 2. The framework of ISFP-LUAM.

3.2.1. Economic Objective

In this model, the objective function is the net benefit from land-use system, and it equals all benefit from agricultural land, water land and urban land minus cost from all types of land-use. In detail, benefit is from the industries on the lands. For example, benefit from agricultural land comes from all agricultural industries (planting industry); benefit from urban land comes from all urban industries such as coal industry, paper industry, textile industry, and so on. The cost is from maintenance fees of all types of land-use. For example, we must be able to afford agricultural land and urban land with energy and water. Based on above settings, our objective function can be expressed as:

$$\begin{array}{l}MaxN{B}^{\pm }\cong {\displaystyle \sum _{i=1}^3{\displaystyle \sum _{k=1}^3\left(A{P}_{i,j=1,k}^{\pm }\times x_{i,j=1,k}^{\pm }\right)}}+{\displaystyle \sum _{i=1}^3{\displaystyle \sum _{k=1}^{\text{3}}\left(W{P}_{i,j=4,k}^{\pm }\times x_{i,j=4,k}^{\pm }\right)}}+{\displaystyle \sum _{i=1}^3{\displaystyle \sum _{k=1}^{\text{3}}\left(U{P}_{i,j=5,k}^{\pm }\times x_{i,j=5,k}^{\pm }\right)}}\\ -{\displaystyle \sum _{i=1}^3{\displaystyle \sum _{k=1}^{\text{3}}\left[\left(NW{C}_{i,j=1,k}^{\pm }+NS{C}_{i,j=1,k}^{\pm }+NE{C}_{i,j=1,k}^{\pm }\right)\times x_{i,j=1,k}^{\pm }\right]}}\\ -{\displaystyle \sum _{i=1}^3{\displaystyle \sum _{k=1}^3\left[\left(NW{C}_{i,j=5,k}^{\pm }+NS{C}_{i,j=5,k}^{\pm }+NE{C}_{i,j=5,k}^{\pm }\right)\times x_{i,j=5,k}^{\pm }\right]}}\\ -{\displaystyle \sum _{i=1}^3{\displaystyle \sum _{k=1}^3\left(FM{C}_{i,j=2,k}^{\pm }\times x_{i,j=2,k}^{\pm }\right)}}-{\displaystyle \sum _{i=1}^3{\displaystyle \sum _{k=1}^3\left(GM{C}_{i,j=3,k}^{\pm }\times x_{i,j=3,k}^{\pm }\right)}}\\ -{\displaystyle \sum _{i=1}^3{\displaystyle \sum _{k=1}^3\left(WM{C}_{i,j=4,k}^{\pm }\times x_{i,j=4,k}^{\pm }\right)}}-{\displaystyle \sum _{i=1}^3{\displaystyle \sum _{k=1}^3\left(UD{C}_{i,j=6,k}^{\pm }\times x_{i,j=6,k}^{\pm }\right)}}\\ -{\displaystyle \sum _{i=1}^3\left(UL{C}_{i,j=7}^{\pm }\times x_{i,j=7}^{\pm }\right)}\end{array}$$

$N{B}^{\pm }$ = net system benefit of the land-use system ($); “x” is the independent variable, means the land areas of each land type. “$\pm$” = interval values; “$\cong$” = fuzzy equal; x are variables; i = name of district, where i = 1 for control development district; i = 2 for core protection district; i = 3 for key development district; j = type of land use, where j = 1 for agricultural land, j = 2 for forest land, j = 3 for grass land, j = 4 for water land, j = 5 for urban land, j = 6 for unused land, j = 7 for landfill; k = land suitability condition, where k = 1 for highly suitable; k = 2 for moderately suitable; k = 3 for lowly suitable; $A{P}_{i,j=1,k}^{\pm }$ = unit benefit of agricultural land (yuan/km²); $W{P}_{i,j=4,k}^{\pm }$ = unit benefit of water land (yuan/km²); $U{P}_{i,j=5,k}^{\pm }$ = unit benefit of urban land (yuan/km²); $NW{C}_{i,j=1,k}^{\pm }$ = unit wastewater-tackling cost of agricultural land (yuan/km²); $NS{C}_{i,j=1,k}^{\pm }$ = unit solid-waste-tackling cost of agricultural land (yuan/km²); $NE{C}_{i,j=1,k}^{\pm }$ = unit electricity cost of agricultural land (yuan/km²); $NW{C}_{i,j=5,k}^{\pm }$ = unit wastewater-tackling cost of urban land (yuan/km²); $NS{C}_{i,j=5,k}^{\pm }$ = unit solid-waste-tackling cost of urban land (yuan/km²); $NE{C}_{i,j=5,k}^{\pm }$ = unit electricity cost of urban land (yuan/km²); $FM{C}_{i,j=2,k}^{\pm }$ = unit maintenance costs of forest land (yuan/km²); $GM{C}_{i,j=3,k}^{\pm }$ = unit maintenance costs of grass land (yuan/km²); $WM{C}_{i,j=4,k}^{\pm }$ = unit maintenance costs of water land (yuan/km²); $UD{C}_{i,j=6,k}^{\pm }$ = unit developing costs of unused land (yuan/km²); $UL{C}_{i,j=7,k}^{\pm }$ = unit maintenance costs of landfill (yuan/km²).

3.2.2. Economic Constraints

(i) Government investment constraint

All costs will be afforded by government investment, so the government investment constraint can be expressed as:

$$\begin{array}{l}{\displaystyle \sum _{i=1}^3{\displaystyle \sum _{k=1}^3\left[\left(NW{C}_{i,j=1,k}^{\pm }+NS{C}_{i,j=1,k}^{\pm }+NE{C}_{i,j=1,k}^{\pm }\right)\times x_{i,j=1,k}^{\pm }\right]}}\\ +{\displaystyle \sum _{i=1}^3{\displaystyle \sum _{k=1}^3\left[\left(NW{C}_{i,j=5,k}^{\pm }+NS{C}_{i,j=5,k}^{\pm }+NE{C}_{i,j=5,k}^{\pm }\right)\times x_{i,j=5,k}^{\pm }\right]}}\\ +{\displaystyle \sum _{i=1}^3{\displaystyle \sum _{k=1}^3\left(FM{C}_{i,j=2,k}^{\pm }\times x_{i,j=2,k}^{\pm }\right)}}-{\displaystyle \sum _{i=1}^3{\displaystyle \sum _{k=1}^3\left(GM{C}_{i,j=3,k}^{\pm }\times x_{i,j=3,k}^{\pm }\right)}}\\ +{\displaystyle \sum _{i=1}^3{\displaystyle \sum _{k=1}^3\left(WM{C}_{i,j=4,k}^{\pm }\times x_{i,j=4,k}^{\pm }\right)}}-{\displaystyle \sum _{i=1}^3{\displaystyle \sum _{k=1}^3\left(UD{C}_{i,j=6,k}^{\pm }\times x_{i,j=6,k}^{\pm }\right)}}\\ +{\displaystyle \sum _{i=1}^3\left(UL{C}_{i,j=7}^{\pm }\times x_{i,j=7}^{\pm }\right)}\lesssim MG{I}^{\pm }\end{array}$$

$MG{I}^{\pm }$ = maximum government investment (yuan); “$\lesssim$” means fuzzy less than.

(ii) Agricultural production input-output constraint

$${\displaystyle \sum _{i=1}^3{\displaystyle \sum _{k=1}^3\left(UA{B}_{i,k}^{\pm }\times x_{i,j=1,k}^{\pm }\right)}}\gtrsim DA{B}^{\pm }$$

$UA{B}_{i,k}^{\pm }$ = unit production from agriculture land (ton/ km²); $DA{B}^{\pm }$ = demand agricultural production (ton). “$\gtrsim$”means fuzzy greater than.

(iii) Water production input-output constraint

$${\displaystyle \sum _{i=1}^3{\displaystyle \sum _{k=1}^3\left(UW{P}_{i,k}^{\pm }\times x_{i,j=4,k}^{\pm }\right)}}\gtrsim DW{P}^{\pm }$$

$UW{P}_{i,k}^{\pm }$ = unit production from water land (ton/ km²); $DW{P}^{\pm }$ = demand aquatic production(ton).

(iv) Available water consumption constraint

$${\displaystyle \sum _{i=1}^3{\displaystyle \sum _{j=1}^6{\displaystyle \sum _{k=1}^3\left(W{C}_{i,k}^{\pm }\times x_{i,j,k}^{\pm }\right)}}}+{\displaystyle \sum _{i=1}^3\left(W{C}_i^{\pm }\times x_{i,j=7}^{\pm }\right)}\lesssim A{W}^{\pm }$$

$W{C}_{i,k}^{\pm }$ = unit water consumption of all types of land uses (ton/ km²); $A{W}^{\pm }$ = available water (ton).

(v) Available electricity power consumption constraint

$${\displaystyle \sum _{i=1}^3{\displaystyle \sum _{j=1}^6{\displaystyle \sum _{k=1}^3\left(E{C}_{i,k}^{\pm }\times x_{i,j,k}^{\pm }\right)}}}+{\displaystyle \sum _{i=1}^3\left(E{C}_i^{\pm }\times x_{i,j=7}^{\pm }\right)}\lesssim E{W}^{\pm }$$

$E{C}_{i,k}^{\pm }$ = unit electric power consumption of all types of land uses (kilowatt hour/ km², KWH/ km²); $E{W}^{\pm }$ = available electric power (kilowatt hour, KWH).

3.2.3. Social Constraints

(i) Maximum people in a unit land area constraint

$$T{P}^{\pm }/({\displaystyle \sum _{i=1}^3{\displaystyle \sum _{j=1}^6{\displaystyle \sum _{k=1}^3{x}_{i,j,k}^{\pm }}}}+{\displaystyle \sum _{i=1}^3{x}_{i,j=7}^{\pm }})\lesssim MI{P}^{\pm }$$

$T{P}^{\pm }$ = total population (person); $MI{P}^{\pm }$ = minimum population in a unit area (person/ km²).

(ii) Available labor constraint

$${\displaystyle \sum _{i=1}^3{\displaystyle \sum _{j=1}^6{\displaystyle \sum _{k=1}^3\left(L{C}_{i,k}^{\pm }\times x_{i,j,k}^{\pm }\right)}}}+{\displaystyle \sum _{i=1}^3{\left(L{C}_i^{\pm }\times x_{i,j=7}^{\pm }\right)}_{k=4}^{\pm }}\lesssim A{L}^{\pm }$$

$L{C}_{i,k}^{\pm }$ = labors in a unit land area (person/ km²); $A{L}^{\pm }$ = available labors(person).

3.2.4. Land Suitability Constraints

$${\displaystyle \sum _{i=1}^3{\displaystyle \sum _{j=1}^6{\displaystyle \sum _{k=1}^3{x}_{i,j,k}^{\pm }+}}}{\displaystyle \sum _{i=1}^3{x}_{i,j=7}^{\pm }}\lesssim {\displaystyle \sum _{j=1}^{7}MI{L}_j^{\pm }}$$

$MI{L}_j^{\pm }$ = maximum area of land-use j (km²).

3.2.5. Environmental Constraints

(i) Wastewater treatment capacity constraint

$${\displaystyle \sum _{i=1}^3{\displaystyle \sum _{k=1}^3\left(AW{F}_{i,j=1,k}^{\pm }\times x_{i,j=1,k}^{\pm }\right)}}+{\displaystyle \sum _{i=1}^3{\displaystyle \sum _{k=1}^3\left(UW{F}_{i,j=5,k}^{\pm }\times x_{i,j=5,k}^{\pm }\right)}}\lesssim AW{D}^p$$

$AW{F}_{i,j=1,k}^{\pm }$ = wastewater discharging factor of agricultural land (ton/km²); $UW{F}_{i,j=5,k}^{\pm }$ = wastewater discharging factor of urban land (ton/km²); $AWD$ = wastewater treatment plant capacity (ton); p = probability of violating the constraints of environmental capacities, and p ∈ [0,1].

(ii) Solid-waste treatment capacity constraint

$${\displaystyle \sum _{i=1}^3{\displaystyle \sum _{k=1}^3\left(AS{F}_{i,j=1,k}^{\pm }\times x_{i,j=1,k}^{\pm }\right)}}+{\displaystyle \sum _{i=1}^3{\displaystyle \sum _{k=1}^3\left(US{F}_{i,j=5,k}^{\pm }\times x_{i,j=5,k}^{\pm }\right)}}-{\displaystyle \sum _{i=1}^3\left(LH{P}_i^{\pm }\times x_{i,j=7}^{\pm }\right)}\lesssim AS{D}^p$$

$AS{F}_{i,j=1,k}^{\pm }$ = solid-waste discharging factor of agricultural land (ton/km²); $US{F}_{i,j=5,k}^{\pm }$ = solid-waste discharging factor of urban land (ton/km²); $ASD$ = solid-waste treatment plant capacity (except landfill) (ton); $LH{P}_i^{\pm }$ = solid-waste discharging factor (landfill) (ton). The environmental impacts are mainly caused by industrial activities in the land-use system. Otherwise, environmental impacts are also caused by domestic wastewater/solid waste.

3.2.6. Ecological Constraints

(i) Available soil erosion constraint

$${\displaystyle \sum _{i=1}^3{\displaystyle \sum _{j=1}^6{\displaystyle \sum _{k=1}^3\left(O{P}_{i,k}^{\pm }\times x_{i,j,k}^{\pm }\right)}}}+{\displaystyle \sum _{i=1}^{3}O{P}_i^{\pm }\times x_{i,j=7}^{\pm }}\lesssim A{O}^p$$

$O{P}_i^{\pm }$ = soil erosion rate (%); $A{O}^{\pm }$ = available soil erosion area (km²).

(ii) Forest and grass cover rate constraints

$$({\displaystyle \sum _{i=1}^3{\displaystyle \sum _{k=1}^3\left(x_{i,j=2,k}^{\pm }+x_{i,j=3,k}^{\pm }\right)}})/\left({\displaystyle \sum _{i=1}^3{\displaystyle \sum _{j=1}^6{\displaystyle \sum _{k=1}^3{x}_{i,j,k}^{\pm }}+}{\displaystyle \sum _{i=1}^3{x}_{i,j=7}^{\pm }}}\right)\gtrsim M{R}^p$$

$M{R}^{\pm }$ = minimum forest and grass cover rate (%)

(iii) Fertilizer consumption constraints

$${\displaystyle \sum _{i=1}^3{\displaystyle \sum _{k=1}^3\left(F{P}_{i,k}^{\pm }\times x_{i,j=1,k}^{\pm }\right)}}\lesssim M{P}^p$$

$F{P}_i^{\pm }$ = fertilizer consumption for unit agricultural land (ton/ km²); $M{P}^{\pm }$ = maximum fertilizer consumption (ton)

3.2.7. Technical Constraints

(i) Total land areas constraint

$${\displaystyle \sum _{i=1}^3{\displaystyle \sum _{j=1}^6{\displaystyle \sum _{k=1}^3{x}_{i,j,k}^{\pm }}+}{\displaystyle \sum _{i=1}^3{x}_{i,j=7}^{\pm }}}=TU{L}^{\pm }$$

$TU{L}^{\pm }$ = total land area (km²).

(ii) Non-negative constraints

$$x_{i,j,k}^{\pm }\ge 0$$

According to the ISFP solution algorithm in Section 2, the above ISFP-LUAM can be transformed into two deterministic sub-models, which corresponds to the upper and lower bounds for the desired objective function value under different p levels. Then we can calculate the two linear models in the software of Microsoft Office Excel. The framework of the ISFP-LUAM model is shown in Figure 2.

3.3. Data Collection

The parameters of ISFP-LUAM including five types: beneficial and cost parameters; economic and social parameters; land suitability parameters; environmental parameters; ecological parameters (Table 1, Table 2, Table 3 and Table 4). Beneficial and cost parameters can be got from land evaluation. Economic and social parameters can be got though index forecasting model. Land suitability parameters can be got though GIS technology [41]. Environmental/ecological parameters can be got though stochastic models. Data on existing land-uses were obtained from the land-use and land-cover change (LUCC) database established by Chinese Academy of Sciences (CAS), which produces thematic maps at a scale of 1:100,000 [42]. These LUCC data were obtained through visual interpretation and digitization of satellite remote sensing data provided by the US Landsat TM/ETM images, with a hierarchical classification system of 25 land-cover classes [43]. During the process of interpretation and land-cover classifications, Chinese Academy of Sciences (CAS) has verified that the average interpretation accuracies for the LUCC data were more than 92% through an outdoor survey and random sample check (covering a line survey of 70,000 km and 13,300 patches) [6,42].

3.4. The Solution of a General ISFP Land-use Planning Model at a Watershed Level

Based on Section 3.1, we can conclude the general solution steps for the ISFP-LUAM at a watershed level:

• Step 1: Analyze the land-use system in the watershed and formulate the conceptual model;
• Step 2: Transform the conceptual model to mathematical model through ISFP method;
• Step 3: Get economic, beneficial, and cost parameters through forecasting models and land evaluation methods;
• Step 4: Obtain land suitability parameters through GIS technology;
• Step 5: Obtain ecological parameters through ecological models;
• Step 6: Obtain environmental parameters under different p levels through stochastic fitting methods;
• Step 7: Transform the ISFP-LUAM into two sub-models corresponding to the up bound and low bound objective- function values;
• Step 8: Solve two sub-models and obtain their solutions;
• Step 9: Obtain the solutions of the ISFP-LUAM and get the optimal land areas for each user;
• Step 10: Analyze the results and generate decision alternatives.

Table 1. Economic, social, environmental and technical parameters.

Symbol	Lower Bound	Upper Bound	Symbol	Lower Bound	Upper Bound
MGI (1012 yuan)	92.15	103.99	LCi=1,k=1 (people/km2)	312.58	442.19
UABi=1,k=1 (ton/km2)	2.84	3.91	AL (103 people)	4498.00	5643.00
DAB (106 ton)	5.34	6.97	AWFi=1,j=1,k=1 (103 ton/km2)	5.67	7.28
UWPi=1,k=1 (ton/km2)	2.25	6.51	UWFi=1,l=5,k=1 (106 ton/km2)	15.64	22.18
DWP (106 ton)	1.14	2.58	ASFi=1,j=1,k=1 (ton/km2)	42.18	55.47
WCi=1,k=1 (103 m3/km2)	221.38	256.47	USFi=1,l=5,k=1 (103 ton/km2)	105.24	226.37
AW (109 m3)	2.69	4.32	LHPi=1 (ton)	1865.27	2021.34
ECi=1,k=1 (106 kwh/km2)	5.12	7.58	OPi=1,k=1	2%	2.5%
EW (109 kwh)	39.54	72.19	AO (km2)	2564.27	3302.18
TP (106 people)	42.19	59.27	FPi=1,k=1 (ton)	12.34	13.27
MIP (people/km2)	789.00	854.00	TUL (103 km2)	162.00	195.00

Table 1. Economic, social, environmental and technical parameters.

Symbol	Lower Bound	Upper Bound	Symbol	Lower Bound	Upper Bound
MGI (1012 yuan)	92.15	103.99	LCi=1,k=1 (people/km2)	312.58	442.19
UABi=1,k=1 (ton/km2)	2.84	3.91	AL (103 people)	4498.00	5643.00
DAB (106 ton)	5.34	6.97	AWFi=1,j=1,k=1 (103 ton/km2)	5.67	7.28
UWPi=1,k=1 (ton/km2)	2.25	6.51	UWFi=1,l=5,k=1 (106 ton/km2)	15.64	22.18
DWP (106 ton)	1.14	2.58	ASFi=1,j=1,k=1 (ton/km2)	42.18	55.47
WCi=1,k=1 (103 m3/km2)	221.38	256.47	USFi=1,l=5,k=1 (103 ton/km2)	105.24	226.37
AW (109 m3)	2.69	4.32	LHPi=1 (ton)	1865.27	2021.34
ECi=1,k=1 (106 kwh/km2)	5.12	7.58	OPi=1,k=1	2%	2.5%
EW (109 kwh)	39.54	72.19	AO (km2)	2564.27	3302.18
TP (106 people)	42.19	59.27	FPi=1,k=1 (ton)	12.34	13.27
MIP (people/km2)	789.00	854.00	TUL (103 km2)	162.00	195.00

Table 2. Benefits and costs for different land-use types (yuan/hm²).

Land-use Type	Symbol	Lower Bound	Upper Bound
Benefits of land use	APi=1,j=1,k=1 (106)	0.13	0.15
	APi=2,j=1,k=1 (106)	0.09	0.11
	APi=3,j=1,k=1 (106)	0.25	0.34
	WPi=1,j=4,k=1 (103)	25.69	36.98
	WPi=2,j=4,k=1 (103)	18.21	20.12
	WPi=3,j=4,k=1 (103)	78.91	105.21
	UPi=1,j=5,k=1 (106)	54.32	66.87
	UPi=2,j=5,k=1 (106)	27.35	35.64
	UPi=3,j=5,k=1 (106)	158.98	225.21
Costs of land use	NWCi=1,j=1,k=1 (103)	115.32	126.31
	NSCi=1,j=1,k=1 (103)	261.32	298.54
	NECi=1,j=1,k=1 (103)	98.35	115.21
	NWCi=1,j=5,k=1 (103)	2132.12	2564.89
	NSCi=1,j=5,k=1 (103)	5698.25	7789.24
	NECi=1,j=5,k=1 (103)	229.65	339.17
	FMCi=1,j=2,k=1 (103)	112.31	152.13
	GMCi=1,j=3,k=1 (103)	258.14	265.38
	WMCi=1,j=4,k=1 (103)	118.25	156.38
	UDCi=1,j=6,k=1 (103)	196.35	256.28
	ULCi=1,j=7,k=1 (103)	95.23	98.25

Table 2. Benefits and costs for different land-use types (yuan/hm²).

Land-use Type	Symbol	Lower Bound	Upper Bound
Benefits of land use	APi=1,j=1,k=1 (106)	0.13	0.15
	APi=2,j=1,k=1 (106)	0.09	0.11
	APi=3,j=1,k=1 (106)	0.25	0.34
	WPi=1,j=4,k=1 (103)	25.69	36.98
	WPi=2,j=4,k=1 (103)	18.21	20.12
	WPi=3,j=4,k=1 (103)	78.91	105.21
	UPi=1,j=5,k=1 (106)	54.32	66.87
	UPi=2,j=5,k=1 (106)	27.35	35.64
	UPi=3,j=5,k=1 (106)	158.98	225.21
Costs of land use	NWCi=1,j=1,k=1 (103)	115.32	126.31
	NSCi=1,j=1,k=1 (103)	261.32	298.54
	NECi=1,j=1,k=1 (103)	98.35	115.21
	NWCi=1,j=5,k=1 (103)	2132.12	2564.89
	NSCi=1,j=5,k=1 (103)	5698.25	7789.24
	NECi=1,j=5,k=1 (103)	229.65	339.17
	FMCi=1,j=2,k=1 (103)	112.31	152.13
	GMCi=1,j=3,k=1 (103)	258.14	265.38
	WMCi=1,j=4,k=1 (103)	118.25	156.38
	UDCi=1,j=6,k=1 (103)	196.35	256.28
	ULCi=1,j=7,k=1 (103)	95.23	98.25

Table 3. The minimum area of every type of land (hm²).

Symbol	Lower Bound	Upper Bound
MILj=1 (106)	53.58	55.45
MILj=2 (106)	31.77	33.64
MILj=3 (106)	0.12	0.15
MILj=4 (106)	21.18	22.43
MILj=5 (106)	8.10	11.21
MILj=6 (103)	93.45	105.91
MILj=7 (103)	79.74	83.48

Table 3. The minimum area of every type of land (hm²).

Symbol	Lower Bound	Upper Bound
MILj=1 (106)	53.58	55.45
MILj=2 (106)	31.77	33.64
MILj=3 (106)	0.12	0.15
MILj=4 (106)	21.18	22.43
MILj=5 (106)	8.10	11.21
MILj=6 (103)	93.45	105.91
MILj=7 (103)	79.74	83.48

Table 4. Eco-environmental capacity under different p levels.

Eco-environmental Capacity	p level
	p = 0.01	p = 0.05	p = 0.10	p = 0.15
AWD(109 ton)	17.72	19.25	29.34	42.68
ASD(106 ton)	146.79	168.95	198.25	249.67
AO (km2)	2932.15	3269.31	3965.24	4458.21
MR	44%	36%	32%	29%
MP (103)	559.68	665.32	778.98	998.28

Table 4. Eco-environmental capacity under different p levels.

Eco-environmental Capacity	p level
	p = 0.01	p = 0.05	p = 0.10	p = 0.15
AWD(109 ton)	17.72	19.25	29.34	42.68
ASD(106 ton)	146.79	168.95	198.25	249.67
AO (km2)	2932.15	3269.31	3965.24	4458.21
MR	44%	36%	32%	29%
MP (103)	559.68	665.32	778.98	998.28

4. Results Analysis

4.1. Optimized Land-use Patterns under Different p Levels and Land Use Policy Analysis

Figure 3, Figure 4 and Figure 5 present the solutions to land allotment for decision variables obtained through the ISFP-LUAM under different p levels. The results indicate that the variations of funding, resources, ecological and waste generation conditions may lead to the varied LUA patterns. In case of excess investment, allotments to urban land for economic growth should be assigned firstly and then to cultivated land, forest land and grass land, while allotments to unused land due mainly to policy constraints. Analysis of the modeling solutions are provided below.

The optimized LUA patterns in Lake Controlling Development Zone under different p levels are presented in Figure 3. In detail, under p = 0.01, optimized cultivated land, forest land, grass land, water land, urban land, unused land and landfill will be [228234, 237844] ha, [47228, 58451] ha, [20982, 23718] ha, [33897, 35280] ha, [15215, 15907] ha, [528, 879] ha and [1023, 1260] ha. Under p = 0.05, the values will change to [216822, 225951] ha, [45339, 71895] ha, [19093, 26564] ha, [33219, 37044] ha, [19019, 22269] ha [369, 703] ha and [1200, 1387] ha. Under p = 0.10, the optimized land-use patterns will become [190803, 212394] ha, [34004, 46012] ha, [17947, 24173] ha, [32554, 32598] ha, [21300, 26722] ha, [336, 633] ha and [1280, 1500] ha. Under p = 0.15, modeling results will be [152643, 191155] ha, [28903, 42331] ha, [17768, 22723] ha, [29624, 29664] ha, [31951, 40351] ha, [0, 317] ha and [1690, 1900] ha. We can clearly see that cultivated land, urban land and landfill will increase with the p levels. p levels indicate the probabilities that violating environmental/ecological constraints. When the value of p increased, the probability of environmental/ecological risk will increase. However, the environmental/ecological capacity will expand and the ISFP-LUAM will prefer to more economic benefit. Therefore, more lands will be allocated to urban land and cultivated land which can bring more economic revenues for citizens and farmers. The increasing of landfill indicates that a bigger environmental/ecological capacity will request more landfill to afford more solid waste from land-use system. In contrast, forest land, grass land, water land and unused land will decrease with the p levels. First, these four types of land use can create less economic benefit compared with urban land and cultivated land in Poyang Lake watershed; Secondly, more economical benefits will urge citizens and farmers to explore more lands by changing the four types of land use to urban land and cultivated land.

Figure 3. Optimized land-use allocation in Lake Controlling Development Zone under different p levels.

Figure 3. Optimized land-use allocation in Lake Controlling Development Zone under different p levels.

The optimized LUA patterns in other two zones under different p levels are presented in Figure 4 and Figure 5. Figure 4 indicates that in Lake Core Protecting Zone, urban land will increase with the p level and other types of land use will decrease. Modeling results indicate that model will allocate more lands to urban land in Lake Core Protecting Zone if the p level increases. However, when more urban land in this zone is developed, the probability of eco-environmental risk will increase. In this zone, the eco-environmental standard is very strict; therefore, developing more beneficial land will bring a bigger eco-environmental risk than other two zones. Furthermore, LUA to forest land and grass land in this zone will decrease fast with the p level. An increased p level also indicates a radical economic policy, which will lead to more land reclamation and implies more population, industries and urbanization. Correspondingly, forest land and grass land will be decrease fast. Figure 5 indicates that the features of land-use changes in Lake Key Development Zone are similar with Lake Core Protecting Zone. However, we can see that in the Lake Key Development Zone, the model allocates much more urban land than other two zones. That is because in this area government will invest more money to develop the economic. An increased p level will relax eco-environmental constraints and thus raise the risk of violating these constraints. In comparison to other land-use types, urban land is known to have a lower operation cost and conspicuous comparative advantages in yielding economic benefits in Lake Key Development Zone. Thus, when eco-environmental constraints are relaxed, LUA to urban land will increase; however, this situation will lead to considerable loss of cultivated land. This result is consistent with the fact that industry and the booming township and village enterprises are the main forces propelling economic growth in this zone. Furthermore, the decrease of water land is because land occupation associated with urbanization and industrialization has been reduced the lake surface area in this zone.

Figure 4. Optimized land-use allocation in Lake Core Protecting Zone under different p levels.

Figure 4. Optimized land-use allocation in Lake Core Protecting Zone under different p levels.

Results in Figure 3, Figure 4 and Figure 5 also indicate that interval solutions can be generated from the ISFP-LUAM model. Interval solutions can effectively support land policy analysis. For example, in the Lake Controlling Development Zone, solutions for the lower bounds of cultivated land, urban land and landfill and upper bounds of forest land, grass land, water land and unused land correspond to the lower system benefit, which could guarantee social demands, ecological balance and environmental criteria be met, and imply a conservative land-use management strategy. When the values of cultivated land, urban land and landfill aim toward the upper bounds and forest land, grass land, water land and unused land aim toward the lower bounds, the land-use system will get a higher benefit level. However, social demands, ecological risk and environmental criteria will be increased, implying a more radical economic strategy. A solution of the objective function provides two extremes of system benefit over the planning horizon. For example, under p = 0.01, which means the eco-environmental violating probability is the lowest, the eco-environmental constraints will be most strict, the optimized system benefit will be [15.17, 18.29] × 10¹² yuan, which means the expected system benefit would change between 15.17 × 10¹² yuan and 18.29 × 10¹² yuan with varied reliability levels, implying the actual value of each continuous variable varies within its lower and upper bounds. In general, planning with a lower system benefit will be associated with a lower risk of violating the system constraints. Conversely, a plan targeting a higher system benefit may be associated with a higher risk of violating system constraints.

Figure 5. Optimized land-use allocation in the Lake Key Development Zone under different p levels.

Figure 5. Optimized land-use allocation in the Lake Key Development Zone under different p levels.

When land-use patterns are selected through combining land-use area values within their interval solutions, the system benefit value will change within its interval correspondingly. Therefore, decision alternatives can be generated by adjusting different land-use combinations according to projected applicable conditions. This could effectively reflect potential variations of system conditions caused by the existence of parameter uncertainties. The feasible ranges for the decision variables provided by the ISFP-LUAM solutions are also useful for decision makers to justify the generated alternatives directly, or to potentially adjust the decision variable values when they are not satisfied with the provided alternatives. Therefore, the ISFP-LUAM approach allows decision makers to incorporate implicit knowledge within the problem, and thus obtain satisfactory and applicable decision schemes.

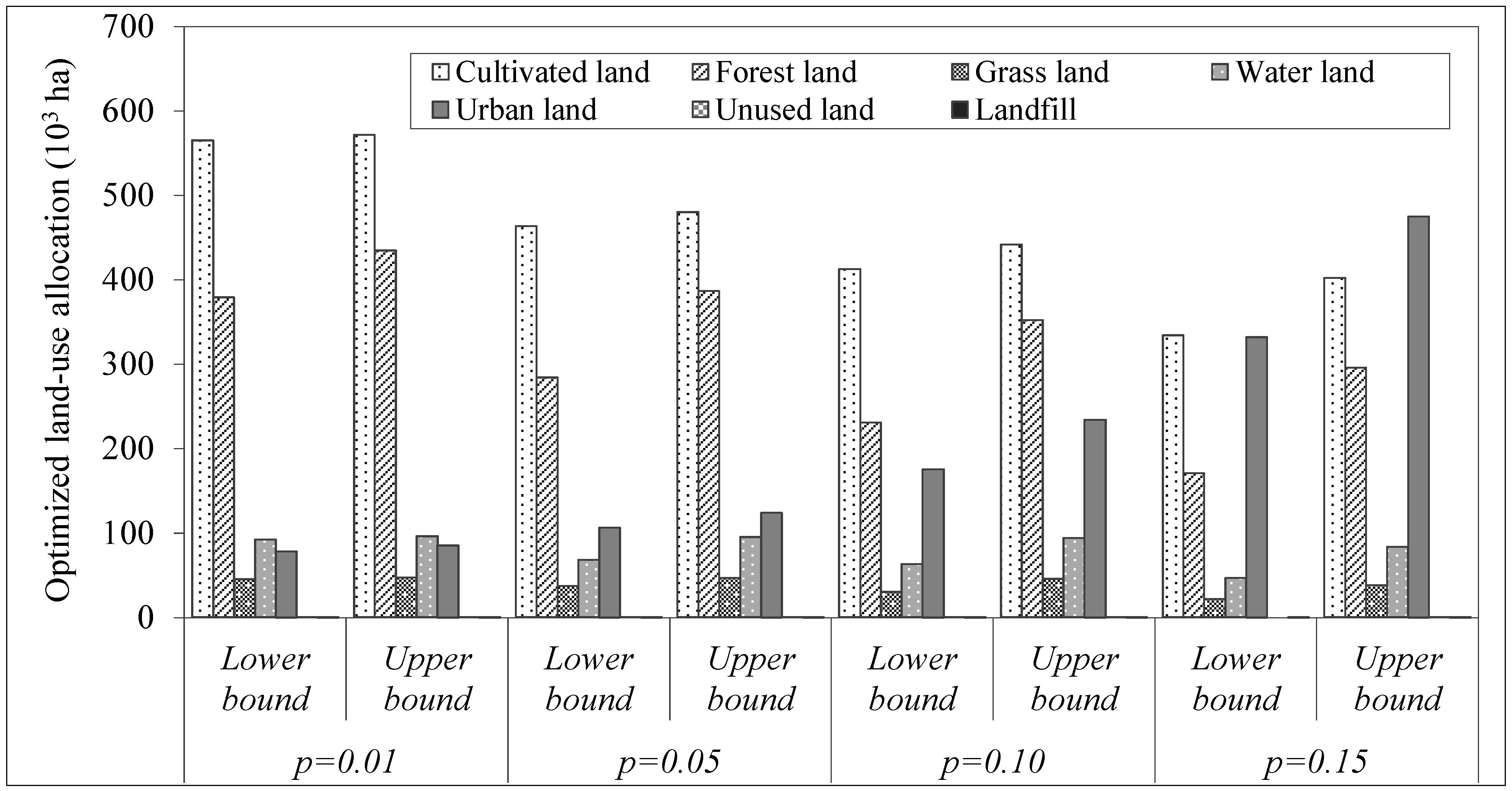
4.2. Optimized Environmental Pollutants Emissions and Ecological Patterns under Different p Levels and Eco-Environmental Policy Analysis

Figure 6 and Figure 7 show the optimized wastewater/solid-waste discharge from ISFP-LUAM. Solutions for lower bounds of optimized wastewater/solid-waste discharge correspond to lower system benefit, which could guarantee that wastewater/solid-waste discharge criteria be met, and imply a conservative environmental management strategy. However, when the decision aims toward the upper-bound wastewater/solid-waste discharge that is linked to a higher system benefit level, the risk of unsafe water quality/solid-waste emission for the LUA system will increase.

Figure 6. Relationship between p and optimized wastewater discharge.

Figure 6. Relationship between p and optimized wastewater discharge.

Figure 7. Relationship between p and optimized solid-waste discharge.

Figure 7. Relationship between p and optimized solid-waste discharge.

4.3. Tradeoff between Economic Objective and Eco-Environmental Constraints

The p levels represent the probability of violating the constraints of eco-environmental capacities. The results in Figure 3, Figure 4 and Figure 5 also indicate that any change in p would yield different wastewater/solid-waste capacities and ecological conditions and thus results in different system benefits. For example, when p = 0.01, system benefit are [15.17, 18.29] × 10¹² yuan. In comparison, when p = 0.05, the values change to [23.18, 36.94] × 10¹² yuan. Similar characteristics exist in solutions under the other significance levels (p = 0.05 and 0.10). The relationship between p and system benefit is shown in Figure 8.

Since the p levels represent probabilities at which the eco-environmental constraints will be violated, relation between system benefit and p demonstrates a tradeoff between economic efficiency and system risk. An increased p level means an increased risk of eco-environmental constraint violation; at the same time, it will lead to a decreased strictness for the constraints (and thus an expanded decision space, e.g., increased waste treatment/disposal capacity and worse ecological conditions). That is, a higher system benefit (under a high p level) represents an alternative with lower waste generation rates and a higher waste treatment/disposal capacity and bad ecological conditions, while a lower system benefit (under a lower p level) represents an alternative with higher waste generation rates and a lower eco-environmental capacity. Usually, planning with lower system benefit can guarantee that waste management requirements and eco-environmental regulations be met; in comparison, with planning aiming toward higher system benefit, these requirements may not be met. Thus, with the increased p level, the reliability of meeting waste treatment/disposal capacity requirements and eco-environmental requirements would decrease.

Figure 8. Relationship between p and optimized system benefit.

Figure 8. Relationship between p and optimized system benefit.

4.4. Tradeoff between Constraints and System Benefit and Economic Policy Analysis

The results also indicate that the optimized λ values are in the range of [0.69, 0.98]. The λ represents the possibility of satisfying all objectives and constraints under all given system conditions. The solutions correspond to conservative strategies when their λ values tend to the lower bound; in comparison, the solutions become more optimistic when their λ values tend to the upper bound. The relationship between λ values and system benefit is showed in Figure 9. From this figure we can see that the λ value and the system benefit have a relationship of positive correlation. The ISFP-LUAM is to achieve a maximized satisfaction degree (λ value) for system objective and constraints under uncertainty. Under λ = 0.69 (p = 0), the system benefit will be [12.17, 15.39] × 10¹² yuan, while under λ = 0.98 (p = 0), the system benefit will be [68.31, 72.19] × 10¹² yuan. The λ values indicate the tradeoff between system benefit and all the constraints (including eco-environmental constraints). Lower λ values would guarantee all the requirements are met, result in a more strict constraints and a lower system benefit; in comparison, a higher λ values lead to a more flexible constraints and a higher system benefit. For example, a higher available electricity power, water and soil erosion corresponding to a higher λ values and give a higher system benefit.

Figure 9. Relationship between λ and optimized system benefit.

Figure 9. Relationship between λ and optimized system benefit.

4.5. Summary

The obtained results indicate that uncertainties that exist in the system parameters can be effectively reflected as intervals, probability distributions, and membership functions in ISFP-LUAM, with reasonable solutions and land use policies generated. The quantitive interactions among land areas, system benefit and environmental capacities can be studied more clearly.

5. Conclusions

In this study, an inexact stochastic fuzzy programming (ISFP) model is proposed for land-use allocation and environmental/ecological planning at a watershed level. ISFP-LUAM is developed through incorporation of interval parameter programming, stochastic programming and fuzzy linear programming approaches within a general optimization framework. It improves upon the previous programming methods, and can reflect uncertainties expressed as discrete intervals, probabilities, fuzzy sets and their combinations. The method can also be used for analyzing a variety of policy scenarios that are associated with different levels of economic/environmental penalties. The ISFP-LUAM can be transformed into two deterministic sub-models, which corresponded to the lower and upper bounds of the desired objective. Solutions are then obtained by solving the two sub-models sequentially. Interval solutions associated with information of system failure risk can then be obtained.

The method is applied to a case study of LUA in Poyang Lake watershed, China. Four scenarios (under four different p levels) are considered and the results indicated that reasonable solutions were generated. The solutions provided desired LUA/eco-environmental protection alternatives with a maximized system benefit and a minimized eco-environmental risk level. All in all, the results demonstrated the inherent interdependences among economic development and eco-environmental effects, as well as the successes of mitigation measures based on an integrated and adaptive LUA optimization approach.

ISFP-LUAM improves upon the existing interval parameter programming, stochastic programming and fuzzy flexible programming techniques, and can efficiently deal with LUA optimization issues under multiple uncertainties and various economic/social/eco-environmental conditions at a watershed lever. However, other environmental wastes such as air pollutant, other environmental/ecological sector such as fungicides, and other social conditions such as behavior intention of stakeholders can be incorporated within a general optimization framework. The approach can also be applied to other micro-LUA management problems involving uncertainties presented in multiple formats as well as complexities in policy dynamics.