Methodological Proposal for Optimal Location of Emergency Operation Centers through Multi-Criteria Approach

Abstract

Territorial vulnerability and risk analysis play a fundamental role in urban planning and emergency management. Requirements analysis of such aspects are possible to define more and more effective risk mitigation strategies providing efficient response plans to events. Many mitigation strategies as well as many response plans have in common the purpose of minimizing response time in order to decrease the level of vulnerability of the concerning area. The response time to a perturbing event is in fact an essential parameter to define the hazard of the considered site and literature is unanimous in considering it. In this context, the article proposes a methodology for the optimization of the location on the territory of emergency operation centers (EOCs), reducing response times and mitigating in this way the vulnerability of the area. The proposed methodology is based on a multi-criteria decision making (MCDM) hybrid type AHP (Analytic Hierarchy Process)-Electre. This method has been applied in the territory of Bressanone and Vipiteno (Bolzano-Italy), simulating the need to build a new barrack of Fire Department. A campaign of interviews with operators and industry experts and the collection of spatial data from the portals of the concerned authorities has been carried out in order to get the number of necessary data for the implementation of the proposed methodology.

1. Introduction: The Best Location as a Tool for Risk Mitigation

Territorial vulnerability and risk analysis play a fundamental role in urban planning and emergency management. Increasingly effective strategies of risk-reduction and providing efficient response plans to events may be defined by analyzing such aspects. Risk mitigation strategies may involve territorial intervention of different kind. Structural and non-structural measures are one of the most common classifications of these interventions.

The non-structural measures are aimed at a reduction of potential damage caused by the occurrence of an event, and they are taken into account when discussing territorial planning and drafting legislation. In order to limit damage as much as possible, especially the vulnerability of the area, can be reduced by technical interventions such as the organization of emergency plans and optimization of rescue.

Maximizing the assistance means first of all minimizing times. The response time to a perturbing event is, in fact, an essential parameter to define the hazard of the concerned site and literature is unanimous in considering it. Effectively allocating emergency operation centers (EOCs) may be a genuine strategy for risk-reduction. Providing an effective response time of assistance is the global criterion under which a site shall be considered “the best” site.

2. Literature Review

Multi-criteria decision making (MCDM) approaches deal with the evaluation of a set of alternatives in terms of numerous decision criteria with the goal of providing a choice highlighting the best alternative among the set of options.

Mulliner et al. [1] elaborated on a comparative analysis of different MCDM methods, comparing the rankings of the alternatives and their tolerance to change in criterion weights amongst the following MCDM methods: the Weighted Sum Model (WSM), the Weighted Product Model (WPM), the revised Analytic Hierarchy Process (AHP), Technique for Order of Preference by Similarity to Ideal Solution (TOPSIS), and Complex Proportional Assessment (COPRAS).

The Decision Making Trial and the Evaluation Laboratory (DEMATEL) methods are used for clarifying interactions in decision models, finding criteria weights, and supporting decisions with AHP [2]. The AHP is based on the use of pair-wise comparisons, for estimating criteria weights and comparing at the same time the alternatives with regard to the decision criteria [3]. Tomic et al. [4] used AHP as a support in making logistic center location decisions, analyzing criteria which affect location decisions. AHP and Analytic Network Process (ANP) models quantify the influence between criteria based upon the pairwise comparisons. Simplifying the hierarchical decomposition of AHP, the ANP approach makes use of clusters, and criteria are placed within the clusters. The connection between criteria is determined by pairwise comparisons, placing the corresponding weights in the appropriate columns of an elaborated supermatrix [2].

Recently, there have been many research studies using the DEMATEL method in conjunction with ANP; these two approaches have been used by Tuzkaya et al. [5] to choose the most convenient locations for emergency logistics centers.

The VIKOR (Višekriterijumska Optimizacija i kompromisno Rešenje) method was elaborated on for multi-criteria optimization of complex systems. Its acronym comes from its Serbian name that means multi-criteria optimization and compromise solution. Because of its stability and ease of use, this method is adopted for the selection problems considering the lowest performance rating with respect to a specified criterion [6]. It is focused on ranking and selecting from a set of alternatives against various, and in most cases conflicting and non-commensurable, decision criteria [7].

Preference Ranking Organization Method for Enrichment Evaluation (PROMETHEE) is a simple ranking method in conception and application, which firstly includes two methodological families (PROMETHEE I for partial ranking and PROMETHEE II for complete ranking) that have been implemented with other versions of the PROMETHEE methods developed during the years [8]. All PROMETHEE methods are based on the generalization of the concept of criterion by generalized criterion functions and by the mathematical relations for ranking which are based on them [9].

The COPRAS technique is used for evaluating complex processes by quantitative multi-criteria methods, both maximizing and minimizing criteria values [10]. This method could be applied selecting the appropriate set of criteria that describes the chosen alternatives, preparing a decision-making matrix and then determining the weights of the criteria [11]. During their research, Bausys et al. [11] studied the aspects of the application of a multicriteria decision making method with single value neutrosophic sets (SVNS), namely COPRAS-SVNS method, considering the selection of the location site for liquefied natural gas terminal.

The TOPSIS method is based on an aggregating function representing closeness to reference points considering that the optimal alternative should have the shortest distance from the ideal solution and the farthest one from the negative-ideal solution [12]. It could be applied as a criteria to maximize benefits and minimize costs assuming that each criterion takes either monotonically increasing or monotonically decreasing utility.

Simple Additive Weighting (SAW) is a widely used method for providing a comparative evaluation procedure using all criterion values of an alternative by means of the regular arithmetical operations of multiplication and addition. Moreover, a reasonable basis on which to form the weights reflecting the importance of each criterion should be determined.

The same input data are required for SAW and TOPSIS, and they can lead to a unique choice by comparing overall evaluations in SAW or closeness coefficients in TOPSIS [13].

Last but not least, Turskis et al. [14] developed a new fuzzy additive ratio assessment method called ARAS-F. This Additive Ratio Assessment method argues that the ratio of the sum of normalized and weighted criteria scores, which describe alternatives under consideration, to the sum of the values of normalized and weighted criteria, which describes the optimal alternative, is the degree of optimality, which is reached by the alternative under comparison [14].

Among the described MCDM methods, AHP was widely used for selections of center locations measuring environmental complexity, understanding the relevance of environmental complexity and facing supply chain operations [4]. Moreover, the Electre approach has been used for the selection of different typologies of logistics center location [15,16,17,18,19].

Therefore, the proposed methodology is based on a hybrid AHP [20]—Electre [21] MCDM approach. Since they were proposed, both methods have been applied to many different contexts. There are numerous examples of these and other method applications to problems of optimal location [22,23,24], in particular about environmental management [25].

The exiting literature on emergency management believes that the response time to a perturbing events is one of the essential parameters to define the hazards of the considered sites [26].

Therefore, this article examines the optimal location of logistic centers through the application of an MCDM [27].

3. Hybrid Methodology AHP-Electre

In literature, there are widespread examples of optimal placement determined by applying the Electre method [21] or AHP method [20]. These examples highlight the decision-making criteria weights. The estimate of the weights is a phase of the decision-making process as important as it is difficult whether they are assigned directly or not. The direct assignment of weights (Electre) is a huge source of arbitrariness, while the pairwise comparison (AHP) provides very simplified but numerous assessments, which may lead the decision-maker into contradictions [28]. Hence, the following decision-maker method shall be proposed, which will be considered as a hybrid type. Thus, both the AHP and Electre methods have been applied jointly in order to get a method, which could limit as much as it can the arbitrariness of the choice.

The Electre method is used basically to gain the organization of the estimates areas based on the decisional criteria. Rather than considering weights as criteria data, chosen by the decision-maker as suggested by the method, a hierarchy is inserted upstream which follows the AHP method to determinate the weights. In particular, hierarchy provides that every decision-maker (or typology of decision-makers) shall assess the importance of the criteria by comparing them in pairs. Subsequently, decision-makers shall be compared in pairs based on their importance. In general, it should not be difficult to estimate the decision-making power of the various parties involved according to the level of responsibility related to the subjects. Every decision-maker will eventually be able to make very simple judgments by comparing from time to time the importance of just two criteria, and the final weights, which will be assigned to the criteria, will not be just a commonplace average of values given by the different makers, but, instead, it will take into account both the roles and the decision-making authority of those who are involved.

Therefore, the proposed methodology is concentrated on the choice of the weights framed into a decisional context which involved more subjects with different priorities and responsibilities. The approach outlined preserves all the advantages of the Electre method, which does not require additional computational costs to the decision-maker, as the choices just mentioned in here. In fact, the method gives cascading alternatives by classifying them from the best to the worst in an very intuitive way and simple to read (see Figure 1).

Figure 1. Analytic hierarchy process.

Figure 1. Analytic hierarchy process.

4. Case Study: Location of an EOC in Valle Isarco and Alta Valle Isarco (Bolzano, Italy)

We face the choice of an EOC location in the territories of Bressanone and Vipiteno, the Isarco Valley and High Isarco Valley in south Tyrol (Italy) (Figure 2). Our aim will be to build a new Fire Department barrack choosing the perfect site planning in this context. Regional sensitivities are typical of a mountainous area so landslides, avalanches and the seasonal flooding are the risks that can possibly happen. The natural environment is very important and it must be absolutely protected.

Figure 2. Study area.

Figure 2. Study area.

4.1. The Options: Six Possible Locations

Six sites have been identified in the territory to be a potential locations for the new EOC. The sites have been selected for studies with the solo purpose of presenting as disparate features as possible to test the decision-making’ strategy.

The first alternative (site 1) refers to the opportunity of expanding the current barrack of the Fire Department in Sant’ Andrea connected only by Provincial Road to Bressanone. There are many dangers linked to landslides or avalanches neither hydraulic risks in this locality. The place is excluded from environment restrictions despite being adjacent to agricultural areas of landscape interest with chestnut groves and forests.

The second option (site 2) provides for the establishment of a center in a mainly rural area connected only by local roads. The site has a negligible level of risk. The whole agricultural area is of environmental interest although excluded from environmental constraints.

The third option (site 3) refers to the possibility of expanding the actual barrack of the Fire Department in Bressanone, which is connected with Highway and State Highway. Bressanone has previously been the subject of flood events during the flooding of Isarco river, which joins the Rienza River close to the aforementioned city. In particular, the center of the city is at flood risk. The area is quite populated, and there are not landscaping neither environmental constraints.

The fourth option (site 4) provides for the construction of the center in an industrial area: the usage as a trade or industrial area has already affected the same, which seems without any environmental interest, although it is bordering rural areas of environmental interest. The industrial area is right at the State Highway connecting Brenner Highway to Brunico, and it can be reached by alternative routes due to the presence of county and local roads, it is just 3 km from the Highway. The area is devoid of significant risks even if the surrounding areas are prone to collapse and widespread overturning.

The fifth option (site 5) is the possibility of adapting the existing barracks in Vipiteno, a town located right at the intersection of three State Highways, and it is quickly hooked up to the Highway. This site is not covered by any environmental restrictions, and it does not present any particular risks.

The sixth site (site 6) figures out how to recover a former quarry-area. The site is directly connected to the Highway and to the State Highway. It is not covered by any environmental restrictions nor does it present any particular risks (Figure 3).

Figure 3. Location of the six alternatives.

Figure 3. Location of the six alternatives.

4.2. Survey, Criteria and Weights

As mentioned before, the proposed approach focuses on the choice of the criteria weights applying a hierarchy of the AHP type framed in a decisional context, which sees more subjects involved with different priorities and responsibilities. There are five decisional criteria to be considered in this case of study: (1) building cost of the center; (2) site accessibility; (3) dangerousness; (4) environmental impact; (5) communications quality at the site considered.

A specific questionnaire has been drawn up just to consult about different types of decision-makers regarding the assigned weights to these criteria. The questionnaire has been sent to almost three hundred experts and insiders (Directors and Heads of Units of: county and local Civil Protection—PC; County Fire Department—VVF; Italian Red Cross—CRI; university professors and researchers of Emergency Management—Research). In accordance with Legislative Decree 196/2003 (Data Protection Code), the questionnaire was anonymous, but, in order to track the origin of the answers and the information about the composition of the sample, the first question was concerning the kind of organization. Most of the responses obtained come from academic researchers and operative realities (VVF, CRI and PC), but nothing has came from administrative or political organizations (Figure 4).

Figure 4. Distribution of answers in percentage points.

Figure 4. Distribution of answers in percentage points.

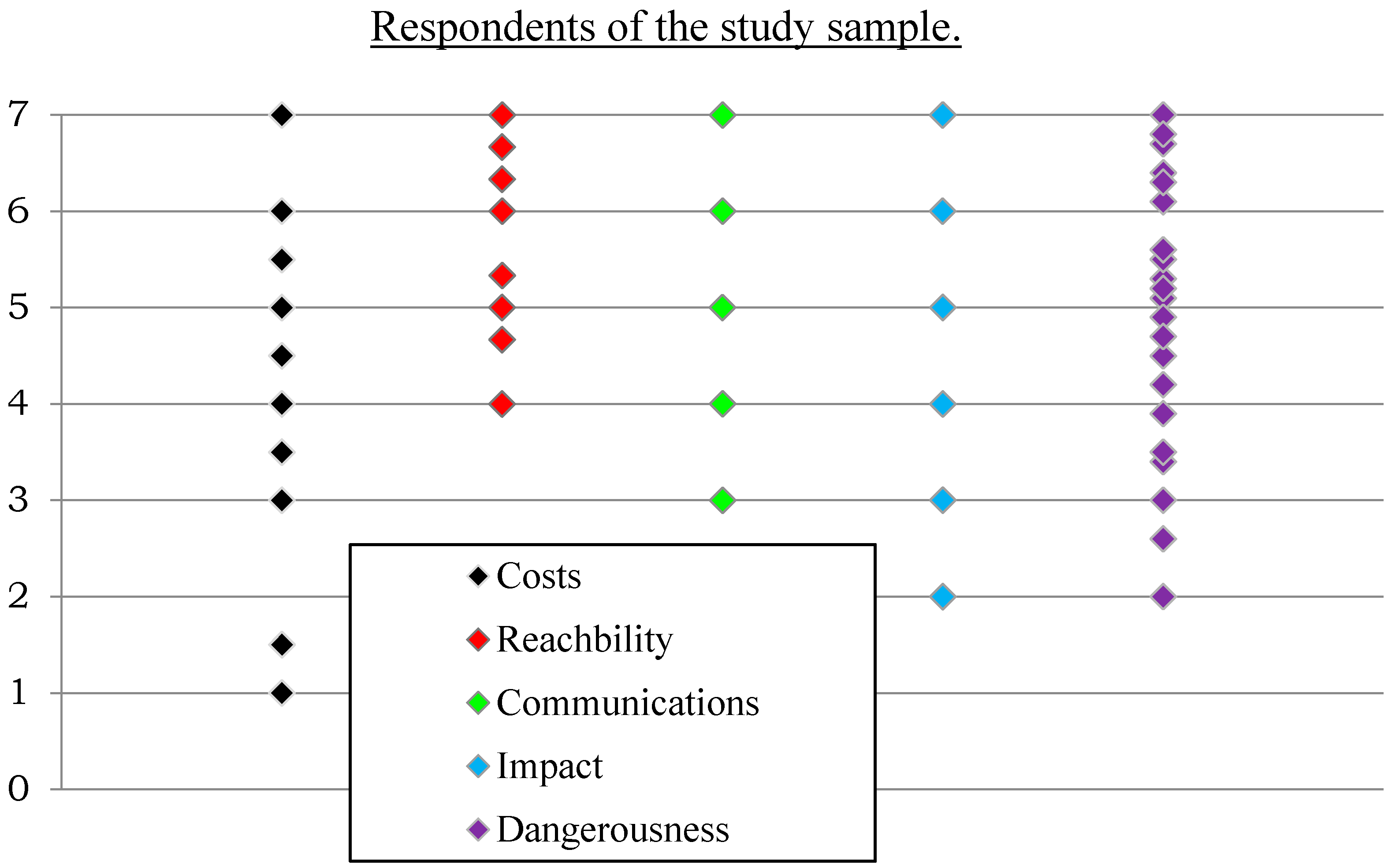
The questionnaire was designed to test the decisional criteria chosen for the respondents’ samples with the purpose of obtaining an important indication (from a minimum value of 1 up to a maximum value of 7) for each proposed criteria. The results appear to be very scattered when they are received globally (Figure 5).

Figure 5. Variability of the weight coefficient for each criterion.

Figure 5. Variability of the weight coefficient for each criterion.

If we consider separately the answers obtained from each type of respondent, it is noted that values given for weights tend to cluster. For some criteria, all of the respondents belong to the same category, which has showed the same weight value. This scenario emphasizes how membership of a group involved in a specific way in the management could affect the mindset of the respondent by raising awareness in each member’s mind, by giving special emphasis to certain decision criteria while leaving others in the background.

In the responses of the survey, a line of thought was pretty clear that characterizes each different operating structure. As it sets out above, the academic group and the researchers are the exception because of their extremely dispersed results.

Thanks to the opinions collected, it has been possible to apply the AHP method to calculate the weights of the criteria starting from the matrix of pairwise comparison of criteria related to each decision-maker (see Table 1, Table 2, Table 3 and Table 4).

Table 1. Weights matrix—VVF decision-maker.

VVF	Costs	Reachbility	Communications	Impact	Dangerousness
costs	1	0.25	0.33	4	2
reachbility	4	1	2	9	5
communications	3	0.5	1	8	4
impact	0.25	0.11	0.125	1	0.33
dangerousness	0.5	0.2	0.25	3	1

Table 1. Weights matrix—VVF decision-maker.

VVF	Costs	Reachbility	Communications	Impact	Dangerousness
costs	1	0.25	0.33	4	2
reachbility	4	1	2	9	5
communications	3	0.5	1	8	4
impact	0.25	0.11	0.125	1	0.33
dangerousness	0.5	0.2	0.25	3	1

Table 2. Weights matrix—CRI decision-maker.

CRI	Costs	Reachbility	Communications	Impact	Dangerousness
costs	1	0.25	0.33	3	0.8
reachbility	4	1	1.5	9	5
communications	3	0.66	1	8	4
impact	0.33	0.11	0.125	1	0.33
dangerousness	1.25	0.2	0.25	3	1

Table 2. Weights matrix—CRI decision-maker.

CRI	Costs	Reachbility	Communications	Impact	Dangerousness
costs	1	0.25	0.33	3	0.8
reachbility	4	1	1.5	9	5
communications	3	0.66	1	8	4
impact	0.33	0.11	0.125	1	0.33
dangerousness	1.25	0.2	0.25	3	1

Table 3. Weights matrix—PC decision-maker.

PC	Costs	Reachbility	Communications	Impact	Dangerousness
costs	1	0.18	0.16	3	2.5
reachbility	5.5	1	0.66	7.5	6.5
communications	6	1.5	1	8	7
impact	0.33	0.13	0.125	1	0.5
dangerousness	0.4	0.15	0.14	2	1

Table 3. Weights matrix—PC decision-maker.

PC	Costs	Reachbility	Communications	Impact	Dangerousness
costs	1	0.18	0.16	3	2.5
reachbility	5.5	1	0.66	7.5	6.5
communications	6	1.5	1	8	7
impact	0.33	0.13	0.125	1	0.5
dangerousness	0.4	0.15	0.14	2	1

Table 4. Weights matrix—Research decision-maker.

Research	Costs	Reachbility	Communications	Impact	Dangerousness
costs	1	0.25	0.2	0.5	2.5
reachbility	4	1	0.5	3	5
communications	5	2	1	4	6
impact	2	0.33	0.25	1	2.5
dangerousness	0.4	0.2	0.16	0.4	1

Table 4. Weights matrix—Research decision-maker.

Research	Costs	Reachbility	Communications	Impact	Dangerousness
costs	1	0.25	0.2	0.5	2.5
reachbility	4	1	0.5	3	5
communications	5	2	1	4	6
impact	2	0.33	0.25	1	2.5
dangerousness	0.4	0.2	0.16	0.4	1

Regarding the matrix of pairwise comparisons of the decision-makers (Table 5), it is considered far more authoritative the opinion of the VVF. In fact, the case study concerns the placement of one of their barracks, and there is a lack of answers from the political and administration world. The other two operational decision-makers—CRI and PC—are considered equally important, albeit much less of VVF. In the end, it has been considered that rarely does the reality of the research gain a true decisional power in such kind of territorial planning context.

Table 5. Pairwise comparison matrix.

Decision	VVF	CRI	PC	Research
vvf	1	5	5	9
cri	0.2	1	1	5
pc	0.2	1	1	5
research	0.11	0.2	0.2	1

Table 5. Pairwise comparison matrix.

Decision	VVF	CRI	PC	Research
vvf	1	5	5	9
cri	0.2	1	1	5
pc	0.2	1	1	5
research	0.11	0.2	0.2	1

As showed in Table 6, we have calculated the weights of the criteria, which were used in the case study, applying a recombination matrix, specified by the method.

Table 6. Final weights matrix.

WC(VVF)	WC(CRI)	WC(PC)	WC(R)		WD(G)		WC(G)
0.13	0.10	0.11	0.10		0.63		0.12
0.45	0.42	0.42	0.32	x	0.17	=	0.44
0.30	0.32	0.51	0.49		0.17		0.35
0.04	0.04	0.04	0.14		0.04		0.04
0.08	0.10	0.06	0.06				0.08

Table 6. Final weights matrix.

WC(VVF)	WC(CRI)	WC(PC)	WC(R)		WD(G)		WC(G)
0.13	0.10	0.11	0.10		0.63		0.12
0.45	0.42	0.42	0.32	x	0.17	=	0.44
0.30	0.32	0.51	0.49		0.17		0.35
0.04	0.04	0.04	0.14		0.04		0.04
0.08	0.10	0.06	0.06				0.08

4.3. Scale of Compliance

Once we have set the options and the decision criteria, the sites are evaluated numerically on each criterion in order to compose the evaluation matrix. Data were largely derived from institutional portals of Bolzano Province, and they were minimally supplemented by plausible values from the literature. In particular, it is being mentioned for the study values of the costs and communication quality while it was possible to obtain data on the criteria of dangerousness, environmental impact and accessibility of the sites by institutional portals. For some time, the Autonomous Provincia of Bolzano has arranged to implement an open access Geoportal, on an Geographic Information System (GIS) open source platform, which provides many of the datasets on the Province in accordance with the requirements of the INSPIRE (Directive 2007/2/CE of European Parliament).

Thus, it is necessary to collect all the data needed and structure compliance scales for each criterion in order to transform qualitative information in quantitative scores. Most of the criteria considered in the case study (three out of five) respects a trend for which higher values correspond to conditions increasingly unfavorable: the cost requirement is the obvious example of this trend. Based on the majority of the criteria, therefore, the best alternatives should be based on the minimization of the scores. Since this is the dominant trend, it has been chosen to adapt the remaining two criteria with the opposite pattern (accessibility and quality communication). Obviously, the choice made is based on the minimization of values, and it is completely arbitrary and irrelevant in order to identify the best alternative. Then, we define the scale of compliance for each criterion.

Cost: evaluations are already expressed in terms of numbers, and, therefore, there is no need to introduce further scales of compliance. We only report the cost for each option in the evaluation matrix.

Dangerousness and Environmental impact: these criteria, showed in Table 7 and Table 8, have intuitively the trend that we have chosen to follow.

Table 7. Attribute scores for “Dangerousness-Criteria”.

Dangerousness
Very low	1
Low	2
Mid-low	3
Medium	4
Mid-high	5
High	6

Table 7. Attribute scores for “Dangerousness-Criteria”.

Dangerousness
Very low	1
Low	2
Mid-low	3
Medium	4
Mid-high	5
High	6

Table 8. Attribute scores for “Environmental Impact-Criteria“.

Environmental Impact
Very low	1
Low	2
Medium	3
High	4
Very high	5

Table 8. Attribute scores for “Environmental Impact-Criteria“.

Environmental Impact
Very low	1
Low	2
Medium	3
High	4
Very high	5

Reachability: we have the amount of roads links and their type as input data for each site. Therefore, we choose to assign a rating to each type of road as shown below, and we add these scores to calculate the goodness of links (Table 9).

Table 9. Attribute scores for “Reachability-Criteria”.

Reachability
LR	+1
PR	+2
SH	+3
H	+4

Table 9. Attribute scores for “Reachability-Criteria”.

Reachability
LR	+1
PR	+2
SH	+3
H	+4

Any way that the resulting value does not respect the trend chosen because of a well-connected site will have a high score. We chose an evaluation of the accessibility of the site as the complement to 20 of the scores obtained in the manner set out above. The value 20 is arbitrary, and it has been chosen as the highest ideal because it is sufficiently large if compared to the scores of the alternatives under consideration to represent an area optimally connected.

Communication Quality: for the latter criterion, we must reserve the intuitive trend of scores because, in this case, it is desirable to minimize the scores (Table 10).

Table 10. Attribute scores for “Communication Quality-Criteria”.

Communication Quality
Low	4
Medium	3
High	2
Very high	1

Table 10. Attribute scores for “Communication Quality-Criteria”.

Communication Quality
Low	4
Medium	3
High	2
Very high	1

4.4. Attributes of Alternatives, Evaluation Matrix and Sorting

First of all, we compile a matrix with the information obtained by analysing the available data. Based on this, we can estimate qualitative judgments integrated with assumptions (cost and quality of communication), and, finally, we compile the evaluation matrix transforming qualitative values into quantitative scores using the scale of compliance (see Table 11, Table 12 and Table 13).

Table 11. Available information matrix.

Alternative	Cost	Reachability	Dangerousness	Environmental Impact	Communication Quality
Site 1	No data	PR	No particular risks observed	Location without constraints, adjacent to scenic areas	No data
Site 2	No data	several LR	No particular risks observed	Location without constraints, farmland of environmental interest	No data
Site 3	No data	H, SH	Area historically subject to flood risk where Isarco River joins Rienza River in urban context.	Populated area, location without constraints	No data
Site 4	No data	Next to H, SH, PR, LR	Area with no significant risks, adjacent to areas subject to frequent collapses and rollovers	Area deteriorated by industrial use, bordering areas of environmental interest	No data
Site 5	No data	H, three SH	No particular risks observed	Populated area, location without constraints	No data
Site 6	No data	H, two SH	No particular risks observed	Location without constraints	No data

Table 11. Available information matrix.

Alternative	Cost	Reachability	Dangerousness	Environmental Impact	Communication Quality
Site 1	No data	PR	No particular risks observed	Location without constraints, adjacent to scenic areas	No data
Site 2	No data	several LR	No particular risks observed	Location without constraints, farmland of environmental interest	No data
Site 3	No data	H, SH	Area historically subject to flood risk where Isarco River joins Rienza River in urban context.	Populated area, location without constraints	No data
Site 4	No data	Next to H, SH, PR, LR	Area with no significant risks, adjacent to areas subject to frequent collapses and rollovers	Area deteriorated by industrial use, bordering areas of environmental interest	No data
Site 5	No data	H, three SH	No particular risks observed	Populated area, location without constraints	No data
Site 6	No data	H, two SH	No particular risks observed	Location without constraints	No data

Table 12. Added information matrix.

Alternative	Cost	Reachability	Dangerousness	Environmental Impact	Communication Quality
Site 1	€500.000,00	PR	Very low	low	high
Site 2	€500.000,00	several LR	Very low	high	low
Site 3	€1.000.000,00	H, SH	Mid high	Very low	Very high
Site 4	€1.600.000,00	Next to H, SH, PR, LR	low	low	Medium
Site 5	€5.000.000,00	H, three SH	Very low	Very low	high
Site 6	€1.500.000,00	H, two SH	Very low	Very low	low

Table 12. Added information matrix.

Alternative	Cost	Reachability	Dangerousness	Environmental Impact	Communication Quality
Site 1	€500.000,00	PR	Very low	low	high
Site 2	€500.000,00	several LR	Very low	high	low
Site 3	€1.000.000,00	H, SH	Mid high	Very low	Very high
Site 4	€1.600.000,00	Next to H, SH, PR, LR	low	low	Medium
Site 5	€5.000.000,00	H, three SH	Very low	Very low	high
Site 6	€1.500.000,00	H, two SH	Very low	Very low	low

Table 13. Evaluation matrix.

Alternative	Cost	Reachability	Dangerousness	Environmental Impact	Communication Quality
Site 1	€500.000,00	18	1	2	2
Site 2	€500.000,00	18	1	4	4
Site 3	€1.000.000,00	13	5	1	1
Site 4	€1.600.000,00	11	2	2	3
Site 5	€5.000.000,00	7	1	1	2
Site 6	€1.500.000,00	10	1	1	4

Table 13. Evaluation matrix.

Alternative	Cost	Reachability	Dangerousness	Environmental Impact	Communication Quality
Site 1	€500.000,00	18	1	2	2
Site 2	€500.000,00	18	1	4	4
Site 3	€1.000.000,00	13	5	1	1
Site 4	€1.600.000,00	11	2	2	3
Site 5	€5.000.000,00	7	1	1	2
Site 6	€1.500.000,00	10	1	1	4

We get the following ranking of the alternatives processing the matrix obtained by the Electre method. The preferred alternative is site 5, as in the Table 14, thanks to the system of weights chosen.

Table 14. Ranking of the alternatives.

Ranking	Alternative
1	Site 5
2	Site 3
3	Site 6
4	Site 4
5	Site 1
6	Site 2

Table 14. Ranking of the alternatives.

Ranking	Alternative
1	Site 5
2	Site 3
3	Site 6
4	Site 4
5	Site 1
6	Site 2

5. Conclusions

The introductory part clearly indicates the necessity of the application of complex procedures in solving location problems of EOC. In fact, the EOC are structures potentially very impactful (appropriate roads, helicopters area, large storage areas, parking, etc.); however, the real problem is not simply to minimize the building environmental impacts but to establish a process to optimize the best place to situate these centers. In particular, many mitigation strategies, as well as many response plans have in common the purpose of minimizing response time in order to decrease the level of vulnerability of the study area.

The purpose of this study was to develop a methodology for evaluating and selecting EOC locations, which is a multidimensional and multilevel decision making problem. The proposed methodology retains the advantages of the Electre method, simplifying the assignment of the weights in contexts characterized by the presence of more decision-makers or more types of decision-makers. The method is extremely versatile and applicable to different problems. It would be interesting to proceed with another survey with experts and professionals on the proposed hybrid methodology.