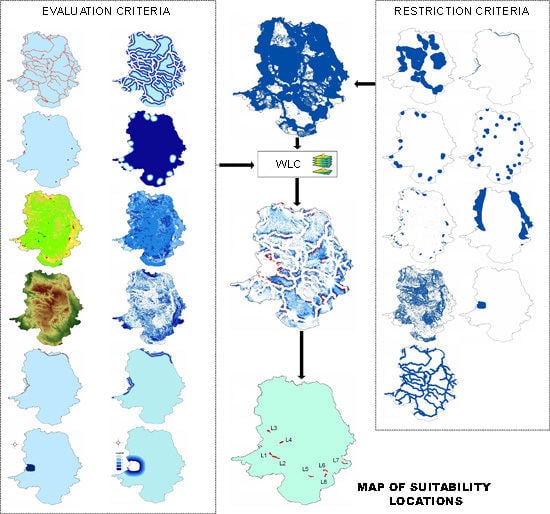
This phase concerns standardization and evaluation of all criteria used in the analysis.
2.4.3. Comparison and Relative Assessment of Criteria Weight (DEMATEL-ANP)
While solving real problems, criteria do not have the same degree of significance so the DM has to define significance factors for some criteria using weighting coefficients (weights) or criteria evaluation. The WLC method demands normalized weights, meaning that the sum of all weights must be 1.
DEMATEL and ANP (DANP) method is used for the calculation of normalized criteria weights followed then by WLC method. The DEMATEL method was originally developed by the Science and Human Affairs Program of the Battelle Memorial Institute of Geneva, with the purpose of studying a complex and intertwined problem [
43]. It has been widely accepted as one of the best tools to solve the cause and effect relationship among evaluation criteria [
43,
44,
45,
46,
47]. The original DEMATEL method is modified by some researchers so as to make it comply with their problems. The modified DEMATEL method which is used in this paper is adapted from the study of [
48] (
Figure 2).
The full procedure of the previously defined DEMATEL method is explained as follows:
Step 1. Gather experts’ opinions and calculate the average matrix Z. The modified DEMATEL method is built first creating the direct-relation matrix Z where Z is (n × n) matrix, n represents the number of criteria. The direct relation matrices are all obtained by holding a pair-wise comparison among the criteria themselves in which Zij indicates the degree to which the criterion affects criterion . Therefore, the relationship among the criteria could be held within a matrix. In this method, the effects of the criteria on each other are expressed in terms of linguistic equations.
A group of
e experts and
n factors are used in this step. Each expert is asked to view the degree of direct influence between two factors based on a pair-wise comparison. The degree to which the expert perceived factor
i impacts factor
j is denoted as
. For each expert, a
n ×
n non-negative matrix is constructed (
n represents the number of criteria) as
, where
e is the expert number of participating in evaluation process with 1 ≤
e ≤
k. Thus,
are the matrices from
m experts. In this method, the effects of the criteria on each other are expressed in terms of linguistic equations. Aggregation of experts’ opinions gives the final matrix
where
denotes preference of expert number
e,
k is total number of experts.
Step 2. Calculate the normalized initial direct-relation matrix
D. The normalized initial direct-relation matrix
, where value of each element in matrix
D is ranged between [0,1]. The calculation is shown below.
where the elements of the initial direct-relation matrix is calculated from
where
n denotes total number of criteria.
Step 3. Derive the total relation matrix
T. The total-influence matrix
T is obtained by utilizing Equation (7), in which,
I is an
n ×
n identity matrix. The element of
tij represents the indirect effects that factor
i had on factor
j, then the matrix
T reflects the total relationship between each pair of system factors. Initial normalized direct-relation matrix can be separated into separate sub matrices
i.e., (
,
,
). It was proven that
And
where
0 is the null matrix and
I is the identity matrix [
49,
50]. Therefore, the total-relation matrix
T can be acquired by calculating the following term [
51]:
As it is previously shown, the total relation matrix for the criteria (
T) can be presented as:
where
tij is the overall influence rating of decision maker for each alternative
against criterion
.
Step 4. Calculate the sums of rows and columns of matrix
T. The sum of rows and sum of columns of the sub-matrices
,
and
denoted by the numbers
Di and
Ri, respectively, can be obtained through Equations (9) and (10), respectively:
where
n denotes number of criteria.
Step 5. Determination of the threshold value
α. Threshold value
α is used for creating a cause and effect relationship diagram. Threshold value
α is calculated as the median of elements (
tij) from the matrix
T, according to Equation (11). This calculation aims eliminate some minor effects of elements in matrix
T [
52].
where
N is the total number of elements in matrix
T.
Step 6. Creating a cause and effect relationship diagram. The cause and effect diagram is constructed by mapping all coordinate sets of (
Di +
Rj,
Di −
Rj) to visualize the complex interrelationship and provide information in order to determine the most important factors and how they influence the affected factors [
53]. The factors
tij that are greater than
α are selected and shown in the cause and effect diagram [
52].
After designing the cause and effect relationship diagram, weighted coefficients of criteria are calculated using the ANP method in the next phase. Afterwards, the implementation of DEMATEL method into the ANP method is elaborated.
The ANP method was developed to avoid the hierarchical restrictions that exist in the AHP method [
54]. ANP presents a generalized AHP method, designed so that the hierarchy is replaced by a network. The ANP method, unlike hierarchy structured problems, takes into account different forms of dependency and feedback. The structure of the feedback is not linear and is more close to the network where interdependent loops frequently appear. The calculation of relative weights of criteria using traditional ANP means the levels of interdependence of factors are treated as reciprocal values. On the contrary, using the DEMATEL method, the levels of interdependence of factors do not have reciprocal value, which is closer to real circumstances [
55].
The traditional ANP method calculates weighted supermatrix by normalization of unweighted supermatrix. Each column of the unweighted supermatrix is divided by the number of criteria so that each column will add up to 1. It means that every criterion has the same weight. However, then, that is not a good assumption, because the mutual influence of two criteria can be different. Although it is easy to normalize using such a method, this neglects the fact that different groups should have different degrees of influence. Thus, we need to find another way of normalizing the unweighted supermatrix that relaxes this assumption of equal weight among criteria. Here, we turn to the total-influence matrix
T in DEMATEL and its threshold value
α for help [
56].
In order to address the mentioned faults, the total relation matrix (matrix T) is used to calculate the weighted coefficient of criteria, according to the DEMATEL method (step 3, Equation (8)). Hence, the mentioned problem is easily resolved by merging DEMATEL with the ANP method (DANP) so the obtained results are more reflective of the real situation. The hybrid DANP method, or the integration of DEMATEL and ANP methods, is conducted through five steps. They are completed after finishing the effect relationship diagram (ERD).
Elements of the unweighted supermatrix are defined in the first step. Before unweighted supermatrix design is completed, it is necessary to define the network model for the ANP method. The network model is designed on the basis of the total relation matrix and ERD.
Unweighted supermatrix is created when each level with the total degree of influence from the total relation matrix
T is normalized. Total sum of matrix elements by columns needs to be calculated before its normalization.
where
matrix contains factors from group K1 and influences in respect to the factors from group K1.
Elements of the normalized total influence matrix for criteria
Tcα are calculated in the next step. After that, the normalization of the matrix
Tc is done. Normalized matrix
Tcα is shown in Equation (13)
For an example, an explanation for the normalization of
Tcα11 on dimension K1 is shown with Equations (14) and (15). Factor sum
c11, ..., c1m1 inside the group K1 is obtained from Equation (14).
where
tcj11 denotes values of factor influences
c11, ..., c1m1 in relation to factors from group D1, and elements
tc11α11 and their normalized values.
The calculation procedure for other matrixes Tcαnn inside the matrix Tcα is identical and it will not be further explained.
The calculation of the unweighted supermatrix
W is completed in the third step. Because the total influence matrix
Tc and fills the interdependence among dimensions and criteria, we can transpose the normalized total influence matrix
Tcα by the dimensions based on the basic concept of ANP resulting in the unweighted supermatrix
W =
(Tcα)', as shown in Equation (16)
where matrix
W11 presents values of factor influences from group K1 in relation to factors from group K1.
The calculation of weighted normalized supermatrix
Wα (Step 4) is conducted by multiplying elements of unweighted supermatrix
W with corresponding elements of the normalized total influence matrix
. Elements of the normalized total influence matrix.
were obtained by normalization of the total influence matrix
TD, according to the Equations (17) and (18).
The normalization of the total influence matrix
of the dimensions, Equation (17), gave a new normalized total influence matrix
, Equation (18).
where
.
The elements of new weighted supermatrix
Wα were calculated after determining the elements of the matrix
. The elements of matrix
Wα are obtained by multiplying normalized total influence matrix of the dimensions
with the unweighted supermatrix
W, Equation (19)
The limit of the weighted supermatrix Wα is calculated in the last step. Afterwards, the weight of each evaluation criteria is obtained. The weighted supermatrix can be raised to the limiting powers until the supermatrix has converged and becomes a long-term stable supermatrix. In this way, the global priority vectors, called DANP influence weights, were obtained such as , where W denotes the limit supermatrix, while k denotes any integer.
2.4.5. Extraction and Ranking of Suitable Locations
The extraction of suitable locations presents the extraction of cells with the highest xi values from the final suitability map. They represent potentially the most suitable alternatives for the AD locations. The filtration of the most suitable alternatives (cells with the highest xi) is conducted with the combined use of GIS arithmetic operations and inquiries. As a result, the suitable locations were obtained which are converted in the vector form meeting a certain level of suitability.
The final decision or recommendation should be based on the suitable locations’ ranking. The ranking is completed in order to assess every location with the established goals of the analysis. This model proposes the use of MAIRCA (MultiAttributive Ideal-Real Comparative Analysis) method for the selection of the most suitable location. MAIRCA was developed in 2014 by the Center for Logistics Research at the University of Defence in Belgrade [
58].
The main assumption of MAIRCA method is in the determination of the gap between ideal and empirical weights. The summation of gaps for each criterion gives the total gap for every observed alternative. At the end, it comes to the alternatives ranking, where the best ranked alternative is the one with the smallest value for the total gap. The alternative with the smallest value for the total gap is the alternative which had values closest to the ideal weights according to the largest number of criteria (ideal criteria values). The MAIRCA method is conducted in six steps:
Step 1. The formation of the initial decision matrix (
X). The criteria values (
xij,
i = 1, 2, ….
n;
j = 1, 2, …
m) are determined in the initial decision Equation (22) for each of the observed alternatives.
Equation (22) are obtained according to the personal preferences of the DM or by aggregation of experts’ decisions.
Step 2. Preference determination according to the alternative selection
. During alternative selection, the DM is neutral to the process. In fact, he does not have preference to any of the proposed alternatives. The main assumption is that DM does not take into account the probabilities of any alternative selection. The DM perceives the alternatives as if any of them can have equal probability of appearance, so the preference to choose one of them from
m possible alternatives is:
where
m denotes the total number of choices.
In the decision making analysis, with the given probabilities we assume that the DM is neutral towards the risk. In that case, all the preferences are equal according to the selection of certain alternatives
where
m denotes the total number of choices.
Step 3. The calculations of theoretical evaluation matrix elements (
). Theoretical evaluation matrix is created (
) with format
n ×
m (
n is the total criteria number,
m is the total number of alternatives). Theoretical evaluation matrix elements (
) are calculated as the multiplication of the preferences according to the alternatives
and criteria weights (
)
Because the DM is neutral to the initial selection of the alternatives, all preferences (
) are equal for all alternatives. Then, the Equation (25) can be shown in the Equation (26)
where
n is the total number of criteria,
is theoretical evaluation.
Step 4. Determination of real evaluation Equation (27).
where
n is the total number of criteria,
m is the total number of alternatives.
The calculation of real evaluation matrix elements (
) is conducted by multiplying the real evaluation matrix elements (
) and elements of the initial decision making matrix (
) according to the equation:
- (a)
For the “benefit” type criteria (the bigger criterion value is desirable)
- (b)
For the “cost” type criteria (the smaller criterion value is desirable)
where
,
i
denote elements of the initial decision making matrix (
),
and
are defined as:
are the maximum values of the marked criterion by its alternatives.
are the minimum values of the marked criterion by its alternatives.
Step 5. The calculation of the total gap matrix (
). The elements of the matrix
are calculated as the difference (gap) between theoretical (
) and real evaluations (
), or by actually subtracting the elements of the theoretical evaluation matrix (
) with the elements of the real evaluation matrix (
).
where
n is the total number of criteria,
m is the total number of alternatives.
Gap
takes values from the interval
, according to Equation (31)
It is desirable that goes to zero () because the alternative with the smallest difference between the theoretical () and real evaluation () is chosen. If the alternative for the criterion has a theoretical evaluation value equal to the real evaluation value (), then the gap for the alternative for the criterion is . In fact, the alternative for the criterion is the best (ideal) alternative ().
If the alternative for the criterion. has a theoretical evaluation value. and the real ponder value , than the gap for the alternative. for the criterion is . In fact, the alternative is for the criterion the worst (anti-ideal) alternative ().
Step 6. The calculation of the final values of the criteria functions (
) for the alternatives. The values of the criteria functions are obtained from the sum of gaps (
) for the alternatives, or just the sum of the matrix elements (
) in columns, using Equation (32)