Revisiting the “Guns versus Butter” Argument in China (1950–2014): New Evidence from the Continuous Wavelet Analysis
Abstract
:1. Introduction
2. Literature Review
2.1. Theoretical Basis
2.2. Empirical Analysis
3. Continuous Wavelet Analysis
3.1. The Continuous Wavelet Transform
3.2. The Power of Wavelet and Cross-Wavelet
3.3. The Wavelet Coherency and the Phase-Difference
3.4. The Partial Wavelet Coherency and the Partial Phase-Difference
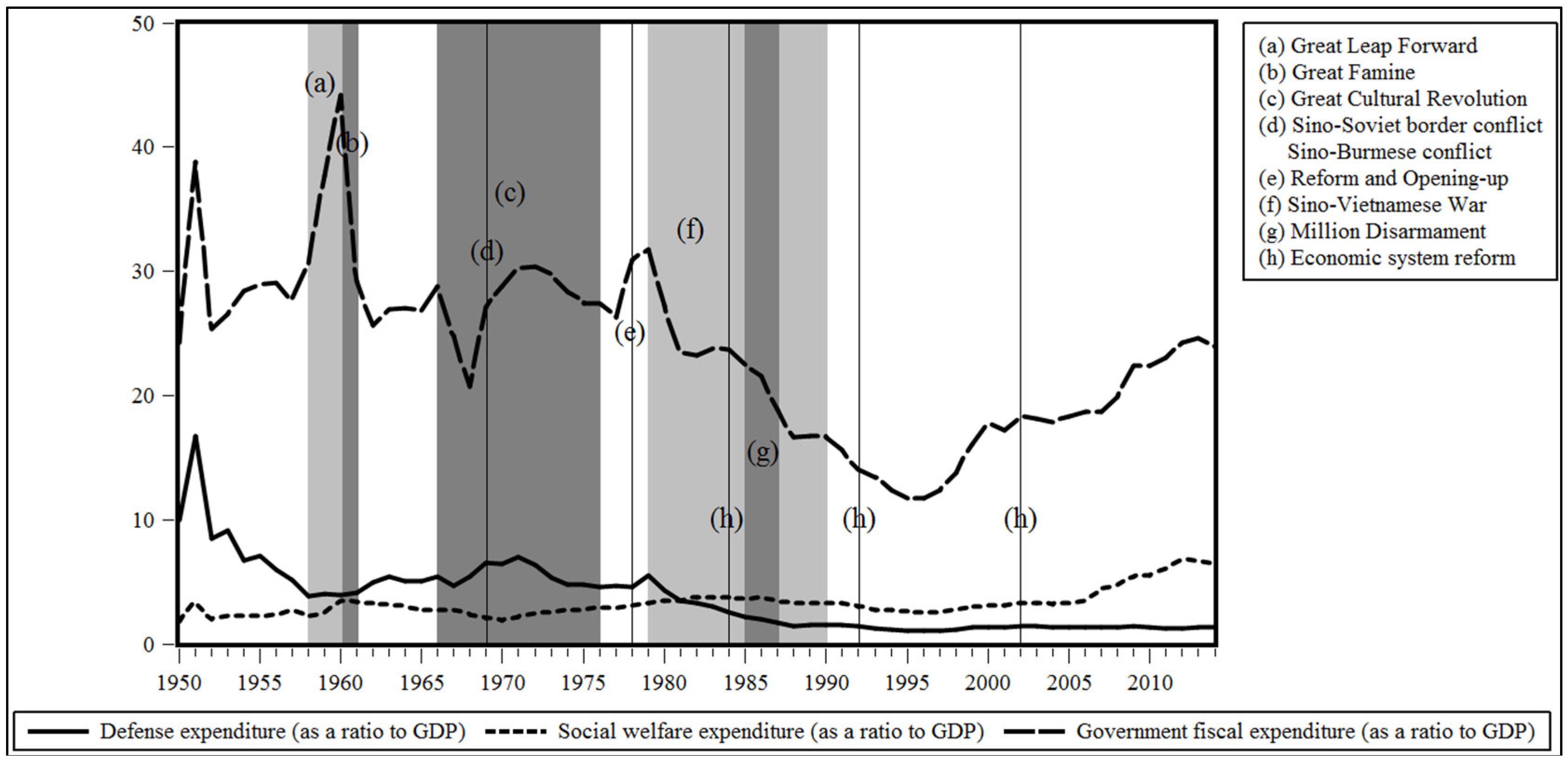
4. Data Description
5. Empirical Analysis of Defense and Social Welfare
5.1. Wavelet Power Spectrum Analysis
5.2. Partial Wavelet Coherency
6. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- China Statistical Yearbook, 2015; China Statistics Press: Beijing, China, 2015.
- Aguiar-Conraria, L.; Soares, M.J. The continuous wavelet transform: Moving beyond uni- and bivariate analysis. J. Econ. Surv. 2014, 28, 344–375. [Google Scholar] [CrossRef]
- Kollias, C.; Paleologou, S.M. Budgetary trade-offs between defence, education and social spending in Greece. Appl. Econ. Lett. 2011, 18, 1071–1075. [Google Scholar] [CrossRef]
- Lin, E.S.; Ali, H.E.; Lu, Y.L. Does military spending crowd out social welfare expenditures? Evidence from a panel of OECD countries. Defence Peace Econ. 2015, 26, 33–38. [Google Scholar] [CrossRef]
- Yildirim, J.; Sezgin, S. Military expenditure and employment in Turkey. Defence Peace Econ. 2003, 14, 129–139. [Google Scholar] [CrossRef]
- Zhang, Y.; Liu, X.; Xu, J.; Wang, R. Does military spending promote social welfare? A comparative analysis of the BRICS and G7 countries. Defence Peace Econ. 2016. [Google Scholar] [CrossRef]
- Apostolakis, B.E. Warfare–welfare expenditure substitutions in Latin America, 1953–87. J. Peace Res. 1992, 29, 85–98. [Google Scholar] [CrossRef]
- Dabelko, D.; McCormick, J.M. Opportunity costs of defense: Some cross-national evidence. J. Peace Res. 1977, 14, 145–154. [Google Scholar] [CrossRef]
- Deger, S. Human resource, government’s education expenditure and the military burden in less developed countries. J. Dev. Areas 1985, 20, 37–48. [Google Scholar]
- Ozsoy, O. Budgetary trade-offs between defense, education and health expenditures: The case of Turkey. Defence Peace Econ. 2002, 13, 129–136. [Google Scholar] [CrossRef]
- Peroff, K.; Podolak-Warren, M. Does spending on defence cut spending on health? A time-Series analysis of the U.S. Economy: 1929–74. Brit. J. Polit. Sci. 1979, 9, 21–39. [Google Scholar] [CrossRef]
- Russett, B.M. Who pays for defense? Am. Polit. Sci. Rev. 1969, 63, 412–426. [Google Scholar] [CrossRef]
- Frederiksen, P.C.; Looney, R.E. Budgetary consequences of defense expenditures in Pakistan: Short-run impacts and long-run adjustments. J. Peace Res. 1994, 31, 11–18. [Google Scholar] [CrossRef]
- Mintz, A. Guns versus butter: A disaggregated analysis. Am. Polit. Sci. Rev. 1989, 83, 1285–1293. [Google Scholar] [CrossRef]
- Russett, B. Defense expenditures and national well-being. Am. Polit. Sci. Rev. 1982, 76, 767–777. [Google Scholar] [CrossRef]
- Peroff, K. The warfare-welfare trade-off: Health, public aid, and housing. J. Sociol. Soc. Welfare 1976, 4, 366–381. [Google Scholar]
- Harris, G.; Kelly, M.; Pranowo. Trade-offs between defence and education/health expenditures in developing countries. J. Peace Res. 1988, 25, 165–177. [Google Scholar] [CrossRef]
- Verner, J.G. Budgetary trade-offs between education and defence in Latin American: A research note. J. Dev. Areas 1983, 18, 77–92. [Google Scholar]
- Caputo, D.A. New perspectives on the public policy implications of defense and welfare expenditures in four modern democracies: 1950–1970. Policy Sci. 1975, 6, 423–446. [Google Scholar] [CrossRef]
- Davis, D.R.; Chan, S. The security–welfare relationship: Longitudinal evidence from Taiwan. J. Peace Res. 1990, 27, 87–100. [Google Scholar] [CrossRef]
- Domke, W.K.; Eichenberg, R.C.; Kelleher, C.M. The illusion of choice: Defense and welfare in advanced industrial democracies, 1948–1978. Am. Polit. Sci. Rev. 1983, 77, 19–35. [Google Scholar] [CrossRef]
- Eichenberg, R.C. The Expenditure and revenue effects of defense spending in the frederal republic of Germany. Policy Sci. 1984, 16, 391–411. [Google Scholar] [CrossRef]
- Hess, P.; Mullan, B. The military burden and public education expenditures in contemporary developing nations: Is there a trade-off? J. Dev. Areas 1988, 22, 497–514. [Google Scholar]
- Cazelles, B.; Chavez, M.; de Magny, G.C.; Guegan, J.F.; Hales, S. Time-dependent spectral analysis of epidemiological time-series with wavelets. J. R. Soc. Interface 2007, 4, 625–636. [Google Scholar] [CrossRef] [PubMed]
- Cazelles, B.; Chavez, M.; Berteaux, D.; Ménard, F.; Vik, J.O.; Jenouvrier, S.; Stenseth, N.C. Wavelet analysis of ecological time series. Oecologia 2008, 156, 287–304. [Google Scholar] [CrossRef] [PubMed]




| Theories | Authors | Details |
|---|---|---|
| Keynesian theory | Yildirim and Sezgin [5]; Kollias and Paleologou [3]; Lin, Ali and Lu [4]; Zhang, et al. [6] | Defense expenditure can stimulate social welfare spending by increasing the aggregate demand. |
| Crowding-out effect | Russett [12]; Dabelko and McCormick [8]; Peroff and Podolak-Warren [11]; Deger [9]; Apostolakis [7]; Ozsoy [10]; Zhang, et al. [6] | Defense expenditure can crowd out the social welfare spending. |
| No relationship | Russett [15]; Mintz [14]; Frederiksen and Looney [13] | Defense expenditure has no relationship with social welfare spending. |
| Findings | Authors | Sample | Method |
|---|---|---|---|
| Positive | Verner [18] | 10 Latin American countries, 1948–1979 | Time-series regression analysis |
| Harris, Kelly and Pranowo [17] | Korea, Malaysia and Sri Lanka, 1967–1982 | Time-series data, a longitudinal regression analysis | |
| Kollias and Paleologou [3] | Greece, 1972–2004 | Time-series analysis, VAR | |
| Lin, Ali and Lu [4] | 29 OECD countries, 1988–2005 | Panel data analysis, GMM | |
| Zhang, et al. [6] | BRICS and G7 countries, 1993–2007 | Panel cointegration, impulse response function | |
| Negative | Russett [12] | The US, the UK, France and Canada, 1939–1968 | Time-series analysis, OLS (ordinary least squares) |
| Peroff [16] | The US, 1929–1971 | Time-series analysis, OLS | |
| Dabelko and McCormick [8] | 77 countries, 1950–1972 | Cross-sectional time-series, OLS | |
| Peroff and Podolak-Warren [11] | The US, 1929–1974 | Time-series analysis, OLS | |
| Deger [9] | 50 LDCs, 1967–1973 | Cross-sectional time-series, 3SLS | |
| Apostolakis [7] | 19 Latin American countries, 1953–1987 | Time-series analysis | |
| Ozsoy [10] | Turkey, 1925–1998 | Time-series analysis, OLS | |
| No Relationship | Caputo [19] | Australia, Sweden, the UK and the US, 1950–1970 | Standardized regressions and Pearson coefficients |
| Russett [15] | The US, 1941–1971 | Time-series analysis, OLS | |
| Domke, Eichenberg, and Kelleher [21] | The US, the UK, Germany and France, 1948–1980 | Time-series analysis, OLS | |
| Eichenberg [22] | Germany, 1950–1979 | Time-series analysis, OLS and GLS | |
| Hess and Mullan [23] | 77 LDCs, 1982–1983 | Cross-sectional time-series, 2SLS | |
| Mintz [14] | The US, 1947–1980 | Time-series analysis, OLS | |
| Davis and Chan [20] | Taiwan, 1961–1985 | Time-series analysis, 3SLS | |
| Frederiksen and Looney [13] | Pakistan, 1973–1986 | Time-series analysis, short-run and long-run model |
| Variable | Description | Time Period | Data Source |
|---|---|---|---|
| Defense | Government defense expenditure/GDP | 1950–2014 | National Bureau of Statistics of China, 2015 [1] |
| SW (social welfare) | Government expenditures of education, health, culture and technology/GDP | 1950–2014 | National Bureau of Statistics of China, 2015 [1] |
| GFE (government fiscal expenditure) | Government fiscal expenditure/GDP | 1950-2014 | National Bureau of Statistics of China, 2015 [1] |
| Frequency Time | 1–2 Years Band | 2–4 Years Band | 4–8 Years Band | |||
|---|---|---|---|---|---|---|
| Leading | Correlation | Leading | Correlation | Leading | Correlation | |
| 1951–1960 | ||||||
| 1961–1968 | Defense | positive | ||||
| 1969 | Defense | positive | ||||
| 1970–1976 | ||||||
| 1977 | Defense | positive | ||||
| 1978–1983 | ||||||
| 1984–1985 | SW | positive | ||||
| 1986–1988 | SW | negative | SW | positive | ||
| 1989–1991 | Defense | negative | ||||
| 1992–1993 | ||||||
| 1994 | SW | positive | ||||
| 1995 | SW | positive | SW | positive | ||
| 1996–1998 | SW | positive | ||||
| 1999–2004 | ||||||
| 2005 | Defense | positive | ||||
| 2006–2014 | ||||||
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, Y.; Liu, X.; Wang, R.; Tang, R. Revisiting the “Guns versus Butter” Argument in China (1950–2014): New Evidence from the Continuous Wavelet Analysis. Sustainability 2016, 8, 655. https://doi.org/10.3390/su8070655
Zhang Y, Liu X, Wang R, Tang R. Revisiting the “Guns versus Butter” Argument in China (1950–2014): New Evidence from the Continuous Wavelet Analysis. Sustainability. 2016; 8(7):655. https://doi.org/10.3390/su8070655
Chicago/Turabian StyleZhang, Ying, Xiaoxing Liu, Rui Wang, and Ruobing Tang. 2016. "Revisiting the “Guns versus Butter” Argument in China (1950–2014): New Evidence from the Continuous Wavelet Analysis" Sustainability 8, no. 7: 655. https://doi.org/10.3390/su8070655
APA StyleZhang, Y., Liu, X., Wang, R., & Tang, R. (2016). Revisiting the “Guns versus Butter” Argument in China (1950–2014): New Evidence from the Continuous Wavelet Analysis. Sustainability, 8(7), 655. https://doi.org/10.3390/su8070655





