Next Article in Journal
Sun Glint Correction of High and Low Spatial Resolution Images of Aquatic Scenes: a Review of Methods for Visible and Near-Infrared Wavelengths
Next Article in Special Issue
Upliftment Estimation of the Zagros Transverse Fault in Iran Using Geoinformatics Technology
Previous Article in Journal
Spectroscopic Analysis of Arsenic Uptake in Pteris Ferns
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Remote Sensing
Volume 1
Issue 4
10.3390/rs1040676
remotesensing-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles thumb_up
...
Endorse textsms
...
Comment
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

Detection and Monitoring of Active Faults in Urban Environments: Time Series Interferometry on the Cities of Patras and Pyrgos (Peloponnese, Greece)

by
Issaak Parcharidis
1,*,
Sotiris Kokkalas
2,
Ioannis Fountoulis
3 and
Michael Foumelis
4
1
Harokopio University of Athens, Department of Geography, El. Venizelou 70, 17671 Athens, Greece
2
University of Patras, Department of Geology, Division of Physical Geology, Marine Geology and Geodynamics, 265 00 Patras, Greece
3
National and Kappodistrian University of Athens, Faculty of Geology and Geoenvironment, Department of Dynamic Tectonic and Applied Geology, Panepistimioupolis Zografou, 157 84 Athens, Greece
4
National and Kappodistrian University of Athens, Faculty of Geology and Geoenvironment, Department of Geophysics and Geothermics, Panepistimioupolis Zografou, 157 84 Athens, Greece
*
Author to whom correspondence should be addressed.
Remote Sens. 2009, 1(4), 676-696; https://doi.org/10.3390/rs1040676
Submission received: 26 August 2009 / Revised: 21 September 2009 / Accepted: 25 September 2009 / Published: 30 September 2009
(This article belongs to the Special Issue Remote Sensing in Seismology)
Browse Figures
Versions Notes

Abstract

:
Monitoring of active faults in urban areas is of great importance, providing useful information to assess seismic hazards and risks. The present study concerns the monitoring of the potential ground deformation caused by the active tectonism in the cities of Patras and Pyrgos in Western Greece. A PS interferometric analysis technique was applied using a rich data–set of ERS–1 & 2 SLC images. The results of the interferometric analysis were compared with the tectonic maps of the two cities. Patras show clearer uplift–subsidence results due to the more distinct fault pattern and intense deformation compared to the Pyrgos area, where more diffused deformation is observed, with no significant displacements on the surface.

1. Introduction

The earthquake cycle of an active fault may include coseismic rupture and interseismic deformation. During the interseismic stage that usually ranges from a few hundreds to thousands of years, crustal tectonic strain may be silently accumulated. The strain is released during the interseismic period, especially along creeping active faults.
Understanding active tectonic processes and related energy release through monitoring of the transient deformation of strain accumulation process has become fundamental for several human activities. Additionally, local deformation type of a fault and the area near the fault may determine the extent of the seismic hazard as well. This allows taking into consideration measures and activities for seismic hazard mitigation.
Monitoring of active faults’ interseismic behavior in urban areas is of great importance, as the local exposure (population, infrastructures etc.) increases the risks. Recently, interseismic crustal velocities and strains have been determined for a number of active areas, through repeated measurements using a Global Position System. In some cases the terrain is remote and the accessibility is difficult and thus the density of GPS measurements is relatively sparse, or in the case of urban environments, the operation of GPS receivers may be interrupted due to the frequent blockage of signals [1,2].
During the last two decades the SAR Differential Interferometric (DInSAR) technique based on radar satellite data has become a useful tool for ground deformation detection and monitoring [3,4]. Recent developments (since the end of the 90s) in DInSAR have demonstrated the potential to overcome some of the known limitations of repeat–pass interferometry. By examining interferometric phase from stable, point like targets, it is possible to monitor stability and cover an area that is normally characterized by low coherence. Additionally, millimetric target displacement along the line of sight (LOS) directions can be detected allowing the measurement of slow terrain motion [5]. Permanent or Persistent Scatterers Interferometry (PSI) is a technique used to calculate fine motions of individual ground and structure points over wide areas. These reflectors should remain stable (interferometric phase stability over time). Interferometric Point Target Analysis (IPTA) is a specific method of PSI to exploit temporal and spatial characteristics of interferometric signatures collected from point targets to map scatterer deformation history [6]. Monitoring faults in urban environments using different interferormetric techniques (repeat–pass, stacking and PS) has been widely used in seismically active areas of the globe [1,7,8,9,10,11,12,13,14].
During 1993 catastrophic earthquakes affected northwestern Peloponnese in the southern part of Greece. They caused serious damages to the greater area of two densely populated cities, Patras and Pyrgos. These are the capital cities of the neighboring prefectures of Achaia and Ilia. This study concerns the use of the PS interferometric analysis of ERS–1 and 2 satellite data, over the cities of Pyrgos and Patras in order to monitor and reveal the spatial distribution of creep along active faults.

2. Tectonic and Geological framework—Active tectonics

Western Greece is an area that characterized by high seismicity and a fairly complex three-dimensional setting, with along strike changes in the progress of subduction zone. It comprises continent–continent collision in the north and ocean–continent subduction in the south [15,16,17,18,19]. The change between continent–continent and ocean–continent subduction occurs at the Kephalonia Transform Fault (KTF) [20], which is characterized by a dextral strike–slip sense of shear. GPS data from western Greece show a small amount of motion north of the KTF and southwest-directed rapid motion of the overriding plate south of it that reaches rates of 30–35 mm/yr in the western parts of the Peloponnese along with dextral kinematics of the KTF [21,22].
The NW Peloponnese about 70–80 km east of the present day NNW–SSE trending Hellenic Trench (Figure 1) has a complex geological history of tectonics and erosion. However, the active deformation in western Greece could be described in spatio–temporal continuation with the foreland–propagated fold and thrust belt of the External Hellenides, which can be followed along the Hellenic arc [15,19]. During the Eocene, the Peloponnese was characterized by an Alpine collisional history, which led to assemblage of intra-Tethyan continental fragments (e.g., Apulia and Pelagonian microcontinents) and the formation of the Hellenic mountain range [23]. Within this context, Mesozoic early Cenozoic carbonate rocks, originally deposited on a series of platforms (Pre-Apulian and Gavrovo isopic zones) and basins (Ionian and Pindos isopic zones), were telescoped by a system of N–S striking and east-dipping thrust faults that propagated upward and westward into overlying flysch deposits [24,25,26]. From the late Miocene and onwards thrust processes progressively shifted westward from the Peloponnese area to the Ionian Sea [15,27]. Compressional structures of Upper Miocene to Quaternary age have been recognized in Ionian Islands from field based studies, as well as in deep seismic profiles [15,28].
An extensional stress field, in turn, has prevailed in the northwestern Peloponnese from the early Pliocene up to present day generating three major sets of active normal faults with NE–SW, WNW–ESE and ENE–WSW trends, respectively [27,29,30,31,32]. The complexity of the structure in the westernmost end of the Hellenic subduction is imprinted on the great variety of earthquake focal mechanisms.

2.1. Patras

The Patras graben is a 40 km long and 15 km wide fault zone which extends from Cape Araxos in the west to the village of Hellinikon in the east. It comprises thick fluvio–deltaic conglomerates, and floodplain or shallow lacustrine sands and clays of Pleistocene age. Towards its eastern part these deposits pass gradually into a coarse conglomerate sequence that was formed as debris flow facies in a fan environment [27]. Holocene sediments, with a thickness of 40 m, are arranged in a series of tilted fault blocks bounded by WNW–trending normal faults that accommodate the extension in the area [33]. Generally, WNW trending faults are clearly segmented along strike and most are characterized by variable displacement. Such differences are accommodated by NNE–oriented transfer faults, which permit abrupt changes in depositional conditions along the WNW–trending downthrown blocks and bound small subbasins at the southern margin of the basin. On the onshore part of the graben, a major WNW–trending fault scarp is formed on the southern part of the graben along the pre-Neogene margin. ENE–directed faults are also present and displace fluviatile terraces. Holocene net vertical slip on the central parts of Patras basin is about 3–5 mm/yr, while on its northern and southern margin is about 1.2 mm/yr [34]. Rifting in the Patras area may have initiated some 1.3–1.5 Ma ago [35].
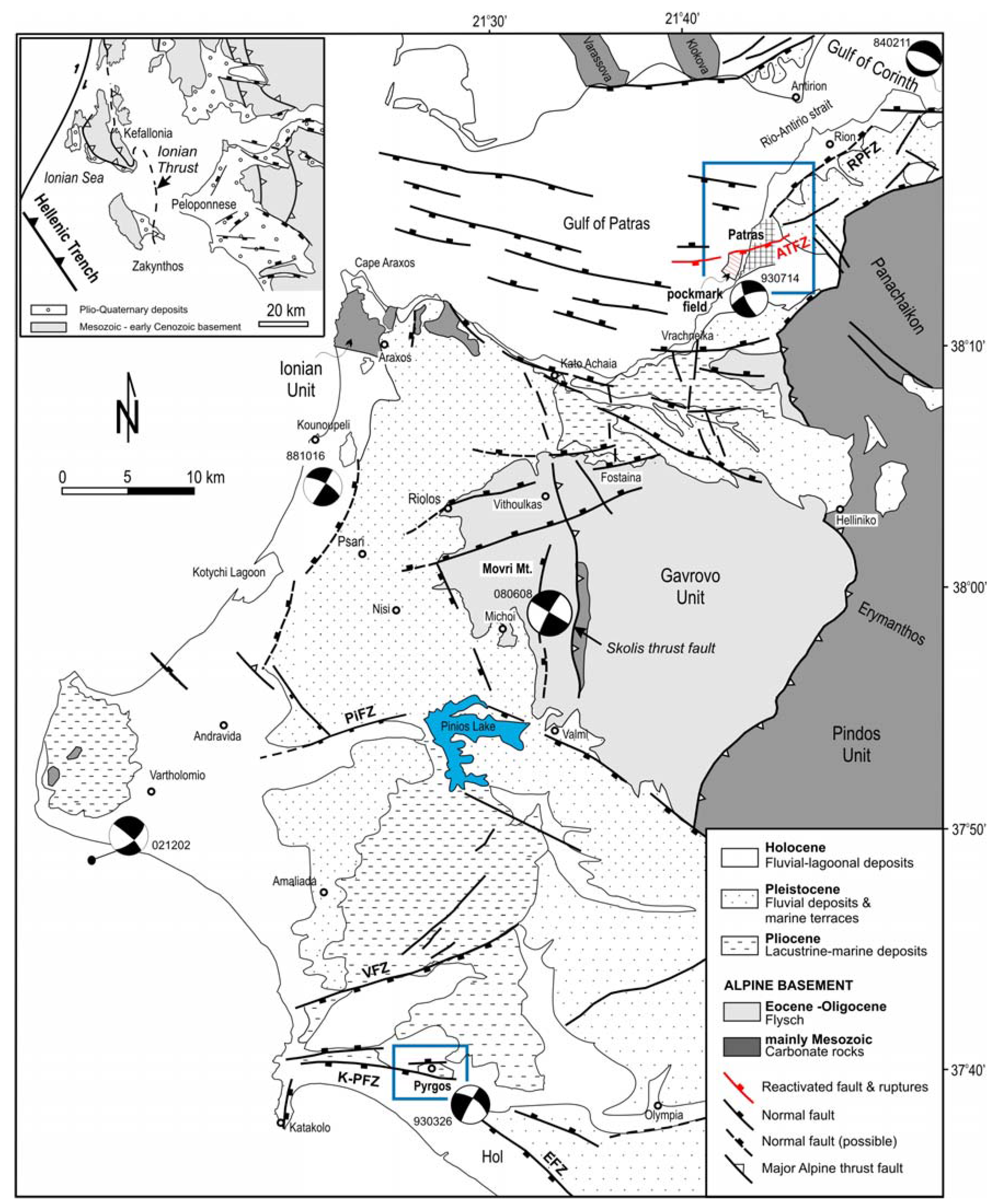
Remotesensing 01 00676 g001 1024
Figure 1. Tectonic setting of the broader study area (ATFZ: Ag. Triada Fault Zone, EFZ: Epitalio fault Zone, RPFZ: Rio–Patra fault Zone, K–PFZ: Katakolo– Pyrgos Fault Zone, PiFZ: Pinios Fault Zone, VFZ: Vounargo Fault Zone, blue frames indicate the study areas, map modified from Koukouvelas et al. [50].
Figure 1. Tectonic setting of the broader study area (ATFZ: Ag. Triada Fault Zone, EFZ: Epitalio fault Zone, RPFZ: Rio–Patra fault Zone, K–PFZ: Katakolo– Pyrgos Fault Zone, PiFZ: Pinios Fault Zone, VFZ: Vounargo Fault Zone, blue frames indicate the study areas, map modified from Koukouvelas et al. [50].
Remotesensing 01 00676 g001
Further to the east, the Rio graben is developed from the village of Vrahneika to the city of Patras and continues further east through Rio to Nafpaktos town. The Rio graben displays two distinct sedimentary cycles: (a) thick silts and clays deposited during Upper Pliocene into a lacustrine to shallow marine environment and (b) coarse fluvial deposits and alluvial fans of Pleistocene age. Pleistocene Rion series are found uplifted up to 500–600 m high in the hills of Ano Kastritsi. A fairly straight NE–trending fault slope limits this hilly morphology from the narrow Patras littoral plain. Major structural trends in this area vary between NE and ENE (55°–70°). Rio graben acted as a transfer zone between the differently extending Patras and Corinth grabens by reactivation of preexisting NE–SW trending faults in the Pliocene [27].
Remotesensing 01 00676 g002 1024
Figure 2. Geological map of Patras City (ATFZ: Ag. Triada Fault Zone, RPFZ: Rio–Patra fault Zone), map modified from Doutsos et al. and Koukis et al. [27,36].
Figure 2. Geological map of Patras City (ATFZ: Ag. Triada Fault Zone, RPFZ: Rio–Patra fault Zone), map modified from Doutsos et al. and Koukis et al. [27,36].
Remotesensing 01 00676 g002
The city of Patras is founded mainly on Quaternary deposits and Plio–Pleistocene sediments (Figure 2) with a thickness exceeding 300 m, based on borehole data [36]. The fault trace map of the broader residential area of the city, based on fieldwork and air photo interpretation [36] shows a NE–SW main fault trend at the northern part of the city and a more prominent WNW–ESE trend in the southern part. This complex fault interplay in the area is due to the location of Patras city in the junction between Patras and Rio grabens. Some ENE–trending faults are also present, such as the Ag. Triada fault zone (ATFZ). This fault was reactivated during the August 31 (Ms 4.8) 1989 earthquake event and caused serious damage to new multistorey and old buildings, in a narrow elongated zone about 1.5 km long and 50 m wide parallel to the fault. Surveying of the fault motion with geodetic methods for almost eight months after the main shock showed a total subsidence of 25 mm and horizontal displacement of 14 mm [37]. The total estimated throw on the Plio–Pleistocene sediments is on the order of 40 m towards the eastern part of fault and decreases to 15–20 m towards the coastal areas [36,37]. Surface ruptures were also observed in a N70° E orientation for almost 1.5 km. Towards the coastal western parts, the surface rupture follows the course of Diakoniaris river for more than 500 m and continues offshore in the Gulf of Patras dipping towards the south, showing tilting of Holocene sediments and clear evidence of faulting with a total throw between 0.5–5.0 m [38].
Along this fault trace and south of it, a pockmark field with craters of gas expulsion was observed. This pockmark field is located close to Patras new harbor, confined between the 10 m and 45 m isobaths and was activated during another strong earthquake (Ms 5.4) on 1993. The earthquake focal mechanism [39] shows a N058° trending nodal plane. If this nodal plane is the active one, the slip on this plane is dextral with a dip–slip component. Anomalously temperature increase and gas expulsion along an ENE–pockmark string of craters recorded prior the earthquake activity suggesting that this fault system is active and plays an important role in fluid circulation [40].

2.2. Pyrgos

The city of Pyrgos is located about 70–80 km east of the NNW–SSE trending Hellenic Trench. Neotectonic structures in the area are not oriented parallel to the arc in the NNW–SSE direction [41]. Instead, there are several WNW–ESE, E–W, and NE–SW trending normal faults forming the margins of the post-Alpine basins developed on top of the thrust sheets of the Hellenides, with alternating horst and graben structures [32,42,43,44].
The broader Pyrgos–Olympia area corresponds to a large 1st order graben structure bounded to the north by the Erymanthos horst, to the east by the Tropea horst and to the south by the Lapithas Mt. horst all of which are built of alpine age sediments. In the Pyrgos–Olympia graben there are more than 3 km of Plio–Quaternary sediments, including some diapiric structures related to the existence of Upper Miocene evaporites at depth, detected from geophysical prospecting and drilling [45]. Continental and lacustrine Pliocene–Lower Pleistocene deposits occur mainly at the eastern part of the Olympia basin whereas marine sediments occurring along the coastal zone of the gulf are mainly of Lower Pleistocene age. The neotectonic evolution of the Pyrgos graben was not the same in all its extent [29]. It was differentiated due to the creation and evolution of smaller size tectonic blocks (2nd, 3rd order macrostructures). One of these smaller order structures is the Pyrgos horst. A great number of faults have been located and studied during neotectonic surveys; some of these were active in previous neotectonic periods (e.g., Late Miocene, Pliocene, Early Pleistocene), whereas others are active Holocene structures [46]. The E–W trending active faults in the Pyrgos area within the Pyrgos–Olympia basin have been analysed after the 1993 destructive earthquake event [30,47].
The outcrops in the broader Pyrgos area (Figure 3) consist of: (i) Alluvial deposits, which crop out in the flat area of the broader Pyrgos area and overlay unconformably the older formations, while their thickness does not exceed 12 m; (ii) Erymanthos Formation, which outcrops over a limited area and consists of red to brown red clays and yellow brown sandy clays of Pleistocene age. It overlies unconformably the Vounargo formation and its thickness varies from 2 m to 8 m; (iii) Vounargo Formation, comprises continuous intercalation of clays, silts, sandstones, sands and marls of Plio–Pleistocene age, with a total thickness up to 600 m [29,46]. The deposits that occur in the area of Pyrgos have undergone neotectonic deformation and are crossed by a number of faults of E–W mean strike that form part of the Katakolo–Pyrgos fault zone, which was responsible for the earthquakes of 26 March 1993 [29].
Remotesensing 01 00676 g003 1024
Figure 3. Geological map of Pyrgos City (NPFZ: North Pyrgos Fault Zone; SPFZ: South Pyrgos Fault Zone).
Figure 3. Geological map of Pyrgos City (NPFZ: North Pyrgos Fault Zone; SPFZ: South Pyrgos Fault Zone).
Remotesensing 01 00676 g003
More specifically, the elongated outcrop of the lower member terminates at the South Pyrgos fault, south of which the upper member of the Vounargo formations occurs. It is a normal fault, accompanied by a morphological discontinuity (to the south of the city main square); its throw is at least 50 m (estimated from morphotectonic features) and eastwards it branches into two faults.
To the north there is an identical setting with the North Pyrgos fault (av. strike NE–SW), which also branches into two minor faults to the east. The North Pyrgos fault juxtaposes the outcrops of upper members, while it also crosses some outcrops of Erymanthos formation. Its throw is smaller, (20–30 m) and all along it, seismic fractures caused by the shock of 26 March 1993, were recognized.
The main shock as well as the aftershocks caused extensive damage in Pyrgos and the surrounding area. Several secondary geological effects such as liquefaction, sandblows, landslides and fractures, were observed.

3. SAR Interferometric Processing and Anaslysis

Interferometric processing for the selected study areas was performed using 42 ERS–1/–2 SAR scenes acquired between 1992 and 2000 along descending track 279 (Table 1) for the Patras case and 39 ERS–1/–2 SAR scenes along descending track 279 for Pyrgos (Table 2).
Table
Table 1. ERS–1 & 2 scenes (Track = 279, Frame = 2835) that have been used (in bold the master reference image).
Table 1. ERS–1 & 2 scenes (Track = 279, Frame = 2835) that have been used (in bold the master reference image).
CountMaster (date)SatelliteSlave (date)OrbitBp (meters)dT (days)
103/06/1995ERS–112/11/1992693773.9−933
203/06/1995ERS–110/06/19939943−477.4−723
303/06/1995ERS–119/08/199310945−323.7−653
403/06/1995ERS–128/10/199311947569.7−583
503/06/1995ERS–125/03/199519305−1169.9−70
603/06/1995ERS–129/04/199519806−518.5−35
703/06/1995ERS–103/06/19952030700
803/06/1995ERS–108/07/199520808−583.435
903/06/1995ERS–213/08/1995163682.971
1003/06/1995ERS–217/09/19952137−360.1106
1103/06/1995ERS–121/10/199522311761.3140
1203/06/1995ERS–231/12/19953640186.2211
1303/06/1995ERS–219/05/1996564471.0351
1403/06/1995ERS–223/06/19966145−83.8386
1503/06/1995ERS–201/09/19967147−514.6456
1603/06/1995ERS–206/10/19967648−392.7491
1703/06/1995ERS–210/11/199681491064.9526
1803/06/1995ERS–215/12/19968650−309.2561
1903/06/1995ERS–219/01/19979151−28.7596
2003/06/1995ERS–223/02/19979652−182.3631
2103/06/1995ERS–204/05/199710654−360.3701
2203/06/1995ERS–208/06/199711155−166.9736
2303/06/1995ERS–213/07/199711656−124.9771
2403/06/1995ERS–217/03/199712157111.5806
2503/06/1995ERS–221/09/199712658−263.2841
2603/06/1995ERS–230/11/199713660177.5911
2703/06/1995ERS–204/01/199814161116.4946
2803/06/1995ERS–219/04/199815664193.11051
2903/06/1995ERS–224/05/199816165−160.71086
3003/06/1995ERS–228/06/199816666−834.91121
3103/06/1995ERS–202/08/19981716756.71156
3203/06/1995ERS–206/09/19981766847.01191
3303/06/1995ERS–228/02/199920173302.91366
3403/06/1995ERS–213/06/199921676−559.81471
3503/06/1995ERS–218/07/199922177455.91506
3603/06/1995ERS–222/08/1999226781012,11541
3703/06/1995ERS–226/09/199923179448.61576
3803/06/1995ERS–231/10/199923680357.31611
3903/06/1995ERS–205/12/199924181−121.91646
4003/06/1995ERS–209/01/200024682−140.11681
4103/06/1995ERS–223/04/200026185953.71786
4203/06/1995ERS–228/05/200026686806.61821
Table
Table 2. ERS–1 & 2 scenes (Track = 279, Frame = 2846) that have been used (in bold the master reference image).
Table 2. ERS–1 & 2 scenes (Track = 279, Frame = 2846) that have been used (in bold the master reference image).
CountMaster (date)SatelliteSlave (date)OrbitBp (meters)dT (days)
117/8/1997ERS–112/11/19926937−44.7−1739
217/8/1997ERS–110/6/19939943−581.5−1529
317/8/1997ERS–119/8/199310945−432.0−1459
417/8/1997ERS–128/10/199311947455.7−1389
517/8/1997ERS–125/3/199519305−1274.8−876
617/8/1997ERS–129/4/199519806−624.8−841
717/8/1997ERS–13/6/199520307−107.5−806
817/8/1997ERS–213/8/19951636−28.5−735
917/8/1997ERS–121/10/199522311653.7−666
1017/8/1997ERS–118/5/19962531739.4−456
1117/8/1997ERS–223/6/19966145−196.6−420
1217/8/1997ERS–21/9/19967147−622.8−350
1317/8/1997ERS–210/11/19968149954.8−280
1417/8/1997ERS–215/12/19968650−415.3−245
1517/8/1997ERS–219/1/19979151−139.1−210
1617/8/1997ERS–223/2/19979652−288.6−175
1717/8/1997ERS–24/5/199710654−466.7−105
1817/8/1997ERS–28/6/199711155−276.1−70
1917/8/1997ERS–213/7/199711656−235.9−35
2017/8/1997ERS–217/8/19971215700
2117/8/1997ERS–221/9/199712658−370.435
2217/8/1997ERS–230/11/19971366063.3105
2317/8/1997ERS–24/1/1998141619.9140
2417/8/1997ERS–219/4/19981566478.8245
2517/8/1997ERS–224/5/199816165−271.3280
2617/8/1997ERS–228/6/199816666−941.3315
2717/8/1997ERS–22/8/199817167−47.8350
2817/8/1997ERS–26/9/199817668−60.7385
2917/8/1997ERS–228/2/199920173186.5560
3017/8/1997ERS–213/6/199921676−674.8665
3117/8/1997ERS–218/7/199922177341.6700
3217/8/1997ERS–222/8/199922678898.1735
3317/8/1997ERS–226/9/199923179345.9770
3417/8/1997ERS–231/10/199923680247.4805
3517/8/1997ERS–25/12/199924181−236.6840
3617/8/1997ERS–29/1/200024682−247.4875
3717/8/1997ERS–223/4/200026185838.9980
3817/8/1997ERS–219/11/200029191839.01190
3917/8/1997ERS–224/12/200029692−567.11225
Initial estimates of the interferometric baselines were calculated from available precise orbit state vectors from Delft Institute (NL) for Earth–Oriented Space Research (DEOS) [48]. The topographic phase was simulated based on SRTM V3 DEM of approximate spatial resolution of 90 m, resampled to 40 m to fit the SAR data resolution.
Time-series analysis was based on the IPTA processing scheme [6]. Temporal and spatial characteristics of interferometric signatures collected from point targets are exploited to accurately map average ground deformation rates and deformation histories.
The selection of the reference points is regarded to be the most critical part of the IPTA, as final deformation rates and histories are greatly affected by this decision. Some criteria for the selection of the reference point are dictated by the applied method, such as the high quality of the point in terms of phase stability overtime. Others are related to the regional tectonic setting of the area and the related pattern of deformation which needs to be extracted.

3.1. Interferometric point target analysis

Starting from a stack of coregistered Single Look Complex (SLC) images, the selection of the reference scene was based primarily on the baseline minimization criteria. In addition, the selection of a reference scene acquired near the temporal average of the available SAR acquisitions is also of interest.
The first step of the analysis involves the identification of candidate point targets for which the time-series analysis will be performed. In this case two different approaches were applied. The first approach is based on the spectral properties of each individual SLC image. This is done by identifying point targets of low spectral phase diversity. The second approach involves the identification of candidate point targets based on low intensity variability, since by definition point targets do not show speckle behavior as simple coherent scatterer dominates the echo.
The analysis of the differential interferometric phases in the temporal direction is an important element of an interferometric point target analysis. Point data stack of differential interferograms was generated and analyzed by means of phase regression analysis in the temporal domain using two dimensional bilinear regression model.
Two-dimensional regression analysis is done with the dimensions corresponding to the perpendicular baseline of the interferometric pairs and to the time difference between the two SLC of the interferometric pairs according to:
a0 + a1 × bperp [i] + a2 × delta_t [i]
where a0: phase offset, a1: slope in baseline dimension (can be converted into point height correction), a2: slope in time dimension (can be converted into linear deformation rate), bperp: perpendicular baseline component of interferograms, and delta_t: time interval of interferograms.
The model examines linear dependence of the topographic phase on the perpendicular baseline component as well as linear phase dependence with time, solving respectively for both height correction and constant deformation rate of the point target relative to the reference. The regression analysis of the entire stack of observations was first conducted using multiple patches, within each patch one reference is determined, and then using the selected single reference point as a global reference. This procedure was followed in order to minimize the effect of distance between the two pairs of phase components, as the atmospheric distortion, baseline error (residual orbital phase trends) and higher relative deformation rates result in higher deviations of the individual points from the regression plain. The quality of the preliminary candidate points were then carefully evaluated based on the estimated standard deviation of the differential interferometric phase from the 2-D regression model.
Points with a phase standard deviation larger than the indicated threshold (in this case 1.0) were rejected, significantly reducing the number of scatterers. The majority of the rejected points were located over mountainous areas. A total number of 6,613 and 1,829 targets for Patras and Pyrgos respectively were detected.
The general phase model for IPTA that used is the same as the conventional interferometry. The unwrapped interferometric phase Φunw is expressed as the sum of topographic phase Φtopo, deformation phase Φdef, path delay Φatm (atmospheric phase) and the phase noise Φnoise:
Φunw = Φtopo + Φdef + Φatm + Φnoise
Phase terms related to the atmosphere, nonlinear deformation, baseline errors and noise can be discriminated within the residual phases based on their differing spatial and temporal dependencies [6].
Unwrapped phases calculated from the regression analysis described above and the corresponding topographic phases were then used in a least-squares approach for baseline refinement. The analysis was limited over areas exhibiting no deformation as dictated by the linear deformation estimates. Introducing the refined baselines and taking into consideration the early estimated height corrections and linear deformation rates, the interferometric phase model was updated in a second iteration.
Additional processing includes temporal and spatial filtering of newly estimated residual phases to compensate for atmosphere and noise. Atmospheric screen was attributed to large scale nonlinear residuals and subtracted from the model by applying low-pass spatial filtering on the residual phases. Phase noise was treated by spatially filtering of phases around the reference, assuming stability of the area considered.
Further iteration applying the additional corrections results in the final regression model. Results consist of point heights, linear deformation rates, atmospheric phase, refined baselines, quality information (temporal coherence) and nonlinear deformation histories for each point. It is important to mention that the final deformation model, as a consequence of the assumptions made during the estimation of atmospheric phase contribution to the signal, includes nonlinear components of only local scale phase variations.

4. Results

After transformation of the interferometric results from range–Doppler coordinates into map geometry (geographic coordinates), point targets were imported in a GIS environment and plotted on a panchromatic Landsat–7 ETM+ image and in the Google Earth environment for point target identification (Figure 4 and Figure 5).
Here we should note that, although the reference points are considered stable there are no absolute stable points in the area. In this way, negative velocities do not necessarily represent subsidence, but possibly slower uplift according to the reference point. Thus, when we use the terms subsidence and uplift we refer to relative values with regard to the picked reference point.
Remotesensing 01 00676 g004 1024
Figure 4. Linear component of ground deformation obtained by IPTA over Patras city. Point targets are plotted on a Panchromatic Landsat–7 ETM+ image. The star on the image refers to the location of the reference point.
Figure 4. Linear component of ground deformation obtained by IPTA over Patras city. Point targets are plotted on a Panchromatic Landsat–7 ETM+ image. The star on the image refers to the location of the reference point.
Remotesensing 01 00676 g004
Remotesensing 01 00676 g005 1024
Figure 5. Linear component of ground deformation obtained by IPTA over Pyrgos city. Point targets plotted on a QuickBird Pan–Sharpened image. The star on the image refers to the location of the reference point.
Figure 5. Linear component of ground deformation obtained by IPTA over Pyrgos city. Point targets plotted on a QuickBird Pan–Sharpened image. The star on the image refers to the location of the reference point.
Remotesensing 01 00676 g005

4.1. Patras

From Figure 6 it is indicated that generally the relative vertical velocities toward and away from the satellite range in the LOS, vary between maximum values of +5 mm/yr and −5 mm/yr, respectively. A remarkable aspect is that there is contrasting subsidence and uplift of PS points along discrete and specific zones, such as the Ag. Triada fault zone in the south of the city and along a W–E trending lineament, north of the Patras port, that doesn’t relate with any visible mapped fault trace (Figure 7). Between these two zones only uplift even with low rates is observed. This area represents in a way the relay zone and the hanginwall block of both Ag. Triada and Rio–Patras fault zone, consisting of Plio–Pleistocene sediments. Maximum uplift velocities on the order of +4.0 mm/yr to +5.5 mm/yr are constricted on the footwall block of Pio–Patras fault, while in the relay zone between that fault zone and Ag. Triada fault lower values between +2.5 mm/yr and +4.0 mm/yr are observed. Similar values are also calculated towards west close to the basin bounding Kastritsi fault.
Remotesensing 01 00676 g006 1024
Figure 6. Point targets plotted over the fault map for Patras area (ATFZ: Ag. Triada Fault Zone), solid line corresponds to the section of figure 7, fault pattern modified from Koukis et al. [36].
Figure 6. Point targets plotted over the fault map for Patras area (ATFZ: Ag. Triada Fault Zone), solid line corresponds to the section of figure 7, fault pattern modified from Koukis et al. [36].
Remotesensing 01 00676 g006
Remotesensing 01 00676 g007 1024
Figure 7. Spatial profile showing the displacement field as observed by IPTA and plotting targets within 150 meters in both sides of the profile (upper), and the related topography (down), red lines correspond to the faults.
Figure 7. Spatial profile showing the displacement field as observed by IPTA and plotting targets within 150 meters in both sides of the profile (upper), and the related topography (down), red lines correspond to the faults.
Remotesensing 01 00676 g007
Accordingly, maximum subsidence values on the order of −4.5 mm/yr to −5.5 mm/yr are restricted mainly on the hanging wall block of Rio–Patras fault and specifically towards its NE–termination. Lower values between −1.0 mm/yr and −2.8 mm/yr are observed along the downthrown block of Ag. Triada fault, indicating a lower deformation rate compared to the Rio graben. The footwall block of this fault displays low uplift rates between +0.4 and +1.0 mm/yr. Based on the relative uplift and subsidence velocities on footwall and hanginwall blocks of Ag. Triada fault, a vertical velocity between 1.4 mm/yr and 3.8 mm/yr can be estimated for an almost 10 year period of time. Along the main fault trace and in a 50 m width zone, relatively small ground movements, such as cracks on road pavement and buildings, small scale subsidence and fissures are periodically observed. Typical historic deformation diagrams are shown in Figure 8 for two targets from the footwall and hanging wall of Agia Triada fault.

4.2. Pyrgos

Based on the spatial distribution of the PS points, the size and the kind of the vertical movement (uplift or subsidence) for the time period 1992–2000, three areas can be distinguished for the Pyrgos city area: the northern, the central and the southern (Figure 9).
Remotesensing 01 00676 g008 1024
Figure 8. Typical displacement histories obtained by IPTA for specific point targets from the footwall (left diagram) and from the hanginwall (right diagram) of the Agia Triada fault zone.
Figure 8. Typical displacement histories obtained by IPTA for specific point targets from the footwall (left diagram) and from the hanginwall (right diagram) of the Agia Triada fault zone.
Remotesensing 01 00676 g008
Remotesensing 01 00676 g009 1024
Figure 9. Point targets plotted over the fault map of Pyrgos area, solid line corresponds to the section of Figure 10.
Figure 9. Point targets plotted over the fault map of Pyrgos area, solid line corresponds to the section of Figure 10.
Remotesensing 01 00676 g009
For the northern area the PS points indicate mainly subsidence with values varying from −0.8 to −2.5 mm/yr, while there are few targets, indicating stability. In this area loose alluvial deposits occur, which locally are marshy deposits and the water table of the aquifer is very close to the surface. The area is bounded to the north by the Vounargo fault zone and to the south by the North Pyrgos fault.
The central area, which corresponds to the Pyrgos tectonic horst, is bounded to the north and south by the North and South Pyrgos fault correspondingly [29]. The lower members of the Vounargo formation (thickness >400m, Plio–pleistocene age) occur and the majority of the PS points indicate uplift from +1.5 mm/yr up to +2.5 mm/yr, with very few points presenting subsidence (Figure 10).
Remotesensing 01 00676 g010 1024
Figure 10. Spatial profile showing the displacement field as observed by IPTA and plotting targets within 150 meters in both sides of the profile (upper), and the related topography (down), red lines correspond to the faults.
Figure 10. Spatial profile showing the displacement field as observed by IPTA and plotting targets within 150 meters in both sides of the profile (upper), and the related topography (down), red lines correspond to the faults.
Remotesensing 01 00676 g010
At the southern part of Pyrgos, where loose alluvial deposits outcrop, the majority of the targets indicate subsidence, with few being stable and a minority showing uplift.
Typical historic deformation diagram is shown in Figure 11 for a target from the northern part of the city. It has to be mentioned that the measured vertical movements and more specifically the uplift ones are not so intensive. This is in accordance with the low elevation of the Late Pleistocene marine terraces of the broader area, which do not exceed 100 m.
On the contrary, the most destructive earthquakes are related with fault plane solutions of strike slip movements [18,49]. This can explain why the areas of subsidence and uplift are not so clear in the case of Pyrgos being a minor order young neotectonic structure, which has been created after the Middle Pleistocene [29].
Remotesensing 01 00676 g011 1024
Figure 11. Displacement history obtained by IPTA for specific point target from the northern part of the city.
Figure 11. Displacement history obtained by IPTA for specific point target from the northern part of the city.
Remotesensing 01 00676 g011

5. Discussion

Measurement of ground deformation is a direct and valuable input to models of earthquake risk and for prone areas is of great importance. Given sufficient SAR scenes the submillimeter accuracy of PSI does represent an effective tool for the measurement of tectonic related ground motions.
The PSI technique has proven to be an excellent tool for identifying zones of ground deformation inside urban areas that cannot be easily visible or determined by conventional survey means with unprecedented detail and accuracy. Specifically, the PSI method provides much more information (on both a local and regional scale) on the ground displacements than data obtained by leveling and D–GPS techniques.
Superimposition of several natural and anthropogenic mechanisms that act in different time and scale and provoking ground deformation should be considered. Finally, a complete multidisciplinary approach (including active tectonic, GPS monitoring and seismology) is the appropriate study scheme.
For this specific study, our results of Patras show clearer uplift–subsidence rates due to the more distinct fault pattern and intense deformation compared to Pyrgos area, where more diffused deformation is observed with no significant displacements on surface. This is maybe due to hidden blind structures activating as strike slip at depth, as it is confirmed by recent earthquakes with such focal mechanisms [49,50].

Acknowledgements

Data provided by ESA in the frame of CAT–1 projects. The part of the study concerning Pyrgos city was supported by John S. Latsis Public Benefit Foundation and the Patras city case was supported by ESA in the frame of the 1st Call for Ideas for Greek institutions.

References

  1. Wright, T.; Parsons, B.; Fielding, E. Measurement of interseismic strain accumulation across the North Anatolian Fault by satellite radar interferometry. Geophys. Res. Lett. 2001, 28, 2117–2120. [Google Scholar] [CrossRef]
  2. Tosi, L.; Teatini, P.; Carbognin, L.; Brancolini, G. Using high resolution data to reveal depth–dependent mechanisms that drive land subsidence: The Venice coast, Italy. Tectonophysics 2009. [Google Scholar] [CrossRef]
  3. Massonnet, D.; Rossi, M.; Carmona, C.; Adragna, F.; Peltzer, G.; Feigl, K.; Rabaute, T. The displacement field of the Landers earthquake mapped by radar interferometry. Nature 1993, 364, 138–142. [Google Scholar] [CrossRef]
  4. Zebker, H.A.; Rosen, P.A.; Goldstein, R.M.; Gabriel, A.; Werner, C.L. On the derivation of coseismic displacement fields using differential radar interferometry. The Landers earthquake. J. Geophys. Res. 1994, 99, 19617–19634. [Google Scholar] [CrossRef]
  5. Ferretti, A.; Prati, C.; Rocca, F. Permanent scatterers in SAR interferometry. IEEE T. Geosci. Remote 2001, 39, 8–20. [Google Scholar] [CrossRef]
  6. Werner, C.; Wegmüller, U.; Strozzi, T.; Wiesmann, A. Interferometric point target anaysis for deformation mapping. In Proceedings of the IEEE International Geoscience and Remote Sensing Symposium, Toulouse, France, July 2003; pp. 4362–4364.
  7. Rosen, P.; Werner, C.; Fielding, E.; Hensley, S.; Buckley, S.; Vincent, P. Aseismic creep along the San Andreas fault northwest of Parkfield, CA measured by radar interferometry. Geophys. Res. Lett. 1998, 25, 825–828. [Google Scholar] [CrossRef]
  8. Colesanti, C.; Ferretti, A.; Ferrucci, F.; Prati, C.; Rocca, F. Monitoring known seismic faults using the Permanent Scatterers (PS) technique. In Proceedings of the IEEE International Geoscience and Remote Sensing Symposium, Honolulu, HI, USA, July 2000; pp. 2221–2223.
  9. Lee, J.C.; Angelier, J.; Chu, H.T.; Hu, J.C.; Jeng, F.S.; Rau, R.J. Active fault creep variations at Chihshang, Taiwan, revealed by creep meter monitoring, 1998 – 2001. J. Geophys. Res-Sol. Ea. 2003, 108, ETG 4–1–ETG 4–21. [Google Scholar] [CrossRef]
  10. Cunha, T.A.; Sarti, F. SAR interferometry as a tool for the detection of active tectonic regions: Preliminary results on the algarve region of the south Portugal. In Proceedings of the FRINGE 2003 Workshop, Frascati, Italy, 1–5 December 2003. ESA SP-550.
  11. Taylor, M.; Peltzer, G. Current slip rates on conjugate strike–slip faults in central Tibet using synthetic aperture radar interferometry. J. Geophys. Res-Sol. Ea. 2006, 111, B1240. [Google Scholar] [CrossRef]
  12. Biggs, J.; Wright, T.; Lu, Z.; Parsons, B. Multi-interferogram method for measuring interseismic deformation: Denali Fault, Alaska. Geophys. J. Int. 2007, 170, 1165–1179. [Google Scholar] [CrossRef]
  13. Cavalié, O.; Lasserre, C.; Doin, M.; Peltzer, G.; Sun, J.; Xu, X.; Shen, Z. Present-day deformation across the Haiyuan fault (Gansu, China), measured by SAR interferometry. In Dragon 1 Programme Final Results 2004–2007, Proceedings of the 2008 Dragon Symposium, Beijing, China, 21–25 April 2008; Lacoste, H., Ouwehand, L., Eds.; ESA Communication Production Office ESTEC: Noordwijk, The Netherlands, 2008. ESA SP-655. [Google Scholar]
  14. Huang, M.; Hu, J.; Ching, K.; Rau, R.; Hsieh, C.; Pathier, E.; Fruneau, B.; Deffontaines, B. Active deformation of Tainan tableland of southwestern Taiwan based on geodetic measurements and SAR interferometry. Tectonophysics 2009, 466, 322–334. [Google Scholar] [CrossRef]
  15. Underhill, J.R. Late Cenozoic deformation of the Hellenide foreland, western Greece. Geo. Soc. Am. Bull. 1989, 101, 613–634. [Google Scholar] [CrossRef]
  16. Hatzfeld, D.; Pedotti, G.; Hatzidimitriou, P.; Makropoulos, K. The strain pattern in the western Hellenic arc deduced from a microearthquake survey. Geophys. J. Int. 1990, 101, 181–202. [Google Scholar] [CrossRef]
  17. Hatzfeld, D.; Kassaras, I.; Panagiotopoulos, D.; Amorese, D.; Makropoulos, K.; Karakaisis, G.; Coutant, O. Microseismicity and strain pattern in northwestern Greece. Tectonics 1995, 14, 773–785. [Google Scholar] [CrossRef]
  18. Sachpazi, M.; Hirn, A.; Clément, C.; Haslinger, F.; Laigle, M.; Kissling, E.; Charvis, P.; Hello, Y.; Lépine, J.C.; Sapin, M.; Ansorge, J. Western Hellenic subduction and Cephalonia Transform: local earthquakes and plate transport and strain. Tectonophysics 2000, 319, 301–319. [Google Scholar] [CrossRef]
  19. Doutsos, T.; Koukouvelas, I.K.; Xypolias, P. A new orogenic model for the External Hellenides. In Tectonic Development of the Eastern Mediterranean Region; Robertson, Α.H.F., Mountrakis, D., Eds.; Geological Society: London, UK, 2006; pp. 507–520. [Google Scholar]
  20. Kokkalas, S.; Xypolias, P.; Koukouvelas, I.K.; Doutsos, T. Post-Ccollisional Contractional and Extensional Deformation in the Aegean Region. In Post-Collisional Tectonics and Magmatism in the Mediterranean region and Asia (GSA Special Paper); Dilek, Y., Pavlides, S., Eds.; Geol. Soc. Am. S.; 2006; Volume 409, pp. 97–123. [Google Scholar]
  21. Lagios, E.; Sakkas, V.; Papadimitriou, P.; Parcharidis, I.; Damiata, B.N.; Chousianitis, K.; Vassilopoulou, S. Crustal deformation in the Central Ionian Islands (Greece): Results from DGPS and DInSAR analyses (1995–2006). Tectonophysics 2007, 444, 119–145. [Google Scholar] [CrossRef]
  22. Hollenstein, Ch.; Müller, M.D.; Geiger, A.; Kahle, H.G. Crustal motion and deformation in Greece from a decade of GPS measurements, 1993–2003. Tectonophysics 2008, 449, 17–40. [Google Scholar] [CrossRef]
  23. Doutsos, T.; Pe-Piper, G.; Boronkay, K.; Koukouvelas, I. Kinematics of the Central Hellenides. Tectonics 1993, 12, 936–953. [Google Scholar] [CrossRef]
  24. Xypolias, P.; Doutsos, T. Kinematics of rock flow in a crustal scale shear zone: implication for the orogenic evolution of the SW Hellenides. Geol. Mag. 2000, 137, 81–96. [Google Scholar] [CrossRef]
  25. Skourlis, K.; Doutsos, T. The Pindos Fold and Thrust Belt (Greece): Inversion kinematics of a passive continental margin. Int. J. Earth Sci. 2003, 92, 891–903. [Google Scholar] [CrossRef]
  26. Sotiropoulos, S.; Kamberis, E.; Triantaphyllou, M.; Doutsos, T. Thrust sequences at the central part of the External Hellenides. Geol. Mag. 2003, 140, 661–668. [Google Scholar] [CrossRef]
  27. Doutsos, T.; Kontopoulos, N.; Poulimenos, G. The Corinth–Patras rift as the initial stage of continental fragmentation behind an active island arc (Greece). Basin Res. 1988, 1, 177–190. [Google Scholar] [CrossRef]
  28. Doutsos, T.; Kontopoulos, N.; Frydas, D. Neotectonic evolution of northwestern continental Greece. Geol. Rundsch. 1987, 76, 433–452. [Google Scholar] [CrossRef]
  29. Lekkas, E.; Papanikolaou, D.; Fountoulis, I. The Pyrgos Earthquake: The geological and geotechnical conditions of Pyrgos area (W. Peloponnese, Greece). In Field–guide for the Pre–Congress Excursion of the XV Congress of the Carpatho–Balcan Geological Association, Athens, Greece, September 1995; pp. 42–46.
  30. Koukouvelas, I.; Mpresiakas, A.; Sokos, E.; Doutsos, T. The tectonic setting and earthquake ground hazards of the 1993 Pyrgos earthquake, Peloponnese, Greece. J. Geol. Soc. London 1996, 153, 39–49. [Google Scholar] [CrossRef]
  31. Doutsos, T.; Kokkalas, S. Stress and deformation patterns in the Aegean region. J. Struct. Geol. 2001, 23, 455–472. [Google Scholar] [CrossRef]
  32. Papanikolaou, D.; Fountoulis, I.; Metaxas, C. Active faults, deformation rates and Quaternary paleogeography at Kyparissiakos Gulf (SW Greece) deduced from on-shore and off-shore data. Quatern. Int. 2007, 171–172, 14–30. [Google Scholar] [CrossRef]
  33. Zelilidis, A.; Koukouvelas, I.; Doutsos, T. Neogene paleostress changes behind the forearc fold belt in the Patraikos Gulf area, Western Greece. Neues Jahrb. Geol. P. M. 1988, 311–325. [Google Scholar]
  34. Flotte, N.; Sorel, D.; Muller, C.; Tensi, J. Along strike changes in the structural evolution over a brittle detachment fault: example of the Pleistocene Corinth – Patras rift (Greece). Tectonophysics 2005, 403, 77–94. [Google Scholar] [CrossRef]
  35. Chronis, G.; Piper, D.W.; Anagnostou, C. Late Quaternary evolution of the Gulf of Patras, Greece: Tectonism, deltaic sedimentation and sea–level change. Mar. Geol. 1991, 97, 191–209. [Google Scholar] [CrossRef]
  36. Koukis, G.; Sabatakakis, N.; Tsiambaos, G.; Katrivesis, N. Engineering geological approach to the evaluation of seismic risk in metropolitan regions: Case study of Patras, Greece. Bull. Eng. Geol. Environ. 2005, 64, 219–235. [Google Scholar] [CrossRef]
  37. Kalteziotis, N.; Koukis, G.; Tsiambaos, G.; Sabatakakis, N.; Zervogiannis, H. Structural damage in a populated area due to an active fault. In Proceedings of the 2nd International Conference on Recent Advancces in geotechnical Earthquake Engineering and soil Dynamics, Rolla, MO, USA, 11–15 March 1991; pp. 1709–1716.
  38. Hasiotis, T.; Papatheodorou, G.; Kastanos, N.; Ferentinos, G. A pockmark field in the Patras Gulf (Greece) and its activation during the 14/7/93 seismic event. Mar. Geol. 1996, 130, 333–344. [Google Scholar] [CrossRef]
  39. Papazachos, B.C.; Papazachou, C. The Earthquakes of Greece; Ziti Publications: Thessaloniki, Greece, 1997. [Google Scholar]
  40. Papatheodorou, G.; Christodoulou, D.; Geraga, M.; Etiope, G.; Ferentinos, G. The pockmark field of the Gulf of Patras: An ideal natural laboratory for studying seabed fluid flow. In Filed trips guide book “Sedimentology of western and central Greece from Triassic to recent”, Proceedings of the 25th IAS Meeting of Sedimentology, Patras, Greece, 4–7 September 2007.
  41. Lepichon, X.; Angelier, J. The Hellenic arc and trench system: a key to the neotectonic evolution of the Eastern Mediterranean area. Tectonophysics 1979, 60, 1–42. [Google Scholar]
  42. Mariolakos, I.; Papanikolaou, D. The neogene basins of the Aegean Arc from the Paleogeographic and the Geodynamic point of view. In Proceedings of the Int. Symp. Hell. Arc and Trench (HEAT), Athens, Greece, 1981; Vol. I, pp. 383–399.
  43. Mariolakos, I.; Papanikolaou, D. Deformation pattern and relation between deformation and seismicity in the Hellenic arc. Bull. Geol. Soc. Greece 1987, XIX, 59–76. (in Greek). [Google Scholar]
  44. Mariolakos, I.; Papanikolaou, D.; Lagios, E. A neotectonic geodynamic model of Peloponnesus based on: morphotectonics, repeated gravity measurements and seismicity. Geol. Jb. 1985, 50, 3–17. [Google Scholar]
  45. Kamberis, E. Geology and petroleum geology study of NW Peloponnese, Greece. Ph.D. Thesis, National Technical University of Athens, Athens, Greece, 1987. [Google Scholar]
  46. Lekkas, E.; Papanikolaou, D.; Fountoulis, I. Neotectonic map of Greece, sheet "Pyrgos" – "Tropaia" (scale 1/100.000). Project-University of Athens: Athens, Greece, 1992; 120. (in Greek) [Google Scholar]
  47. Lekkas, E.; Fountoulis, I.; Papanikolaou, D. Intensity distribution and Neotectonic macrostructure Pyrgos Earthquake data (Greece, 26 March 1993). Nat. Hazards 2000, 21, 19–33. [Google Scholar] [CrossRef]
  48. Scharoo, R.; Visser, P.N.A.M. Precise orbit determination and gravity field improvement for the ERS satellites. J. Geophys. Res. 1998, 103, 8113–8127. [Google Scholar] [CrossRef]
  49. Roumelioti, Z.; Benetatos, Ch.; Kiratzi, A.; Stavrakakis, G.; Melis, N. A study of the 2 December 2002 (M5.5) Vartholomio (western Peloponnese, Greece) earthquake and of its largest aftershocks. Tectonophysics 2004, 387, 65–79. [Google Scholar] [CrossRef]
  50. Koukouvelas, I.; Kokkalas, S.; Xypolias, P. Surface deformation during the Mw 6.4 (8 June 2008) Movri earthquake in the Peloponnese and its implications for the seismotectonics of Western Greece. Int. Geol. Rev. 2009. [Google Scholar] [CrossRef]

Share and Cite

MDPI and ACS Style

Parcharidis, I.; Kokkalas, S.; Fountoulis, I.; Foumelis, M. Detection and Monitoring of Active Faults in Urban Environments: Time Series Interferometry on the Cities of Patras and Pyrgos (Peloponnese, Greece). Remote Sens. 2009, 1, 676-696. https://doi.org/10.3390/rs1040676

AMA Style

Parcharidis I, Kokkalas S, Fountoulis I, Foumelis M. Detection and Monitoring of Active Faults in Urban Environments: Time Series Interferometry on the Cities of Patras and Pyrgos (Peloponnese, Greece). Remote Sensing. 2009; 1(4):676-696. https://doi.org/10.3390/rs1040676

Chicago/Turabian Style

Parcharidis, Issaak, Sotiris Kokkalas, Ioannis Fountoulis, and Michael Foumelis. 2009. "Detection and Monitoring of Active Faults in Urban Environments: Time Series Interferometry on the Cities of Patras and Pyrgos (Peloponnese, Greece)" Remote Sensing 1, no. 4: 676-696. https://doi.org/10.3390/rs1040676

APA Style

Parcharidis, I., Kokkalas, S., Fountoulis, I., & Foumelis, M. (2009). Detection and Monitoring of Active Faults in Urban Environments: Time Series Interferometry on the Cities of Patras and Pyrgos (Peloponnese, Greece). Remote Sensing, 1(4), 676-696. https://doi.org/10.3390/rs1040676

Article Metrics

Back to TopTop