1. Introduction
The persistence of forest ecosystem resources is the key to protecting wild coverage of reproductive trees in order to alleviate global warming or the impact of climate change. Specifically, the variance in the area of woods, the accumulation of forest biomass/carbon storage, and the improvement of healthy forests are the periodic evaluation indices of global forest resources for forest sustainability, according to Forest Resources Assessment FAO (Food and Agriculture Organization of the United Nations) [
1]. Therefore, using telemetry to monitor the health level of forest ecosystems has a critical effect on the subject of global warming control. Climate change may affect phenological events such as the onset of green-up and dormancy [
2]. Trees start to sprout once they sense the growing signals in early spring. After the leaf initiation stage, the newly sprouted leaflet will gradually develop and further facilitate tree growth in crown width, height, diameter, and carbon storage [
3]. As a result, the newly grown leaves (NGL) can be seen as the first objects of trees in response to a change in temperature, and can therefore provide critical information for the early detection of climate changes [
4]. UAV-sensed images are generally collected at low altitude; the images are supposedly free of atmospheric effects [
5], and provide very high spatial resolution for applications. Taking the strengths of UAV-sensed images, NGL over a forest area can be detected via appropriate remote sensing techniques.
In forest science, remote sensing has been applied to investigate species classification [
6,
7], tree delineation [
8,
9], and biomass productivity estimation [
10,
11]. The detection of NGL is a new application in respect to the previous applications. The target of interest may occur under a very low probability or probably has a relatively smaller size than the background, such as the damaged portion of crown in the forest canopy or the new leaf crown in the forest canopy. In this case, the traditional spatial domain (i.e., literal)-based image processing techniques [
12,
13,
14,
15] may fail to extract these targets effectively, especially when the target size is smaller than the pixel resolution. In contrast, the technique using spectral characteristics to detect the subpixel level is one of the more feasible methods. From the angle of multispectral/hyperspectral detection, the spectral information-based target detection technique [
16,
17,
18] should be able to solve these problems.
Hyperspectral subpixel detection techniques can be divided into active and passive manners. In the active methods, the detectors only use single or multiple spectral signatures of targets of interest for detection purposes; e.g., Constrained Energy Minimization (CEM) [
19], Correlation Mahalanobis Distance (RMD) [
7,
20], Mahalanobis Distance (KMD) [
17,
21], Adaptive Coherence Estimator (ACE) [
22], Target-Constrained Interference-Minimized Filter (TCIMF) [
17,
18,
23], etc. The correctness of target information plays an important role. Incorrect information results in a false alarm and omission of a target detection result. Therefore, how to provide the correct target object information is a very important step. The Optimal Signature Generation Process (OSGP) that is proposed in this paper increases the accuracy of selecting a target iteratively so as to solve the previously mentioned problem.
Hyperspectral algorithms have been developed for many different target detections in recent years and are used in different areas [
24,
25,
26,
27,
28,
29]. Many studies have proposed CEM based algorithms [
30,
31] in the last decade. However, using hyperspectral algorithms to detect targets in RGB images presents several issues since spectral information is insufficient and spatial information is not used, and thus a false alarm is likely to occur where there is a similar spectral characteristic. In order to solve this dilemma, this paper proposes three innovative CEM based detectors-Subset CEM, Sliding Window-based CEM, and Adaptive Sliding Window-based CEM to establish their own autocorrelation matrix, and uses sliding window point-to-point scanning for calculation. As the sliding window passes through, the contrast between a NGL and the background can be enhanced. When compared with traditional CEM results that incur too many false alarms, our proposed methods can solve this issue and produce more stable results.
2. Materials and Methods
2.1. Constrained Energy Minimization
Traditional Constrained Energy Minimization (CEM) [
16,
17,
18,
19] of active hyperspectral target detection is the major technique that is adopted in this paper. The CEM only needs the spectral signature of one specific target of interest during target detection; it is free of the spectral signature of other targets or background. Many target detection methods have been proposed in recent years, among those, the CEM only needs the signature of one target of interest and the detection is stable. Thus, this paper selects CEM to compare local improvement methods. In the CEM algorithm, only one spectral signature (desired signature or target of interest) is given, referred to as
d, any prior knowledge is not required, e.g., multiple targets of interest or background. In other words, users can extract the specific target of interest without any background information, implementing target detection. This is one of the major advantages of CEM. Another advantage of CEM is that as many signal sources cannot be recognized or observed with the naked eye, some materials may be detected by sensors leading to false alarm. However, the CEM transposes the correlation matrix
R of data samples before the desired signature
d is extracted. The sample autocorrelation matrix can be defined as
, so that the background can be suppressed by
R, and the filter is matched with signature d to enhance the capability of detecting signature, the execution is more efficient. The CEM is evolved from the LCMV proposed by Frost [
32]. If there are
N pixels
in a hyperspectral image with
L band, which are
, where
, the desired target to be looked for is represented by
d, defined as
, the desired target to be looked for can be detected by finite impulse response filter (FIR) based on CEM and desired target
d. The filter coefficient is defined as
, the
w can be obtained with the minimum average energy, defined as
. Therefore, if
is defined as
and imported into FIR, and then
can be expressed as
With the minimum average energy, the optimal solution of
w can be obtained
According to the theory of Harsanyi [
19], the optimal solution to the weight vector of one
L band is
Equation (3) is substituted in Equation (2), the result of CEM is
2.2. Subset CEM
The first target detection algorithm using autocorrelation matrix
S that is proposed in this paper is a novel method using subsets, known as Subset CEM. The Subset CEM splits the image into several small square images; these small images are the subsets of the original image. The CEM detection is then implemented, and the results of subsets are patched up to obtain a complete resulting image. In other words, the small image of each subset has its own autocorrelation matrix
S. For example, a 1200 × 1500 image is divided into nine small images; the resolution of each small image is 400 × 500, the autocorrelation matrix
S is
S1,
S2,
S3, …,
S9, respectively, and the corresponding
Sn of each pixel is substituted into CEM for detection, thus obtaining the result.
Figure 1 is the schematic diagram of the autocorrelation matrix in the image. The subset image size of the local autocorrelation matrix
S is obtained by trial and error. Normally, using five times smaller than the original size is a good first try. The image resolution used in this paper is 1000 × 1300, and thus the image is divided into 200 × 260 subset images.
The results show that this method can effectively suppress the background pixels that are too similar to the desired target. Because the image is divided into the set of small images, the autocorrelation matrix of each small image changes accordingly. There is a different
S for suppressing the background according to different images, and
S is calculated according to the pixels in a small area; thus, the small difference between similar spectral signatures is enlarged. It is easier to judge the difference between two RGB values for suppression, so as to increase the detection rate.
Figure 2 shows the detection process after the Subset CEM splits the image into subsets.
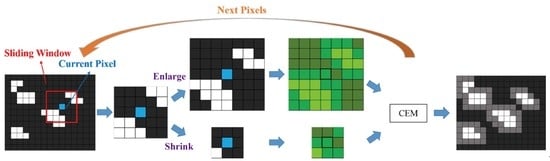
2.3. Sliding Window-Based CEM (SW CEM)
Section 2.2 mentioned that the Subset CEM can effectively reduce the false alarm rate of similar background spectrums using the concept of the local autocorrelation matrix
S. The Subset CEM divides the image into small square images, where each small image has its own autocorrelation matrix
S. In other words, every two small images have dissimilar
S. However, Subset CEM uses non-overlapped windows, which causes artifacts at the borders of subset images. In order to resolve such an issue, this paper proposes the pixel-by-pixel sliding window-based CEM (SW CEM) for detection. The sliding window concept is used in many studies [
27,
33,
34,
35]. The pixel-by-pixel CEM uses a sliding window of fixed size to obtain the RGB values around each pixel, according to different spectral characteristics around each pixel, so as to determine its autocorrelation matrix
Sn. In other words, if the Subset CEM divides the image into small square images, then the pixel-by-pixel CEM divides the image into pixels, combined with a sliding window, to acquire the pixels around the pixel to determine the autocorrelation matrix
Sn.
Figure 3 shows the sliding window and direction.
This means that each pixel in the image has its
Sn, and each
Sn is independent and different. Hence, the SW CEM can be defined as:
where,
is the current pixel value, and
is the autocorrelation matrix of
, if the size of the sliding window is 2
k + 1, as shown in
Figure 4.
When the size of a sliding window is known,
can be defined as:
where,
represents each pixel in the sliding window, and
is a constant, if
is simplified by
.
We substitute Equation (8) into Equation (6) to obtain:
where,
is the autocorrelation matrix of current pixel
, and the capability of suppressing the background can be enhanced for each region by
.
2.4. Adaptive Sliding Window-Based CEM (ASW CEM)
The adaptive window concept has been applied to targets detection in many applications in the last decade, such as vehicles detection [
36,
37], adaptive filters [
38], and anomaly detection [
39,
40]. When compared to SW CEM, which uses a fixed window size to calculate autocorrelation matrices
S, AWS CEM determines the window size according to the spatial and spectral characteristics around each pixel, so as to suppress the background. The optimum size of the sliding window varies with the quantity of NGL around each pixel, and thus the sliding window improves based on the local CEM in this paper. The size of sliding window is determined by acquiring the proportion of sprouts around the current pixel. When the sliding window size 2
K + 1 of the current pixel is determined, the result of SW CEM target detection can be obtained. In this case, we developed Adaptive Sliding Window-based CEM (ASW CEM) to combine adaptive window concept in CEM.
Figure 5 illustrates the flowchart of ASW CEM. ASW CEM can change the size of the sliding window according to the ratio of the NGL around the current pixel to enhance NGL and suppress background.
The execution of ASW CEM comprises six steps:
Input image
Decide the default size of the sliding window
Calculate the rate of the sprout in the sliding window
If the rate of the sprout meets the set condition or the window size has reached the default maximum or minimum window, then the S in Equation (10) is calculated according to the pixel values of the current window size. If the rate of the sprout is not met or the window size has not reached the limit value, then the size of the sliding window is changed and return to Step 3; otherwise, proceed to Step 5.
The S obtained in Step 4 is used to calculate CEM to obtain the result value of the current pixel.
If all pixels of the image have been calculated, then ASW CEM detection is finished; otherwise, return to Step 2.
The calculation of the rate of the sprout in the sliding window in Step 3 and the sliding window change conditions in Steps 2 and 4 are introduced below.
2.4.1. Acquire the Rate of the NGL around the Current Pixel (NGL Map)
In order to enable the sliding window of each pixel to decide whether or not to enlarge or to shrink the current window according to the proportion of peripheral NGL, this paper requires a sprout map for judgment and reading. To set up the sprout distribution map, the spectral comparison is conducted on the he Spectral Information Divergence (SID) [
17,
41] for experimental multispectral images before ASW CEM, so as to obtain a preliminary sprout detection result. This result contains a small false alarm, but according to this result, when deciding whether or not to enlarge or shrink the sliding window, only the relative rate of the sprout in the sliding window shall be calculated, as the actual number of NGL is not required. The SID resulting image is segmented several times by using Otsu’s method [
42]. The rate of the sprout in the image is preliminarily estimated at 1~2%, so as to minimize the false alarm, and the major sprout points are maintained for calculation. When the image with a preliminary estimate of the sprout is obtained, the proportion of NGL can be calculated by using the default sliding window size, and the size of the sliding window is changed according to the number of NGL.
Figure 6 is the flowchart of this step.
2.4.2. Adaptive Sliding Window
To calculate the rate of the sprout around the current pixel, a sliding window of preset size needs to be made. The rate of the sprout in this window decides whether or not to enlarge or shrink the sliding window for subsequent algorithmic detection.
Figure 7 is the flowchart of this step. A larger sliding window size is required in the region with a higher rate of the sprout; the optimum size of maximum window is set as
m2; on the contrary, a smaller sliding window size is required in the region with a lower rate of the sprout, and the optimum size of the smallest window is set as
n2. When the maximum window
m2 and minimum window
n2 are obtained, the default window is set as an intermediate between maximum and minimum windows, i.e.,
. The advantage is that as the initial window is intermediately sized, the window is enlarged or shrunk to the limit relatively fast. Afterwards, the sliding window is enlarged or shrunk gradually, according to the rate of the sprout in the window.
As the distribution of NGL is not even, when the window is shrunk or enlarged, the rate of the sprout does not always increase or decrease. This method can enlarge and shrink the window. In order to avoid the non-uniform rate of the sprout leading to an infinite circulation of window enlargement or shrinkage, the initial window is used to calculate the sprout as a watershed. When the rate of the sprout in the initial window is higher than a threshold, the sliding window is enlarged gradually until the rate of the sprout in the window is lower than a threshold or the window is maximized before CEM detection. If the rate of the sprout in the initial window is lower than a threshold, then the sliding window is shrunk gradually until the rate of the sprout in the window is higher than a threshold, or the window is minimized before CEM detection. In order to adjust the window size conditionally in the stable level, this paper includes a parameter ε as initial NGL rate in the window, where ε is the proportion of the number of NGL in the window to the total number of pixels in the sliding window. When the rate of the sprout in the window is lower than ε, the window is shrunk; if the rate of the sprout in the window is higher than ε, then the window is enlarged.
2.5. Optimal Signature Generation Process (OSGP)
In order to remedy the defect in the CEM-related algorithm in that only one desired target can be selected, the Optimal Signature Generation Process (OSGP) is used herein to obtain a stable desired target by the iterative process. The idea of the iterative process is similar to K-means [
43], iterative self-organizing data (ISODATA) [
44] and iterative FLDA [
45]. The OSGP implements Subset CEM target detection for the image iteratively. When the result of CEM is obtained, the image is segmented by using Otsu’s method until the number of result pixels is 2–3%, which is the target pixel with the highest probability of the sprout. These pixels correspond to the same pixel RGB values in the original image, averaged as a new target
d’. If the pixel value of
d’ is not similar enough to that of
d, then
d’ is substituted in the next CEM, a new desired target is obtained. This is repeated until this and the last Spectral Angle Mapper [
46] are smaller than a value θ, and then the current target
d is exported. The threshold of spectral angle was tested continuously, and the threshold was set as 0.003.
Figure 8 is the flowchart of OSGP.
It is noteworthy that CEM uses the global correlation matrix R to suppress the background, and it is likely that the background has similar spectral signatures. Simply iterating CEM is the same condition, and some background pixels that do not belong to the desired target will be misrecognized as the result pixels, and the averaging of them influences the new desired target. A stable target d is still obtained after iteration, but the misrecognized pixels may result in errors in d, thus reducing the detection accuracy slightly. To solve this dilemma, this paper proposes Optimal Signature Generation Process (OSGP) and replaces CEM by subset CEM. The Subset CEM splits the image into many small sets; in the global view of the full image, the small square image of a subset is the local concept. The local algorithm can effectively suppress the pixel RGB values similar to the desired target, which is substituted into the iterative algorithm. This not only reduces the misrecognized result of pixels during iteration, but also obtains a better desired target d, so that the precision of detection increases and the probability of a false alarm decreases.
2.6. Parameter Settings of Different Algorithms
For different parameter settings of algorithms in this paper, the results are different, and so the parameter settings of the multiple CEM algorithm are listed in this section, as shown in
Table 1. The input
d of CEM, Subset CEM, SW CEM, and ASW CEM is the randomly selected desired target. The desired target
d’ is iterated by using OSGP. The OSGP iteration stop condition is that the SAM value of two adjacent targets
d shall be smaller than
θ; if tenable, then the desired target
d’ is exported. Here,
ε is the condition value of the rate of the sprout when the sliding window of ASW CEM is enlarged or shrunk. In the following experiments in this study,
ε is set to 1%. However, this parameter depends on the proportion of the number of target pixel in the entire image.
In the following experiments the Subset image size is set as 200 × 260 pixel, and each small image uses the same d and d’, where each small image takes the pixels of its image size to calculate S. The subset image size of the local autocorrelation matrix S is obtained by trial and error. When each small image has calculated CEM, the results are exported and merged into the original picture size, and the merged picture is the result of Subset CEM.
The window size of SW CEM varied by different application and images. Normally, 5–6 times smaller than the entire images are the good try as the initial setting. This study sets the sliding window size as 151 × 151 pixel. It extracts the pixels of 151 × 151 pixel around each pixel to calculate S in Equation (10), which are substituted into CEM in order to work out the result value of the pixel. When each pixel is calculated, the output result of SW CEM is obtained.
ASW CEM uses the original image for SID measurement and gives the preliminarily estimated NGL map, and then ASW CEM employs the sliding window of preset size to calculate the rate of the sprout. When the rate of the sprout mismatches the stop condition, the window size is changed and this rate in the window is recalculated, until the window size reaches the threshold or the rate of the sprout is equivalent to ε. The pixel values in this window are used to calculate S, which is substituted into CEM to work out the result value of the pixel. When each pixel has been calculated, the output result of ASW CEM is obtained. For this experiment, the maximum size of the sliding window is set as 151 × 151, the minimum window is 31 × 31, and the initial window is 91 × 91. The initial window size can be set as the average of the maximum and minimum size.
4. Discussion
A variety of target detection techniques have been published during the last few decades [
12,
13,
14,
15,
25,
59], with several studies applying support vector machines (SVM) [
60] or Fisher’s linear discriminant analysis (FLDA) [
60] to solve target detection problems as a binary classification problem [
61,
62,
63,
64,
65]. These algorithms require a number of classes, and their class distribution model must be known in advance. In order to avoid any biased selection of training samples, the partition must be performed randomly. In other words, training samples must be randomly selected from a dataset to form a training sample set for cross validation. As a result, such a validation is not repeatable and cannot be re-produced. The results are inconsistent. To alleviate this dilemma, this paper proposes a novel Constrained Energy Minimization (CEM) based technique that takes advantage of spectral and spatial information and developed Optimal Signature Generation Process (OSGP) in terms of the iterative process point of view to solve the issues mentioned above. CEM only requires one desired target information for the specific target of interest, regardless of other background information, which is its major advantage. Theoretically, CEM subpixel detection is generally performed by two operations that involve background suppression and matched filter [
16]. First, it performs background suppression via the inverse of
R so as to enhance a detected target contrast against the background. Second, CEM operates a matched filter using
d as the desired matched signature so as to increase intensity of the target of interest. Since only one target signature can be used as the
d in Equation (5), selecting an appropriate
d is a very crucial step for detection results. Although CEM has many applications [
27,
30,
31], very few studies investigated the issues of selecting a desire target signature. Therefore, this paper developed the Optimal Signature Generation Process (OSGP) to resolve this issue.
When compared to the classification based approaches that require very precise prior knowledge to generate a set of training samples and features, applying OSGP on the proposed CEM based methods required only one target signature information and provided stable results even if the initial desire target information is bias or not reliable. In the iterative process of OSGP in
Figure 24, the iteration results of different desired signatures
d after different numbers of iterations give a stable AUC result, so that the originally worse desired target obtains a relatively better desired target.
Figure 25 shows different
d’s have different results in the same algorithm. However, the
d’ iterated by OSGP used in CEM, Subset CEM, SW CEM, and ASW CEM can enhance the original desired target to some extent. Moreover, the results are approximately identical, meaning OSGP can determine the appropriate desired target automatically when selecting inappropriate
d as initial, and the result is still very stable.
CEM technique only takes advantages of spectral information to detect target of interests. However, when spectral information is insufficient to distinguish between targets and some materials have similar spectral signature, this likely causes false alarms in the multispectral images. In this case, our proposed window-based techniques actually include spatial information into the CEM algorithms via fixed or adaptive windows to compensate for the insufficient spectral information. According to the experimental results and the resulting images in
Figure 14,
Figure 15,
Figure 16 and
Figure 17, among our proposed local CEM algorithms, the Subset CEM, Sliding Window-based CEM (SW CEM) of the fixed window size, or Adaptive Window-based CEM (ASW CEM) enhances the contrast between the target and the background better than the general CEM. Because the autocorrelation matrix
R of the CEM algorithm is different, CEM uses
R of the full image, whereas our proposed local CEMs uses local autocorrelation matrix
S in Equation (10) to suppress the background. According to effect of the background suppression [
58], it is obvious that using local autocorrelation
S is better than global autocorrelation
R in this study.
Figure 26 and
Figure 27 show the RGB signatures corresponding to different objects in the study site. As seen, some RGB signatures of leaves and grass are very close to NGL. In the upper left of Region 1, as the grass is too similar to the sprout shown in
Figure 26, the CEM detection is likely to give a false alarm. Because the
R that is used by CEM is generated according to the pixel value of the full image, the difference between NGL and grass is not obvious in the full image. In the entire image, the house and soil are larger than the RGB difference between grass and the sprout, and so the grass is likely to be misrecognized as NGL. On the contrary, in our proposed CEM based algorithms using
S, because
S is generated by pixels around the current pixel value and the proportion of soil and house is not high in a small area, the difference in RGB values between grass and NGL is enlarged, and the grass is likely to be suppressed, thus reducing the false alarm rate. In the same way, the lower right of Region 2 also easily gives a false alarm. Because the pixel values of some leaves are very similar to NGL in the region shown in
Figure 27, when
R is used to suppress the background, it is likely to be influenced by pixel values with a larger difference, and this problem can be solved by using
S.
ASW CEM can change the size of the sliding window, according to the ratio of NGL around the current pixel. When there are too many NGL in the window, the difference between them is likely to be enlarged, and NGL that is very different from the desired target will be suppressed, leading to detection omission. Therefore, the sliding window shall be enlarged to reduce the rate of NGL and enhance the difference from the background, thus increasing the detected value. On the contrary, if the rate of NGL is too low, then the difference between backgrounds increase, and the RGB values that are similar to NGL is likely to be misrecognized. At this point, the sliding window is shrunk, the rate of NGL increases, the difference between NGL and background are more apparent, and the result value of the non-NGL is reduced for suppression. When NGL are enhanced and background is suppressed; their difference is enlarged, so as to highlight NGL.
Briefly, CEM technique was originally designed to catch (1) low probability of infrequent occurrence, (2) relatively small sample size, and (3) most importantly, the target pixel has spectrally distinct from its surrounding pixels [
16]. Obviously, the NGL in RGB images shows the same features. This explains why the window-based CEM techniques can achieve satisfied results of NGL detection even only three spectral signatures is used.