The Effects of Higher-Order Ionospheric Terms on GPS Tropospheric Delay and Gradient Estimates
Abstract
:1. Introduction
2. Materials and Methods
2.1. Datasets and Processing Strategies
2.2. Methodology
2.2.1. Ionospheric Delay Expression
2.2.2. GPS Observation Equation
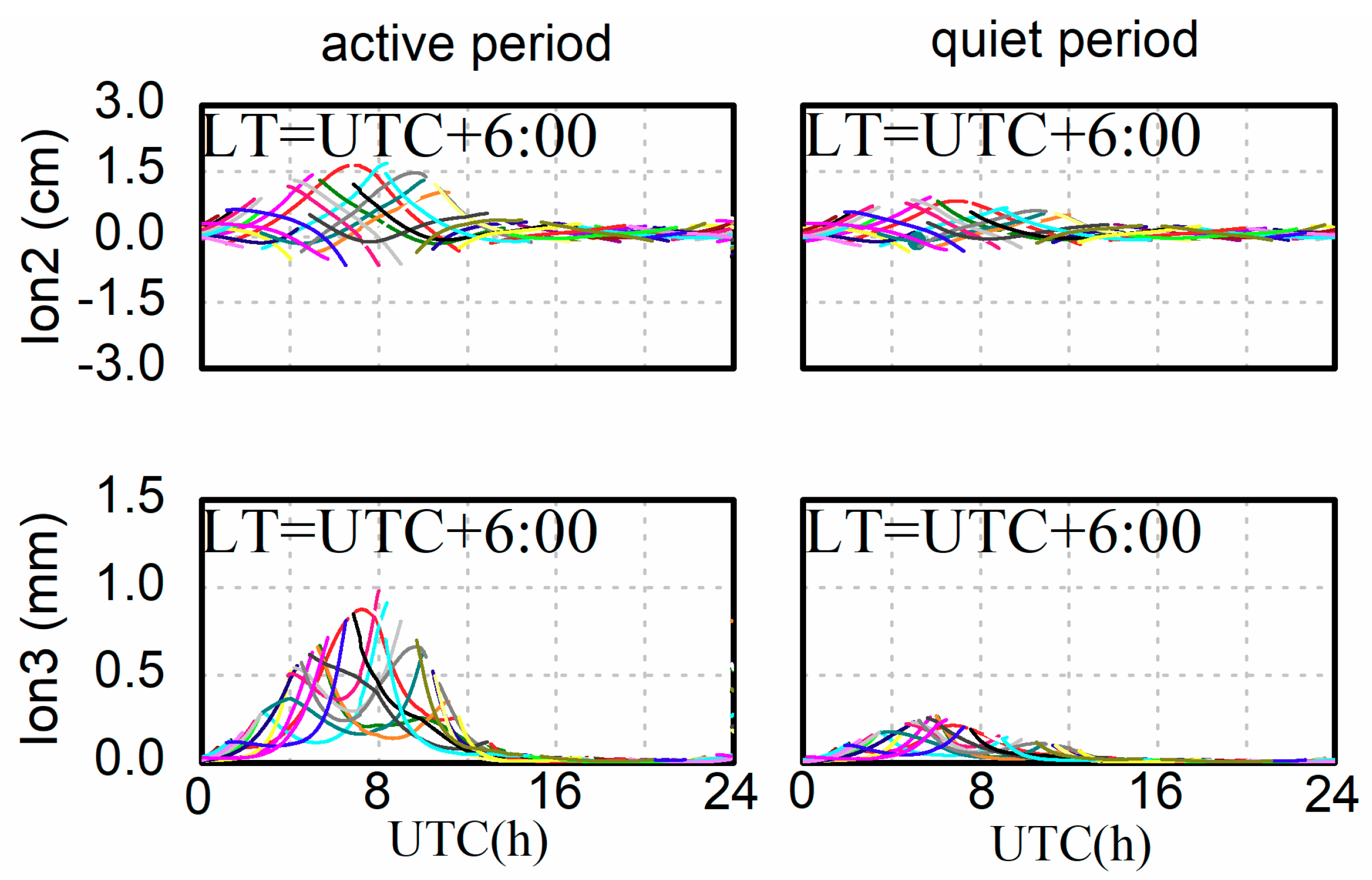
2.2.3. HOI Correction and Tropospheric Delay Estimation
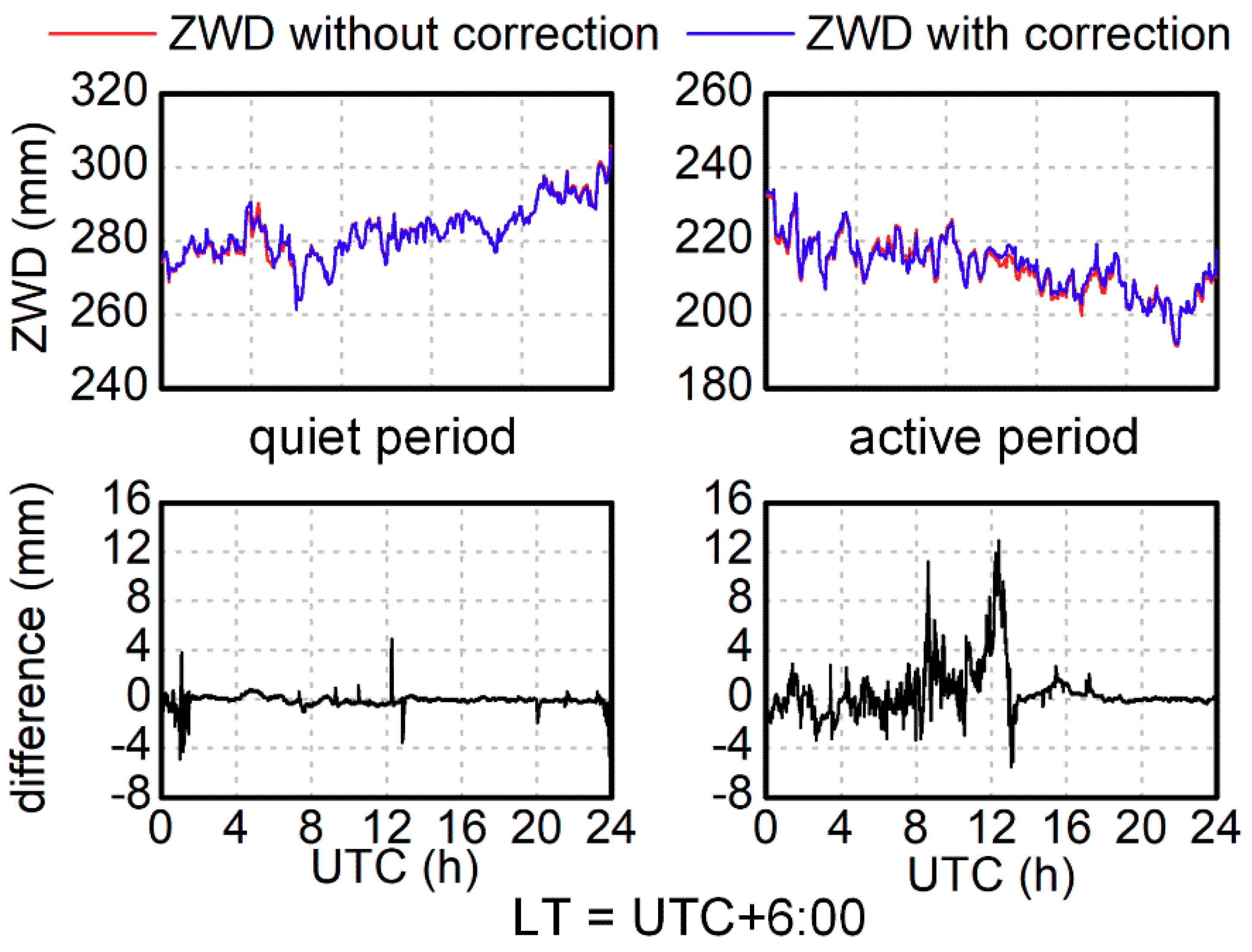
3. Results and Discussion
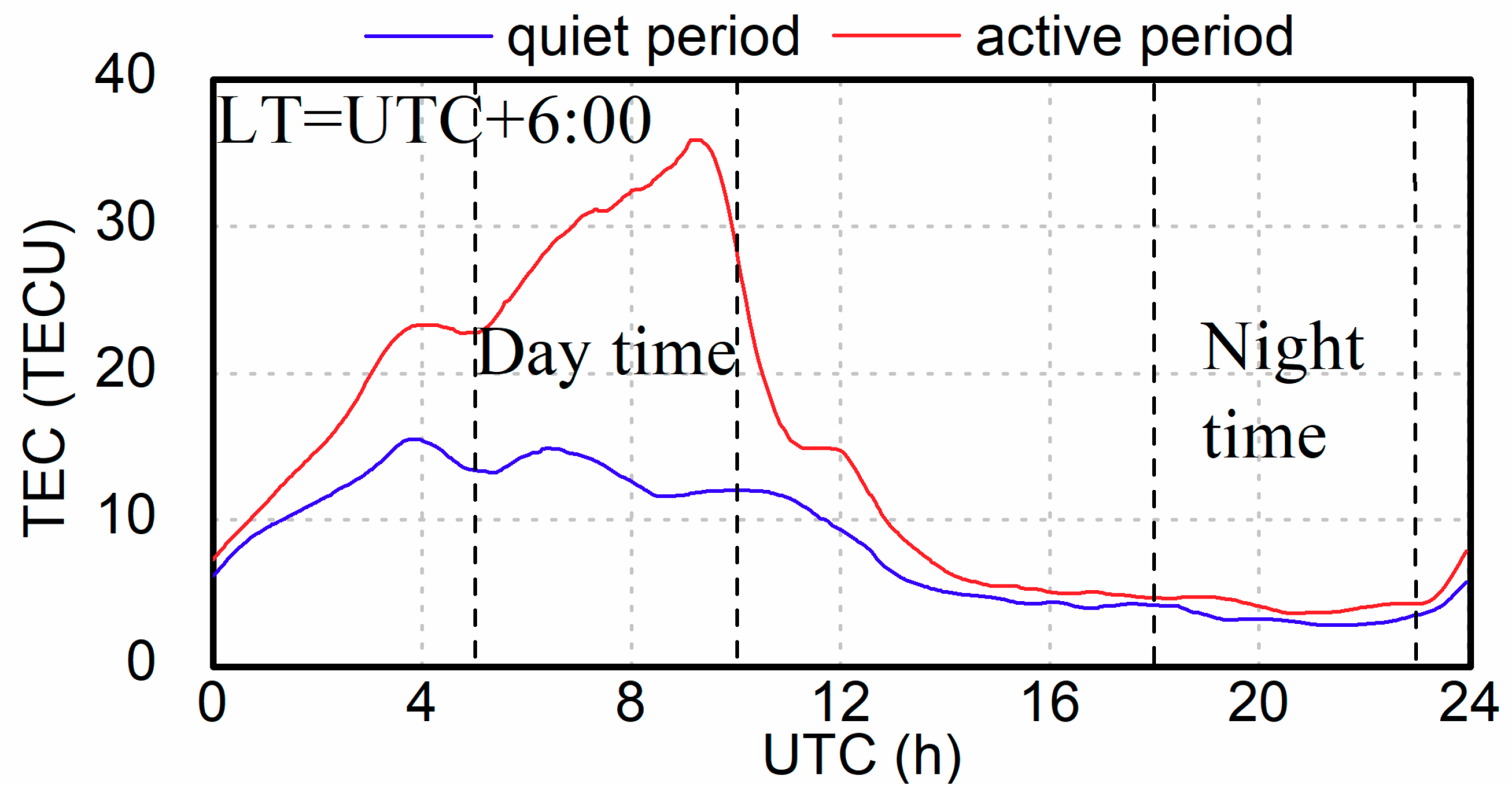
3.1. HOI Effects in Different TEC Conditions
3.2. HOI Effects in Different Geomagnetic Conditions
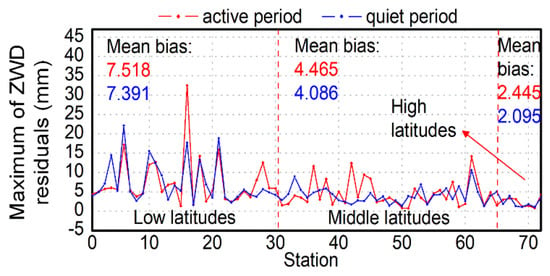
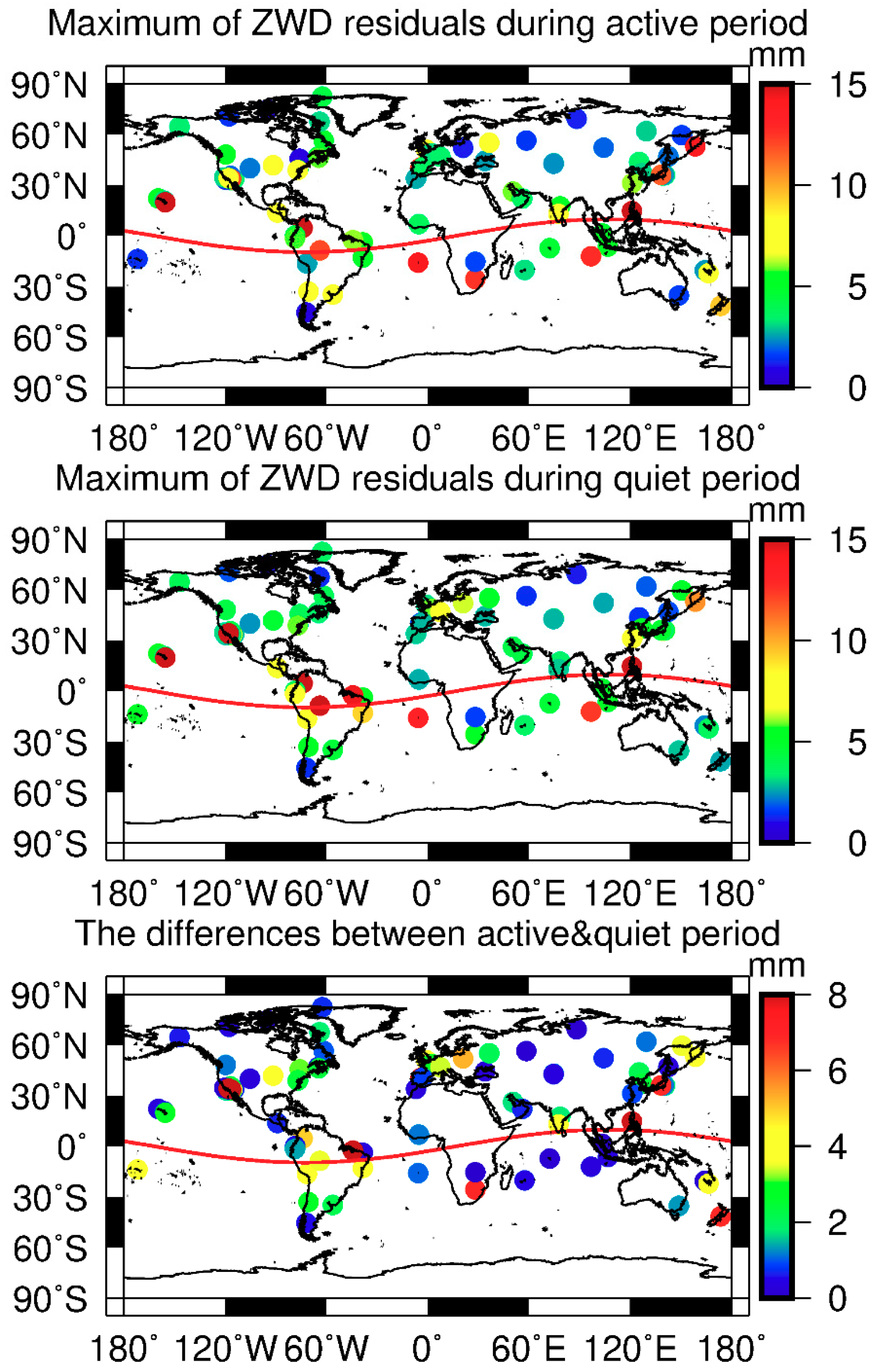
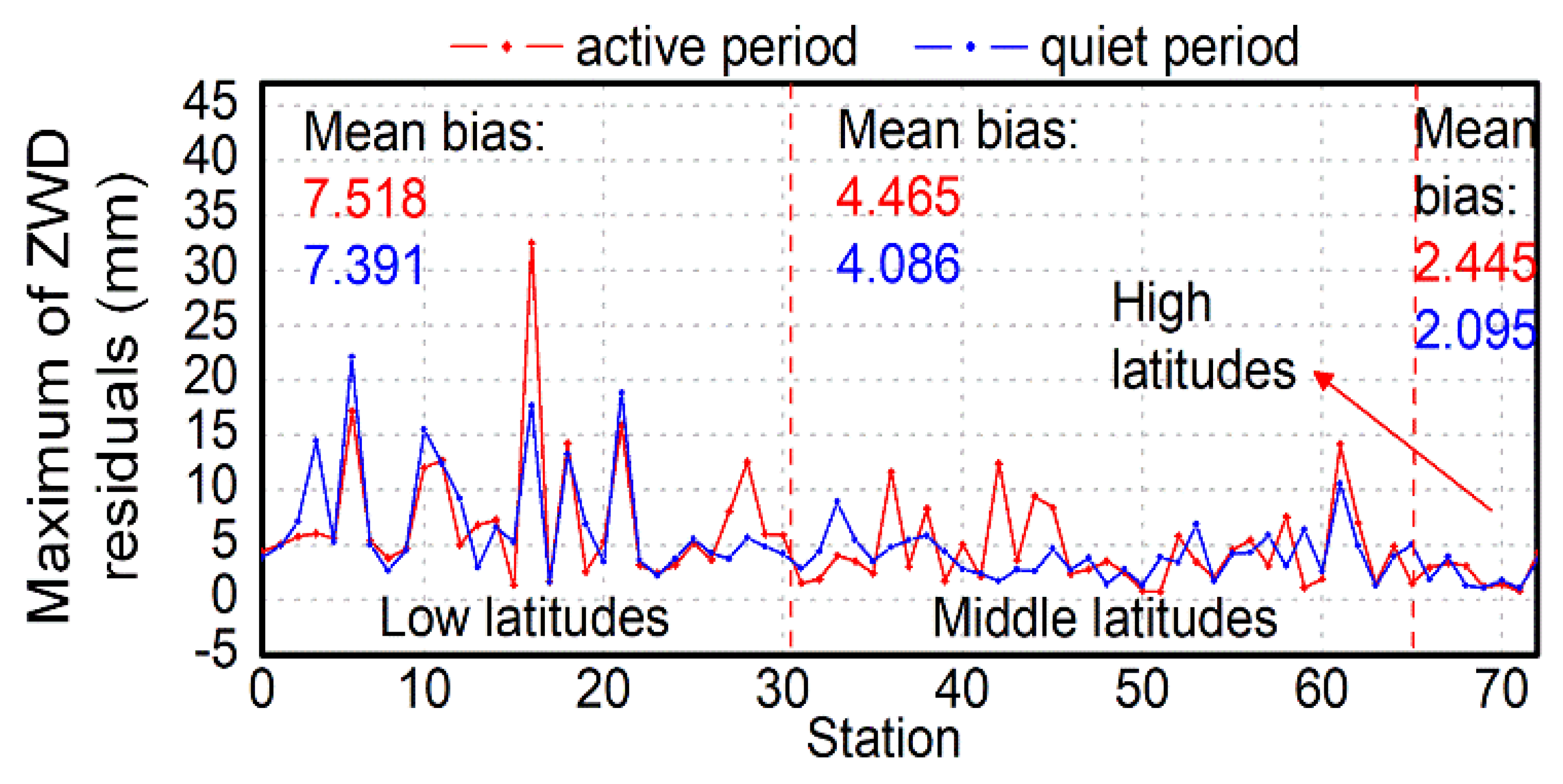
3.3. HOI Effects in Different Spatial Locations
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Tregoning, P.; Boers, R.; O’Brien, D.; Hendy, M. Accuracy of absolute precipitable water vapor estimates from GPS observations. J. Geophys. Res. Atmos. 1998, 103, 28701–28710. [Google Scholar] [CrossRef] [Green Version]
- Böhm, J.; Niell, A.; Tregoning, P.; Schuh, H. Global Mapping Function (GMF): A new empirical mapping function based on numerical weather model data. Geophys. Res. Lett. 2006, 33, L07304. [Google Scholar] [CrossRef]
- Saastamoinen, J. Contributions to the theory of atmospheric refraction. Bull. Géod. (1946–1975) 1973, 107, 13–34. [Google Scholar] [CrossRef]
- Hopfield, H.S. Tropospheric effect on electromagnetically measured range: Prediction from surface weather data. Radio Sci. 1971, 6, 357–367. [Google Scholar] [CrossRef]
- Klobuchar, J.A. Ionospheric effects on GPS. Glob. Position. Syst. Theory Appl. 1996, 1, 485–515. [Google Scholar]
- Hoque, M.M.; Jakowski, N. Estimate of higher order ionospheric errors in GNSS positioning. Radio Sci. 2008, 43, 1–15. [Google Scholar] [CrossRef]
- Elmas, Z.G.; Aquino, M.; Marques, H.; Monico, J.F. Higher order ionospheric effects in GNSS positioning in the European region. Proc. Ann. Geophys. 2011, 29, 1383–1399. [Google Scholar] [CrossRef] [Green Version]
- Wang, Z.; Wu, Y.; Zhang, K.; Meng, Y. Triple-frequency method for high-order ionospheric refractive error modelling in GPS modernization. J. Glob. Position. Syst. 2005, 4, 291–295. [Google Scholar] [CrossRef]
- Brunner, F.K.; Gu, M. An improved model for the dual frequency ionospheric correction of GPS observations. Manuscr. Geod. 1991, 16, 205–214. [Google Scholar]
- Bassiri, S.; Hajj, G.A. Higher-order ionospheric effects on the global positioning system observables and means of modeling them. Manuscr. Geod. 1993, 18, 280. [Google Scholar]
- Petrie, E.J.; King, M.A.; Moore, P.; Lavallée, D.A. Higher-order ionospheric effects on the GPS reference frame and velocities. J. Geophys. Res. Solid Earth 2010, 115, B03417. [Google Scholar] [CrossRef]
- Fritsche, M.; Dietrich, R.; Knöfel, C.; Rülke, A.; Vey, S.; Rothacher, M.; Steigenberger, P. Impact of higher-order ionospheric terms on GPS estimates. Geophys. Res. Lett. 2005, 32, L23311. [Google Scholar] [CrossRef]
- Garcia-Fernandez, M.; Desai, S.; Butala, M.; Komjathy, A. Evaluation of different approaches to modeling the second-order ionospheric delay on GPS measurements. J. Geophys. Res. Space Phys. 2013, 118, 7864–7873. [Google Scholar] [CrossRef] [Green Version]
- Elsobeiey, M.; El-Rabbany, A. Impact of second-order ionospheric delay on GPS precise point positioning. J. Appl. Geophys. 2011, 5, 37–45. [Google Scholar] [CrossRef]
- Hernandez-Pajares, M.; Juan, J.; Sanz, J.; Orús, R. Second-order ionospheric term in GPS: Implementation and impact on geodetic estimates. J. Geophys. Res. Solid Earth 2007, 112, B08417. [Google Scholar] [CrossRef]
- Deng, L.; Jiang, W.; Li, Z.; Chen, H.; Wang, K.; Ma, Y. Assessment of second-and third-order ionospheric effects on regional networks: Case study in China with longer CMONOC GPS coordinate time series. J. Geod. 2017, 91, 207–227. [Google Scholar] [CrossRef]
- Hadas, T.; Krypiak-Gregorczyk, A.; Hernández-Pajares, M.; Kaplon, J.; Paziewski, J.; Wielgosz, P.; Garcia-Rigo, A.; Kazmierski, K.; Sosnica, K.; Kwasniak, D. Impact and Implementation of Higher-Order Ionospheric Effects on Precise GNSS Applications. J. Geophys. Res. Solid Earth 2017, 122, 9420–9436. [Google Scholar] [CrossRef]
- Liu, Z.; Li, Y.; Guo, J.; Li, F. Influence of higher-order ionospheric delay correction on GPS precise orbit determination and precise positioning. Geod. Geodyn. 2016, 7, 369–376. [Google Scholar] [CrossRef]
- Zus, F.; Deng, Z.; Wickert, J. The impact of higher-order ionospheric effects on estimated tropospheric parameters in Precise Point Positioning. Radio Sci. 2017, 52, 963–971. [Google Scholar] [CrossRef] [Green Version]
- Douša, J.; Dick, G.; Kačmařík, M.; Brožková, R.; Zus, F.; Brenot, H.; Stoycheva, A.; Möller, G.; Kaplon, J. Benchmark campaign and case study episode in central Europe for development and assessment of advanced GNSS tropospheric models and products. Atmos. Meas. Tech. 2016, 9, 2989–3008. [Google Scholar] [CrossRef] [Green Version]
- Marques, H.A.; Monico, J.F.; Aquino, M. RINEX_HO: Second-and third-order ionospheric corrections for RINEX observation files. GPS Solut. 2011, 15, 305–314. [Google Scholar] [CrossRef]
- Schmid, R.; Steigenberger, P.; Gendt, G.; Ge, M.; Rothacher, M. Generation of a consistent absolute phase-center correction model for GPS receiver and satellite antennas. J. Geod. 2007, 81, 781–798. [Google Scholar] [CrossRef]
- Wu, J.-T.; Wu, S.C.; Hajj, G.A.; Bertiger, W.I.; Lichten, S.M. Effects of antenna orientation on GPS carrier phase. Adv. Astronaut. Sci. 1992, 76, 1647–1660. [Google Scholar]
- Budden, K.G. The Propagation of Radio Waves: The Theory of Radio Waves of Low Power in the Ionosphere and Magnetosphere, 1st ed.; Cambridge University Press: Cambridge, UK, 1988; pp. 328–356. ISBN 978-0521369527. [Google Scholar]
- Davies, K. Ionospheric Radio, 1st ed.; IET: Stevenage, UK, 1990; pp. 89–124. ISBN 978-0863411861. [Google Scholar]
- Rawer, K. Wave Propagation in the Ionosphere, 1st ed.; Springer Science & Business Media: Berlin, Germany, 2013; pp. 109–139. ISBN 978-9401736657. [Google Scholar]
- Hoque, M.M.; Jakowski, N. Higher order ionospheric effects in precise GNSS positioning. J. Geod. 2007, 81, 259–268. [Google Scholar] [CrossRef]
- Zus, F.; Deng, Z.; Heise, S.; Wickert, J. Ionospheric mapping functions based on electron density fields. GPS Solut. 2017, 21, 873–885. [Google Scholar] [CrossRef]
- Kedar, S.; Hajj, G.A.; Wilson, B.D.; Heflin, M.B. The effect of the second order GPS ionospheric correction on receiver positions. Geophys. Res. Lett. 2003, 30, 1829. [Google Scholar] [CrossRef]
- Odijk, D. Fast Precise GPS Positioning in the Presence of Ionospheric Delays. Ph.D. Thesis, Faculty of Civil Engineering and Geosciences, Delft University of Technology, Delft, The Netherlands, 2002. [Google Scholar]
- Zumberge, J.; Heflin, M.; Jefferson, D.; Watkins, M.; Webb, F.H. Precise point positioning for the efficient and robust analysis of GPS data from large networks. J. Geophys. Res. Solid Earth 1997, 102, 5005–5017. [Google Scholar] [CrossRef] [Green Version]
- Kouba, J.; Héroux, P. Precise point positioning using IGS orbit and clock products. GPS Solut. 2001, 5, 12–28. [Google Scholar] [CrossRef]








| Item | Processing Strategies |
|---|---|
| Observation | Ionosphere-free (IF) combination |
| Signal selection | L1 and L2 |
| Sampling rate | 30 s |
| Elevation mask | 10° |
| Weight for observations | Elevation-dependent weighting scheme |
| Estimator | Kalman filter |
| Ionosphere | with and without HOI corrections [21] |
| Tropospheric mapping function | GMF [2] |
| Satellite orbit | IGS final precise ephemeris products |
| Satellite clock | IGS final precise clock products |
| Coordinates of stations | Fixed with SINEX product |
| Phase center offset and variation | IGS Convention [22] |
| Phase windup effect | Corrected [23] |
| Receiver clock | Estimated as white noise |
| Tropospheric wet delay | Estimated as random-walk model. RWPN*: |
| Tropospheric gradients | Estimated as random-walk model. RWPN: |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, Z.; Guo, F.; Zhang, X. The Effects of Higher-Order Ionospheric Terms on GPS Tropospheric Delay and Gradient Estimates. Remote Sens. 2018, 10, 1561. https://doi.org/10.3390/rs10101561
Zhang Z, Guo F, Zhang X. The Effects of Higher-Order Ionospheric Terms on GPS Tropospheric Delay and Gradient Estimates. Remote Sensing. 2018; 10(10):1561. https://doi.org/10.3390/rs10101561
Chicago/Turabian StyleZhang, Zhiyu, Fei Guo, and Xiaohong Zhang. 2018. "The Effects of Higher-Order Ionospheric Terms on GPS Tropospheric Delay and Gradient Estimates" Remote Sensing 10, no. 10: 1561. https://doi.org/10.3390/rs10101561
APA StyleZhang, Z., Guo, F., & Zhang, X. (2018). The Effects of Higher-Order Ionospheric Terms on GPS Tropospheric Delay and Gradient Estimates. Remote Sensing, 10(10), 1561. https://doi.org/10.3390/rs10101561