Evaluating the Temporal Dynamics of Uncertainty Contribution from Satellite Precipitation Input in Rainfall-Runoff Modeling Using the Variance Decomposition Method
Abstract
:1. Introduction
2. Study Area and Data
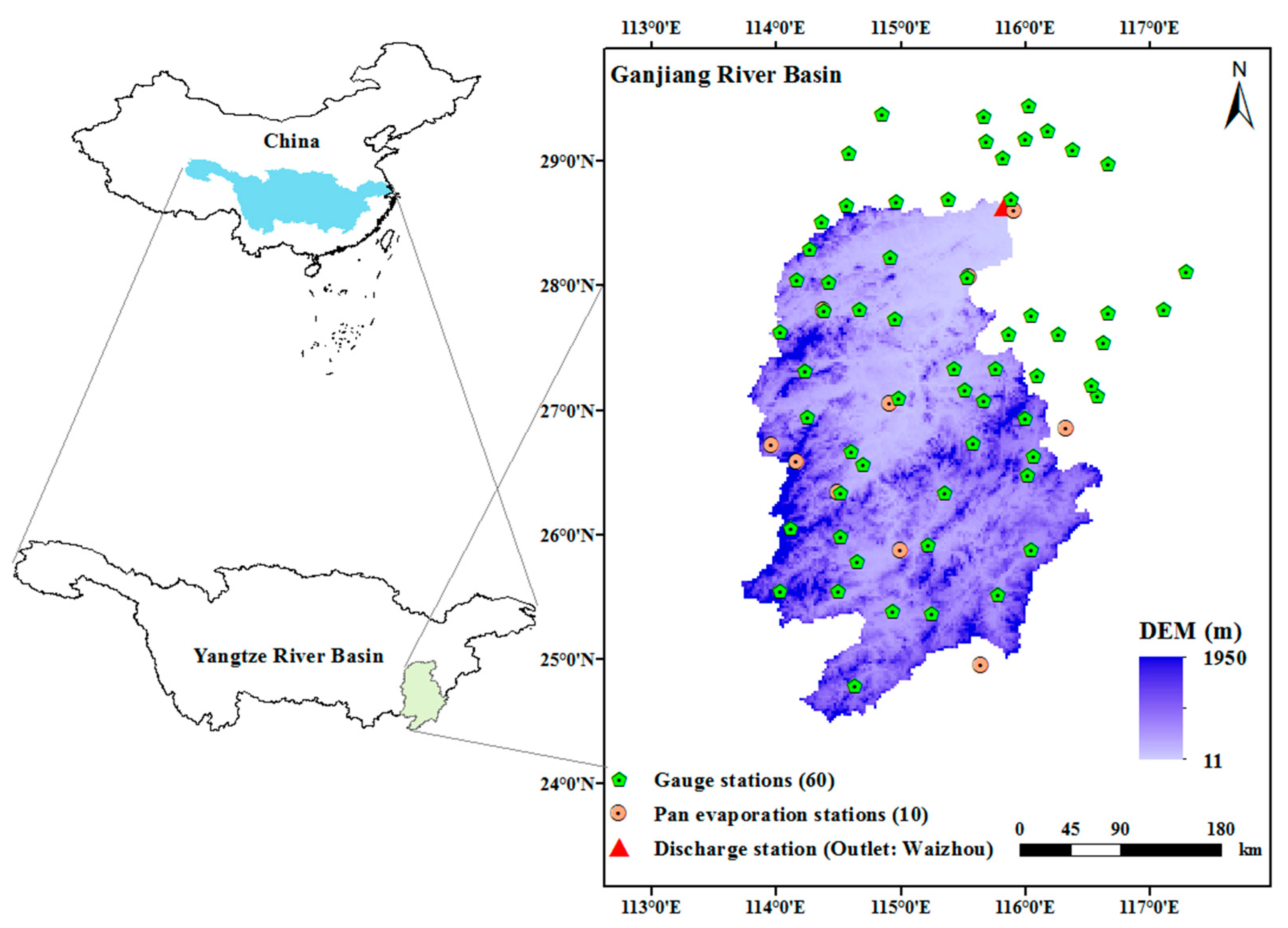
2.1. Ganjiang River Basin
2.2. Precipitation Datasets
3. Methodology
3.1. GR and CREST Models
3.2. Configuration of the Modeling
3.3. Variance-Based Decomposition of Uncertainty Sources
3.4. Evaluation Criteria
4. Results and Discussion
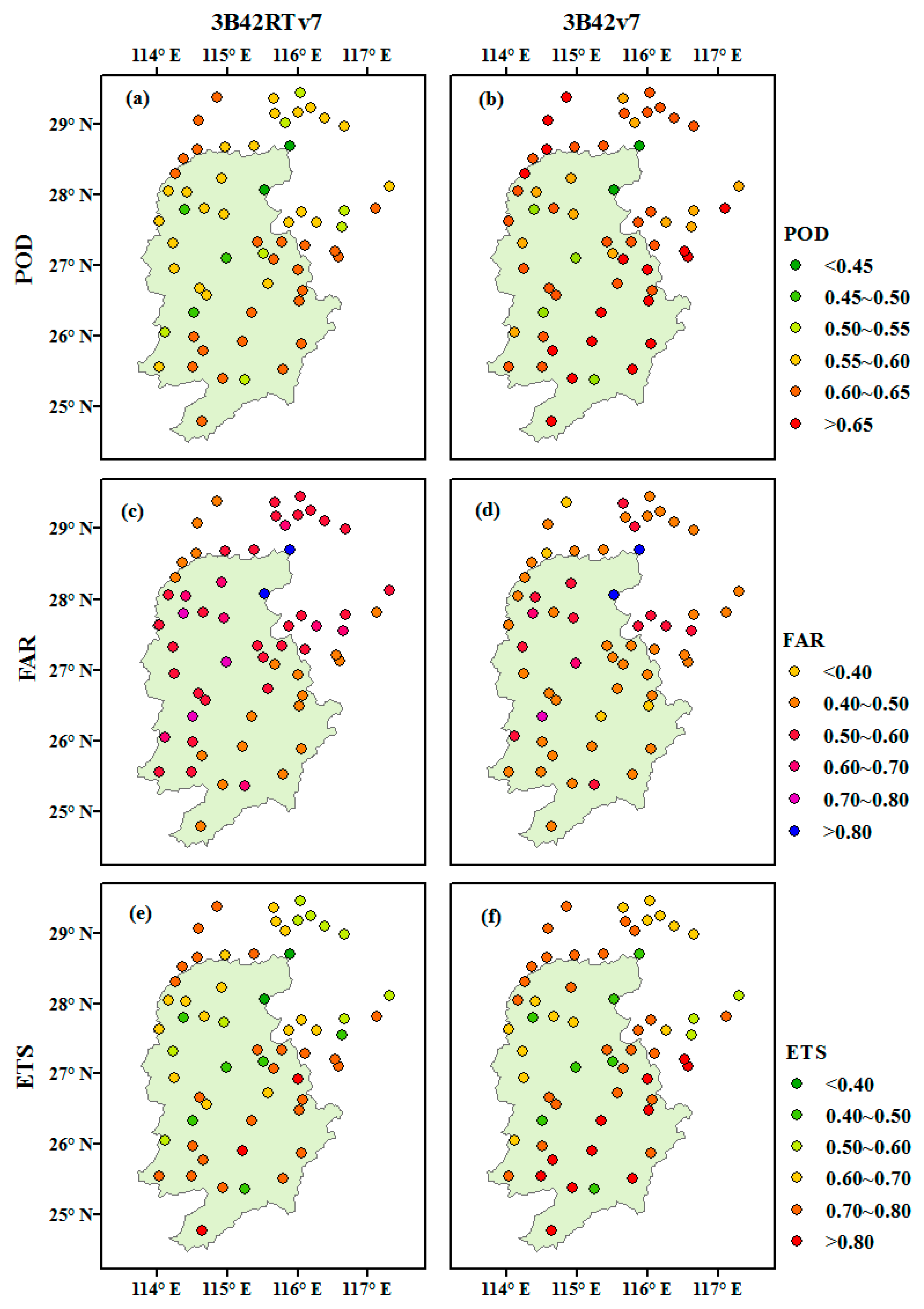
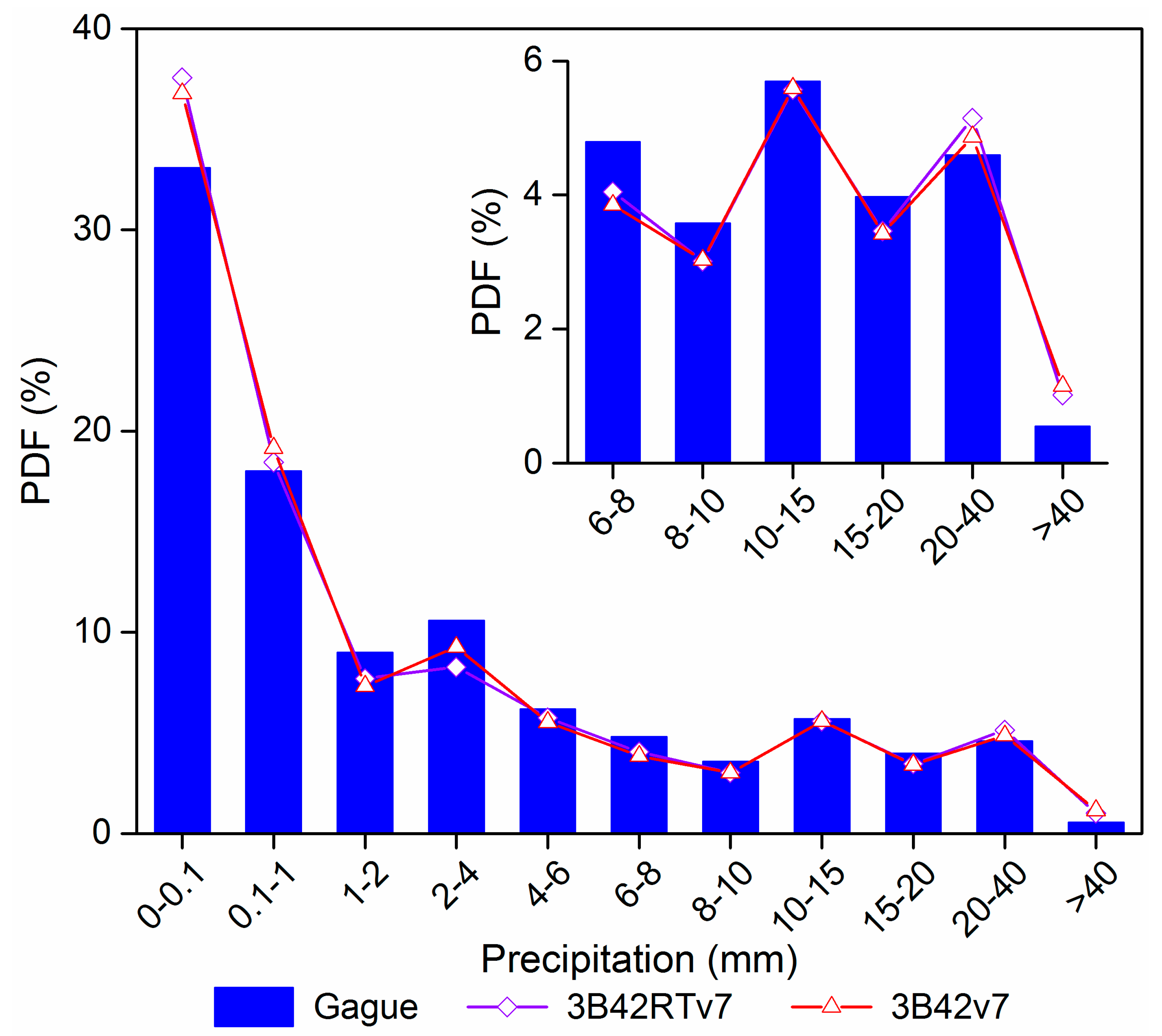
4.1. Evaluating the Consistency of Two SPE Products and Gauge-Based Reference
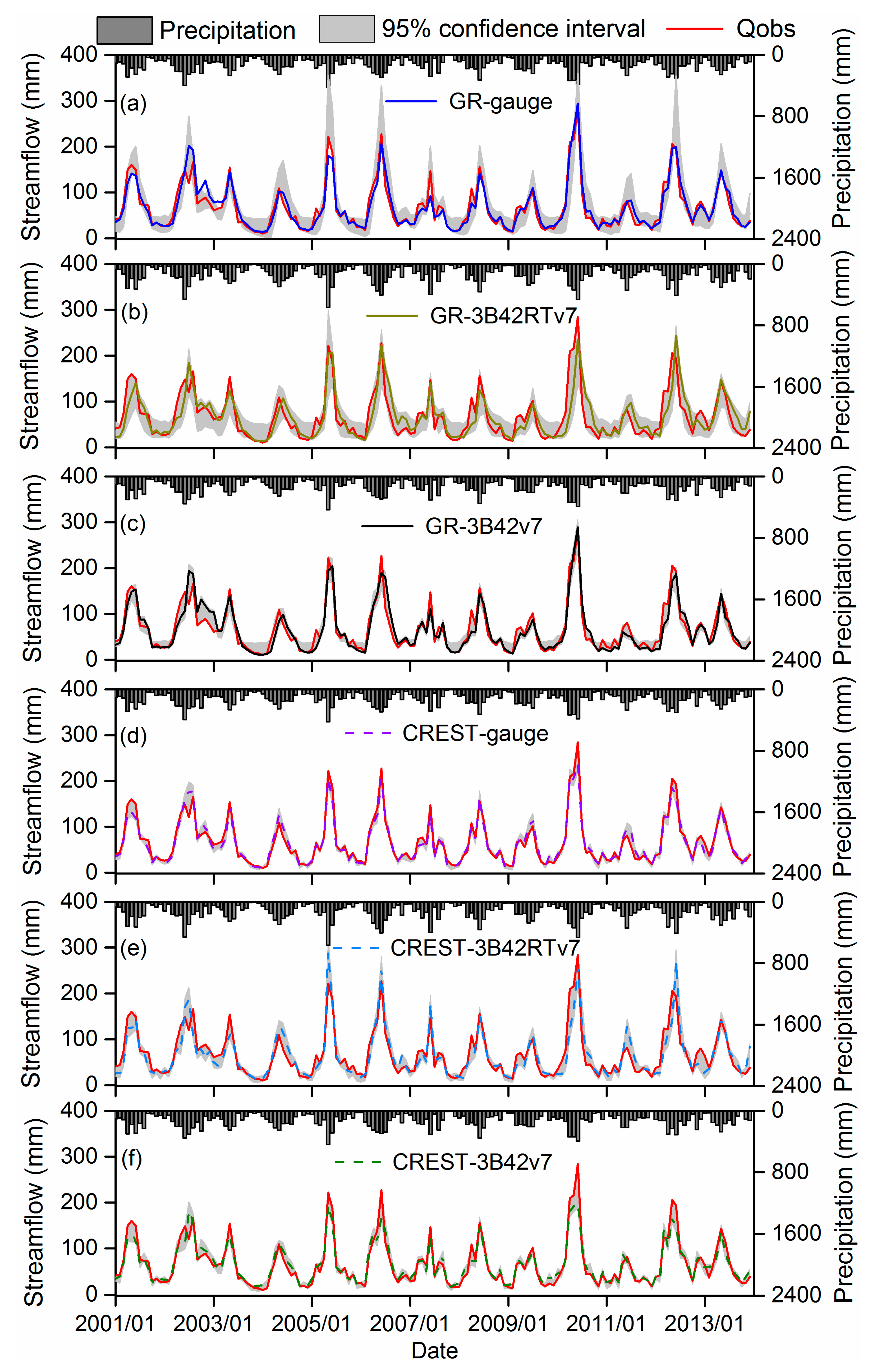
4.2. Hydrologic Evaluation of SPE
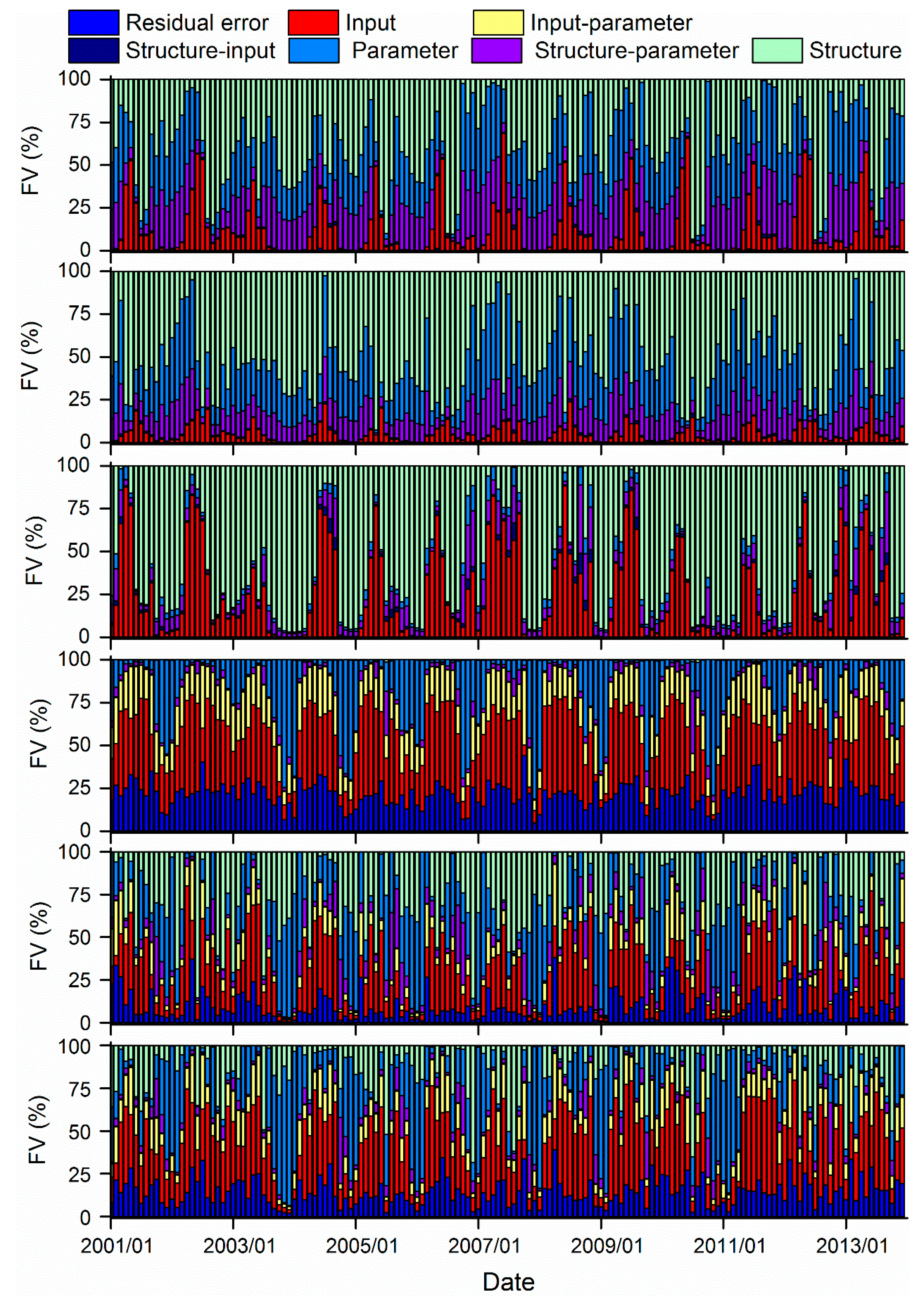
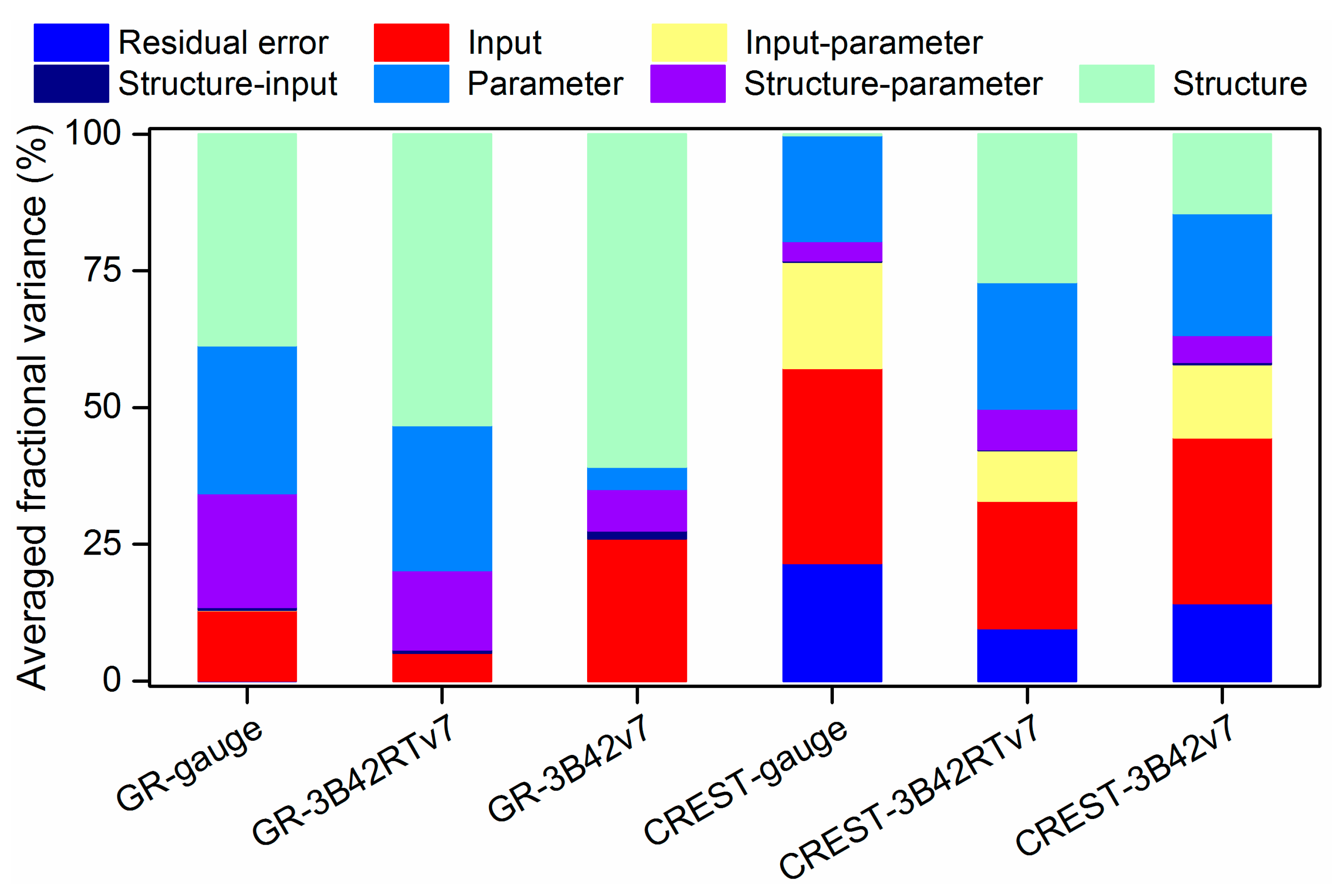
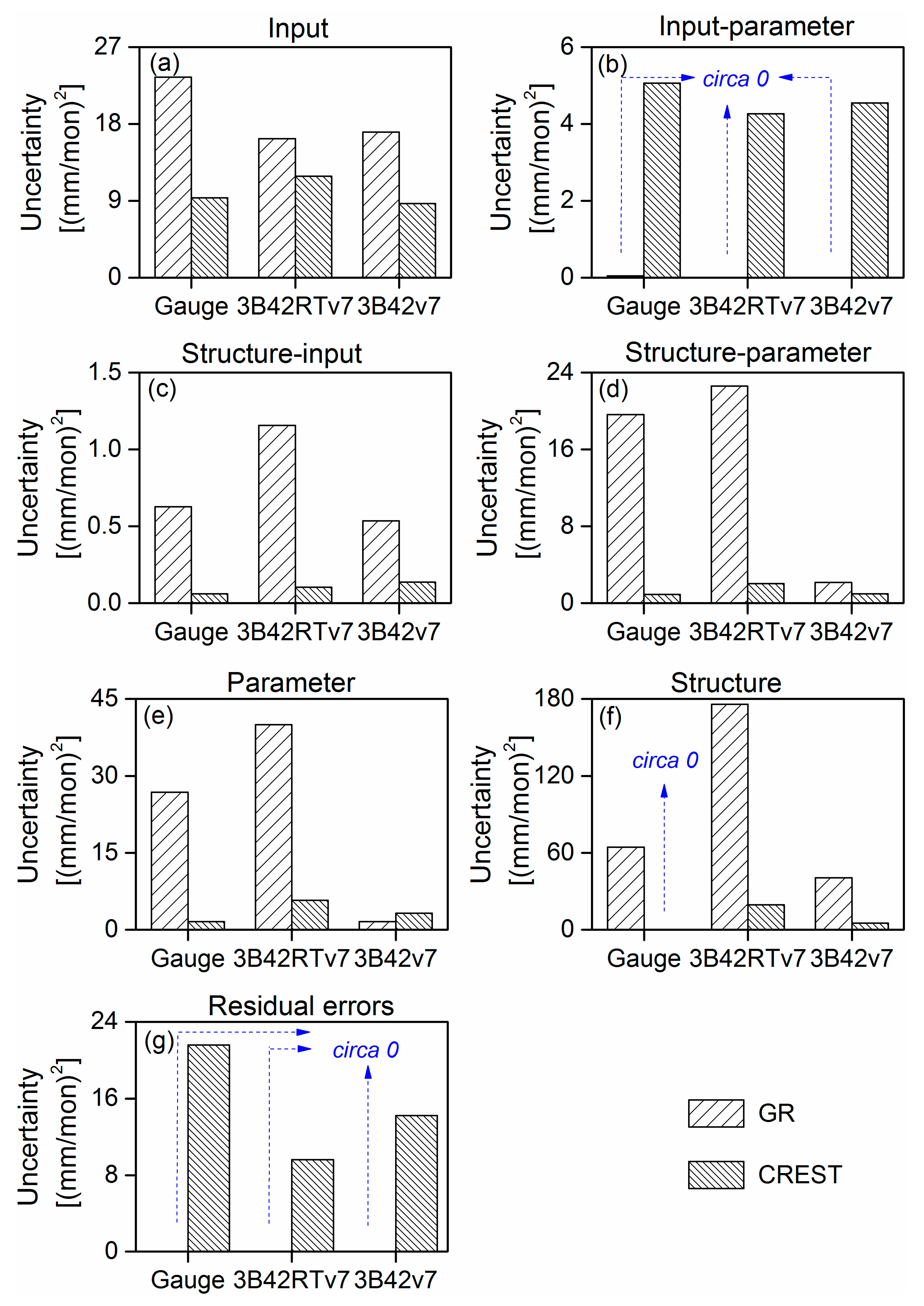
4.3. Variance-Based Uncertainty Component Analysis
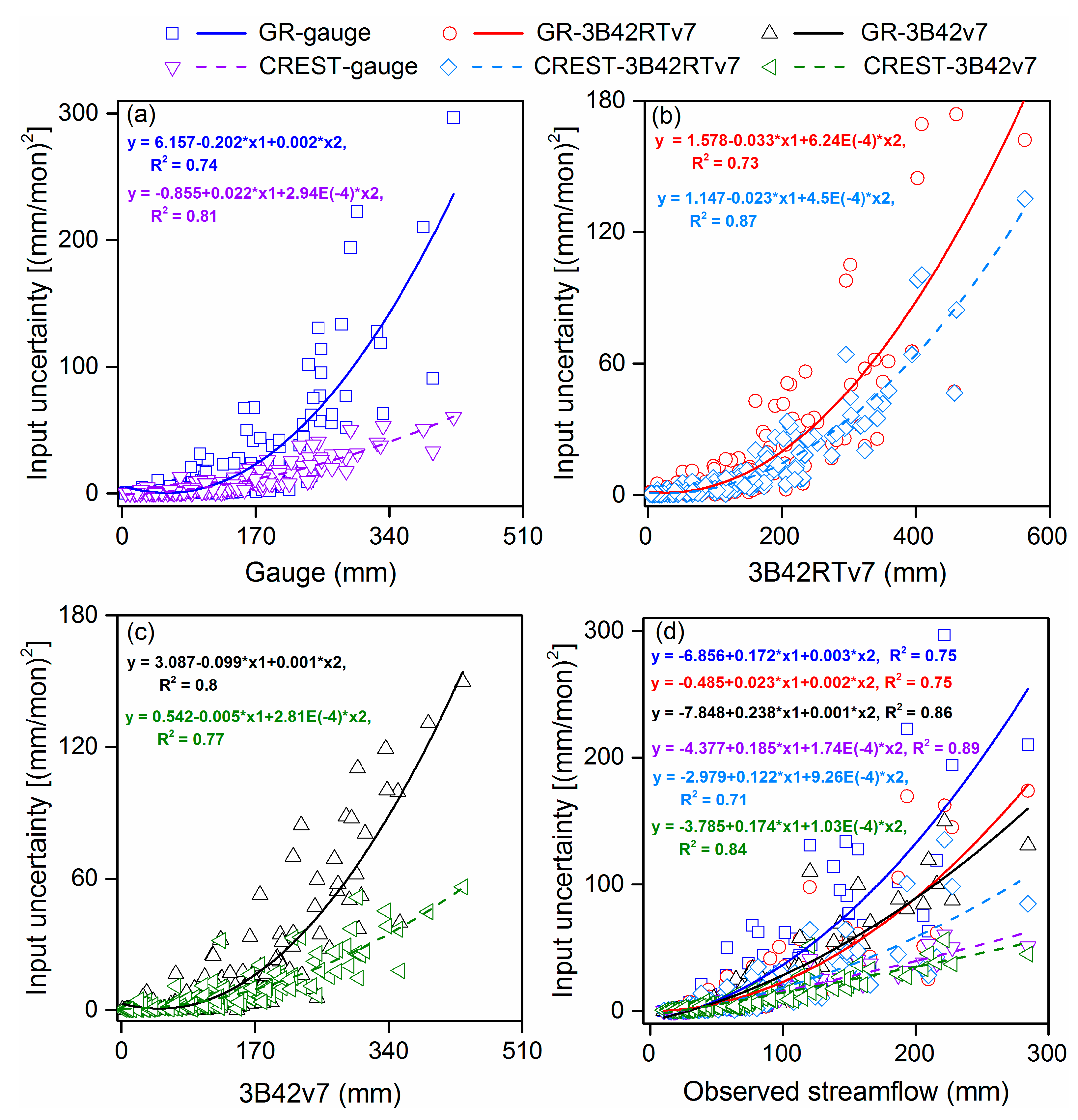
4.3.1. Inter-comparison of Uncertainties in Precipitation Input with Other Sources
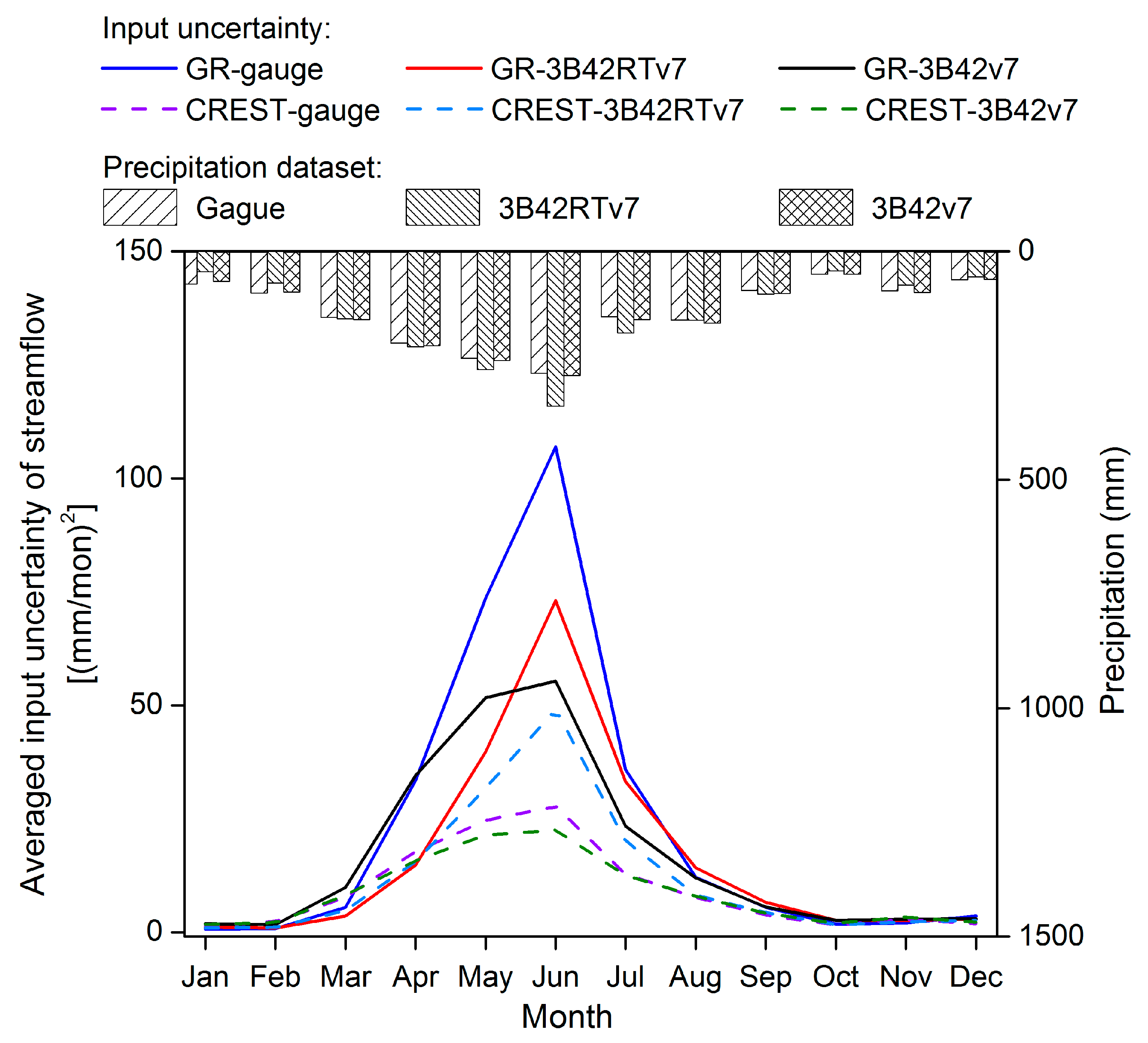
4.3.2. Inter-comparison of Input Uncertainties among Six Schemes
4.4. Discussion
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Katiraie-Boroujerdy, P.; Asanjan, A.A.; Hsu, K.; Sorooshian, S. Intercomparison of PERSIANN-CDR and TRMM-3B42V7 precipitation estimates at monthly and daily time scales. Atmos. Res. 2017, 193, 36–49. [Google Scholar] [CrossRef]
- Sunilkumar, K.; Rao, T.N.; Satheeshkumar, S. Assessment of small-scale variability of rainfall and multi-satellite precipitation estimates using measurements from a dense rain gauge network in Southeast India. Hydrol. Earth Syst. Sci. 2016, 20, 1719–1735. [Google Scholar] [CrossRef] [Green Version]
- Renard, B.; Kavetski, D.; Kuczera, G.; Thyer, M.; Franks, S.W. Understanding predictive uncertainty in hydrologic modeling: The challenge of identifying input and structural errors. Water Resour. Res. 2010, 46, W5521. [Google Scholar] [CrossRef]
- McMillan, H.; Jackson, B.; Clark, M.; Kavetski, D.; Woods, R. Rainfall uncertainty in hydrological modelling: An evaluation of multiplicative error models. J. Hydrol. 2011, 400, 83–94. [Google Scholar] [CrossRef]
- Yen, H.; Su, Y.; Wolfe, J.E.; Chen, S.; Hsu, Y.; Tseng, W.; Brady, D.M.; Jeong, J.; Arnold, J.G. Assessment of input uncertainty by seasonally categorized latent variables using SWAT. J. Hydrol. 2015, 531, 685–695. [Google Scholar] [CrossRef] [Green Version]
- Mockler, E.M.; Chun, K.P.; Sapriza-Azuri, G.; Bruen, M.; Wheater, H.S. Assessing the relative importance of parameter and forcing uncertainty and their interactions in conceptual hydrological model simulations. Adv. Water Resour. 2016, 97, 299–313. [Google Scholar] [CrossRef]
- Yong, B.; Hong, Y.; Ren, L.L.; Gourley, J.J.; Huffman, G.J.; Chen, X.; Wang, W.; Khan, S.I. Assessment of evolving TRMM-based multisatellite real-time precipitation estimation methods and their impacts on hydrologic prediction in a high latitude basin. J. Geophys. Res. Atmos. 2012, 117, D9108. [Google Scholar] [CrossRef]
- Gebregiorgis, A.S.; Tian, Y.; Peters Lidard, C.D.; Hossain, F. Tracing hydrologic model simulation error as a function of satellite rainfall estimation bias components and land use and land cover conditions. Water Resour. Res. 2012, 48, W11509. [Google Scholar] [CrossRef]
- Li, D.; Christakos, G.; Ding, X.; Wu, J. Adequacy of TRMM satellite rainfall data in driving the SWAT modeling of Tiaoxi catchment (Taihu lake basin, China). J. Hydrol. 2018, 556, 1139–1152. [Google Scholar] [CrossRef]
- Gao, Z.; Long, D.; Tang, G.; Zeng, C.; Huang, J.; Hong, Y. Assessing the potential of satellite-based precipitation estimates for flood frequency analysis in ungauged or poorly gauged tributaries of China’s Yangtze River basin. J. Hydrol. 2017, 550, 478–496. [Google Scholar] [CrossRef]
- Tong, K.; Su, F.; Yang, D.; Hao, Z. Evaluation of satellite precipitation retrievals and their potential utilities in hydrologic modeling over the Tibetan Plateau. J. Hydrol. 2014, 519, 423–437. [Google Scholar] [CrossRef]
- Knoche, M.; Fischer, C.; Pohl, E.; Krause, P.; Merz, R. Combined uncertainty of hydrological model complexity and satellite-based forcing data evaluated in two data-scarce semi-arid catchments in Ethiopia. J. Hydrol. 2014, 519, 2049–2066. [Google Scholar] [CrossRef]
- Li, Z.; Yang, D.; Gao, B.; Jiao, Y.; Hong, Y.; Xu, T. Multiscale Hydrologic Applications of the Latest Satellite Precipitation Products in the Yangtze River Basin using a Distributed Hydrologic Model. J. Hydrometeorol. 2015, 16, 407–426. [Google Scholar] [CrossRef]
- Yang, Z.; Hsu, K.; Sorooshian, S.; Xu, X.; Braithwaite, D.; Zhang, Y.; Verbist, K.M. Merging High-resolution Satellite-based Precipitation Fields and Point-scale Rain-gauge Measurements—A Case Study in Chile. J. Geophys. Res. Atmos. 2017, 122, 5267–5284. [Google Scholar] [CrossRef]
- Jing, W.; Yang, Y.; Yue, X.; Zhao, X. A spatial downscaling algorithm for satellite-based precipitation over the Tibetan plateau based on NDVI, DEM, and land surface temperature. Remote Sens. 2016, 8, 655. [Google Scholar] [CrossRef]
- Maggioni, V.; Sapiano, M.R.; Adler, R.F. Estimating uncertainties in high-resolution satellite precipitation products: Systematic or random error? J. Hydrometeorol. 2016, 17, 1119–1129. [Google Scholar] [CrossRef]
- Yong, B.; Chen, B.; Tian, Y.; Yu, Z.; Hong, Y. Error-component analysis of TRMM-based multi-satellite precipitation estimates over Mainland China. Remote Sens. 2016, 8, 440. [Google Scholar] [CrossRef]
- Maggioni, V.; Nikolopoulos, E.I.; Anagnostou, E.N.; Borga, M. Modeling satellite precipitation errors over mountainous terrain: The influence of gauge density, seasonality, and temporal resolution. IEEE Trans. Geosci. Remote Sens. 2017, 55, 4130–4140. [Google Scholar] [CrossRef]
- Shah, H.L.; Mishra, V. Uncertainty and bias in satellite-based precipitation estimates over indian subcontinental basins: Implications for real-time streamflow simulation and flood prediction. J. Hydrometeorol. 2016, 17, 615–636. [Google Scholar] [CrossRef]
- Mendoza, P.A.; Clark, M.P.; Mizukami, N.; Gutmann, E.D.; Arnold, J.R.; Brekke, L.D.; Rajagopalan, B. How do hydrologic modeling decisions affect the portrayal of climate change impacts? Hydrol. Process. 2016, 30, 1071–1095. [Google Scholar] [CrossRef]
- Sapriza Azuri, G.; Jódar, J.; Navarro, V.; Slooten, L.J.; Carrera, J.; Gupta, H.V. Impacts of rainfall spatial variability on hydrogeological response. Water Resour. Res. 2015, 51, 1300–1314. [Google Scholar] [CrossRef] [Green Version]
- Li, M.; Yang, D.; Chen, J.; Hubbard, S.S. Calibration of a distributed flood forecasting model with input uncertainty using a Bayesian framework. Water Resour. Res. 2012, 48, W8510. [Google Scholar] [CrossRef]
- Kavetski, D.; Kuczera, G.; Franks, S.W. Bayesian analysis of input uncertainty in hydrological modeling: 1. Theory. Water Resour. Res. 2006, 42, W3407. [Google Scholar] [CrossRef]
- Ajami, N.K.; Duan, Q.; Sorooshian, S. An integrated hydrologic Bayesian multimodel combination framework: Confronting input, parameter, and model structural uncertainty in hydrologic prediction. Water Resour. Res. 2007, 43, W1403. [Google Scholar] [CrossRef]
- Addor, N.; Rössler, O.; Köplin, N.; Huss, M.; Weingartner, R.; Seibert, J. Robust changes and sources of uncertainty in the projected hydrological regimes of Swiss catchments. Water Resour. Res. 2014, 50, 7541–7562. [Google Scholar] [CrossRef] [Green Version]
- Ren, Z.H.; Zhao, P.; Zhang, Q.; Zhang, Z.F.; Cao, L.J.; Yang, Y.R.; Zou, F.L.; Zhao, Y.F.; Zhao, H.M.; Chen, Z. Quality control procedures for hourly precipitation data from automatic weather stations in China. Meteorol. Mon. 2010, 36, 123–132. [Google Scholar]
- Gebremichael, M.; Hossain, F. Satellite Rainfall Applications for Surface Hydrology; Springer: Berlin, Germany, 2010; pp. 3–22. [Google Scholar]
- Huffman, G.J.; Bolvin, D.T. TRMM and Other Data Precipitation Data Set Documentation; NASA: Greenbelt, MD, USA, 2013; Volume 28, pp. 1–46.
- Liu, Z. Comparison of precipitation estimates between Version 7 3-hourly TRMM Multi-Satellite Precipitation Analysis (TMPA) near-real-time and research products. Atmos. Res. 2015, 153, 119–133. [Google Scholar] [CrossRef]
- Bowman, K.P.; Hong, Y.; Stocker, E.F.; Wol, D.B. The TRMM multi-satellite precipitation analysis: Quasi-global, multi-year, combined-sensor precipitation estimates at finescale. J. Hydrometeorol. 2007, 8, 3855. [Google Scholar]
- Coron, L.; Perrin, C.; Delaigue, O.; Andréassian, V.; Thirel, G. airGR: A suite of lumped hydrological models in an R-package. Environ. Modell. Softw. 2017, 94, 166–171. [Google Scholar] [CrossRef]
- Shin, M.; Kim, C. Assessment of the suitability of rainfall-runoff models by coupling performance statistics and sensitivity analysis. Hydrol. Res. 2017, 48, 1192–1213. [Google Scholar] [CrossRef]
- Pushpalatha, R.; Perrin, C.; Le Moine, N.; Mathevet, T.; Andréassian, V. A downward structural sensitivity analysis of hydrological models to improve low-flow simulation. J. Hydrol. 2011, 411, 66–76. [Google Scholar] [CrossRef]
- Khan, S.I.; Adhikari, P.; Hong, Y.; Vergara, H.; F Adler, R.; Policelli, F.; Irwin, D.; Korme, T.; Okello, L. Hydroclimatology of Lake Victoria region using hydrologic model and satellite remote sensing data. Hydrol. Earth Syst. Sci. 2011, 15, 107–117. [Google Scholar] [CrossRef] [Green Version]
- Khan, S.I.; Hong, Y.; Wang, J.; Yilmaz, K.K.; Gourley, J.J.; Adler, R.F.; Brakenridge, G.R.; Policelli, F.; Habib, S.; Irwin, D. Satellite remote sensing and hydrologic modeling for flood inundation mapping in Lake Victoria basin: Implications for hydrologic prediction in ungauged basins. IEEE Trans. Geosci. Remote Sens. 2011, 49, 85–95. [Google Scholar] [CrossRef]
- Wang, J.; Hong, Y.; Li, L.; Gourley, J.J.; Khan, S.I.; Yilmaz, K.K.; Adler, R.F.; Policelli, F.S.; Habib, S.; Irwn, D. The coupled routing and excess storage (CREST) distributed hydrological model. Hydrol. Sci. J. 2011, 56, 84–98. [Google Scholar] [CrossRef] [Green Version]
- Perrin, C.; Michel, C.; Andréassian, V. Improvement of a parsimonious model for streamflow simulation. J. Hydrol. 2003, 279, 275–289. [Google Scholar] [CrossRef]
- Duan, Q.; Sorooshian, S.; Gupta, V. Effective and efficient global optimization for conceptual rainfall-runoff models. Water Resour. Res. 1992, 28, 1015–1031. [Google Scholar] [CrossRef]
- Yip, S.; Ferro, C.A.; Stephenson, D.B.; Hawkins, E. A simple, coherent framework for partitioning uncertainty in climate predictions. J. Clim. 2011, 24, 4634–4643. [Google Scholar] [CrossRef]
- Lovenduski, N.S.; McKinley, G.A.; Fay, A.R.; Lindsay, K.; Long, M.C. Partitioning uncertainty in ocean carbon uptake projections: Internal variability, emission scenario, and model structure. Glob. Biogeochem. Cycles 2016, 30, 1276–1287. [Google Scholar] [CrossRef]
- Guo, H.; Chen, S.; Bao, A.; Behrangi, A.; Hong, Y.; Ndayisaba, F.; Hu, J.; Stepanian, P.M. Early assessment of integrated multi-satellite retrievals for global precipitation measurement over China. Atmos. Res. 2016, 176, 121–133. [Google Scholar] [CrossRef]
- Wȩglarczyk, S. The interdependence and applicability of some statistical quality measures for hydrological models. J. Hydrol. 1998, 206, 98–103. [Google Scholar] [CrossRef]
- Xiong, L.; Wan, M.; Wei, X.; O’Connor, K.M. Indices for assessing the prediction bounds of hydrological models and application by generalised likelihood uncertainty estimation/Indices pour évaluer les bornes de prévision de modèles hydrologiques et mise en œuvre pour une estimation d’incertitude par vraisemblance généralisée. Hydrol. Sci. J. 2009, 54, 852–871. [Google Scholar]
- Tang, G.; Li, Z.; Xue, X.; Hu, Q.; Yong, B.; Hong, Y. A study of substitutability of TRMM remote sensing precipitation for gauge-based observation in Ganjiang River basin. Adv. Water Sci. 2015, 26, 340–346. [Google Scholar]
- Jiang, S.; Zhang, Z.; Huang, Y.; Chen, X.; Chen, S. Evaluating the TRMM Multisatellite Precipitation Analysis for Extreme Precipitation and Streamflow in Ganjiang River Basin, China. Adv. Meteorol. 2017, 2017, 2902493. [Google Scholar] [CrossRef]
- Tian, Y.; Booij, M.J.; Xu, Y. Uncertainty in high and low flows due to model structure and parameter errors. Stoch. Environ. Res. Risk Access. 2014, 28, 319–332. [Google Scholar] [CrossRef]
- Zeng, Q.; Chen, H.; Xu, C.; Jie, M.; Hou, Y. Feasibility and uncertainty of using conceptual rainfall-runoff models in design flood estimation. Hydrol. Res. 2016, 47, 701–717. [Google Scholar] [CrossRef]


| Symbol | Description | Numerical Range | Unit | |
|---|---|---|---|---|
| GR | X1 | Production store capacity | 100–1400 | mm |
| X2 | Intercatchment exchange coefficient | −4–4 | mm/d | |
| X3 | Routing store capacity | 0–500 | mm | |
| X4 | Unit hydrograph time constant | 0–10 | d | |
| X5 | Intercatchment exchange threshold | −4–4 | – | |
| X6 | Coefficient for emptying exponential store | 0–20 | mm | |
| CREST | Ksat | The soil saturate hydraulic conductivity | 10–3000 | mm/d |
| WM | The mean water capacity | 80–200 | mm | |
| B | The exponent of the variable infiltration curve | 0.05–1.5 | – | |
| IM | Impervious area ratio | 0–0.2 | – | |
| KE | The factor to convert the potential evapotranspiration to local actual | 0.1–1.5 | – | |
| coeM | Overland runoff velocity coefficient | 1.0–150 | – | |
| expM | Overland flow speed exponent | 0.1–2.0 | – | |
| coeR | Multiplier used to convert overland flow speed to channel flow speed | 1.0–3.0 | – | |
| coeS | Multiplier used to convert overland flow speed to interflow speed | 0.001–1.0 | – | |
| KS | Overland reservoir discharge parameter | 0–1.0 | – | |
| KI | Interflow reservoir discharge parameter | 0–1.0 | – |
| Sources of Uncertainty | Difference/Variance | Expression |
|---|---|---|
| Input from precipitation (I) | Difference | |
| Variance | ||
| Parameter set (P) | Difference | |
| Variance | ||
| Model structure (S) | Difference | |
| Variance | ||
| Interaction between input and parameter (IP) | Difference | |
| Variance | ||
| Interaction between input and structure (IS) | Difference | |
| Variance | ||
| Interaction between parameter and structure (PS) | Difference | |
| Variance | ||
| Residual error (v) | Difference | |
| Variance |
| Gauge | 3B42RTv7 | 3B42v7 | |||||||
|---|---|---|---|---|---|---|---|---|---|
| NSE | r | Bias (%) | NSE | r | Bias (%) | NSE | r | Bias (%) | |
| GR4J | 0.82 | 0.91 | 0.66 | 0.61 | 0.78 | −0.13 | 0.75 | 0.87 | −2.16 |
| GR5J | 0.81 | 0.91 | −6.58 | 0.66 | 0.82 | −6.04 | 0.76 | 0.88 | −7.03 |
| GR6J | 0.83 | 0.91 | −6.53 | 0.67 | 0.82 | −6.84 | 0.77 | 0.88 | −7.30 |
| CREST v1 | 0.86 | 0.93 | −2.49 | 0.68 | 0.83 | −3.83 | 0.74 | 0.86 | −1.57 |
| CREST v2 | 0.86 | 0.93 | −2.49 | 0.49 | 0.75 | −3.83 | 0.72 | 0.85 | −1.98 |
| GR | CREST | |||||
|---|---|---|---|---|---|---|
| CR (%) | B (mm) | D (mm) | CR (%) | B (mm) | D (mm) | |
| Gauge | 58.97 | 38.47 | 20.28 | 81.41 | 16.91 | 6.94 |
| 3B42RTv7 | 71.79 | 52.42 | 20.49 | 47.44 | 20.87 | 15.84 |
| 3B42v7 | 63.46 | 24.76 | 12.05 | 77.56 | 20.63 | 8.53 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ma, Q.; Xiong, L.; Liu, D.; Xu, C.-Y.; Guo, S. Evaluating the Temporal Dynamics of Uncertainty Contribution from Satellite Precipitation Input in Rainfall-Runoff Modeling Using the Variance Decomposition Method. Remote Sens. 2018, 10, 1876. https://doi.org/10.3390/rs10121876
Ma Q, Xiong L, Liu D, Xu C-Y, Guo S. Evaluating the Temporal Dynamics of Uncertainty Contribution from Satellite Precipitation Input in Rainfall-Runoff Modeling Using the Variance Decomposition Method. Remote Sensing. 2018; 10(12):1876. https://doi.org/10.3390/rs10121876
Chicago/Turabian StyleMa, Qiumei, Lihua Xiong, Dedi Liu, Chong-Yu Xu, and Shenglian Guo. 2018. "Evaluating the Temporal Dynamics of Uncertainty Contribution from Satellite Precipitation Input in Rainfall-Runoff Modeling Using the Variance Decomposition Method" Remote Sensing 10, no. 12: 1876. https://doi.org/10.3390/rs10121876
APA StyleMa, Q., Xiong, L., Liu, D., Xu, C.-Y., & Guo, S. (2018). Evaluating the Temporal Dynamics of Uncertainty Contribution from Satellite Precipitation Input in Rainfall-Runoff Modeling Using the Variance Decomposition Method. Remote Sensing, 10(12), 1876. https://doi.org/10.3390/rs10121876









