Physically-Based Retrieval of Canopy Equivalent Water Thickness Using Hyperspectral Data
Abstract
:1. Introduction
2. Materials
2.1. Munich-North-Isar Test Site
2.1.1. Biomass Sampling and Water Content Determination
2.1.2. Spectroscopic Measurements
2.2. Leaf Optical Data
2.3. Radiative Transfer Models and Look-Up Tables
3. Methods
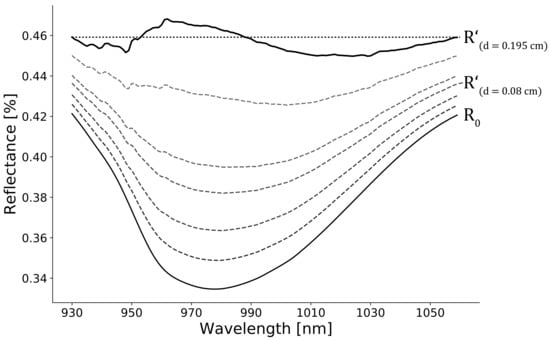
3.1. The Beer-Lambert Law and Retrieval Method Development
3.2. Global Sensitivity Analysis
3.3. Using PROSPECT for Calibration of the PWR Model
4. Results
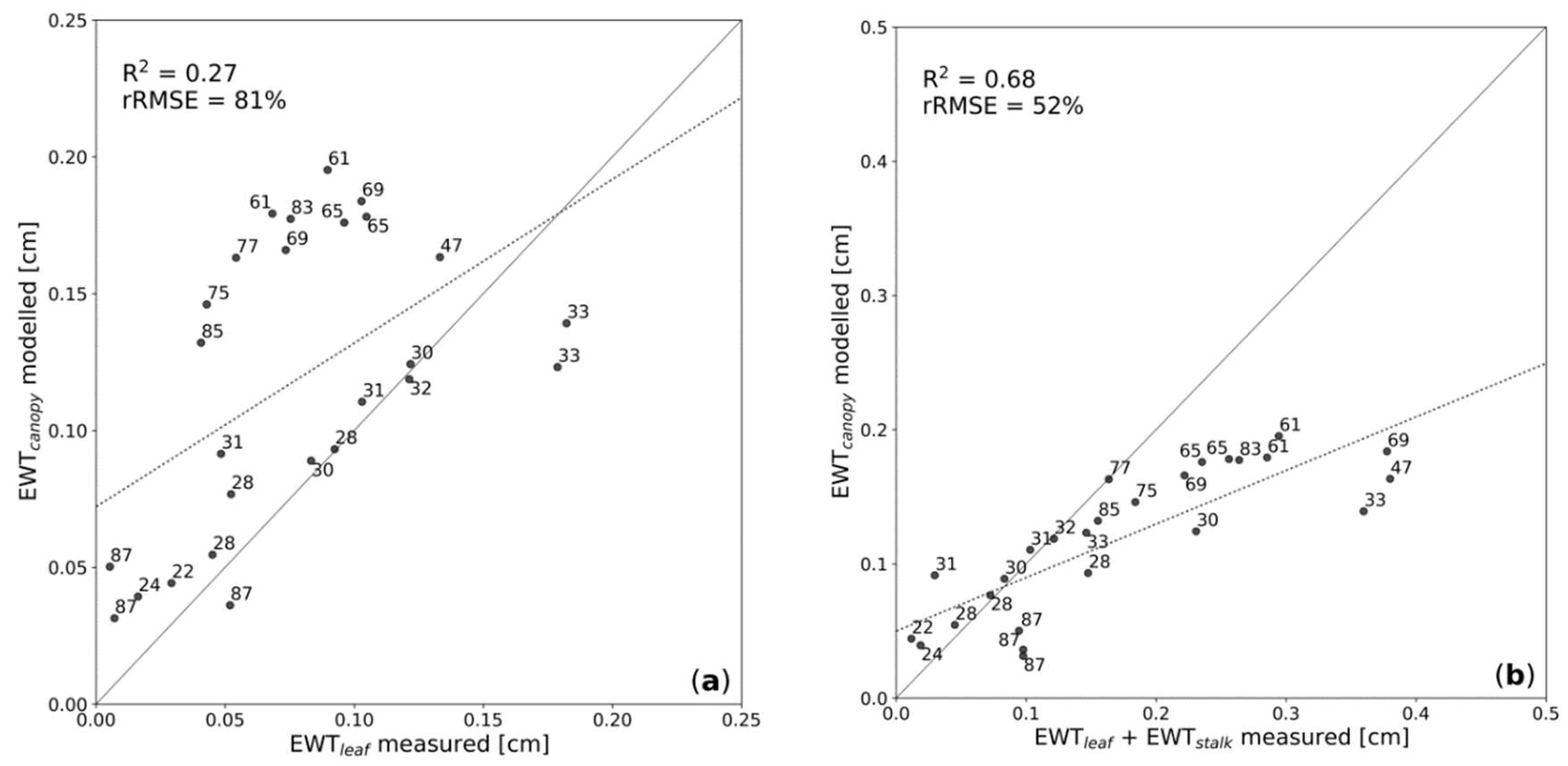
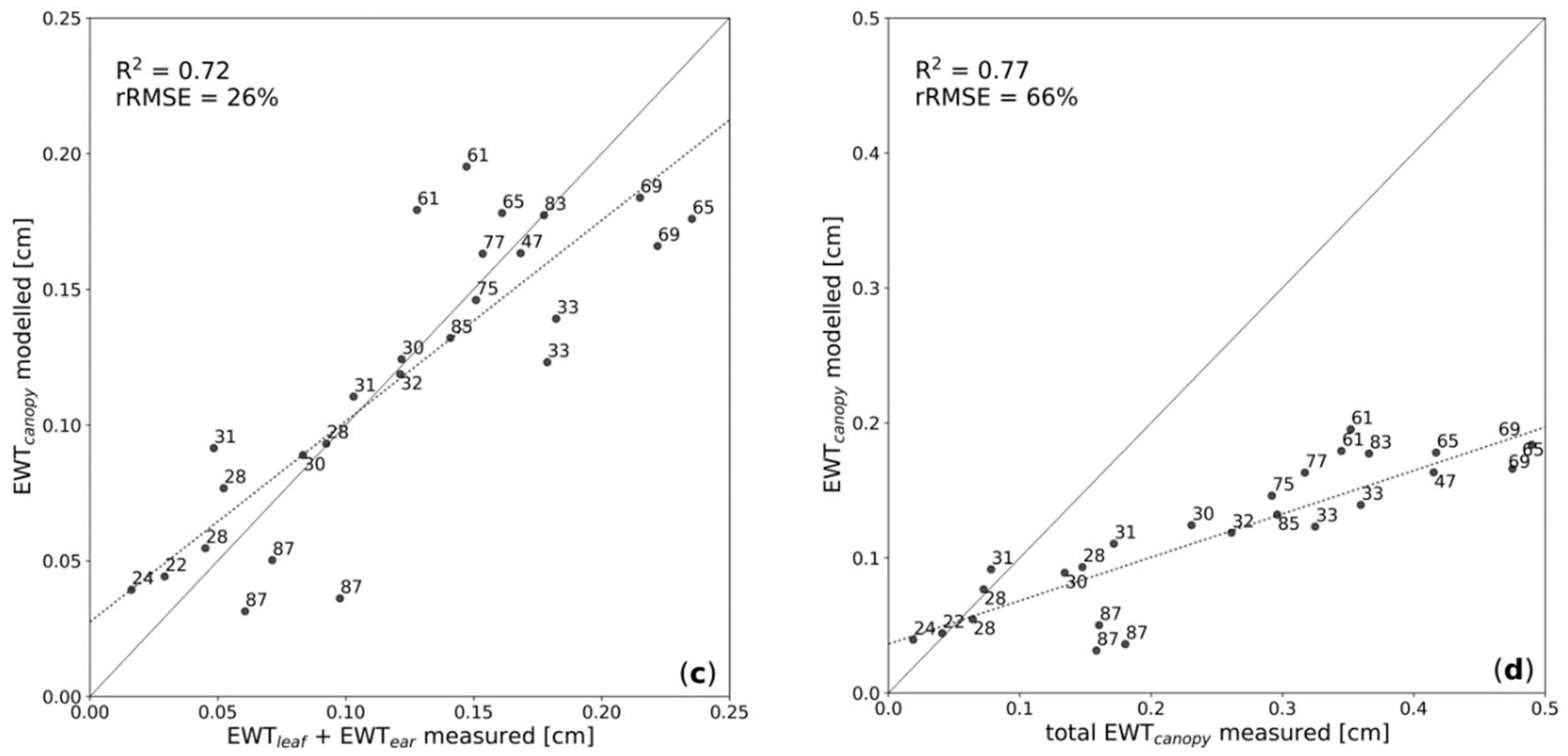
4.1. Winter Wheat Data
4.2. Corn Data
5. Discussion
5.1. Inversion of the Beer-Lambert Law for Water Content Retrieval
5.2. Dependency of Canopy Water Detection on Canopy Structure
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Running, S.W.; Gower, S. Forest-BGC, a general model of forest ecosystem processes for regional applications. Ii. Dynamic carbon allocation and nitrogen budgets. Tree Physiol. 1991, 9, 147–160. [Google Scholar] [CrossRef] [PubMed]
- Running, S.W.; Nemani, R.R. Regional hydrologic and carbon balance responses of forests resulting from potential climate change. Clim. Chang. 1991, 19, 349–368. [Google Scholar] [CrossRef]
- Vohland, M. Using imaging and non-imaging spectroradiometer data for the remote detection of vegetation water content. J. Appl. Remote Sens. 2008, 2, 023520. [Google Scholar] [CrossRef]
- Hank, T.; Bach, H.; Mauser, W. Using a remote sensing-supported hydro-agroecological model for field-scale simulation of heterogeneous crop growth and yield: Application for wheat in central Europe. Remote Sens. 2015, 7, 3934–3965. [Google Scholar] [CrossRef]
- Clevers, J.G.P.W.; Kooistra, L.; Schaepman, M.E. Estimating canopy water content using hyperspectral remote sensing data. Int. J. Appl. Earth Obs. Geoinf. 2010, 12, 119–125. [Google Scholar] [CrossRef]
- Peñuelas, J.; Filella, I.; Biel, C.; Serrano, L.; Savé, R. The reflectance at the 950–970 nm region as an indicator of plant water status. Int. J. Remote Sens. 1993, 14, 1887–1905. [Google Scholar] [CrossRef]
- Peñuelas, J.; Pinol, J.; Ogaya, R.; Filella, I. Estimation of plant water concentration by the reflectance water index wi (r900/r970). Int. J. Remote Sens. 1997, 18, 2869–2875. [Google Scholar] [CrossRef]
- Hank, T.B.; Berger, K.; Bach, H.; Clevers, J.G.P.W.; Gitelson, A.; Zarco-Tejada, P.; Mauser, W. Spaceborne imaging spectroscopy for sustainable agriculture: Contributions and challenges. Surv. Geophys. 2018. [Google Scholar] [CrossRef]
- Tucker, C.J. Remote sensing of leaf water content in the near infrared. Remote Sens. Environ. 1980, 10, 23–32. [Google Scholar] [CrossRef]
- Danson, F.M.; Steven, M.D.; Malthus, T.J.; Clark, J.A. High-spectral resolution data for determining leaf water content. Int. J. Remote Sens. 1992, 13, 461–470. [Google Scholar] [CrossRef]
- Kou, L.; Labrie, D.; Chylek, P. Refractive indices of water and ice in the 0.65- to 2.5-μm spectral range. Appl. Opt. 1993, 32, 3531–3540. [Google Scholar] [CrossRef] [PubMed]
- Hardisky, M.; Klemas, V.; Smart, R.M. The influence of soil salinity, growth form, and leaf moisture on the spectral radiance of spartina alterniflora canopies. Photogramm. Eng. Remote Sens. 1983, 49, 77–83. [Google Scholar]
- Hunt, E.R.; Rock, B.N.; Nobel, P.S. Measurement of leaf relative water content by infrared reflectance. Remote Sens. Environ. 1987, 22, 429–435. [Google Scholar] [CrossRef]
- Hunt, E.R.; Rock, B.N. Detection of changes in leaf water content using near- and middle-infrared reflectances. Remote Sens. Environ. 1989, 30, 43–54. [Google Scholar]
- Gao, B.-C. NDWI—A normalized difference water index for remote sensing of vegetation liquid water from space. Remote Sens. Environ. 1996, 58, 257–266. [Google Scholar] [CrossRef]
- Datt, B. Remote sensing of water content in eucalyptus leaves. Aust. J. Bot. 1999, 47, 909–923. [Google Scholar] [CrossRef]
- Jacquemoud, S.; Verhoef, W.; Baret, F.; Bacour, C.; Zarco-Tejada, P.J.; Asner, G.P.; François, C.; Ustin, S.L. Prospect+SAIL models: A review of use for vegetation characterization. Remote Sens. Environ. 2009, 113, S56–S66. [Google Scholar] [CrossRef]
- Lillesaeter, O. Spectral reflectance of partly transmitting leaves: Laboratory measurements and mathematical modeling. Remote Sens. Environ. 1982, 12, 247–254. [Google Scholar] [CrossRef]
- Newton, J.E.; Blackman, G.E. The penetration of solar radiation through leaf canopies of different structure. Ann. Bot. 1970, 34, 329–348. [Google Scholar] [CrossRef]
- Bull, C.R. Wavelength selection for near-infrared reflectance moisture meters. J. Agric. Eng. Res. 1991, 49, 113–125. [Google Scholar] [CrossRef]
- Sims, D.A.; Gamon, J.A. Estimation of vegetation water content and photosynthetic tissue area from spectral reflectance: A comparison of indices based on liquid water and chlorophyll absorption features. Remote Sens. Environ. 2003, 84, 526–537. [Google Scholar] [CrossRef]
- Ghulam, A.; Li, Z.-L.; Qin, Q.; Yimit, H.; Wang, J. Estimating crop water stress with ETM+ NIR and SWIR data. Agric. For. Meteorol. 2008, 148, 1679–1695. [Google Scholar] [CrossRef]
- Clevers, J.G.P.W.; Kooistra, L.; Schaepman, M.E. Using spectral information from the NIR water absorption features for the retrieval of canopy water content. Int. J. Appl. Earth Obs. Geoinf. 2008, 10, 388–397. [Google Scholar] [CrossRef]
- Cernicharo, J.; Verger, A.; Camacho, F. Empirical and physical estimation of canopy water content from CHRIS/PROBA data. Remote Sens. 2013, 5, 5265. [Google Scholar] [CrossRef]
- Verrelst, J.; Camps-Valls, G.; Muñoz-Marí, J.; Rivera, J.P.; Veroustraete, F.; Clevers, J.G.P.W.; Moreno, J. Optical remote sensing and the retrieval of terrestrial vegetation bio-geophysical properties—A review. ISPRS J. Photogramm. Remote Sens. 2015, 108, 273–290. [Google Scholar] [CrossRef]
- Ceccato, P.; Flasse, S.; Tarantola, S.; Jacquemoud, S.; Grégoire, J.-M. Detecting vegetation leaf water content using reflectance in the optical domain. Remote Sens. Environ. 2001, 77, 22–33. [Google Scholar] [CrossRef]
- Zarco-Tejada, P.J.; Rueda, C.A.; Ustin, S.L. Water content estimation in vegetation with MODIS reflectance data and model inversion methods. Remote Sens. Environ. 2003, 85, 109–124. [Google Scholar] [CrossRef]
- Yilmaz, M.T.; Hunt, E.R.; Jackson, T.J. Remote sensing of vegetation water content from equivalent water thickness using satellite imagery. Remote Sens. Environ. 2008, 112, 2514–2522. [Google Scholar] [CrossRef]
- Baret, F.; Guyot, G. Potentials and limits of vegetation indices for LAI and APAR assessment. Remote Sens. Environ. 1991, 35, 161–173. [Google Scholar] [CrossRef]
- Houborg, R.; Soegaard, H.; Boegh, E. Combining vegetation index and model inversion methods for the extraction of key vegetation biophysical parameters using terra and aqua MODIS reflectance data. Remote Sens. Environ. 2007, 106, 39–58. [Google Scholar] [CrossRef]
- Verrelst, J.; Malenovský, Z.; Van der Tol, C.; Camps-Valls, G.; Gastellu-Etchegorry, J.-P.; Lewis, P.; North, P.; Moreno, J. Quantifying vegetation biophysical variables from imaging spectroscopy data: A review on retrieval methods. Surv. Geophys. 2018. [Google Scholar] [CrossRef]
- Jacquemoud, S.; Bacour, C.; Poilvé, H.; Frangi, J.P. Comparison of four radiative transfer models to simulate plant canopies reflectance: Direct and inverse mode. Remote Sens. Environ. 2000, 74, 471–481. [Google Scholar] [CrossRef]
- Atzberger, C.; Richter, K. Spatially constrained inversion of radiative transfer models for improved LAI mapping from future sentinel-2 imagery. Remote Sens. Environ. 2012, 120, 208–218. [Google Scholar] [CrossRef]
- Labate, D.; Ceccherini, M.; Cisbani, A.; De Cosmo, V.; Galeazzi, C.; Giunti, L.; Melozzi, M.; Pieraccini, S.; Stagi, M. The PRISMA payload optomechanical design, a high performance instrument for a new hyperspectral mission. Acta Astronaut. 2009, 65, 1429–1436. [Google Scholar] [CrossRef]
- Lee, C.M.; Cable, M.L.; Hook, S.J.; Green, R.O.; Ustin, S.L.; Mandl, D.J.; Middleton, E.M. An introduction to the NASA hyperspectral InfraRed imager (HyspIRI) mission and preparatory activities. Remote Sens. Environ. 2015, 167, 6–19. [Google Scholar] [CrossRef]
- Feingersh, T.; Eyal, B.D. SHALOM—A commercial hyperspectral space mission. In Optical Payloads for Space Missions; Qian, S.-E., Ed.; John Wiley & Sons: Hoboken, NJ, USA, 2015. [Google Scholar]
- Nieke, J.; Rast, M. Towards the copernicus hyperspectral imaging mission for the environment (CHIME). In Proceedings of the IGGARS 2018, Valencia, Spain, 22–27 July 2018; pp. 157–159. [Google Scholar]
- Guanter, L.; Kaufmann, H.; Segl, K.; Foerster, S.; Rogass, C.; Chabrillat, S.; Kuester, T.; Hollstein, A.; Rossner, G.; Chlebek, C.; et al. The enmap spaceborne imaging spectroscopy mission for earth observation. Remote Sens. 2015, 7, 8830–8857. [Google Scholar] [CrossRef] [Green Version]
- Green, R.O.; Conel, J.E.; Margolis, J.; Bruegge, J.C.; Hoover, L.G. An inversion algorithm for retrieval of atmospheric and leaf water absorption from AVIRIS radiance with compensation for atmospheric scattering. In Third Airborne Visible/Infrared Imaging Spectrometer (AVIRIS) Workshop; Green, O.R., Ed.; NASA: Pasadena, CA, USA, 1991; pp. 51–61. [Google Scholar]
- Green, R.O.; Conel, J.E.; Roberts, D.A. Estimation of aerosol optical depth, pressure elevation, water vapor, and calculation of apparent surface reflectance from radiance measured by the airborne visible/infrared imaging spectrometer (AVIRIS). In Proceedings of the Summaries of the 4th Annual JPL Airborne Geoscience Workshop, AVJRIS Workshop, Washington, DC, USA, 25–29 October 1993; Volume 1937, pp. 73–76. [Google Scholar]
- Ustin, S.L.; Riaño, D.; Hunt, E.R. Estimating canopy water content from spectroscopy. Isr. J. Plant Sci. 2012, 60, 9–23. [Google Scholar] [CrossRef]
- Hunt, E.R.; Ustin, S.L.; Riaño, D. Remote sensing of leaf, canopy, and vegetation water contents for satellite environmental data records. In Satellite-Based Applications on Climate Change; Qu, J., Powell, A., Sivakumar, M.V.K., Eds.; Springer: Dordrecht, The Netherlands, 2013; pp. 335–357. [Google Scholar]
- Knipling, E.B. Physical and physiological basis for the reflectance of visible and near-infrared radiation from vegetation. Remote Sens. Environ. 1970, 1, 155–159. [Google Scholar] [CrossRef]
- Carter, G.A. Primary and secondary effects of water content on the spectral reflectance of leaves. Am. J. Bot. 1991, 78, 916–924. [Google Scholar] [CrossRef]
- Gao, B.-C.; Goetz, A.F.H. Column atmospheric water vapor and vegetation liquid water retrievals from airborne imaging spectrometer data. J. Geophys. Res. Atmos. 1990, 95, 3549–3564. [Google Scholar] [CrossRef]
- Gao, B.-C.; Goetz, A.F.H. Retrieval of equivalent water thickness and information related to biochemical components of vegetation canopies from AVIRIS data. Remote Sens. Environ. 1995, 52, 155–162. [Google Scholar] [CrossRef]
- Green, R.O.; Painter, T.H.; Roberts, D.A.; Dozier, J. Measuring the expressed abundance of the three phases of water with an imaging spectrometer over melting snow. Water Resour. Res. 2006, 42. [Google Scholar] [CrossRef] [Green Version]
- Thompson, D.R.; Gao, B.-C.; Green, R.O.; Roberts, D.A.; Dennison, P.E.; Lundeen, S.R. Atmospheric correction for global mapping spectroscopy: ATREM advances for the HyspIRI preparatory campaign. Remote Sens. Environ. 2015, 167, 64–77. [Google Scholar] [CrossRef]
- Yi, Q.; Wang, F.; Bao, A.; Jiapaer, G. Leaf and canopy water content estimation in cotton using hyperspectral indices and radiative transfer models. Int. J. Appl. Earth Obs. Geoinf. 2014, 33, 67–75. [Google Scholar] [CrossRef]
- Pasqualotto, N.; Delegido, J.; Van Wittenberghe, S.; Verrelst, J.; Rivera, J.P.; Moreno, J. Retrieval of canopy water content of different crop types with two new hyperspectral indices: Water absorption area index and depth water index. Int. J. Appl. Earth Obs. Geoinf. 2018, 67, 69–78. [Google Scholar] [CrossRef]
- Bach, H. Die Bestimmung Hydrologischer und Landwirtschaftlicher Oberflächenparameter aus Hyperspektralen Fernerkundungsdaten; Geobuch-Verlag: München, Germany, 1995. [Google Scholar]
- Ustin, S.L.; Roberts, D.A.; Pinzón, J.; Jacquemoud, S.; Gardner, M.; Scheer, G.; Castañeda, C.M.; Palacios-Orueta, A. Estimating canopy water content of chaparral shrubs using optical methods. Remote Sens. Environ. 1998, 65, 280–291. [Google Scholar] [CrossRef]
- Champagne, C.M.; Staenz, K.; Bannari, A.; McNairn, H.; Deguise, J.-C. Validation of a hyperspectral curve-fitting model for the estimation of plant water content of agricultural canopies. Remote Sens. Environ. 2003, 87, 148–160. [Google Scholar] [CrossRef]
- Meier, U. Growth Stages of Mono- and Dicotyledonous Plants: BBCH Monograph; Open Agrar Repositorium: Quedlinburg, Germany, 2018. [Google Scholar]
- Hosgood, B.; Jacquemoud, S.; Andreoli, J.; Verdebout, A.; Pedrini, A.; Schmuck, G. Leaf Optical Properties Experiment 93 (LOPEX93); European Commission: Brussels, Belgium, 1995. [Google Scholar]
- Jacquemoud, S.; Bidel, C.; Pavan, F.G. Angers Leaf Optical Properties Database. 2003. Available online: http://ecosis.org (accessed on 14 November 2017).
- Jacquemoud, S.; Baret, F. Prospect: A model of leaf optical properties spectra. Remote Sens. Environ. 1990, 34, 75–91. [Google Scholar] [CrossRef]
- Verhoef, W. Light scattering by leaf layers with application to canopy reflectance modeling: The sail model. Remote Sens. Environ. 1984, 16, 125–141. [Google Scholar] [CrossRef]
- Verhoef, W.; Bach, H. Coupled soil–leaf-canopy and atmosphere radiative transfer modeling to simulate hyperspectral multi-angular surface reflectance and TOA radiance data. Remote Sens. Environ. 2007, 109, 166–182. [Google Scholar] [CrossRef]
- Féret, J.B.; Gitelson, A.A.; Noble, S.D.; Jacquemoud, S. Prospect-D: Towards modeling leaf optical properties through a complete lifecycle. Remote Sens. Environ. 2017, 193, 204–215. [Google Scholar] [CrossRef]
- Feret, J.-B.; François, C.; Asner, G.P.; Gitelson, A.A.; Martin, R.E.; Bidel, L.P.R.; Ustin, S.L.; le Maire, G.; Jacquemoud, S. Prospect-4 and 5: Advances in the leaf optical properties model separating photosynthetic pigments. Remote Sens. Environ. 2008, 112, 3030–3043. [Google Scholar] [CrossRef]
- Cannavó, F. Sensitivity analysis for volcanic source modeling quality assessment and model selection. Comput. Geosci. 2012, 44, 52–59. [Google Scholar] [CrossRef]
- Wang, Z.; Skidmore, A.K.; Darvishzadeh, R.; Wang, T. Mapping forest canopy nitrogen content by inversion of coupled leaf-canopy radiative transfer models from airborne hyperspectral imagery. Agric. For. Meteorol. 2018, 253–254, 247–260. [Google Scholar] [CrossRef]
- Zhang, Q.; Li, Q.; Zhang, G. Scattering impact analysis and correction for leaf biochemical parameter estimation using vis-NIR spectroscopy. Spectroscopy 2011, 26, 28–39. [Google Scholar]
- Dorigo, W.A. Improving the robustness of cotton status characterisation by radiative transfer model inversion of multi-angular CHRIS/PROBA data. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2012, 5, 18–29. [Google Scholar] [CrossRef]
- Zou, X.; Hernandez Clemente, R.; Tammeorg, P.; Lizarazo, C.; Stoddard, F.; Mäkelä, P.; Pellikka, P.; Mõttus, M. Retrieval of leaf chlorophyll content in field crops using narrow-band indices: Effects of leaf area index and leaf mean tilt angle. Int. J. Remote Sens. 2015, 36, 6031–6055. [Google Scholar] [CrossRef]
- Combal, B.; Baret, F.; Weiss, M.; Trubuil, A.; Macé, D.; Pragnère, A.; Myneni, R.; Knyazikhin, Y.; Wang, L. Retrieval of canopy biophysical variables from bidirectional reflectance: Using prior information to solve the ill-posed inverse problem. Remote Sens. Environ. 2003, 84, 1–15. [Google Scholar] [CrossRef]
- Kuester, T.; Spengler, D. Structural and spectral analysis of cereal canopy reflectance and reflectance anisotropy. Remote Sens. 2018, 10, 1767. [Google Scholar] [CrossRef]
- Serrano, L.; Ustin, S.L.; Roberts, D.A.; Gamon, J.A.; Peñuelas, J. Deriving water content of chaparral vegetation from AVIRIS data. Remote Sens. Environ. 2000, 74, 570–581. [Google Scholar] [CrossRef]
- Trombetti, M.; Riaño, D.; Rubio, M.A.; Cheng, Y.B.; Ustin, S.L. Multi-temporal vegetation canopy water content retrieval and interpretation using artificial neural networks for the continental USA. Remote Sens. Environ. 2008, 112, 203–215. [Google Scholar] [CrossRef]
- Berger, K.; Hank, T.; Vuolo, F.; Mauser, W.; D’Urso, G. Optimal exploitation of the sentinel-2 spectral capabilities for crop leaf area index mapping. Remote Sens. 2012, 4, 561–582. [Google Scholar]
- Richter, K.; Hank, T.B.; Mauser, W.; Atzberger, C. Derivation of biophysical variables from earth observation data: Validation and statistical measures. J. Appl. Remote Sens. 2012, 6, 063557. [Google Scholar] [CrossRef]
- Transon, J.; d’Andrimont, R.; Maugnard, A.; Defourny, P. Survey of hyperspectral earth observation applications from space in the sentinel-2 context. Remote Sens. 2018, 10, 157. [Google Scholar] [CrossRef]
- Verrelst, J.; Rivera, J.P.; Gitelson, A.; Delegido, J.; Moreno, J.; Camps-Valls, G. Spectral band selection for vegetation properties retrieval using Gaussian processes regression. Int. J. Appl. Earth Obs. Geoinf. 2016, 52, 554–567. [Google Scholar] [CrossRef]
- Danner, M.; Berger, K.; Wocher, M.; Mauser, W.; Hank, T. Retrieval of biophysical crop variables from multi-angular canopy spectroscopy. Remote Sens. 2017, 9, 726. [Google Scholar] [CrossRef]
- van der Linden, S.; Rabe, A.; Held, M.; Jakimow, B.; Leitão, P.; Okujeni, A.; Schwieder, M.; Suess, S.; Hostert, P. The EnMAP-Box—A toolbox and application programming interface for EnMAP data processing. Remote Sens. 2015, 7, 11249. [Google Scholar] [CrossRef]








| Crop Type | Coordinates | Sampling Period | No. of Samplings | No. of Spectral Measurements |
|---|---|---|---|---|
| Winter wheat | 48°14′51.46″N 11°42′24.10″E | 10 April–29 July 2015 | 17 | 7 |
| Winter wheat | 48°14′56.70″N 11°43′03.60″E | 29 March–17 July 2017 | 16 | 12 |
| Winter wheat | 48°14′52.27″N 11°42′57.06″E | 04 April–13 July 2018 | 12 | 7 |
| Corn | 48°17′06.56″N 11°42′49.98″E | 8 June–15 September 2017 | 11 | 8 |
| Corn | 48°14′56.70″N 11°43′03.60″E | 25 May–29 August 2018 | 13 | 6 |
| Year | 2015 | 2017 | 2018 | ||
|---|---|---|---|---|---|
| Crop Type | Winter Wheat | Winter Wheat | Corn | Winter Wheat | Corn |
| BBCH range [-] | 22–87 | 25–87 | 30–85 | 28–87 | 32–83 |
| EWTleaf: range [cm] | 0.007–0.179 | 0.005–0.182 | 0.009–0.104 | 0.045–0.121 | 0.095–0.161 |
| mean (std) [cm] | 0.066 (0.058) | 0.082 (0.050) | 0.059 (0.035) | 0.082 (0.027) | 0.132 (0.023) |
| EWTstalk: range [cm] | 0.012–0.256 | 0.003–0.275 | 0.008–0.295 | 0.019–0.268 | 0.252–0.619 |
| mean (std) [cm] | 0.123 (0.084) | 0.144 (0.089) | 0.161 (0.115) | 0.126 (0.099) | 0.472 (0.126) |
| EWTfruit: range [cm] | 0.000–0.100 | 0.000–0.112 | 0.000–0.248 | 0.000–0.148 | 0.000–0.306 |
| mean (std) [cm] | 0.044 (0.045) | 0.045 (0.045) | 0.068 (0.100) | 0.048 (0.068) | 0.171 (0.123) |
| Total EWTcanopy: range [cm] | 0.041–0.417 | 0.019–0.490 | 0.017–0.606 | 0.064–0.503 | 0.347–1.019 |
| mean (std) [cm] | 0.233 (0.141) | 0.271 (0.145) | 0.289 (0.221) | 0.256 (0.170) | 0.775 (0.227) |
| PROSPECT-D-Parameters | Range | Notation [Unit] | 4SAIL-Parameters | Range | Notation [Unit] |
|---|---|---|---|---|---|
| N | 1.0–3.0 | [-] | LAI | 0.5–8.0 | [m2 m−2] |
| Cab | 55 | [µg cm−2] | ALA | 0–90 | [deg] |
| Cw | 0.0002–0.07 | [g cm−2] | hspot | 0.01–0.5 | [-] |
| Cm | 0.001–0.02 | [g cm−2] | OZA | 0 | [deg] |
| Cbrown | 0.0–1.0 | [-] | SZA | 35–50 | [deg] |
| Car | 15 | [µg cm−2] | rAA | 0 | [deg] |
| Canth | 5 | [µg cm−2] | psoil | 0.0–1.0 | [-] |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wocher, M.; Berger, K.; Danner, M.; Mauser, W.; Hank, T. Physically-Based Retrieval of Canopy Equivalent Water Thickness Using Hyperspectral Data. Remote Sens. 2018, 10, 1924. https://doi.org/10.3390/rs10121924
Wocher M, Berger K, Danner M, Mauser W, Hank T. Physically-Based Retrieval of Canopy Equivalent Water Thickness Using Hyperspectral Data. Remote Sensing. 2018; 10(12):1924. https://doi.org/10.3390/rs10121924
Chicago/Turabian StyleWocher, Matthias, Katja Berger, Martin Danner, Wolfram Mauser, and Tobias Hank. 2018. "Physically-Based Retrieval of Canopy Equivalent Water Thickness Using Hyperspectral Data" Remote Sensing 10, no. 12: 1924. https://doi.org/10.3390/rs10121924
APA StyleWocher, M., Berger, K., Danner, M., Mauser, W., & Hank, T. (2018). Physically-Based Retrieval of Canopy Equivalent Water Thickness Using Hyperspectral Data. Remote Sensing, 10(12), 1924. https://doi.org/10.3390/rs10121924