Abstract
We describe an approach (ESMAP; Evaporation–Soil Moisture Active Passive) to estimate direct evaporation from soil, Esoil, by combining remotely-sensed soil drying rates with model calculations of the vertical fluxes in and out of the surface soil layer. Improved knowledge of Esoil can serve as a constraint in how total evapotranspiration is partitioned. The soil drying rates used here are based on SMAP data, but the method could be applied to data from other sensors. We present results corresponding to ten SMAP pixels in North America to evaluate the method. The ESMAP method was applied to intervals between successive SMAP overpasses with limited precipitation (<2 mm) to avoid uncertainty associated with precipitation, infiltration, and runoff. We used the Hydrus 1-D model to calculate the flux of water across the bottom boundary of the 0 to 50 mm soil layer sensed by SMAP, qbot. During dry intervals, qbot typically transfers water upwards into the surface soil layer from below, usually <0.5 mm day−1. Based on a standard formulation, transpiration from the surface soil layer, ET_s, is usually < 0.1 mm day−1, and, thus, generally not an important flux. Soil drying rates (converted to equivalent water thickness) are typically between 0 and 1 mm day−1. Evaporation is almost always greater than soil drying rates because qbot is typically a source of water to the surface soil and ET_s is negligible. Evaporation is typically between 0 and 1.5 mm day−1, with the highest values following rainfall. Soil evaporation summed over SMAP overpass intervals with precipitation <2 mm (60% of days) accounts for 15% of total precipitation. If evaporation rates are similar during overpasses with substantial precipitation, then the total evaporation flux would account for ~25% of precipitation. ESMAP could be used over spatially continuous domains to provide constraints on Esoil, but model-based Esoil would be required during intervals with substantial precipitation.
1. Introduction
Evapotranspiration (ET) and precipitation represent the two largest terms in the terrestrial water balance [1] and, hence, are fundamental processes driving the global water, energy, and carbon cycles. Despite recent improvements in estimating precipitation from space, for example, the Global Precipitation Measurement (GPM) mission [2], our ability to observe the return-flow of moisture (on timescales of days to years) from the land to the atmosphere is still poor [3,4]. The flux of water vapor from the land surface to the atmosphere is the sum of three components: evaporation from the soil surface, Esoil; transpiration from vegetation, ET; and evaporation of intercepted water from vegetation canopies, Ec. At present, we lack the in-situ observations needed to study the processes that control the three component fluxes at basin to global scales. Nearly all ground-based and remotely sensed observations represent the total ET flux. Estimates of the individual components are subject to considerable uncertainties. Many land surface models (LSMs) calculate the soil evaporation, transpiration, and canopy evaporation fluxes separately. However, the simulated component fluxes depend on model structure and parameters, and errors in one flux may be compensated by errors in the other [5]. We consider the potential of using satellite-based soil moisture to monitor evaporation from soil. An evaluation of this methodology at a diverse set of sites across the conterminous U.S. is described here. Our goal is to understand this method’s viability in producing a global observation-based soil evaporation dataset to provide a more complete understanding of the land-to-atmosphere vapor flux.
Many remote sensing methods exist to estimate ET, largely relying on thermal data as a key input to the ET algorithm (e.g., [6,7,8,9]). These algorithms depend upon complex relationships between models, in-situ measurements, and multiple remote sensing products (e.g., [4]). Kalma et al. (2008) [10] summarized 30 published ET validation studies that used flux measurements: the average root mean squared error value was 50 W m−2 (or 1.7 mm day−1 water equivalent). Importantly, this does not provide information specifically about the individual components of ET, only the total ET flux. The exception is for locations or times when transpiration is known to be zero, for example, over bare soil. In these cases, Esoil is equivalent to the total ET flux.
Typical ground-based techniques, for example, the eddy covariance or Bowen Ratio energy balance methods, also provide measurements of the total ET flux. Similar to remotely-sensed data, the ground-based observations only provide specific information about Esoil when transpiration is known to be zero. However, there are several ground-based methods that can provide measurements of Esoil, including: (i) relating soil moisture changes to soil thermal properties (i.e., the soil heat pulse approach, [11,12]), (ii) the use of chambers to measure changes in gas concentrations in a closed volume above the soil surface (e.g., [13]), (iii) repeat weighing of soil in vegetation-free lysimeters or microlysimeters (e.g., [14,15]). Similarly, there are techniques that provide estimates or measurements of transpiration alone, including sap flow [16] and leaf or plant-chamber techniques. These ground-based techniques that measure Esoil and transpiration are labor intensive, and thus cannot be applied at the regional scale or for long-term monitoring.
Without observation-based estimates of how ET is partitioned into the component fluxes, it is not possible to improve the representation of soil evaporation or transpiration in hydrologic models, or the controls exerted by ecosystem type, land cover, and climate. Whereas the total ET simulated by NLDAS models has been validated, there has been no similar effort to evaluate either transpiration or direct evaporation, as datasets do not exist for this purpose. Here we show that Esoil simulated by three of the four NLDAS models is highly inconsistent across models. Given these differences, it is not possible to use evaporation from the NLDAS models for validation. In addition, the NLDAS models do not include irrigation, yet irrigation affects the surface soil moisture and evaporation flux in many regions. This difference complicates the comparison between satellite- and model-based estimates of soil moisture and fluxes [17]. Recently, three remote sensing algorithms were evaluated to understand global ET partitioning [18] finding major differences among components, even with disagreement on which of the three components is the largest. Using the same dataset, Talsma et al. (2018) [19] found notable divergence between the magnitudes of the remotely sensed ET components relative to ground observations, noting the greatest uncertainty for remotely sensed Esoil.
Given the observational limitations that exist, quantifying a single ET component, here Esoil, at landscape to continental scales is challenging, even with a combination of observations, models, and theory (e.g., [20]). Isotope methods can provide long-term (time-invariant) estimates of evaporation and transpiration (e.g., [21]), with the caveat that these methods have been shown to overestimate the ratio of ET to ET [22]. Greater uncertainty in this ratio was later demonstrated [23], with its spatial variation largely dependent upon growing season stage and leaf area index [24]. Commonly, ET partitioning is based on bio-geophysical and LSMs [5,25,26]. These models depend critically on physics assumptions and parameter selection. Therefore, there exists a wide range of simulated partitioning into evaporation and transpiration. Even different versions of the same model can yield very large differences in ET partitioning [5]. These approaches show that the partitioning of ET into soil evaporation and transpiration varies greatly from site to site, depending upon a number of factors including vegetation type, meteorological conditions, and soil texture [27]. For example, the percentage of ET that comes from Esoil can exceed 50% in both dry areas with limited vegetation, and also in very wet systems, such as irrigated crops and wetlands. Improving knowledge of Esoil can serve as a constraint in how total ET is partitioned, aiding in the study of connections between the water and carbon cycles, forecast seasonal water resource availability, and to resolve uncertainties in the coupling of water and biogeochemical models [28,29].
Surface soil drying rates can potentially provide an estimate of Esoil, for conditions when other fluxes in or out of the surface soil are minimal. Several recent studies have used SMAP surface soil moisture data to observe soil drying following rainfall events. Shellito et al. (2016) [30] compared the rate of soil drying observed by SMAP to that from upscaled in-situ observations at thirteen Core Validation Sites (CVS). They found that SMAP dependably records soil dry-down events, but the rate of drying calculated from SMAP was often faster than observed in-situ. The different drying rates were attributed to SMAP’s variable (and often shallower) sensing depth. McColl et al. (2017) [31] reported that less than 14% of precipitation was retained in surface soils three days after rainfall events, based on a global analysis of soil drying from SMAP. Shellito et al. (2018) [32] analyzed the factors that control soil drying, using SMAP and NLDAS-2 Noah data over CONUS. Soil drying was shown to be most rapid for areas with limited vegetation and high potential evapotranspiration (PET). Soil drying rates based on SMAP are typically less than 10% of PET, even within several days after rainfall—the time when evaporation from soil should be greatest. The soil drying rates observed by SMAP are considerably less than observed at smaller scales or over shorter time intervals [33]. This CONUS-wide analysis demonstrated that SMAP drying rates are consistently faster than simulated by Noah, which can partly be explained by the difference between Noah’s surface layer thickness and SMAP’s sensing depth.
Here, we describe how surface soil drying rates determined from passive or active microwave remote sensing can be used to provide a unique estimate of soil evaporation. The approach, which we call ESMAP, combines drying rates from NASA’s SMAP satellite with estimates of the vertical fluxes in or out of the surface soil layer. The soil drying rates used here are based on SMAP soil moisture data, but the method could be applied to data from other passive or active sensors. The ESMAP approach offers an independent estimate of Esoil, referred to in this article as ESMAPsoil, (Appendix A). This estimate could be used to improve and validate existing models at the footprint scale of the remote sensing product. Here, we only present results from a set of locations in North America, although the method is envisioned for use at the continental or global scale. The goals are (1) to describe the ESMAP method; (2) compare the magnitude of the various fluxes that affect the surface-layer water balance, including their uncertainty; (3) describe soil evaporation time series from the sites and compare these to corresponding estimates from two NLDAS models; and (4) consider the limitations and errors associated with the method.
2. Materials and Methods
2.1. Evaporation and Water Balance of the Surface Soil Layer
The water balance equation for the surface soil layer can be written:
where θs is volumetric soil moisture in the surface layer (mm3 mm−3), D is the thickness of the layer (mm), and the terms on the right hand side are fluxes in and out of the surface layer (mm day−1) (Figure 1): I is infiltration, Esoil is evaporation from the surface soil layer, ET_s is transpiration from the surface layer, and qbot is the flux across the bottom boundary of the surface soil layer. We define the thickness of surface soil layer, D, to be equivalent to the SMAP sensing depth (50 mm) [34], noting that this sensing depth does actually vary through time with soil moisture [35]. ET_s is only a fraction of total transpiration (ET), specifically the portion that is due to extraction of soil water by any roots in the top 50 mm of the soil. Most plant roots exist below the surface soil layer [36], and thus a majority of water extraction that supplies transpiration is from depths below 50 mm. We define qbot as positive when water moves from the surface layer to deeper soil and negative when water moves from deeper soil to the surface layer.
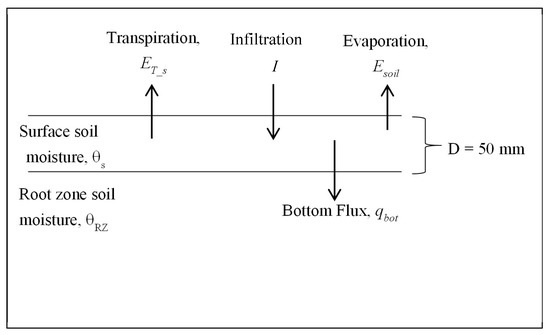
Figure 1.
Fluxes affecting water balance of the surface soil layer (50 mm thick). The transpiration flux, ET_s, only includes water extracted by roots in the surface layer.
Here we use SMAP soil moisture time series to estimate soil evaporation based on the idea that soil evaporation, Esoil, is typically the largest flux in Equation (1), excluding times when infiltration is actively occurring due to precipitation or snowmelt. For any interval when infiltration is zero, ESMAPsoil can be estimated from the water balance equation for the surface layer:
The observed θs time series is used to calculate for intervals defined by successive SMAP overpasses [30]. Therefore, absolute values of soil moisture are not used in the method, only the rate of change in soil moisture. The remaining terms on the right-hand side of Equation (2) are estimated using a combination of auxiliary data and models. We hypothesize that soil drying is dominated by evaporation at most times: thus ESMAPsoil is large compared to ET_s and qbot. For intervals when ESMAPsoil is not the largest flux in Equation (2), the estimate of ESMAPsoil will be largely dependent on the calculation of the other two fluxes, rather than the drying rate measured via SMAP.
The ESMAP approach is analogous to using SMAP as a lysimeter with a sensing scale equivalent to SMAP’s footprint, or 9 km × 9 km for the enhanced SMAP product [37]. When using an actual lysimeter, it is possible to measure Esoil via repeated weighing of the monitored soil volume, as long as the soil volume is kept free of plant roots (ET = 0) and the bottom of the soil volume is closed (qbot = 0) [15]. Alternatively, when the lysimeter volume includes vegetation, the lysimeter provides a measurement of ET. If the SMAP sensing depth was 10’s of cm (100’s of mm, e.g., like P-band AirMOSS; [38]), it would make sense to use SMAP soil moisture to monitor ET (i.e., to include the transpiration component). However, the SMAP sensing depth is only 50 mm, so the sensed soil volume includes only a small fraction of plant roots in most ecosystems [36]. Therefore, it is more practical to use SMAP to estimate Esoil than total ET, although transpiration from the surface (ET_s) must be accounted for. Although other fluxes affecting the surface soil balance must be estimated, ESMAP provides a lysimeter-type approach that can be applied at the global scale, is continuous through time, and provides information at scales relevant to various hydrologic applications.
2.2. Soil Moisture Data and Spatial Support
Here we use data from NASA’s SMAP satellite, but any surface soil time series could be incorporated into the ESMAP approach. SMAP was launched in January 2015 and provides morning and evening (6 AM and 6 PM local time) estimates of θs time, in mm3 mm−3, globally every 1–3 days [34]. Retrievals are estimates of soil moisture based on passive microwave (1.41 GHz) brightness temperature, so the sensing depth is approximately 0–50 mm. We use the “enhanced” level 3 soil moisture data product (SCA-V polarization), version 1, which is available from the National Snow and Ice Data Center. The SMAP radiometer has a native spatial resolution of 36 km, but this product utilizes the Backus-Gilbert optimal interpolation algorithm to post soil moisture retrievals onto the 9 km Equal-Area Scalable Earth grid version 2 (EASE-2) [39]. The enhanced resolution version reveals spatial features not apparent in the 36 km standard product and similarly meets the mission goal of 0.04 mm3 mm−3 unbiased root-mean-squared-error [37]. We use only AM overpasses because the SMAP algorithm assigns one temperature to both the soil and its overlying canopy, a condition that is best met in the morning hours [34,40]. We exclude data that have been flagged for uncertain quality due to dense vegetation (>5 kg m−2), mountainous terrain (>3° slope standard deviation), and >5% of the sensing area comprising frozen ground, snow, ice, precipitation, or static water. Our study utilizes SMAP, NLDAS-2, and NDVI data from the first 30 months of SMAP’s data stream: 1 April 2015, through 17 October 2017.
The ESMAP approach provides an estimate of Esoil, referred to as ESMAPsoil, that is representative of the sensing footprint of the satellite. For example, the initial SMAP passive soil moisture product has a spatial resolution of 36 km × 36 km [41], so these data would have yielded ESMAPsoil at this scale. The enhanced product [42] used here has a resolution of 9 km × 9 km, and thus the resulting ESMAPsoil time series is an estimate at this scale. The auxiliary data and models required to estimate the remaining components of the surface soil balance (Equation (2)) should represent a similar spatial scale.
The analysis presented here is based on SMAP data, auxiliary remote sensing and NLDAS products for ten locations in North America. Eight of the sites are official CVSs [43] and two (Viara and Tonzi Ranch) are not (Table 1). Less than 10% of the SMAP sensing footprint at each site is affected by irrigation. This greatly simplifies the comparison to evaporation simulated by NLDAS models. The NLDAS models do not represent irrigation, yet irrigation affects remotely-sensed soil moisture [44], and thus drying rates derived from these data. Any CONUS-wide comparison of ESMAP to NLDAS must consider this fundamental difference, otherwise, the source of any differences or inconsistencies cannot be identified. SMAP data from these pixel locations was used because SMAP performance has already been evaluated at eight of the ten sites, demonstrating achievement of mission goals (unbiased RMSE < 0.04 mm3 mm−3, [37]). The two California sites (Viara and Tonzi Ranch, non CVS) were included because of the long seasonal drought that occurs at each summer, providing a broader range of climate conditions to evaluate ESMAP. One strength of data from a satellite such as SMAP is spatial continuity, which would allow the ESMAP approach to be applied at the continental or the global scale. However, the site-focused analysis presented here is needed to first evaluate and identify the limitations and errors associated with the ESMAP method, prior to application at larger spatial scales.

Table 1.
Site descriptions for locations used, including: site name, latitude, longitude, vegetation coverage type and dominant soil type from NLDAS soil texture information.
2.3. Precipitation
The ESMAP approach cannot be applied to intervals between successive SMAP overpasses during which precipitation yields substantial infiltration (Figure 2). During these intervals, the plant canopy traps some precipitation, leading to canopy evaporation, Ec. Some portion of the precipitation that falls through the vegetation canopy infiltrates, while the remainder runs off. The amount of infiltration is unknown and is challenging to estimate. It depends on precipitation amount and intensity, throughfall, and runoff generation. Given that the uncertainty in infiltration may be greater than Esoil itself, we do not use the water balance approach to estimate Esoil at these times. Although this does limit the times when ESMAP can be applied, dry days are more common than days with substantial precipitation. For example, across the conterminous U.S. (CONUS), there is less than 2 mm of precipitation during 65% of the SMAP overpasses (Figure 3b). The prevalence of dry days varies greatly through space, so ESMAP will yield more data (without gap filling) in some locations than others (Figure 3a). Therefore, on the basis of the above considerations, intervals between successive SMAP overpasses with <2 mm of precipitation are hereafter referred to as ‘valid intervals’, while those with larger precipitation values are considered to be ‘non-valid’. The valid intervals that immediately follow large precipitation events will include a large portion of the drying signal, and thus will be useful for calculating soil evaporation resulting from precipitation that accumulates during the preceding non-valid interval.
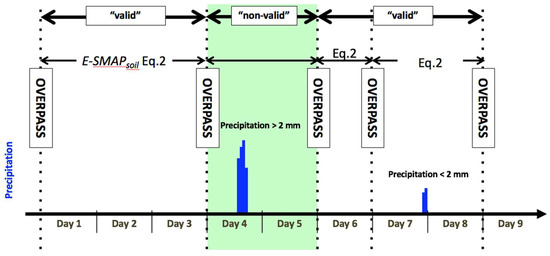
Figure 2.
Example time sequence for estimating ESMAPsoil based on SMAP descending overpasses for a midlatitude site. ESMAPsoil will be estimated from Equation (2) for overpass intervals where precipitation is less than 2 mm, e.g., “valid” overpasses. Any interval where precipitation exceeds 2 mm is termed “non-valid” for the ESMAP method.
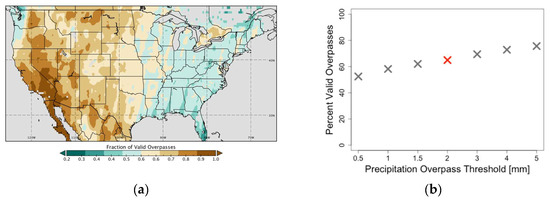
Figure 3.
(a) Map of percent “valid” SMAP overpasses, defined as having less than 2 mm precipitation in the overpass interval. (b) Percent of valid overpasses for given precipitation thresholds. The red-X denotes the chosen threshold, 2 mm.
Here, we use precipitation data from the NLDAS-2 primary forcing fields [45,46]. This precipitation data is based on the NCEP Climate Prediction Center’s unified gauge-based precipitation, which has been adjusted for orographic effects [47]. We do not use data from individual precipitation gauges at the study locations (Table 1). Our intent is to estimate ESMAPsoil at the scale of the SMAP pixel (9 × 9 km), thus the NLDAS data is expected to be more representative than that from individual gauges. The NLDAS grid (1/8th degree) is of similar scale to the SMAP product. Therefore, we use data from the NLDAS grid cell that most closely corresponds in space to the SMAP EASE grid. The magnitude of precipitation does not directly affect ESMAPsoil determined from the water balance. We only attempt to identify the presence of precipitation during each SMAP overpass interval, using a threshold of 2 mm. This threshold was selected based on SMAP’s accuracy and sensing depth [34]: 2 mm of infiltrated water is expected to yield a measurable change (>0.040 mm3 mm−3) over SMAP’s sensing depth.
2.4. Bottom Flux
We now consider the flux that transfers water vertically across the bottom boundary of the 0–50 mm surface soil layer, qbot (Figure 1). During and after rainfall, water moves from the surface soil to deeper layers. Once the surface soil dries sufficiently, the matric potential gradient is reversed and water flows to the surface layer from below. No method exists to measure this flux in-situ. Soil moisture or soil water potential can be measured at different depths in the soil column. These measurements can be used to calculate water potential gradients for use in flux calculations [48]. However, this approach is problematic near the soil-atmosphere interface, where vertical potential gradients tend to be extreme and soil hydraulic properties are variable. In addition, in-situ soil probes sample small soil volumes that are not representative of an entire SMAP pixel. Given these challenges, the qbot at the scale of SMAP may be best estimated with models.
We use the Hydrus 1-D model to estimate qbot. Hydrus simulates one-dimensional variably saturated water flow by numerically solving the mixed form of the Richards equation [49]. We used a modeled soil column with depth of 1000 mm, discretized by nodes of 10 mm. We used the flux at the bottom of the 50 mm deep node for qbot. Soil type at each site was determined from the NLDAS-2 soil texture map. The Hydrus default van Genuchten [50] soil hydraulic property parameters for the mapped soil type were used for the simulations. The bottom boundary condition (1 m soil depth) is set to free drainage. The top boundary condition is set to replicate observed atmospheric boundary conditions: hourly precipitation and PET were derived from NLDAS forcing. Hydrus simulates water loss from the profile by both evaporation and transpiration. These two fluxes are not used directly in the ESMAP water balance (Equations (1) and (2)) but are necessary for a realistic evolution of soil moisture profiles, which does affect qbot. Hydrus calculates transpiration using the Feddes water stress response function. Simulated qbot is not sensitive to the root distribution used. In a series of test simulations, we used a wide range of root profiles (uniform with depth, increasing with depth, etc.) and found differences in qbot of less than several percent. The top surface boundary condition also requires specification of the minimum allowed pressure head at the soil surface. We found that the modeled qbot was not sensitive to this parameter within the allowable range, so −1000 m was used for all sites. For model spin up, Hydrus was first run for one full year at each site (1 April 2015 to 31 March 2016), and the resulting soil moisture profile was used as initial conditions. Then, the model was run for the 931-day SMAP record (1 April 2015, through 17 October 2017). Hydrus uses a variable time step, depending on matric potential gradients. The simulated fluxes are accumulated first to 30-min intervals, and then to SMAP overpass intervals for comparison with drying rates.
The benefit of using Hydrus to estimate qbot is that the flux across the bottom boundary of the sensing depth (Figure 1) is calculated from the vertical soil moisture gradient simulated at 10 mm resolution, which captures the passage of wetting fronts. An alternative approach is to calculate qbot using a model with thicker layers typical of LSMs (e.g., [51]). Even if there is a layer boundary at 50 mm, this approach is still problematic because both the matric potential gradient and hydraulic conductivity must be calculated from averaged values representing soil layers ~100 mm thick, much thicker than the SMAP sensing depth. We have compared qbot from Hydrus to that using a Noah-type calculation. The simulated fluxes are similar, although the latter is clearly unrealistic, particularly as the surface soil layer approaches residual water content. In order for Hydrus to provide a reasonable estimate of qbot, the simulated ET and soil moisture time series must be accurate. We compare Hydrus soil moisture, averaged over the top 50 mm, to SMAP surface soil moisture in Table 2. This comparison uses all unflagged, 6 AM SMAP observations and the Hydrus soil moisture values that correspond to each SMAP measurement. We calculate RMSE on the order of SMAP’s accuracy (0.04 mm3 mm−3) and high correlation at all sites but one (Table 2). SMAP soil moisture is lower than Hydrus, by an average of 0.07 mm3 mm−3 across sites, similar to the known dry bias of SMAP relative to in situ observations [37].

Table 2.
Table showing unbiased RMSE (ubRMSE) of Hydrus-1D VSM (mm/mm) with observed SMAP VSM (mm/mm) for all times, correlation of Hydrus-1D VSM (mm/mm) with observed SMAP VSM (mm/mm), mean bias of Hydrus-1D VSM (mm/mm) versus SMAP VSM (mm/mm), mean drying rate during valid overpasses (mm/day), mean qbot (mm/day) during valid overpasses, mean ET_s (mm/day) during valid overpasses, mean Noah Esoil (mm/day), mean Mosaic Esoil (mm/day), mean ESMAPsoil (mm/day) during valid overpasses, mean precipitation (mm/day) over the entire time-period, number of days in valid overpasses (<2 mm precipitation), and number of days in invalid overpasses (>2 mm precipitation).
Uncertainty in the calculation of qbot is due to imperfect soil hydraulic properties, spatial scaling issues, model structure, and meteorological forcing. We provide an estimate of the magnitude of uncertainty by varying model parameters only. We repeated the Hydrus simulations using a range of soil hydraulic properties [52], varying both saturated hydraulic conductivity and the van Genuchten ‘n’ parameter [50]. Then, we calculate uncertainty based on the simulated distribution of qbot values.
2.5. Transpiration from the Surface Soil
The final component of the surface soil water balance is transpiration from the 50 mm surface soil layer, (ET_s; transpiration from the surface layer), which is only a portion of total transpiration. We generate a time series of ET_s for each site based on the calculation of total transpiration of Mu et al. (2011) [53]. We complete a standard calculation of PET, in units of W m−2 as follows:
where s is the slope of the saturated water vapor pressure curve (Pa K−1), A is net radiation (W m−2), is air density (kg m−3), Cp is specific heat capacity of air (1005 J kg−1 K−1), esat − e is vapor pressure deficit, ra aerodynamic resistance (s m−1), is the psychometric constant (Pa K−1), and rs is surface resistance. The aerodynamic resistance is based on Equations (10) and (11) in Mu et al. (2007) [54] and the surface resistance is from biome specific constants described by Mu et al. (2011) [53]. The input meteorological forcing comes from the NLDAS-2 data. Using a modified form of the Penman-Monteith equation, potential transpiration (Figure 4) is then calculated using a variant of Equation (3) that accounts for fraction of the land surface covered by vegetation, FC [53], based on the Enhanced Vegetation Index (EVI) derived from the Global Modis MOD13A2 product [55]. We did not upscale the MODIS data to SMAP’s sensing footprint, as this would have had virtually no impact on the final time series. An example time series is shown in Figure 4. The PET calculated from Equation (3) varies largely due to seasonal variations in available energy. The potential transpiration is lower than PET because FC is less than one, more so in the winter than in the summer.
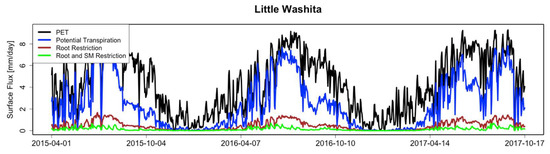
Figure 4.
Time-series of PET (black), potential transpiration (blue), root restricted transpiration from the surface layer (brown), and root and soil moisture restricted transpiration (green) from the surface layer. The root and soil moisture restricted transpiration (green) are the estimates used in ESMAP calculation.
We then calculate ET_s from potential transpiration by applying two restrictions. First, potential transpiration is multiplied by the fraction of roots in the surface soil layer: 20% or less of total roots exist in the top 50 mm of the soil profile across Earth’s common biomes [36]. This results in a large decrease in transpiration from the surface relative to total potential transpiration (Figure 4), usually to values less than 1 mm day−1. For each site, the fraction of roots in the surface layer is determined from root distribution parameters as used in the National Center for Atmospheric Research (NCAR) Community Land Model (CLM) [36]; CLM uses vegetation dependent root distributions based on an assumption of exponential decay of root densities in the soil column. Second, we include an additional restriction due to soil water stress, using the standard linear formulation that scales transpiration between a reference soil moisture value and a wilting point [56,57]. Scaling the potential transpiration by both the fraction of roots in the surface layer and a soil moisture stress factor is equivalent to a non-compensatory root extraction function [58]. We estimate uncertainty in the ET_s by varying three of the parameters in the calculation as follows: (1) adding random noise from a uniform distribution within the range of uncertainty of SMAP (0.04 mm3 mm−3), (2) adding random noise from a uniform distribution within the range of uncertainty of EVI to the observed EVI values (0.025), and (3) randomly selecting rooting depth parameters from a range of comparable vegetation commonly used in GCM and land-surface model land cover classifications (e.g., BATS, IGBP, and SiB2; 35). By adding random noise to the entire record of the observational components and using constant rooting depth profiles for each of the 100 sensitivity simulations, we are able to deduce what variables and processes most impact ET_s in our water-balance calculations. Adding noise within the range of uncertainty for both SMAP and EVI had little impact on the ET_s response, while ET_s responds in a largely linear fashion as parameter combinations place varying amounts of roots in the surface layer.
3. Results
First, we examine qbot and uncertainty (Section 3.1), then transpiration and uncertainty (Section 3.2). These are then compared to rates of soil drying and evaporation based on the ESMAP framework (Section 3.3). Finally, we evaluate the components of the surface soil water balance (Section 3.4).
3.1. Vertical Flux in the Soil
The calculation of qbot depends on the vertical soil moisture profile simulated by Hydrus. Observations do not exist to validate either the simulated vertical gradient or the resulting flux. As a gauge of model performance, we use SMAP surface soil moisture to evaluate if the soil moisture simulated by Hydrus is reasonable. SMAP soil moisture has been validated at the eight CVS sites to be within 0.04 mm3 mm−3, the performance standard set and achieved for the SMAP mission [37]. Averaged over the top 50 mm, Hydrus soil moisture is very similar to SMAP at all ten locations used (eight CVS and Viara and Tonzi Ranch) (Figure 5a and Table 2). The unbiased RMSE between SMAP and Hydrus is around 0.04 mm3 mm−3. This provides evidence that the soil water fluxes simulated by Hydrus are reasonable: if Hydrus qbot or surface evaporation was too high (low), the simulated soil moisture would dry faster (slower) than observed. Of course, it is not possible with this comparison alone to prove the simulated qbot is correct. Although unlikely, it is possible that compensating errors in qbot and evaporation could also yield a time series consistent with SMAP. We have also compared Hydrus soil moisture (averaged over the top 50 mm) to in-situ observations at several CVS [59]. This comparison also shows the soil moisture time series simulated by Hydrus is reasonable (e.g., Figure 5a).
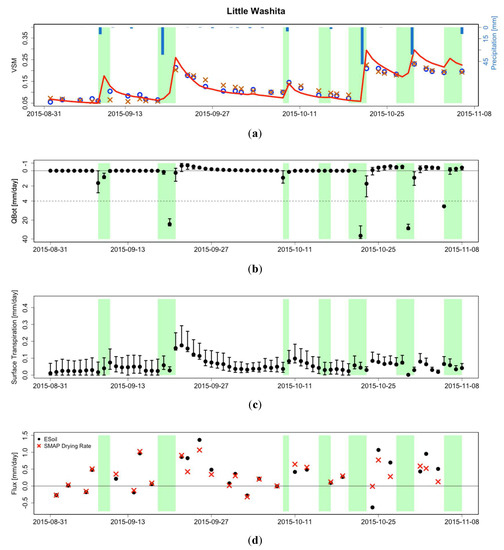
Figure 5.
(a) Soil moisture time-series for SMAP (blue-circles), in situ observations (orange-X), and Hydrus-1D (red-line). Both the in situ and Hydrus data have been adjusted for average bias relative to SMAP. The shading denotes invalid overpasses of precipitation greater than 2 mm, precipitation is plotted as the blue-bars, in mm day−1 (b) qbot time-series, with error bars ranging from 5th to 95th percentiles of sensitivity simulations. The dashed line shows a change in scale in the y-axis. Note that the y-axis goes from positive values at the bottom to negative values at the top (c) ET_s time-series, with error bars ranging from 5th to 95th percentiles of sensitivity simulation. (d) ESMAPsoil estimates (black-dots) and SMAP drying rate (red-X).
The simulated qbot varies in magnitude and direction as the soil is wetted by precipitation and subsequently dries (Figure 5b). During and after rainfall, water moves from the surface soil to deeper layers (positive qbot), driven by a combination of gravity and the gradient in matric potential. During these intervals, several mm of water may pass the bottom boundary of the sensing depth (50 mm) per day. Rates are even higher on shorter timescales (not shown). The magnitude of qbot decreases on a timescale of days as the surface soil dries. Once the surface soil dries sufficiently, the matric potential gradient is reversed and water flows to the surface layer from below. The magnitude of the upward-directed fluxes is approximately an order of magnitude less than downward fluxes following rainfall, usually less than 0.2 mm day−1. This upward flux is maintained as long as the root zone is wetter than the surface soil and the gradient is sufficient to overcome gravity.
We split the simulated qbot data into SMAP overpass intervals with (non-valid) and without (valid) precipitation that exceeds the prescribed threshold (2 mm). During non-valid intervals, qbot is almost always positive (downward flow) with values of several mm day−1 or more (Figure 6). During these intervals, uncertainty of qbot, based on parametric uncertainty of saturated hydraulic conductivity (Ks) and van Genuchten n [50] is one to several mm day−1 (Figure 7). The magnitude of qbot and its uncertainty is of similar magnitude to drying rates (converted to depth of water) typically observed from SMAP (Section 3.3). Thus, any calculation of evaporation during these intervals is highly dependent on parameter selection in Hydrus, and less so on the soil drying observed by SMAP. During valid overpasses (<2 mm total precipitation), the absolute magnitude of qbot is almost always <0.5 mm day−1 and the flow is upwards (negative flux) (Figure 5b and Figure 6). Uncertainty during these intervals is usually approximately 0.1 mm day−1 or less (Figure 7), with the greatest uncertainty for the combination of low saturated hydraulic conductivity and n values. Thus, compared to evaporation rates based on soil drying, the importance of parameter selection and the Hydrus qbot calculation is relatively unimportant during valid overpass intervals when precipitation is limited (<2 mm).
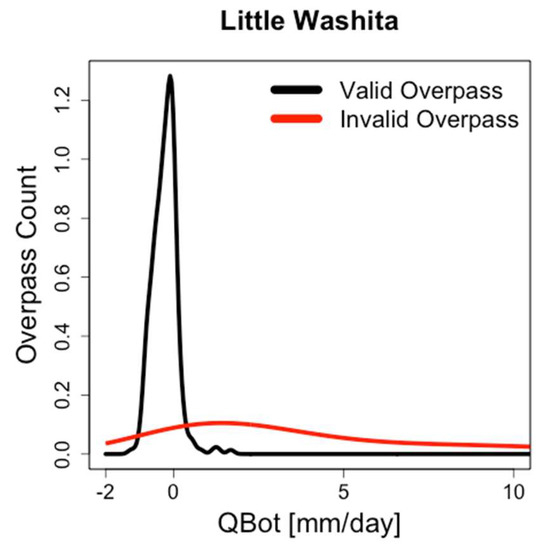
Figure 6.
qbot distributions for valid overpasses (black) and invalid overpasses (red).

Figure 7.
(a) qbot values from sensitivity analysis for a rainy day and (b) 2 days post-rain. X-axis are Ks (saturated hydraulic conductivity, cm day−1) values used in the sensitivity analysis. Colors represent the range of n values used. The black-asterisk represents the qbot value used in ESMAPsoil calculation for the Little Washita site.
3.2. Transpiration from the Surface Layer
The surface transpiration, ET_s, is the component of total transpiration due to extraction of soil water by roots in the top 50 mm of the soil. There are large seasonal variations in potential evapotranspiration and potential transpiration, the former caused by changes in available energy and the latter by fluctuations in active vegetation cover as determined by EVI (Figure 4). The prescription that only a small fraction (<20%) of plant roots exist in the surface layer (root restriction) is time invariant and lowers the potential transpiration from several mm day−1 to values usually <0.2 mm day−1. The soil moisture restriction then lowers transpiration further (Figure 4). In addition, it superimposes temporal fluctuations in ET_s on timescales of days to weeks (Figure 5c). For example, at Little Washita, ET_s is <0.05 mm day−1 prior to precipitation when the surface soil layer is dry. After precipitation, ET_s jumps to values >0.2 mm day−1 before decreasing in concert with surface soil moisture (Figure 5a,c).
The values of ET_s calculated according to Mu et al. (2007 and 2011) [53,54] are small in magnitude, compared to both qbot during and after storms as well as soil drying rates measured by SMAP. However, excluding ET_s from the surface soil layer calculation would yield an overestimate of Esoil, on the order of 10% for a soil evaporation rate of one to several mm day−1, and even greater when evaporation is close to zero. Thus, even though the surface transpiration flux is small, it is important to quantify the reasonability and uncertainty of the ET_s calculation. Total transpiration has been validated [53], but the component from the surface soil used here has not, and no data exists for this purpose. We have estimated uncertainty in ET_s of ~25% by varying the key parameters over a reasonable range, including soil moisture, EVI, and fraction of roots in the surface layer (Figure 8). As the component of the transpiration from the root layer depends linearly on fraction of roots in the surface layer, this parameter holds the greatest explanatory power in the sensitivity analysis.
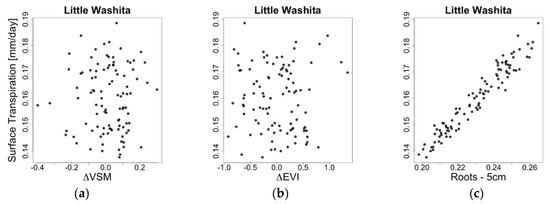
Figure 8.
(a) Transpiration sensitivity to variations in VSM, (b) EVI and (c) root distribution. ∆VSM and ∆EVI corresponds to the net change in VSM and EVI when adding noise from a uniform random distribution within the uncertainty of the observations.
3.3. Soil Drying and Evaporation
We report surface soil drying rates as mm day−1 water equivalent, by multiplying the rate of volumetric soil moisture drying (mm3 mm−3 day−1) by the sensing depth (50 mm). Drying rates are almost always less than 2 mm day−1 and tend to decrease through time after rainfall (e.g., Figure 5d), consistent with that reported by Shellito et al. (2018) [32] and McColl et al. (2017) [31]. Negative drying rates (i.e., soil is wetting) between 0 and 0.5 mm day−1 are not uncommon (Figure 5d), even during intervals when the soil is expected to dry from day to day (e.g., see early October observation in Figure 5d). Noise in consecutive SMAP observations is the likely source of negative drying observations. Small precipitation events may also lead to soil wetting during valid overpass intervals, even though there is less than 2 mm total precipitation. Finally, condensation of atmospheric water vapor on the soil surface is another possible source.
Soil evaporation rates are typically greater than drying rates (Figure 5d and Figure 9). This is most obviously the case during the ~10 day intervals following rainfall when the soil is drying. During these intervals, soil water is usually flowing upwards into the surface soil layer (qbot < 0) (Figure 5b and Figure 6). Therefore, the evaporation rate is greater in magnitude than the corresponding soil drying rate. This is shown in Figure 9: the points that fall furthest above the 1:1 line between soil drying and evaporation have the most negative qbot values. During these same intervals, transpiration removes water from the surface layer. In the absence of vertical soil water redistribution, transpiration would lead to evaporation rates that are smaller in magnitude than drying rates. However, transpiration is typically an order of magnitude smaller than qbot, so this effect is usually negligible. However, there are instances where evaporation is less than the drying rate (points below the 1:1 line) even when qbot is negative. These are times where surface transpiration most strongly affects the calculated ESMAPsoil.
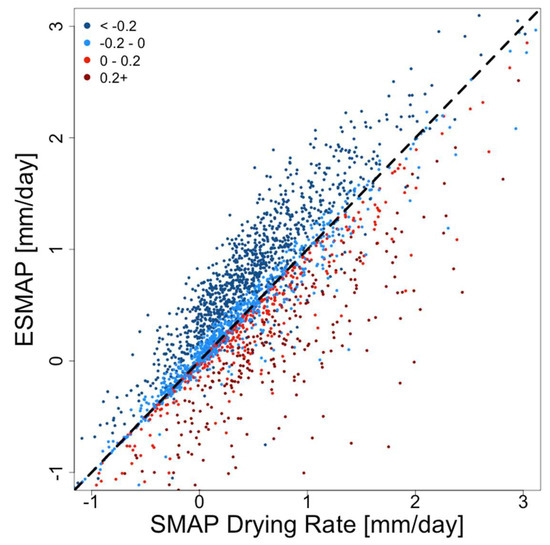
Figure 9.
ESMAPsoil estimates and SMAP drying rates for valid overpasses, black-dashed line represents a 1-1 relationship. Shading follows qbot for the respective overpasses with negative (blue) values indicating upward movement into the surface layer and positive (red) values indicating downward movement into the sub-surface layer.
The evaporation time series are not always smoothly varying: a monotonic decrease through time after precipitation is not always observed. As mentioned above, noise in the SMAP soil moisture observations or small precipitation events introduce fluctuations in drying rate (Figure 5d). These fluctuations affect the estimated evaporation rate. In addition, day-to-day changes in qbot or transpiration can add additional variations in the evaporation time series.
3.4. Simulated Water Balance
We now compare the water balance components summed over the valid overpasses. Esoil is the largest term in the surface water balance at all sites (Figure 10). Net qbot is the second largest flux at eight of the sites. At all sites except South Fork, qbot yields a net upward flow into the surface soil layer from below during the valid overpasses. If overpasses with precipitation were included, net qbot would be downward and of much larger magnitude. ET_s is generally much smaller than the other two fluxes. We note that the sum of all three terms does not equal zero because changes in soil moisture are almost always observed at the transition between valid and invalid overpasses. Because net qbot is upwards, ESMAPsoil is higher than drying rates, usually by ~10–50% (Figure 9).
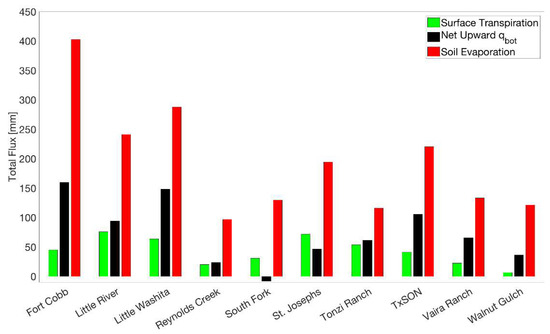
Figure 10.
Bar plots of surface transpiration (green), net qbot with positive values indicating net upward flow (black) and Esoil (red) for valid overpasses at 10 SMAP core validation sites. Flux values are summed over all valid overpasses.
When summed over the valid overpasses across the period of SMAP data analyzed, direct evaporation from soil varies from 100 to 400 mm across the sites (Table 2). Because the number of days included in valid overpasses differs between sites, the total evaporation is more readily compared once converting to an evaporation rate (mm day−1). The average ESMAPsoil for the valid overpass intervals varies between ~0.2 and 0.7 mm day−1 from site to site. The estimates from ESMAP are more similar to those from the NLDAS-Mosaic model than the NLDAS-Noah model (Table 2). Evaporation from NLDAS-Mosaic is roughly twice that from NLDAS-Noah at all ten sites. We have compared evaporation from these two models across CONUS and found a similar result: evaporation from Mosaic is consistently about two times that from Noah. The NLDAS-VIC evaporation is zero, resulting from the model canopy formulation (applicable to versions 4.1 and older). Given the drastic differences between these three models with identical forcing, we conclude that NLDAS LSM fields are not suitable for validating the ESMAP estimates. At the continental scale, the NLDAS fields would be even less useful because the models do not represent irrigation. In contrast, SMAP and thus ESMAPsoil would be affected by irrigation, obfuscating any comparisons.
As a percent of total precipitation that accumulated during the 30-month period analyzed, ESMAPsoil during valid overpasses represents between 7.5% and 25% of precipitation depending on the site. This is a minimum estimate of the total flux from evaporation, as it does not include SMAP overpass intervals during which rainfall exceeds 2 mm. Across sites, there is a positive correlation between ESMAPsoil and precipitation rate (or total precipitation) (Figure 11). In contrast, there is no consistent relationship between ESMAPsoil and PET across sites (not shown).
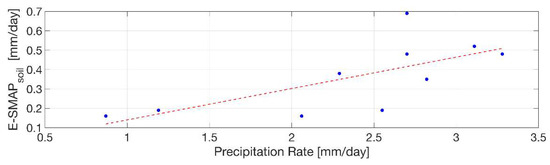
Figure 11.
Scatter plot of mean precipitation rate (x-axis) in comparison to mean ESMAPsoil rate (y-axis) at 10 SMAP core validation sites. R2 = 0.57.
4. Discussion
We have described a methodology to calculate evaporation from the surface soil. The method is only applied during SMAP overpass intervals when NLDAS precipitation is <2 mm. During the 2.5-year analysis period, this accounts for approximately 60% of the time across the ten sites examined (Table 2). While this method excludes overpass intervals with large precipitation inputs (e.g., ‘non-valid’ intervals), we have demonstrated that a large portion of the subsequent soil drying and evaporation is captured during the subsequent ‘valid’ overpasses (e.g., Figure 5).
The ESMAP approach yields the following consistent results across ten locations in North America. First, the vertical flux of soil water between the surface soil layer (50 mm) and the underlying soil, qbot, is generally upwards during intervals without precipitation, with an absolute magnitude between 0 and 0.5 mm day−1. This is in contrast to intervals during, and within several days following, precipitation when the flow is downwards and of a much greater magnitude. Transpiration from the surface soil layer is typically <0.1 mm day−1, and thus almost always of smaller magnitude than qbot. Soil drying rates (converted to equivalent water thickness) are typically between 0 and 1 mm day−1, with the highest values following rainfall. ESMAPsoil is of comparable magnitude to soil drying, but is almost always greater, because qbot is typically a source of water into the surface layer and transpiration is negligible. Therefore, ESMAPsoil is typically between 0 and 1.5 mm day−1. At the ten sites, ESMAPsoil is higher than that simulated by NLDAS Noah. This result is consistent with the CONUS-wide study of drying rates by Shellito et al. [30], who found SMAP soil drying was consistently faster than from Noah.
We now evaluate the reliability of these results. The qbot calculation results in a net upward flow of water into the surface soil during SMAP overpass intervals with minimal precipitation (Table 2) and yields ESMAPsoil rates that are higher than soil drying rates observed directly from SMAP. The net upward flow during intervals with minimal precipitation is qualitatively consistent with theory and observations that describe how soil dries from the surface downwards in the first ~10 days following rainfall. The actual magnitude and temporal fluctuations of qbot cannot be evaluated directly with field observations, beyond the demonstrated consistency with surface soil moisture time series (Table 2). The vertical fluxes simulated by Hydrus depend on the soil hydraulic properties used. We used the NLDAS soil texture classification for each site and their corresponding default soil hydraulic properties for that soil type in Hydrus. However, there is a wide range of values for these parameters within each soil type [60]. As demonstrated above, the parameter values used do not greatly influence the magnitude or direction of qbot during SMAP overpass intervals without precipitation (Figure 5b and Figure 7), with uncertainty of ~0.1 mm day−1 (or <20%) for most conditions. Choosing different parameter values would not change the basic result that water generally flows into the surface soil layer. Other sources of uncertainty have not been quantitatively evaluated, so caution is warranted. Here, the soil profile is modeled as vertically homogeneous, though soil texture typically varies with depth. In addition, Hydrus as applied does not treat spatial variations within a SMAP pixel, associated with topography, soil type, land-cover, or meteorological input. The roles of changing water table depths and lateral redistribution of water are neglected in the methodology due to both 1-dimensional model assumptions and SMAP’s sensing footprint. Therefore, the method is unresponsive to changes in moisture that come from topographical gradients and surface water-groundwater interactions that are not detected by the SMAP sensor.
Further uncertainty is associated with the calculation of transpiration from the surface soil layer. The most critical parameter in the calculation is the fraction of roots that exist in the surface layer, which is expected to be less than 20% in most environments [36]. In locations where the fraction of roots in the surface soil layer is greater, transpiration may be more important than shown here (Figure 10). However, given the limited sensing depth of SMAP and other similar sensors, we expect this flux to be of secondary importance in the calculation of soil evaporation. This does not mean that transpiration from the surface layer should be ignored, as it does reduce the calculated evaporation rate by ~10%.
ESMAPsoil accounts for an average of 15% of total precipitation, with a range of 8 to 26%, across the ten sites. ESMAPsoil rates tend to be higher at sites with more precipitation (Figure 11), consistent with the fact that precipitation is the primary source for ET in most environments. This calculation is based on evaporation accumulated over SMAP overpass intervals with precipitation <2 mm (60% of days), whereas precipitation is aggregated across all days in the record. If evaporation rates are similar during overpasses with precipitation, then the total evaporation flux would account for ~25% of precipitation. It is possible that evaporation rates are even higher during overpass intervals with precipitation. ET is often most rapid soon after precipitation ends [61]. It follows that some of the longer overpass intervals, e.g., 2 or 3 days long, flagged as invalid (>2 mm precipitation) may include 1 or 2 dry days after the precipitation ends. In these cases, the soil evaporation rates would be higher than ESMAPsoil in the subsequent interval with drier soil.
The ESMAP approach was not applied during overpass intervals with precipitation exceeding 2 mm since the uncertainties in precipitation, infiltration, runoff, and canopy evaporation would far exceed the magnitude of direct soil evaporation calculated via Equation (1). Evaluating the importance of the direct soil evaporation flux relative to transpiration and other water cycle components requires Esoil estimation during rainy intervals. One potential approach would combine a standard LSM with the ESMAP methodology: the model simulating continuous estimates of evaporation, with ESMAP providing a constraint on evaporation during overpass intervals with minimal precipitation. Data assimilation is an obvious way to bring together the LSM and ESMAP, but parameter estimation (i.e., calibration) might work equally well. Even if surface soil moisture is assimilated to improve a state variable, this does not guarantee improvement in the simulated evaporation flux. The results shown in Table 2 suggest that the formulation for evaporation in the Noah and Mosaic LSMs are very different (and VIC has zero evaporation), such that there is low confidence that assimilation could bring the models in line with each other or observations.
Here, we used data from ten sites in an attempt to evaluate the challenges and uncertainty with ESMAP. The true appeal of remotely-sensed data, such as that from SMAP, is the ability to examine fluxes and storage changes at continental to global scales. Clearly the variation in evaporation in Figure 11 cannot be explained solely by precipitation. Rather it is expected that other factors, for example, soil and vegetation type, also impact site-to-site differences in evaporation. These are targets for future research as the study domain increases to continental scales. All datasets used here are available at the global scale. The Hydrus estimates of qbot and Mu (2011) [53] transpiration calculation could be applied at all SMAP pixels within an extended domain. One challenge of applying ESMAP spatially would be to account for the spatial heterogeneity within SMAP grid boxes within the 1-D ESMAP calculation. Specifically, variations in soil texture within SMAP grid boxes would affect qbot calculation. In addition, meteorological uncertainty, particularly in data scarce areas, will impact the <2 mm screening procedure and the Hydrus forcing calculation. Hyper-arid regions may pose a unique challenge. Finally, in its current form, the ESMAP method has little applicability to very wet areas—e.g., coastal and/or tropical regions—due to the prevalence of rainy intervals, as well as QC issues with SMAP sensing over dense vegetation.
5. Conclusions
We have described a methodology to calculate evaporation from the surface soil by combining a time series of SMAP soil moisture observations with auxiliary observations and model calculations. This approach was evaluated at ten locations in North America. During overpass intervals without precipitation, qbot typically transfers water upwards into the surface soil layer from below, at rates usually <0.5 mm day−1. Transpiration from the surface soil layer, ET_s, is usually much less than qbot and does not substantially influence the surface soil water balance. Evaporation is almost always greater than soil drying rates because qbot is typically a source of water to the surface soil and ET_s is negligible. Evaporation is typically between 0 and 1.5 mm day−1, with the highest values following rainfall.
Soil evaporation summed over SMAP overpass intervals with precipitation <2 mm (60% of days) accounts for 15% of total precipitation, averaged over the ten sites. If evaporation rates are similar during rainy intervals, then the total evaporation flux would account for ~25% of precipitation, suggesting that its magnitude would be similar to that of transpiration or runoff, for the sites evaluated. ESMAP could be used over spatially continuous domains to provide constraints on Esoil, but model-based Esoil would be required during non-valid intervals with substantial precipitation.
Author Contributions
E.E.S. and B.L. were responsible for the original concept. All four authors were responsible for data processing, calculations, and analysis. All four authors contributed to writing of the manuscript.
Funding
This research was funded by the National Aeronautics and Space Administration: NASA SUSMAP Grant, NNX16AQ46G: Monitoring soil evaporation using SMAP surface soil moisture in a water balance framework.
Acknowledgments
The MOD13A2 was retrieved from the online Terra Modis, courtesy of the NASA EOSDIS Land Processes Distributed Active Archive Center (LP DAAC), USGS/Earth Resources Observation and Science (EROS) Center, Sioux Falls, South Dakota, https://e4ftl01.cr.usgs.gov/MOLT/.
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A

Table A1.
Variables.
Table A1.
Variables.
| Variable | Description | Units |
|---|---|---|
| qbot | Flux of water across the bottom boundary of the surface soil layer sensed by SMAP (0–50 mm). Downward fluxes out of the surface soil layer were considered positive; whereas upwards fluxes into the surface soil layer were considered negative. | mm day−1 |
| ET_s | Transpiration from the surface soil layer (0–50 mm) | mm day−1 |
| Esoil | Soil evaporation from the surface soil layer (00–50 mm) | mm day−1 |
| ESMAPsoil | Soil evaporation from the surface soil layer (0–50 mm) estimated with the presented ESMAP approach | mm day−1 |
References
- Tateishi, R.; Ahn, C.H. Mapping Evapotranspiration and Water Balance for Global Land Surfaces. ISPRS J. Photogramm. Remote Sens. 1996, 51, 209–215. [Google Scholar] [CrossRef]
- Hou, A.Y.; Kakar, R.K.; Neeck, S.; Azarbarzin, A.A.; Kummerow, C.D.; Kojima, M.; Oki, R.; Nakamura, K.; Iguchi, T. The Global Precipitation Measurement Mission. Bull. Am. Meteorol. Soc. 2014, 95, 701–722. [Google Scholar] [CrossRef]
- Dolman, A.J.; De Jeu, R.A.M. Evaporation in Focus. Nat. Geosci. 2010, 3, 296. [Google Scholar] [CrossRef]
- Miralles, D.G.; Holmes, T.R.H.; de Jeu, R.A.M.; Gash, J.H.; Meesters, A.G.C.A.; Dolman, A.J. Global Land-Surface Evaporation Estimated from Satellite-Based Observations. Hydrol. Earth Syst. Sci. 2011, 15, 453–469. [Google Scholar] [CrossRef]
- Lawrence, D.M.; Thornton, P.E.; Oleson, K.W.; Bonan, G.B. The Partitioning of Evapotranspiration into Transpiration, Soil Evaporation, and Canopy Evaporation in a GCM: Impacts on Land–Atmosphere Interaction. J. Hydrometeorol. 2007, 8, 862–880. [Google Scholar] [CrossRef]
- Kustas, W.P.; Norman, J.M. Evaluation of Soil and Vegetation Heat Flux Predictions Using a Simple Two-Source Model with Radiometric Temperatures for Partial Canopy Cover. Agric. For. Meteorol. 1999, 94, 13–29. [Google Scholar] [CrossRef]
- Allen, R.G.; Tasumi, M.; Morse, A.; Trezza, R.; Wright, J.L.; Bastiaanssen, W.; Kramber, W.; Lorite, I.; Robison, C.W. Satellite-Based Energy Balance for Mapping Evapotranspiration with Internalized Calibration (METRIC)—Applications. J. Irrig. Drain. Eng. 2007, 133, 395–406. [Google Scholar] [CrossRef]
- Anderson, M. A Two-Source Time-Integrated Model for Estimating Surface Fluxes Using Thermal Infrared Remote Sensing. Remote Sens. Environ. 1997, 60, 195–216. [Google Scholar] [CrossRef]
- Bastiaanssen, W.G.; Menenti, M.; Feddes, R.A.; Holtslag, A.A.M. A Remote Sensing Surface Energy Balance Algorithm for Land (SEBAL). 1. Formulation. J. Hydrol. 1998, 212–213, 198–212. [Google Scholar] [CrossRef]
- Kalma, J.D.; McVicar, T.R.; McCabe, M.F. Estimating Land Surface Evaporation: A Review of Methods Using Remotely Sensed Surface Temperature Data. Surv. Geophys. 2008, 29, 421–469. [Google Scholar] [CrossRef]
- Heitman, J.L.; Xiao, X.; Horton, R.; Sauer, T.J. Sensible Heat Measurements Indicating Depth and Magnitude of Subsurface Soil Water Evaporation. Water Resour. Res. 2008, 44. [Google Scholar] [CrossRef]
- Xiao, Z.; Lu, S.; Heitman, J.; Horton, R.; Ren, T. Measuring Subsurface Soil-Water Evaporation with an Improved Heat-Pulse Probe. Soil Sci. Soc. Am. J. 2012, 76, 876. [Google Scholar] [CrossRef]
- Stannard, D.I.; Weltz, M.A. Partitioning Evapotranspiration in Sparsely Vegetated Rangeland Using a Portable Chamber. Water Resour. Res. 2006, 42. [Google Scholar] [CrossRef]
- Shawcroft, R.W.; Gardner, H.R. Direct Evaporation from Soil under a Row Crop Canopy. Agric. Meteorol. 1983, 28, 229–238. [Google Scholar] [CrossRef]
- Herbst, M.; Kappen, L.; Thamm, F.; Vanselow, R. Simultaneous Measurements of Transpiration, Soil Evaporation and Total Evaporation in a Maize Field in Northern Germany. J. Exp. Bot. 1996, 47, 1957–1962. [Google Scholar] [CrossRef]
- Wullschleger, S.D.; Hanson, P.J.; Tschaplinski, T.J. Whole-Plant Water Flux in Understory Red Maple Exposed to Altered Precipitation Regimes. Tree Physiol. 1998, 18, 71–79. [Google Scholar] [CrossRef] [PubMed]
- Kumar, S.V.; Peters-Lidard, C.D.; Santanello, J.A.; Reichle, R.H.; Draper, C.S.; Koster, R.D. Evaluating the utility of satellite soil moisture retrievals over irrigated areas and the ability of land data assimilation methods to correct for unmodeled processes. Hydrol. Earth Syst. Sci. 2015, 19, 4463–4478. [Google Scholar] [CrossRef]
- Miralles, D.G.; Jimenez, C.; Jung, M.; Michel, D.; Ershadi, A.; McCabe, M.F.; Hirschi, M.; Martes, B.; Dolman, A.J.; Fisher, J.B.; et al. The WACMOS-ET project—Part 2: Evaluation of global terrestrial evaporation data sets. Hydrol. Earth Syst. Sci. 2016, 20, 823–842. [Google Scholar] [CrossRef]
- Talsma, C.J.; Good, S.P.; Jimenez, C.; Martens, B.; Fisher, J.B.; Miralles, D.G.; McCabe, M.F.; Purdy, A.J. Partitioning of evapotranspiration in remote sensing-based models. Agric. For. Meteorol. 2018, 260, 131–143. [Google Scholar] [CrossRef]
- Moran, M.S.; Scott, R.L.; Keefer, T.O.; Emmerich, W.E.; Hernandez, M.; Nearing, G.S.; Paige, G.B.; Cosh, M.H.; O’Neil, P.E. Partitioning Evapotranspiration in Semiarid Grassland and Shrubland Ecosystems Using Time Series of Soil Surface Temperature. Agric. For. Meteorol. 2009, 149, 59–72. [Google Scholar] [CrossRef]
- Jasechko, S.; Sharp, Z.D.; Gibson, J.J.; Birks, S.J.; Yi, Y.; Fawcett, P.J. Terrestrial Water Fluxes Dominated by Transpiration. Nature 2013, 496, 347–350. [Google Scholar] [CrossRef] [PubMed]
- Brooks, J.R.; Barnard, H.R.; Coulombe, R.; McDonnell, J.J. Ecohydrologic Separation of Water between Trees and Streams in a Mediterranean Climate. Nat. Geosci. 2009, 3, 100–104. [Google Scholar] [CrossRef]
- Coenders-Gerrits, A.M.J.; van der Ent, R.J.; Bogaard, T.A.; Wang-Erlandsson, L.; Hrachowitz, M.; Savenije, H.H.G. Uncertainties in Transpiration Estimates. Nature 2014, 506. [Google Scholar] [CrossRef] [PubMed]
- Wang, L.; Good, S.P.; Caylor, K.K. Global Synthesis of Vegetation Control on Evapotranspiration Partitioning. Geophys. Res. Lett. 2014, 41, 6753–6757. [Google Scholar] [CrossRef]
- Choudhury, B.J.; Monteith, J.L. A Four-Layer Model for the Heat Budget of Homogeneous Land Surfaces. Q. J. R. Meteorol. Soc. 1988, 114, 373–398. [Google Scholar] [CrossRef]
- Dirmeyer, P.A. The Land Surface Contribution to the Potential Predictability of Boreal Summer Season Climate. J. Hydrometeorol. 2005, 6, 618–632. [Google Scholar] [CrossRef]
- Kool, D.; Ben-Gal, A.; Agam, N.; Šimůnek, J.; Heitman, J.L.; Sauer, T.J.; Lazarovitch, N. Spatial and Diurnal below Canopy Evaporation in a Desert Vineyard: Measurements and Modeling. Water Resour. Res. 2014, 50, 7035–7049. [Google Scholar] [CrossRef]
- Troch, P.A.; Martinez, G.F.; Pauwels, V.R.N.; Durcik, M.; Sivapalan, M.; Harman, C.; Brooks, P.D.; Gupta, H.; Huxman, T. Climate and Vegetation Water Use Efficiency at Catchment Scales. Hydrol. Processes 2009, 23, 2409–2414. [Google Scholar] [CrossRef]
- Wang, L.; Caylor, K.K.; Villegas, J.C.; Barron-Gafford, G.A.; Breshears, D.D.; Huxman, T.E. Partitioning Evapotranspiration across Gradients of Woody Plant Cover: Assessment of a Stable Isotope Technique. Geophys. Res. Lett. 2010, 37. [Google Scholar] [CrossRef]
- Shellito, P.J.; Small, E.E.; Colliander, A.; Bindlish, R.; Cosh, M.H.; Berg, A.A.; Bosch, D.D.; Caldwell, T.G.; Goodrich, D.C.; McNairn, H.; et al. SMAP Soil Moisture Drying More Rapid than Observed in Situ Following Rainfall Events. Geophys. Res. Lett. 2016, 43, 8068–8075. [Google Scholar] [CrossRef]
- McColl, K.A.; Alemohammad, S.H.; Akbar, R.; Konings, A.G.; Yueh, S.; Entekhabi, D. The Global Distribution and Dynamics of Surface Soil Moisture. Nat. Geosci. 2017, 10, 100–104. [Google Scholar] [CrossRef]
- Shellito, P.J.; Small, E.E. Controls on Surface Soil Drying Rates Observed by SMAP and Simulated by the Noah Land Surface Model. Hydrol. Earth Syst. Sci. 2018, 22, 1649–1663. [Google Scholar] [CrossRef]
- Kurc, S.A.; Small, E.E. Soil Moisture Variations and Ecosystem-Scale Fluxes of Water and Carbon in Semiarid Grassland and Shrubland. Water Resour. Res. 2007, 43. [Google Scholar] [CrossRef]
- Entekhabi, D.; Yueh, S.; O’Neill, P.E.; Kellogg, K.H.; Allen, A.; Bindlish, R.; Brown, M.; Chan, S.; Colliander, A.; Crow, W.T.; et al. SMAP Handbook; Laboratory, J.P., Ed.; JPL Publication JPL 400-1567; NASA CalTech: Pasadena, CA, USA, 2014.
- Njoku, E.G.; Kong, J.A. Theory for Passive Microwave Remote Sensing of near-Surface Soil Moisture. J. Geophys. Res. 1977, 82, 3108–3118. [Google Scholar] [CrossRef]
- Zeng, X. Global Vegetation Root Distribution for Land Modeling. J. Hydrometeorol. 2001, 2, 525–530. [Google Scholar] [CrossRef]
- Chan, S.; Bindlish, R.; O’Neill, P.E.; Jackson, T.J.; Njoku, E.; Dunbar, R.S.; Chaubell, J.; Peipmeier, J.; Yueh, S.; Entekhabi, D.; et al. Development and assessment of the SMAP enhanced passive soil moisture product. Remote Sens. Environ. 2018, 204, 931–941. [Google Scholar] [CrossRef]
- Chapin, E.; Chau, A.; Chen, J.; Heavey, B.; Hensley, S.; Lou, Y.; Machuzak, R.; Moghaddam, M. AirMOSS: An Airborne P-Band SAR to Measure Root-Zone Soil Moisture. In Proceedings of the 2012 IEEE Radar Conference, Atlanta, GA, USA, 7–11 May 2012. [Google Scholar] [CrossRef]
- O’Neill, P.E.; Chan, S.; Njoku, E.G.; Jackson, T.; Bindlish, R. SMAP Enhanced L3 Radiometer Global Daily 9 km EASE-Grid Soil Moisture, Version 1; NASA National Snow and Ice Data Center Distributed Active Archive Center: Boulder, CO, USA, 2016. [CrossRef]
- Jackson, T.J.; Bindlish, R.; Cosh, M.H.; Zhao, T.; Starks, P.J.; Bosch, D.D.; Seyfried, M.; Moran, M.S.; Goodrich, D.C.; Kerr, Y.H.; et al. Validation of Soil Moisture and Ocean Salinity (SMOS) Soil Moisture Over Watershed Networks in the U.S. IEEE Trans. Geosci. Remote Sens. 2012, 50, 1530–1543. [Google Scholar] [CrossRef]
- Chan, S.K.; Bindlish, R.; O’Neil, P.E.; Njoku, E.; Jackson, T.; Colliander, A.; Chen, F.; Burgin, M.; Dunbar, S.; Piepmeier, J.; et al. Assessment of the SMAP passive soil moisture product. IEEE Trans. Geosci. Remote Sens. 2016, 54, 4994–5007. [Google Scholar] [CrossRef]
- O’Neill, P.E.; Chan, S.; Njoku, E.G.; Jackson, T.; Bindlish, R. SMAP Enhanced L3 Radiometer Global Daily 9 km EASE-Grid Soil Moisture, Version 2; NASA National Snow and Ice Data Center Distributed Active Archive Center: Boulder, CO, USA, 2018. [CrossRef]
- Colliander, A.; Jackson, T.J.; Bindlish, R.; Chan, S.; Das, N.; Kim, S.B.; Cosh, M.H.; Dunbar, R.S.; Dang, L.; Pashaian, L.; et al. Validation of SMAP surface soil moisture products with core validation sites. Remote Sens. Environ. 2017, 191, 215–231. [Google Scholar] [CrossRef]
- Lawston, P.M.; Santanello, J.A.; Franz, T.E.; Rodell, M. Assessment of irrigation physics in a land surface modelling framework using non-traditional and human-practice datasets. Hydrol. Earth Syst. Sci. 2017, 21, 2953–2966. [Google Scholar] [CrossRef]
- NCEP/EMC. NLDAS Primary Forcing Data L4 Hourly 0.125 × 0.125 Degree V002; Goddard Earth Sciences Data and Information Services Center (GESDISC): Greenbelt, MD, USA, 2009. [CrossRef]
- Xia, Y.; Mitchell, K.; Ek, M.; Sheffield, J.; Cosgrove, B.; Wood, E.; Luo, L.; Alonge, C.; Wei, H.; Meng, J.; et al. Continental-scale water and energy flux analysis and validation for the North American Land Data Assimilation System project phase 2 (NLDAS-2): 1. Intercomparison and application of model products. J. Geophys. Res. 2012, 117, D03109. [Google Scholar] [CrossRef]
- Daly, C.; Neilson, R.P.; Philips, D.L. A Statistical-Topographic Model for Mapping Climatological Precipitation over Mountainous Terrain. J. Appl. Meteorol. 1994, 33, 140–158. [Google Scholar] [CrossRef]
- Scanlon, B.R. Water and heat fluxes in desert soils—1. Field Studies. Water Resour. Res. 1994, 30, 709–719. [Google Scholar] [CrossRef]
- Šimůnek, J.; Jarvis, N.J.; Van Genuchten, M.T.; Gärdenäs, A.L. Review and Comparison of Models for Describing Non-Equilibrium and Preferential Flow and Transport in the Vadose Zone. J. Hydrol. 2003, 272, 14–35. [Google Scholar] [CrossRef]
- Van Genuchten, M.T. A Closed-Form Equation for Predicting the Hydraulic Conductivity of Unsaturated Soils. Soil Sci. Soc. Am. J. 1980, 44, 892. [Google Scholar] [CrossRef]
- Chen, F.; Dudhia, J. Coupling an Advanced Land Surface–Hydrology Model with the Penn State–NCAR MM5 Modeling System. Part I: Model Implementation and Sensitivity. Mon. Weather Rev. 2001, 129, 569–585. [Google Scholar] [CrossRef]
- Gutmann, E.; Small, E. The effect of soil hydraulic properties versus soil texture in land surface models. Geophys. Res. Lett. 2005, 32, L02402. [Google Scholar] [CrossRef]
- Mu, Q.; Zhao, M.; Running, S.W. Improvements to a MODIS Global Terrestrial Evapotranspiration Algorithm. Remote Sens. Environ. 2011, 115, 1781–1800. [Google Scholar] [CrossRef]
- Mu, Q.; Heinsch, F.A.; Zhao, M.; Running, S.W. Development of a Global Evapotranspiration Algorithm Based on MODIS and Global Meteorology Data. Remote Sens. Environ. 2007, 111, 519–536. [Google Scholar] [CrossRef]
- Didan, K.; Barreto Munoz, A.; Solano, R.; Huete, A. MODIS Vegetation Index User’s Guide; Collection 6; NASA: Washington, DC, USA, 2015.
- Ek, M.B.; Mitchell, K.E.; Lin, Y.; Rogers, E.; Grunmann, P.; Koren, V.; Gayno, G.; Tarpley, J.D. Implementation of Noah land surface model advances in the National Centers for Environmental Prediction operational mesoscale Eta model. J. Geophys. Res. 2003, 108, 8851. [Google Scholar] [CrossRef]
- Xia, Y.; Mitchell, K.; Ek, M.; Cosgrove, B.; Sheffield, J.; Luo, L.; Alonge, C.; Wei, H.; Meng, J.; Livneh, B.; et al. Continental-scale water and energy flux analysis and validation for North American Land Data Assimilation System project phase 2 (NLDAS-2): 2. Validation of model-simulated streamflow. J. Geophys. Res. 2012, 117, D03110. [Google Scholar] [CrossRef]
- Guswa, A.J.; Celia, M.A.; Rodriguez-Iturbe, I. Models of soil moisture dynamics in ecohydrology: A comparative study. Water Resour. Res. 2002, 38, 5-1–5-15. [Google Scholar] [CrossRef]
- Colliander, A. SMAP/In Situ Core Validation Site Land Surface Parameters Match-Up Data, Version 1; NASA National Snow and Ice Data Center Distributed Active Archive Center: Boulder, CO, USA, 2017. [CrossRef]
- Gutmann, E.D.; Small, E.E. A comparison of land surface model soil hydraulic properties estimated by inverse modeling and pedotransfer functions. Water Resour. Res. 2007, 43, W05418. [Google Scholar] [CrossRef]
- Kurc, S.A.; Small, E.E. Dynamics of evapotranspiration in semiarid grassland and shrubland ecosystems during the summer monsoon season, central New Mexico. Water Resour. Res. 2004, 40, W09305. [Google Scholar] [CrossRef]
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).