Evaluation of the Weak Constraint Data Assimilation Approach for Estimating Turbulent Heat Fluxes at Six Sites
Abstract
:1. Introduction
2. Methodology
2.1. Heat Diffusion Equation
2.2. Surface Energy Balance (SEB) equation
2.3. Adjoint State Formulation
3. Study Domain and Data
4. Results and Discussions
4.1. Neutral Bulk Heat Transfer Coefficient
4.2. Evaporative Fraction
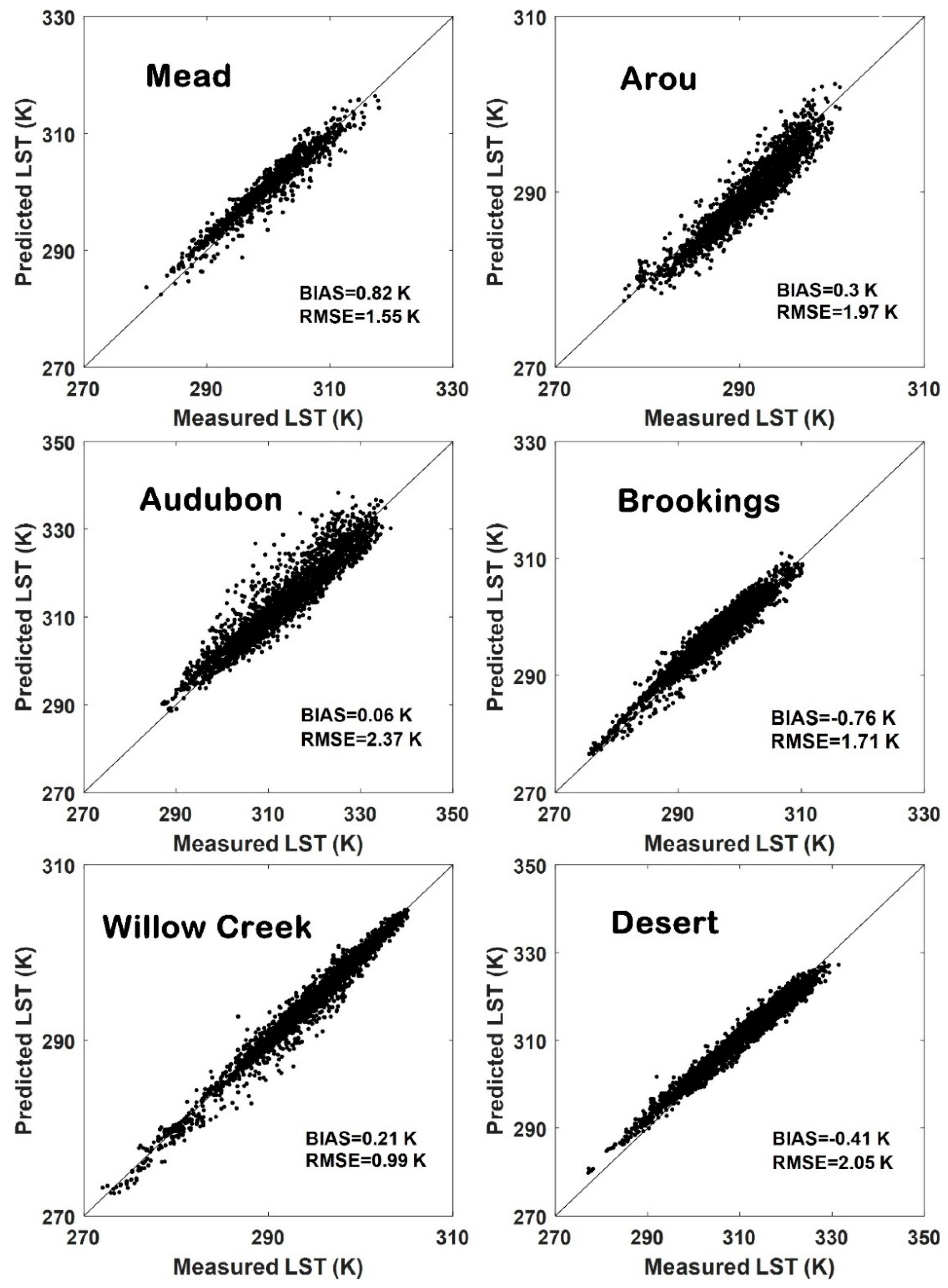
4.3. Land Surface Temperature
4.4. Sensible and Latent Heat Fluxes
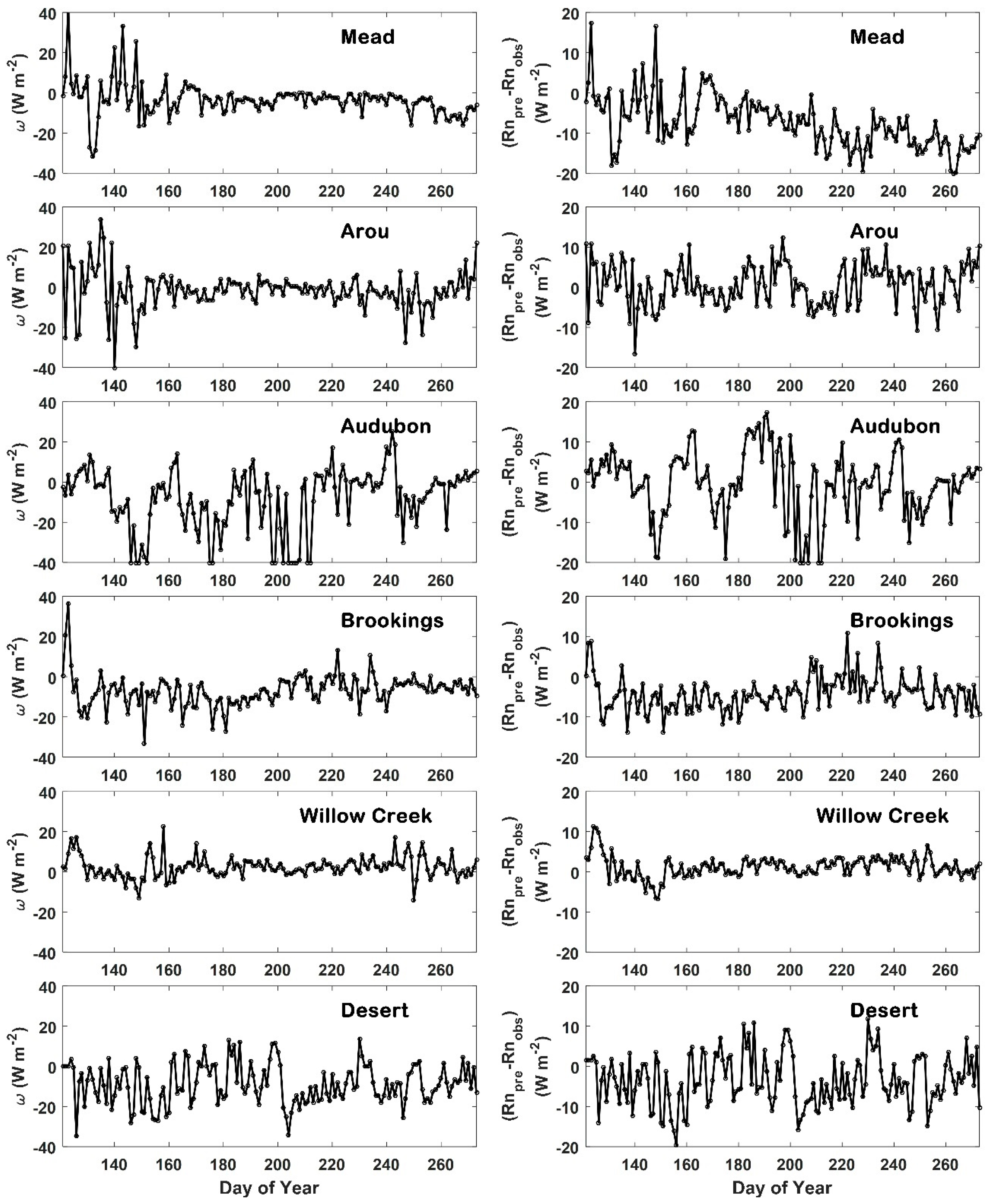
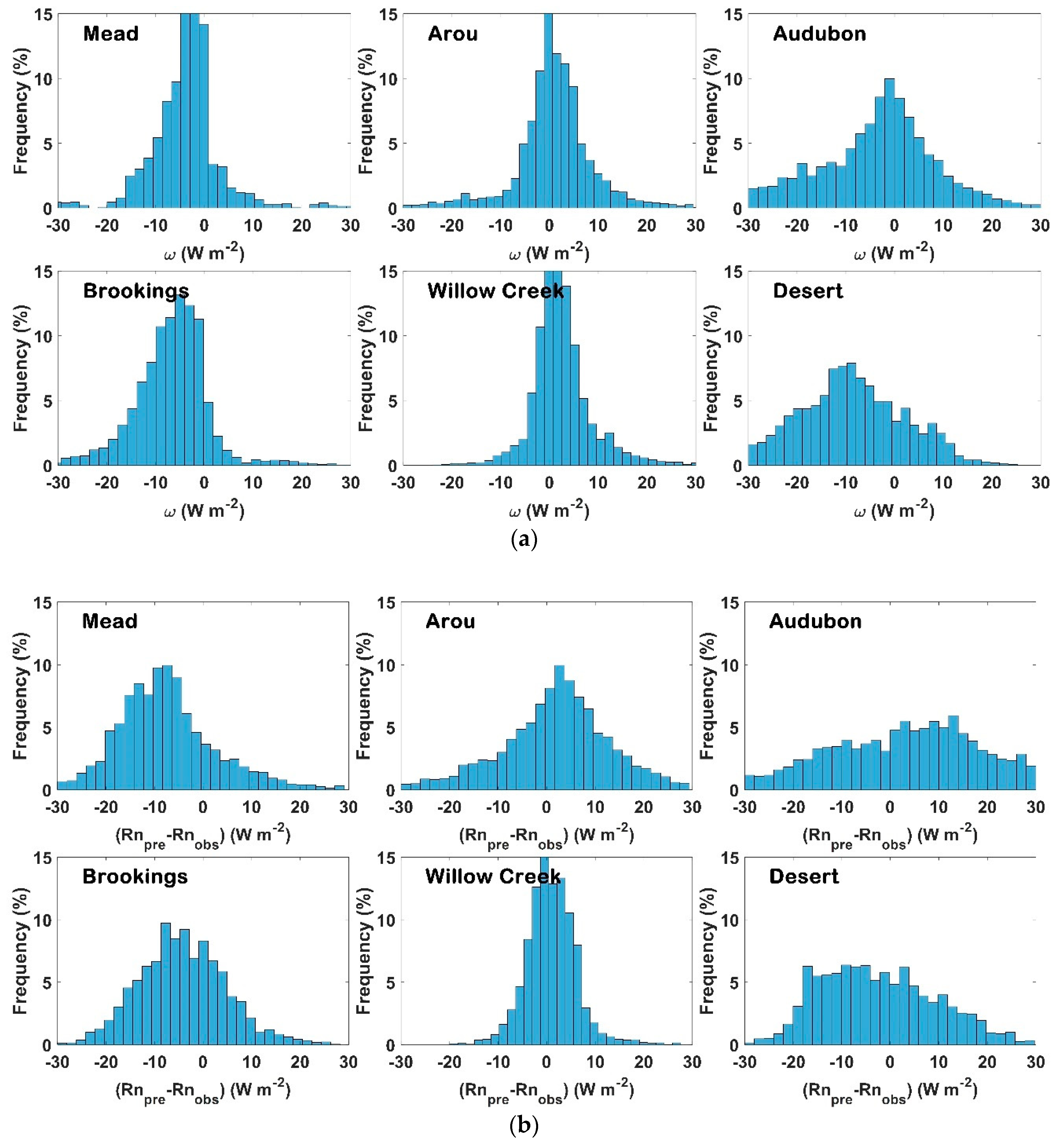
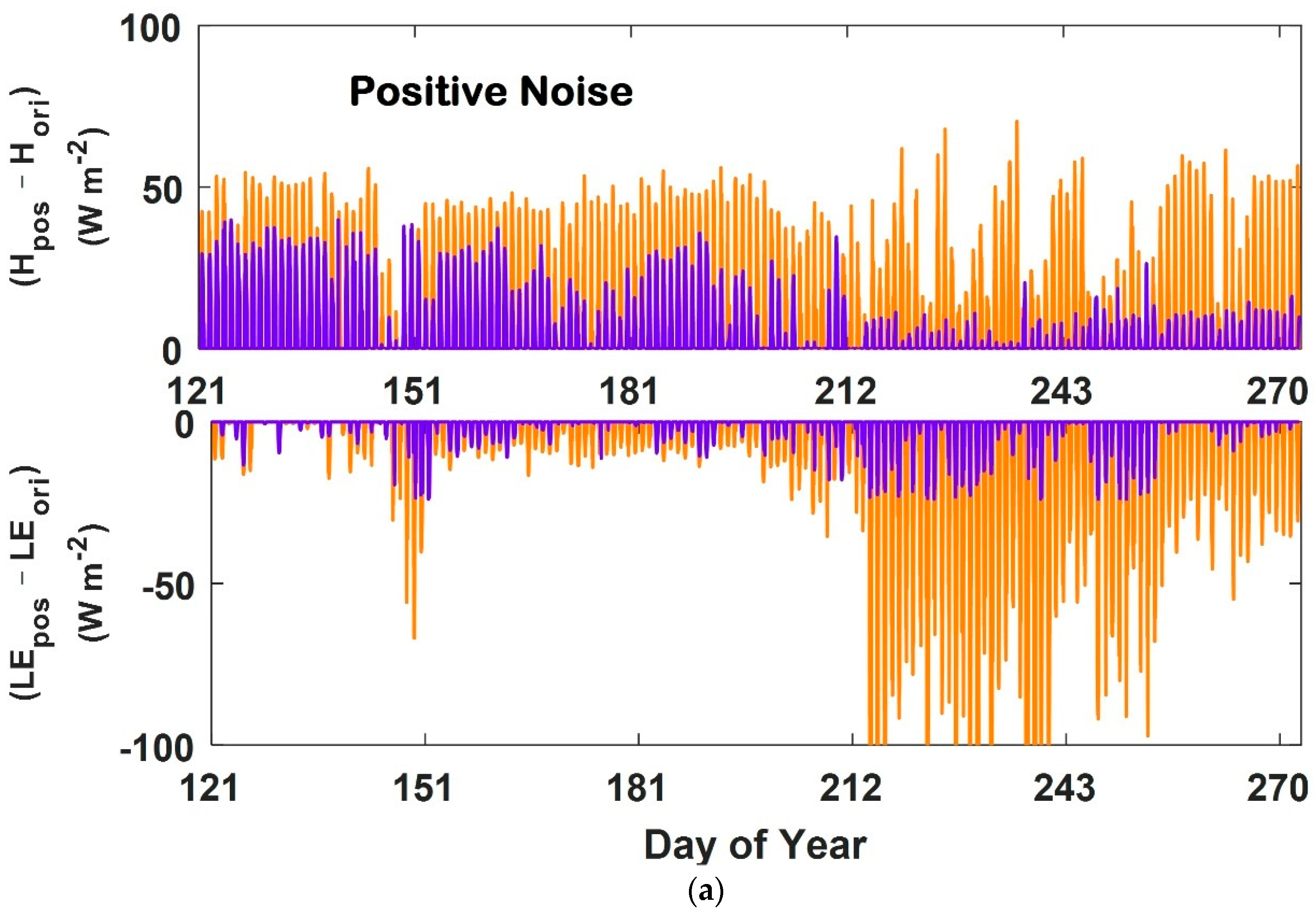
4.5. Model Error Analysis
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A. Difference between the 3D- and 4D-VDA Approaches
Appendix B. Euler-Lagrange Equations
References
- Alfieri, J.G.; Blanken, P.D.; Smith, D.; Morgan, J. Concerning the measurement and magnitude of heat, watervapor, and carbon dioxide exchange from a semiarid grassland. J. Appl. Meteorol. Climatol. 2009, 48, 982–996. [Google Scholar] [CrossRef]
- Stephens, G.L.; Li, J.; Wild, M.; Clayson, C.A.; Loeb, N.; Kato, S.; L’Ecuyer, T.; Stackhouse, P.W.; Lebsock, M.; Andrews, T. An update on Earth’s energy balance in light of the latest global observations. Nat. Geosci. 2012, 5, 691–696. [Google Scholar] [CrossRef]
- Xu, T.; Guo, Z.; Liu, S.; He, X.; Meng, Y.; Xu, Z.; Xia, Y.; Xiao, J.; Zhang, Y.; Ma, Y.; et al. Evaluating different machine learning methods for upscaling evapotranspiration from flux towers to the regional scale. J. Geophys. Res. Atmos. 2018, 123, 8674–8690. [Google Scholar] [CrossRef]
- Norman, J.M.; Kustas, W.P.; Humes, K. Source approach for estimating soil and vegetation energy fluxes in observations of directional radiometric surface temperature. Agric. For. Meteorol. 1995, 77, 263–293. [Google Scholar] [CrossRef]
- Bastiaanssen, W.G.M.; Menenti, M.; Feddes, R.A.; Holtslag, A.A.M. A remote sensing surface energy balance algorithm for land (SEBAL): 1. Formulation. J. Hydrol. 1998, 212–213, 198–212. [Google Scholar] [CrossRef]
- Bastiaanssen, W.G.M.; Pelgrum, H.; Wang, J.; Ma, Y.; Moreno, J.F.; Roerink, G.J.; van der Wal, T. A remote sensing surface energy balance algorithm for land (SEBAL): 2. Validation. J. Hydrol. 1998, 212–213, 213–229. [Google Scholar] [CrossRef]
- Jiang, L.; Islam, S. Estimation of surface evaporation map over Southern Great Plain using remote sensing data. Water Resour. Res. 2001, 37, 329–340. [Google Scholar] [CrossRef]
- Su, Z. The Surface Energy Balance System (SEBS) for estimation of turbulent heat fluxes. Hydrol. Earth Syst. Sci. 2002, 6, 85–100. [Google Scholar] [CrossRef] [Green Version]
- Wang, K.C.; Dickinson, R.E. A review of global terrestrial evapotranspiration: Observation, modeling, climatology, and climatic variability. Rev. Geophys. 2012, 50. [Google Scholar] [CrossRef] [Green Version]
- Yao, Y.; Liang, S.; Li, X.; Chen, J.; Wang, K.; Jia, K.; Cheng, J.; Jiang, B.; Fisher, J.; Mu, Q.; et al. A satellite-based hybrid algorithm to determine the Priestley-Taylor parameter for global terrestrial latent heat flux estimation across multiple biomes. Remote Sens. Environ. 2015, 165, 216–233. [Google Scholar] [CrossRef]
- Song, L.S.; Kustas, W.P.; Liu, S.M.; Colaizzi, P.D.; Nieto, H.; Xu, Z.W.; Ma, Y.F.; Li, M.S.; Xu, T.R.; Agam, N.; et al. Applications of a thermal-based two-source energy balance model using Priestley-Taylor approach for surface temperature partitioning under advective conditions. J. Hydrol. 2016, 540, 574–587. [Google Scholar] [CrossRef] [Green Version]
- Fisher, J.B.; Melton, F.; Middleton, E.; Hain, C.; Anderson, M.; Allen, R.; McCabe, M.; Hook, S.; Baldocchi, D.; Townsend, P.A.; et al. The Future of Evapotranspiration: Global requirements for ecosystem functioning, carbon and climate feedbacks, agricultural management, and water resources. Water Resour. Res. 2017, 53, 2618–2626. [Google Scholar] [CrossRef]
- Ma, Y.; Liu, S.; Song, L.; Xu, Z.; Liu, Y.; Xu, T.; Zhu, T. Estimation of daily evapotranspiration and irrigation water efficiency at a Landsat-like scale for an arid irrigation area using multi-source remote sensing data. Remote Sens. Environ. 2018, 216, 715–734. [Google Scholar] [CrossRef]
- Bateni, S.; Entekhabi, D. Surface heat flux estimation with the ensemble Kalman smoother: Joint estimation of state and parameters. Water Resour. Res. 2012, 48, W08521. [Google Scholar] [CrossRef]
- Jiang, L.; Islam, S. An intercomparison of regional latent heat flux estimation using remote sensing data. Int. J. Remote Sens. 2003, 24, 2221–2236. [Google Scholar] [CrossRef]
- Nishida, K.; Nemani, R.R.; Glassy, J.M.; Running, S.W. Development of an evapotranspiration Index from Aqua/MODIS for monitoring surface moisture status. IEEE Geosci. Remote Sens. 2003, 41, 493–500. [Google Scholar] [CrossRef]
- Wang, K.; Li, Z.; Cribb, M. Estimating of evaporative fraction from a combination of day and night land surface temperature and NDVI: A new method to determine the Priestley-Taylor parameter. Remote Sens. Environ. 2006, 102, 293–305. [Google Scholar] [CrossRef]
- Tang, R.; Li, Z.L.; Tang, B. An application of the Ts-VI triangle method with enhanced edges determination for evapotranspiration estimation from MODIS data in arid and semi-arid regions: Implementation and validation. Remote Sens. Environ. 2010, 114, 540–551. [Google Scholar] [CrossRef]
- Sun, L.; Liang, S.; Yuan, W.; Chen, Z. Improving a Penman-Monteith evapotranspiration model by incorporating soil moisture control on soil evaporation in semiarid areas. Int. J. Digit. Earth 2013, 6, 134–156. [Google Scholar] [CrossRef]
- Zhu, W.; Jia, S.; Lv, A. A universal Ts-VI triangle method for the continuous retrieval of evaporative fraction from MODIS products. J. Geophys. Res. Atmos. 2017, 122, 10206–10227. [Google Scholar] [CrossRef]
- Liu, S.M.; Hu, G.; Lu, L. Estimation of regional evapotranspiration by TM/ETM+ data over heterogeneous surfaces. Photogramm. Eng. Remote Sens. 2007, 73, 1169–1178. [Google Scholar] [CrossRef]
- Jia, L.; Xi, G.; Liu, S.; Huang, C.; Yan, Y.; Liu, G. Regional estimation of daily to annual regional evapotranspiration with MODIS data in the Yellow River Delta wetland. Hydrol. Earth Syst. Sci. 2009, 13, 1775–1787. [Google Scholar] [CrossRef]
- Mallick, K.; Jarvis, A.J.; Fisher, J.B.; Tu, K.P.; Boegh, E.; Niyogi, D. Latent heat flux and canopy conductance based on Penman-Monteith, Priestly-Taylor equation, and Bouchets complementary hypothesis. J. Hydrometeorol. 2013, 14, 419–442. [Google Scholar] [CrossRef]
- Mallick, K.; Jarvis, A.J.; Boegh, E.; Fisher, J.B.; Drewry, D.T.; Tu, K.P.; Hook, S.J.; Hulley, G.; Ardö, J.; Beringer, J.; et al. A surface temperature initiated closure (STIC) for surface energy balance fluxes. Remote Sens. Environ. 2014, 141, 243–261. [Google Scholar] [CrossRef]
- Peters-Lidard, C.D.; Kumar, S.V.; Mocko, D.M.; Tian, Y. Estimating evapotranspiration with land data assimilation systems, hydrological processes. Hydrol. Processes 2011, 25, 3979–3992. [Google Scholar] [CrossRef]
- Xu, T.R.; Liu, S.M.; Liang, S.; Qin, J. Improving predictions of water and heat fluxes by assimilating MODIS land surface temperature products into common land model. J. Hydrometeorol. 2011, 12, 227–244. [Google Scholar] [CrossRef]
- Xu, T.R.; Liang, S.; Liu, S. Estimating turbulent fluxes through assimilation of geostationary operational environmental satellites data using ensemble Kalman filter. J. Geophys. Res. 2011, 116, D09109. [Google Scholar] [CrossRef]
- Xu, T.R.; Liu, S.M.; Xu, Z.W.; Liang, S.; Xu, L. A dual-pass data assimilation scheme for estimating surface fluxes with FY3A-VIRR land surface temperature. Sci. China Earth Sci. 2015, 58, 211–230. [Google Scholar] [CrossRef]
- Xia, Y.; Sheffield, J.S.; Ek, M.B.; Dong, J.; Chaney, N.; Wei, H.; Meng, J.; Wood, E.F. Evaluation of multi-model simulated soil moisture in NLDAS-2. J. Hydrol. 2014, 512, 107–125. [Google Scholar] [CrossRef]
- Xia, Y.; Ek, M.; Mocko, D.; Peters-Lidard, C.; Sheffield, J.; Dong, J.; Wood, E. Uncertainties, correlations, and optimal blends of drought indices from the NLDAS multiple land surface model ensemble. J. Hydrometeor. 2014. [Google Scholar] [CrossRef]
- Carrera, M.; Belair, S.; Bilodeau, B. The Canadian Land Data Assimilation System (CaLDAS): Description and synthetic evaluation study. J. Hydrometeor. 2015, 16, 1293–1314. [Google Scholar] [CrossRef]
- Crow, W.T.; Kustas, W.P. Utility of assimilating surface radiometric temperature observations for evaporative fraction and heat transfer coefficient retrieval. Bound. Layer Meteorol. 2005, 115, 105–130. [Google Scholar] [CrossRef]
- Sini, F.; Boni, G.; Caparrini, F.; Entekhabi, D. Estimation of large-scale evaporation fields based on assimilation of remotely sensed land temperature. Water Resour. Res. 2008, 44, W06410. [Google Scholar] [CrossRef]
- Bateni, S.M.; Liang, S. Estimating surface energy fluxes using a dual-source data assimilation approach adjoined to the heat diffusion equation. J. Geophys. Res. 2012, 117, D17118. [Google Scholar] [CrossRef]
- Bateni, S.M.; Entekhabi, D.; Jeng, D.S. Variational assimilation of land surface temperature and the estimation of surface energy balance components. J. Hydrol. 2013, 481, 143–156. [Google Scholar] [CrossRef]
- Xu, T.R.; Bateni, S.M.; Liang, S.; Entekhabi, D.; Mao, K.B. Estimation of surface turbulent heat fluxes via variational assimilation of sequences of land surface temperatures from Geostationary Operational Environmental Satellites. J. Geophys. Res. 2014, 119, 10780–10798. [Google Scholar] [CrossRef]
- Xu, T.R.; Bateni, S.M.; Liang, S. Estimating turbulent heat fluxes with a weak-constraint data assimilation scheme: A case study (HiWATER-MUSOEXE). IEEE Geosci. Remote Sens. 2015, 12, 68–72. [Google Scholar]
- Xu, T.R.; Bateni, S.M.; Margulis, S.A.; Song, L.; Liu, S.M.; Xu, Z.W. Partitioning Evapotranspiration into Soil Evaporation and Canopy Transpiration via a Two-Source Variational Data Assimilation System. J. Hydrometeorol. 2016, 17, 2353–2370. [Google Scholar] [CrossRef]
- Xu, T.; Bateni, S.M.; Neale, C.M.U.; Auligne, T.; Liu, S. Estimation of turbulent heat fluxes by assimilation of land surface temperature observations from GOES satellites into an ensemble Kalman smoother framework. J. Geophys. Res. Atmos. 2018, 123, 2409–2423. [Google Scholar] [CrossRef]
- Abdolghafoorian, A.; Farhadi, L.; Bateni, S.M.; Margulis, S.; Xu, T.R. Characterizing the effect of vegetation dynamics on the bulk heat transfer coefficient to improve variational estimation of surface turbulent fluxes. J. Hydrometeorol. 2017, 18, 321–333. [Google Scholar] [CrossRef]
- Hu, Z.; Islam, S. Prediction of ground temperature and soil moisture content by the force–restore method. Water Resour. Res. 1995, 31, 2531–2539. [Google Scholar] [CrossRef]
- Bateni, S.M.; Entekhabi, D.; Castelli, F. Mapping evaporation and estimation of surface control of evaporation using remotely sensed land surface temperature from a constellation of satellites. Water Resour. Res. 2013, 49, 950–968. [Google Scholar] [CrossRef] [Green Version]
- Gentine, P.; Entekhabi, D.; Chehbouni, A.; Boulet, G.; Duchemin, B. Analysis of evaporative fraction diurnal behaviour. Agric. For. Meteorol. 2007, 143, 13–29. [Google Scholar] [CrossRef] [Green Version]
- Reichle, R.H. Data assimilation methods in the earth sciences. Adv. Water Resour. 2008, 31, 1411–1418. [Google Scholar] [CrossRef]
- Margulis, S.; Entekhabi, D. Variational assimilation of surface temperature and micrometeorology into a model of the atmospheric boundary layer and land surface. Mon. Weather Rev. 2003, 131, 1272–1288. [Google Scholar] [CrossRef]
- Rodgers, C. Inverse Methods for Atmospheric Sounding; World Scientific: Singapore, 2000. [Google Scholar]
- Tremolet, Y. Accounting for an imperfect model in 4d-var. Quart. J. R. Meteorol. Soc. 2006, 132, 2483–2504. [Google Scholar] [CrossRef]
- Baldocchi, D.; Falge, E.; Gu, L.H.; Olson, R. FLUXNET: A new tool to study the temporal and spatial variability of ecosystem-scale carbon dioxide, water vapor, and energy flux densities. Bull. Am. Meteorol. Soc. 2001, 82, 2415–2434. [Google Scholar] [CrossRef]
- Liu, S.M.; Xu, Z.W.; Wang, W.Z.; Bai, J.; Jia, Z.; Zhu, M.; Wang, J.M. A comparison of eddy-covariance and large aperture scintillometer measurements with respect to the energy balance closure problem. Hydrol. Earth Syst. Sci. 2011, 15, 1291–1306. [Google Scholar] [CrossRef] [Green Version]
- Li, X.; Cheng, G.D.; Liu, S.M.; Xiao, Q.; Ma, M.G.; Jin, R.; Che, T.; Liu, Q.H.; Wang, W.Z.; Qi, Y.; et al. Heihe Watershed Allied Telemetry Experimental Research (HiWATER): Scientific objectives and experimental design. Bull. Am. Meteorol. Soc. 2013, 94, 1145–1160. [Google Scholar] [CrossRef]
- Xiao, Z.; Liang, S.; Wang, J.; Chen, P.; Yin, X.; Zhang, L.; Song, J. Use of general regression neural networks for generating the GLASS leaf area index product from time-series MODIS surface reflectance. IEEE Trans. Geosci. Remote Sens. 2013, 52, 209–223. [Google Scholar] [CrossRef]
- Xiao, Z.; Liang, S.; Wang, J.; Xiang, Y.; Zhao, X.; Song, J. Long-Time-Series Global Land Surface Satellite Leaf Area Index Product Derived From MODIS and AVHRR Surface Reflectance. IEEE Trans. Geosci. Remote Sens. 2016, 54, 5301–5318. [Google Scholar] [CrossRef]
- Chen, S.X. Thermal conductivity of sands. Heat Mass Transf. 2008, 44, 1241–1246. [Google Scholar] [CrossRef]
- Farouki, O.T. Thermal Properties of Soils; TransTech: Clausthal-Zellerfeld, Germany, 1986. [Google Scholar]
- Usowicz, B.; Lipiec, J.; Marczewski, W.; Ferrero, A. Thermal conductivity modeling of terrestrial soil media—A comparative study. Planet. Space Sci. 2006, 54, 1086–1095. [Google Scholar] [CrossRef]
- Song, X.; Liu, F.; Zhang, G.; Li, D.; Zhao, Y. Estimation of soil texture at a regional scale using local soil-landscape models. Soil Sci. 2016, 181, 435–445. [Google Scholar] [CrossRef]
- Brutsaert, W. Heat and mass transfer to and from surfaces with dense vegetation or similar permeable roughness. Bound. Layer Meteorol. 1979, 16, 365–388. [Google Scholar] [CrossRef]
- Duynkerke, P.G. The roughness length for heat and other vegetation parameters for a surface of short grass. J. Appl. Meteorol. 1992, 31, 579–586. [Google Scholar] [CrossRef]
- Shokri, N.; Lehmann, P.; Vontobel, P.; Or, D. Drying front and water content dynamics during evaporation from sand delineated by neutron radiography. Water Resour. Res. 2008, 44, W06418. [Google Scholar] [CrossRef]
- Shokri, N.; Lehmann, P.; Or, D. Characteristics of evaporation from partially wettable porous media. Water Resour. Res. 2008, 45, W02415. [Google Scholar] [CrossRef]
- Mazzarella, V.; Maiello, I.; Capozzi, V.; Budillon, G.; Ferretti, R. Comparison between 3D-Var and 4D-Var data assimilation methods for the simulation of a heavy rainfall case in central Italy. Adv. Sci. Res. 2017, 14, 271–278. [Google Scholar] [CrossRef] [Green Version]
- Errico, R.M. What is an adjoint method? Bull. Am. Meteorol. Soc. 1997, 78, 2577–2591. [Google Scholar] [CrossRef]
- Errico, R.M.; Reader, K.D. An examination of the accuracy of the linearization of a mesoscale model with moist physics. Q. J. R. Meteorol. Soc. 1999, 125, 169–195. [Google Scholar] [CrossRef]
- Errico, R.M.; Vukicevic, T.; Reader, K. Examination of the accuracy of a tangent linear model. Tellus 1993, 45A, 462–477. [Google Scholar] [CrossRef]






| Site | Location | Land Cover | LAI | fc | SM | Elevation (m) |
|---|---|---|---|---|---|---|
| Mead | 41.18N, 96.44W | Cropland | 1.75 | 0.53 | 0.25 | 363 |
| Arou | 38.04N, 100.46E | Grassland | 2.53 | 0.72 | 0.34 | 3033 |
| Audubon | 31.59N, 110.51W | Grassland | 0.39 | 0.17 | 0.07 | 1469 |
| Brookings | 44.34N, 96.83W | Grassland | 2.24 | 0.67 | 0.45 | 510 |
| Willow Creek | 45.80N, 90.08W | Forest | 4.8 | 0.91 | 0.30 | 520 |
| Desert | 42.11N, 100.99E | Barren land | 0 | 0 | 0.01 | 1000 |
| Site | 121–151 | 152–181 | 182–212 | 213–243 | 244–273 | |
|---|---|---|---|---|---|---|
| Mead | CHN | 0.22 × 10−2 | 0.40 × 10−2 | 1.22 × 10−2 | 1.48 × 10−2 | 0.78 × 10−2 |
| LAI | 0.77 | 1.28 | 2.42 | 2.70 | 1.54 | |
| Arou | CHN | 0.12 × 10−2 | 0.46 × 10−2 | 3.35 × 10−2 | 5.12 × 10−2 | 1.98 × 10−2 |
| LAI | 0.46 | 1.77 | 3.79 | 4.22 | 2.42 | |
| Audubon | CHN | 0.31 × 10−2 | 0.35 × 10−2 | 0.42 × 10−2 | 0.31 × 10−2 | 0.25 × 10−2 |
| LAI | 0.23 | 0.30 | 0.35 | 0.54 | 0.53 | |
| Brookings | CHN | 0.72 × 10−2 | 1.54 × 10−2 | 3.12 × 10−2 | 1.55 × 10−2 | 0.62 × 10−2 |
| LAI | 1.30 | 2.37 | 2.85 | 2.74 | 1.94 | |
| Willow Creek | CHN | 6.33 × 10−2 | 7.45 × 10−2 | 8.61 × 10−2 | 14.35 × 10−2 | 8.13 × 10−2 |
| LAI | 2.64 | 5.35 | 5.88 | 5.73 | 4.40 | |
| Desert | CHN | 0.13 × 10−3 | 0.14 × 10−3 | 0.18 × 10−3 | 0.19 × 10−3 | 0.12 × 10−3 |
| LAI | 0 | 0 | 0 | 0 | 0 |
| Bias (K) | RMSE (K) | |||
|---|---|---|---|---|
| Study Sites | WC-VDA | SC-VDA | WC-VDA | SC-VDA |
| Mead | 0.82 | −1.23 | 1.55 | 1.71 |
| Arou | 0.30 | 0.5 | 1.97 | 2.07 |
| Audubon | 0.06 | 0.23 | 2.37 | 2.75 |
| Brookings | −0.76 | −0.86 | 1.71 | 1.72 |
| Willow Creek | 0.21 | 0.56 | 0.99 | 1.06 |
| Desert | −0.41 | −0.92 | 2.05 | 2.53 |
| Six-sites-average | 0.04 | −0.29 | 1.77 | 1.97 |
| a | |||||
| Study Site | Method | H (W·m−2) | LE (W·m−2) | ||
| Bias | RMSE | Bias | RMSE | ||
| Mead | WC-VDA (SC-VDA) | 8.73 (10.21) | 64.60 (69.25) | −3.81 (−8.65) | 63.07 (75.55) |
| Arou | WC-VDA (SC-VDA) | −11.64 (−15.75) | 52.28 (55.63) | −0.49 (5.32) | 70.54 (79.88) |
| Audubon | WC-VDA (SC-VDA) | 16.25 (20.21) | 56.44 (67.82) | 7.95 (12.19) | 54.37 (57.55) |
| Brookings | WC-VDA (SC-VDA) | 4.77 (10.88) | 42.72 (45.35) | −7.31 (−11.60) | 81.36 (83.86) |
| Willow Creek | WC-VDA (SC-VDA) | 7.67 (22.17) | 86.74 (91.18) | 19.88 (32.49) | 110.82 (125.60) |
| Desert | WC-VDA (SC-VDA) | 7.08 (12.68) | 54.30 (68.21) | 0.95 (1.25) | 24.45 (27.91) |
| b | |||||
| Study Site | Method | H (W·m−2) | LE (W·m−2) | ||
| Bias | RMSE | Bias | RMSE | ||
| Mead | WC-VDA (SC-VDA) | 5.32 (9.45) | 40.89 (43.28) | −3.05 (−7.51) | 40.75 (47.62) |
| Arou | WC-VDA (SC-VDA) | −0.37 (−3.43) | 31.56 (38.69) | 3.56 (17.74) | 32.71 (50.58) |
| Audubon | WC-VDA (SC-VDA) | 12.04 (16.15) | 31.95 (42.09) | 0.51 (−7.32) | 28.86 (22.98) |
| Brookings | WC-VDA (SC-VDA) | 2.50 (8.82) | 33.91 (36.54) | −13.13 (−17.61) | 60.52 (64.87) |
| Willow Creek | WC-VDA (SC-VDA) | 5.38 (19.88) | 52.46 (57.23) | 19.12 (25.76) | 56.59 (73.18) |
| Desert | WC-VDA (SC-VDA) | 7.51 (12.69) | 33.30 (49.64) | 0.43 (0.97) | 10.04 (12.71) |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
He, X.; Xu, T.; Bateni, S.M.; Neale, C.M.U.; Auligne, T.; Liu, S.; Wang, K.; Mao, K.; Yao, Y. Evaluation of the Weak Constraint Data Assimilation Approach for Estimating Turbulent Heat Fluxes at Six Sites. Remote Sens. 2018, 10, 1994. https://doi.org/10.3390/rs10121994
He X, Xu T, Bateni SM, Neale CMU, Auligne T, Liu S, Wang K, Mao K, Yao Y. Evaluation of the Weak Constraint Data Assimilation Approach for Estimating Turbulent Heat Fluxes at Six Sites. Remote Sensing. 2018; 10(12):1994. https://doi.org/10.3390/rs10121994
Chicago/Turabian StyleHe, Xinlei, Tongren Xu, Sayed M. Bateni, Christopher M. U. Neale, Thomas Auligne, Shaomin Liu, Kaicun Wang, Kebiao Mao, and Yunjun Yao. 2018. "Evaluation of the Weak Constraint Data Assimilation Approach for Estimating Turbulent Heat Fluxes at Six Sites" Remote Sensing 10, no. 12: 1994. https://doi.org/10.3390/rs10121994
APA StyleHe, X., Xu, T., Bateni, S. M., Neale, C. M. U., Auligne, T., Liu, S., Wang, K., Mao, K., & Yao, Y. (2018). Evaluation of the Weak Constraint Data Assimilation Approach for Estimating Turbulent Heat Fluxes at Six Sites. Remote Sensing, 10(12), 1994. https://doi.org/10.3390/rs10121994











