Optical Tracking Velocimetry (OTV): Leveraging Optical Flow and Trajectory-Based Filtering for Surface Streamflow Observations
Abstract
:1. Introduction
2. Case Studies and Methodology
2.1. Case Studies
2.1.1. Controlled Outdoor Tests in the Brenta River
2.1.2. A Moderate Flood Event in The Tiber River
2.2. Optical Tracking Velocimetry
2.2.1. Feature Detectors
2.2.2. Tracking Approach
2.2.3. Trajectory-Based Filtering
2.3. Alternative Algorithms
2.4. Velocity Data Extraction and Comparison
3. Results
3.1. Assessment of OTV through Controlled Outdoor Tests in the Brenta River
3.1.1. Average Surface Streamflow Velocity
3.1.2. Subsampled Video Acquisition Frequency
3.1.3. Subsampled Image Resolution
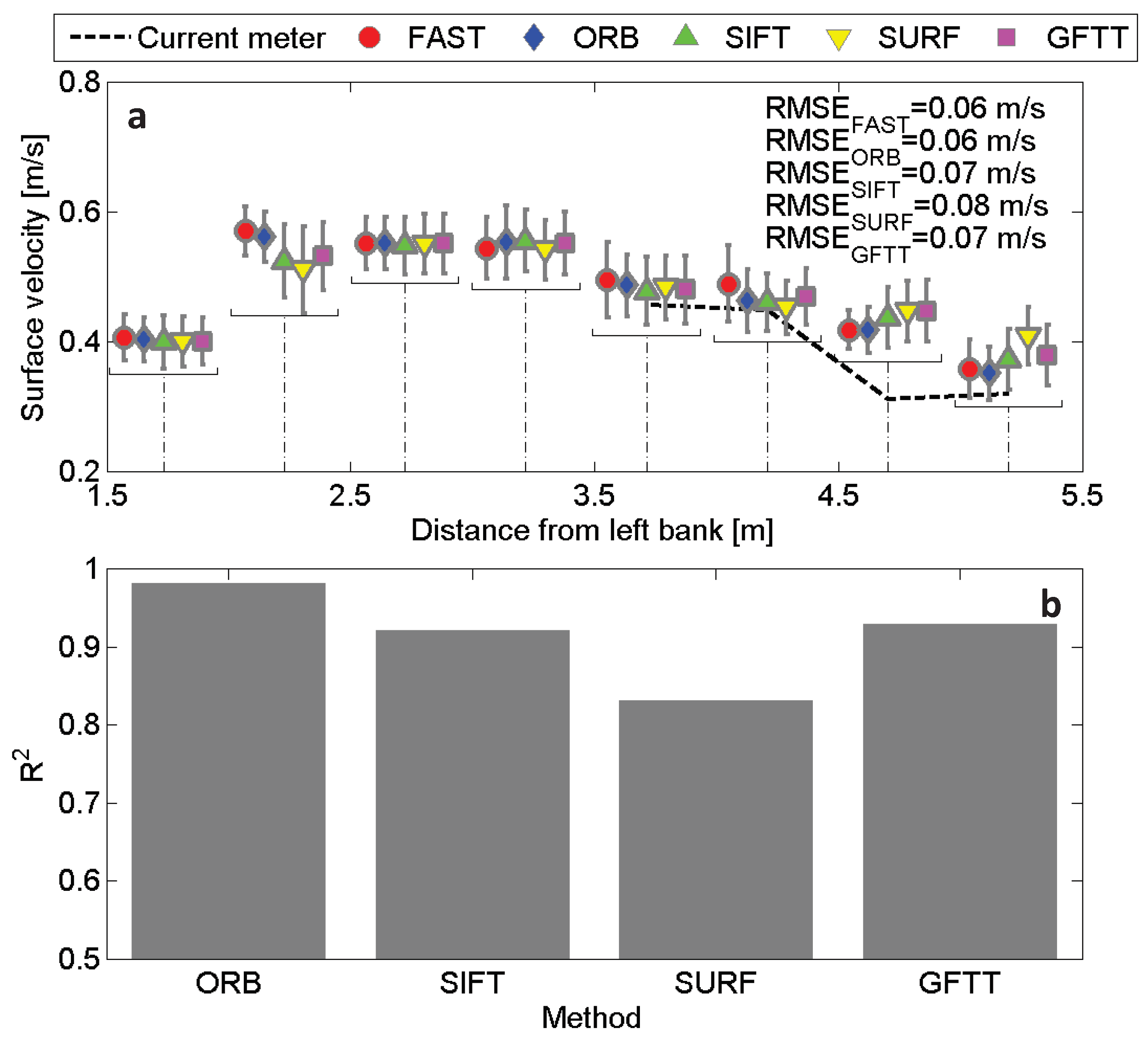
3.1.4. Feature Detector Performance
3.1.5. Comparison to Alternative Velocimetry Algorithms
3.2. Proof of Concept Moderate Flood in the Tiber River
3.2.1. OTV Observations
3.2.2. Comparison to Alternative Velocimetry Algorithms
4. Discussion and Recommendations
4.1. Suitability of OTV for Streamflow Observations
4.2. Comparison to Alternative Velocimetry Algorithms
4.3. Criticalities and Future Developments
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Clarke, T.R. Uncertainty in the estimation of mean annual flood due to rating-curve indefinition. J. Hydrol. 1999, 222, 185–190. [Google Scholar] [CrossRef]
- Di Baldassarre, G.; Montanari, A. Uncertainty in river discharge observations: A quantitative analysis. Hydrol. Earth Syst. Sci. 2009, 13, 913–921. [Google Scholar] [CrossRef]
- McMillan, H.; Freer, J.; Pappenberger, F.; Krueger, T.; Clark, M. Impacts of uncertain river flow data on rainfall-runoff model calibration and discharge predictions. Hydrol. Process. 2010, 24, 1270–1284. [Google Scholar] [CrossRef]
- Hairsine, P.B.; Rose, C.W. Modeling water erosion due to overland flow using physical principles: 1. Sheet flow. Water Resour. Res. 1992, 28, 237–243. [Google Scholar] [CrossRef]
- Yorke, T.H.; Oberg, K.A. Measuring river velocity and discharge with acoustic Doppler profilers. Flow Meas. Instrum. 2002, 13, 191–195. [Google Scholar] [CrossRef]
- Czuba, J.A.; Foufoula-Georgiou, E.; Gran, K.B.; Belmont, P.; Wilcock, P.R. Interplay between spatial explicit sediment sourcing, hierarchical river-network structure, and in-channel bed material sediment transport and storage dynamics. J. Geophys. Res. Earth Surf. 2017, 122, 1090–1120. [Google Scholar] [CrossRef]
- Costa, J.; Spicer, K.; Cheng, R.; Haeni, F.; Melcher, N.; Thurman, E.; Plant, W.; Keller, W. Measuring stream discharge by non-contact methods—A proof-of-concept experiment. Geophys. Res. Lett. 2000, 27, 553–556. [Google Scholar] [CrossRef]
- Tauro, F.; Petroselli, A.; Grimaldi, S. Optical sensing for stream flow observations: A review. J. Agric. Eng. 2018, 49. [Google Scholar] [CrossRef]
- Legleiter, C.J.; Mobley, C.D.; Overstreet, B.T. A framework for modeling connections between hydraulics, water surface roughness, and surface reflectance in open channel flows. J. Geophys. Res. Earth Surf. 2017, 122, 1715–1741. [Google Scholar] [CrossRef]
- Legleiter, C.J.; Kinzel, P.J.; Nelson, J.M. Remote measurement of river discharge using thermal particle image velocimetry (PIV) and various sources of bathymetric information. J. Hydrol. 2017, 554, 490–506. [Google Scholar] [CrossRef]
- Adrian, R.J. Particle-imaging techniques for experimental fluid-mechanics. Annu. Rev. Fluid Mech. 1991, 23, 261–304. [Google Scholar] [CrossRef]
- Adrian, R.J. Twenty years of particle image velocimetry. Exp. Fluids 2005, 39, 159–169. [Google Scholar] [CrossRef] [Green Version]
- Raffel, M.; Willert, C.E.; Wereley, S.T.; Kompenhans, J. Particle Image Velocimetry. A Practical Guide; Springer: New York, NY, USA, 2007. [Google Scholar]
- Fujita, I.; Muste, M.; Kruger, A. Large-scale particle image velocimetry for flow analysis in hydraulic engineering applications. J. Hydraul. Res. 1997, 36, 397–414. [Google Scholar] [CrossRef]
- Lloyd, P.M.; Stansby, P.K.; Ball, D.J. Unsteady surface-velocity field measurement using particle tracking velocimetry. J. Hydraul. Res. 1995, 33, 519–534. [Google Scholar] [CrossRef]
- Brevis, W.; Niño, Y.; Jirka, G.H. Integrating cross-correlation and relaxation algorithms for particle tracking velocimetry. Exp. Fluids 2011, 50, 135–147. [Google Scholar] [CrossRef]
- DalSasso, S.F.; Pizarro, A.; Samela, C.; Mita, L.; Manfreda, S. Exploring the optical experimental setup for surface flow velocity measurements using PTV. Environ. Monit. Assess. 2018, 190, 460. [Google Scholar] [CrossRef] [PubMed]
- Tauro, F.; Piscopia, R.; Grimaldi, S. Streamflow observations from cameras: Large-scale particle image velocimetry or particle tracking velocimetry? Water Resour. Res. 2017, 53, 10374–10394. [Google Scholar] [CrossRef]
- Tauro, F.; Piscopia, R.; Grimaldi, S. PTV-Stream: A simplified particle tracking velocimetry framework for stream surface flow monitoring. Catena 2019, 172, 378–386. [Google Scholar] [CrossRef]
- Horn, B.K.P.; Schunck, B.G. Determining optical flow. Artif. Intell. 1981, 17, 185–203. [Google Scholar] [CrossRef] [Green Version]
- Barron, J.L.; Fleet, D.J.; Beauchemin, S.S. Performance of optical flow techniques. Int. J. Comput. Vis. 1994, 12, 43–77. [Google Scholar] [CrossRef] [Green Version]
- Chao, H.; Gu, Y.; Napolitano, M. A survey of optical flow techniques for robotics navigation applications. J. Intell. Robot. Syst. 2014, 73, 361–372. [Google Scholar] [CrossRef]
- James, M.R.; Pinkerton, H.; Robson, S. Image-based measurement of flux variation in distal regions of active lava flows. Geochem. Geophys. Geosyst. 2007, 8, Q03006. [Google Scholar] [CrossRef]
- Raaf, O.; Adane, A. The determination of rainy clouds motion using optical flow. In Nonlinear and Complex Dynamics; Springer: New York, NY, USA, 2011; pp. 179–191. [Google Scholar]
- Li, L.; Chen, S.; Mai, X.F. Sub-pixel precipitation nowcasting over Guangdong province using opitcal flow algorithm. In Proceedings of the IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Fort Worth, TX, USA, 23–28 July 2017; pp. 4638–4641. [Google Scholar]
- Reinoso, J.F.; León, C.; Mataix, J. Optical flow algorithm as estimator of horizontal discrepancy between features derived from DEMs: Rivers and creeks as case study. Surv. Rev. 2013, 46, 149–154. [Google Scholar] [CrossRef]
- Mémin, E.; Pérez, P. Fluid motion recovery by coupling dense and parametric vector fields. In Proceedings of the 7th IEEE International Conference on Computer Vision, Kerkyra, Greece, 20–27 September 1999. [Google Scholar]
- Wildes, R.P.; Amabile, M.J.; Lanzillotto, A.M.; Leu, T.S. Recovering estimates of fluid flow from image sequence data. Comput. Vis. Image Understand. 2000, 80, 246–266. [Google Scholar] [CrossRef]
- Corpetti, T.; Heitz, D.; Arroyo, G.; Mémin, E. Fluid experimental flow estimation based on an optical-flow scheme. Exp. Fluids 2006, 40, 80–97. [Google Scholar] [CrossRef]
- Yuan, J.; Schnörr, C.; Mémin, E. Discrete orthogonal decomposition and variational fluid flow estimation. J. Math. Imaging Vis. 2007, 28, 67–80. [Google Scholar] [CrossRef]
- Liu, T.; Shen, L. Fluid flow and optical flow. J. Fluid Mech. 2008, 614, 253–291. [Google Scholar] [CrossRef]
- Sakaino, H. Fluid motion estimation method based on physical properties of waves. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Anchorage, AK, USA, 23–28 June 2008. [Google Scholar]
- Doshi, A.; Bors, A.G. Robust processing of optical flow of fluids. IEEE Trans. Image Process. 2010, 19, 2332–2344. [Google Scholar] [CrossRef]
- Liu, T.; Merat, A.; Makhmalbaf, M.H.M.; Fajardo, C.; Merati, P. Comparison between optical flow and cross-correlation methods for extraction of velocity fields from particle images. Exp. Fluids 2015, 56, 166. [Google Scholar] [CrossRef]
- Bruhn, A.; Weickert, J.; Schnörr, C. Pattern Recognition. In Lecture Notes in Computer Science; Chapter Combining the Advantages of Local and Global Optic Flow Methods; Springer: Berlin, Germany, 2002; Volume 2449, pp. 454–462. [Google Scholar]
- Plyer, A.; Le Besnerais, G.; Champagnat, F. Massively parallel Lucas Kanade optical flow for real-time video processing applications. J. Real-Time Image Process. 2016, 11, 713–730. [Google Scholar] [CrossRef]
- Quénot, G.M.; Pakleza, J.; Kowalewski, T.A. Particle image velocimetry with optical flow. Exp. Fluids 1998, 25, 177–189. [Google Scholar] [CrossRef]
- Shindler, L.; Moroni, M.; Cenedese, A. Using optical flow equation for particle detection and velocity prediction in particle tracking. Appl. Math. Comput. 2012, 218, 8684–8694. [Google Scholar] [CrossRef]
- Bacharidis, K.; Moirogiorgou, K.; Sibetheros, I.A.; Savakis, A.E.; Zervakis, M. River flow estimation using video data. In Proceedings of the IEEE International Conference on Imaging Systems and Techniques (IST) Proceedings, Santorini, Greece, 14–17 October 2014. [Google Scholar]
- Chang, J.; Edwards, D.; Yu, Y. Statistical estimation of fluid flow fields. In Proceedings of the ECCV Workshop on Statistical Methods in Video Processing, Lyon, France, 21–26 July 2002; pp. 91–96. [Google Scholar]
- Bung, D.B.; Valero, D. Application of the optical flow method to velocity determination in hydraulic structure models. In Proceedings of the 6th International Symposium on Hydraulic Structures, Portland, OR, USA, 27–30 June 2016; pp. 240–249. [Google Scholar]
- Dérian, P.; Almar, R. Wavelet-based optical flow estimation of instant surface currents from shore-based and UAV videos. IEEE Trans. Geosci. Remote Sens. 2017, 55, 5790–5797. [Google Scholar] [CrossRef]
- Ghalenoei, E.; Hasanlou, M. Monitoring of sea surface currents by using sea surface temperature and satellite altimetry data in the Caspian Sea. Earth Obs. Geomat. Eng. 2017, 1, 36–46. [Google Scholar]
- Vogel, C.; Bauder, A.; Schindler, K. Optical flow for glacier motion estimation. In Proceedings of the ISPRS Annals of the Photogrammetry, Remote Sensing and Spatial Information Sciences (XXII ISPRS Congress), Melbourne, Australia, 25 August–1 September 2012; Volume I-3, pp. 359–364. [Google Scholar]
- Karvonen, J. Virtual radar ice buoys—A method for measuring fine-scale sea ice drift. Cryosphere 2016, 10, 29–42. [Google Scholar] [CrossRef]
- Krout, D.W.; Okopal, G.; Jessup, A.; Hanusa, E. Tracking drifting surface objects with aerial infrared and electro-optical sensors. In Proceedings of the 2012 Oceans, Hampton Roads, VA, USA, 14–19 October 2012; pp. 1–4. [Google Scholar] [CrossRef]
- Waghmare, A.; Naik, A.A. Water velocity measurement using contact and non-contact type sensor. In Proceedings of the 2015 Communication, Control and Intelligent Systems (CCIS), Mathura, India, 7–8 November 2015; pp. 334–338. [Google Scholar]
- Zhang, G.; Chanson, H. Application of local opticl flow methods to high-velocity free-surface flows: Validation and application to stepped chutes. Exp. Therm. Fluid Sci. 2018, 90, 186–199. [Google Scholar] [CrossRef]
- Perks, M.T.; Russell, A.J.; Large, A.R.G. Technical Note: Advances in flash flood monitoring using unmanned aerial vehicles (UAVs). Hydrol. Earth Syst. Sci. 2016, 20, 4005–4015. [Google Scholar] [CrossRef]
- Tauro, F.; Porfiri, M.; Grimaldi, S. Orienting the camera and firing lasers to enhance large scale particle image velocimetry for streamflow monitoring. Water Resour. Res. 2014, 50, 7470–7483. [Google Scholar] [CrossRef] [Green Version]
- Forsyth, D.A.; Ponce, J. Computer Vision: A Modern Approach; Pearson: Prentice Hall, NJ, USA, 2011. [Google Scholar]
- Tauro, F.; Petroselli, A.; Porfiri, M.; Giandomenico, L.; Bernardi, G.; Mele, F.; Spina, D.; Grimaldi, S. A novel permanent gauge-cam station for surface-flow observations on the Tiber River. Geosci. Instrum. Methods Data Syst. 2016, 5, 241–251. [Google Scholar] [CrossRef] [Green Version]
- Tauro, F.; Salvatori, S. Surface flows from images: Ten days of observations from the Tiber River gauge-cam station. Hydrol. Res. 2016, 48, 646–655. [Google Scholar] [CrossRef]
- Tuytelaars, T.; Mikolajczyk, K. Local invariant feature detectors: A survey. Found. Trends® Comput. Graph. Vis. 2008, 3, 177–280. [Google Scholar] [CrossRef]
- Mikolajczyk, K.; Schmid, C. A performance evaluation of local descriptors. IEEE Trans. Pattern Anal. Mach. Intell. 2005, 27, 1615–1630. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Shi, J.; Tomasi, C. Good features to track. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Seattle, WA, USA, 21–23 June 1994. [Google Scholar]
- Lowe, D.G. Object recognition from local scale-invariant features. In Proceedings of the International Conference on Computer Vision (ICCV’99), Kerkyra, Greece, 20–27 September 1999; IEEE Computer Society: Washington, DC, USA, 1999; Volume 2, p. 1150. [Google Scholar]
- Valgren, C.; Lilienthal, A.J. SIFT, SURF & seasons: Appearance-based long-term localization in outdoor environments. Robot. Auton. Syst. 2010, 58, 149–156. [Google Scholar]
- Rosten, E.; Drummond, T. Machine learning for high-speed corner detection. In Proceedings of the ECCV, Graz, Austria, 7–13 May 2006. [Google Scholar]
- Bay, H.; Ess, A.; Tuytelaars, T.; Van Gool, L. Speeded-up robust features (SURF). Comput. Vis. Image Understand. 2008, 110, 346–359. [Google Scholar] [CrossRef]
- Rublee, E.; Rabaud, V.; Konolige, K.; Bradski, G. ORB: An efficient alternative to SIFT or SURF. In Proceedings of the 2011 International Conference on Computer Vision, Barcelona, Spain, 6–13 November 2011; pp. 2564–2571. [Google Scholar]
- Nourani-Vatani, N.; Borges, P.V.K.; Roberts, J.M. A study of feature extraction algorithms for optical flow tracking. In Proceedings of the Australasian Conference on Robotics and Automation, Wellington, New Zealand, 3–5 December 2012. [Google Scholar]
- Lucas, B.D.; Kanade, T. An iterative image registration technique with an application to stereo vision. In Proceedings of the 7th International Joint Conference On Artificial Intelligence (IJCAI’81), Vancouver, BC, Canada, 24–28 August 1981; Morgan Kaufmann Publishers Inc.: Vancouver, BC, Canada, 1981; Volume 2, pp. 674–679. [Google Scholar]
- Bouguet, J.Y. Pyramidal Implementation of the Lucas Kanade Feature Tracker—Description of the Algorithm; Technical Report; Intel Microprocessor Research Labs: Santa Clara, CA, USA, 1999. [Google Scholar]
- Hassan, Y.A.; Canaan, R.E. Full-field bubbly flow velocity measurements using a multiframe particle tracking technique. Exp. Fluids 1991, 12, 49–60. [Google Scholar] [CrossRef]
- Tauro, F.; Grimaldi, S. Ice dices for monitoring stream surface velocity. J. Hydro-Environ. Res. 2017, 14, 143–149. [Google Scholar] [CrossRef]
- Niroumand-Jadidi, M.; Vitti, A.; Lyzenga, D.R. Multiple Optimal Depth Predictors Analysis (MODPA) for river bathymetry: Findings from spectroradiometry, simulations, and satellite imagery. Remote Sens. Environ. 2018, 218, 132–147. [Google Scholar] [CrossRef]
- Tauro, F.; Selker, J.; van de Giesen, N.; Abrate, T.; Uijlenhoet, R.; Porfiri, M.; Manfreda, S.; Caylor, K.; Moramarco, T.; Benveniste, J.; et al. Measurements and Observations in the XXI century (MOXXI): Innovation and multidisciplinarity to sense the hydrological cycle. Hydrol. Sci. J. 2018, 63, 169–196. [Google Scholar] [CrossRef]
- Manfreda, S.; McCabe, M.F.; Miller, P.E.; Lucas, R.; Madrigal, V.P.; Mallinis, G.; Ben Dor, E.; Helman, D.; Estes, L.; Ciraolo, G.; et al. On the use of unmanned aerial systems for environmental monitoring. Remote Sens. 2018, 10, 641. [Google Scholar] [CrossRef]
- Hauet, A.; Kruger, A.; Krajewski, W.; Bradley, A.; Muste, M.; Creutin, J.; Wilson, M. Experimental system for real-time discharge estimation using an image-based method. J. Hydrol. Eng. 2008, 13, 105–110. [Google Scholar] [CrossRef]
- Huang, W.C.; Young, C.C.; Liu, W.C. Application of an automated discharge imaging system and LSPIV during typhoon events in Taiwan. Water 2018, 10, 280. [Google Scholar] [CrossRef]
- Chiu, C.L. Application of entropy concept in open-channel flow study. J. Hydraul. Eng. 1991, 117, 615–628. [Google Scholar] [CrossRef]
- Moramarco, T.; Saltalippi, C.; Singh, V.P. Estimation of mean velocity in natural channels based on Chiu’s velocity distribution equation. J. Hydraul. Eng. 2004, 9, 42–50. [Google Scholar] [CrossRef]







| 0.46 | 0.45 | 0.31 | 0.32 | |
| 0.04 | 0.03 | 0.02 | 0.02 |
| Method | Processing Time () | Frame-by-Frame Average Detected Features () | Total Tracked Features () |
|---|---|---|---|
| FAST | 43 | 19,098 | 18,076 |
| ORB | 61 | 37,968 | 18,325 |
| SIFT | 235 | 7656 | 24,119 |
| SURF | 83 | 10,076 | 21,887 |
| GFTT | 67 | 7788 | 24,747 |
| Random | 50 | 20,000 | 23,215 |
| FAST | ORB | SIFT | SURF | GFTT | LSPIV | Unf. PTV | Filt. PTV | PTV-Stream | |
|---|---|---|---|---|---|---|---|---|---|
| average velocity () | 1.54 | 1.57 | 1.50 | 1.49 | 1.52 | 0.39 | 0.66 | 1.4 | 1.6 |
| standard deviation () | 0.32 | 0.38 | 0.36 | 0.34 | 0.35 | 0.07 | 0.27 | 0.2 | 0.09 |
| trajectories () | 214,884 | 223,706 | 163,599 | 144,735 | 149,834 | – | 19,000 | 68 | 24 |
| time () | 34 | 40 | 94 | 43 | 42 | >3000 | >3000 | >3000 | >1000 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tauro, F.; Tosi, F.; Mattoccia, S.; Toth, E.; Piscopia, R.; Grimaldi, S. Optical Tracking Velocimetry (OTV): Leveraging Optical Flow and Trajectory-Based Filtering for Surface Streamflow Observations. Remote Sens. 2018, 10, 2010. https://doi.org/10.3390/rs10122010
Tauro F, Tosi F, Mattoccia S, Toth E, Piscopia R, Grimaldi S. Optical Tracking Velocimetry (OTV): Leveraging Optical Flow and Trajectory-Based Filtering for Surface Streamflow Observations. Remote Sensing. 2018; 10(12):2010. https://doi.org/10.3390/rs10122010
Chicago/Turabian StyleTauro, Flavia, Fabio Tosi, Stefano Mattoccia, Elena Toth, Rodolfo Piscopia, and Salvatore Grimaldi. 2018. "Optical Tracking Velocimetry (OTV): Leveraging Optical Flow and Trajectory-Based Filtering for Surface Streamflow Observations" Remote Sensing 10, no. 12: 2010. https://doi.org/10.3390/rs10122010
APA StyleTauro, F., Tosi, F., Mattoccia, S., Toth, E., Piscopia, R., & Grimaldi, S. (2018). Optical Tracking Velocimetry (OTV): Leveraging Optical Flow and Trajectory-Based Filtering for Surface Streamflow Observations. Remote Sensing, 10(12), 2010. https://doi.org/10.3390/rs10122010








