A Region Merging Segmentation with Local Scale Parameters: Applications to Spectral and Elevation Data
Abstract
1. Introduction
2. Materials and Methods
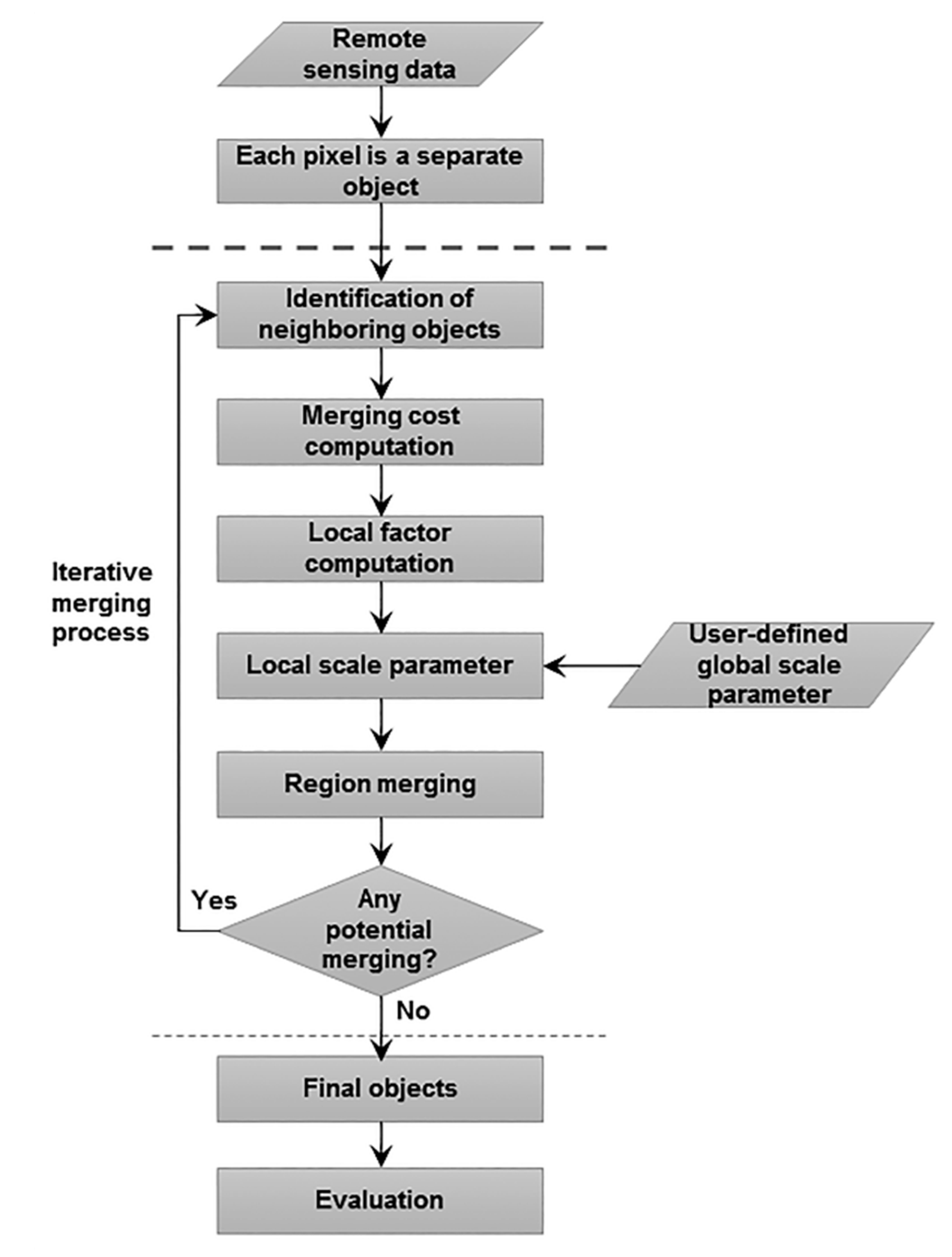
2.1. Overview
2.2. Segmentation
2.2.1. Merging Cost (MC)
2.2.2. Local Scale Parameter (SPlocal) Definition
2.2.3. Merging Order
2.3. Segmentation Comparison
2.4. Supervised Evaluation
2.5. Unsupervised Evaluation
3. Results
3.1. Remote Sensing Applications
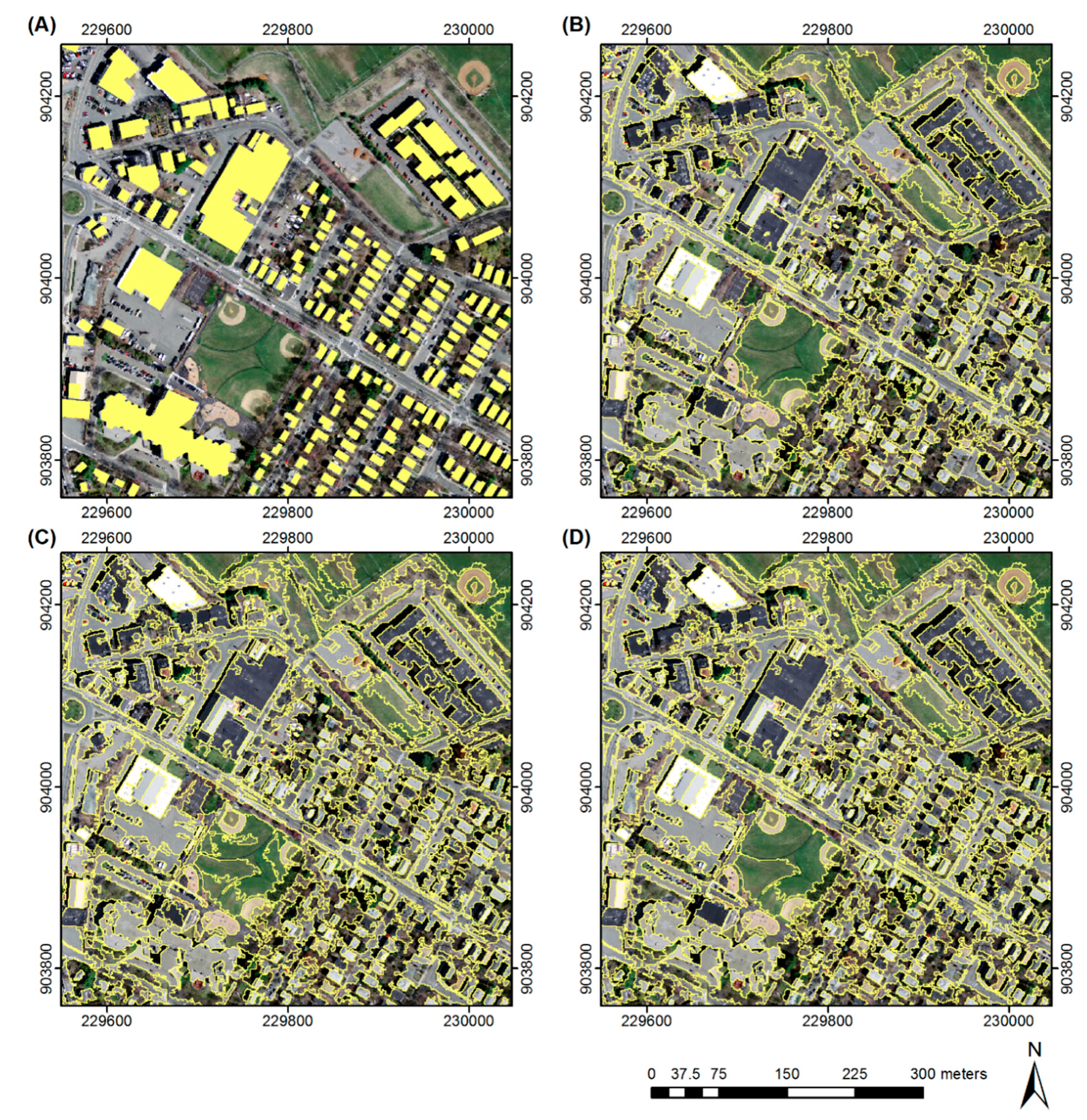
3.1.1. Building Delimitation from Spectral Data
3.1.2. Impact Crater Delimitation from Elevation Data
3.2. Building Delimitation from Spectral Data
3.3. Impact Crater Delimitation from Elevation Data
3.4. Comparison with a Relative Hybrid Segmentation Method
4. Discussion
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Blaschke, T.; Hay, G.J.; Kelly, M.; Lang, S.; Hofmann, P.; Addink, E.; Feitosa, R.Q.; Meer, F.V.D.; Werff, H.V.D.; Coillie, F.V. Geographic object-based image analysis—Towards a new paradigm. ISPRS J. Photogramm. Remote Sens. 2014, 87, 180–191. [Google Scholar] [CrossRef] [PubMed]
- Hay, G.J.; Castilla, G. Geographic Object-Based Image Analysis (GEOBIA): A new name for a new discipline. In Object-Based Image Analysis—Spatial Concepts for Knowledge-Driven Remote Sensing Applications; Blaschke, T., Lang, S., Hay, G., Eds.; Springer: Heidelberg/Berlin, Germany; New York, NY, USA, 2008; pp. 75–89. [Google Scholar]
- Schiewe, J. Segmentation of high-resolution remotely sensed data-concepts, applications and problems. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2002, 4, 380–385. [Google Scholar]
- Meinel, G.; Neubert, M. A Comparison of segmentation programs for high resolution remote sensing data. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2004, 35, 1097–1102. [Google Scholar]
- Baatz, M.; Schäpe, A. Multiresolution Segmentation—An Optimization Approach for High Quality Multi-Scale Image Segmentation. In Angewandte Geographische Informations-Verarbeitung; Strobl, J., Blaschke, T., Griesebner, G., Eds.; Wichmanm Verlag: Karlsruhe, Germany, 2000; pp. 12–23. [Google Scholar]
- Kim, M.; Warner, T.A.; Madden, M.; Atkinson, D.S. Multi-scale GEOBIA with very high spatial resolution digital aerial imagery: Scale, texture and image objects. Int. J. Remote Sens. 2011, 32, 2825–2850. [Google Scholar] [CrossRef]
- Espindola, G.M.; Camara, G.; Reis, I.A.; Bins, L.S.; Monteiro, A.M. Parameter selection for region-growing image segmentation algorithms using spatial autocorrelation. Int. J. Remote Sens. 2006, 27, 3035–3040. [Google Scholar] [CrossRef]
- Liu, J.; Du, M.; Mao, Z. Scale computation on high spatial resolution remotely sensed imagery multi-scale segmentation. Int. J. Remote Sens. 2017, 38, 5186–5214. [Google Scholar] [CrossRef]
- Johnson, B.; Xie, Z. Unsupervised image segmentation evaluation and refinement using a multi-scale approach. ISPRS J. Photogramm. Remote Sens. 2011, 66, 473–483. [Google Scholar] [CrossRef]
- Chen, J.; Deng, M.; Mei, X.M.; Chen, T.Q.; Shao, Q.B.; Hong, L. Optimal segmentation of a high-resolution remote-sensing image guided by area and boundary. Int. J. Remote Sens. 2014, 35, 6914–6939. [Google Scholar] [CrossRef]
- Yang, J.; He, Y.H.; Caspersen, J. Region merging using local spectral angle thresholds: A more accurate method for hybrid segmentation of remote sensing images. Remote Sens. Environ. 2017, 190, 137–148. [Google Scholar] [CrossRef]
- Wang, Y.; Meng, Q.; Qi, Q.; Yang, J.; Liu, Y. Region merging considering within- and between-segment heterogeneity: An improved hybrid remote-sensing image segmentation method. Remote Sens. 2018, 10, 781. [Google Scholar] [CrossRef]
- Benedek, C.; Descombes, X.; Zerubia, J. Building Development Monitoring in Multitemporal Remotely Sensed Image Pairs with Stochastic Birth-Death Dynamics. IEEE Trans. Pattern Anal. Mach. Intell. 2012, 34, 33–50. [Google Scholar] [CrossRef] [PubMed]
- Tilton, J.C.; Tarabalka, Y.; Montesano, P.M.; Gofman, E. Best merge region-growing segmentation with integrated nonadjacent region object aggregation. IEEE Trans. Geosci. Remote 2012, 50, 4454–4467. [Google Scholar] [CrossRef]
- Anselin, L. Local indicators of spatial association: LISA. Geogr. Anal. 1995, 27, 93–115. [Google Scholar] [CrossRef]
- Drăguţ, L.; Tiede, D.; Levick, S. ESP: A tool to estimate scale parameters for multiresolution image segmentation of remotely sensed data. Int. J. Geogr. Inf. Sci. 2010, 24, 859–871. [Google Scholar] [CrossRef]
- Woodcock, C.; Strahler, A. The factor of scale in remote sensing. Remote Sens. Environ. 1987, 21, 311–332. [Google Scholar] [CrossRef]
- Lassalle, P.; Inglada, J.; Michel, J.; Grizonnet, M. A scalable tile-based framework for region-merging segmentation. IEEE Trans. Geosci. Remote 2015, 53, 5473–5485. [Google Scholar] [CrossRef]
- Zhang, X.L.; Xiao, P.F.; Feng, X.Z.; Wang, J.G.; Wang, Z. Hybrid region merging method for segmentation of high-resolution remote sensing images. ISPRS J. Photogramm. 2014, 98, 19–28. [Google Scholar] [CrossRef]
- Clinton, N.; Holt, A.; Scarborough, J.; Yan, L.; Gong, P. Accuracy assessment measures for object-based image segmentation goodness. Photogramm. Eng. Remote Sens. 2010, 76, 289–299. [Google Scholar] [CrossRef]
- Lucieer, A.; Stein, A. Existential uncertainty of spatial objects segmented from satellite sensor imagery. IEEE Trans. Geosci. Remote 2002, 40, 2518–2521. [Google Scholar] [CrossRef]
- Zhang, X.; Feng, X.; Xiao, P.; He, G.; Zhu, L. Segmentation quality evaluation using region-based precision and recall measures for remote sensing images. ISPRS J. Photogramm. Remote Sens. 2015, 102, 73–84. [Google Scholar] [CrossRef]
- Johnson, B.A.; Bragais, M.; Endo, I.; Magcale-Macandog, D.B.; Macandog, P.B.M. Image segmentationparameter optimization considering within- and between-segment heterogeneity at multiple scale levels: Test case for mapping residential areas using landsat imagery. ISPRS Int. J. Geo-Inf. 2015, 4, 2292–2305. [Google Scholar] [CrossRef]
- Tsai, Y.H.; Stow, D.; Weeks, J. Comparison of Object-Based Image Analysis approaches to mapping new buildings in Accra, Ghana Using multi-temporal QuickBird satellite imagery. Remote Sens. 2011, 3, 2707–2726. [Google Scholar] [CrossRef]
- Doxani, G.; Karantzalos, K.; Tsakiri-Strati, M. Object-based building change detection from a single multispectral image and pre-existing geospatial information. Photogramm. Eng. Remote Sens. 2015, 81, 481–489. [Google Scholar] [CrossRef]
- Mnih, V. Machine Learning for Aerial Image Labeling. Ph.D. Thesis, University of Toronto, Toronto, ON, Canada, 2013. [Google Scholar]
- Drăguţ, L.; Blaschke, T. Automated classification of landform elements using object-based image analysis. Geomorphology 2006, 81, 330–344. [Google Scholar] [CrossRef]
- Van Asselen, S.; Seijmonsbergen, A.C. Expert-driven semi-automated geomorphological mapping for a mountainous area using a laser DTM. Geomorphology 2006, 78, 309–320. [Google Scholar] [CrossRef]
- Miliaresis, G.C.; Argialas, D.P. Segmentation of physiographic features from the global digital elevation model/GTOPO30. Comput. Geosci. 1999, 25, 715–728. [Google Scholar] [CrossRef]
- MacMillan, R.A.; Pettapiece, W.W.; Nolan, S.C.; Goddard, T.W. A generic procedure for automatically segmenting landforms into landform elements using DEMs, heuristic rules and fuzzy logic. Fuzzy Sets Syst. 2000, 113, 81–109. [Google Scholar] [CrossRef]
- Miliaresis, G.C. Geomorphometric mapping of Zagros Ranges at regional scale. Comput. Geosci. 2001, 27, 775–786. [Google Scholar] [CrossRef]
- Blaschke, T.; Strobl, J. Defining landscape units through integrated morphometric characteristics. In Landscape Modelling: Digital Techniques for Landscape Architecture; Buhmann, E., Ervin, S., Eds.; Wichmann-Verlag: Heidelberg, Germany, 2003; pp. 104–113. [Google Scholar]
- Van Niekerk, A. A comparison of land unit delineation techniques for land evaluation in the Western Cape, South Africa. Land Use Policy 2010, 27, 937–945. [Google Scholar] [CrossRef]
- Eisank, C.; Smith, M.; Hillier, J. Assessment of multiresolution segmentation for delimiting drumlins in digital elevation models. Geomorphology 2014, 214, 452–464. [Google Scholar] [CrossRef]
- Vamshi, G.T.; Martha, T.R.; Kumar, K.V. An object-based classification method for automatic detection of lunar impact craters from topographic data. Adv. Space Res. 2016, 57, 1978–1988. [Google Scholar] [CrossRef]
- Robinson, M.S.; Brylow, S.M.; Tschimmel, M.; Humm, D.; Lawrence, S.J.; Thomas, P.C.; Denevi, B.W.; Bowman-Cisneros, E.; Zerr, J.; Caplinger, M.A.; et al. Lunar Reconnaissance Orbiter Camera (LROC) instrument overview. Space Sci. Rev. 2010, 150, 81–124. [Google Scholar] [CrossRef]
- Robinson, D.J.; Redding, N.J.; Crisp, D.J. Implementation of a Fast Algorithm for Segmenting SAR Imagery; DSTO-TR-1242; Defence Science Technology Organisation: Fairbairn, Australia, 2002.
- Neubert, M.; Herold, H.; Meinel, G. Assessing image segmentation quality—Concepts, methods and application. In Object-based Image Analysis—Spatial Concepts for Knowledge-Driven Remote Sensing Applications; Blaschke, T., Lang, S., Hay, G., Eds.; Springer: Heidelberg/Berlin, Germany; New York, NY, USA, 2008; pp. 769–784. [Google Scholar]
- Congalton, R.G. A review of assessing the accuracy of classifications of remotely sensed data. Remote Sens. Environ. 1991, 37, 35–46. [Google Scholar] [CrossRef]







| Image | OGf | ||||
|---|---|---|---|---|---|
| MRS | Global | Local | OHRH 1 | FLSA 1 | |
| Côte d’Azur | 0.7224 | 0.7674 | 0.7375 | 0.5864 | 0.5902 |
| Manchester | 0.7648 | 0.7780 | 0.7923 | 0.5151 | 0.5012 |
| Szada | 0.7823 | 0.7996 | 0.7967 | 0.6983 | 0.6794 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dekavalla, M.; Argialas, D. A Region Merging Segmentation with Local Scale Parameters: Applications to Spectral and Elevation Data. Remote Sens. 2018, 10, 2024. https://doi.org/10.3390/rs10122024
Dekavalla M, Argialas D. A Region Merging Segmentation with Local Scale Parameters: Applications to Spectral and Elevation Data. Remote Sensing. 2018; 10(12):2024. https://doi.org/10.3390/rs10122024
Chicago/Turabian StyleDekavalla, Maria, and Demetre Argialas. 2018. "A Region Merging Segmentation with Local Scale Parameters: Applications to Spectral and Elevation Data" Remote Sensing 10, no. 12: 2024. https://doi.org/10.3390/rs10122024
APA StyleDekavalla, M., & Argialas, D. (2018). A Region Merging Segmentation with Local Scale Parameters: Applications to Spectral and Elevation Data. Remote Sensing, 10(12), 2024. https://doi.org/10.3390/rs10122024





