Differing Responses to Rainfall Suggest More Than One Functional Type of Grassland in South Africa
Abstract
:1. Introduction
- How sensitive is the productivity of grasslands in semi-arid regions to mean rainfall and inter-annual variability?
- Which factors affect this sensitivity, and what is the role of legacy effects?
- What factors differentiate or correlate the sensitivity of these ecosystems to average precipitation and inter-annual variability?
- What are the implications of grassland sensitivity for their vulnerability under future climates?
2. Materials and Methods
2.1. Datasets
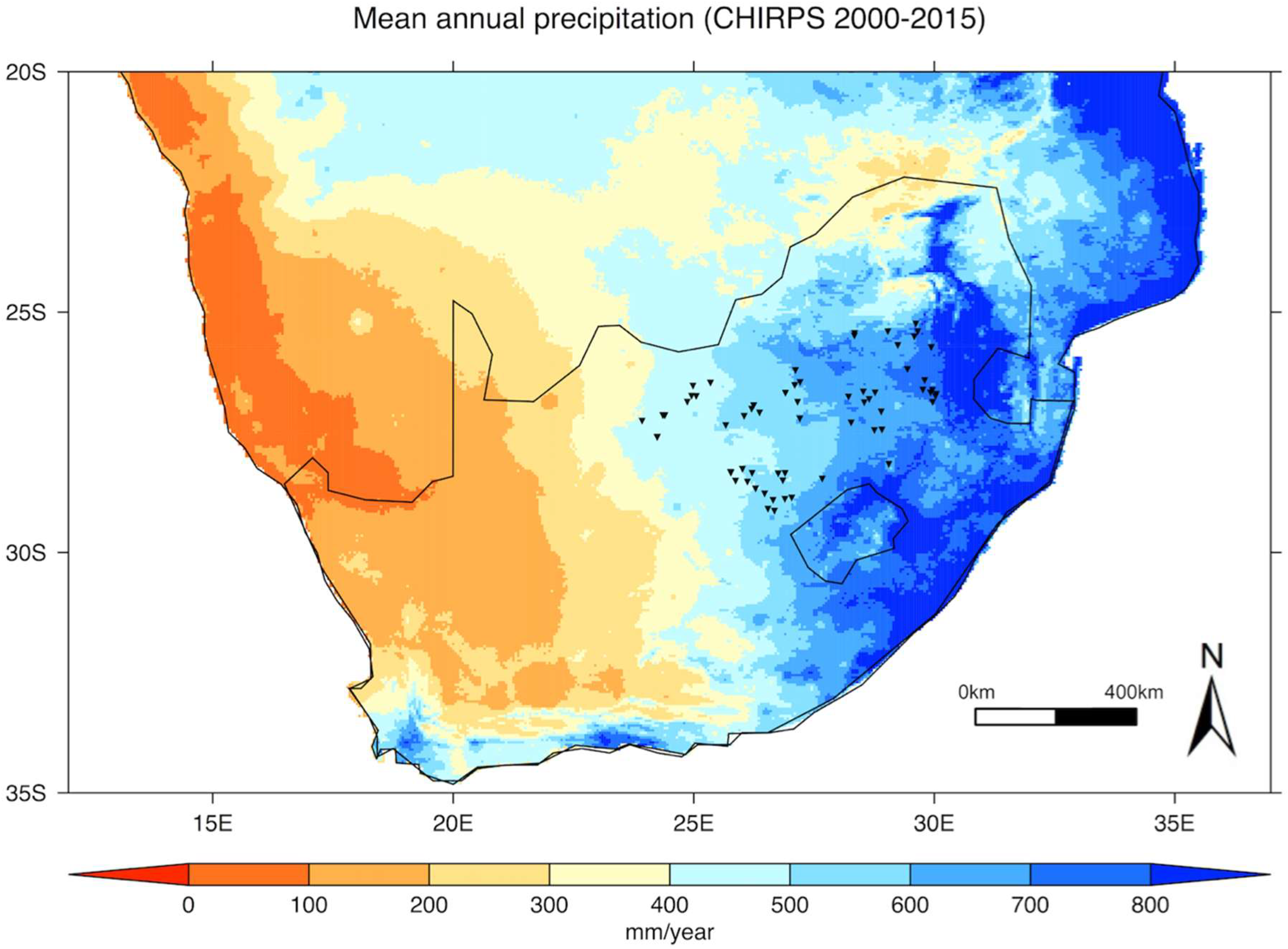
- Monthly precipitation data were extracted from the Climate Hazards Group InfraRed Precipitation with Station data, CHIRPS v2.0 [29], which covers the latitude band 50°S–50°N at all longitudes, from 1981 to the near-present, at a 0.05° spatial resolution (available from http://chg.geog.ucsb.edu/data/index.html). This dataset incorporates monthly precipitation climatology from the Climate Hazards Group’s Precipitation Climatology version 1 (CHPClim), infrared satellite observations from the Climate Prediction Center (CPC) and the National Climate Data Center (NCDC), the Tropical Rainfall Measuring Mission (TRMM) product, atmospheric model rainfall fields from the Coupled Forecast System version 2 (CFSv2), and in situ precipitation observations obtained from a variety of sources including national and regional meteorological services. The relevance and applicability of this dataset for this study were evaluated by comparing it to precipitation records independently provided by the South African Weather Service for five weather stations located within the study area (Bloemfontein, Vryburg, Potchefstroom, Johannesburg and Witbank).
- The seasonally-accumulated FAPAR, estimated from the high resolution MISR-HR satellite product [27], were used as a proxy for grassland productivity. These FAPAR data, at a spatial resolution of 275 m, have been available since late February 2000 from the Global Change Institute, University of the Witwatersrand (free on request to webmaster@misrhr.org). The product is delivered in the Space Oblique Mercator projection format. The repeat frequency of observation of an arbitrary site (under identical observation geometries) is 16 days. However, due to the overlap of successive paths and the fact that any site in South Africa can be observed from three such paths, the revisit frequency is much higher, at around six times per month. This feature partially mitigates the problem of missing data due to cloud cover, especially during the rainy season.
- Natural grassland areas (i.e., excluding croplands, abandoned fields, plantations and other land uses within the grassland biome) were extracted from the 30 × 30 m 2013–2014 South African National Land-Cover Dataset [30] which was derived from an analysis of the 2013–2014 Landsat 8 satellite imagery. This data can be found at http://bgis.sanbi.org/DEA_Landcover/project.asp. The potential grassland sites were further assessed against the “grassland” class of the 2010 global land cover map from the European Space Agency (ESA), available at a 300 m resolution based on MERIS [31], and the same class of the 2014 global land cover GLC map, available at a 1 km resolution based on global and national datasets [32]. These datasets can be downloaded respectively at https://www.esa-landcover-cci.org and at http://www.earthenv.org/landcover.
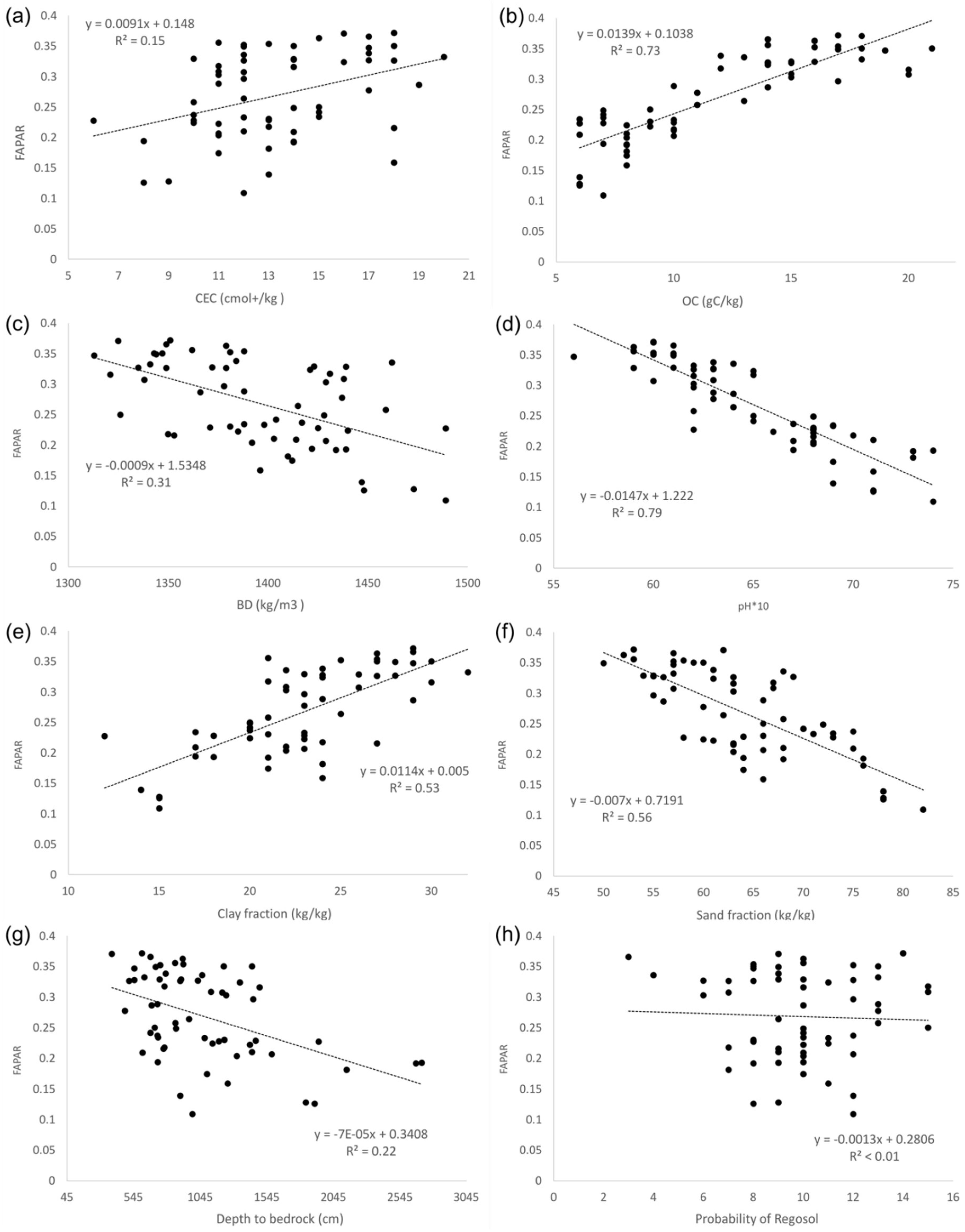
- Soil information for the selected grassland sites were acquired from the AfSoilGrids 25 dataset [33]. The dataset contains soil characteristics—including soil organic carbon (gC/kg), pH (in H2O), fraction of sand (kg/kg), silt (kg/kg) and clay (kg/kg), bulk density (kg/m3), and cation-exchange capacity (CEC, cmol +/kg), in addition to estimates of depth to the bedrock (cm), the probability of occurrence of R horizon or bedrock within 20 m, and the distribution of soil classes based on the World Reference Base (WRB) and the United States Department of Agriculture (USDA) classification systems—for the whole African continent at 25 spatial resolution at seven standard soil depths (0, 5, 15, 30, 60, 100, and 200 cm). This gridded dataset was derived using machine learning techniques from ca. 150,000 soil profiles and a stack of 158 soil covariates, mostly derived from the Moderate Resolution Imaging Spectroradiometer (MODIS) land products, Shuttle Radar Topography Mission (SRTM) digital elevation model (DEM) derivatives, spatially interpolated climate data on grids, and global landform and lithology maps. This dataset can be found at https://www.isric.online/projects/soil-property-maps-africa-250-m-resolution.
- Data on herbivory and fire were taken from Archibald et al. [3] who produced maps for sub-Saharan Africa at a resolution of 0.5° × 0.5° of the mean consumption of above ground NPP by fire and herbivory. These data were made available for this study by S. Archibald. The fire data are an aggregate of 50 resolution MODIS burned area data for the period from 2000 to 2015. There is no reliable source of high-resolution herbivory data; this product combines livestock census data with estimates of wildlife biomass.
2.2. Method
2.2.1. Grassland Sites and Selection
2.2.2. Data Preparation
2.2.3. Data Analysis
3. Results
3.1. Spatial Variability in Grassland Productivity
3.1.1. Factors Affecting Spatial Variability in Productivity
3.1.2. Sensitivity of Grassland Productivity to Spatial Variation in Precipitation
3.2. Temporal Variability in Grassland Productivity at a Site
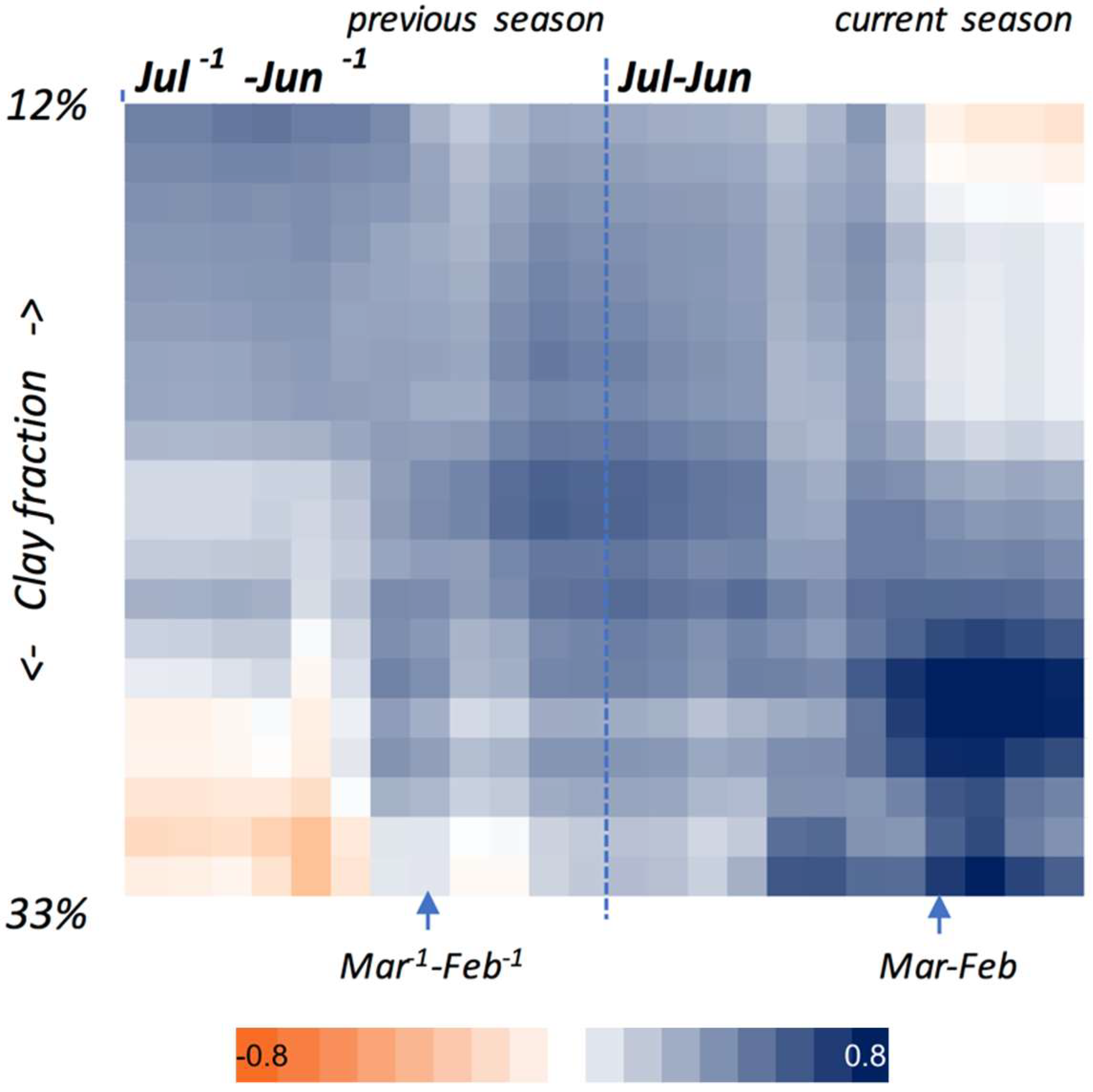
3.2.1. Sensitivity to Rainfall and the Factors Affecting It
3.2.2. Relationship with in-Season Grassland Productivity
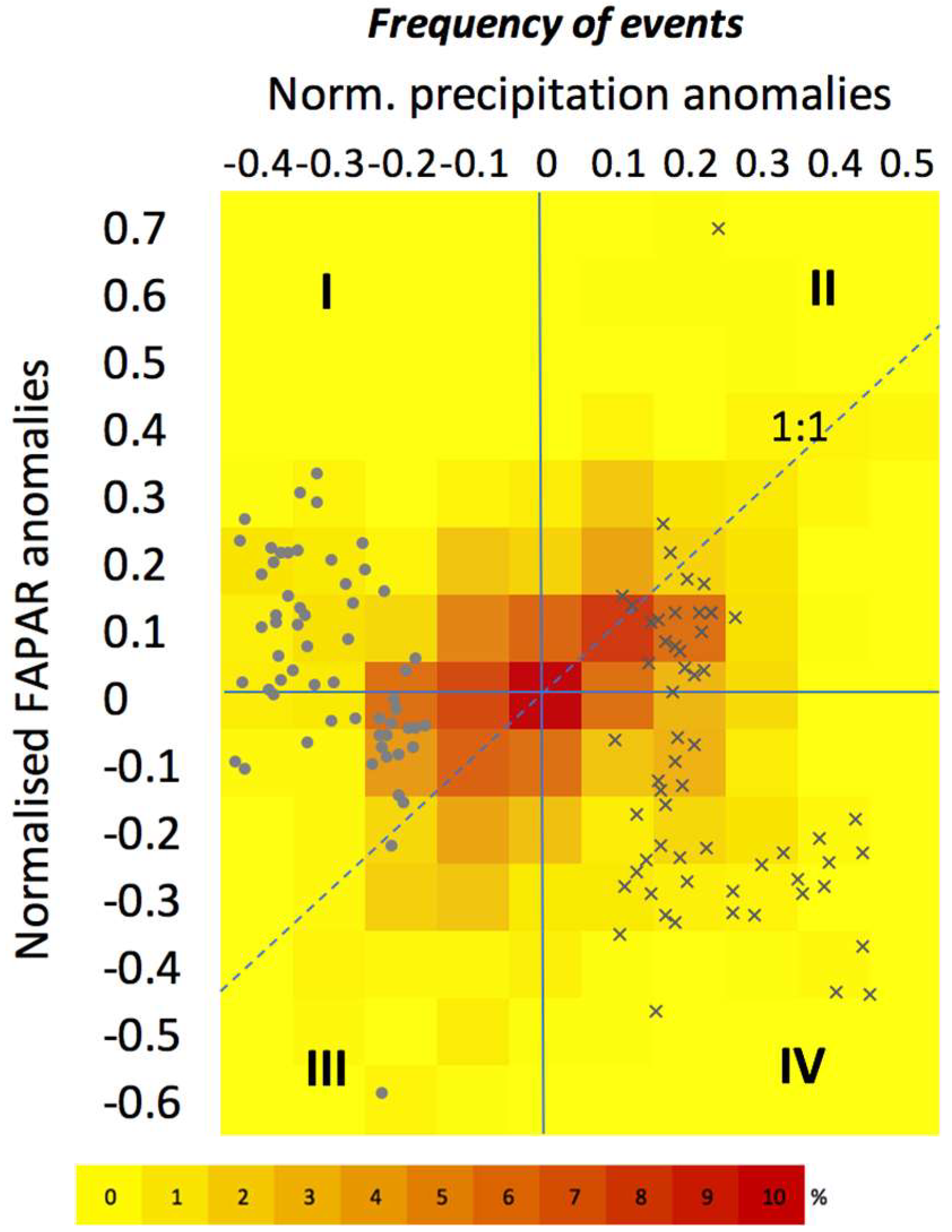
3.3. The Impact of Extreme Precipitation Events
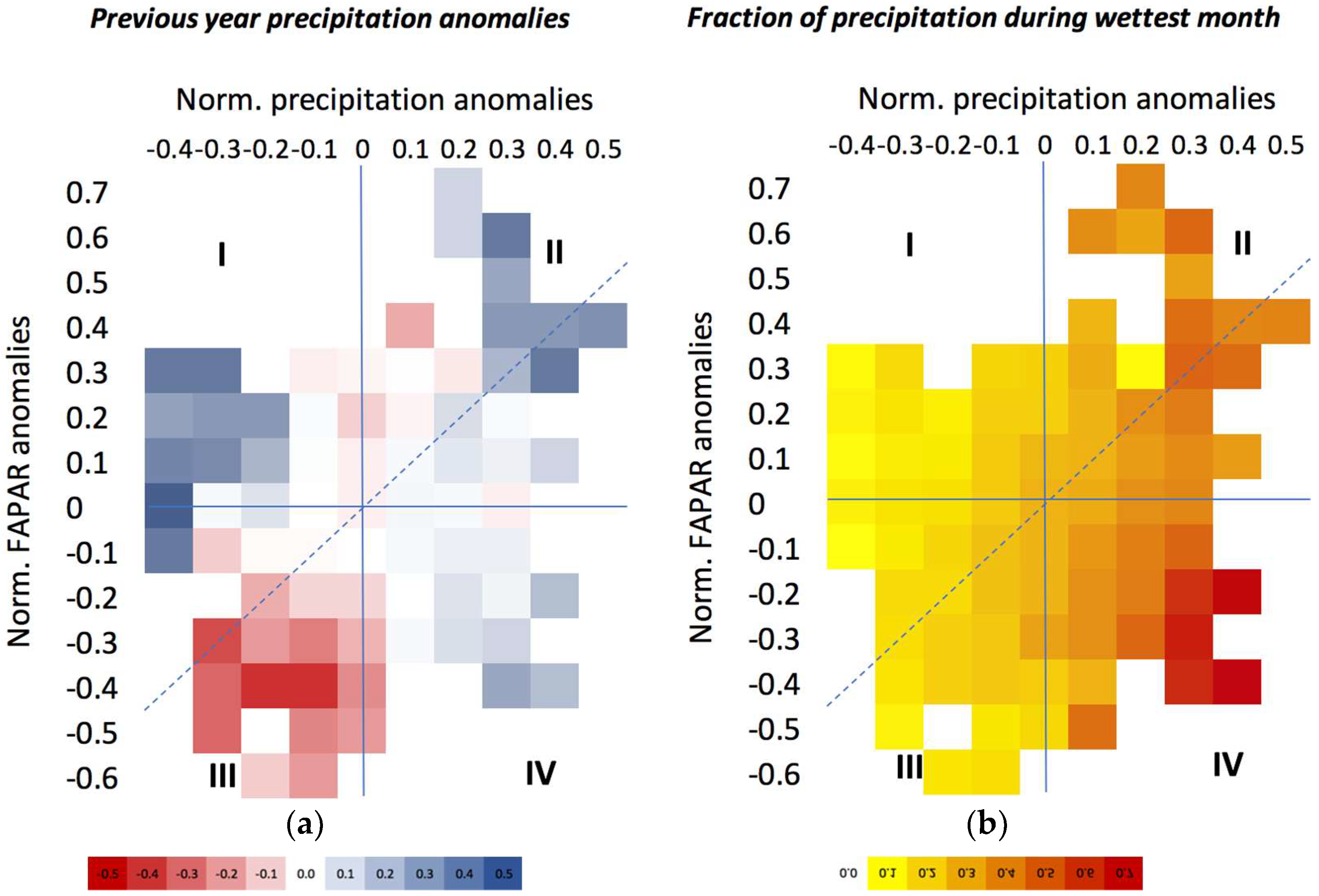
3.3.1. Nature of Precipitation Event
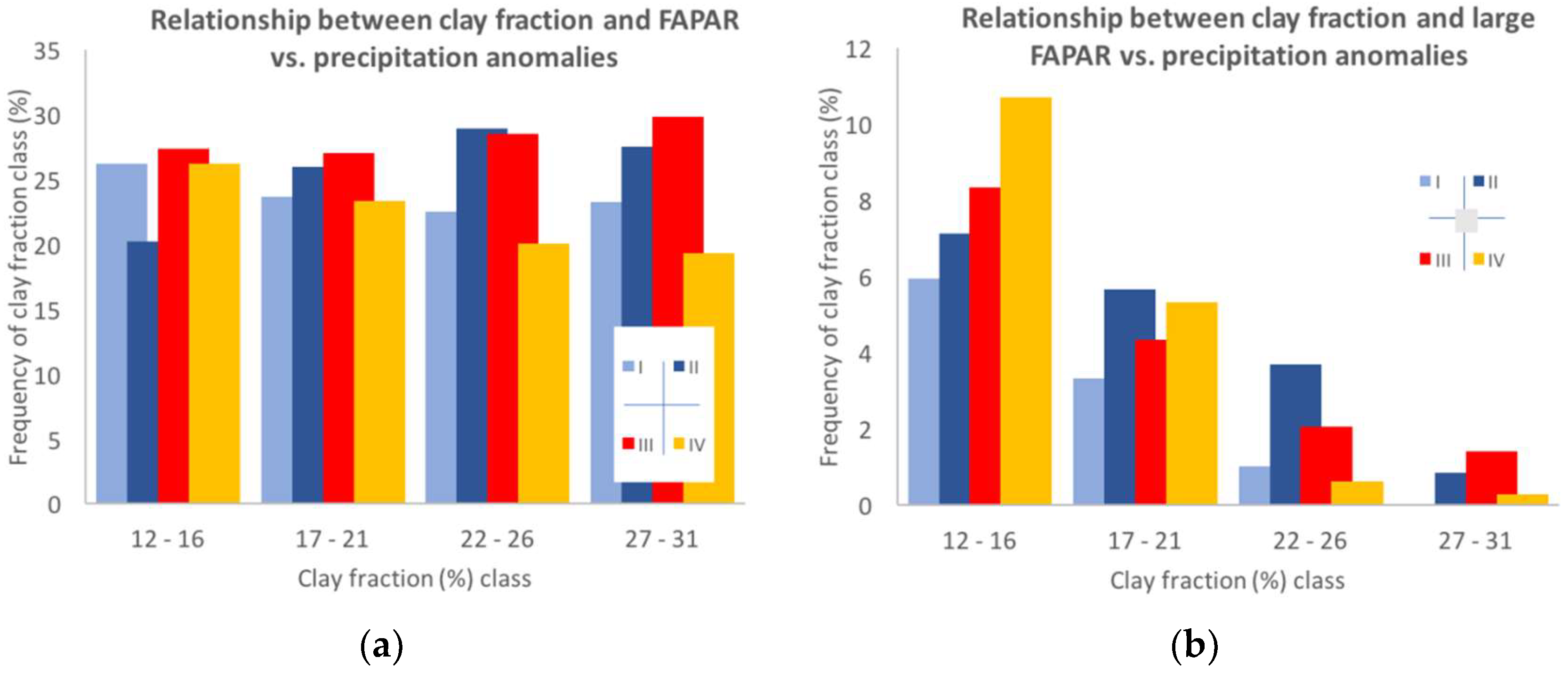
3.3.2. Site-Specific Characteristics
4. Discussion
4.1. Spatial Variability in Grassland Productivity
4.1.1. Factors Affecting Spatial Variability in Grassland Productivity
4.1.2. Factors Affecting the Sensitivity of Productivity to Precipitation Spatial Variability
4.2. Temporal Variability in Grassland Productivity
4.2.1. Factors Affecting the Sensitivity to Rainfall Variability at a Site
4.2.2. The Impact of Extreme Precipitation Events on Grassland Productivity
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
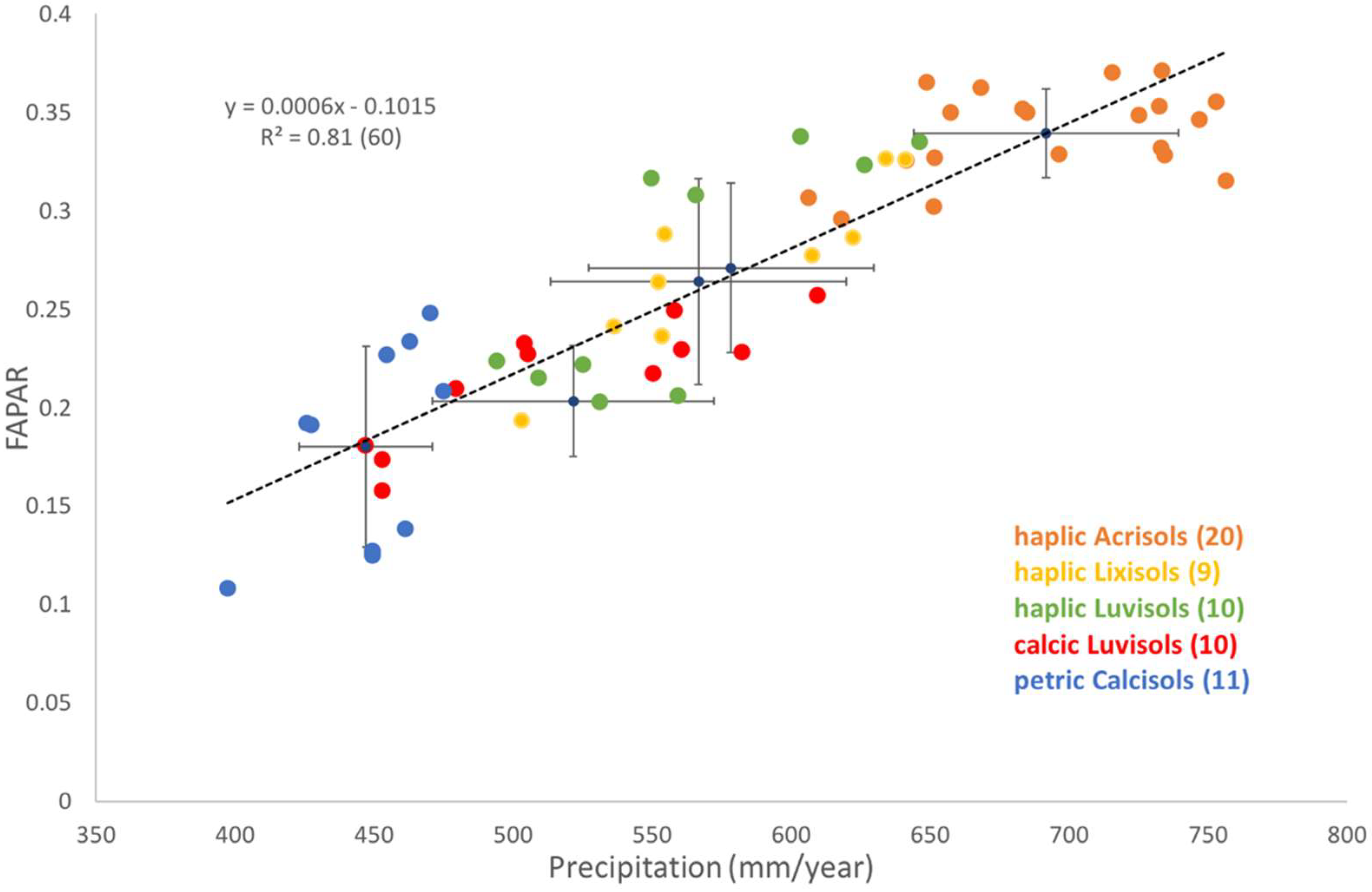
Appendix A. This Appendix Summarizes the Key Properties of the 5 Soil Classes (WRB) found in the Study Area
- petric Calcisols (10 sites): Calcisols develop in dry climate, arid to semi-arid, and have a substantial accumulation of calcium carbonate, CaCO2. Petric Calcisols have a continuous cemented horizon, to the extent that dry fragments do not slake in water and roots cannot enter. It has a low base saturation (<50%) and CEC (<24). They are well drained and have a good water-holding capacity.
- haplic Luvisols (10 sites): Luvisols develop in wet–dry climates, and are soils in which clay is washed down from the surface to a deeper horizon. It has a high base saturation (>50%) and CEC (>24). Luvisols are moderately weathered. Most Luvisols are well drained, but those with a high silt content may be sensitive to slaking and erosion. Luvisols are generally fertile.
- calcic Luvisols (11 sites): They have similar general proprieties as the haplic Luvisols but have additional calcic proprieties. Calcic soils are a result of the continuing accumulation of CaCO2 over a long period. If the surface soil is silty, crusts may form that restrict rapid infiltration of rain and root penetration.
- haplic Lixisols (nine sites): Lixisols have an argic B-horizon which has a CEC < 24. The argic B-horizon is a subsurface horizon which has a distinctly higher clay content than the overlying horizon. These soils are strongly weathered (low level of available nutrients: low fertility but better than acrisols), which results in a low silt/clay ratio. They have a higher pH (base saturation > 50%) than other tropical soils (better chemical properties than Acrisols). The structure stability is lower than in Acrisols, and slaking and caking of the surface soil is a serious problem (an issue when exposed to the direct impact of rain drops). The moisture content at low pF is higher than in Acrisols.
- haplic Acrisols (20 sites): Acrisols are associated with humid, tropical climates. They have an argic B-horizon (clay rich) which has a CEC < 24 and a base saturation < 50%. These soils are strongly weathered. They have a low fertility and a high Al toxicity. During rain showers, crusting and erosion of the top soil can occur. They mostly develop on acid rock, and in strongly weathered clays, which are undergoing further degradation.
Appendix B. CHIRPS vs South African Weather Service Precipitation Data for Five Weather Stations

Appendix C. Multi-Year FAPAR Vs. Soil Variables
Appendix D. Factors Affecting the Sensitivity of Mean Productivity to Spatial Variations in Precipitation
| Nbr. of variables | Variables | MSE | R² | Akaike’s AIC |
|---|---|---|---|---|
| 1 | Mean precip | 0.001 | 0.805 | 412.225 |
| 2 | st dev precip/Mean precip | 0.001 | 0.851 | −426.178 |
| 3 | st dev precip/Mean precip/fire DMI | 0.001 | 0.861 | −428.381 |
| 4 | st dev precip/Mean precip/BD/fire DMI | 0.001 | 0.865 | −428.411 |
| 5 | st dev precip/Mean precip/BD/Clay/fire DMI | 0.001 | 0.869 | −428.250 |
| 6 | st dev precip/Mean precip/BD/Clay/Depth to bedrock/fire DMI | 0.001 | 0.872 | −427.575 |
| 7 | st dev precip/Mean precip/BD/Clay/Sand/Depth to bedrock/fire DMI | 0.001 | 0.875 | −426.858 |
| …… |
References
- White, R.P.; Murray, S.; Rohweder, M.; Prince, S.D.; Thompson, K.M. Grassland Ecosystems; World Resources Institute: Washington, DC, USA, 2000. [Google Scholar]
- Morrison, J. Grasslands of the World. In Experimental Agriculture, 1st ed.; Suttie, J.M., Reynolds, S.G., Batello, C., Eds.; Food and Agriculture Organization of the United Nations: Rome, Italy, 2006; Volume 42, pp. 254–255. ISBN 92-5-105337-5. [Google Scholar]
- Archibald, S.; Hempson, G.P. Competing consumers: Contrasting the patterns and impacts of fire and mammalian herbivory in Africa. Philos. Trans. R. Soc. B 2016, 371, 1–14. [Google Scholar] [CrossRef] [PubMed]
- O’Mara, F.P. The role of grasslands in food security and climate change. Ann. Bot. 2012, 110, 1263–1270. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Zhihui, G.; Peijun, S.; Jin, C. Estimation of grassland degradation based on historical maximum growth model using with remote sensing data. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2008, 37, 895–900. [Google Scholar]
- MEA, Millennium Ecosystem Assessment. Ecosystems and Human Well-Being Scenarios. Findings of the Scenarios Working Group; Island Press: Washington, DC, USA, 2005. [Google Scholar]
- Scholes, R.J.; Montanarella, L.; Brainich, E.; Barger, N.; Ten Brink, B.; Cantele, M.; Erasmus, B.; Fisher, J.; Gardner, T.; Holland, T.G.; et al. IPBES: Summary for Policymakers of the Assessment Report on Land Degradation and Restoration of the Intergovernmental Science-Policy Platform on Biodiversity and Ecosystem Services; IPBES Secretariat: Bonn, Germany, 2018. [Google Scholar]
- Thiombiano, L.; Tourino-Soto, I. Status and trends in land degradation in Africa. In Climate and Land Degradation; Springer: Berlin/Heidelberg, Germany, 2007; pp. 39–53. [Google Scholar]
- Scholes, R.J. Syndromes of dryland degradation in southern Africa. Afr. J. Range Forage Sci. 2009, 26, 113–125. [Google Scholar] [CrossRef]
- Bai, Z.G.; Dent, D.L.; Olsson, L.; Schaepman, M.E. Proxy global assessment of land degradation. Soil Use Manag. 2008, 24, 223–234. [Google Scholar] [CrossRef] [Green Version]
- Adeel, Z. Findings of the global desertification assessment by the millennium ecosystem assessment—A perspective for better managing scientific knowledge. In The Future of Drylands; Springer: Dordrecht, The Netherlands, 2008; pp. 677–685. [Google Scholar]
- Sommer, S.; Zucca, C.; Grainger, A.; Cherlet, M.; Zougmore, R.; Sokona, Y.; Hill, J.; Della Peruta, R.; Roehrig, J.; Wang, G. Application of indicator systems for monitoring and assessment of desertification from national to global scales. Land Degrad. Dev. 2011, 22, 184–197. [Google Scholar] [CrossRef]
- Winslow, M.D.; Vogt, J.V.; Thomas, R.J.; Sommer, S.; Martius, C.; Akhtar-Schuster, M. Science for improving the monitoring and assessment of dryland degradation. Land Degrad. Dev. 2012, 2, 145–149. [Google Scholar] [CrossRef]
- Stocker, T.F.; Qin, D.; Plattner, G.K.; Tignor, M.; Allen, S.K.; Boschung, J.; Nauels, A.; Xia, Y.; Bex, V.; IPCC. Climate Change; IPCC: Geneva, Switzerland, 2013. [Google Scholar]
- Asner, G.P.; Heidebrecht, K.B. Desertification alters regional ecosystem–climate interactions. Glob. Chang. Biol. 2005, 11, 182–194. [Google Scholar] [CrossRef]
- Busby, J.W.; Smith, T.G.; White, K.L.; Strange, S.M. Climate change and insecurity: Mapping vulnerability in Africa. Int. Secur. 2013, 37, 132–172. [Google Scholar] [CrossRef]
- Knapp, A.K.; Smith, M.D. Variation among biomes in temporal dynamics of aboveground primary production. Science 2001, 291, 481–484. [Google Scholar] [CrossRef] [PubMed]
- Knapp, A.K.; Fay, P.A.; Blair, J.M.; Collins, S.L.; Smith, M.D.; Carlisle, J.D.; Harper, C.W.; Danner, B.T.; Lett, M.S.; McCarron, J.K. Rainfall variability, carbon cycling, and plant species diversity in a mesic grassland. Science 2001, 298, 2202–2205. [Google Scholar] [CrossRef] [PubMed]
- Noy-Meir, I. Desert ecosystems: Environment and producers. Ann. Rev. Ecol. Syst. 1973, 4, 25–51. [Google Scholar] [CrossRef]
- Le Houerou, H.N. Rain use efficiency: A unifying concept in arid-land ecology. J. Arid Environ. 1984, 7, 213–247. [Google Scholar]
- Zhao, M.; Running, S.W. Drought-induced reduction in global terrestrial net primary production from 2000 through 2009. Science 2010, 329, 940–943. [Google Scholar] [CrossRef] [PubMed]
- Ruppert, J.C.; Holm, A.; Miehe, S.; Muldavin, E.; Snyman, H.A.; Wesche, K.; Linstädter, A. Meta-analysis of ANPP and rain-use efficiency confirms indicative value for degradation and supports non-linear response along precipitation gradients in drylands. J. Veg. Sci. 2012, 23, 1035–1050. [Google Scholar] [CrossRef]
- Sala, O.E.; Gherardi, L.A.; Reichmann, L.; Jobbagy, E.; Peters, D. Legacies of precipitation fluctuations on primary production: Theory and data synthesis. Philos. Trans. R. Soc. Lond. B Biol. Sci. 2012, 367, 3135–3144. [Google Scholar] [CrossRef] [PubMed]
- Chapin, F.S.; Matson, P.A.; Mooney, H.A. Principles of Terrestrial Ecosystem Ecology; Springer: New York, NY, USA, 2002; pp. 151–175. [Google Scholar]
- Reichmann, L.G.; Sala, O.E.; Peters, D.P. Precipitation legacies in desert grassland primary production occur through previous-year tiller density. Ecology 2013, 94, 435–443. [Google Scholar] [CrossRef] [PubMed]
- Reichmann, L.G.; Sala, O.E. Differential sensitivities of grassland structural components to changes in precipitation mediate productivity response in a desert ecosystem. Funct. Ecol. 2014, 28, 1292–1298. [Google Scholar] [CrossRef] [Green Version]
- Verstraete, M.; Hunt, L.; Scholes, R.; Clerici, M.; Pinty, B.; Nelson, D. Generating 275-m resolution land surface products from the Multi-angle Imaging SpectroRadiometer data. IEEE Trans. Geosci. Remote Sens. 2012, 50, 3980–3990. [Google Scholar] [CrossRef]
- Gobron, N.; Belward, A.; Pinty, B.; Knorr, W. Monitoring biosphere vegetation 1998–2009. Geophys. Res. Lett. 2010, 37. [Google Scholar] [CrossRef]
- Funk, C.; Verdin, A.; Michaelsen, J.; Peterson, P.; Pedreros, D.; Husak, G. A global satellite assisted precipitation climatology. Earth Syst. Sci. Data Discuss. 2015, 8. [Google Scholar] [CrossRef]
- DEA, Department of Environmental Affairs. 2013–14 SA National Land-Cover—Broad Parent Classes. Technical Report. 2015. Available online: http://bgis.sanbi.org/DEA_Landcover/ project.asp (accessed on 20 February 2017).
- Defourny, P.; Bontemps, S.; Lamarche, C.; Brockmann, C.; Kirches, G.; Boettcher, M.; Arino, O. ESA Climate Change Initiative—Land Cover Project, Products User Guide, Version 2.4. 2014. Available online: http://maps.elie.ucl.ac.be/CCI/viewer/index.php (accessed on 20 February 2017).
- Tuanmu, M.-N.; Jetz, W. A global 1-km consensus land-cover product for biodiversity and ecosystem modelling. Glob. Ecol. Biogeogr. 2014, 23, 1031–1045. [Google Scholar] [CrossRef]
- Hengl, T.; de Jesus, J.M.; Heuvelink, G.B.; Gonzalez, M.R.; Kilibarda, M.; Blagoti’c, A.; Shangguan, W.; Wright, M.N.; Geng, X.; Bauer-Marschallinger, B.; et al. SoilGrids250m: Global gridded soil information based on machine learning. PLoS ONE 2017, 12. [Google Scholar] [CrossRef] [PubMed]
- Akaikei, H. Information theory and an extension of maximum likelihood principle. In Proc. 2nd International Symposium on Information Theory; Akadémiai Kiadó: Budapest, Hungary, 1973; pp. 267–281. [Google Scholar]
- Lauenroth, W.K. Grassland primary production: North American grasslands in perspective. In Perspectives in Grassland Ecology; Springer: New York, NY, USA, 1979; pp. 3–24. [Google Scholar]
- Slessarev, E.; Lin, Y.; Bingham, N.; Johnson, J.; Dai, Y.; Schimel, J.; Chadwick, O. Water balance creates a threshold in soil pH at the global scale. Nature 2016, 540, 567–569. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Bot, A.; Benites, J. The Importance of Soil Organic Matter: Key to Drought-Resistant Soil and Sustained Food Production; Food and Agriculture Organisation: Rome, Italy, 2005. [Google Scholar]
- Barshad, I. The effect of a variation in precipitation on the nature of clay mineral formation in soils from acid and basic igneous rocks. In Proceedings of the International Clay Conference, Jerusalem, Israel, 20–24 June 1966; CIPEA: Israel, Jerusalem, 1966; Volume 1, pp. 167–173. [Google Scholar]
- Barger, N.N.; Archer, S.R.; Campbell, J.L.; Huang, C.-Y.; Morton, J.A.; Knapp, A.K. Woody plant proliferation in North American dry-lands: A synthesis of impacts on ecosystem carbon balance. J. Geophys. Res. Biogeosci. 2011, 116. [Google Scholar] [CrossRef]
- Scholes, R.J. Convex relationships in ecosystems containing mixtures of trees and grass. Environ. Res. Econ. 2003, 26, 559–574. [Google Scholar] [CrossRef]
- Hill, M.J.; Hanan, N.P. Ecosystem Function in Savannas: Measurement and Modeling at Landscape to Global Scales; CRC Press: Boca Raton, FL, USA, 2010. [Google Scholar]
- Dangal, S.R.; Tian, H.; Lu, C.; Pan, S.; Pederson, N.; Hessl, A. Synergistic effects of climate change and grazing on net primary production of Mongolian grasslands. Ecosphere 2016, 7, 1–20. [Google Scholar] [CrossRef]
- Pastor, J.; Cohen, Y. Herbivores, the functional diversity of plants species, and the cycling of nutrients in ecosystems. Theor. Popul. Biol. 1997, 5, 165–179. [Google Scholar] [CrossRef]
- Schönbach, P.; Wan, H.; Gierus, M.; Bai, Y.; Müller, K.; Lin, L.; Susenbeth, A.; Taube, F. Grassland responses to grazing: Effects of grazing intensity and management system in an Inner Mongolian steppe ecosystem. Plant Soil 2011, 340, 103–115. [Google Scholar] [CrossRef]
- Frank, A.B. Carbon dioxide fluxes over a grazed prairie and seeded pasture in the Northern Great Plains. Environ. Pollut. 2002, 116, 397–403. [Google Scholar] [CrossRef]
- McNaughton, S.J.; Banyikwa, F.F.; McNaughton, M.M. Promotion of the cycling of diet-enhancing nutrients by African grazers. Science 1997, 278, 1798–1800. [Google Scholar] [CrossRef] [PubMed]
- Irisarri, J.G.N.; Derner, J.D.; Porensky, L.M.; Augustine, D.J.; Reeves, J.L.; Mueller, K.E. Grazing intensity differentially regulates ANPP response to precipitation in North American semiarid grasslands. Ecol. Appl. 2016, 26, 1370–1380. [Google Scholar] [CrossRef] [PubMed]
- Dangal, S.R.; Tian, H.; Lu, C.; Ren, W.; Pan, S.; Yang, J.; Di Cosmo, N.; Hessl, A. Integrating herbivore population dynamics into a global land biosphere model: Plugging animals into the earth system. J. Adv. Model. Earth Syst. 2017, 9, 2920–2945. [Google Scholar] [CrossRef]
- Asner, G.P.; Elmore, A.J.; Olander, L.P.; Martin, R.E.; Harris, A.T. Grazing systems, ecosystem responses, and global change. Annu. Rev. Environ. Resour. 2004, 29, 261–299. [Google Scholar] [CrossRef]
- McNaughton, S.J. Interactive regulation of grass yield and chemical properties by defoliation, a salivary chemical, and inorganic nutrition. Oecologia 1985, 65, 478–486. [Google Scholar] [CrossRef] [PubMed]
- Van de Vijver, C.A.D.M.; Poot, P.; Prins, H.H.T. Causes of increased nutrient concentrations in post-fire regrowth in an East African savanna. Plant Soil 1999, 214, 173–185. [Google Scholar] [CrossRef]
- Gherardi, L.A.; Sala, O.E. Enhanced precipitation variability decreases grass- and increases shrub-productivity. Proc. Natl. Acad. Sci. USA 2015, 112, 12735–12740. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Hsu, J.S.; Powell, J.; Adler, P.B. Sensitivity of mean annual primary production to precipitation. Glob. Chang. Biol. 2012, 18, 2246–2255. [Google Scholar] [CrossRef]
- Hsu, J.S.; Adler, P.B. Anticipating changes in variability of grassland production due to increases in interannual precipitation variability. Ecosphere 2014, 5, 1–15. [Google Scholar] [CrossRef]
- Rutherford, M.C. Field identification of roots of woody plants of the savanna ecosystem study area, Nylsvley. Bothalia 1980, 13, 171–184. [Google Scholar] [CrossRef]
- Scholes, R.J. Nutrient cycling in semi-arid grasslands and savannas: Its influence on pattern, productivity and stability. In Proceedings of the XII International Grassland Congress, Palmerston North, New Zealand, 8–21 February 1993. [Google Scholar]
- Austin, A.T.; Yahdjian, L.; Stark, J.M.; Belnap, J.; Porporato, A.; Norton, U.; Ravetta, D.A.; Schaeffer, S.M. Water pulses and biogeochemical cycles in arid and semiarid ecosystems. Oecologia 2004, 141, 221–235. [Google Scholar] [CrossRef] [PubMed]
- Jackson, R.B.; Canadell, J.; Ehleringer, J.R.; Mooney, H.A.; Sala, O.E.; Schulze, E.D. A global analysis of root distributions for terrestrial biomes. Oecologia 1996, 108, 389–411. [Google Scholar] [CrossRef] [PubMed]
- Van den Hoof, C.; Lambert, F. Mitigation of drought negative effect on ecosystem productivity by vegetation mixing. J. Geophys. Res. Biogeosci. 2016, 121, 2667–2683. [Google Scholar] [CrossRef]
- Zhang, Y.; Moran, M.S.; Nearing, M.A.; Campos, G.E.P.; Huete, A.R.; Buda, A.R.; Bosch, D.D.; Gunter, S.A.; Kitchen, S.G.; McNab, W.H.; et al. Extreme precipitation patterns and reductions of terrestrial ecosystem production across biomes. J. Geophys. Res. Biogeosci. 2013, 118, 148–157. [Google Scholar] [CrossRef] [Green Version]
- Engelbrecht, C.J.; Engelbrecht, F.A.; Dyson, L.L. High-resolution model-projected changes in mid-tropospheric closed-lows and extreme rainfall events over southern Africa. Int. J. Climatol. 2013, 33, 173–187. [Google Scholar] [CrossRef]
- Arora, V.K.; Chiew, F.H.; Grayson, R.B. Effect of sub-grid-scale variability of soil moisture and precipitation intensity on surface runoff and streamflow. J. Geophys. Res. Atmos. 2001, 106, 17073–17091. [Google Scholar] [CrossRef] [Green Version]
- Porporato, A.; D’odorico, P.; Laio, F.; Ridolfi, L.; Rodriguez-Iturbe, I. Ecohydrology of water-controlled ecosystems. Adv. Water Resour. 2002, 25, 1335–1348. [Google Scholar] [CrossRef]
- Garland, R.M.; Matooane, M.; Engelbrecht, F.A.; Bopape, M.J.M.; Landman, W.A.; Naidoo, M.; Merwe, J.V.D.; Wright, C.Y. Regional projections of extreme apparent temperature days in Africa and the related potential risk to human health. Int. J. Environ. Res. Public Health 2015, 12, 12577–12604. [Google Scholar] [CrossRef] [PubMed]

© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Van den Hoof, C.; Verstraete, M.; Scholes, R.J. Differing Responses to Rainfall Suggest More Than One Functional Type of Grassland in South Africa. Remote Sens. 2018, 10, 2055. https://doi.org/10.3390/rs10122055
Van den Hoof C, Verstraete M, Scholes RJ. Differing Responses to Rainfall Suggest More Than One Functional Type of Grassland in South Africa. Remote Sensing. 2018; 10(12):2055. https://doi.org/10.3390/rs10122055
Chicago/Turabian StyleVan den Hoof, Catherine, Michel Verstraete, and Robert J. Scholes. 2018. "Differing Responses to Rainfall Suggest More Than One Functional Type of Grassland in South Africa" Remote Sensing 10, no. 12: 2055. https://doi.org/10.3390/rs10122055
APA StyleVan den Hoof, C., Verstraete, M., & Scholes, R. J. (2018). Differing Responses to Rainfall Suggest More Than One Functional Type of Grassland in South Africa. Remote Sensing, 10(12), 2055. https://doi.org/10.3390/rs10122055





