Retrieval of Reflected Shortwave Radiation at the Top of the Atmosphere Using Himawari-8/AHI Data
Abstract
:1. Introduction
2. Materials
2.1. Input Data
2.2. Validation Data
3. Methods
3.1. Theoretical Background
3.2. Reflected Shortwave Radiation Retrieval Algorithm
3.2.1. Anisotropy Consideration
3.2.2. Sun Glint Removal
4. Results
4.1. Evaluation of the Reflected Shortwave Radiation Algorithm
4.1.1. Anisotropy Consideration
4.1.2. Sun Glint Removal
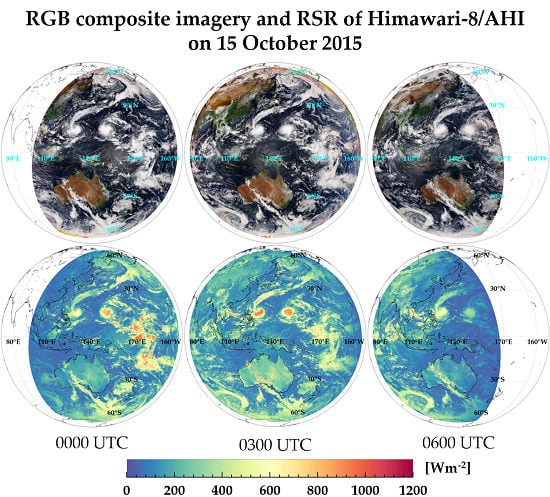
4.1.3. Reflected Shortwave Radiation
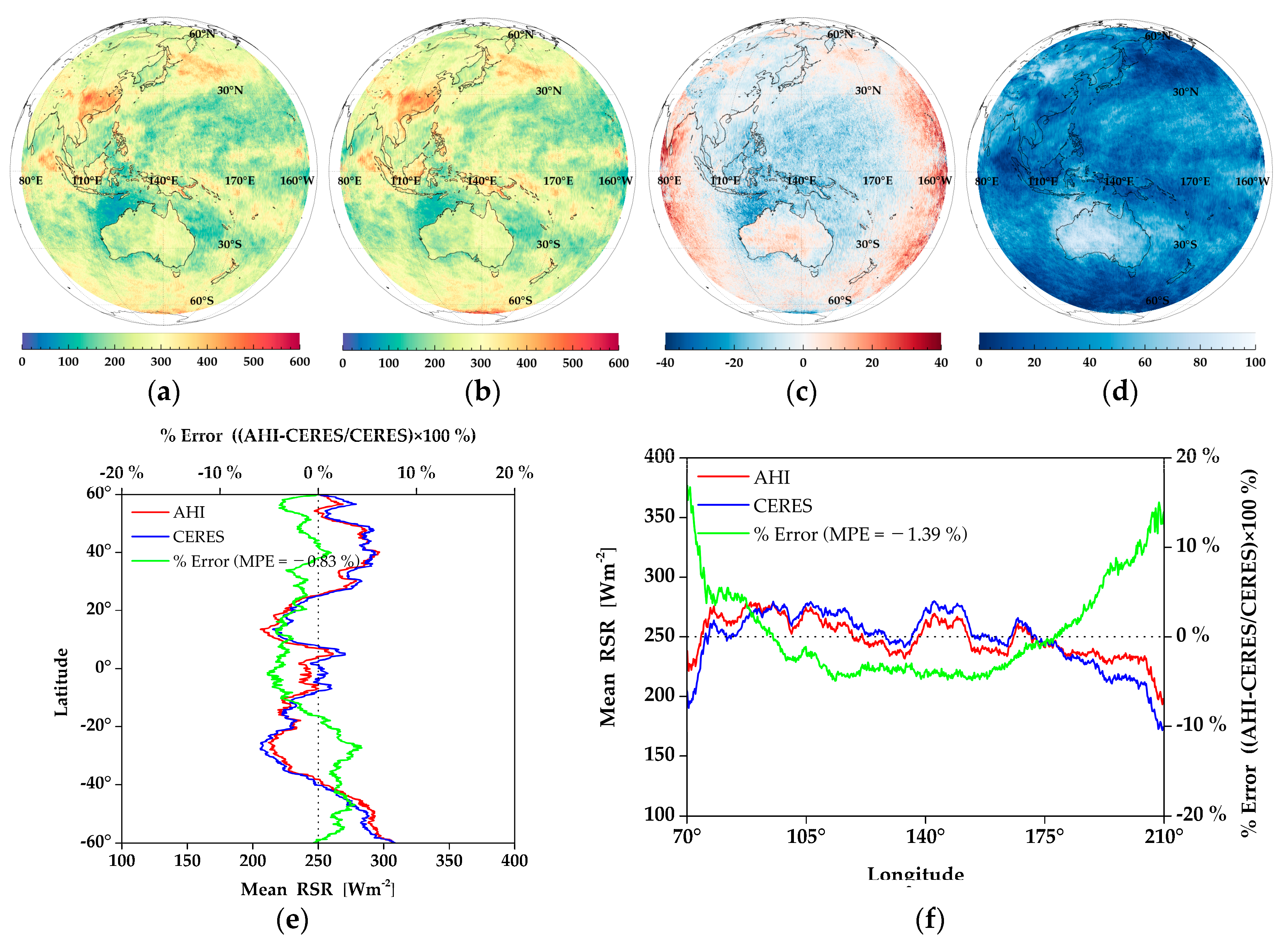
4.2. Validation of Reflected Shortwave Radiation Algorithm Using CERES Data
5. Discussion
6. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- AWG Radiation Budget Application Team. GOES-R Advanced Baseline Imager (ABI) Algorithm Theoretical Basis Document for Downward Shortwave Radiation (Surface), and Reflected Shortwave Radiation (TOA), NOAA NESDIS Center for Satellite Applications and Research, 27 September 2010. Available online: https://www.goes-r.gov/products/ATBDs/baseline/baseline-DSR-v2.0.pdf (accessed on 28 November 2017).
- Bhartia, P.K. Top-of-the-atmosphere shortwave flux estimation from satellite observations: An empirical neural network approach applied with data from the a-train constellation. Atmos. Meas. Tech. 2016, 9, 2813–2826. [Google Scholar]
- Kim, Y.-J.; Kim, B.-G.; Miller, M.; Min, Q.; Song, C.-K. Enhanced aerosol-cloud relationships in more stable and adiabatic clouds. Asia-Pac. J. Atmos. Sci. 2012, 48, 283–293. [Google Scholar] [CrossRef]
- Trenberth, K.E.; Dai, A.; Van Der Schrier, G.; Jones, P.D.; Barichivich, J.; Briffa, K.R.; Sheffield, J. Global warming and changes in drought. Nat. Clim. Chang. 2014, 4, 17–22. [Google Scholar] [CrossRef]
- Doelling, D.R.; Loeb, N.G.; Keyes, D.F.; Nordeen, M.L.; Morstad, D.; Nguyen, C.; Wielicki, B.A.; Young, D.F.; Sun, M. Geostationary enhanced temporal interpolation for CERES flux products. J. Atmos. Ocean. Technol. 2013, 30, 1072–1090. [Google Scholar] [CrossRef]
- Stephens, G.L.; O’Brien, D.; Webster, P.J.; Pilewski, P.; Kato, S.; Li, J.L. The albedo of earth. Rev. Geophys. 2015, 53, 141–163. [Google Scholar] [CrossRef]
- Hatzianastassiou, N.; Matsoukas, C.; Fotiadi, A.; Pavlakis, K.; Drakakis, E.; Hatzidimitriou, D.; Vardavas, I. Global distribution of earth’s surface shortwave radiation budget. Atmos. Chem. Phys. 2005, 5, 2847–2867. [Google Scholar] [CrossRef]
- Stubenrauch, C.; Rossow, W.; Kinne, S. Assessment of global cloud data sets from satellites a project of the world climate research programme global energy and water cycle experiment (GEWEX) radiation panel lead authors. Am. Meteorol. Soc. 2012. [Google Scholar] [CrossRef]
- Luther, M.; Cooper, J.; Taylor, G. The earth radiation budget experiment nonscanner instrument. Rev. Geophys. 1986, 24, 391–399. [Google Scholar] [CrossRef]
- Wielicki, B.A.; Barkstrom, B.R.; Harrison, E.F.; Lee, R.B., III; Louis Smith, G.; Cooper, J.E. Clouds and the earth’s radiant energy system (CERES): An earth observing system experiment. Bull. Am. Meteorol. Soc. 1996, 77, 853–868. [Google Scholar] [CrossRef]
- Wang, D.; Liang, S. Estimating high-resolution top of atmosphere albedo from moderate resolution imaging spectroradiometer data. Remote Sens. Environ. 2016, 178, 93–103. [Google Scholar] [CrossRef]
- Niu, X.; Pinker, R.T. Revisiting satellite radiative flux computations at the top of the atmosphere. Int. J. Remote Sens. 2012, 33, 1383–1399. [Google Scholar] [CrossRef]
- Buriez, J.C.; Parol, F.; Poussi, Z.; Viollier, M. An improved derivation of the top-of-atmosphere albedo from POLDER/ADEOS-2: 2. Broadband albedo. J. Geophys. Res. Atmos. 2007, 112. [Google Scholar] [CrossRef]
- Laszlo, I.; Gruber, A.; Jacobowitz, H. The relative merits of narrowband channels for estimating broadband albedos. J. Atmos. Ocean. Technol. 1988, 5, 757–773. [Google Scholar] [CrossRef]
- Wydick, J.E.; Davis, P.A.; Gruber, A. Estimation of Broadband Planetary Albedo from Operational Narrowband Satellite Measurements; National Oceanic and Atmospheric Administration: Washington, DC, USA, 1987.
- Loeb, N.G.; Manalo-Smith, N.; Kato, S.; Miller, W.F.; Gupta, S.K.; Minnis, P.; Wielicki, B.A. Angular distribution models for top-of-atmosphere radiative flux estimation from the clouds and the earth’s radiant energy system instrument on the tropical rainfall measuring mission satellite. Part I: Methodology. J. Appl. Meteorol. 2003, 42, 240–265. [Google Scholar] [CrossRef]
- Viollier, M. Restitution of longwave and shortwave radiative fluxes at the top of the atmosphere from combination of scarab and meteosat data. In Proceedings of the Megha-Tropiques 2nd Scientific Workshop, Paris, France, 2–6 July 2001. [Google Scholar]
- Vazquez-Navarro, M.; Mayer, B.; Mannstein, H. A fast method for the retrieval of integrated longwave and shortwave top-of-atmosphere upwelling irradiances from MSG/SEVIRI (RRUMS). Atmos. Meas. Tech. 2013, 6, 2627–2640. [Google Scholar] [CrossRef] [Green Version]
- Berk, A.; Bernstein, L.; Robertson, D. Modtran: A Moderate Resolution Model for LOWTRAN 7; Rep. AFGL-TR-83-0187; Air Force Geophysical Laboratory, Hanscom Air Force Base: Hanscom, MA, USA, 1983. [Google Scholar]
- Kim, B.-Y.; Lee, K.-T.; Jee, J.-B.; Zo, I.-S. Retrieval of outgoing longwave radiation at top-of-atmosphere using himawari-8 AHI data. Remote Sens. Environ. 2018, 204, 498–508. [Google Scholar] [CrossRef]
- Choi, Y.-S.; Ho, C.-H. Earth and environmental remote sensing community in South Korea: A review. Remote Sens. Appl. Soc. Environ. 2015, 2, 66–76. [Google Scholar] [CrossRef]
- Murata, H.; Takahashi, M.; Kosaka, Y. Vis and IR bands of Himawari-8/AHI compatible with those of MTSAT-2/Imager. 2015. Available online: www.data.jma.go.jp/mscweb/technotes/msctechrep60.pdf (accessed on 30 January 2018).
- Lee, S.-H.; Lee, K.-T.; Kim, B.-Y.; Zo, I.-S.; Jung, H.-S.; Rim, S.-H. Retrieval Algorithm for Broadband Albedo at the Top of the Atmosphere. Asia Pac. J. Atmos. Sci. 2017, accepted. [Google Scholar]
- Ricchiazzi, P.; Yang, S.; Gautier, C.; Sowle, D. Sbdart: A research and teaching software tool for plane-parallel radiative transfer in the earth’s atmosphere. Bull. Am. Meteorol. Soc. 1998, 79, 2101–2114. [Google Scholar] [CrossRef]
- Bessho, K.; Date, K.; Hayashi, M.; Ikeda, A.; Imai, T.; Inoue, H.; Kumagai, Y.; Miyakawa, T.; Murata, H.; Ohno, T. An introduction to himawari-8/9—Japan’s new-generation geostationary meteorological satellites. J. Meteorol. Soc. Jpn. Ser. II 2016, 94, 151–183. [Google Scholar] [CrossRef]
- Puschell, J.J.; Lowe, H.A.; Jeter, J.W.; Kus, S.M.; Hurt, W.T.; Gilman, D.; Rogers, D.L.; Hoelter, R.L.; Ravella, R. Japanese Advanced Meteorological Imager: A next-generation geo imager for MTSAT-1R. In Proceedings of the Earth Observing Systems VII, Seattle, WA, USA, 7–11 July 2002; International Society for Optics and Photonics: Bellingham, WA, USA, 2002; pp. 152–162. [Google Scholar]
- Cao, C.; De Luccia, F.J.; Xiong, X.; Wolfe, R.; Weng, F. Early on-orbit performance of the visible infrared imaging radiometer suite onboard the Suomi National Polar-Orbiting Partnership (S-NPP) satellite. IEEE Trans. Geosci. Remote Sens. 2014, 52, 1142–1156. [Google Scholar] [CrossRef]
- Yu, F.; Wu, X. Radiometric inter-calibration between Himawari-8 AHI and S-NPP VIIRS for the solar reflective bands. Remote Sens. 2016, 8, 165. [Google Scholar] [CrossRef]
- Paden, J.; Smith, G.L.; Lee, R.B.; Pandey, D.K.; Thomas, S. Reality check: A point response function (PRF) comparison of theory to measurements for the clouds and the earth’s radiant energy system (CERES) tropical rainfall measuring mission (TRMM) instrument. In Proceedings of the Visual Information Processing VI, Orlando, FL, USA, 21–25 April 1997; International Society for Optics and Photonics: Bellingham, WA, USA, 1997; pp. 109–118. [Google Scholar]
- Su, W.; Corbett, J.; Eitzen, Z.; Liang, L. Next-generation angular distribution models for top-of-atmosphere radiative flux calculation from CERES instruments: Validation. Atmos. Meas. Tech. 2015, 8, 3297–3313. [Google Scholar] [CrossRef]
- Zerefos, C.S.; Isaksen, I.S.; Ziomas, I. Chemistry and Radiation Changes in the Ozone Layer; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2012; Volume 557. [Google Scholar]
- Blanc, P.; Gschwind, B.; Lefevre, M.; Wald, L. Twelve monthly maps of ground albedo parameters derived from MODIS data sets. In Proceedings of the IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Quebec City, QC, Canada, 13–18 July 2014; pp. 3270–3272. [Google Scholar]
- Liang, S. Quantitative Remote Sensing of Land Surfaces; John Wiley & Sons: Hoboken, NJ, USA, 2005; Volume 30. [Google Scholar]
- Qu, X.; Hall, A. Surface contribution to planetary albedo variability in cryosphere regions. J. Clim. 2005, 18, 5239–5252. [Google Scholar] [CrossRef]
- Kopp, G.; Lean, J.L. A new, lower value of total solar irradiance: Evidence and climate significance. Geophys. Res. Lett. 2011, 38. [Google Scholar] [CrossRef]
- Michalsky, J.J. The astronomical almanac’s algorithm for approximate solar position (1950–2050). Sol. Energy 1988, 40, 227–235. [Google Scholar] [CrossRef]
- Nanni, M.R.; Demattê, J.A.M. Spectral reflectance methodology in comparison to traditional soil analysis. Soil Sci. Soc. Am. J. 2006, 70, 393–407. [Google Scholar] [CrossRef]
- Mokhtari, M.H.; Busu, I. Downscaling albedo from moderate-resolution imaging spectroradiometer (MODIS) to advanced space-borne thermal emission and reflection radiometer (ASTER) over an agricultural area utilizing aster visible-near infrared spectral bands. Int. J. Phys. Sci. 2011, 6, 5804–5821. [Google Scholar]
- Draper, N.R.; Smith, H.; Pownell, E. Applied Regression Analysis; Wiley: New York, NY, USA, 1966; Volume 3. [Google Scholar]
- Kleinbaum, D.; Kupper, L.; Nizam, A.; Rosenberg, E. Applied Regression Analysis and Other Multivariable Methods; Nelson Education: Scarborough, ON, Canada, 2013. [Google Scholar]
- Loeb, N.G.; Hinton, P.O.R.; Green, R.N. Top-of-atmosphere albedo estimation from angular distribution models: A comparison between two approaches. J. Geophys. Res. Atmos. 1999, 104, 31255–31260. [Google Scholar] [CrossRef]
- Loeb, N.G.; Parol, F.; Buriez, J.-C.; Vanbauce, C. Top-of-atmosphere albedo estimation from angular distribution models using scene identification from satellite cloud property retrievals. J. Clim. 2000, 13, 1269–1285. [Google Scholar] [CrossRef]
- Kato, S.; Marshak, A. Solar zenith and viewing geometry-dependent errors in satellite retrieved cloud optical thickness: Marine stratocumulus case. J. Geophys. Res. Atmos. 2009, 114. [Google Scholar] [CrossRef]
- Gardner, A.S.; Sharp, M.J. A review of snow and ice albedo and the development of a new physically based broadband albedo parameterization. J. Geophys. Res. Earth Surf. 2010, 115. [Google Scholar] [CrossRef]
- Loeb, N.G.; Kato, S. Top-of-atmosphere direct radiative effect of aerosols over the tropical oceans from the clouds and the earth’s radiant energy system (CERES) satellite instrument. J. Clim. 2002, 15, 1474–1484. [Google Scholar] [CrossRef]
- Geier, E.; Green, R.; Kratz, D.; Minnis, P.; Miller, W.; Nolan, S.; Franklin, C. Clouds and the Earth’s Radiant Energy System (CERES). Data Management System: Single Satellite Footprint TOA/Surface Fluxes and Clouds (SSF) Collection Document. Release 2 Version 1; 2003. Available online: https://ceres.larc.nasa.gov/documents/collect_guide/pdf/SSF_CG.pdf (accessed on 28 November 2017).
- Zhang, H.; Wang, M. Evaluation of sun glint models using MODIS measurements. J. Quant. Spectrosc. Radiat. Transf. 2010, 111, 492–506. [Google Scholar] [CrossRef]
- Kay, S.; Hedley, J.D.; Lavender, S. Sun glint correction of high and low spatial resolution images of aquatic scenes: A review of methods for visible and near-infrared wavelengths. Remote Sens. 2009, 1, 697–730. [Google Scholar] [CrossRef]
- Wilks, D.S. Statistical Methods in the Atmospheric Sciences; Academic Press: Cambridge, MA, USA, 2011; Volume 100. [Google Scholar]
- Benesty, J.; Chen, J.; Huang, Y.; Cohen, I. Pearson correlation coefficient. In Noise Reduction in Speech Processing; Springer: New York, NY, USA, 2009; pp. 1–4. [Google Scholar]
- Livezey, R.E.; Chen, W. Statistical field significance and its determination by Monte Carlo techniques. Mon. Weather Rev. 1983, 111, 46–59. [Google Scholar] [CrossRef]
- Thomas, S.; Priestley, K.; Shankar, M.; Smith, N.; Timcoe, M. Pre-launch sensor characterization of the CERES flight model 5 (FM5) instrument on NPP mission. Proc. SPIE 2011. [Google Scholar] [CrossRef]
- Lu, N.; Liu, R.; Liu, J.; Liang, S. An algorithm for estimating downward shortwave radiation from GMS 5 visible imagery and its evaluation over china. J. Geophys. Res. Atmos. 2010, 115. [Google Scholar] [CrossRef]
- Vermote, E.F.; Kotchenova, S. Atmospheric correction for the monitoring of land surfaces. J. Geophys. Res. Atmos. 2008, 113. [Google Scholar] [CrossRef]
- Sena, E.; Artaxo, P.; Correia, A. The effects of smoke aerosols, land-use change and water vapor reduction on the shortwave radiative budget over the Amazônia. In Proceedings of the EGU General Assembly Conference Abstracts, Vienna, Austria, 27 April–2 May 2014; Volume 16. [Google Scholar]
- Bertrand, C.; Clerbaux, N.; Ipe, A.; Dewitte, S.; Gonzalez, L. Angular distribution models anisotropic correction factors and sun glint: A sensitivity study. Int. J. Remote Sens. 2006, 27, 1741–1757. [Google Scholar] [CrossRef]
- Urraca, R.; Gracia-Amillo, A.M.; Koubli, E.; Huld, T.; Trentmann, J.; Riihelä, A.; Lindfors, A.V.; Palmer, D.; Gottschalg, R.; Antonanzas-Torres, F. Extensive validation of CM SAF surface radiation products over europe. Remote Sens. Environ. 2017, 199, 171–186. [Google Scholar] [CrossRef] [PubMed]
- Madhavan, B. Interactive comment on “shortwave surface radiation budget network for observing small-scale cloud inhomogeneity fields” by B.L. Madhavan et al. Atmos. Meas. Tech. Discuss. 2015, 8, C2233–C2250. [Google Scholar] [CrossRef]
- Li, Z.; Cribb, M.; Chang, F.L.; Trishchenko, A.; Luo, Y. Natural variability and sampling errors in solar radiation measurements for model validation over the atmospheric radiation measurement southern great plains region. J. Geophys. Res. Atmos. 2005, 110. [Google Scholar] [CrossRef]
- Wang, D.; Liang, S. Estimating top-of-atmosphere daily reflected shortwave radiation flux over land from modis data. IEEE Trans. Geosci. Remote Sens. 2017, 55, 4022–4031. [Google Scholar] [CrossRef]
- He, L.; Wang, L.; Lin, A.; Zhang, M.; Bilal, M.; Tao, M. Aerosol optical properties and associated direct radiative forcing over the Yangtze River basin during 2001–2015. Remote Sens. 2017, 9, 746. [Google Scholar] [CrossRef]
- Katagiri, S.; Kikuchi, N.; Nakajima, T.Y.; Higurashi, A.; Shimizu, A.; Matsui, I.; Hayasaka, T.; Sugimoto, N.; Takamura, T.; Nakajima, T. Cirrus cloud radiative forcing derived from synergetic use of MODIS analyses and ground-based observations. Sola 2010, 6, 25–28. [Google Scholar] [CrossRef]
- Allan, R.P.; Slingo, A.; Milton, S.F.; Culverwell, I. Exploitation of geostationary earth radiation budget data using simulations from a numerical weather prediction model: Methodology and data validation. J. Geophys. Res. Atmos. 2005, 110. [Google Scholar] [CrossRef]
- Urbain, M.; Clerbaux, N.; Ipe, A.; Tornow, F.; Hollmann, R.; Baudrez, E.; Velazquez Blazquez, A.; Moreels, J. The CM SAF TOA radiation data record using MVIRI and SEVIRI. Remote Sens. 2017, 9, 466. [Google Scholar] [CrossRef]
- Congalton, R.G.; Gu, J.; Yadav, K.; Thenkabail, P.; Ozdogan, M. Global land cover mapping: A review and uncertainty analysis. Remote Sens. 2014, 6, 12070–12093. [Google Scholar] [CrossRef]
- Doelling, D.R.; Sun, M.; Nguyen, L.T.; Nordeen, M.L.; Haney, C.O.; Keyes, D.F.; Mlynczak, P.E. Advances in geostationary-derived longwave fluxes for the CERES synoptic (SYN1deg) product. J. Atmos. Ocean. Technol. 2016, 33, 503–521. [Google Scholar] [CrossRef]














| Channel | Wavelength (µm) | Resolution | Main Purpose of Use | ||
|---|---|---|---|---|---|
| Spatial | Numbers of Pixels | Temporal | |||
| CH1 (Blue) | 0.47 (0.43–0.48) | 1.0 km | 11,000 | 10-min Full Disk | Weather forecasting Climate modeling |
| CH2 (Green) | 0.51 (0.50–0.52) | 1.0 km | 11,000 | ||
| CH3 (Red) | 0.64 (0.63–0.66) | 0.5 km | 22,000 | ||
| CH4 (NIR) | 0.86 (0.85–0.87) | 1.0 km | 11,000 | ||
| CH5 (NIR) | 1.61 (1.60–1.62) | 2.0 km | 5500 | ||
| CH6 (NIR) | 2.26 (2.25–2.27) | 2.0 km | 5500 | ||
| Parameter | Values Used for Look-Up-Table | Number |
|---|---|---|
| Spectral range | 0.2 to 3.3 at 0.005 µm | 620 |
| Solar zenith angle | 0°, 10°, 20°, 30°, 40°, 50°, 60°, 70°, 75°, 80°, and 85° | 12 |
| Viewing zenith angle | 0° to 85° at 5° increments | 18 |
| Relative azimuth angle | 0° to 180° at 10° increments | 19 |
| Atmospheric profiles | Tropical, Mid-latitude summer, Mid-latitude winter Subarctic summer, Subarctic winter, and US62 standard | 6 |
| Surface types | Ocean, Lake, Vegetation, Snow, and Sand | 5 |
| Aerosol types | Rural, Urban, Marine, and Tropospheric | 4 |
| Aerosol visibilities | 5, 10, 15, and 20 km | 4 |
| Cloud height | 2, 4, 6, 8, 10, 12, 14, and 16 km | 8 |
| Cloud optical thickness | 8, 16, 32, 64, and 128 | 5 |
| Date | Isotropy | Anisotropy | N | ||||||
|---|---|---|---|---|---|---|---|---|---|
| R2 | %Bias | %RMSE | MPE | R2 | %Bias | %RMSE | MPE | ||
| 15 July 2015 | 0.892 | 1.07 | 21.61 | 2.34 | 0.892 | −4.77 | 21.78 | −3.56 | 382,868 |
| 15 August 2015 | 0.881 | 3.99 | 22.99 | 4.98 | 0.882 | −2.80 | 21.98 | −1.72 | 765,902 |
| 15 September 2015 | 0.896 | 7.54 | 23.44 | 7.96 | 0.897 | 0.66 | 20.86 | 1.25 | 748,431 |
| 15 October 2015 | 0.894 | 8.17 | 24.55 | 8.65 | 0.889 | 1.27 | 21.94 | 2.60 | 769,128 |
| 15 November 2015 | 0.907 | 7.63 | 23.23 | 8.33 | 0.897 | −0.43 | 21.80 | 0.95 | 346,584 |
| 15 December 2015 | 0.894 | 4.08 | 21.94 | 5.37 | 0.885 | −1.74 | 21.56 | 0.00 | 318,051 |
| 15 January 2016 | 0.908 | 1.76 | 20.52 | 3.35 | 0.905 | −0.79 | 20.47 | 1.03 | 209,119 |
| 15 February 2016 | 0.904 | 8.13 | 22.09 | 9.47 | 0.899 | 1.39 | 19.73 | 3.56 | 700,569 |
| 15 March 2016 | 0.906 | 6.93 | 21.49 | 7.53 | 0.902 | 0.23 | 19.56 | 1.53 | 608,431 |
| 15 April 2016 | 0.900 | 4.43 | 22.57 | 4.63 | 0.900 | −1.18 | 21.15 | −0.54 | 622,010 |
| 15 May 2016 | 0.910 | −0.06 | 20.18 | −0.98 | 0.910 | −4.58 | 20.24 | −5.43 | 457,664 |
| 15 June 2016 | 0.895 | −0.91 | 20.07 | −0.98 | 0.897 | −6.11 | 20.33 | −6.32 | 414,194 |
| 15 July 2016 | 0.889 | 0.45 | 21.73 | 1.14 | 0.887 | −4.56 | 21.94 | −4.18 | 350,007 |
| 15 August 2016 | 0.880 | 4.25 | 23.00 | 4.54 | 0.891 | −2.65 | 20.73 | −2.47 | 673,663 |
| 15 September 2016 | 0.874 | 5.69 | 24.20 | 5.88 | 0.892 | −0.69 | 20.63 | −0.57 | 729,884 |
| 15 October 2016 | 0.900 | 5.59 | 22.04 | 5.78 | 0.900 | −0.81 | 20.05 | −0.12 | 769,781 |
| 15 November 2016 | 0.892 | 4.28 | 22.79 | 4.89 | 0.885 | −1.29 | 22.19 | −0.28 | 585,544 |
| 15 December 2016 | 0.900 | 3.49 | 21.33 | 4.86 | 0.892 | −0.59 | 21.17 | 0.92 | 451,665 |
| 15 January 2017 | 0.900 | 5.85 | 22.22 | 5.99 | 0.887 | −0.77 | 21.40 | 0.29 | 626,594 |
| 15 February 2017 | 0.887 | 9.59 | 25.63 | 8.82 | 0.878 | 0.94 | 22.14 | 1.36 | 578,772 |
| All | 0.893 | 5.16 | 22.67 | 5.58 | 0.893 | −1.14 | 21.04 | −0.33 | 11,108,861 |
| Statistics | R2 | Mean | RMSE (%RMSE) | MPE | N | ||
|---|---|---|---|---|---|---|---|
| Clear Fraction Land & Ocean | AHI | CERES | |||||
| Cloudy | 0.869 | 302.70 | 313.46 | 56.02 (17.87) | −2.34 | 2,006,927 | |
| –Partly | 0.639 | 195.27 | 198.39 | 38.17 (19.24) | −0.25 | 574,000 | |
| Land | –Mostly | 0.657 | 270.61 | 277.79 | 59.52 (21.42) | −1.66 | 630,676 |
| –Overcast | 0.861 | 404.78 | 423.82 | 64.4. (14.97) | −4.36 | 802,251 | |
| All | 0.880 | 274.26 | 282.03 | 51.29 (18.29) | −0.51 | 2,632,865 | |
| Cloudy | 0.902 | 256.18 | 256.59 | 54.14 (21.10) | −0.60 | 7,417,530 | |
| –Partly | 0.429 | 105.49 | 111.12 | 30.62 (27.56) | −5.25 | 1,864,210 | |
| Ocean | –Mostly | 0.625 | 192.29 | 183.33 | 57.95 (31.61) | 3.98 | 1,999,843 |
| –Overcast | 0.874 | 371.19 | 374.14 | 61.12 (16.34) | −0.74 | 3,553,477 | |
| All | 0.909 | 243.16 | 244.24 | 52.39 (21.45) | −1.37 | 8,000,530 | |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lee, S.-H.; Kim, B.-Y.; Lee, K.-T.; Zo, I.-S.; Jung, H.-S.; Rim, S.-H. Retrieval of Reflected Shortwave Radiation at the Top of the Atmosphere Using Himawari-8/AHI Data. Remote Sens. 2018, 10, 213. https://doi.org/10.3390/rs10020213
Lee S-H, Kim B-Y, Lee K-T, Zo I-S, Jung H-S, Rim S-H. Retrieval of Reflected Shortwave Radiation at the Top of the Atmosphere Using Himawari-8/AHI Data. Remote Sensing. 2018; 10(2):213. https://doi.org/10.3390/rs10020213
Chicago/Turabian StyleLee, Sang-Ho, Bu-Yo Kim, Kyu-Tae Lee, Il-Sung Zo, Hyun-Seok Jung, and Se-Hun Rim. 2018. "Retrieval of Reflected Shortwave Radiation at the Top of the Atmosphere Using Himawari-8/AHI Data" Remote Sensing 10, no. 2: 213. https://doi.org/10.3390/rs10020213
APA StyleLee, S.-H., Kim, B.-Y., Lee, K.-T., Zo, I.-S., Jung, H.-S., & Rim, S.-H. (2018). Retrieval of Reflected Shortwave Radiation at the Top of the Atmosphere Using Himawari-8/AHI Data. Remote Sensing, 10(2), 213. https://doi.org/10.3390/rs10020213