An Information Entropy-Based Sensitivity Analysis of Radar Sensing of Rough Surface
Abstract
:1. Introduction
2. Materials and Methods
2.1. Surface Scattering Model
2.2. Information Theoretic Criteria
3. Results
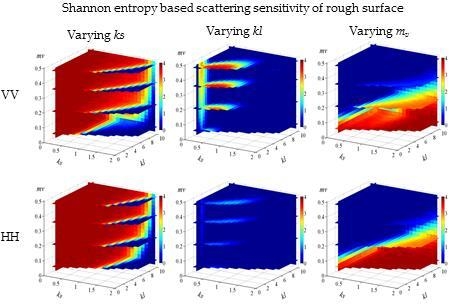
3.1. SA of Surface Condition
3.2. Sensitivity of Observation Configuration
3.3. SA of Dual-Polarization and Multi-Angle
4. Discussion
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Ulaby, F.T.; Long, D.G. Microwave Radar and Radiometric Remote Sensing; University of Michigan Press: Ann Arbor, MI, USA, 2014. [Google Scholar]
- Crosson, W.L.; Limaye, A.S.; Laymon, C.A. Parameter sensitivity of soil moisture retrievals from airborne L-band radiometer measurements in SMEX02. IEEE Trans. Geosci. Remote Sens. 2005, 43, 1517–1528. [Google Scholar] [CrossRef]
- Du, Y.; Ulaby, F.T.; Dobson, M.C. Sensitivity to soil moisture by active and passive microwave sensors. IEEE Trans. Geosci. Remote Sens. 2000, 38, 105–114. [Google Scholar] [CrossRef]
- Zribi, M.; Dechambre, M. A new empirical model to retrieve soil moisture and roughness from C-band radar data. Remote Sens. Environ. 2003, 84, 42–52. [Google Scholar] [CrossRef]
- Verhoest, N.E.; Lievens, H.; Wagner, W.; Álvarez-Mozos, J.; Moran, M.S.; Mattia, F. On the soil roughness parameterization problem in soil moisture retrieval of bare surfaces from synthetic aperture radar. Sensors 2008, 8, 4213–4248. [Google Scholar] [CrossRef] [PubMed]
- Lievens, H.; Verhoest, N.E.; De Keyser, E.; Vernieuwe, H.; Matgen, P.; Álvarez-Mozos, J.; De Baets, B. Effective roughness modeling as a tool for soil moisture retrieval from C-and L-band SAR. Hydrol. Earth Syst. Sci. 2011, 15, 151–162. [Google Scholar] [CrossRef] [Green Version]
- Zribi, M.; Gorrab, A.; Baghdadi, N. A new soil roughness parameter for the modelling of radar backscattering over bare soil. Remote Sens. Environ. 2014, 152, 62–73. [Google Scholar] [CrossRef] [Green Version]
- Bindlish, R.; Jackson, T.J.; Wood, E.; Gao, H.; Starks, P.; Bosch, D.; Lakshmi, V. Soil moisture estimates from TRMM Microwave Imager observations over the Southern United States. Remote Sens. Environ. 2003, 85, 507–515. [Google Scholar] [CrossRef]
- Chen, K.S.; Yen, S.K.; Huang, W.P. A simple-model for retrieving bare soil-moisture from radar-scattering coefficients. Remote Sens. Environ. 1995, 54, 121–126. [Google Scholar] [CrossRef]
- Mao, K.B.; Tang, H.J.; Zhang, L.X.; Li, M.C.; Guo, Y.; Zhao, D.Z. A method for retrieving soil moisture in Tibet region by utilizing microwave index from TRMM/TMI data. Int. J. Remote Sens. 2008, 29, 2903–2923. [Google Scholar] [CrossRef]
- Brogioni, M.; Pettinato, S.; Macelloni, G.; Paloscia, S.; Pampaloni, P.; Pierdicca, N.; Ticconi, F. Sensitivity of bistatic scattering to soil moisture and surface roughness of bare soils. Int. J. Remote Sens. 2010, 31, 4227–4255. [Google Scholar] [CrossRef]
- Saltelli, A.; Ratto, M.; Andres, T.; Campolongo, F.; Cariboni, J.; Gatelli, D.; Saisana, M.; Tarantola, S. Global Sensitivity Analysis: The Primer; John Wiley & Sons: West Sussex, UK, 2008. [Google Scholar]
- Wagner, S. Global sensitivity analysis of predictor models in soft- ware engineering. In Proceedings of the International Workshop on Predictor Models in Software Engineering, Minneapolis, MN, USA, 20–26 May 2007; p. 3. [Google Scholar]
- Petropoulos, G.; Srivastava, P.K. (Eds.) Sensitivity Analysis in Earth Observation Modelling; Elsevier: Oxford, UK, 2016. [Google Scholar]
- Ma, C.F.; Li, X.; Wang, S.G. A global sensitivity analysis of soil parameters associated with backscattering using the advanced integral equation model. IEEE Trans. Geosci. Remote Sens. 2015, 53, 5613–5623. [Google Scholar]
- McNairn, H.; Jackson, T.J.; Wiseman, G.; Belair, S.; Berg, A.; Bullock, P.; Colliander, A.; Cosh, M.H.; Kim, S.B.; Magagi, R.; et al. The soil moisture active passive validation experiment 2012 (SMAPVEX12): Prelaunch calibration and validation of the SMAP soil moisture algorithms. IEEE Trans. Geosci. Remote Sens. 2015, 53, 2784–2801. [Google Scholar] [CrossRef]
- Wang, J.; Li, X.; Lu, L.; Fang, F. Parameter sensitivity analysis of crop growth models based on the extended Fourier amplitude sensitivity test method. Environ. Model. Softw. 2013, 48, 171–182. [Google Scholar] [CrossRef]
- Estrada, V.; Diaz, M.S. Global sensitivity analysis in the development of first principle-based eutrophication models. Environ. Model. Softw. 2010, 25, 1539–1551. [Google Scholar] [CrossRef]
- Li, D.; Jin, R.; Zhou, J.; Kang, J. Analysis and reduction of the uncertainties in soil moisture estimation with the L-MEB model using EFAST and ensemble retrieval. IEEE Geosci. Remote Sens. Lett. 2015, 12, 1337–1341. [Google Scholar]
- Lentini, N.E.; Hackett, E.E. Global sensitivity of parabolic equation radar wave propagation simulation to sea state and atmospheric refractivity structure. Radio Sci. 2015, 50, 1027–1049. [Google Scholar] [CrossRef]
- Neelam, M.; Mohanty, B.P. Global sensitivity analysis of the radiative transfer model. Water Resour. Res. 2015, 51, 2428–2443. [Google Scholar] [CrossRef]
- Sobol, I.M. Sensitivity estimates for nonlinear mathematical models. Math. Model. Comput. Exp. 1993, 1, 407–414. [Google Scholar]
- Sudret, B. Global sensitivity analysis using polynomial chaos expansions. Reliab. Eng. Syst. Saf. 2008, 93, 964–979. [Google Scholar] [CrossRef]
- Saltelli, A.; Sobol, I.M. About the use of rank transformation in sensitivity of model output. Reliab. Eng. Syst. Saf. 1995, 50, 225–239. [Google Scholar]
- Saltelli, A.; Annoni, P. How to avoid a perfunctory sensitivity analysis. Environ. Model. Softw. 2010, 25, 1508–1517. [Google Scholar] [CrossRef]
- Shannon, C.E. A mathematical theory of communication. In ACM SIGMOBILE Mobile Computing and Communications Review; ACM: New York, NY, USA, 2001; Volume 5, pp. 3–55. [Google Scholar]
- Chen, K.S.; Wu, T.D.; Tsang, L.; Li, Q.; Shi, J.C.; Fung, A.K. Emission of rough surfaces calculated by the integral equation method with comparison to three-dimensional moment method simulations. IEEE Trans. Geosci. Remote Sens. 2003, 41, 90–101. [Google Scholar] [CrossRef]
- Wu, T.D.; Chen, K.S.; Shi, J.C.; Lee, H.W.; Fung, A.K. A study of AIEM Model for Bistatic Scattering from Randomly Surfaces. IEEE Trans. Geosci. Remote Sens. 2008, 46, 2584–2598. [Google Scholar]
- Chen, K.L.; Chen, K.S.; Li, Z.L.; Liu, Y. Extension and validation of an advanced integral equation model for bistatic scattering from rough surfaces. Prog. Electromagn. Res. 2015, 152, 59–76. [Google Scholar] [CrossRef]
- Dobson, M.C.; Ulaby, F.T.; Hallikainen, M.T.; El-Rayes, M.A. Microwave dielectric behavior of wet soil—Part II. Dielectric mixing models. IEEE Trans. Geosci. Remote Sens. 1985, 1, 35–46. [Google Scholar] [CrossRef]
- Peplinski, N.R.; Ulaby, F.T.; Dobson, M.C. Dielectric-properties of soils in the 0.3–1.3-GHz range. IEEE Trans. Geosci. Remote Sens. 1995, 33, 803–807. [Google Scholar] [CrossRef]
- Chen, K.S.; Wu, T.D.; Shi, J.C. A model- based inversion of rough surface parameters from radar measurements. J. Electromagn. Waves Appl. 2001, 15, 173–200. [Google Scholar] [CrossRef]
- Rényi, A. On measures of entropy and information. In Proceedings of the Fourth Berkeley Symposium on Mathematical Statistics and Probability, Berkeley, CA, USA, 20 June–30 July 1960; Volume 1, pp. 547–561. [Google Scholar]
- Liu, H.; Chen, W.; Sudjianto, A. Relative entropy based method for probabilistic sensitivity analysis in engineering design. J. Mech. Des. 2006, 128, 326–336. [Google Scholar] [CrossRef]
- Ziviani, A.; Gomes, A.T.A.; Monsores, M.L.; Rodrigues, P.S. Network anomaly detection using nonextensive entropy. IEEE Commun. Lett. 2007, 11, 1034–1036. [Google Scholar] [CrossRef]
- Phillips, S.J.; Dudík, M.; Schapire, R.E. A maximum entropy approach to species distribution modeling. In Proceedings of the Twenty-First International Conference on Machine Learning, Banff, AB, Canada, 4–8 July 2004; ACM: New York, NY, USA, 2004; p. 83. [Google Scholar]
- Parzen, E. On the estimation of a probability density function and the mode. Ann. Math. Stat. 1962, 33, 1065–1076. [Google Scholar] [CrossRef]











| Parameters | Range | ||
|---|---|---|---|
| Surface Parameter | ks | Normalized root mean surfaces height | 0.01~2 |
| kl | Normalized correlation length | 0.01~10 | |
| mv | Moisture content (m3m−3) | 0.01~0.45 | |
| Radar Parameter | θi | Incident angle | 10°~70° |
| θs | Scattering angle | =θi | |
| φs | Scattering azimuthal angle | 180° | |
| Distribution | Equation 1 | Number | Parameters | SE (nat) | RE (nat) | |||
|---|---|---|---|---|---|---|---|---|
| Uniform | Case 1 | 0.01 | −1.18 | 0.57 | 3.75 | 3.76 | ||
| Exponential | Case 2 | 1.90 | 5.59 | 1.99 | 3.42 | 3.28 | ||
| Normal | Case 3 | −0.01 | 0 | 0.13 | 3.88 | 3.78 | ||
| Case 4 | −0.02 | 0.17 | 0.25 | 3.90 | 3.76 | |||
| Case 5 | 0.00 | −0.03 | 1.25 | 3.88 | 3.77 | |||
| Beta | 2 | Case 6 | −3.30 | 11.86 | 0.14 | 1.47 | −0.23 | |
| Case 7 | −2.03 | 3.8 | 0.18 | 2.66 | 1.77 | |||
| Case 8 | −0.59 | −0.55 | 0.23 | 3.77 | 3.67 | |||
| Weibull | Case 9 | 0.61 | 0.21 | 0.33 | 3.90 | 3.74 | ||
| Case 10 | −0.61 | 0.45 | 0.11 | 3.90 | 3.72 | |||
| Case 11 | −0.84 | 1.14 | 0.06 | 3.84 | 3.73 | |||
| Lognormal | Case 12 | 0.18 | 0.08 | 0.47 | 3.88 | 3.78 | ||
| Case 13 | 0.86 | 1.33 | 1.96 | 3.86 | 3.72 | |||
| Case 14 | 1.56 | 3.45 | 4.38 | 3.63 | 3.56 | |||
| Gamma | Case 15 | 1.33 | 2.47 | 0.35 | 3.69 | 3.58 | ||
| Case 16 | 1.36 | 2.7 | 1.76 | 3.64 | 3.61 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, Y.; Chen, K.-S. An Information Entropy-Based Sensitivity Analysis of Radar Sensing of Rough Surface. Remote Sens. 2018, 10, 286. https://doi.org/10.3390/rs10020286
Liu Y, Chen K-S. An Information Entropy-Based Sensitivity Analysis of Radar Sensing of Rough Surface. Remote Sensing. 2018; 10(2):286. https://doi.org/10.3390/rs10020286
Chicago/Turabian StyleLiu, Yu, and Kun-Shan Chen. 2018. "An Information Entropy-Based Sensitivity Analysis of Radar Sensing of Rough Surface" Remote Sensing 10, no. 2: 286. https://doi.org/10.3390/rs10020286
APA StyleLiu, Y., & Chen, K.-S. (2018). An Information Entropy-Based Sensitivity Analysis of Radar Sensing of Rough Surface. Remote Sensing, 10(2), 286. https://doi.org/10.3390/rs10020286