Combining Fractional Order Derivative and Spectral Variable Selection for Organic Matter Estimation of Homogeneous Soil Samples by VIS–NIR Spectroscopy
Abstract
:1. Introduction
2. Materials and Methods
2.1. Study Area and Field Sampling
2.2. Spectral Measurement and Pre-Processing
2.3. Chemical Analysis
2.4. Fractional Order Derivative (FOD)
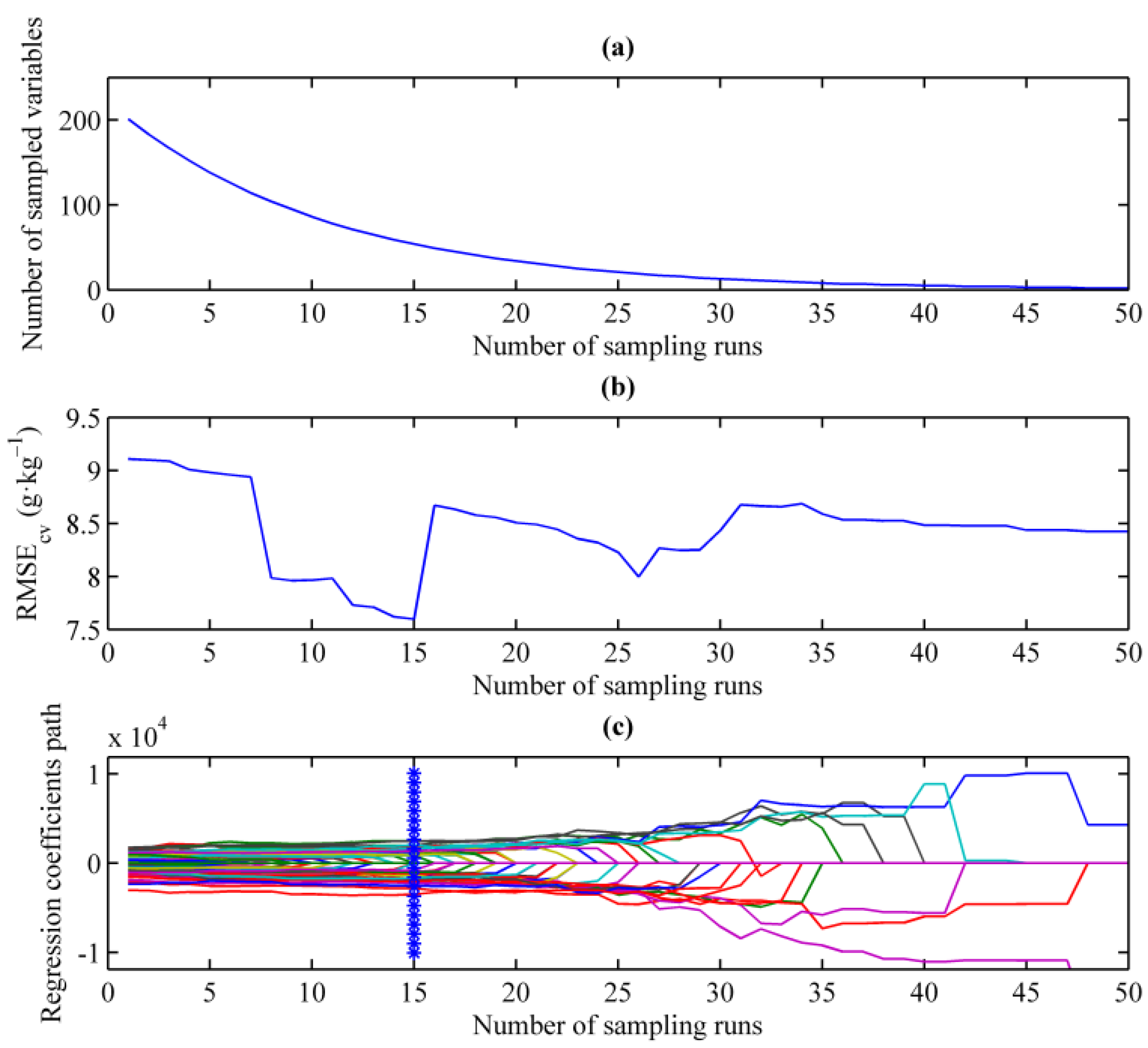
2.5. Spectral Variable Selection Techniques
2.6. Model Calibration and Validation
3. Results
3.1. SOM, Soil Water Content and VIS–NIR Spectra
3.2. FOD Spectra
3.3. Full-Spectrum SVM Models
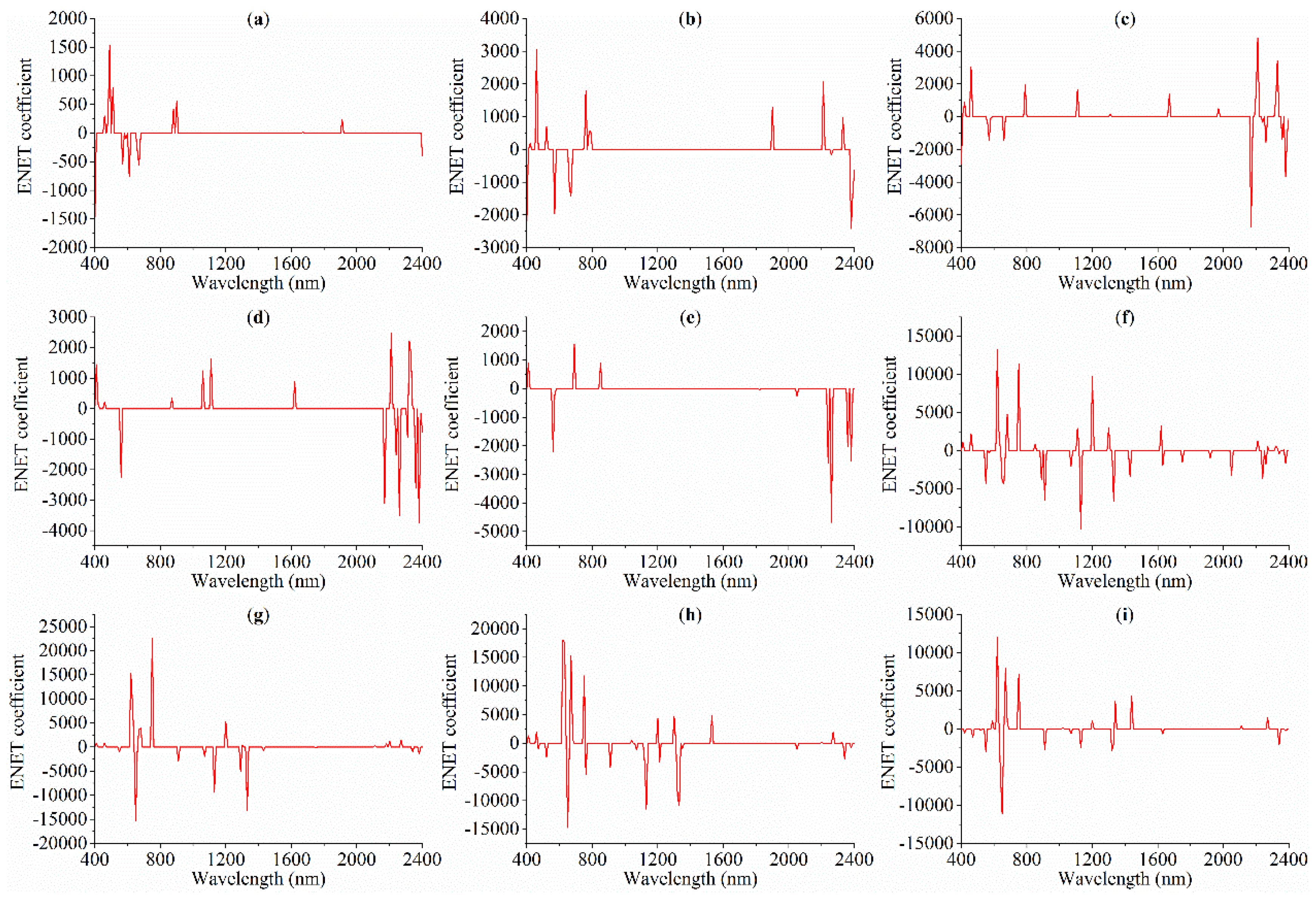
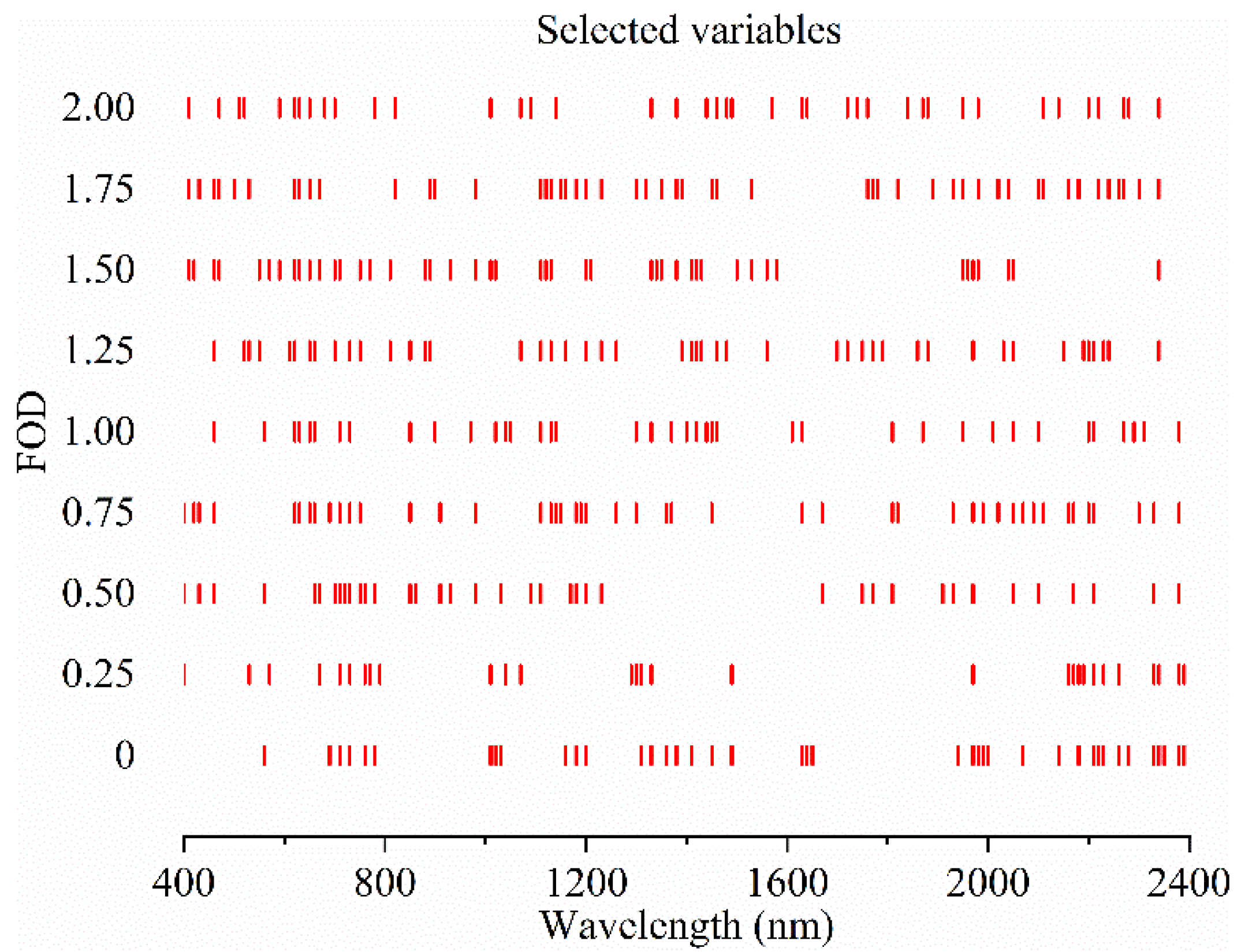
3.4. Spectral Variables Selected by CARS, ENET and GA
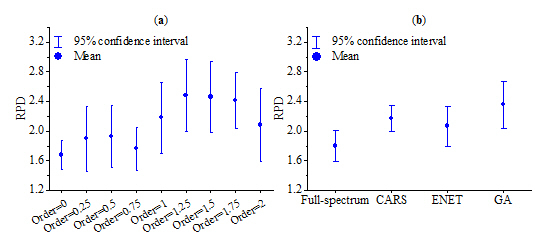
3.5. Comparison of Predictions Using Different FOD Transformations and Variable Selection Techniques
4. Discussion
5. Conclusions
- (1)
- The overall reflectance of moist spectra was lower than dried ground spectra. With increasing order of derivative, the overlapping peaks and baseline drifts were gradually removed, but the spectral strength decreased simultaneously.
- (2)
- In some cases, FOD (e.g., 1.25-order and 1.5-order) could generate better estimation than integer order derivatives (i.e., 1-order and 2-order) and original reflectance spectra.
- (3)
- The SVM model based on 1.5 derivative spectra and GA method provided the optimal model prediction, with validation RPD of 2.89. Our study confirms the potential of moist VIS–NIR spectra to estimate SOM.
- (4)
- Variable selection (i.e., CARS, ENET and GA) was able to select the useful spectral variables, and the simplified models showed the improved prediction accuracies. Overall, GA produced the best predictive result, but it also consumed long computation time. One alternative is to apply CARS method because it takes less time to process the algorithm without significantly reducing the model performance.
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Schlesinger, W.H.; Andrews, J.A. Soil respiration and the global carbon cycle. Biogeochemistry 2000, 48, 7–20. [Google Scholar] [CrossRef]
- Lal, R. Soil carbon sequestration to mitigate climate change. Geoderma 2004, 123, 1–22. [Google Scholar] [CrossRef]
- Lobsey, C.R.; Viscarra Rossel, R.A.; Roudier, P.; Hedley, C.B. Rs-local data-mines information from spectral libraries to improve local calibrations. Eur. J. Soil Sci. 2017, 68, 840–852. [Google Scholar] [CrossRef]
- Kuhnel, A.; Bogner, C. In-situ prediction of soil organic carbon by VIS–NIR spectroscopy: An efficient use of limited field data. Eur. J. Soil Sci. 2017, 68, 689–702. [Google Scholar] [CrossRef]
- Hong, Y.S.; Yu, L.; Chen, Y.Y.; Liu, Y.F.; Liu, Y.L.; Liu, Y.; Cheng, H. Prediction of soil organic matter by VIS–NIR spectroscopy using normalized soil moisture index as a proxy of soil moisture. Remote Sens. 2018, 10, 28. [Google Scholar] [CrossRef]
- Ogen, Y.; Neumann, C.; Chabrillat, S.; Goldshleger, N.; Ben Dor, E. Evaluating the detection limit of organic matter using point and imaging spectroscopy. Geoderma 2018, 321, 100–109. [Google Scholar] [CrossRef]
- Mouazen, A.M.; Maleki, M.R.; De Baerdemaeker, J.; Ramon, H. On-line measurement of some selected soil properties using a VIS–NIR sensor. Soil Tillage Res. 2007, 93, 13–27. [Google Scholar] [CrossRef]
- Nocita, M.; Kooistra, L.; Bachmann, M.; Muller, A.; Powell, M.; Weel, S. Predictions of soil surface and topsoil organic carbon content through the use of laboratory and field spectroscopy in the Albany Thicket Biome of Eastern Cape Province of South Africa. Geoderma 2011, 167–168, 295–302. [Google Scholar] [CrossRef] [Green Version]
- Li, S.; Shi, Z.; Chen, S.C.; Ji, W.J.; Zhou, L.Q.; Yu, W.; Webster, R. In situ measurements of organic carbon in soil profiles using VIS–NIR spectroscopy on the Qinghai-Tibet plateau. Environ. Sci. Technol. 2015, 49, 4980–4987. [Google Scholar] [CrossRef] [PubMed]
- Nawar, S.; Buddenbaum, H.; Hill, J.; Kozak, J.; Mouazen, A.M. Estimating the soil clay content and organic matter by means of different calibration methods of VIS–NIR diffuse reflectance spectroscopy. Soil Tillage Res. 2016, 155, 510–522. [Google Scholar] [CrossRef]
- Rinnan, Å.; Berg, F.v.d.; Engelsen, S.B. Review of the most common pre-processing techniques for near-infrared spectra. TrAC Trend Anal. Chem. 2009, 28, 1201–1222. [Google Scholar]
- Dotto, A.C.; Dalmolin, R.S.D.; ten Caten, A.; Grunwald, S. A systematic study on the application of scatter-corrective and spectral-derivative preprocessing for multivariate prediction of soil organic carbon by VIS–NIR spectra. Geoderma 2018, 314, 262–274. [Google Scholar] [CrossRef]
- Tong, P.J.; Du, Y.P.; Zheng, K.Y.; Wu, T.; Wang, J.J. Improvement of NIR model by fractional order Savitzky-Golay derivation (FOSGD) coupled with wavelength selection. Chemom. Intell. Lab. 2015, 143, 40–48. [Google Scholar] [CrossRef]
- Li, Y.L.; Pan, C.; Meng, X.; Ding, Y.Q.; Chen, H.X. Haar wavelet based implementation method of the non-integer order differentiation and its application to signal enhancement. Meas. Sci. Rev. 2015, 15, 101–106. [Google Scholar] [CrossRef]
- Zhang, D.; Tiyip, T.; Ding, J.L.; Zhang, F.; Nurmemet, I.; Kelimu, A.; Wang, J.Z. Quantitative estimating salt content of saline soil using laboratory hyperspectral data treated by fractional derivative. J. Spectrosc. 2016, 2016, 1081674. [Google Scholar] [CrossRef]
- Viscarra Rossel, R.A.; Behrens, T. Using data mining to model and interpret soil diffuse reflectance spectra. Geoderma 2010, 158, 46–54. [Google Scholar] [CrossRef]
- Vohland, M.; Ludwig, M.; Thiele-Bruhn, S.; Ludwig, B. Quantification of soil properties with hyperspectral data: Selecting spectral variables with different methods to improve accuracies and analyze prediction mechanisms. Remote Sens. 2017, 9, 1103. [Google Scholar] [CrossRef]
- Xu, S.X.; Zhao, Y.C.; Wang, M.Y.; Shi, X.Z. Comparison of multivariate methods for estimating selected soil properties from intact soil cores of paddy fields by VIS–NIR spectroscopy. Geoderma 2018, 310, 29–43. [Google Scholar] [CrossRef]
- Chong, I.G.; Jun, C.H. Performance of some variable selection methods when multicollinearity is present. Chemom. Intell. Lab. 2005, 78, 103–112. [Google Scholar] [CrossRef]
- Jarvis, R.M.; Goodacre, R. Genetic algorithm optimization for pre-processing and variable selection of spectroscopic data. Bioinformatics 2005, 21, 860–868. [Google Scholar] [CrossRef] [PubMed]
- Galvão, R.K.H.; Araújo, M.C.U.; Fragoso, W.D.; Silva, E.C.; José, G.E.; Soares, S.F.C.; Paiva, H.M. A variable elimination method to improve the parsimony of MLR models using the successive projections algorithm. Chemom. Intell. Lab. 2008, 92, 83–91. [Google Scholar] [CrossRef]
- Li, H.D.; Liang, Y.Z.; Xu, Q.S.; Cao, D.S. Key wavelengths screening using competitive adaptive reweighted sampling method for multivariate calibration. Anal. Chim. Acta 2009, 648, 77–84. [Google Scholar] [CrossRef] [PubMed]
- Vohland, M.; Ludwig, M.; Harbich, M.; Emmerling, C.; Thiele-Bruhn, S. Using variable selection and wavelets to exploit the full potential of visible-near infrared spectra for predicting soil properties. J. Near Infrared Spec. 2016, 24, 255–269. [Google Scholar] [CrossRef]
- Vohland, M.; Harbich, M.; Ludwig, M.; Emmerling, C.; Thiele-Bruhn, S. Quantification of soil variables in a heterogeneous soil region with VIS–NIR–SWIR data using different statistical sampling and modeling strategies. IEEE J. Sel. Top. Appl. 2016, 9, 4011–4021. [Google Scholar] [CrossRef]
- Vohland, M.; Ludwig, M.; Thiele-Bruhn, S.; Ludwig, B. Determination of soil properties with visible to near- and mid-infrared spectroscopy: Effects of spectral variable selection. Geoderma 2014, 223, 88–96. [Google Scholar] [CrossRef]
- Xu, S.X.; Zhao, Y.C.; Wang, M.Y.; Shi, X.Z. Determination of rice root density from VIS–NIR spectroscopy by support vector machine regression and spectral variable selection techniques. Catena 2017, 157, 12–23. [Google Scholar] [CrossRef]
- Zou, H.; Hastie, T. Regularization and variable selection via the elastic net. J. R. Stat. Soc. B 2005, 67, 301–320. [Google Scholar] [CrossRef]
- Liu, W.Y.; Li, Q. An efficient elastic net with regression coefficients method for variable selection of spectrum data. PLoS ONE 2017, 12, e0171122. [Google Scholar] [CrossRef] [PubMed]
- Niazi, A.; Leardi, R. Genetic algorithms in chemometrics. J. Chemom. 2012, 26, 345–351. [Google Scholar] [CrossRef]
- Leardi, R.; Lupiáñez González, A. Genetic algorithms applied to feature selection in PLS regression: How and when to use them. Chemom. Intell. Lab. 1998, 41, 195–207. [Google Scholar] [CrossRef]
- Jiang, Q.H.; Liu, M.X.; Wang, J.; Liu, F. Feasibility of using visible and near-infrared reflectance spectroscopy to monitor heavy metal contaminants in urban lake sediment. Catena 2018, 162, 72–79. [Google Scholar] [CrossRef]
- Shi, T.Z.; Chen, Y.Y.; Liu, H.Z.; Wang, J.J.; Wu, G.F. Soil organic carbon content estimation with laboratory-based visible-near-infrared reflectance spectroscopy: Feature selection. Appl. Spectrosc. 2014, 68, 831–837. [Google Scholar] [CrossRef] [PubMed]
- Liu, Y.L.; Jiang, Q.H.; Fei, T.; Wang, J.J.; Shi, T.Z.; Guo, K.; Li, X.R.; Chen, Y.Y. Transferability of a visible and near-infrared model for soil organic matter estimation in riparian landscapes. Remote Sens. 2014, 6, 4305–4322. [Google Scholar] [CrossRef]
- Qi, H.J.; Paz-Kagan, T.; Karnieli, A.; Li, S.W. Linear multi-task learning for predicting soil properties using field spectroscopy. Remote Sens. 2017, 9, 1099. [Google Scholar] [CrossRef]
- Romero, D.J.; Ben-Dor, E.; Demattê, J.A.M.; Souza, A.B.E.; Vicente, L.E.; Tavares, T.R.; Martello, M.; Strabeli, T.F.; Barros, P.P.D.; Fiorio, P.R.; et al. Internal soil standard method for the Brazilian soil spectral library: Performance and proximate analysis. Geoderma 2018, 312, 95–103. [Google Scholar] [CrossRef]
- Savitzky, A.; Golay, M.J.E. Smoothing and differentiation of data by simplified least squares procedures. Anal. Chem. 1964, 36, 1627–1639. [Google Scholar] [CrossRef]
- Clark, R.N.; Roush, T.L. Reflectance spectroscopy—Quantitative-analysis techniques for remote-sensing applications. J. Geophys. Res. 1984, 89, 6329–6340. [Google Scholar] [CrossRef]
- Benkhettou, N.; da Cruz, A.; Torres, D.F.M. A fractional calculus on arbitrary time scales: Fractional differentiation and fractional integration. Signal Process. 2015, 107, 230–237. [Google Scholar] [CrossRef]
- Leardi, R.; Boggia, R.; Terrile, M. Genetic algorithms as a strategy for feature-selection. J. Chemometr. 1992, 6, 267–281. [Google Scholar] [CrossRef]
- Wang, J.J.; Cui, L.J.; Gao, W.X.; Shi, T.Z.; Chen, Y.Y.; Gao, Y. Prediction of low heavy metal concentrations in agricultural soils using visible and near-infrared reflectance spectroscopy. Geoderma 2014, 216, 1–9. [Google Scholar] [CrossRef]
- Vapnik, V.N. An overview of statistical learning theory. IEEE Trans. Neural Netw. 1999, 10, 988–999. [Google Scholar] [CrossRef] [PubMed]
- Chang, C.C.; Lin, C.J. LIBSVM: A library for support vector machines. ACM Trans. Intell. Syst. Technol. 2011, 2. [Google Scholar] [CrossRef]
- Thissen, U.; Pepers, M.; Ustun, B.; Melssen, W.J.; Buydens, L.M.C. Comparing support vector machines to PLS for spectral regression applications. Chemom. Intell. Lab. 2004, 73, 169–179. [Google Scholar] [CrossRef]
- Luca, F.; Conforti, M.; Castrignano, A.; Matteucci, G.; Buttafuoco, G. Effect of calibration set size on prediction at local scale of soil carbon by VIS–NIR spectroscopy. Geoderma 2017, 288, 175–183. [Google Scholar] [CrossRef]
- Franceschini, M.H.D.; Demattê, J.A.M.; Kooistra, L.; Bartholomeus, H.; Rizzo, R.; Fongaro, C.T.; Molin, J.P. Effects of external factors on soil reflectance measured on-the-go and assessment of potential spectral correction through orthogonalisation and standardisation procedures. Soil Tillage Res. 2018, 177, 19–36. [Google Scholar] [CrossRef]
- Ji, W.; Rossel, R.A.V.; Shi, Z. Accounting for the effects of water and the environment on proximally sensed VIS–NIR soil spectra and their calibrations. Eur. J. Soil Sci. 2015, 66, 555–565. [Google Scholar] [CrossRef]
- Ackerson, J.P.; Morgan, C.L.S.; Ge, Y. Penetrometer-mounted VIS–NIR spectroscopy: Application of EPO-PLS to in situ VIS–NIR spectra. Geoderma 2017, 286, 131–138. [Google Scholar] [CrossRef]
- Wijewardane, N.K.; Ge, Y.F.; Morgan, C.L.S. Moisture insensitive prediction of soil properties from VNIR reflectance spectra based on external parameter orthogonalization. Geoderma 2016, 267, 92–101. [Google Scholar] [CrossRef]
- Roudier, P.; Hedley, C.B.; Lobsey, C.R.; Rossel, R.A.V.; Leroux, C. Evaluation of two methods to eliminate the effect of water from soil VIS–NIR spectra for predictions of organic carbon. Geoderma 2017, 296, 98–107. [Google Scholar] [CrossRef]
- Minasny, B.; McBratney, A.B.; Bellon-Maurel, V.; Roger, J.M.; Gobrecht, A.; Ferrand, L.; Joalland, S. Removing the effect of soil moisture from NIR diffuse reflectance spectra for the prediction of soil organic carbon. Geoderma 2011, 167–168, 118–124. [Google Scholar] [CrossRef]
- Yu, L.; Hong, Y.S.; Zhu, Y.X.; Huang, P.; He, Q.; Qi, F. Removing the effect of soil moisture content on hyperspectral reflectance for the estimation of soil organic matter content. Spectrosc. Spectr. Anal. 2017, 37, 2146–2151. (In Chinese) [Google Scholar]
- Lobell, D.B.; Asner, G.P. Moisture effects on soil reflectance. Soil Sci. Soc. Am. J. 2002, 66, 722–727. [Google Scholar] [CrossRef]
- Terra, F.S.; Demattê, J.A.M.; Viscarra Rossel, R.A. Proximal spectral sensing in pedological assessments: VIS–NIR spectra for soil classification based on weathering and pedogenesis. Geoderma 2018, 318, 123–136. [Google Scholar] [CrossRef]
- Schmitt, J.M. Fractional derivative analysis of diffuse reflectance spectra. Appl. Spectrosc. 1998, 52, 840–846. [Google Scholar] [CrossRef]
- Wang, J.Z.; Tiyip, T.; Ding, J.L.; Zhang, D.; Liu, W.; Wang, F.; Tashpolat, N. Desert soil clay content estimation using reflectance spectroscopy preprocessed by fractional derivative. PLoS ONE 2017, 12, e0184836. [Google Scholar] [CrossRef] [PubMed]
- Wiggins, K.; Palmer, R.; Hutchinson, W.; Drummond, P. An investigation into the use of calculating the first derivative of absorbance spectra as a tool for forensic fibre analysis. Sci. Justice 2007, 47, 9–18. [Google Scholar] [CrossRef] [PubMed]
- Srivastava, R.; Sarkar, D.; Mukhopadhayay, S.S.; Sood, A.; Singh, M.; Nasre, R.A.; Dhale, S.A. Development of hyperspectral model for rapid monitoring of soil organic carbon under precision farming in the Indo-Gangetic Plains of Punjab, India. J. Indian Soc. Remote Sens. 2015, 43, 751–759. [Google Scholar] [CrossRef]
- Liu, L.F.; Ji, M.; Dong, Y.Y.; Zhang, R.C.; Buchroithner, M. Quantitative retrieval of organic soil properties from visible near-infrared shortwave infrared (VIS–NIR–SWIR) spectroscopy using fractal-based feature extraction. Remote Sens. 2016, 8, 1035. [Google Scholar] [CrossRef]
- Demattê, J.A.M.; Ramirez-Lopez, L.; Marques, K.P.P.; Rodella, A.A. Chemometric soil analysis on the determination of specific bands for the detection of magnesium and potassium by spectroscopy. Geoderma 2017, 288, 8–22. [Google Scholar] [CrossRef]
- Liu, L.; Ji, M.; Buchroithner, M. Combining partial least squares and the gradient-boosting method for soil property retrieval using visible near-infrared shortwave infrared spectra. Remote Sens. 2017, 9, 1299. [Google Scholar] [CrossRef]
- Raj, A.; Chakraborty, S.; Duda, B.M.; Weindorf, D.C.; Li, B.; Roy, S.; Sarathjith, M.C.; Das, B.S.; Paulette, L. Soil mapping via diffuse reflectance spectroscopy based on variable indicators: An ordered predictor selection approach. Geoderma 2018, 314, 146–159. [Google Scholar] [CrossRef]
- Pang, G.J.; Wang, T.; Liao, J.; Li, S. Quantitative model based on field-derived spectral characteristics to estimate soil salinity in Minqin county, china. Soil Sci. Soc. Am. J. 2014, 78, 546–555. [Google Scholar] [CrossRef]
- Vohland, M.; Emmerling, C. Determination of total soil organic c and hot water-extractable c from VIS–NIR soil reflectance with partial least squares regression and spectral feature selection techniques. Eur. J. Soil Sci. 2011, 62, 598–606. [Google Scholar] [CrossRef]
- Peon, J.; Recondo, C.; Fernandez, S.; Calleja, J.F.; De Miguel, E.; Carretero, L. Prediction of topsoil organic carbon using airborne and satellite hyperspectral imagery. Remote Sens. 2017, 9, 1211. [Google Scholar] [CrossRef]







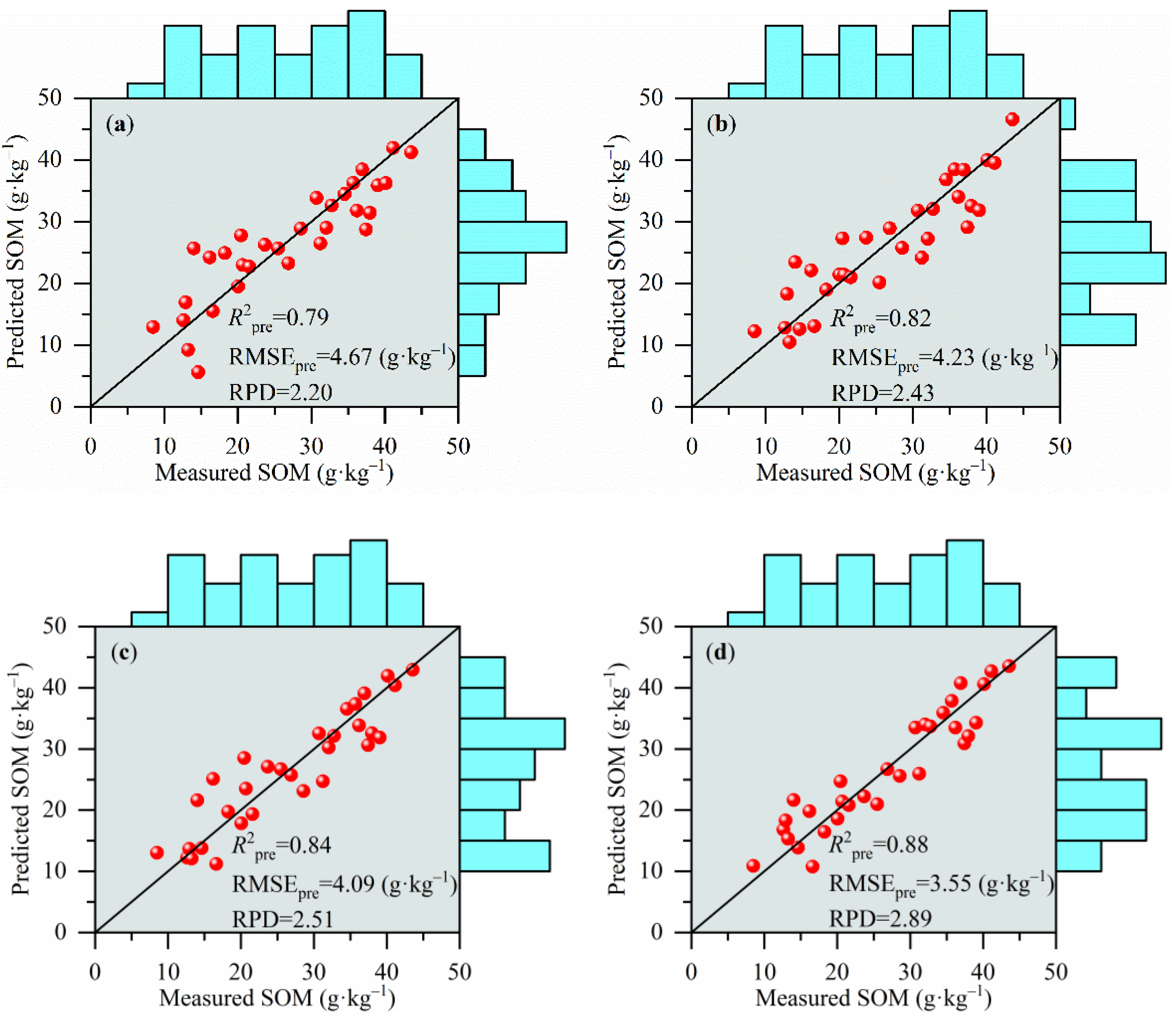

| FOD | N a | Calibration Dataset (n = 60) | Validation Dataset (n= 31) | |||
|---|---|---|---|---|---|---|
| R2cv | RMSEcv (g·kg–1) | R2pre | RMSEpre (g·kg–1) | RPD | ||
| Order = 0 | 201 | 0.61 | 6.27 | 0.55 | 6.75 | 1.52 |
| Order = 0.25 | 201 | 0.71 | 5.37 | 0.59 | 6.67 | 1.54 |
| Order = 0.5 | 201 | 0.67 | 5.74 | 0.60 | 6.62 | 1.55 |
| Order = 0.75 | 201 | 0.68 | 5.69 | 0.61 | 6.54 | 1.57 |
| Order = 1 | 201 | 0.71 | 5.38 | 0.69 | 5.84 | 1.76 |
| Order = 1.25 | 201 | 0.84 | 4.03 | 0.77 | 4.85 | 2.12 |
| Order = 1.5 | 201 | 0.83 | 4.18 | 0.79 | 4.67 | 2.20 |
| Order = 1.75 | 201 | 0.79 | 4.64 | 0.76 | 4.90 | 2.09 |
| Order = 2 | 201 | 0.76 | 4.95 | 0.72 | 5.53 | 1.86 |
| Variable Selection Techniques | FOD | Variable Selection | Calibration Dataset (n = 60) | Validation Dataset (n = 31) | ||||
|---|---|---|---|---|---|---|---|---|
| N a | Time (s) b | R2cv | RMSEcv (g·kg–1) | R2pre | RMSEpre (g·kg–1) | RPD | ||
| CARS | Order = 0 | 28 | 0.38 | 0.80 | 4.46 | 0.70 | 5.68 | 1.81 |
| Order = 0.25 | 28 | 0.37 | 0.83 | 4.10 | 0.79 | 4.67 | 2.20 | |
| Order = 0.5 | 12 | 0.35 | 0.81 | 4.42 | 0.77 | 4.85 | 2.12 | |
| Order = 0.75 | 7 | 0.32 | 0.77 | 4.83 | 0.70 | 5.71 | 1.80 | |
| Order = 1 | 54 | 0.30 | 0.83 | 4.13 | 0.79 | 4.60 | 2.23 | |
| Order = 1.25 | 37 | 0.33 | 0.89 | 3.26 | 0.82 | 4.23 | 2.43 | |
| Order = 1.5 | 21 | 0.32 | 0.89 | 3.26 | 0.81 | 4.43 | 2.32 | |
| Order = 1.75 | 16 | 0.32 | 0.88 | 3.49 | 0.82 | 4.26 | 2.41 | |
| Order = 2 | 19 | 0.32 | 0.85 | 3.84 | 0.78 | 4.69 | 2.19 | |
| ENET | Order = 0 | 19 | 0.63 | 0.66 | 5.85 | 0.62 | 6.22 | 1.65 |
| Order = 0.25 | 20 | 0.65 | 0.76 | 4.89 | 0.72 | 5.55 | 1.85 | |
| Order = 0.5 | 28 | 0.33 | 0.80 | 4.46 | 0.72 | 5.30 | 1.94 | |
| Order = 0.75 | 19 | 0.20 | 0.71 | 5.41 | 0.66 | 6.06 | 1.69 | |
| Order = 1 | 11 | 0.15 | 0.81 | 4.41 | 0.80 | 4.53 | 2.26 | |
| Order = 1.25 | 34 | 0.10 | 0.89 | 3.20 | 0.84 | 4.09 | 2.51 | |
| Order = 1.5 | 24 | 0.09 | 0.88 | 3.42 | 0.82 | 4.23 | 2.43 | |
| Order = 1.75 | 29 | 0.08 | 0.89 | 3.34 | 0.83 | 4.13 | 2.48 | |
| Order = 2 | 26 | 0.09 | 0.76 | 4.95 | 0.70 | 5.68 | 1.81 | |
| GA | Order = 0 | 40 | 136.77 | 0.71 | 5.43 | 0.66 | 5.89 | 1.74 |
| Order = 0.25 | 29 | 115.29 | 0.78 | 4.76 | 0.74 | 5.12 | 2.00 | |
| Order = 0.5 | 38 | 126.38 | 0.80 | 4.50 | 0.77 | 4.87 | 2.11 | |
| Order = 0.75 | 46 | 123.33 | 0.78 | 4.73 | 0.74 | 5.12 | 2.00 | |
| Order = 1 | 39 | 106.74 | 0.88 | 3.52 | 0.83 | 4.13 | 2.48 | |
| Order = 1.25 | 46 | 108.19 | 0.92 | 2.86 | 0.87 | 3.58 | 2.87 | |
| Order = 1.5 | 45 | 114.69 | 0.96 | 1.94 | 0.88 | 3.55 | 2.89 | |
| Order = 1.75 | 50 | 136.56 | 0.87 | 3.65 | 0.85 | 3.85 | 2.66 | |
| Order = 2 | 40 | 109.47 | 0.85 | 3.91 | 0.83 | 4.13 | 2.48 | |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hong, Y.; Chen, Y.; Yu, L.; Liu, Y.; Liu, Y.; Zhang, Y.; Liu, Y.; Cheng, H. Combining Fractional Order Derivative and Spectral Variable Selection for Organic Matter Estimation of Homogeneous Soil Samples by VIS–NIR Spectroscopy. Remote Sens. 2018, 10, 479. https://doi.org/10.3390/rs10030479
Hong Y, Chen Y, Yu L, Liu Y, Liu Y, Zhang Y, Liu Y, Cheng H. Combining Fractional Order Derivative and Spectral Variable Selection for Organic Matter Estimation of Homogeneous Soil Samples by VIS–NIR Spectroscopy. Remote Sensing. 2018; 10(3):479. https://doi.org/10.3390/rs10030479
Chicago/Turabian StyleHong, Yongsheng, Yiyun Chen, Lei Yu, Yanfang Liu, Yaolin Liu, Yong Zhang, Yi Liu, and Hang Cheng. 2018. "Combining Fractional Order Derivative and Spectral Variable Selection for Organic Matter Estimation of Homogeneous Soil Samples by VIS–NIR Spectroscopy" Remote Sensing 10, no. 3: 479. https://doi.org/10.3390/rs10030479
APA StyleHong, Y., Chen, Y., Yu, L., Liu, Y., Liu, Y., Zhang, Y., Liu, Y., & Cheng, H. (2018). Combining Fractional Order Derivative and Spectral Variable Selection for Organic Matter Estimation of Homogeneous Soil Samples by VIS–NIR Spectroscopy. Remote Sensing, 10(3), 479. https://doi.org/10.3390/rs10030479