Evaluation of Groundwater Storage Variations Estimated from GRACE Data Assimilation and State-of-the-Art Land Surface Models in Australia and the North China Plain
Abstract
:1. Introduction
2. Data Processing and Land Surface Models
2.1. GRACE
2.2. Land Surface Models
2.2.1. PCR-GLOBWB Model and Uncertainties
2.2.2. CABLE, WGHM, and W3 Models
2.3. In Situ Groundwater Data
3. GRACE Data Assimilation
4. Results
4.1. Data Assimilation Process and Impact on ∆TWS Estimates
4.2. Evaluation of ∆TWS Estimates
4.3. Seasonality and Long-Term Trends of ∆TWS and ∆GWS Estimates
4.3.1. Seasonal Variation
4.3.2. Long-Term Trend Estimates
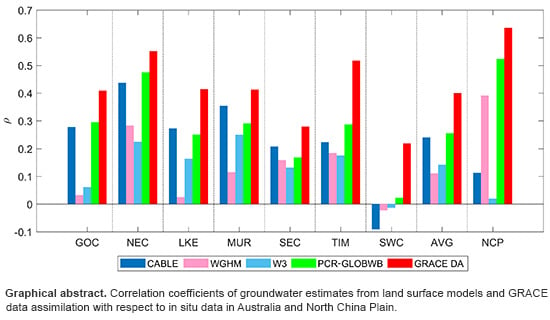
4.4. Validation of ∆GWS Estimates
4.4.1. Validation of ∆GWS Estimates against In Situ Data
4.4.2. Impact of Climate Variation on Groundwater Variation
4.5. Groundwater Depletion
5. Discussion
6. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Siebert, S.; Burke, J.; Faures, J.M.; Frenken, K.; Hoogeveen, J.; Döll, P.; Portmann, F.T. Groundwater use for irrigation—A global inventory. Hydrol. Earth Syst. Sci. 2010, 14, 1863–1880. [Google Scholar] [CrossRef] [Green Version]
- Döll, P.; Müller Schmied, H.; Schuh, C.; Portmann, F.T.; Eicker, A. Global-scale assessment of groundwater depletion and related groundwater abstractions: Combining hydrological modeling with information from well observations and GRACE satellites. Water Resour. Res. 2014, 50, 5698–5720. [Google Scholar] [CrossRef]
- Konikow, L.F.; Kendy, E. Groundwater depletion: A global problem. Hydrogeol. J. 2005, 13, 317–320. [Google Scholar] [CrossRef]
- Leblanc, M.J.; Tregoning, P.; Ramillien, G.; Tweed, S.O.; Fakes, A. Basin-scale, integrated observations of the early 21st century multiyear drought in southeast Australia. Water Resour. Res. 2009, 45, W04408. [Google Scholar] [CrossRef]
- Crosbie, R.S.; McCallum, J.L.; Walker, G.R.; Chiew, F.H.S. Modelling climate-change impacts on groundwater recharge in the Murray-Darling Basin, Australia. Hydrogeol. J. 2010, 18, 1639–1656. [Google Scholar] [CrossRef]
- McCallum, J.L.; Crosbie, R.S.; Walker, G.R.; Dawes, W.R. Impacts of climate change on groundwater in Australia: A sensitivity analysis of recharge. Hydrogeol. J. 2010, 18, 1625–1638. [Google Scholar] [CrossRef]
- Cao, G.; Zheng, C.; Scanlon, B.R.; Liu, J.; Li, W. Use of flow modeling to assess sustainability of groundwater resources in the North China Plain. Water Resour. Res. 2013, 49, 159–175. [Google Scholar] [CrossRef]
- Tapley, B.D.; Bettadpur, S.; Ries, J.C.; Thompson, P.F.; Watkins, M.M. GRACE Measurements of Mass Variability in the Earth System. Science 2004, 305, 503–505. [Google Scholar] [CrossRef] [PubMed]
- Rodell, M.; Velicogna, I.; Famiglietti, J.S. Satellite-based estimates of groundwater depletion in India. Nature 2009, 460, 999–1002. [Google Scholar] [CrossRef] [PubMed]
- Famiglietti, J.S.; Lo, M.; Ho, S.L.; Bethune, J.; Anderson, K.J.; Syed, T.H.; Swenson, S.C.; de Linage, C.R.; Rodell, M. Satellites measure recent rates of groundwater depletion in California’s Central Valley. Geophys. Res. Lett. 2011, 38, L03403. [Google Scholar] [CrossRef]
- Feng, W.; Zhong, M.; Lemoine, J.-M.; Biancale, R.; Hsu, H.-T.; Xia, J. Evaluation of groundwater depletion in North China using the Gravity Recovery and Climate Experiment (GRACE) data and ground-based measurements. Water Resour. Res. 2013, 49, 2110–2118. [Google Scholar] [CrossRef]
- Huang, Z.; Pan, Y.; Gong, H.; Yeh, P.J.-F.; Li, X.; Zhou, D.; Zhao, W. Subregional-scale groundwater depletion detected by GRACE for both shallow and deep aquifers in North China Plain. Geophys. Res. Lett. 2015, 42, 1791–1799. [Google Scholar] [CrossRef]
- Forootan, E.; Rietbroek, R.; Kusche, J.; Sharifi, M.A.; Awange, J.L.; Schmidt, M.; Omondi, P.; Famiglietti, J. Separation of large scale water storage patterns over Iran using GRACE, altimetry and hydrological data. Remote Sens. Environ. 2014, 140, 580–595. [Google Scholar] [CrossRef]
- Long, D.; Chen, X.; Scanlon, B.R.; Wada, Y.; Hong, Y.; Singh, V.P.; Chen, Y.; Wang, C.; Han, Z.; Yang, W. Have GRACE satellites overestimated groundwater depletion in the Northwest India Aquifer? Sci. Rep. 2016, 6, 24398. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Andrew, R.; Guan, H.; Batelaan, O. Estimation of GRACE water storage components by temporal decomposition. J. Hydrol. 2017, 552, 341–350. [Google Scholar] [CrossRef]
- Forootan, E.; Safari, A.; Mostafaie, A.; Schumacher, M.; Delavar, M.; Awange, J.L. Large-Scale Total Water Storage and Water Flux Changes over the Arid and Semiarid Parts of the Middle East from GRACE and Reanalysis Products. Surv. Geophys. 2017, 38, 591–615. [Google Scholar] [CrossRef]
- Zaitchik, B.F.; Rodell, M.; Reichle, R.H. Assimilation of GRACE Terrestrial Water Storage Data into a Land Surface Model: Results for the Mississippi River Basin. J. Hydrometeorol. 2008, 9, 535–548. [Google Scholar] [CrossRef]
- Tangdamrongsub, N.; Steele-Dunne, S.C.; Gunter, B.C.; Ditmar, P.G.; Weerts, A.H. Data assimilation of GRACE terrestrial water storage estimates into a regional hydrological model of the Rhine River basin. Hydrol. Earth Syst. Sci. 2015, 19, 2079–2100. [Google Scholar] [CrossRef]
- Khaki, M.; Ait-El-Fquih, B.; Hoteit, I.; Forootan, E.; Awange, J.; Kuhn, M. A two-update ensemble Kalman filter for land hydrological data assimilation with an uncertain constraint. J. Hydrol. 2017, 555, 447–462. [Google Scholar] [CrossRef]
- Tian, S.; Tregoning, P.; Renzullo, L.J.; van Dijk, A.I.J.M.; Walker, J.P.; Pauwels, V.R.N.; Allgeyer, S. Improved water balance component estimates through joint assimilation of GRACE water storage and SMOS soil moisture retrievals. Water Resour. Res. 2017, 53, 1820–1840. [Google Scholar] [CrossRef]
- Khaki, M.; Hoteit, I.; Kuhn, M.; Awange, J.; Forootan, E.; van Dijk, A.I.J.M.; Schumacher, M.; Pattiaratchi, C. Assessing sequential data assimilation techniques for integrating GRACE data into a hydrological model. Adv. Water Resour. 2017, 107, 301–316. [Google Scholar] [CrossRef]
- Tangdamrongsub, N.; Han, S.-C.; Yeo, I.-Y. Enhancement of water storage estimates using GRACE data assimilation with particle filter framework. In Proceedings of the 22nd International Congress on Modelling and Simulation (MODSIM), Hobart, Australia, 8–11 December 2017; pp. 1041–1047. [Google Scholar]
- Girotto, M.; De Lannoy, G.J.M.; Reichle, R.H.; Rodell, M. Assimilation of gridded terrestrial water storage observations from GRACE into a land surface model. Water Resour. Res. 2016, 52, 4164–4183. [Google Scholar] [CrossRef]
- Khaki, M.; Schumacher, M.; Forootan, E.; Kuhn, M.; Awange, J.L.; van Dijk, A.I.J.M. Accounting for spatial correlation errors in the assimilation of GRACE into hydrological models through localization. Adv. Water Resour. 2017, 108, 99–112. [Google Scholar] [CrossRef]
- Eicker, A.; Schumacher, M.; Kusche, J.; Döll, P.; Müller Schmied, H. Calibration/Data Assimilation Approach for Integrating GRACE Data into the WaterGAP Global Hydrology Model (WGHM) Using an Ensemble Kalman Filter: First Results. Surv. Geophys. 2014, 35, 1285–1309. [Google Scholar] [CrossRef]
- Schumacher, M.; Kusche, J.; Döll, P. A systematic impact assessment of GRACE error correlation on data assimilation in hydrological models. J. Geod. 2016, 90, 537–559. [Google Scholar] [CrossRef]
- Tangdamrongsub, N.; Steele-Dunne, S.C.; Gunter, B.C.; Ditmar, P.G.; Sutanudjaja, E.H.; Sun, Y.; Xia, T.; Wang, Z. Improving estimates of water resources in a semi-arid region by assimilating GRACE data into the PCR-GLOBWB hydrological model. Hydrol. Earth Syst. Sci. 2017, 21, 2053–2074. [Google Scholar] [CrossRef]
- Kumar, S.V.; Zaitchik, B.F.; Peters-Lidard, C.D.; Rodell, M.; Reichle, R.; Li, B.; Jasinski, M.; Mocko, D.; Getirana, A.; De Lannoy, G.; et al. Assimilation of Gridded GRACE Terrestrial Water Storage Estimates in the North American Land Data Assimilation System. J. Hydrometeorol. 2016, 17, 1951–1972. [Google Scholar] [CrossRef]
- Girotto, M.; De Lannoy, G.J.M.; Reichle, R.H.; Rodell, M.; Draper, C.; Bhanja, S.N.; Mukherjee, A. Benefits and pitfalls of GRACE data assimilation: A case study of terrestrial water storage depletion in India. Geophys. Res. Lett. 2017, 44, 4017–4115. [Google Scholar] [CrossRef]
- Schumacher, M.; Forootan, E.; van Dijk, A.I.J.M.; Müller Schmied, H.; Crosbie, R.S.; Kusche, J.; Döll, P. Improving drought simulations within the Murray-Darling Basin by combined calibration/assimilation of GRACE data into the WaterGAP Global Hydrology Model. Remote Sens. Environ. 2018, 204, 212–228. [Google Scholar] [CrossRef]
- Van Dijk, A.I.J.M.; Peña-Arancibia, J.L.; Wood, E.F.; Sheffield, J.; Beck, H.E. Global analysis of seasonal streamflow predictability using an ensemble prediction system and observations from 6192 small catchments worldwide. Water Resour. Res. 2013, 49, 2729–2746. [Google Scholar] [CrossRef]
- Sutanudjaja, E.H.; van Beek, R.; Wanders, N.; Wada, Y.; Bosmans, J.H.C.; Drost, N.; Ent, R.J.; van der Graaf, I.E.M.; de Hoch, J.M.; Jong, K.; et al. PCR-GLOBWB 2: A 5 ARC-minute global hydrological and water resources model. Geosci. Model Dev. Discuss. 2017. [Google Scholar] [CrossRef]
- De Lannoy, G.J.M.; Reichle, R.H.; Houser, P.R.; Arsenault, K.R.; Verhoest, N.E.C.; Pauwels, V.R.N. Satellite-Scale Snow Water Equivalent Assimilation into a High-Resolution Land Surface Model. J. Hydrometeorol. 2009, 11, 352–369. [Google Scholar] [CrossRef]
- Decker, M. Development and evaluation of a new soil moisture and runoff parameterization for the CABLE LSM including subgrid-scale processes. J. Adv. Model. Earth Syst. 2015, 7, 1788–1809. [Google Scholar] [CrossRef]
- Müller Schmied, H. Evaluation, Modification and Application of a Global Hydrological Model. Ph.D. Thesis, Institute of Physical Geography, Goethe University Frankfurt, Frankfurt am Main, Germany, 2017. [Google Scholar]
- Bettadpur, S. Gravity Recovery and Climate Experiment UTCSR Level-2 Processing Standards Document for Level-2 Product Release 0005; Center for Space Research, The University of Texas: Austin, TX, USA, 2012. [Google Scholar]
- Swenson, S.; Chambers, D.; Wahr, J. Estimating geocenter variations from a combination of GRACE and ocean model output. J. Geophys. Res. Solid Earth 2008, 113, B08410. [Google Scholar] [CrossRef]
- Cheng, M.; Tapley, B.D. Variations in the Earth’s oblateness during the past 28 years. J. Geophys. Res. Solid Earth 2004, 109, B09402. [Google Scholar] [CrossRef]
- Swenson, S.; Wahr, J. Post-processing removal of correlated errors in GRACE data. Geophys. Res. Lett. 2006, 33, L08402. [Google Scholar] [CrossRef]
- Jekeli, C. Alternative Methods to Smooth the Earth’s Gravity Field; Scientific Report, 327; The Ohio State University: Columbus, OH, USA, 1981. [Google Scholar]
- Wahr, J.; Molenaar, M.; Bryan, F. Time variability of the Earth’s gravity field: Hydrological and oceanic effects and their possible detection using GRACE. J. Geophys. Res. Solid Earth 1998, 103, 30205–30229. [Google Scholar] [CrossRef]
- Tangdamrongsub, N.; Ditmar, P.G.; Steele-Dunne, S.C.; Gunter, B.C.; Sutanudjaja, E.H. Assessing total water storage and identifying flood events over Tonlé Sap basin in Cambodia using GRACE and MODIS satellite observations combined with hydrological models. Remote Sens. Environ. 2016, 181, 162–173. [Google Scholar] [CrossRef]
- Zhou, H.; Luo, Z.; Tangdamrongsub, N.; Wang, L.; He, L.; Xu, C.; Li, Q. Characterizing Drought and Flood Events over the Yangtze River Basin Using the HUST-Grace2016 Solution and Ancillary Data. Remote Sens. 2017, 9, 1100. [Google Scholar] [CrossRef]
- Van Beek, L.P.H.; Wada, Y.; Bierkens, M.F.P. Global monthly water stress: 1. Water balance and water availability. Water Resour. Res. 2011, 47, W07517. [Google Scholar] [CrossRef]
- Erkens, G.; Sutanudjaja, E.H. Towards a global land subsidence map. Proc. Int. Assoc. Hydrol. Sci. 2015, 372, 83–87. [Google Scholar] [CrossRef]
- Huffman, G.J.; Bolvin, D.T.; Nelkin, E.J.; Wolff, D.B.; Adler, R.F.; Gu, G.; Hong, Y.; Bowman, K.P.; Stocker, E.F. The TRMM Multisatellite Precipitation Analysis (TMPA): Quasi-Global, Multiyear, Combined-Sensor Precipitation Estimates at Fine Scales. J. Hydrometeorol. 2007, 8, 38–55. [Google Scholar] [CrossRef]
- Dee, D.P.; Uppala, S.M.; Simmons, A.J.; Berrisford, P.; Poli, P.; Kobayashi, S.; Andrae, U.; Balmaseda, M.A.; Balsamo, G.; Bauer, P.; et al. The ERA-Interim reanalysis: Configuration and performance of the data assimilation system. Q. J. R. Meteorol. Soc. 2011, 137, 553–597. [Google Scholar] [CrossRef]
- Lu, J.; Sun, G.; McNulty, S.G.; Amatya, D.M. A Comparison of Six Potential Evapotranspiration Methods for Regional Use in the Southeastern United States1. JAWRA J. Am. Water Resour. Assoc. 2005, 41, 621–633. [Google Scholar] [CrossRef]
- Huffman, G.J. Estimates of Root-Mean-Square Random Error for Finite Samples of Estimated Precipitation. J. Appl. Meteorol. 1997, 36, 1191–1201. [Google Scholar] [CrossRef]
- Bi, D.; Dix, M.; Marsland, S.; O’Farrell, S.; Rashid, H.; Uotila, P.; Hirst, T.; Kowalczyk, E.; Golebiewski, M.; Sullivan, A.; et al. The ACCESS Coupled Model: Description, Control Climate and Evaluation. Aust. Meteorol. Oceanogr. J. 2013, 63, 41–64. [Google Scholar] [CrossRef]
- Ukkola, A.M.; Pitman, A.J.; Decker, M.; De Kauwe, M.G.; Abramowitz, G.; Kala, J.; Wang, Y.-P. Modelling evapotranspiration during precipitation deficits: Identifying critical processes in a land surface model. Hydrol. Earth Syst. Sci. 2016, 20, 2403–2419. [Google Scholar] [CrossRef]
- Decker, M.; Zeng, X. Impact of Modified Richards Equation on Global Soil Moisture Simulation in the Community Land Model (CLM3.5). J. Adv. Model. Earth Syst. 2009, 1, 5. [Google Scholar] [CrossRef]
- Rodell, M.; Houser, P.R.; Jambor, U.; Gottschalck, J.; Mitchell, K.; Meng, C.-J.; Arsenault, K.; Cosgrove, B.; Radakovich, J.; Bosilovich, M.; et al. The Global Land Data Assimilation System. Bull. Am. Meteorol. Soc. 2004, 85, 381–394. [Google Scholar] [CrossRef]
- Tangdamrongsub, N.; Han, S.-C.; Decker, M.; Yeo, I.-Y.; Kim, H. On the use of the GRACE normal equation of inter-satellite tracking data for estimation of soil moisture and groundwater in Australia. Hydrol. Earth Syst. Sci. 2018, 22, 1811–1829. [Google Scholar] [CrossRef]
- Döll, P.; Kaspar, F.; Lehner, B. A global hydrological model for deriving water availability indicators: Model tuning and validation. J. Hydrol. 2003, 270, 105–134. [Google Scholar] [CrossRef]
- Müller Schmied, H.; Eisner, S.; Franz, D.; Wattenbach, M.; Portmann, F.T.; Flörke, M.; Döll, P. Sensitivity of simulated global-scale freshwater fluxes and storages to input data, hydrological model structure, human water use and calibration. Hydrol. Earth Syst. Sci. 2014, 18, 3511–3538. [Google Scholar] [CrossRef]
- Weedon, G.P.; Balsamo, G.; Bellouin, N.; Gomes, S.; Best, M.J.; Viterbo, P. The WFDEI meteorological forcing data set: WATCH Forcing Data methodology applied to ERA-Interim reanalysis data. Water Resour. Res. 2014, 50, 7505–7514. [Google Scholar] [CrossRef]
- Van Dijk, A. Landscape Model (Version 0.5); AWRA Technical Report 3; WIRADA/CSIRO Water for a Healthy Country Flagship: Canberra, Australia, 2010. [Google Scholar]
- Evensen, G. The Ensemble Kalman Filter: Theoretical formulation and practical implementation. Ocean Dyn. 2003, 53, 343–367. [Google Scholar] [CrossRef]
- Tregoning, P.; McClusky, S.; Van Dijk, A.; Crosbie, R.; Pena Arancibia, J. Assessment of GRACE Satellites for Groundwater Estimation in Australia; National Water Commission: Canberra, Australia, 2012; ISBN 978-1-921853-54-8. [Google Scholar]
- Tregoning, P.; Lambeck, K.; Ramillien, G. GRACE estimates of sea surface height anomalies in the Gulf of Carpentaria, Australia. Earth Planet. Sci. Lett. 2008, 271, 241–244. [Google Scholar] [CrossRef]
- Peel, M.C.; Finlayson, B.L.; McMahon, T.A. Updated world map of the Köppen-Geiger climate classification. Hydrol. Earth Syst. Sci. 2007, 11, 1633–1644. [Google Scholar] [CrossRef]
- Khandu; Forootan, E.; Schumacher, M.; Awange, J.L.; Müller Schmied, H. Exploring the influence of precipitation extremes and human water use on total water storage (TWS) changes in the Ganges-Brahmaputra-Meghna River Basin. Water Resour. Res. 2016, 52, 2240–2258. [Google Scholar] [CrossRef]
- Mcgrath, G.; Sadler, R.; Fleming, K.; Tregoning, P.; Hinz, C.; Veneklaas, E. Tropical cyclones and the ecohydrology of Australia’s recent continental-scale drought. Geophys. Res. Lett. 2012, 39, 1–6. [Google Scholar] [CrossRef]
- Van Dijk, A.I.J.M.; Beck, H.E.; Crosbie, R.S.; de Jeu, R.A.M.; Liu, Y.Y.; Podger, G.M.; Timbal, B.; Viney, N.R. The Millennium Drought in southeast Australia (2001–2009): Natural and human causes and implications for water resources, ecosystems, economy, and society. Water Resour. Res. 2013, 49, 1040–1057. [Google Scholar] [CrossRef]
- Chen, J.L.; Wilson, C.R.; Tapley, B.D.; Scanlon, B.; Güntner, A. Long-term groundwater storage change in Victoria, Australia from satellite gravity and in situ observations. Glob. Planet. Chang. 2016, 139, 56–65. [Google Scholar] [CrossRef]
- CSIRO. Water Yields and Demands in South-West Western Australia; A Report to the Australian Government from the CSIRO South-West Western Australia Sustainable Yields Project; Department of the Environment, Water, Heritage and the Arts, CSIRO Water for a Healthy Country Flagship: Canberra, Australia, 2009.
- García-García, D.; Ummenhofer, C.C.; Zlotnicki, V. Australian water mass variations from GRACE data linked to Indo-Pacific climate variability. Remote Sens. Environ. 2011, 115, 2175–2183. [Google Scholar] [CrossRef]
- Webber, M.; Crow-Miller, B.; Rogers, S. The South–North Water Transfer Project: Remaking the geography of China. Reg. Stud. 2017, 51, 370–382. [Google Scholar] [CrossRef]
- Houborg, R.; Rodell, M.; Li, B.; Reichle, R.; Zaitchik, B.F. Drought indicators based on model-assimilated Gravity Recovery and Climate Experiment (GRACE) terrestrial water storage observations. Water Resour. Res. 2012, 48, W07525. [Google Scholar] [CrossRef]
- Müller Schmied, H.; Adam, L.; Eisner, S.; Fink, G.; Flörke, M.; Kim, H.; Oki, T.; Portmann, F.T.; Reinecke, R.; Riedel, C.; et al. Impact of climate forcing uncertainty and human water use on global and continental water balance components. Proc. Int. Assoc. Hydrol. Sci. 2016, 374, 53–62. [Google Scholar]
- Hunger, M.; Döll, P. Value of river discharge data for global-scale hydrological modeling. Hydrol. Earth Syst. Sci. 2008, 12, 841–861. [Google Scholar] [CrossRef]
- Sutanudjaja, E.H.; van Beek, L.P.H.; de Jong, S.M.; van Geer, F.C.; Bierkens, M.F.P. Large-scale groundwater modeling using global datasets: A test case for the Rhine-Meuse basin. Hydrol. Earth Syst. Sci. 2011, 15, 2913–2935. [Google Scholar] [CrossRef] [Green Version]













| River Basin | CABLE | WGHM | W3 | PCR-GLOBWB | GRACE DA |
|---|---|---|---|---|---|
| GOC | 0.70 | 0.68 | 0.76 | 0.59 | 0.81 |
| IND | 0.33 | 0.31 | 0.37 | 0.43 | 0.54 |
| LKE | 0.73 | 0.36 | 0.64 | 0.61 | 0.65 |
| MRD | 0.71 | 0.40 | 0.69 | 0.69 | 0.76 |
| NEC | 0.73 | 0.51 | 0.66 | 0.70 | 0.82 |
| NWP | 0.66 | 0.35 | 0.58 | 0.49 | 0.65 |
| SEC | 0.55 | 0.55 | 0.51 | 0.56 | 0.73 |
| SWC | 0.25 | 0.45 | 0.54 | 0.46 | 0.66 |
| SWP | 0.46 | 0.21 | 0.45 | 0.46 | 0.66 |
| TIM | 0.72 | 0.61 | 0.76 | 0.57 | 0.78 |
| Average | 0.58 | 0.44 | 0.60 | 0.56 | 0.71 |
| NCP | 0.35 | 0.36 | 0.35 | 0.42 | 0.60 |
| River Basin | CABLE | WGHM | W3 | PCR-GLOBWB | GRACE DA |
|---|---|---|---|---|---|
| GOC | 12.75 | 10.94 | 9.97 | 18.97 | 7.74 |
| IND | 4.43 | 2.94 | 3.20 | 3.75 | 2.62 |
| LKE | 4.41 | 3.39 | 2.88 | 3.86 | 2.85 |
| MRD | 5.02 | 5.63 | 4.21 | 5.97 | 3.77 |
| NEC | 10.92 | 7.57 | 7.66 | 18.49 | 5.10 |
| NWP | 5.22 | 5.22 | 4.32 | 5.08 | 4.14 |
| SEC | 8.73 | 7.90 | 7.40 | 10.37 | 5.51 |
| SWC | 5.46 | 4.41 | 4.01 | 6.02 | 3.59 |
| SWP | 3.45 | 2.81 | 2.55 | 4.87 | 2.06 |
| TIM | 7.79 | 8.46 | 6.83 | 14.02 | 5.43 |
| Average | 6.82 | 5.93 | 5.30 | 9.14 | 4.28 |
| NCP | 5.46 | 5.51 | 4.14 | 3.38 | 2.93 |
| CABLE | WGHM | W3 | PCR-GLOBWB | GRACE DA | TRMM () | ∆GL | |
|---|---|---|---|---|---|---|---|
| Correlation | |||||||
| MUR | 0.80 | 0.68 | 0.34 | 0.82 | 0.84 | 0.83 | 1.0 |
| PB | −0.15 | 0.03 | 0.07 | −0.25 | 0.45 | 0.18 | 1.0 |
| VIC | 0.54 | 0.44 | 0.30 | 0.58 | 0.69 | 0.59 | 1.0 |
| NCP | 0.03 | 0.88 | 0.01 | 0.87 | 0.91 | 0.12 | 1.0 |
| Trend | |||||||
| MUR (2004–2009) | −0.35 ± 0.01 | −0.01 ± 0.005 | −0.01 ± 0.003 | 9 × 10−4 ± 1 × 10−4 | −0.09 ± 0.01 | −6.90 ± 0.14 | −0.20 ± 0.01 |
| PB (2004–009) | 0.45 ± 0.04 | 0.05 ± 0.02 | 0.08 ± 0.03 | 2.61 ± 0.10 | −0.71 ± 0.04 | 1.61 ± 0.21 | −16.03 ± 0.94 |
| VIC (2004 –009) | −0.66 ± 0.01 | −0.21 ± 0.01 | −0.05 ± 0.01 | −0.02 ± 0.01 | −0.25 ± 0.01 | −11.05 ± 0.22 | −2.29 ± 0.18 |
| NCP (2003–2014) | 0.10 ± 0.02 | −3.51 ± 0.04 | −0.005 ± 0.003 | −1.59 ± 0.01 | −1.41 ± 0.01 | −0.21 ± 0.09 | −37.19 ± 0.62 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tangdamrongsub, N.; Han, S.-C.; Tian, S.; Müller Schmied, H.; Sutanudjaja, E.H.; Ran, J.; Feng, W. Evaluation of Groundwater Storage Variations Estimated from GRACE Data Assimilation and State-of-the-Art Land Surface Models in Australia and the North China Plain. Remote Sens. 2018, 10, 483. https://doi.org/10.3390/rs10030483
Tangdamrongsub N, Han S-C, Tian S, Müller Schmied H, Sutanudjaja EH, Ran J, Feng W. Evaluation of Groundwater Storage Variations Estimated from GRACE Data Assimilation and State-of-the-Art Land Surface Models in Australia and the North China Plain. Remote Sensing. 2018; 10(3):483. https://doi.org/10.3390/rs10030483
Chicago/Turabian StyleTangdamrongsub, Natthachet, Shin-Chan Han, Siyuan Tian, Hannes Müller Schmied, Edwin H. Sutanudjaja, Jiangjun Ran, and Wei Feng. 2018. "Evaluation of Groundwater Storage Variations Estimated from GRACE Data Assimilation and State-of-the-Art Land Surface Models in Australia and the North China Plain" Remote Sensing 10, no. 3: 483. https://doi.org/10.3390/rs10030483
APA StyleTangdamrongsub, N., Han, S.-C., Tian, S., Müller Schmied, H., Sutanudjaja, E. H., Ran, J., & Feng, W. (2018). Evaluation of Groundwater Storage Variations Estimated from GRACE Data Assimilation and State-of-the-Art Land Surface Models in Australia and the North China Plain. Remote Sensing, 10(3), 483. https://doi.org/10.3390/rs10030483