Modeling Orbital Error in InSAR Interferogram Using Frequency and Spatial Domain Based Methods

Abstract

Synthetic Aperture Radar Interferometry (SAR, InSAR) is increasingly being used for deformation monitoring. Uncertainty in satellite state vectors is considered to be one of the main sources of errors in applications such as this. In this paper, we present frequency and spatial domain based algorithms to model orbital errors in InSAR interferograms. The main advantage of this method, when applied to the spatial domain, is that the order of the polynomial coefficient is automatically determined according to the features of the orbital errors, using K-cross validation. In the frequency domain, a maximum likelihood fringe rate estimate is deployed to resolve linear orbital patterns in strong noise interferograms, where spatial-domain-based algorithms are unworkable. Both methods were tested and compared with synthetic data and applied to historical Environmental Satellite Advanced Synthetic Aperture Radar (ENVISAT ASAR) sensor and modern instruments such as Gaofen-3 (GF-3) and Sentinel-1. The validation from the simulation demonstrated that an accuracy of ~1mm can be obtained under optimal conditions. Using an independent GPS measurement that is discontinuous from the InSAR measurement over the Tohoku-Oki area, we found a 31.45% and 73.22% reduction in uncertainty after applying our method for ASAR tracks 347 and 74, respectively.

1. Introduction

The precise orbiting position information of space-borne Synthetic Aperture Radar (SAR) systems is of great significance in many Interferometric Synthetic Aperture Radar (InSAR) applications, especially in the case of ground motion monitoring [1,2,3]. The InSAR technique uses two sensors, carried on satellites, with slightly different incidence angles, to measure a displacement along the radar line-of-sight (LOS) between two SAR acquisitions. The theoretical accuracy can be as high as a centimeter to as low as a millimeter. This technique has been widely used to identify many geophysical processes that usually cause long-wavelength crustal deformation, including strain accumulation along locked continental faults, coseismic deformation caused by the occurrence of faulting in the lithosphere, and postseismic deformation caused by afterslip and viscoelastic relaxation [4,5,6].

The radar, the ground, and the intervening medium create a compound observing system; within this, there are several potential sources of errors that have a detrimental impact on the accuracy of InSAR measurements. In particular, satellite orbital errors [7], temporal and spatial decorrelation effects [8,9], atmospheric screens [10], and high-deformation gradients are the main limitations [11]. As far as orbital errors are concerned, they cause long-wavelength phase contributions to interferogram and are often referred to as ‘the phase ramp’. The pattern of the phase ramp usually depends on the satellite–state–vector error, especially on the radial and cross-track components of the orbital error [7]. The influence of orbital errors on the final accuracy of deformation products is largely contingent on the SAR instruments, i.e., the trajectory of the satellite orbit, the radar frequency, and the degree of overlap between the phase ramp and the deformation signals.

Several efforts have been made during the last two decades to mitigate the orbital error, and most of them start with spatial domain analyses of InSAR interferograms. A simple but very effective solution is de-ramping from the InSAR interferogram using a linear or quadratic surface fitting [3,12]. The phase ramp is either subtracted from the original phase or used to refine the spatial baseline to infer a revised interferogram [13,14]. Given a wrapped-phase pattern, the unwrapping operation is always required before fitting. The accuracy of the estimated coefficients in the polynomial model relies on the quality of the observations to be fitted. Error propagation in the unwrapping procedure over fast decorrelation areas with low coherence may distort the signal and, therefore, contribute to surface artifacts. To solve this problem, pixel offsets between bi-temporal-SAR data can be estimated using the cross-correlation algorithm; the baseline is then re-estimated to compensate for the residual phase in the interferogram [15]. Despite many efforts, the accuracy of the estimated offsets, from meter to decimeter, restricts the correction of the baseline components. Kohlhase et al. (2003) suggest counting the fringes caused by orbital errors according to phase gradients in differential interferograms and to adjust the trajectories of satellite orbits [16]. This does not work for coseismic scenes, where a stronger deformation causes dense fringes [7].

Advances related to orbital error correction refer to the time-series-SAR dataset. One such suggestion is to independently estimate the phase ramp on each interferogram using least squares scheme. To ensure consistency in the interferometric network, the polynomial coefficients are refined in a network sense by time-series inversions [17,18]. Considering the inseparability of phase ramp and long-wavelength deformation signals in the spatial dimension, the alternative is to estimate both deformation and orbital errors by exploiting spatio-temporal characteristics of both quantities [17,19]. However, resolving large, linear systems of algebraic equations, error propagation, and underdetermined problems have become the main challenges associated with these methods.

One promising alternative to separating long-wavelength displacement signals and orbit errors is to employ external data, for example, GPS measurement [20,21,22]. GPS displacements located in the SAR scene are projected onto the line-of-sight direction according to the incidence angle and the heading of the SAR geometry. The phase ramp is then estimated by minimizing the residuals between the InSAR interferogram and the phase inverted by the GPS. The final accuracy of the InSAR deformation product depends on the accuracy of the GPS measurements, the number of GPS stations and their spatial distribution.

In summary, the current problems of orbital error removal are two-fold. The first problem originates from the fact that all long-wavelength signals are treated as orbital errors during the correction without ancillary data. Although a few studies try to use wavelet-multiresolution analysis to classify the different components in the unwrapped interferogram automatically [23], the method is still empirical, as the number of levels of wavelet decomposition must be specified manually according to the features of the interferogram. The second problem involves robust regression. As stated in Reference [24], the model selection is subjective and relies on the distribution and the density of the targets showing high coherence, while errors in unwrapping are likely to mislead surface fitting. In fact, the method of estimating the phase ramp in the frequency domain may avoid the unwrapping error. However, few studies discuss using this method for orbital error correction. In the following section, we focus our analyses on the individual interferogram, as it is essential for time-series inversion and many geophysical applications.

The remainder of the paper is organized as follows: In Section 2, we introduce the frequency and spatial domain based methods, respectively, from the image-processing viewpoint. In Section 3, the results and quantitative comparisons are presented using synthetic and real data. In Section 4, the feasibility of these methods, including their merits and faults, are investigated. In Section 5, conclusions are given.

2. Methods

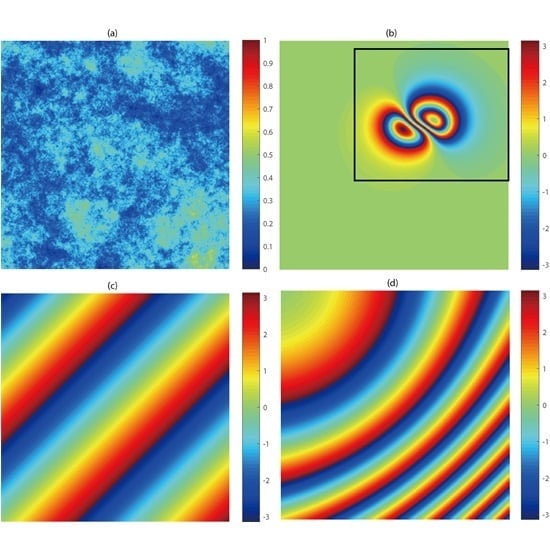
2.1. Modeling Orbital Error in Frequency Domain

The fringe rate of long-wavelength signals in interferogram can be estimated by means of maximum likelihood (ML) frequency algorithms [25,26,27]. The idea is that the orbital error has a dominant term in its Fourier expansion. Assuming original interferogram I can be expressed as:

$$I=e^{i({\varphi }_{def}+{\varphi }_{topo}+{\varphi }_{orbit}+{\varphi }_{other})}=D\cdot e^{i{\varphi }_{topo}}$$

(1)

where ${\varphi }_{def}$, ${\varphi }_{topo}$, ${\varphi }_{orbit}$, ${\varphi }_{other}$ denote deformation phase, topographic phase, orbital ramp, and other phase components related to the atmosphere and decorrelation, respectively. $D$ is the differential interferogram. After atmospheric correction and/or phase filtering, we rewrite $D$ as a sinusoidal model:

$$D=e^{i{\varphi }_{orbit}}\cdot e^{i{\varphi }_{def}}=e^{i2\pi f_{x}x}\cdot e^{i2\pi f_{y}y}\cdot e^{i\rho }\cdot e^{i{\varphi }_{def}}$$

(2)

where $x$ and $y$ denote the pixel index in radar coordinate, $f_x$ and $f_y$ are true fringe frequencies along range and azimuth direction, respectively, and $\rho$ is the residual phase.

$$F=fft(D)$$

(3)

The Fourier filter can be used to obtain the ML estimate of the average stripe rate in Equation (2). The peak location obtained by maximizing the 2D discrete Fourier transform (DFT) corresponds to the estimated frequencies ${\widehat{f}}_x$ and ${\widehat{f}}_y$, respectively, and the phase $\widehat{\rho }$ at the DFT peak is approximate to $\rho$. To better identify the exact frequencies, we increase the DFT frequency sampling by padding the signal in the window with enough zeros. The size of the padded zeros in both directions, $n_x$ and $n_y$, can be determined by the Cramer-Rao bound of the variance of estimated frequency [26]:

$$\{\begin{array}{l}{(\frac{1}{N_x+n_x})}^2\le \frac{6}{SNR\cdot N_x\cdot N_y\cdot (N_x^2-1)}\\ {(\frac{1}{N_y+n_y})}^2\le \frac{6}{SNR\cdot N_x\cdot N_y\cdot (N_y^2-1)}\end{array}$$

(4)

where $SNR$ represents the signal-to-noise ratio, $N_x$ and $N_y$ are equivalent to each of the image sizes. The de-ramped interferogram can be obtained from the cross multiplication of the differential interferogram and the estimated phase ramp under the assumption ${\widehat{f}}_x\approx f_x$, ${\widehat{f}}_y\approx f_y$ and $\widehat{\rho }\approx \rho$.

The significant advantage of this method is its simple computation without the need for phase unwrapping and higher reliability over low-coherence areas (see Section 3.1). However, this method can only estimate the linear terms of orbital error. For non-linear fringe patterns, which are usually present in long-strip images, polynomial fitting in the spatial domain is recommended.

2.2. Modeling Orbital Error in Spatial Domain

The most popular method used in orbital-error correction is surface fitting with linear or quadratic models, using unwrapped phase observations. Its general form can be defined as [23]:

$$z=P_{1}x+P_{2}y+P_3$$

(5)

where $z$ is the polynomial model, $x$ and $y$ indicate the pixel index in radar coordinates. To solve the equation for the unknown coefficients $P_1$, $P_2$ and $P_3$, the least squares scheme is used. The solution can be written as:

$$P={(A^{T}A)}^{-1}{A}^{T}Z$$

(6)

where $P^T=[{\widehat{P}}_1,{\widehat{P}}_2,{\widehat{P}}_3]$ is the estimated vector in which the elements correspond to the coefficients in Equation (5). $Z$ is the observations with size $N$, and $A$ is the $N\times 3$ matrix containing the coordinates $x$ and $y$. However, there are several drawbacks to using this method. Firstly, Equation (6) is not robust to abnormal values, such as unwrapping errors. In addition, the observations contribute to the equivalent weight without the consideration of the interferogram qualities. Secondly, the local deformation will contribute to the polynomial coefficients with the increase of the dimension in $P^T$. Finally, the determination of the order of the polynomial model is not clear yet and is usually empirical. A more sophisticated method is therefore needed.

2.2.1. Preprocess: Multi-Looking and Manually Masking

An increase in looks can enhance the quality of long-wavelength signals and simultaneously mitigate the effect of the short-wavelength signals during the regression. On the other hand, the decreased dimension can reduce the computational burden for unwrapping and the iterative least squares scheme. For those regional deformation signals, manual masking should be undertaken. Although this step is simpler than wavelet decomposition [23], it is still effective without expert knowledge and computational complexity. In addition, masking is important for areas with a high phase gradient, where phase aliasing causes unexpected unwrapping errors [11].

2.2.2. Polynomial Model

For long-strip InSAR interferograms, it is difficult to use the linear or quadric models to incorporate orbit errors. A more general form is needed:

$$z=XM{Y}^T$$

(7)

where $X={[1x{x}^2{x}^3\dots ]}_{1\times (n+1)}$ and $Y^T={[1y{y}^2{y}^3\dots ]}_{1\times (m+1)}$ is the vector with the length $n+1$ and $m+1$ respectively, $M$ is $(n+1)\times (m+1)$ coefficient matrix.

$$M=\left[\begin{array}{ccccc}{P}_{1,1}& P_{1,2}& \dots & P_{1,m}& P_{1,m+1}\\ P_{2,1}& P_{2,2}& \cdots & P_{2,m}& \\ ⋮& ⋮& ⋰& & \\ P_{n,1}& P_{n,2}& & & \\ P_{n+1,1}& & & & 0\end{array}\right]$$

The parameters $n$ and $m$ should be carefully determined to prevent overfitting in terms of the spatial distribution of observations.

2.2.3. Iteratively Reweighted Least Squares Fitting

The main disadvantage of ordinary least squares is that there is a constant deviation in the errors. For observations with different coherence magnitudes, the method of weighted least squares should be used. Moreover, iterative behavior can be employed to reduce the influence of outliers on regression. We designed an iterative version for the least-squares solution according to the phase standard deviation (STD) and robust Bi-square weight. The modification of the parameter estimate $P$ in Equation (6) can be rewritten as:

$$P={(A^{T}WA)}^{-1}{A}^{T}Wz$$

(8)

In this paper, we define weight $W$ in two steps. The prior weight $V=\{v_1,v_2,\dots ,v_N\}$, defined by interferometric phase STD, can be simply written as [27]:

$$v_i=\frac{1}{{\sigma }_i}=\frac{\sqrt{2L}{\gamma }_i}{\sqrt{1-{\gamma }_i^2}}\hspace{1em}L\ge 4$$

(9)

where $L$ is the looks and ${\gamma }_i$ is the coherence observations. Compared with the coherence, phase STD ${\sigma }_i$ is a more appropriate weight, as it takes looks into account. The function model Equation (9) is a close approximation to the complicated stochastic model when looks are greater than four [27]. After initial regression, the robust Bi-square weight $B=\{b_1,b_2,\dots ,b_N\}$, which minimizes a weighted sum of squares, is used during the iteration [28]:

$$\begin{array}{l}{u}_i=\frac{r_i}{cs\sqrt{1-h_i}}\\ b_i=\{\begin{array}{ll}{\left(1-u_i^2\right)}^2& \left|u_i\right|<1\\ 0& \left|u_i\right|\ge 1\end{array}\hspace{1em}\end{array}$$

(10)

where $r_i$ is least-squares residual for each observation from the previous iteration, $c$ is a tuning constant (4.685), and $s$ is the robust variance given by $MAD/0.6745$, where $MAD$ is the absolute deviation of the residuals from their median; $h_i$ is leverage that adjust the residuals. The total weight function $W$, therefore, is:

$$W=\{\begin{array}{ll}V& l=0\\ V\cdot B^{\left(l\right)}& l>0\end{array}$$

(11)

where $l$ denotes the number of iterations. The iterations will stop if the fit converges (minimum change in coefficients <${10}^{-5}$), or the maximum number of iterations allowed for fitting is reached (400).

2.2.4. Model Selection

The presence of the unwanted terms in Equation (7) and the overfitting lead to an unexpected bias or variance in interferograms. A trade-off should be made by taking advantage of K-cross validation, which has been widely used in machine learning [29]. Specifically, we obtained some test data from the same distribution and picked appropriate $m$ and $n$ in Equation (7) to minimize the same sum-of-squares difference that we used for fitting to the training data. This can be achieved by making several different splits in data $Z$. Each subsample is used once for testing, and the rest is used for training. The arrangement of this method is described as follows.

• Split data $Z$ into $K$ subsamples with equivalent size $N$.
• For $k=1,2,\dots ,K$, set validation data $Z_{test}$ to be the $k^{th}$ subsample, and training data $Z_{train}$ to be the other $K-1$ subsamples.
• Fit each model to $Z_{train}$ and evaluate its performance on $Z_{test}$ through weighted root-mean-square error (WRMSE).
• Pick $m$ and $n$ that leads to minimum WRMSE by averaging $K$ results.

Uniform sampling without replacement is used to separate data $Z$, and $K=10$ is set throughout this paper. Considering the different qualities of the validation data, we define WRMSE as:

$$WRMSE=\sqrt{\frac{{\displaystyle \sum _{i=1}^N{v}_i{\left(z_i-Z_{test,i}\right)}^2}}{{\displaystyle \sum _{i=1}^N{v}_i}}}$$

(12)

3. Results

3.1. Synthetic Data

In this section, the performance of the orbital-error corrections are evaluated and compared using a simulation. For notional convenience, we refer to the method in Equations (3) and (4) as DFT, and the method developed in Section 2.2 as adaptive ADP-Poly.

Three phase components, including deformation, random noise, and orbital errors were simulated according to the ENVISAT ASAR geometry. The surface deformation caused by a finite rectangular source was first simulated by the Okada 85 model [30] and then inverted to an interferometric phase (Figure 1b). To add phase noise, the coherence map was simulated under three principle sources of error, i.e., the Doppler, spatial, and temporal decorrelations [25,31], in which the temporal decorrelation was created using an isotropic-2D-fractal surface with a power law spectrum [32]. On the basis of the simulated coherence map under different looks (Figure 1a), the phase-STD map was obtained using the stochastic model (4.2.24) and (4.2.26) in [31]. The phase-noise map was finally generated using pointwise multiplication of the phase-STD map and the standard normal distributed random numbers. The linear and non-linear phase ramps were added to the orbital errors (Figure 1c,d). The combination of all components in synthetic interferograms is given in Figure 2.

To test the methods over fast decorrelation areas, we adjusted the coherence magnitude to an average value of γ = 0.2 under single look, and then added the phase-noise to the interferogram in Figure 2a. Likewise, we set γ = 0.4 under 2-looks to test the capability of both methods on moderate noise scenes, as shown in Figure 2f. For the frequency–domain-based method, the DFT is applied to noisy interferograms directly, while adaptive Goldstein filtering driven by phase STD [33] and minimum cost–flow unwrapping [34] were used before ADP-Poly surface fitting.

Visually, ADP-Poly could not detect the phase ramp in very noisy scenes and left phase residuals in Figure 2c. By contrast, DFT accurately captured the linear phase ramp. The residual between the truth and estimate confirms the potential of using DFT without phase unwrapping (Figure 2d). When the quality of interferogram became better (Figure 2f), ADP-Poly showed its superior performance at detecting nonlinear features (Figure 2h), while DFT could not completely remove the error and left nonlinear residuals in the interferogram (Figure 2g).

To make the results more statistically significant, we performed 500 simulations for each case and evaluated the phase residuals using root-mean-square error (RMSE). It can be seen from Figure 3 that DFT works well in linear orbital error correction over low coherence areas, and the averaged RMSE is up to 0.16 rad (4.99 rad for ADP-Poly). For nonlinear orbital features, ADP-Poly obtained RMSE of 0.10 rad (2.77 rad for DFT), which is equivalent to ~1 mm in deformation monitoring for C-band InSAR measurements.

3.2. Real Data

Four SAR datasets, covering the Datong and Tohoku-Oki areas, were used to validate the methods of orbital error correction, respectively. The information for the interferogram is summarized in

Table 1. ENVISAT ASAR acquisitions over Datong and Tohoku-Oki areas.*

Location	Sensor	Track	Master (yyyy-mm-dd)	Slave (yyyy-mm-dd)	${\mathit{B}}_{\perp }$ (m)	Pass	Char. Def.
Datong	GF-3	-	2017-04-01	2017-06-27	536	D	local
Datong	Sentinel-1	40	2015-10-15	2015-10-27	87	A	local
Tohoku-Oki	ASAR	347	2011-02-19	2011-03-21	163	D	global
Tohoku-Oki	ASAR	74	2011-03-02	2011-04-01	−121	D	global

* Columns show location, satellite platform, track number, acquisition dates, perpendicular baseline, satellite direction (ascending or descending) and characteristics of deformations. “-” denotes unknown track number (Orbit number: 003387/004641).

. The pre-processing includes the co-registration to subpixel accuracy with cross correlation algorithm, multi-looking (3 × 15 looks for ASAR data set along range and azimuth, 4 × 4 looks for GF-3 with stripmap model, 9 × 3 looks for Sentinel-1 with TOPSAR mode), the topography–component removal using the 90-m Shuttle Radar Topography Mission v. 4.1 digital elevation model, and the adaptive Goldstein filtering. The atmospheric delay is not considered any further due to the lack of the external data. For this paper, we assume that this component, together with orbital error, comprises the linear/nonlinear phase ramps.

3.2.1. Datong Area

The deformation feature in the GF-3 interferogram is locally distributed because of the dynamics of land subsidence caused by underground mining activities over the Datong area, China. Errors in the GF-3 satellite state vectors can be observed in the differential interferogram (Figure 4c) and cause a linear phase ramp along the azimuth direction. Because of the relatively low coherence over the area (Figure 4b), we employed DFT to remove the long-wavelength signals (Figure 4d) without the phase unwrapping. The results in the amplified sub-regions (1–3) show that mining-related surface deformation could be monitored after removal of orbital errors. The multi-looking GF-3 SAR image is shown in Figure 4a.

In contrast to GF-3, the better orbital qualities of Sentinel-1 instruments mitigate the phase ramp in the interferogram (Figure 5c). After burst and sub-swath merging, a nonlinear phase ramp with a relatively large spatial coverage can be observed in the upper right part of image. To remove the phase ramp, ADP-Poly is motivated by the high coherence magnitude (Figure 5b). A ten-fold cross validation was performed to select the optimal order of polynomial model. It can be seen from Figure 6a that the overfitting causes a larger bias for regression with the increase in order in polynomial, while the polynomial coefficient with n = 3 and m = 3 reaches the minimum WRMSE (2.15 rad, corresponding to ~9 mm). The final de-ramping interferogram is shown in Figure 5d, where the spatially distributed subsidence bowls can be clearly seen. The multi-looking sentinel-1 SAR image is shown in Figure 5a.

3.2.2. Tohoku-Oki Area

For long-wavelength displacement signals covering the whole image, external GPS measurements should be used to correct the displacement before phase-ramp estimation. To this end, GPS observations, including total 120 stations, were collected from the Advanced Rapid Imaging and Analysis (ARIA) team at Jet Propulsion Laboratory (JPL) and Caltech [20]. During the process, the GPS observations were first projected into the LOS direction using the central unit vector for east, north and vertical directions in descending ASAR (

Table 2. Deformation validation and RMSE before and after orbital error correction over Tohoku-Oki area.

Sensor	Track	Unit Vector of LOS [East North Up]	Number of GPS Station	RMSE before Correction (cm)	RMSE after Correction (cm)	RMSE Reduction (%)
ASAR	347	[0.64 0.11 0.75]	97	35.55	9.52	73.22
ASAR	74	[0.65 0.11 0.75]	23	12.24	8.39	31.45

). Then, all GPS locations were transformed into radar coordinates. The nearest SAR neighbors, with respect to each GPS measurement, were averaged using 3 × 3 boxcar windows, and the weights were determined by means of averaged phase STD with a factor of 1/3. When the phase ramp fitted using ADP-Poly, 90% of the GPS observations located in each SAR track were used to correct the deformation in unwrapped InSAR interferogram, and the remaining 10% were used to evaluate the discrepancies between the GPS observations and the orbit-corrected InSAR coseismic measurements.

We present the results of before and after ADP-Poly orbital error correction in Figure 6 and Figure 7 and Table 2. It can be seen that ADP-Poly suggests a quadratic model to fit the ramps for both tracks (Figure 6b,c). The RMSE values, before and after the orbital error correction, are 35.55 cm and 9.52 cm for track 347, and 12.24 cm and 8.39 cm for track 74, respectively, demonstrating the usefulness of the ADP-poly method developed by the authors. After removal of phase ramp, the displacement caused by earthquakes is rewrapped to 11.8 cm for each fringe, as shown in Figure 7. As stated in previous studies [17,20,35], the discontinuity between GPS measurements and InSAR displacement can be attributed to unwrapping errors over very low coherence area and the aftershock and postseismic deformation that were not covered by the GPS observation period.

4. Discussion

Two methods of modeling orbital error in InSAR interferograms that deploy DFT and the polynomial model with adaptive order determination were presented. DFT is a robust estimator of linear components of the long-wavelength signals, even in strong noise environment. It transfers spatial phase ramps into the frequency spectrum and finds the fringe rate at the peak location of the Fourier transformation. The interpolation of the DFT of the interferogram can better identify the exact fringe rate. A significant advantage of this method is that phase wrapping is not required, and, therefore, the errors caused by the poor quality of the interferograms are avoided. For nonlinear fringe patterns, the polynomial model (ADP-Poly) can compensate for nonlinear components that cannot be estimated with DFT. The development of adaptive order determination for the polynomial model using K-cross validation ensures the model can follow the features of orbital errors more accurately. This step is missed in previous studies, which usually determine the order empirically.

Two problems in orbital error correction should be further pointed out. Firstly, the approach has no capacity to distinguish between orbital errors and long-wavelength atmospheric delays. To our knowledge, this is a common problem in most related studies [12,13,14,20,23]. We therefore made the assumption that the long-wavelength signal only represents the orbital error, implying that part of the tropospheric delay will also be removed from the interferogram. A good alternative is to remove the atmospheric delays prior to orbital error correction, for example, by using the Generic Atmospheric Correction Online Service, applying the Iterative Tropospheric Decomposition model [34].

Secondly, manual masking is used to remove local deformation signals, leading to gaps in the local region, and so, no observation will yield contributions during de-ramping. To solve this problem, a deformation free interferogram can be inverted using a source geophysical model, e.g., Mogi’s formulation for an infinitesimal spherical source in an elastic half-space, by finding the global minimum in the misfit space using a simulated annealing algorithm [36]. To do this, General Inversion of Phase Technique, which estimates parameters in a quantitative model directly from the wrapped-phase data, can be employed [36].

5. Conclusions

This paper has explored orbital error correction in InSAR interferogram using frequency (DFT) and spatial domain (ADP-Poly) based methods. The results reveal that the modeling of orbital error should follow the features of fringe patterns and the quality of the interferogram. To detect linear features of orbital error, the method based on maximum likelihood fringe rate estimation should be deployed. The main advantage of this technique is that it is workable over fast decorrelation areas without the need of unwrapping. However, only linear components can be estimated using this method. For nonlinear features, ADP-Poly, which determines the order of polynomial automatically using K-cross validation, should be used. We evaluated both methods using historical and modern sensors, including ENVISAT ASAR, GF-3 and Sentinel-1. The experiments show that both historical and modern systems can benefit from our method to varying degrees, leading to clearer ground deformation signals, both locally and globally.