A Descriptor-less Well-Distributed Feature Matching Method Using Geometrical Constraints and Template Matching
Abstract
:1. Introduction
1.1. Related Work
1.2. Paper Contribution
2. Overview of the Proposed Method
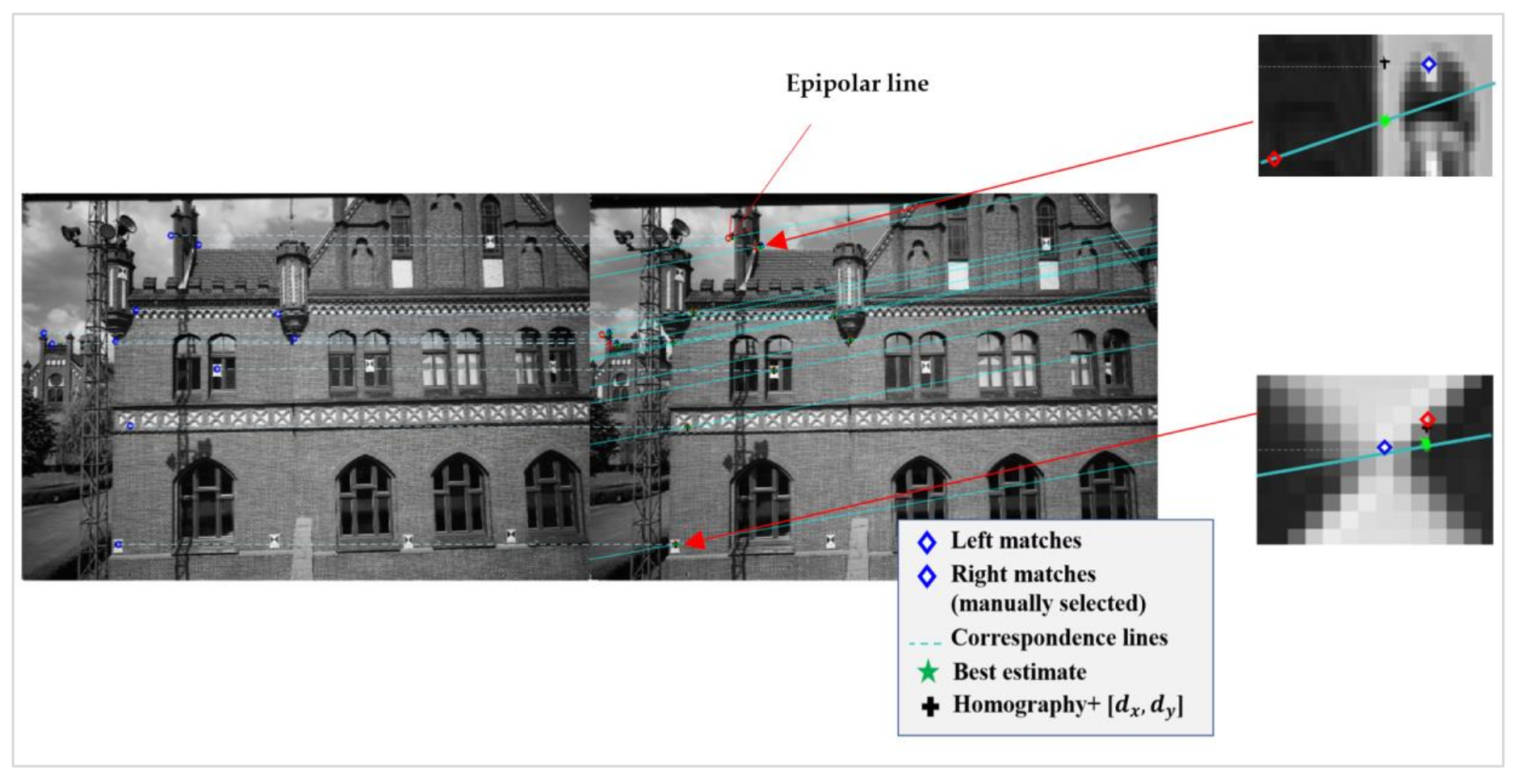
2.1. Epipolar Geometry
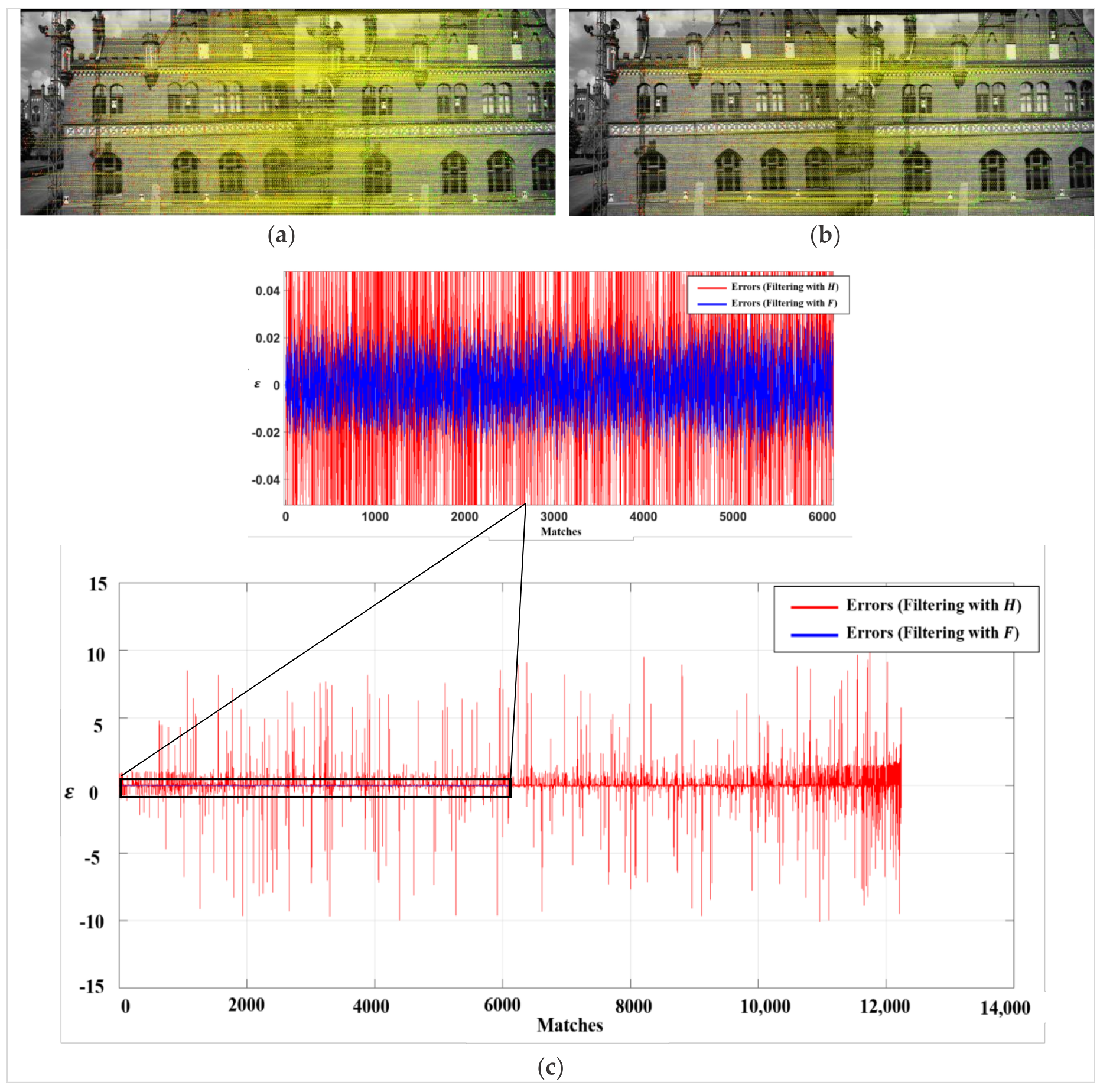
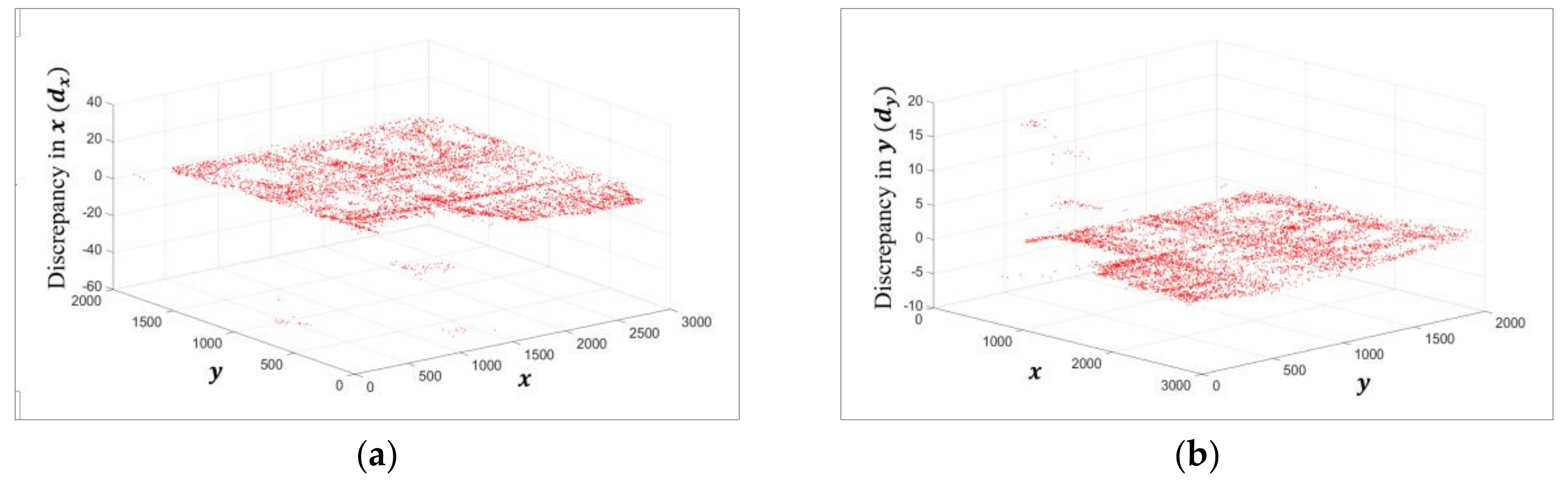
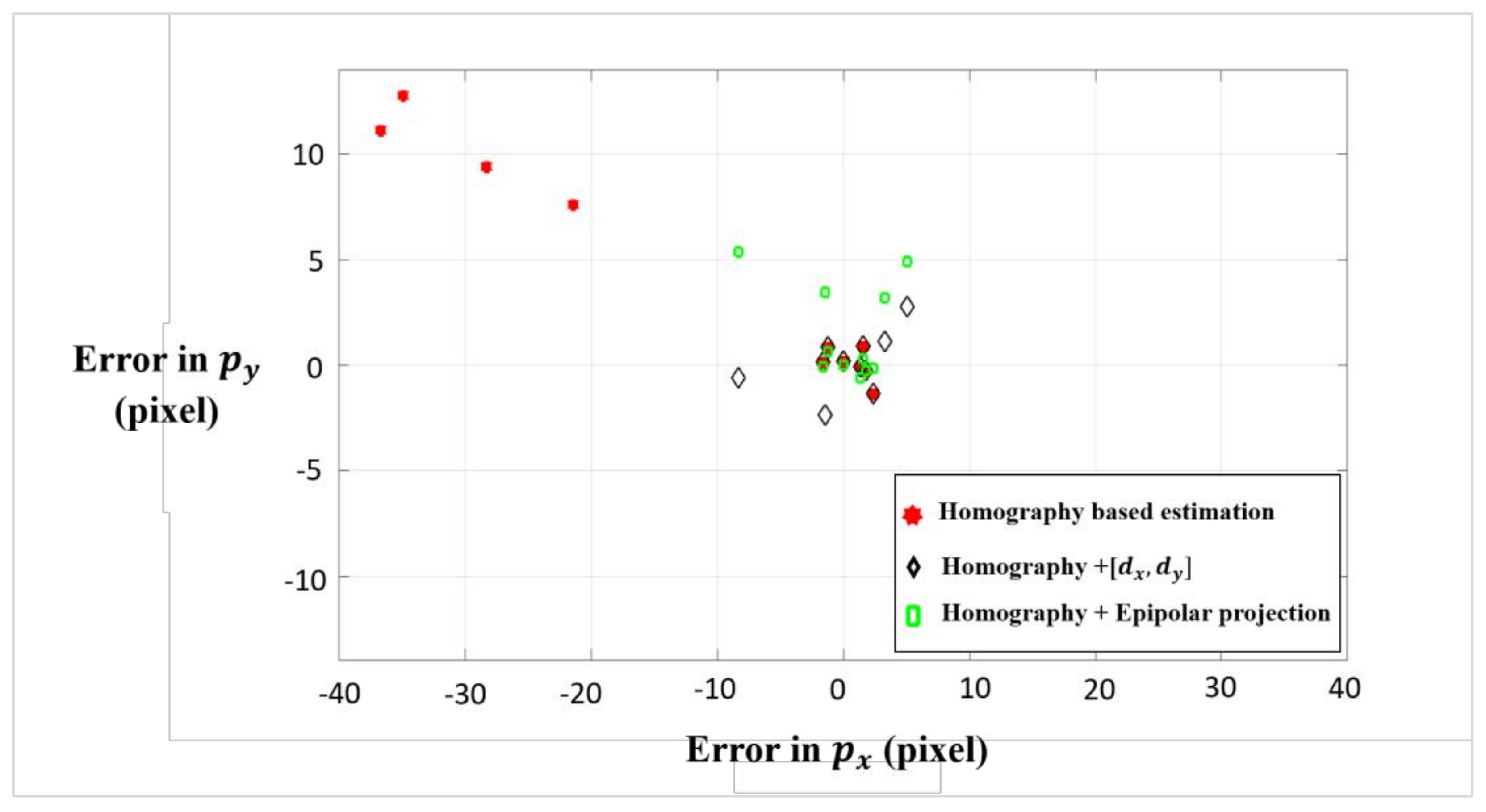
2.2. Discrepancy Assignment
2.3. Feature Detection
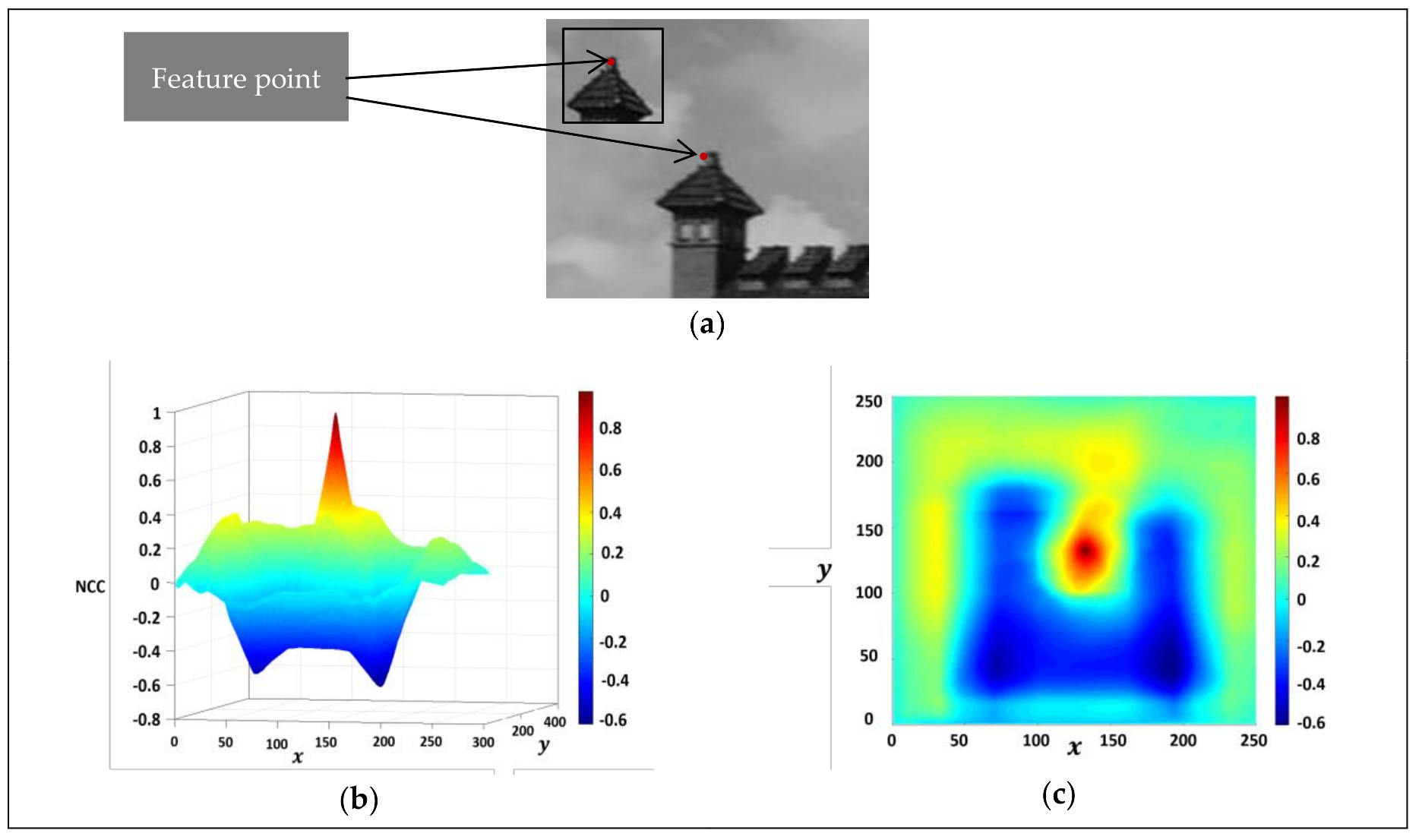
2.4. Template Matching with Normalised Cross-Correlation
2.4.1. Window Size Optimisation
2.5. Scale and Orientation Assignment
2.6. Seed Initialisation
2.7. Summary of the Proposed Methodology
3. Results and Discussions
3.1. Experimental Dataset
3.2. Evaluation Criteria
3.3. Matching Performance
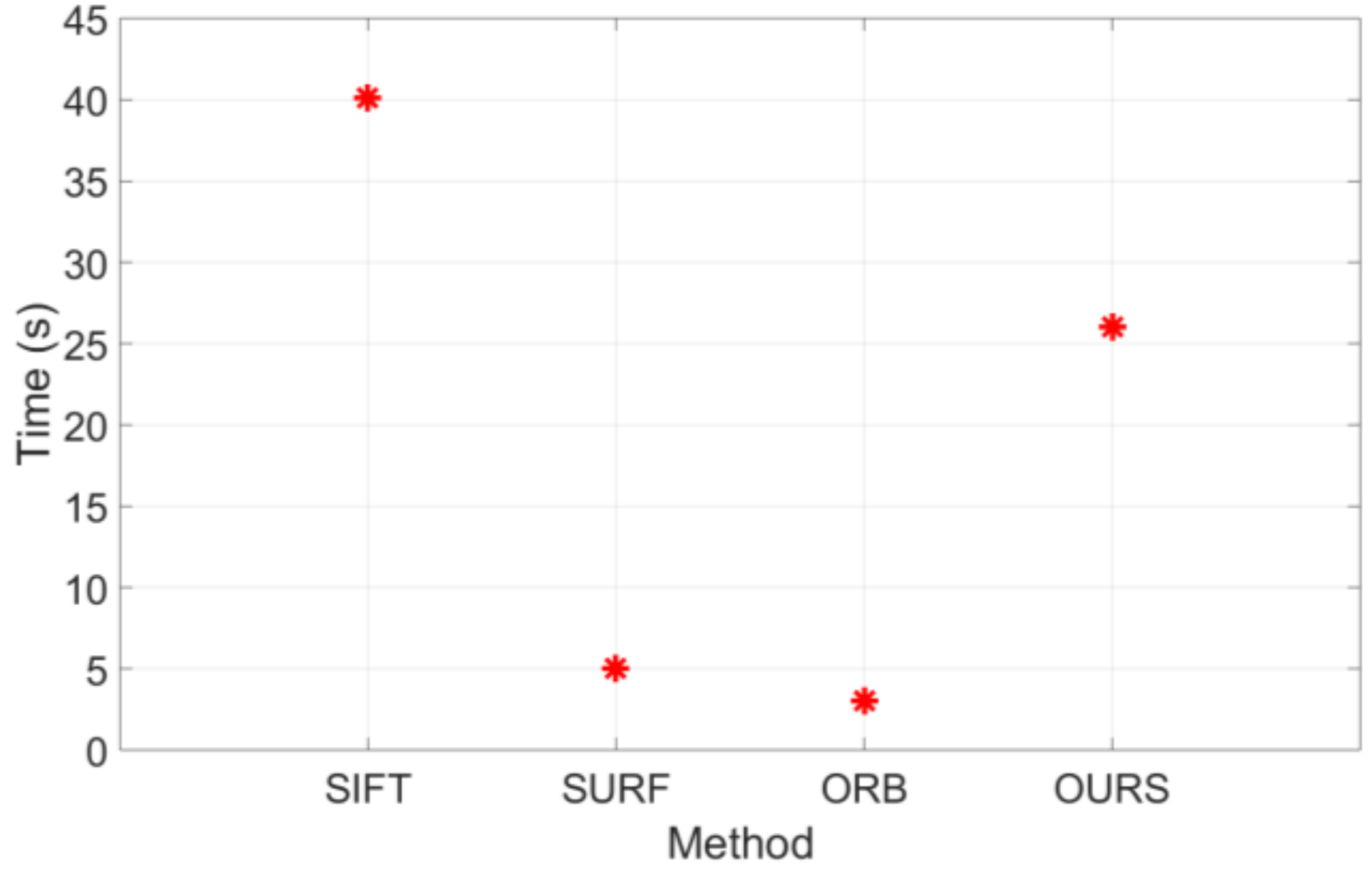
3.4. Processing Time
3.5. Applications
4. Conclusions
Author Contributions
Acknowledgments
Conflicts of Interest
References
- Moravec, H.P. Rover Visual Obstacle Avoidance. In Proceedings of the 7th International Joint Conference on Artificial Intelligence, Vancouver, BC, Canada, 24–28 August 1981; Volume 2, pp. 785–790. [Google Scholar]
- Fischler, M.A.; Bolles, R.C. Random sample consensus: A paradigm for model fitting with applications to image analysis and automated cartography. Commun. ACM 1981, 24, 381–395. [Google Scholar] [CrossRef]
- Torr, P.H.S.; Zisserman, A. MLESAC: A new robust estimator with application to estimating image geometry. Comput. Vis. Image Underst. 2000, 78, 138–156. [Google Scholar] [CrossRef]
- Torr, P.H.S.; Zisserman, A.; Maybank, S.J. Robust detection of degenerate configurations for the fundamental matrix. In Proceedings of the IEEE International Conference on Computer Vision, Cambridge, MA, 20–23 June 1995; pp. 1037–1042. [Google Scholar]
- Chen, C.I.; Sargent, D.; Tsai, C.M.; Wang, Y.F.; Koppel, D. Stabilizing stereo correspondence computation using delaunay triangulation and planar homography. In Proceedings of the 4th International Symposium, ISVC 2008, Las Vegas, NV, USA, 1–3 December 2008; Lecture Notes in Computer Science. Springer: Berlin, Germany, 2008; Volume 5358, pp. 836–845. [Google Scholar] [CrossRef]
- Harris, C.; Stephens, M. A Combined Corner and Edge Detector. In Proceedings of the Alvey Vision Conference, Manchester, UK, 31 August–1 September 1988; pp. 147–152. [Google Scholar]
- Schmid, C.; Mohr, R. Local Greyvalue Invariants for Image Retrieval. IEEE Trans. Pattern Anal. Mach. Intell. 1997, 19, 530–535. [Google Scholar] [CrossRef]
- Lowe, D.G. Object recognition from local scale-invariant features. In Proceedings of the Seventh IEEE International Conference on Computer Vision, Kerkyra, Greece, 20–27 September 1999; Volume 2, pp. 1150–1157. [Google Scholar] [CrossRef]
- Lowe, D.G. Distinctive Image Features from Scale-Invariant Keypoints. Int. J. Comput. Vis. 2004, 60, 91–110. [Google Scholar] [CrossRef]
- Mikolajczyk, K.; Schmid, C. Indexing based on scale invariant interest points. In Proceedings of the Eighth IEEE International Conference on Computer Vision, ICCV 2001, Vancouver, BC, Canada, 7–14 July 2001; Volume 1, pp. 525–531. [Google Scholar] [CrossRef]
- Ke, Y.; Sukthankar, R. PCA-SIFT: A more distinctive representation for local image descriptors. In Proceedings of the 2004 IEEE Computer Society Conference on Computer Vision and Pattern Recognition, CVPR 2004, Washington, DC, USA, 27 June–2 July 2004; Volume 2, pp. 506–513. [Google Scholar] [CrossRef]
- Bay, H.; Ess, A.; Tuytelaars, T.; van Gool, L. Speeded-Up Robust Features (SURF). Comput. Vis. Image Underst. 2008, 110, 346–359. [Google Scholar] [CrossRef]
- Khan, N.Y.; McCane, B.; Wyvill, G. SIFT and SURF performance evaluation against various image deformations on benchmark dataset. In Proceedings of the International Conference on Digital Image Computing Techniques and Applications (DICTA), Noosa, Australia, 6–8 December 2011; pp. 501–506. [Google Scholar]
- Saleem, S.; Bais, A.; Sablatnig, R. A performance evaluation of SIFT and SURF for multispectral image matching. In Proceedings of the 9th International Conference, ICIAR 2012, Aveiro, Portugal, 25–27 June 2012; Lecture Notes in Computer Science. Springer: Berlin, Germany, 2012; Volume 7324, pp. 166–173. [Google Scholar]
- Calonder, M.; Lepetit, V.; Strecha, C.; Fua, P. BRIEF: Binary robust independent elementary features. In Proceedings of the 11th European Conference on Computer Vision, Heraklion, Crete, Greece, 5–11 September 2010; Lecture Notes in Computer Science. Springer: Berlin, Germany, 2010; Volume 6314, pp. 778–792. [Google Scholar]
- Leutenegger, S.; Chli, M.; Siegwart, R.Y. BRISK: Binary Robust invariant scalable keypoints. In Proceedings of the IEEE International Conference on Computer Vision, Barcelona, Spain, 6–13 November 2011; pp. 2548–2555. [Google Scholar]
- Rublee, E.; Rabaud, V.; Konolige, K.; Bradski, G. ORB: An efficient alternative to SIFT or SURF. In Proceedings of the IEEE International Conference on Computer Vision, Barcelona, Spain, 6–13 November 2011; pp. 2564–2571. [Google Scholar]
- Rosten, E.; Drummond, T. Machine Learning for High Speed Corner Detection. In Proceedings of the 9th European Conference on Computer Vision, Graz, Austria, 7–13 May 2006; Springer: Berlin, Germany; Volume 1, pp. 430–443. [Google Scholar] [CrossRef]
- Zhang, Z.; Deriche, R.; Faugeras, O.; Luong, Q.T. A robust technique for matching two uncalibrated images through the recovery of the unknown epipolar geometry. Artif. Intell. 1995, 78, 87–119. [Google Scholar] [CrossRef]
- Torr, P.H.S.; Murray, D.W. Outlier detection and motion segmentation. In Sensor Fusion VI, SPIE 2059; SPIE: Bellingham, WA, USA, 1993; pp. 432–443. [Google Scholar] [CrossRef]
- Isack, H.; Boykov, Y. Energy Based Multi-model Fitting & matching for 3D Reconstruction. In Proceedings of the 2014 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Columbus, OH, USA, 23–28 June 2014; pp. 1146–1153. [Google Scholar]
- Frahm, J.M.; Pollefeys, M. RANSAC for (quasi-) degenerate data (QDEGSAC). In Proceedings of the 2006 IEEE Computer Society Conference on Computer Vision and Pattern Recognition, New York, NY, USA, 17–22 June 2006; Volume 1, pp. 453–460. [Google Scholar] [CrossRef]
- Chum, O.; Matas, J.; Kittler, J. Locally Optimized RANSAC. In Proceedings of the Joint Pattern Recognition Symposium, Magdeburg, Germany, 10–12 September 2003; pp. 236–243. [Google Scholar]
- Tan, X.; Sun, C.; Sirault, X.; Furbank, R.; Pham, T.D. Feature matching in stereo images encouraging uniform spatial distribution. Pattern Recognit. 2015, 48, 2530–2542. [Google Scholar] [CrossRef]
- Kim, H.Y.; de Araújo, S.A. Grayscale Template—Matching Invariant to Rotation, Scale, Translation, Brightness and Contrast. In Proceedings of the Second Pacific Rim Symposium, PSIVT 2007, Santiago, Chile, 17–19 December 2007. [Google Scholar] [CrossRef]
- Hartley, R.; Zisserman, A. Multiple View Geometry in Computer Version, 2nd ed.; Cambridge University Press: Cambridge, UK, 2004; Volume 53. [Google Scholar]
- Bentley, J.L. Multidimensional binary search trees used for associative searching. Commun. ACM 1975, 18, 509–517. [Google Scholar] [CrossRef]
- Rosten, E.; Porter, R.; Drummond, T. Faster and better: A machine learning approach to corner detection. IEEE Trans. Pattern Anal. Mach. Intell. 2010, 32, 105–119. [Google Scholar] [CrossRef] [PubMed]
- Goshtasby, A. Template Matching in Rotated Images. IEEE Trans. Pattern Anal. Mach. Intell. 1985, 7, 338–344. [Google Scholar] [CrossRef] [PubMed]
- Brunelli, R. Template Matching Techniques in Computer Vision: Theory and Practice; Wiley: Hoboken, NJ, USA, 2009. [Google Scholar]
- Lewis, J.P. Fast Template Matching. Pattern Recognit. 1995, 10, 120–123. [Google Scholar]
- Briechle, K.; Hanebeck, U.D. Template matching using fast normalized cross correlation. In Proceedings SPIE 4387, Optical Pattern Recognition XII; SPIE: Bellingham, WA, USA, 2001; pp. 95–102, doi:10.1117/12.42, 1129. [Google Scholar]
- Lewis, J. Fast Normalized Cross-Correlation, Vision Interface. Vis. Interface 1995, 10, 120–123. [Google Scholar]
- Sun, C. Fast optical flow using 3D shortest path techniques. Image Vis. Comput. 2002, 20, 981–991. [Google Scholar] [CrossRef]
- Hartley, R.; Zisserman, A. Multiple View Geometry in Computer Vision. Cambridge University Press: Cambridge, UK, 2003; Volume 1. [Google Scholar]
- Nex, F.; Gerke, M.; Remondino, F.; Przybilla, H.-J.; Bäumker, M.; Zurhorst, A. ISPRS Benchmark for Multi-Platform Photogrammetry. ISPRS Ann. Photogramm. Remote Sens. Spat. Inf. Sci. 2015, II-3/W4, 135–142. [Google Scholar] [CrossRef]
- Chen, M.; Habib, A.; He, H.; Zhu, Q.; Zhang, W. Robust Feature Matching Method for SAR and Optical Images by Using Gaussian-Gamma-Shaped Bi-Windows-Based Descriptor and Geometric Constraint. Remote Sens. 2017, 9, 882. [Google Scholar] [CrossRef]
- Hirschmüller, H. Stereo processing by semiglobal matching and mutual information. IEEE Trans. Pattern Anal. Mach. Intell. 2008, 30, 328–341. [Google Scholar] [CrossRef] [PubMed]















| Image Pair Properties | Left Image | Right Image |
|---|---|---|
| Predominant planar surface Multiple depths Image size: 3000 × 2000 |  |  |
| Relatively larger baseline (different scene structures) Image size: 3000 × 2000 |  |  |
| Projective distortion Image size: 3000 × 2000 |  |  |
| Different scale and orientation (Scale = 0.5, rotation angle = 45°) Image size: 3000 × 2000 |  |  |
| Mobile phone images Indoor environment Uncalibrated Different planar surfaces Image size: 2322 × 4128 |  |  |
| Matching Measures | Matching Methods | |||
|---|---|---|---|---|
| SIFT | SURF | ORB | OURS | |
| Number of Features (F) | 6559 | 6640 | 6500 | 6463 |
| Number of Matches (M) | 2906 | 3706 | 3163 | 4530 |
| Number of Precise Matches (NPM) | 2126 | 1563 | 422 | 4484 |
| Matching Precision (MP) | 73.16% | 42.17% | 13.34% | 98.98% |
| Number of Accurate Matches (NAM) | 2586 | 3237 | 2648 | 4125 |
| Matching Accuracy (MA) | 88.99% | 87.34% | 83.71% | 91.06% |
| Percentage of Correct Matches to Feature number (PCMF) | 39.43% | 48.75% | 40.74% | 63.82% |
| Matching Measures | Matching Methods | |||
|---|---|---|---|---|
| SIFT | SURF | ORB | OURS | |
| F | 5872 | 5497 | 5500 | 5217 |
| M | 748 | 1836 | 802 | 3546 |
| NPM | 112 | 113 | 40 | 2090 |
| MP | 14.97% | 6.15% | 4.99% | 58.94% |
| NAM | 525 | 498 | 371 | 2137 |
| MA | 70.19% | 27.12% | 46.26% | 60.27% |
| PCMF | 8.94% | 9.06% | 6.75% | 40.96% |
| Matching Measures | Matching Methods | |||
| SIFT | SURF | ORB | OURS | |
| F | 6341 | 6392 | 6500 | 6888 |
| M | 144 | 1177 | 254 | 1049 |
| NPM | 135 | 349 | 132 | 457 |
| MP | 93.75% | 29.65% | 51.97% | 43.57% |
| PCMF | 2.13% | 5.46% | 2.03% | 6.63% |
| Matching Measures | Matching Methods | |||
|---|---|---|---|---|
| SIFT | SURF | ORB | OURS | |
| F | 6559 | 6640 | 6500 | 6201 |
| M | 1337 | 1129 | 1920 | 2670 |
| NCM | 1325 | 349 | 1822 | 2661 |
| PCMF | 20.20% | 5.26% | 28.03% | 42.85% |
| MP | 99.10% | 29.65% | 94.84% | 99.63% |
| Matching Measures | Matching Methods | |||
|---|---|---|---|---|
| SIFT | SURF | ORB | OURS | |
| F | 4915 | 4890 | 4700 | 4764 |
| M | 1139 | 1736 | 1523 | 3310 |
| NCM | 973 | 1057 | 1214 | 3024 |
| PCMF | 19.80% | 21.62% | 25.83% | 63.48% |
| MP | 85.43% | 60.89% | 79.71% | 91.36% |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mohammed, H.M.; El-Sheimy, N. A Descriptor-less Well-Distributed Feature Matching Method Using Geometrical Constraints and Template Matching. Remote Sens. 2018, 10, 747. https://doi.org/10.3390/rs10050747
Mohammed HM, El-Sheimy N. A Descriptor-less Well-Distributed Feature Matching Method Using Geometrical Constraints and Template Matching. Remote Sensing. 2018; 10(5):747. https://doi.org/10.3390/rs10050747
Chicago/Turabian StyleMohammed, Hani Mahmoud, and Naser El-Sheimy. 2018. "A Descriptor-less Well-Distributed Feature Matching Method Using Geometrical Constraints and Template Matching" Remote Sensing 10, no. 5: 747. https://doi.org/10.3390/rs10050747
APA StyleMohammed, H. M., & El-Sheimy, N. (2018). A Descriptor-less Well-Distributed Feature Matching Method Using Geometrical Constraints and Template Matching. Remote Sensing, 10(5), 747. https://doi.org/10.3390/rs10050747







