System Noise Removal for Gaofen-4 Area-Array Camera
Abstract
:1. Introduction
2. Materials and Methods
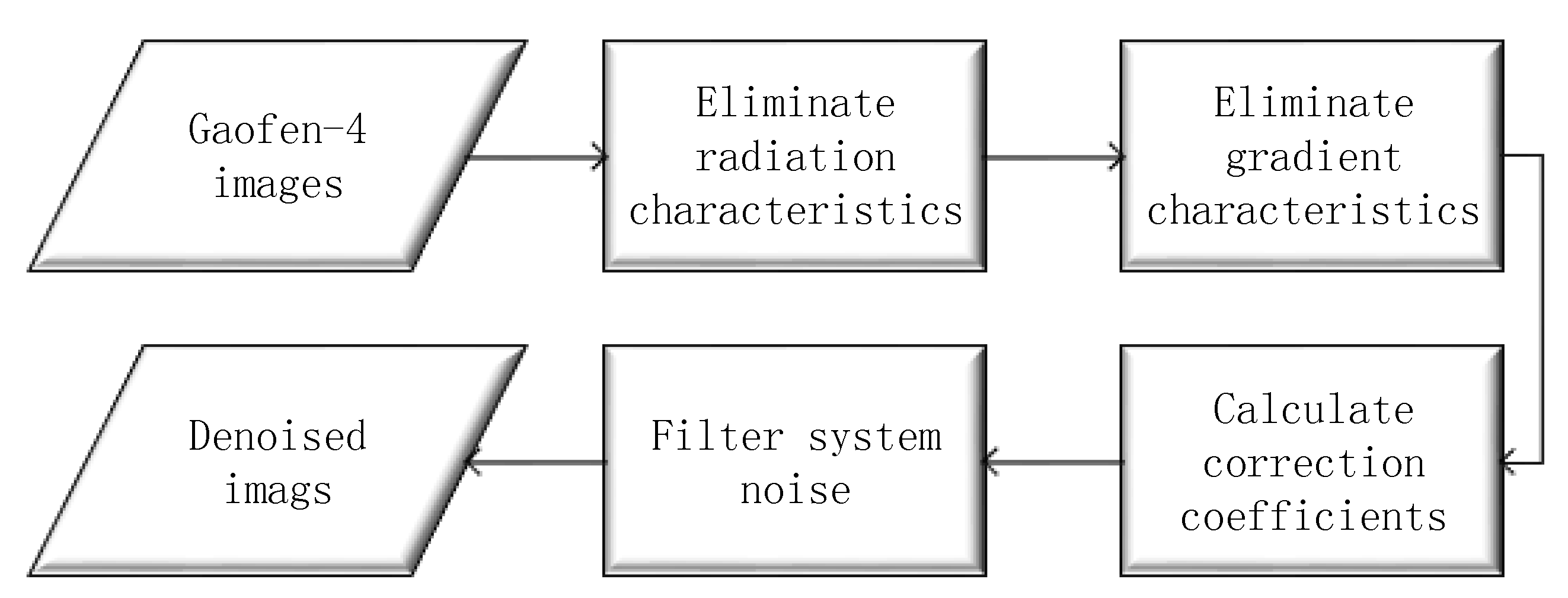
2.1. Principle of Gaofen-4 System Noise Removal
2.2. Elimination of Radiation Characteristics
2.3. Elimination of Gradient Characteristics
2.4. System Noise Removal
3. Results and Discussion
4. Conclusions
Author Contributions
Acknowledgments
Conflicts of Interest
References
- Mendenhall, J.A.; Lencioni, D.E.; Evans, J.B. Earth Observing-1 Advanced Land Imager: Radiometric Response Calibration; MIT/LL Project Report EO-1-3; Massachusetts Institute of Technology: Cambridge, MA, USA, 2000. [Google Scholar]
- Wang, M.; Cheng, Y.; Long, X.; Yang, B. On-Orbit Geometric Calibration Approach for High-Resolution Geostationary Optical Satellite GaoFen-4. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2016, 41, 389–394. [Google Scholar] [CrossRef]
- Gonzalez, R.C.; Woods, R.E. Digital Image Processing; Prentice Hall International: Englewood Cliffs, NJ, USA, 2005; Volume 28, pp. 484–486. [Google Scholar]
- Buades, A.; Coll, B.; Morel, J.M. A Review of Image Denoising Algorithms, with a New One. Siam J. Multiscale Model. Simul. 2005, 4, 490–530. [Google Scholar] [CrossRef]
- Dabov, K.; Foi, A.; Katkovnik, V.; Egiazarian, K. Image Denoising by Sparse 3-D Transform-Domain Collaborative Filtering. IEEE Trans. Image Process. 2007, 16, 2080–2095. [Google Scholar] [CrossRef] [PubMed]
- Witkin, A.P. Scale-space filtering. In Proceedings of the International Joint Conference on Artificial Intelligence, Karlsruhe, Germany, 8–12 August 1983; pp. 1019–1022. [Google Scholar]
- Perona, P.; Malik, J. Scale-Space and Edge Detection Using Anisotropic Diffusion. IEEE Trans. Pattern Anal. Mach. Intell. 1990, 12, 629–639. [Google Scholar] [CrossRef]
- Weickert, J. Theoretical Foundations of Anisotropic Diffusion in Image Processing. In Theoretical Foundations of Computer Vision; Springer: Vienna, Austria, 1996; pp. 221–236. [Google Scholar]
- Lerga, J.; Grbac, E.; Sucic, V. An ICI Based Algorithm for Fast Denoising of Video Signals. Automatika 2014, 55, 351–358. [Google Scholar] [CrossRef]
- Mandić, I.; Peić, H.; Lerga, J.; Štajduhar, I. Denoising of X-ray Images Using the Adaptive Algorithm Based on the LPA-RICI Algorithm. J. Imaging 2018, 4, 34. [Google Scholar] [CrossRef]
- Zorzi, M. An interpretation of the dual problem of the THREE-like approaches. Automatica 2015, 62, 87–92. [Google Scholar] [CrossRef]
- Ringh, A.; Karlsson, J.; Lindquist, A. Multidimensional Rational Covariance Extension with Applications to Spectral Estimation and Image Compression. Mathematics 2016, 306 Pt 1, 823–834. [Google Scholar] [CrossRef]
- Mallat, S.G. A Theory for Multiresolution Signal Decomposition: The Wavelet Representation. IEEE Trans. Pattern Anal. Mach. Intell. 1989, 11, 674–693. [Google Scholar] [CrossRef]
- Chipman, H.; Kolaczyk, E.; Mcculloch, R. Adaptive Bayesian Wavelet Shrinkage. J. Am. Stat. Assoc. 1997, 92, 1413–1421. [Google Scholar] [CrossRef]
- Moulin, P.; Liu, J. Analysis of multiresolution image denoising schemes using generalized Gaussian and complexity priors. IEEE Trans. Inf. Theory 2015, 45, 909–919. [Google Scholar] [CrossRef]
- Romberg, J.K.; Choi, H.; Baraniuk, R.G. Bayesian tree-structured image modeling using wavelet-domain hidden Markov models. IEEE Trans. Image Process. 2001, 10, 1056–1068. [Google Scholar] [CrossRef] [PubMed]
- Donoho, D.L. Ridge Functions and Orthonormal Ridgelets; Academic Press, Inc.: Cambridge, MA, USA, 2001. [Google Scholar]
- Emmanuel, J.C. Monoscale Ridgelets for the Representation of Images with Edges; Technical Report; Department of Statistics Stanford University: Stanford, CA, USA, 1999. [Google Scholar]
- Pennec, E.L.; Mallat, S. Image compression with geometrical wavelets. In Proceedings of the IEEE International Conference on Image Processing, Vancouver, BC, Canada, 10–13 September 2000; Volume 1, pp. 661–664. [Google Scholar]
- Duan, Y.; Zhang, L.; Yan, L.; Wu, T.; Liu, Y.; Tong, Q. Relative radiometric correction methods for remote sensing images and their applicability analysis. J. Remote Sens. 2014, 18, 597–617. [Google Scholar]
- Shen, Y.; Ran, Q.; Liu, Y. Application of Improved Grubbs’ Criterion to Estimation of Signal Detection Threshold. J. Harbin Inst. Technol. 1999, 31, 111–113. [Google Scholar]
- Gao, B.C. An operational method for estimating signal to noise ratios from data acquired with imaging spectrometers. Remote Sens. Environ. 1993, 43, 23–33. [Google Scholar] [CrossRef]






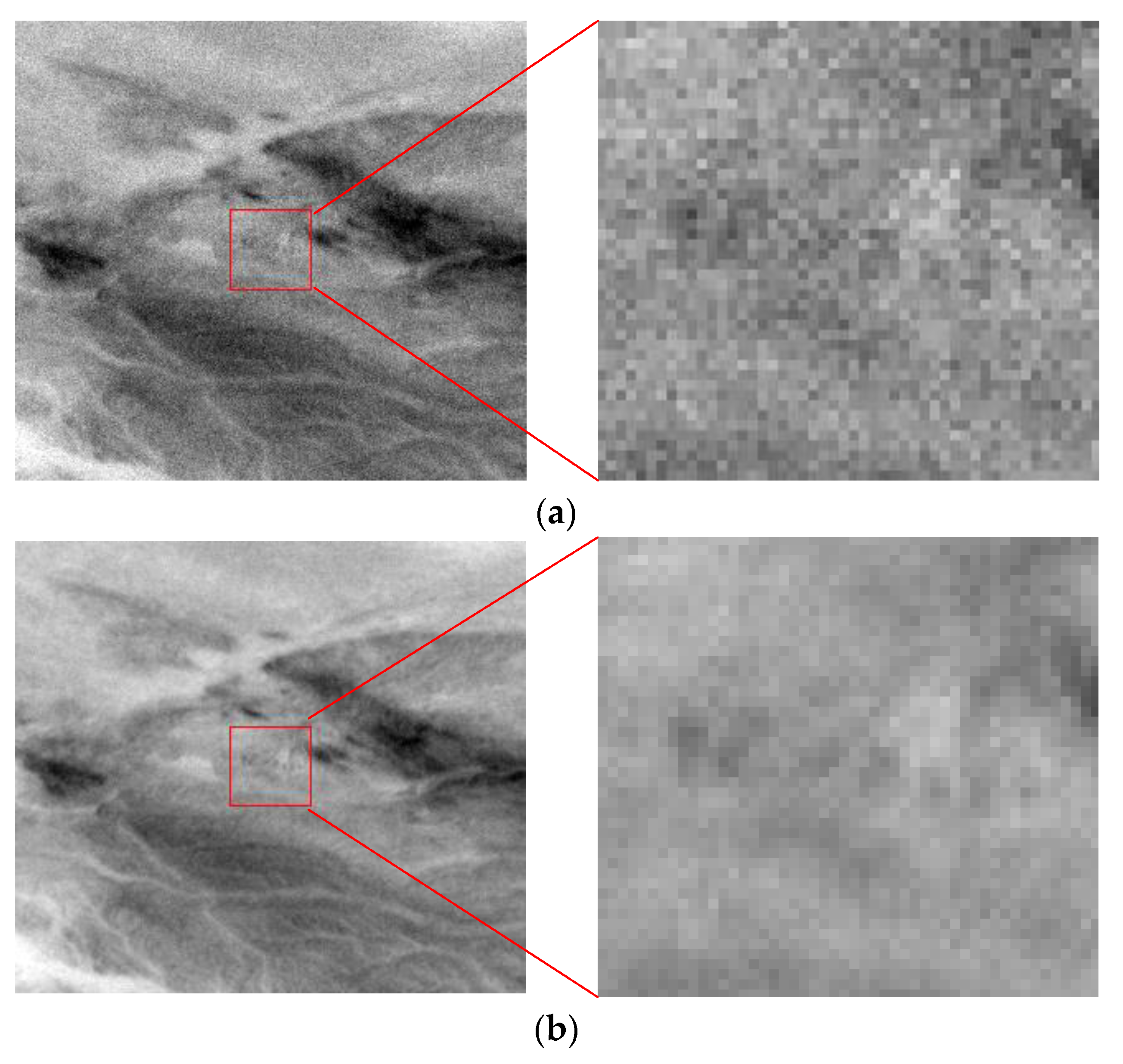


| Method | Mean | Standard Deviation | SNR (dB) |
|---|---|---|---|
| Original Image | 375.3394 | 119.4055 | 27.4280 |
| Local Sigma (sigma = 1) | 375.3642 | 119.2274 | 28.6714 |
| Local Sigma (sigma = 2) | 375.3359 | 118.7214 | 32.7983 |
| Local Sigma (sigma = 3) | 375.3507 | 118.5250 | 35.6646 |
| BM3D (sigma = 1) | 375.3382 | 119.2859 | 28.2042 |
| BM3D (sigma = 2) | 375.3355 | 119.0549 | 31.0448 |
| BM3D (sigma = 3) | 375.3325 | 118.8571 | 37.3436 |
| Proposed Method | 375.4924 | 119.0170 | 35.8638 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chang, X.; He, L. System Noise Removal for Gaofen-4 Area-Array Camera. Remote Sens. 2018, 10, 759. https://doi.org/10.3390/rs10050759
Chang X, He L. System Noise Removal for Gaofen-4 Area-Array Camera. Remote Sensing. 2018; 10(5):759. https://doi.org/10.3390/rs10050759
Chicago/Turabian StyleChang, Xueli, and Luxiao He. 2018. "System Noise Removal for Gaofen-4 Area-Array Camera" Remote Sensing 10, no. 5: 759. https://doi.org/10.3390/rs10050759
APA StyleChang, X., & He, L. (2018). System Noise Removal for Gaofen-4 Area-Array Camera. Remote Sensing, 10(5), 759. https://doi.org/10.3390/rs10050759




