Experimental Study of the Thermal Infrared Emissivity Variation of Loaded Rock and Its Significance
Abstract
:1. Introduction
2. Materials and Methods
2.1. Theoretical Analysis
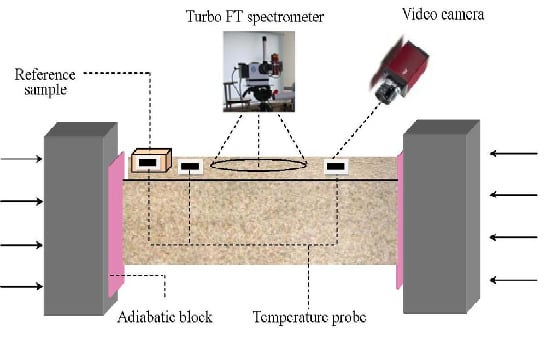
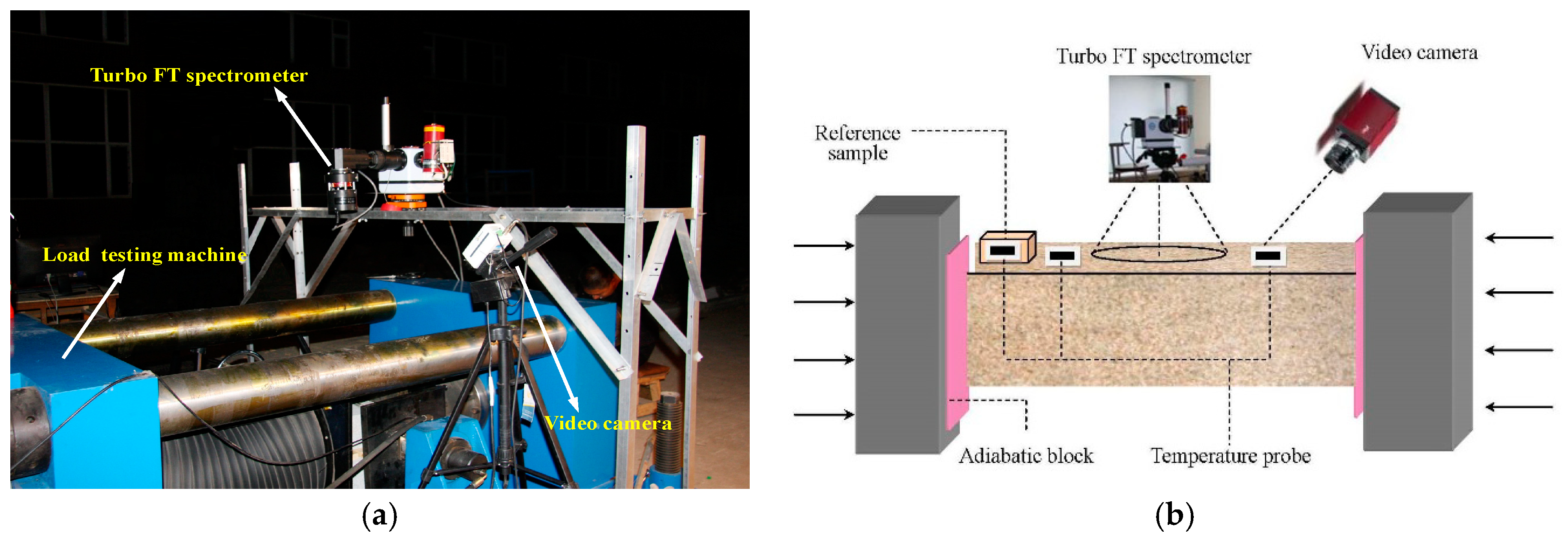
2.2. Components of Experimental System
2.3. Calibration Procedure
2.3.1. Instrument Calibration
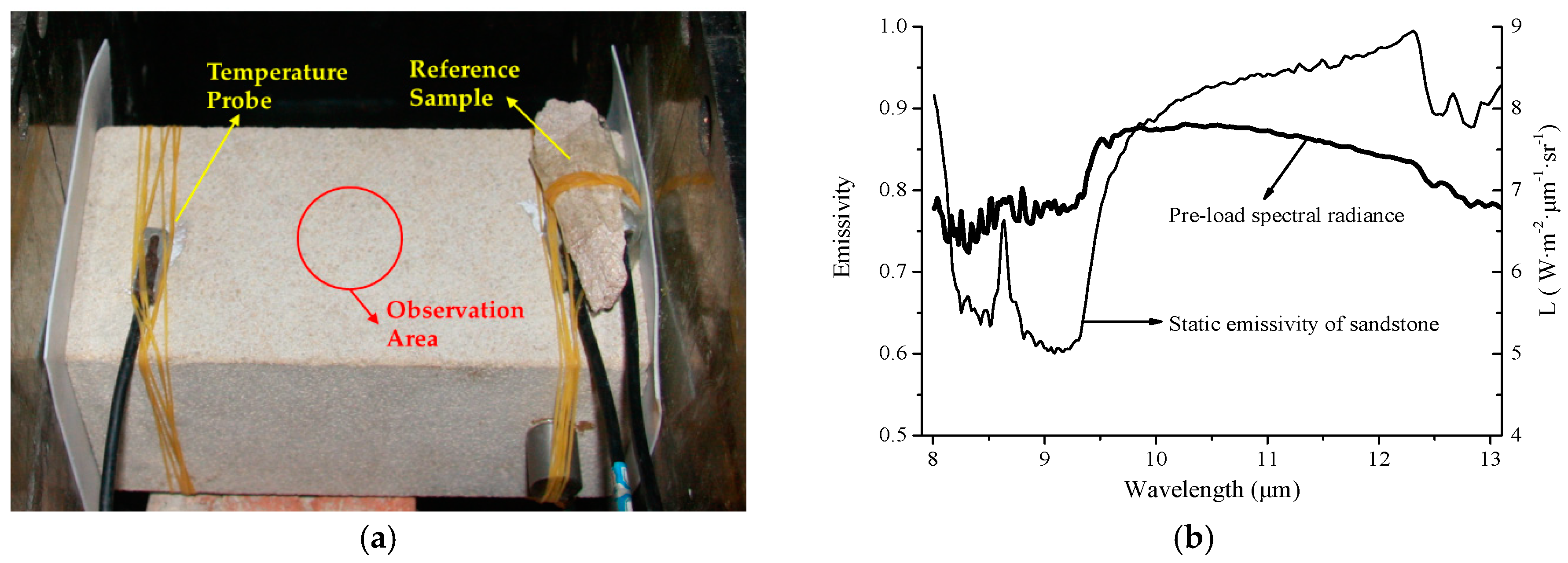
2.3.2. Calibration for the Experimental Environment
2.4. Experimental Method
3. Results
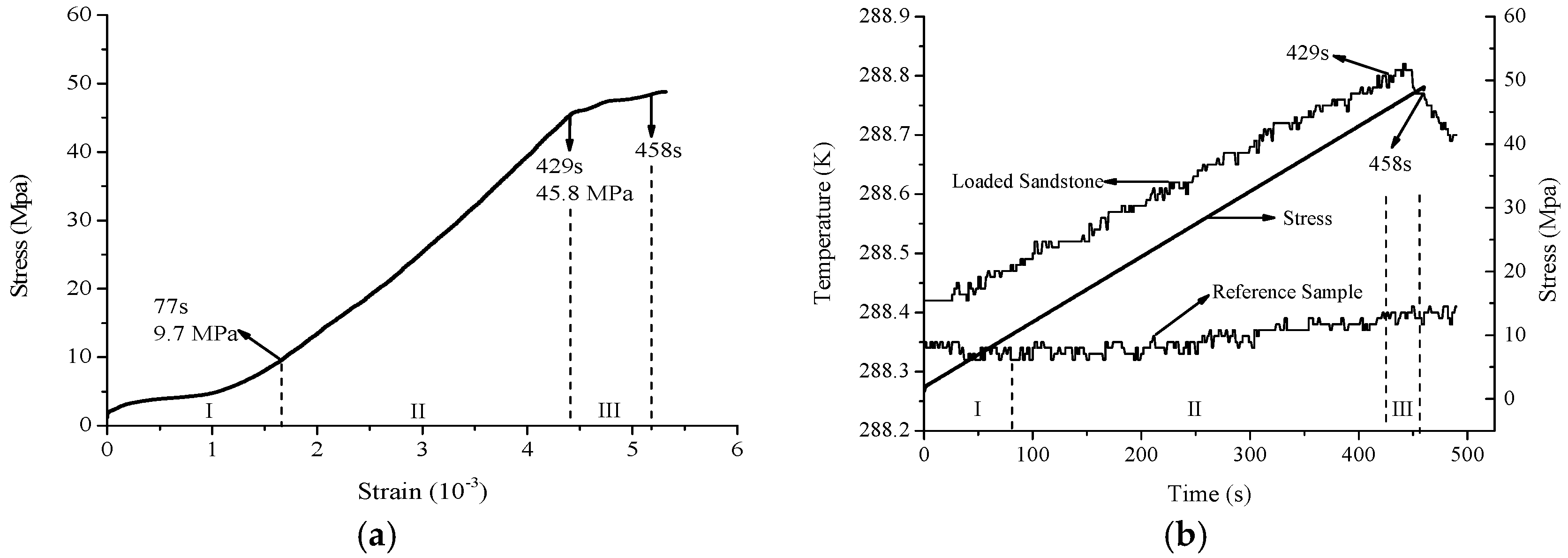
3.1. Variation in Strain and Stress
3.2. Variation in Temperature
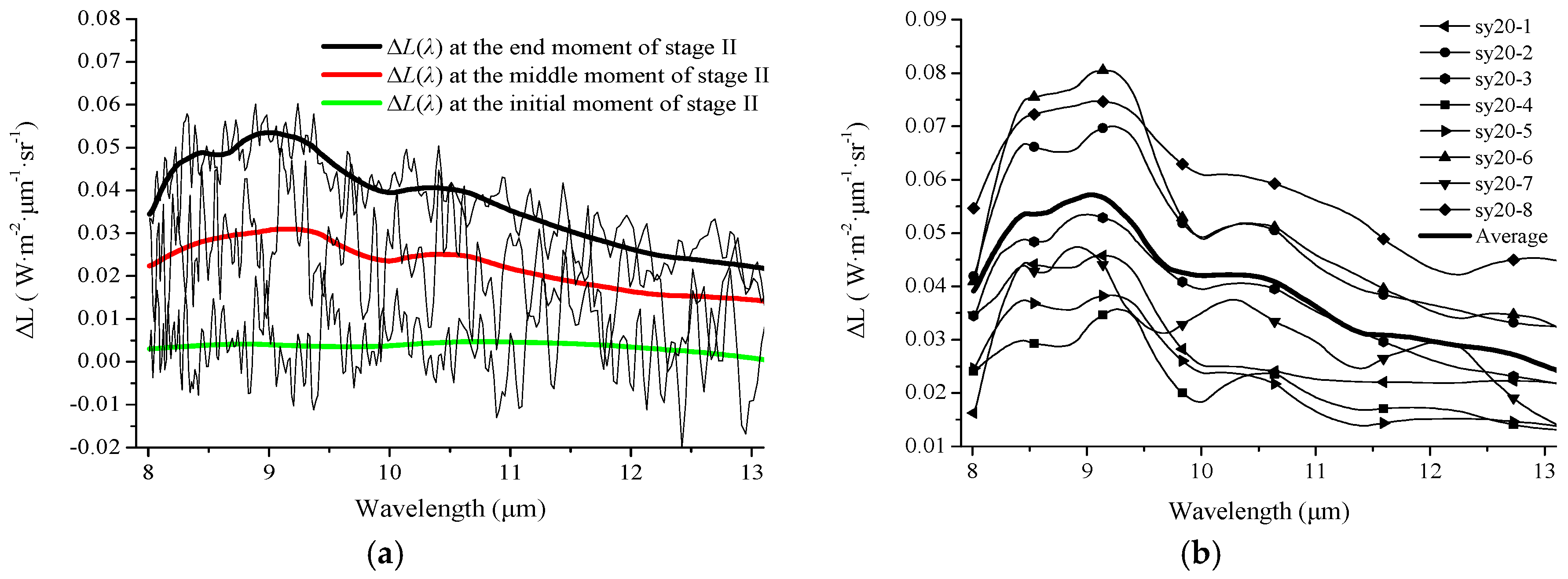
3.3. Variation in Radiance
3.3.1. Measured Radiance Variation
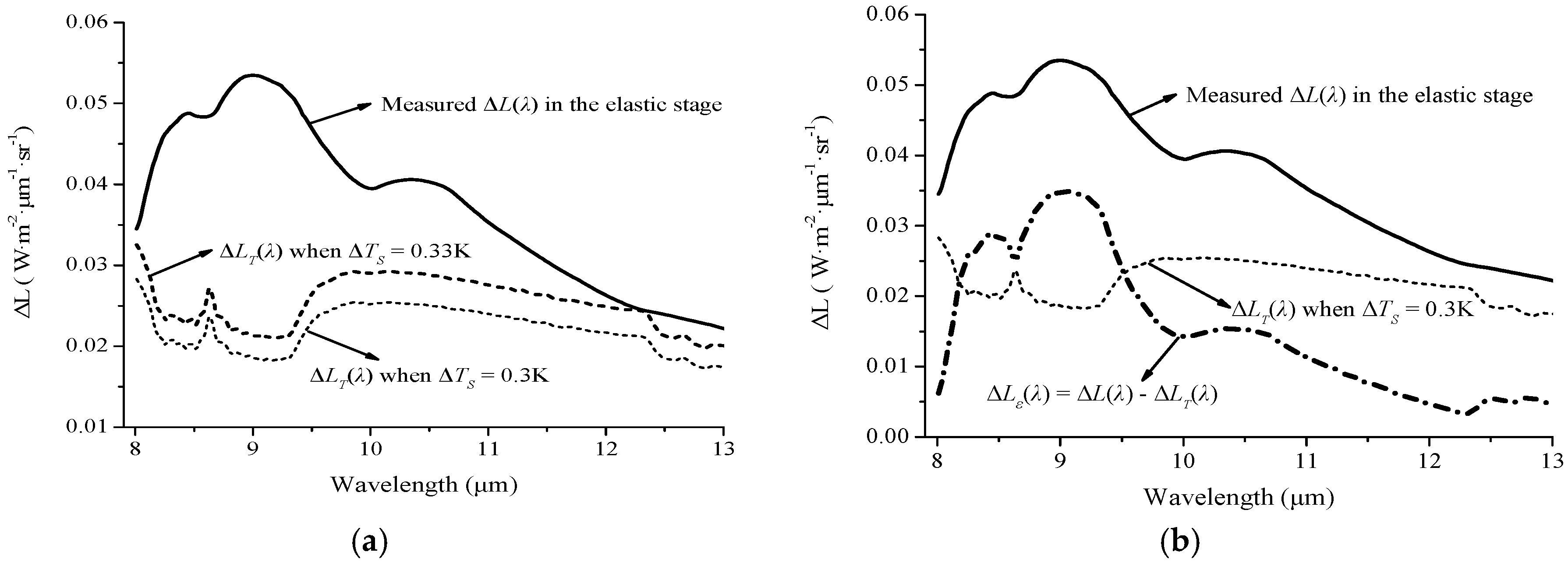
3.3.2. Calculated Results of ΔLT(λ)
3.4. Variation in ε(λ)
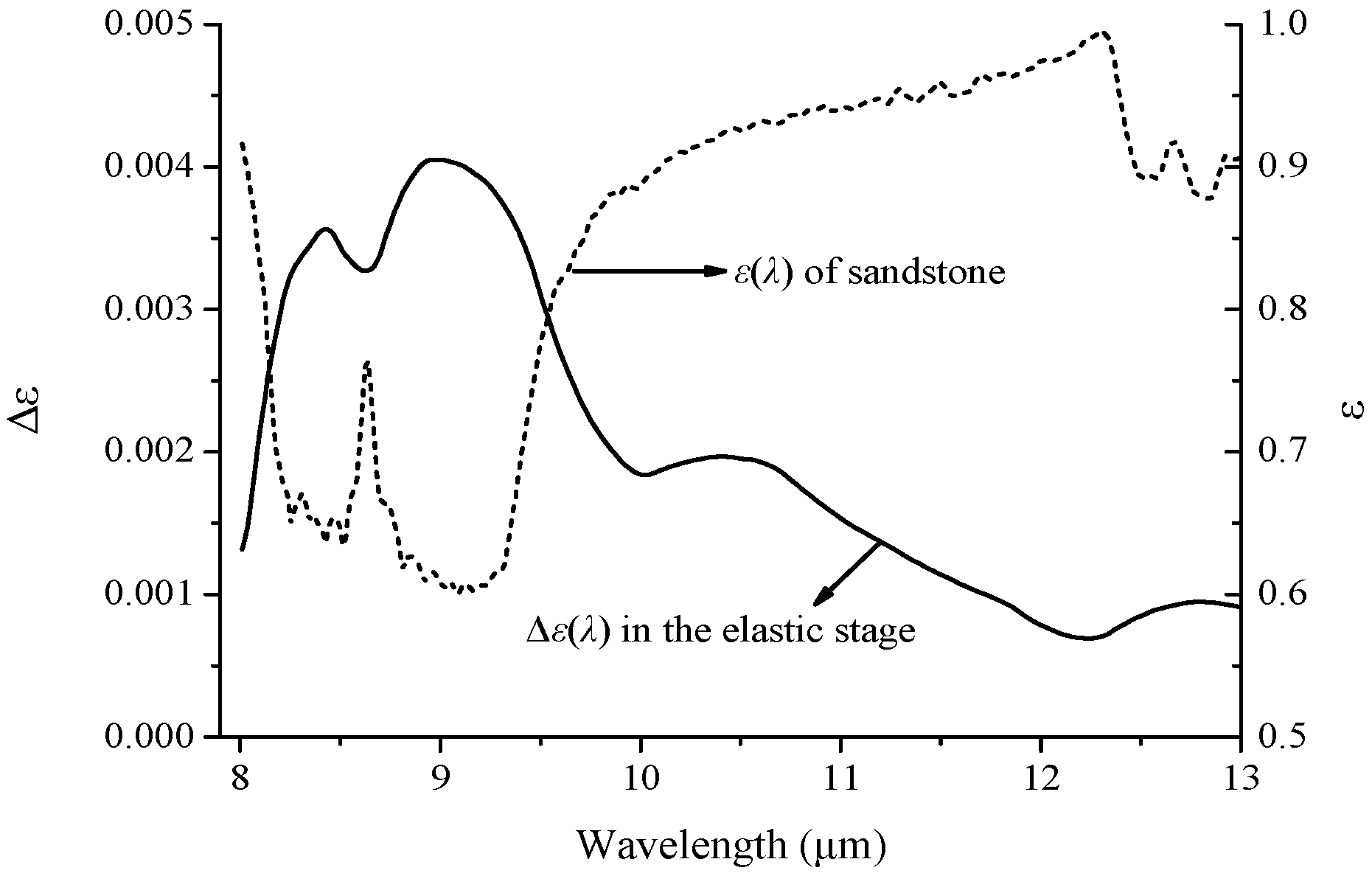
3.4.1. Waveband Features of Δε(λ)
- (1)
- The value of Δε(λ) was positive, and the amplitude varied with wavelength for the entire wavelength range. The curve reaches a local peak in the range of 8.0–10.0 μm and a global maximum with a value of 4.2 × 10−3 at 9.0 μm.
- (2)
- The trends of these two curves were opposite, and the local peaks on the Δε(λ) curve corresponded to local valleys on the ε(λ) curve.
- (3)
- The amplitude range of Δε(λ) was approximately 7 × 10−4–4.2 × 10−3 in the 8.0–13.0 μm range, and the average value is 2.3 × 10−3. Combined with the compressive strain data during the elastic stage, the strain value of sy20-3 was 0.28%, and the average strain of the eight samples was 0.26%. The magnitude of the strain change was consistent with that of Δε(λ).
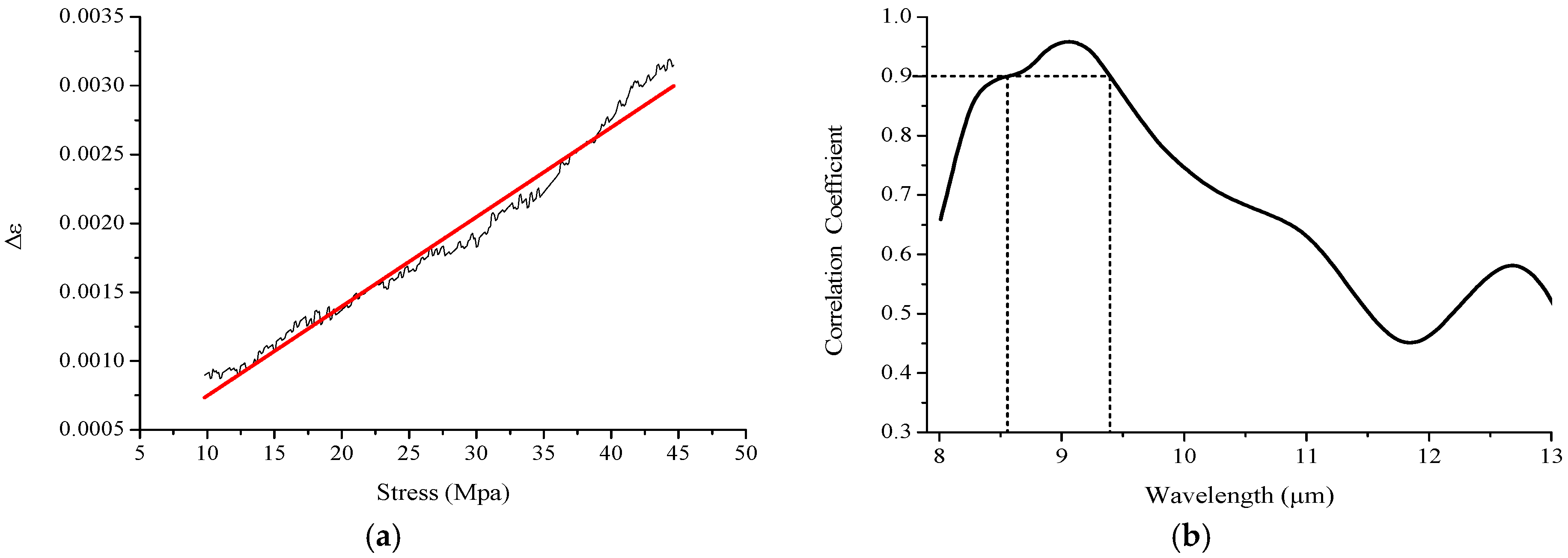
3.4.2. Correlation Analysis between Δε(λ) and Stress
4. Discussion
4.1. Explanation of the Temperature and Emissivity Changes during the Elastic stage
4.1.1. Factors Causing Temperature Change
4.1.2. Factors Causing Emissivity Change
4.2. Significance of the Experimental Results
4.3. The Difficulty
- (1)
- The emissivity change caused by the stress belonged to a weak signal with a magnitude of 10−3 in the elastic stage of rock, which was difficult to be detected based on the radiance and emissivity resolution of the satellite sensor presently. Although some sophisticated algorithms have been developed for extracting the weak TIR anomalies from a relatively strong background [69,70,71,72,73], it remains difficult to obtain the accurate emissivity variation caused by crustal stress.
- (2)
- In the experimental condition, the distance between the spectrometer and the specimen was in the level of meters. However, for satellite observations, the orbit height is about several hundred kilometers. The influence of the atmosphere effect is inevitable and the components of the received radiance are more complex.
- (3)
- In the experimental condition, the observation area was relatively small. There is only one type of rock in the area, and the component of the target is homogeneous. Meanwhile, the stress condition was single. In comparison, because of the spatial resolution for satellite observation, the mixed pixels contain the multiple types of rocks, and the distribution of the crustal stress condition is complex and not uniform. It is difficult to establish the relationship between complex stress condition and emissivity.
5. Conclusions
- (1)
- Both temperature and emissivity changed under the loading conditions. The radiance change caused by the slight emissivity change should be considered in addition to the radiance change caused by temperature change during the loading process.
- (2)
- There were certain waveband features for the emissivity variation, leading to the sensitive waveband of radiance change. The amplitude of the emissivity variations was relatively large in the 8.0–10.0 μm (RF) range and reached a maximum at 9.0 μm.
- (3)
- An obvious linear correlation existed between the emissivity change and the stress change in the 8.6–9.4 μm range. The magnitude of the emissivity change was consistent with that of the strain change during the elastic stage.
Author Contributions
Acknowledgments
Conflicts of Interest
References
- Gorny, V.I.; Sal’Man, A.G.; Tronin, A.A.; Shilin, B.V. Outgoing infrared radiation of the earth as an indicator of seismic activity. Proc. Acad. Sci. USSR 1988, 301, 67–69. [Google Scholar]
- Qiang, Z.J.; Xu, X.D.; Ning, C.G. Abnormal infrared thermal of satellite-forewarning of earthquakes. Chin. Sci. Bull. 1990, 35, 1324–1327. (In Chinese) [Google Scholar]
- Tronin, A.A.; Molchanov, O.A.; Biagi, P.F. Thermal anomalies and well observations in Kamchatka. Int. J. Remote Sens. 2004, 25, 2649–2655. [Google Scholar] [CrossRef]
- Ouzounov, D.; Bryant, N.; Logan, T.; Pulinets, S.; Taylor, P. Satellite thermal IR phenomena associated with some of the major earthquakes in 1999–2003. Phys. Chem. Earth 2006, 31, 154–163. [Google Scholar] [CrossRef]
- Ouzounov, D.; Liu, D.F.; Kang, C.L.; Cervone, G.; Kafatos, M.; Taylor, P. Outgoing long wave radiation variability from IR satellite data prior to major earthquakes. Tectonophysics 2007, 431, 211–220. [Google Scholar] [CrossRef]
- Wu, L.X.; Liu, S.J. Remote Sensing Rock Mechanics and Earthquake Thermal Infrared Anomalies; InTech: Vukovar, Croatia, 2009; pp. 709–741. [Google Scholar]
- Tronin, A.A. Satellite remote sensing in seismology. A review. Remote Sens. 2010, 2, 124–150. [Google Scholar] [CrossRef]
- Wu, L.X.; Qin, K.; Liu, S.J. GEOSS-based thermal parameters analysis for earthquake anomaly recognition. Proc. IEEE. 2012, 100, 2891–2907. [Google Scholar] [CrossRef]
- Piroddi, L.; Ranieri, G. Night Thermal Gradient: A New Potential Tool for Earthquake Precursors Studies. An Application to the Seismic Area of L’Aquila (Central Italy). IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2012, 5, 307–312. [Google Scholar] [CrossRef]
- Piroddi, L.; Ranieri, G.; Freund, F.T.; Trogu, A. Geology, tectonics and topography underlined by L’Aquila earthquake TIR precursors. Geophys. J. Int. 2014, 197, 1532–1536. [Google Scholar] [CrossRef]
- Eleftheriou, A.; Filizzola, C.; Genzano, N.; Lacava, T.; Lisi, M.; Paciello, R.; Pergola, N.; Vallianatos, F.; Tramutoli, V. Long-term RST analysis of anomalous TIR sequences in relation with earthquakes occurred in Greece in the period 2004–2013. Pure Appl. Geophys. 2016, 173, 285–303. [Google Scholar] [CrossRef]
- Bhardwaj, A.; Singh, S.; Sam, L.; Bhardwaj, A.; Martín-Torres, F.J.; Singh, A.; Kumar, R. MODIS-based estimates of strong snow surface temperature anomaly related to high altitude earthquakes of 2015. Remote Sens. Environ. 2017, 188, 1–8. [Google Scholar] [CrossRef]
- Chadha, R.K.; Pandey, A.P.; Kuempel, H.J. Search for earthquake precursors in well water levels in a localized seismically active area of reservoir triggered earthquakes in India. Geophys. Res. Lett. 2003, 30. [Google Scholar] [CrossRef]
- Pulinets, S.A.; Ouzounov, D.; Ciraolo, L.; Singh, R.; Cervone, G.; Leyva, A.; Dunajecka, M.; Karelin, A.V.; Boyarchuk, K.A.; Kotsarenko, A. Thermal, atmospheric and ionospheric anomalies around the time of the colima M7.8 earthquake of 21 January 2003. Ann. Geophys. 2006, 24, 835–849. [Google Scholar] [CrossRef]
- Pulinets, S.A. Physical mechanism of the vertical electric field generation over active tectonic faults. Adv. Space Res. 2009, 44, 767–773. [Google Scholar] [CrossRef]
- Geng, N.G.; Cui, C.Y.; Deng, M.D. Remote sensing detection in rock fracture experiment and the beginning of remote sensing rock mechanics. Acta Seismol. Sin. 1992, 14, 645–652. (In Chinese) [Google Scholar]
- Freund, F. Charge generation and propagation in igneous rocks. J. Geodyn. 2002, 33, 543–570. [Google Scholar] [CrossRef]
- Chen, S.Y.; Ma, J.; Liu, P.X.; Liu, L.Q.; Hu, X.Y.; Ren, Y.Q. Exploring the current tectonic activity with satellite remote sensing thermal information a case of the Wenchuan earthquake. Seismol. Geol. 2014, 36, 775–793. [Google Scholar] [CrossRef]
- Luong, M.P. Nondestructive damage evaluation of reinforced concrete structure using infrared thermography. Proc SPIE Int. Soc. Opt. Eng. 2000, 98–107. [Google Scholar] [CrossRef]
- Wu, L.X.; Liu, S.J.; Wu, Y.H.; Wang, C.Y. Precursors for rock fracturing and failure-part I: IRR image abnormalities. Int. J. Rock Mech. Min. Sci. 2006, 43, 473–482. [Google Scholar] [CrossRef]
- Wu, L.X.; Liu, S.J.; Wu, Y.H.; Wang, C.Y. Precursors for rock fracturing and failure-part II: IRRT-curve abnormalities. Int. J. Rock Mech. Min. Sci. 2006, 43, 483–493. [Google Scholar] [CrossRef]
- Ma, J.; Ma, S.P.; Liu, P.X.; Liu, L.Q. Thermal field indicators for identifying active fault and its instability from laboratory experiments. Seismol. Geol. 2008, 30, 363–382. (In Chinese) [Google Scholar]
- Wang, C.L.; Lu, Z.J.; Liu, L.; Chuai, X.S.; Lu, H. Predicting points of the infrared precursor for limestone failure under uniaxial compression. Int. J. Rock Mech. Min. Sci. 2016, 88, 34–43. [Google Scholar] [CrossRef]
- Sun, X.M.; Xu, H.C.; He, M.C.; Zhang, F. Experimental investigation of the occurrence of rockburst in a rock specimen through infrared thermography and acoustic emission. Int. J. Rock Mech. Min. Sci. 2017, 93, 250–259. [Google Scholar] [CrossRef]
- Yang, X.Q.; Lin, W.R.; Tadai, O.; Zeng, X.; Yu, C.H.; Ye, H.C.; Li, H.B.; Wang, H. Experimental and numerical investigation of the temperature response to stress changes of rocks. J. Geophys. Res. Solid Earth 2017, 122, 5101–5117. [Google Scholar] [CrossRef]
- Salami, Y.; Dano, C.; Hicher, P.Y. Infrared thermography of rock fracture. Géotech. Lett. 2017, 7, 36–40. [Google Scholar] [CrossRef]
- Wu, L.X.; Cui, C.Y.; Geng, N.G.; Wang, J.Z. Remote sensing rock mechanics (RSRM) and associated experimental studies. Int. J. Rock Mech. Min. Sci. 2000, 37, 879–888. [Google Scholar] [CrossRef]
- Pappalardo, G.; Perriello, Z.S.; Cubito, A.; Calcaterra, D. InfraRed Thermography proposed for the estimation of the Cooling Rate Index in the remote survey of rock masses. Int. J. Rock Mech. Min. Sci. 2016, 83, 182–196. [Google Scholar] [CrossRef]
- Pappalardo, G.; Mineo, S.; Calcaterra, D. Geomechanical analysis of unstable rock wedges by means of geostructural and infrared thermography surveys. Italian J. Eng. Geol. Environ. 2017, 1, 93–101. [Google Scholar] [CrossRef]
- Frodella, W.; Gigli, G.; Morelli, S.; Lombardi, L.; Casagli, N. Landslide mapping and characterization through Infrared Thermography (IRT): Suggestions for a methodological approach from some case studies. Remote Sens. 2017, 9, 1281. [Google Scholar] [CrossRef]
- Morello, R. Potentialities and limitations of thermography to assess landslide risk. Meas. J. Int. Meas. Confed. 2018, 116, 658–668. [Google Scholar] [CrossRef]
- Cui, C.Y.; Deng, M.D.; Geng, N.G. Rock spectral radiation signatures under different pressures. Sci. Bull. 1993, 38, 1377–1382. (In Chinese) [Google Scholar]
- Yin, J.Y.; Fang, Z.F.; Qian, J.D.; Deng, M.D.; Geng, N.G.; Hao, J.S.; Wang, Z.; Ji, Q.Q. Research on the application of infrared remote sensing in earthquake prediction and its physical mechanism. Earthq. Res China 2000, 16, 140–148. (In Chinese) [Google Scholar]
- Freund, F.T. On the electrical conductivity structure of the stable continental crust. J. Geodyn. 2003, 35, 353–388. [Google Scholar] [CrossRef]
- Freund, F.T. Rocks that crackle and sparkle and glow: Strange pre-earthquake phenomena. J. Sci. Explor. 2003, 17, 37–71. [Google Scholar]
- Freund, F.T.; Takeuchi, A.; Lau, B.W.S.; Al-Manaseer, A.; Fu, C.C.; Bryant, N.A.; Ouzounov, D. Stimulated infrared emission from rocks: Assessing a stress indicator. eEarth 2007, 2, 7–16. [Google Scholar] [CrossRef]
- Freund, F.T.; Kulahci, I.G.; Cyr, G.; Ling, J.; Winnick, M.; Tregloan-Reed, J.; Freund, M.M. Air ionization at rock surfaces and pre-earthquake signals. J. Atmos. Sol. Terr. Phys. 2009, 71, 1824–1834. [Google Scholar] [CrossRef]
- Freund, F.T. Pre-earthquake signals: Underlying physical processes. J. Asian Earth Sci. 2011, 41, 383–400. [Google Scholar] [CrossRef]
- Freund, F.T.; Freund, M.M. Paradox of Peroxy Defects and Positive Holes in RocksPart I: Effect of Temperature. J. Asian Earth Sci. 2015, 114, 373–383. [Google Scholar] [CrossRef]
- Scoville, J.; Freund, F.T.; Bobrovskiy, V. Stress-Activated Infrared Emission from Rock Surfaces in the Thermal Infrared (TIR) Window. In Proceedings of the AGU Fall Meeting, San Francisco, CA, USA, 12–16 December 2016. [Google Scholar]
- Liu, S.J.; Wu, L.X.; Feng, Z.; Xu, Z.Y. Thermal infrared spectral variation and sensitive waveband of quartzy sandstone under pressure. Spectrosc. Spectr. Anal. 2012, 32, 78–82. [Google Scholar] [CrossRef]
- Lyon, R.J.P. Analysis of rocks by spectral infrared emission (8 to 25 microns). Econ Geol. 1965, 60, 715–736. [Google Scholar] [CrossRef]
- Ruff, S.W.; Christensen, P.R.; Barbera, P.W.; Anderson, D.L. Quantitative thermal emission spectroscopy of minerals: A laboratory technique for measurement and calibration. J. Geophys. Res. 1997, 102, 14899–14913. [Google Scholar] [CrossRef]
- Christensen, P.R.; Bandfield, J.L.; Hamilton, V.E.; Howard, D.A.; Lane, M.D.; Piatek, J.L.; Ruff, S.W.; Stefanov, W.L. A thermal emission spectral library of rock-forming minerals. J. Geophys. Res. 2000, 105, 9735–9739. [Google Scholar] [CrossRef]
- Xu, Z.Y.; Liu, S.J.; Wu, L.X.; Feng, Z. Stress-related thermal infrared spectral variation and sensitive waveband of granite. J. Infrared Millim. Waves 2013, 32, 44–49. [Google Scholar] [CrossRef]
- Huang, J.W.; Liu, S.J.; Xu, Z.Y.; Ma, C.Y.; Wu, L.X. Experimental study on the influence of the radiation background on the variation in thermal infrared radiance of loaded rock. Spectrosc. Spectr. Anal. 2018, 38, 4222–4225. [Google Scholar] [CrossRef]
- Liu, S.J.; Xu, Z.Y.; Wei, J.L.; Huang, J.W.; Wu, L.X. Experimental Study on Microwave Radiation from Deforming and Fracturing Rock under Loading Outdoor. IEEE Trans. Geosci. Remote Sens. 2016, 54, 5578–5587. [Google Scholar] [CrossRef]
- Hook, S.J.; Kahle, A.B. The micro Fourier transform interferometer (μFTIR)—A new field spectrometer for acquisition of infrared data of natural surfaces. Remote Sens. Environ. 1996, 56, 172–181. [Google Scholar] [CrossRef]
- Rubio, E.; Caselles, V.; Coll, C.; Valour, E.; Sospedra, F. Thermal-infrared emissivities of natural surfaces: Improvements on the experimental set-up and new measurements. Int. J. Remote Sens. 2003, 24, 5379–5390. [Google Scholar] [CrossRef]
- Salvaggio, C.; Miller, C.J. Methodologies and protocols for the collection of midwave and longwave infrared emissivity spectral using a portable field spectrometer. Proc. SPIE Int. Soc. Opt. Eng. 2001, 4381, 539–548. [Google Scholar] [CrossRef]
- Salisbury, J.W.; D’Aria, D.M. Emissivity of terrestrial materials in the 8–14 μm atmospheric window. Remote Sens. Environ. 1992, 42, 83–106. [Google Scholar] [CrossRef]
- Song, L.S.; Zhao, Z.Z.; Xu, J.B.; Liu, S.M.; Peng, K.J.; Zhao, K. Improvements in land surface temperature retrieval based on atmospheric water vapour content and atmospheric temperature. Int. J. Remote Sens. 2014, 35, 4881–4904. [Google Scholar] [CrossRef]
- Saikia, B.J.; Parthasarathy, G.; Sarmah, N.C. Fourier transform infrared spectroscopic estimation of crystallinity in SiO2, based rocks. Bull. Mater. Sci. 2008, 31, 775–779. [Google Scholar] [CrossRef]
- Johnson, J.R. Thermal infrared spectra of experimentally shocked andesine anorthosite. Icarus 2012, 221, 359–364. [Google Scholar] [CrossRef]
- Feng, J.; Rivard, B.; Rogge, D.; Sánchez-Azofeifa, A. The longwave infrared (3–14 μm) spectral properties of rock encrusting lichens based on laboratory spectra and airborne SEBASS imagery. Remote Sens. Environ. 2013, 131, 173–181. [Google Scholar] [CrossRef]
- Gillespie, A. Land Surface Emissivity. In Encyclopedia of Remote Sensing; Njoku, E.G., Ed.; Springer: New York, NY, USA, 2014; pp. 303–311. ISBN 978-0-387-36698-2. [Google Scholar]
- Ma, L.Q.; Sun, H.; Zhang, Y.; Zhou, T.; Li, K.; Guo, J.S. Characteristics of Infrared Radiation of Coal Specimens under Uniaxial Loading. Rock Mech. Rock Eng. 2016, 49, 1567–1572. [Google Scholar] [CrossRef]
- Sun, H.; Ma, L.Q.; Adeleke, N.; Zhang, Y. Background Thermal Noise Correction Methodology for Average Infrared Radiation Temperature of Coal under Uniaxial Loading. Infrared Phys. Technol. 2017, 81, 157–165. [Google Scholar] [CrossRef]
- Bandfield, J.L. Effects of surface roughness and graybody emissivity on Martian thermal infrared spectra. Icarus 2009, 202, 414–428. [Google Scholar] [CrossRef]
- Wang, J.X.; Tang, X.B. Wavelet denoise method applied in load spectrum analysis of engineering vehicles. Adv. Mater. Res. 2010, 108–111, 1320–1325. [Google Scholar] [CrossRef]
- Thomson, W. On dynamical theory of heat. Philos. Mag. 1852, 4, 424–434. [Google Scholar] [CrossRef]
- Wong, A.K.; Sparrow, J.G.; Dunn, S.A. On the revised theory of the thermoelastic effect. J. Phys. Chem. Solids 1988, 49, 395–400. [Google Scholar] [CrossRef]
- Garinei, A.; Marsili, R. Thermoelastic Stress Analysis of the contact between a flat plate and a cylinder. Measurement 2014, 52, 102–110. [Google Scholar] [CrossRef]
- Osterloo, M.M.; Hamilton, V.E.; Anderson, F.S. A laboratory study of the effects of roughness on the thermal infrared spectra of rock surfaces. Icarus 2012, 220, 404–426. [Google Scholar] [CrossRef]
- Li, T.Z.; Liu, S.J. A Study on the Effects of Roughness on Thermal Infrared Spectral Unmixing of Rock. Spectrosc. Spectr. Anal. 2017, 37, 3051–3057. [Google Scholar] [CrossRef]
- Korb, A.R.; Salisbury, J.W.; D’Aria, D.M. Thermal-infrared remote sensing and Kirchhoff’s law. 2. Field measurements. J. Geophys. Res. 1999, 104, 15339–15350. [Google Scholar] [CrossRef]
- Ricci, D.; Pacchioni, G.; Szymanski, M.A.; Shluger, A.L.; Stoneham, A.M. Modeling disorder in amorphous silica with embedded clusters: The peroxy bridge defect center. Phys Rev B. 2001, 64, 224104–224108. [Google Scholar] [CrossRef]
- Freund, F.; Ouillon, G.; Scoville, J.; Sornette, D. Earthquake precursors in the light of peroxy defects theory: Critical review of systematic observations. arXiv, 2017; arXiv:1711.01780. [Google Scholar]
- Song, D.M.; Zang, L.; Shan, X.J.; Yuan, Y.; Cui, J.Y.; Shao, H.M.; Shen, C.; Shi, H.T. A study on the algorithm for extracting earthquake thermal infrared anomalies based on the yearly trend of LST. Seismol. Geol. 2016, 38, 680–695. [Google Scholar] [CrossRef]
- Tramutoli, V.; Aliano, C.; Corrado, R.; Filizzola, C.; Genzano, N.; Lisi, M.; Martinelli, G.; Pergola, N. On the possible origin of thermal infrared radiation (TIR) anomalies in earthquake-prone areas observed using robust satellite techniques (RST). Chem. Geol. 2013, 339, 157–168. [Google Scholar] [CrossRef]
- Ma, Y.T.; Liu, S.J.; Wu, L.X.; Xu, Z.Y. Two-step method to extract seismic microwave radiation anomaly: Case study of Ms 8.0 Wenchuan earthquake. Earthq. Sci. 2011, 24, 577–582. [Google Scholar] [CrossRef]
- Guo, X.; Zhang, Y.S.; Wei, C.X.; Zhong, M.J.; Zhang, X. Medium wave infrared brightness anomalies of Wenchuan 8.0 and Zhongba 6.8 earthquakes. Acta Geosci. Sin. 2014, 35, 338–344. [Google Scholar] [CrossRef]
- Lu, X.; Meng, Q.Y.; Gu, X.F.; Zhang, X.D.; Xie, T.; Geng, F. Thermal infrared anomalies associated with multi-year earthquakes in the Tibet region based on China’s FY-2E satellite data. Adv. Space Res. 2016, 58, 989–1001. [Google Scholar] [CrossRef]
| Sample No. | Fluctuant Range (°C) |
|---|---|
| sy20-1 | 17.41–17.46 |
| sy20-2 | 15.36–15.21 |
| sy20-3 | 15.20–15.28 |
| sy20-4 | 17.61–17.68 |
| sy20-5 | 18.41–18.48 |
| sy20-6 | 17.41–17.32 |
| sy20-7 | 17.20–17.28 |
| sy20-8 | 17.13–17.03 |
| Sample No. | Similarity Coefficient |
|---|---|
| sy20-1 | 0.89 |
| sy20-2 | 0.95 |
| sy20-3 | 0.95 |
| sy20-4 | 0.93 |
| sy20-5 | 0.94 |
| sy20-6 | 0.95 |
| sy20-7 | 0.87 |
| sy20-8 | 0.94 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Huang, J.; Liu, S.; Gao, X.; Yang, Z.; Ni, Q.; Wu, L. Experimental Study of the Thermal Infrared Emissivity Variation of Loaded Rock and Its Significance. Remote Sens. 2018, 10, 818. https://doi.org/10.3390/rs10060818
Huang J, Liu S, Gao X, Yang Z, Ni Q, Wu L. Experimental Study of the Thermal Infrared Emissivity Variation of Loaded Rock and Its Significance. Remote Sensing. 2018; 10(6):818. https://doi.org/10.3390/rs10060818
Chicago/Turabian StyleHuang, Jianwei, Shanjun Liu, Xiang Gao, Zhengcang Yang, Qiang Ni, and Lixin Wu. 2018. "Experimental Study of the Thermal Infrared Emissivity Variation of Loaded Rock and Its Significance" Remote Sensing 10, no. 6: 818. https://doi.org/10.3390/rs10060818
APA StyleHuang, J., Liu, S., Gao, X., Yang, Z., Ni, Q., & Wu, L. (2018). Experimental Study of the Thermal Infrared Emissivity Variation of Loaded Rock and Its Significance. Remote Sensing, 10(6), 818. https://doi.org/10.3390/rs10060818