Classifying the Built-Up Structure of Urban Blocks with Probabilistic Graphical Models and TerraSAR-X Spotlight Imagery
Abstract
:1. Introduction
1.1. Descriptive Attributes for Classifying Urban Structure Types
1.2. Main Assumptions and Contributions of This Paper
2. Methods
2.1. Context-Based Classification with Probabilistic Graphical Models
2.2. Model Parameterization and Neighborhood Definition Criteria
2.3. Urban Blocks’ Attributes
3. Experiments
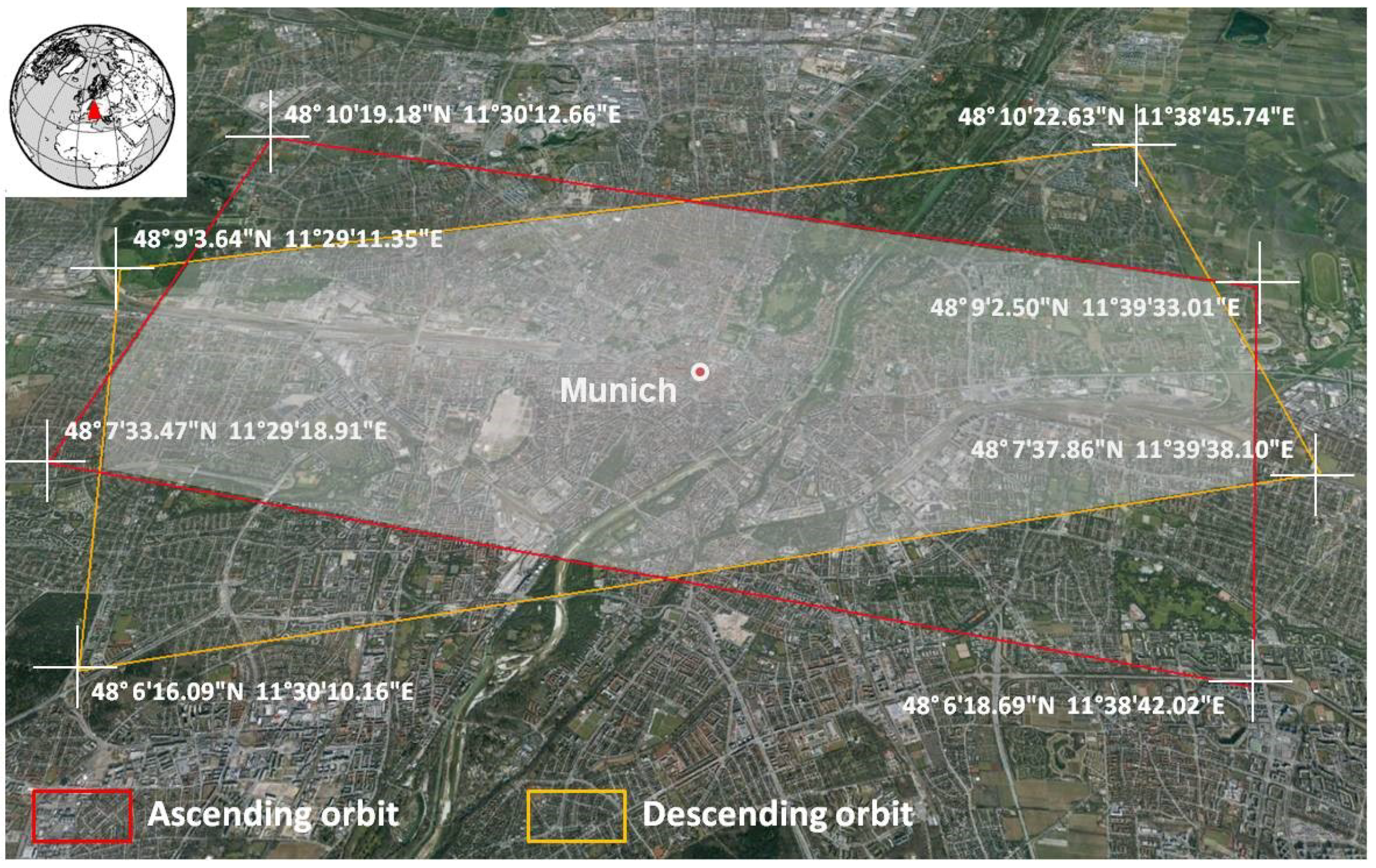
3.1. Image and Auxiliary Data
3.2. Study Area and Urban Structure Type Classes
3.3. Classification Experiments
4. Results
4.1. Model Comparison
4.2. Accuracy Analysis
5. Discussion
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- United Nations. World Urbanization Prospects: The 2017 Revision; Technical Report; United Nations Department of Economic and Social Affairs, Population Division: New York, NY, USA, 2017. [Google Scholar]
- Bundesamt, U. Siedlungs-und Verkehrflaeche. 2015. Available online: https://www.umweltbundesamt.de/daten/flaeche-boden-land-oekosysteme/flaeche/siedlungs-verkehrsflaeche (accessed on 23 May 2018).
- Pauleit, S.; Duhme, F. Assessing the environmental performance of land cover types for urban planning. Landsc. Urban Plan. 2000, 52, 1–20. [Google Scholar] [CrossRef]
- Novack, T.; Stilla, U. Discriminative learning of conditional random fields applied to the classification of urban settlement types. Gemeinsame Tagung 2014 der DGfK, der DGPF, der GfGI und des GiN. 2014. Available online: https://www.pf.bgu.tum.de/pub/2014/novack_co_stilla_dgpf14_pap.pdf (accessed on 23 May 2017).
- Heinzel, J.; Kemper, T. Automated metric characterization of urban structure using building decomposition from very high resolution imagery. Int. J. Appl. Earth Obs. Geoinf. 2015, 35, 151–160. [Google Scholar] [CrossRef]
- Bach, P.; Staalesen, S.; McCarthy, D.; Deletic, A. Revisiting land use classification and spatial aggregation for modeling integrated urban water systems. Landsc. Urban Plan. 2015, 143, 43–55. [Google Scholar] [CrossRef]
- Baud, I.; Kuffer, M.; Pfeffer, K.; Sliuzas, R.; Karuppannan, S. Understanding heterogeneity in metropolitan India: The added value of remote sensing data for analyzing sub-standard residential areas. Int. J. Appl. Earth Obs. Geoinf. 2010, 12, 359–374. [Google Scholar] [CrossRef]
- Yu, B.; Liu, H.; Wu, J.; Hu, Y.; Zhang, L. Automated derivation of urban building density information using airborne LiDAR data and object-based method. Landsc. Urban Plan. 2010, 98, 210–219. [Google Scholar] [CrossRef]
- Banzhaf, E.; Hoefer, R. Monitoring urban structure types as spatial indicators with CIR aerial photographs for a more effective urban environmental management. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2008, 1, 129–138. [Google Scholar] [CrossRef]
- Novack, T.; Kux, H. Urban land cover and land use classification of an informal settlement area using the open-source knowledge-based system InterIMAGE. J. Spat. Sci. 2010, 55, 23–41. [Google Scholar] [CrossRef]
- Heiden, U.; Heldens, W.; Roessner, S.; Segl, K.; Esch, T.; Mueller, A. Urban structure type characterization using hyperspectral remote sensing and height information. Landsc. Urban Plan. 2012, 105, 361–375. [Google Scholar] [CrossRef]
- Voltersen, M.; Berger, C.; Hese, S.; Schmullius, C. Object-based land cover mapping and comprehensive feature calculation for an automated derivation of urban structure types at block level. Remote Sens. Environ. 2014, 154, 192–201. [Google Scholar] [CrossRef]
- Novack, T.; Kux, H.; Feitosa, R.; Costa, G. A knowledge-based, transferable approach for block based urban land use classification. Int. J. Remote Sens. 2014, 35, 4739–4757. [Google Scholar] [CrossRef]
- Walde, I.; Hese, S.; Berger, C.; Schmullius, C. From land cover-graphs to urban structure types. Int. J. Geogr. Inf. Sci. 2014, 28, 584–609. [Google Scholar] [CrossRef]
- Walde, I.; Hese, S.; Berger, C.; Schmullius, C. Graph-based mapping of urban structure types from high-resolution satellite image objects-case study of the german cities Rostock and Erfurt. IEEE Geosci. Remote Sens. Lett. 2013, 10, 932–936. [Google Scholar] [CrossRef]
- Wurm, M.; Taubenboeck, H.; Dech, S. Urban structuring using multi-sensoral remote sensing data by the examples of german cities Cologne and Dresden. In Proceedings of the 2009 Joint Urban Remote Sensing Event, Shanghai, China, 20–22 May 2009; pp. 1–8. [Google Scholar]
- Schmidt, M.; Esch, T.; Klein, D.; Thiel, M.; Dech, S. Estimation of building density using TerraSAR X-data. In Proceedings of the IEEE International Geoscience and Remote Sensing Symposium, Honolulu, HI, USA, 25–30 July 2010; pp. 1936–1939. [Google Scholar]
- Duque, J.C.; Patino, J.E.; Ruiz, L.A.; Pardo-Pascual, J.E. Measuring intra-urban poverty using land cover and texture metrics derived from remote sensing data. Landsc. Urban Plan. 2015, 135, 11–21. [Google Scholar] [CrossRef]
- Wurm, M.; Taubenboeck, H.; Dech, S. Quantification of Urban Structure on Building Block Level Utilizing Multisensoral Remote Sensing Data. In Proceedings of the SPIE 7831 Earth Resources and Environmental Remote Sensing/GIS Applications, Toulouse, France, 21–23 September 2010. [Google Scholar]
- Huck, A.; Hese, S.; Banzhaf, E. Delineating parameters for object-based urban structure mapping in Santiago de Chile using QuickBird data. ISPRS Hannover 2011 Worshop. 2011. Available online: https://pdfs.semanticscholar.org/043d/738e95d2e6ce6d849c53872446da3ad31d3f.pdf?_ga=2.222760539.1140457605.1527174813-91830153.1527174813 (accessed on 23 May 2017).
- Coseo, P.; Larsen, L. How factors of land use/land cover, building configuration, and adjacent heat sources and sinks explain urban heat islands in Chicago. Landsc. Urban Plan. 2014, 125, 117–129. [Google Scholar] [CrossRef]
- Lackner, M.; Conway, T. Determining land use information from land cover through an object oriented classification of IKONOS imagery. Can. J. Remote Sens. 2008, 34, 77–92. [Google Scholar] [CrossRef]
- Linden, S.; Hostert, P. The influence of urban structures on impervious surface maps from airborne hyperspectral data. Remote Sens. Environ. 2009, 113, 2298–2305. [Google Scholar] [CrossRef]
- Benz, U.; Hofmann, P.; Willhauck, G.; Lingenfelder, I.; Heynen, M. Multi resolution object oriented fuzzy analysis of remote sensing data for GIS ready information. ISPRS J. Photogramm. Remote Sens. 2004, 58, 239–258. [Google Scholar] [CrossRef]
- Blaschke, T. Object based image analysis for remote sensing. ISPRS J. Photogramm. Remote Sens. 2010, 65, 2–16. [Google Scholar] [CrossRef]
- Berlin. Bericht zur Dokumentation der Kartiereinheiten und der Aktualisierung des Datenbestandes. 2010. Available online: http://www.stadtentwicklung.berlin.de/umwelt/umweltatlas/dd607_04.htmlk15 (accessed on 24 May 2017).
- Hecht, R.; Herold, H.; Meinel, G.; Buchroithner, M. Automatic Derivation of Urban Structure Types from Topographic Maps by Means of Image Analysis and Machine Learning. In Proceedings of the 26th International Cartographic Conference, Dresden, Germany, 25–30 August 2013. [Google Scholar]
- Vanderhaegen, S.; Canters, F. Developing urban metrics to describe the morphology or urban areas at block level. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2010, 38, 192–197. [Google Scholar]
- Hermosillaa, T.; Ruiza, L.; Recioa, J.; Cambra-Lopezb, M. Assessing contextual descriptive features for plot-based classification of urban areas. Landsc. Urban Plan. 2012, 106, 124–137. [Google Scholar] [CrossRef]
- Tobler, W. A computer movie simulating urban growth in the Detroit region. Econ. Geogr. 1970, 46, 234–240. [Google Scholar] [CrossRef]
- Dekker, R.J. Texture analysis and classification of ERS SAR images for map updating of urban areas in the Netherlands. IEEE Trans. Geosci. Remote Sens. 2003, 41, 1950–1958. [Google Scholar] [CrossRef]
- Gamba, P.; Aldrighi, M. SAR data classification of urban areas by means of segmentation techniques and ancillary optical data. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2012, 5, 1140–1148. [Google Scholar] [CrossRef]
- Salentinig, A.; Gamba, P. A general framework for urban area extraction exploiting multiresolution SAR data fusion. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2016, 9, 2009–2018. [Google Scholar] [CrossRef]
- Amitrano, D.; Belfiore, V.; Cecinati, F.; Martino, D.; Iodice, A.; Mathieu, P.-P.; Medagli, S.; Poreh, D.; Riccio, D.; Ruello, G. Urban areas enhancement in multitemporal SAR RGB images using adaptive coherence window and texture information. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2016, 9, 3740–3752. [Google Scholar] [CrossRef]
- Koller, D.; Friedman, N. Probabilistic Graphical Models: Principles and Techniques; MIT Press: London, UK, 2009. [Google Scholar]
- Kschischang, F.; Frey, B.; Loelinger, H. Factor graphs and the sum-product algorithm. IEEE Trans. Inf. Theory 2001, 47, 498–519. [Google Scholar] [CrossRef]
- Andres, B.; Kappes, J.H.; Koethe, U.; Schnoerr, C.; Hamprecht, F.A. An empirical comparison of inference algorithms for graphical models with higher order factors using OpenGM. In Pattern Recognition; Lecture Notes in Computer Science; Goesele, M., Roth, S., Kuijper, A., Schiele, B., Schindler, K., Eds.; Springer: Berlin/Heidelberg, Germany, 2010; Volume 6376, pp. 353–362. [Google Scholar]
- Szeliski, R.; Scharstein, D.; Veksler, O.; Kolmogorov, V.; Agarwala, A.; Tappen, M.; Rother, C. A comparative study of energy minimization methods for Markov Random Fields with smoothness-based priors. IEEE Trans. Pattern Anal. Mach. Intell. 2008, 30, 1068–1080. [Google Scholar] [CrossRef] [PubMed]
- Quinlan, J.R. Simplifying decision trees. Int. J. Man Mach. Stud. 1987, 27, 221–234. [Google Scholar] [CrossRef]
- Hariharan, S.; Tirodkar, S.; Bhattacharya, A. Polarimetric SAR decomposition parameter subset selection and their optimal dynamic range evaluation for urban area classification using random forest. Int. J. Appl. Earth Obs. Geoinf. 2016, 44, 144–158. [Google Scholar] [CrossRef]
- Du, P.; Samat, A.; Waske, B.; Liu, S.; Li, Z. Random forest and Rotation Forest for fully polarized SAR image classification using polarimetric and spatial features. ISPRS J. Photogramm. Remote Sens. 2015, 105, 38–53. [Google Scholar] [CrossRef]
- Breiman, L. Random forests. Mach. Learn. 2001, 1, 5–32. [Google Scholar] [CrossRef]
- Hastie, T.; Tibshirani, R.; Friedman, J. The Elements of Statistical Learning; Springer: New York, NY, USA, 2001. [Google Scholar]
- Arkin, E.; Chew, L.; Huttenlocher, D.; Kedem, K.; Mitchell, J. An efficiently computable metric for comparing polygonal shapes. IEEE Trans. Pattern Anal. Mach. Intell. 1991, 13, 209–216. [Google Scholar] [CrossRef]
- Novack, N.; Stilla, U. Context-based classification of urban blocks according to their built-up structure. PFG J. Photogramm. Remote Sens. Geoinf. Sci. 2017, 85, 365–376. [Google Scholar] [CrossRef]
- Woodhouse, I. Introduction to Microwave Remote Sensing; CRC Press: Bocaton, FL, USA, 2006. [Google Scholar]
- Stilla, U. High resolution radar imaging of urban areas. In Photogrammetric Week 07; Fritsch, F., Ed.; Wichmann: Berlin/Heidelberg, Germany, 2007; pp. 149–158. [Google Scholar]
- Stilla, U.; Soergel, U.; Thoennessen, U. Potential and limits of InSAR data for building reconstruction in built up areas. ISPRS J. Photogramm. Remote Sens. 2003, 58, 113–123. [Google Scholar] [CrossRef]
- Novack, T. Context-based Classification of Urban Structure Types Using Spaceborne InSAR Images. Ph.D. Thesis, Technische Universität München, München, Germany, 2016; 121p. [Google Scholar]
- Dalal, N.; Triggs, B. Histograms of Oriented Gradients for Human Detection. In Proceedings of the IEEE Computer Society Conference on Computer Vision and Pattern Recognition, San Diego, CA, USA, 20–25 June 2005; pp. 886–893. [Google Scholar]
- West, D.B. Introduction to Graph Theory; Prentice Hall: Upper Saddle River, NJ, USA, 2001; p. 512. [Google Scholar]
- Moran, P. Notes on continuos stochastic phenomena. Biometrika 1950, 37, 17–23. [Google Scholar] [CrossRef] [PubMed]
- DLR—Deutsches Zentrum für Luft und Raumfahrt. The Title of the Cited Contribution. TerraSAR-X—The German Radar Eye in Space. 2009. Available online: http://www.dlr.de/eo/Portaldata/64/Resources/dokumente/TSX_brosch.pdf (accessed on 23 May 2018).
- Tison, C.; Tupin, F. Estimation of urban DSM from mono-aspect InSAR images. In Radar Remote Sensing of Urban Areas; Springer: Berlin/Heidelberg, Germany, 2010; pp. 161–185. [Google Scholar]
- Chen, Z.; Zhang, Y.; Guindon, B.; Esch, T.; Roth, A.; Shang, J. Urban land use mapping using high resolution SAR data based on density analysis and contextual information. Can. J. Remote Sens. 2012, 386, 738–749. [Google Scholar] [CrossRef]
- Newman, M. Mixing patterns in networks. Phys. Rev. 2003, 67, 1–14. [Google Scholar] [CrossRef] [PubMed]
- Congalton, R.G.; Green, K. Assessing the Accuracy of Remotely Sensed Data: Principles and Practices; Mapping Science Series; Lewis Publishers: New York, NY, USA, 1999. [Google Scholar]
- Novack, T.; Stilla, U. Classification of urban settlements types based on space-borne SAR datasets. ISPRS Ann. Photogramm. Remote Sens. Spat. Inf. Sci. 2014, 2, 55–66. [Google Scholar] [CrossRef]




| Dark and bright areas’ attributes: |
| Number of bright areas |
| Number of dark areas |
| Number of bright areas larger than 200 pixels |
| Number of dark areas larger than 200 pixels |
| Number of bright areas larger than 500 pixels |
| Number of dark areas larger than 500 pixels |
| Number of bright areas larger than 1000 pixels |
| Number of dark areas larger than 1000 pixels |
| Sum of bright areas larger than 200 pixels/block’s area |
| Sum of dark areas larger than 200 pixels/block’s area |
| Sum of bright areas larger than 500 pixels/block’s area |
| Sum of dark areas larger than 500 pixels/block’s area |
| Sum of bright areas larger than 1000 pixels/block’s area |
| Sum of dark areas larger than 1000 pixels/block’s area |
| Sum of bright areas/block’s area |
| Sum of dark areas/block’s area |
| Total area of all bright areas |
| Total area of all dark areas |
| Mean area of all bright areas |
| Mean area of all dark areas |
| Maximum area among bright areas |
| Maximum area among dark areas |
| Standard deviation of the area of all bright areas |
| Standard deviation of the area of all dark areas |
| Maximum compactness among bright areas |
| Maximum compactness among dark areas |
| Compactness of the largest bright area |
| Compactness of the largest dark area |
| Maximum length-to-width ratio among bright areas |
| Maximum length-to-width ratio among dark areas |
| Minimum perimeter-area ratio among bright areas |
| Minimum perimeter-area ratio among dark areas |
| Number of bright areas with length-to-width ratio higher than 5 |
| Number of dark areas with length-to-width ratio higher than 5 |
| Number of bright areas with length-to-width ratio higher than 10 |
| Number of dark areas with length-to-width ratio higher than 10 |
| Line attributes: |
| Maximum line length |
| Mean angle difference between a line and its closest line |
| Mean angle diff. between a line and the block boundary closest to it |
| Mean angle diff. between a line and the block boundary most parallel to it |
| Mean angle diff. between a line and the line most parallel to it |
| Mean angle diff. between a line and the line most perpendicular to it |
| Mean distance between a line and its closest line |
| Mean distance between a line and the line most parallel to it |
| Mean distance between a line and the line most perpendicular to it |
| Mean distance between a line and the block boundary closest to it |
| Mean distance between a line and the block boundary most parallel to it |
| Mean distance between a line and the block boundary most perpendicular to it |
| Mean orientation of the lines |
| Mean length of the lines |
| Min. angle diff. between a line and the block boundary closest to it |
| Min. distance between a line and the line most parallel to it |
| Min. distance between a line and the line most perpendicular to it |
| Min. distance between a line and the block boundary most parallel to it |
| Min. distance between a line and the block boundary most perpendicular to it |
| Number of lines |
| Number of lines longer than 50 m |
| Number of lines longer than 100 m |
| Std. dev. of angle difference between a line and its closest line |
| Std. dev. of distance between a line and its closest block boundary |
| Std. dev. of distance between a line and its closest line |
| Std. dev. of distance between a line and the line most parallel to it |
| Std. dev. of distance between a line and the line most perpendicular to it |
| Std. dev. of the lines length |
| Std. dev. of the orientation of all lines |
| Polygon attributes: |
| Maximum pertinence * |
| Mean area |
| Mean angle difference between a polygon and its closest block boundary |
| Mean distance between a polygon and its closest block boundary |
| Mean distance between a polygon and the polygon most parallel to it |
| Mean distance between a polygon and the polygon most perpendicular to it |
| Mean, max. and std. dev. of the polygons area |
| Mean, max. and std. dev. of the polygons length-to-width |
| Mean, max. and std. dev. of the polygons compactness |
| Mean, max. and std. dev. of the polygons orientation |
| Number of pairs of polygons parallel to each other |
| Number of pairs of polygons perpendicular to each other |
| Number of polygons |
| Number of polygons with area > 3rd, 4th and 5th 5-quantiles of the area values |
| Number of polygons with pertinence > [0.05, 0.1, 0.15, 0.2, 0.3, 0.4, 0.5] |
| Number of pol. with pertinence > [3rd, 4th, 5th] of the 5-quantiles of the pertinence values |
| Std. dev. of the angle diff. between a polygon and its closest block boundary |
| Std. dev. of the distance between a polygon and its closest block boundary |
| Std. dev. of the distance between a polygon and the polygon most parallel to it |
| Std. dev. of the distance between a polygon and the polygon most perpendicular to it |
| Std. dev. of the polygons orientation |
| 3rd, 4th and 5th 5-quantiles of the polygons area |
| 3rd, 4th and 5th 5-quantiles of the pertinence values |
| Network structure attributes: |
| Density of the graph [51] |
| Highest mean membership of two connected nodes |
| Mean node pertinence |
| Membership value of the node with highest membership |
| Number of nodes |
| Number of edges |
| Number of edges/number of nodes |
| Number of edges connecting parallel nodes |
| Number of edges connecting parallel nodes/number of edges |
| Number of edges connecting parallel nodes/Number of edges connecting perpendicular nodes |
| Number of edges connecting perpendicular nodes |
| Number of edges connecting perpendicular nodes/number of edges |
| Std. dev. of the membership from the two connected nodes with highest membership mean |
| Network Moran’sIof attributes [52]: |
| Area |
| Distance to closest block boundary |
| Length to width ratio |
| Orientation |
| Orientation difference to closest block boundary |
| Rectangular fit |
| For each of the six attributes above, the following measures were computed: |
| Expected I based on random permutation of the values |
| Expected I under normality assumption |
| Difference between I and expected I based on random permutations |
| Difference between I and expected I under normality assumption |
| p-value of I based on random permutation of the values |
| p-value of I under the normality assumption (one-sided) |
| PVA | DSDH | LBIA | DBD | RBD | Total | User’s Acc. (%) | Prod.’s Acc. (%) | |
|---|---|---|---|---|---|---|---|---|
| Std. class.: | ||||||||
| PVA | 184 | 10 | 3 | 3 | 15 | 215 | 85.58 | 84.40 |
| DSDH | 22 | 144 | 6 | 12 | 35 | 219 | 65.75 | 57.60 |
| LBIA | 2 | 5 | 42 | 6 | 7 | 62 | 67.77 | 30.00 |
| DBD | 3 | 25 | 61 | 491 | 48 | 628 | 78.18 | 85.68 |
| RBD | 7 | 66 | 28 | 64 | 91 | 256 | 35.54 | 46.42 |
| Total | 218 | 250 | 140 | 573 | 196 | |||
| Ctxt. class.: | ||||||||
| PVA | 176 | 8 | 5 | 12 | 14 | 215 | 81.86 | 85.85 |
| DSDH | 15 | 155 | 2 | 6 | 41 | 219 | 70.77 | 65.12 |
| LBIA | 4 | 4 | 45 | 4 | 5 | 62 | 72.25 | 41.66 |
| DBD | 5 | 10 | 33 | 546 | 34 | 628 | 82.94 | 88.63 |
| RBD | 5 | 61 | 23 | 48 | 119 | 256 | 46.48 | 55.86 |
| Total | 205 | 238 | 108 | 616 | 213 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Novack, T.; Stilla, U. Classifying the Built-Up Structure of Urban Blocks with Probabilistic Graphical Models and TerraSAR-X Spotlight Imagery. Remote Sens. 2018, 10, 842. https://doi.org/10.3390/rs10060842
Novack T, Stilla U. Classifying the Built-Up Structure of Urban Blocks with Probabilistic Graphical Models and TerraSAR-X Spotlight Imagery. Remote Sensing. 2018; 10(6):842. https://doi.org/10.3390/rs10060842
Chicago/Turabian StyleNovack, Tessio, and Uwe Stilla. 2018. "Classifying the Built-Up Structure of Urban Blocks with Probabilistic Graphical Models and TerraSAR-X Spotlight Imagery" Remote Sensing 10, no. 6: 842. https://doi.org/10.3390/rs10060842
APA StyleNovack, T., & Stilla, U. (2018). Classifying the Built-Up Structure of Urban Blocks with Probabilistic Graphical Models and TerraSAR-X Spotlight Imagery. Remote Sensing, 10(6), 842. https://doi.org/10.3390/rs10060842






